
INF 1007 – Programação II
Aula 14 – Árvores Binárias
Edirlei Soares de Lima
<elima@inf.puc-rio.br>
Árvores
•
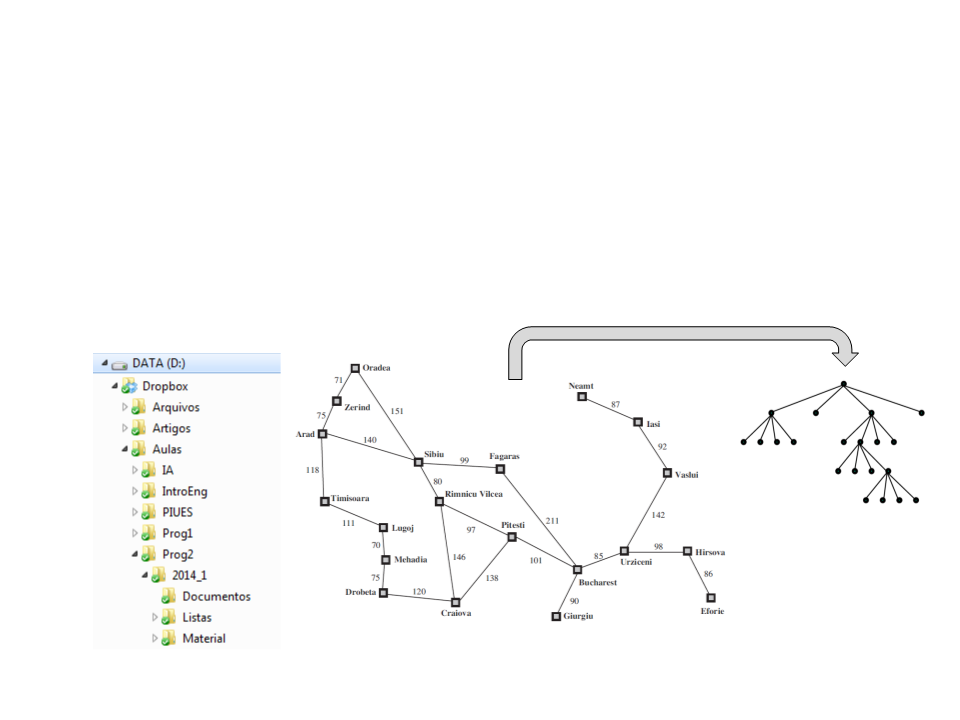
Uma estrutura de dados do tipo árvore permite que dados
sejam organizados de maneira hierárquica.
–
Exemplos: arquivos em diretórios, expressões aritméticas,
planejamento de rotas...
Árvores
•
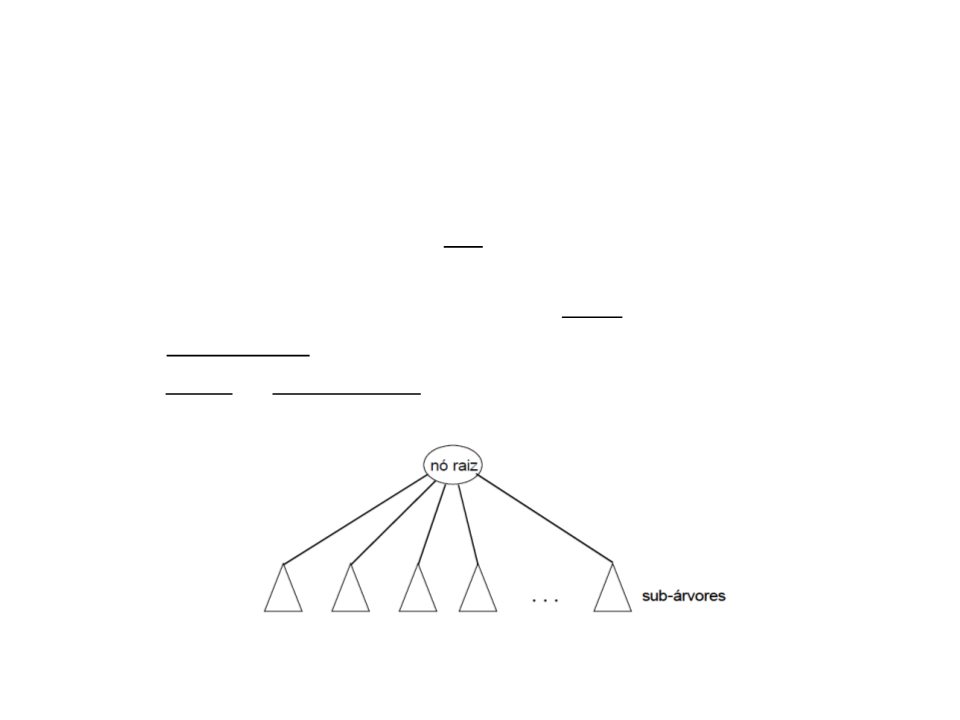
Uma árvore é composta por um conjunto de nós tal que:
–
existe um nó r, denominado raiz, com zero ou mais sub-árvores, cujas
raízes estão ligadas a r;
–
–
–
os nós raízes destas sub-árvores são os filhos de r;
os nós internos da árvore são os nós com filhos;
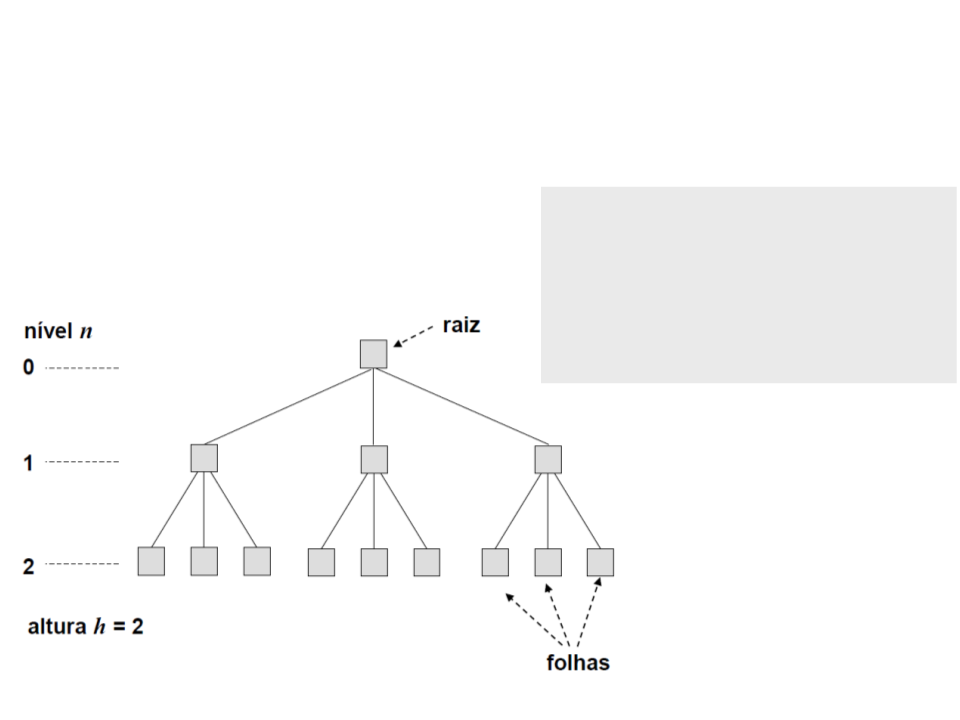
as folhas ou nós externos da árvore são os nós sem filhos;
Árvores
•
Estrutura de uma Árvore:
#define N 3
struct noArvore
{
int info;
struct noArvore* filhos[N];
};
Árvores Binárias
•
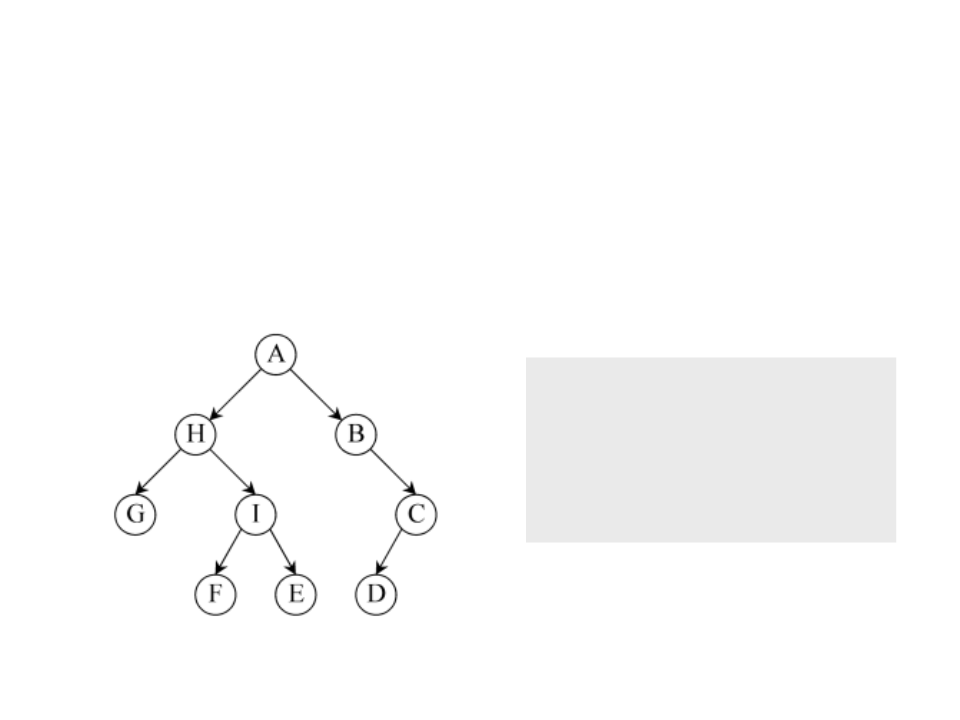
Uma árvore binária é uma árvore em que cada nó tem zero,
um ou dois filhos;
struct noArvore {
char info;
struct noArvore* esq;
struct noArvore* dir;
};
Árvores Binárias
•
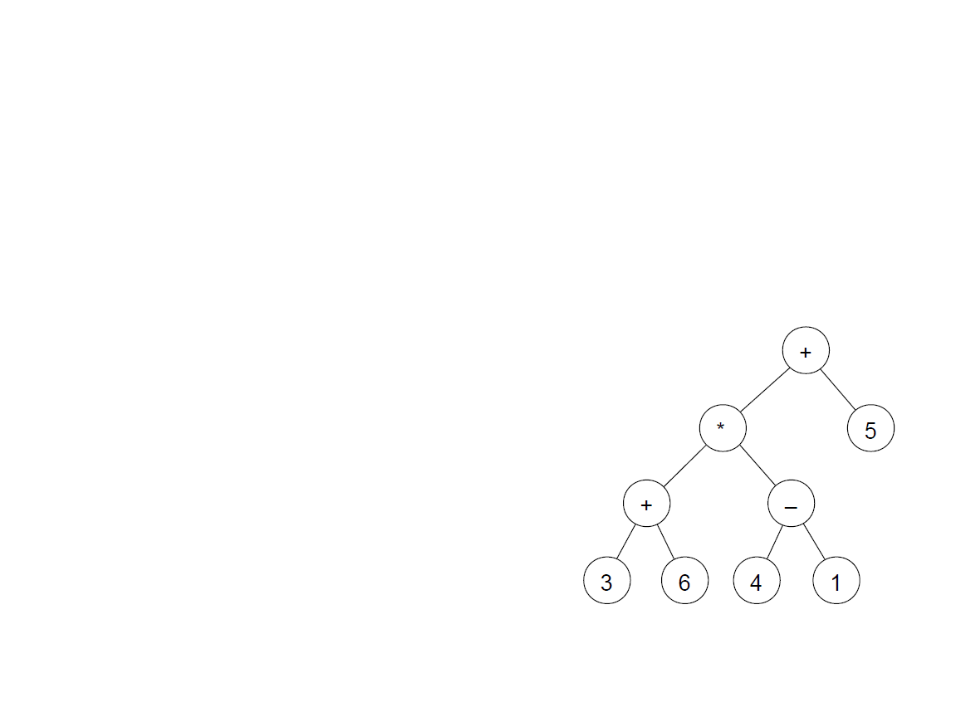
Exemplo: árvores binárias representando expressões
aritméticas:
–
–
nós folhas representam operandos;
nós internos operadores;
–
Exemplo: (3+6)*(4-1)+5

Árvores Binárias

Árvores Binárias – Implementação
•
•
Representação de uma árvore:
–
através de um ponteiro para o nó raiz
Representação de um nó da árvore:
–
Estrutura em C contendo:
•
a informação propriamente dita (exemplo: um caractere);
dois ponteiros para as sub-árvores, à esquerda e à direita;
•
struct noArvore {
char info;
struct noArvore* esq;
struct noArvore* dir;
};

Árvores Binárias – Implementação
Interface do tipo abstrato Árvore Binária: arvore.h
typedef struct noArvore NoArvore;
•
NoArvore* arvore_criavazia(void);
NoArvore* arvore_cria(char c, NoArvore* e, NoArvore* d);
NoArvore* arvore_libera(NoArvore* a);
int arvore_vazia(NoArvore* a);
int arvore_pertence(NoArvore* a, char c);
void arvore_imprime(NoArvore* a);
Árvores Binárias – Implementação
•
•
Implementação das funções:
–
implementação recursiva, em geral;
–
usa a definição recursiva da estrutura;
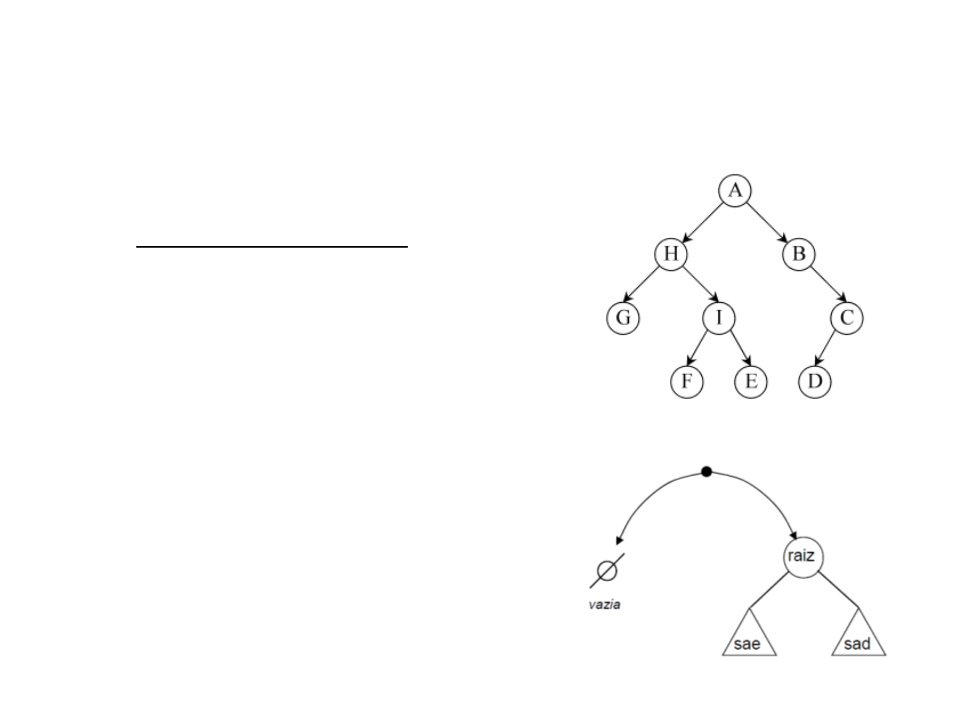
Uma árvore binária é:
–
uma árvore vazia; ou
–
um nó raiz com duas sub-árvores:
•
a sub-árvore da esquerda (sae);
•
a sub-árvore da direita (sad);

Árvores Binárias – Cria Vazia
•
Função arvore_criavazia:
–
cria uma árvore vazia;
NoArvore* arvore_criavazia(void)
{
return NULL;
}

Árvores Binárias – Cria
•
Função arvore_cria:
–
cria um nó raiz dadas a informação e as duas sub-árvores, a da
esquerda e a da direita;
–
retorna o endereço do nó raiz criado;
NoArvore* arvore_cria(char c, NoArvore* sae, NoArvore* sad)
{
NoArvore* p = (NoArvore*)malloc(sizeof(NoArvore));
p->info = c;
p->esq = sae;
p->dir = sad;
return p;
}

Árvores Binárias – Libera
•
Função arvore_libera:
–
–
–
libera memória alocada pela estrutura da árvore;
as sub-árvores devem ser liberadas antes de se liberar o nó raiz;
retorna uma árvore vazia, representada por NULL;
NoArvore* arvore_libera(NoArvore* a)
{
if (!arvore_vazia(a)){
arvore_libera(a->esq);
/* libera sae */
arvore_libera(a->dir); /* libera sad */
free(a);
/* libera raiz */
}
return NULL;
}

Árvores Binárias – Vazia
•
Função arvore_vazia:
–
indica se uma árvore é ou não vazia;
int arvore_vazia(NoArvore* a)
{
return a == NULL;
}

Árvores Binárias – Imprime 1
•
Função arvore_imprime:
–
percorre recursivamente a árvore, visitando todos os nós e
imprimindo sua informação;
void arvore_imprime(NoArvore* a)
{
if (!arvore_vazia(a))
{
printf("%c ", a->info); /* mostra raiz */
arvore_imprime(a->esq); /* mostra sae */
arvore_imprime(a->dir); /* mostra sad */
}
}

Árvores Binárias – Imprime 2
•
Função arvore_imprime:
–
percorre recursivamente a árvore, visitando todos os nós e
imprimindo sua informação formatada de acordo com a sua posição
na árvore;
void arvore_imprime(NoArvore *a, int nivel)
{
int n;
if (arvore_vazia(a))
return;
arvore_imprime(a->dir, nivel + 1);
for (n = 0; n < nivel; n++)
printf("\t");
printf("%d\n\n",a->info);
arvore_imprime(a->esq, nivel + 1);
}

Árvores Binárias – Pertence
•
Função arvore_pertence:
–
verifica a ocorrência de um caractere c em um de nós;
–
retorna um valor booleano (1 ou 0) indicando a ocorrência ou não do
caractere na árvore;
int arvore_pertence (NoArvore* a, char c){
if (arvore_vazia(a))
return 0;
else
/* árvore vazia: não encontrou */
return a->info==c || arvore_pertence(a->esq,c) ||
arvore_pertence(a->dir,c);
}
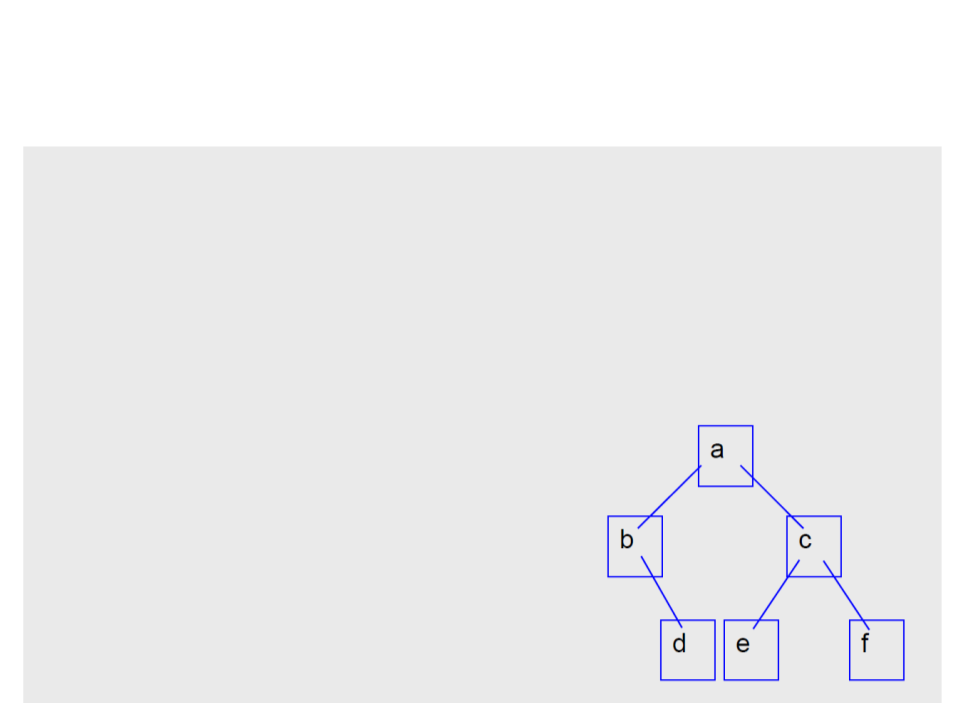
Árvores Binárias – Criação
/
* sub-árvore 'd' */
NoArvore* a1= arvore_cria('d',arvore_criavazia(),arvore_criavazia());
* sub-árvore 'b' */
NoArvore* a2= arvore_cria('b',arvore_criavazia(),a1);
* sub-árvore 'e' */
NoArvore* a3= arvore_cria('e',arvore_criavazia(),arvore_criavazia());
* sub-árvore 'f' */
NoArvore* a4= arvore_cria('f',arvore_criavazia(),arvore_criavazia());
* sub-árvore 'c' */
NoArvore* a5= arvore_cria('c',a3,a4);
* árvore 'a' */
NoArvore* a = arvore_cria('a',a2,a5 );
/
/
/
/
/
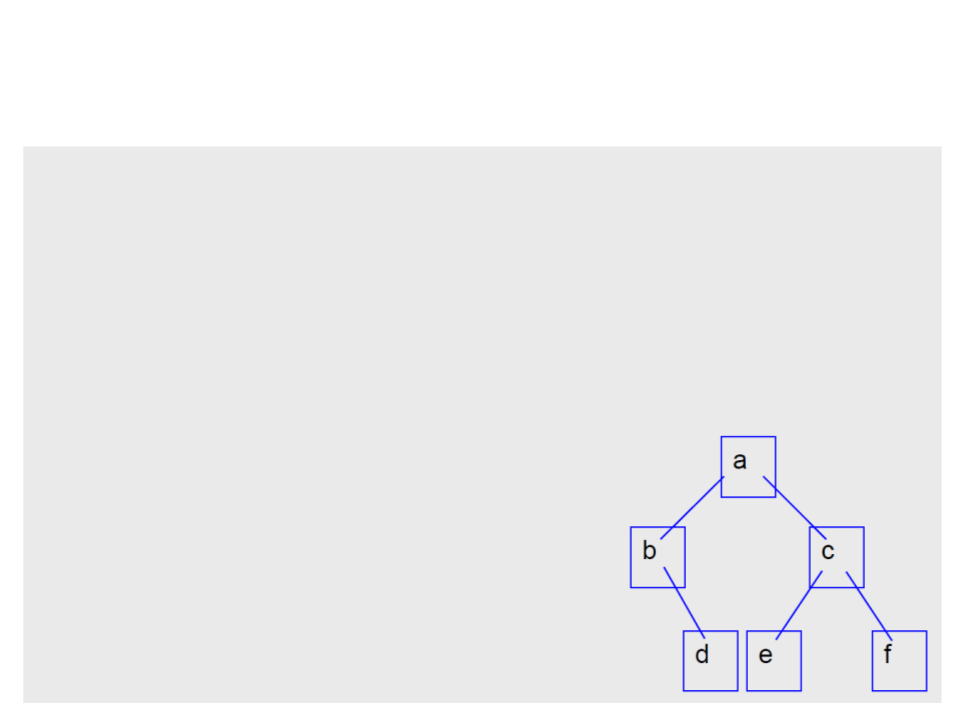
Árvores Binárias – Criação
NoArvore* a = arvore_cria('a',
arvore_cria('b',
arvore_criavazia(),
arvore_cria('d', arvore_criavazia(),
arvore_criavazia())
)
,
arvore_cria('c',
arvore_cria('e', arvore_criavazia(),
arvore_criavazia()),
arvore_cria('f', arvore_criavazia(),
arvore_criavazia())
)
);
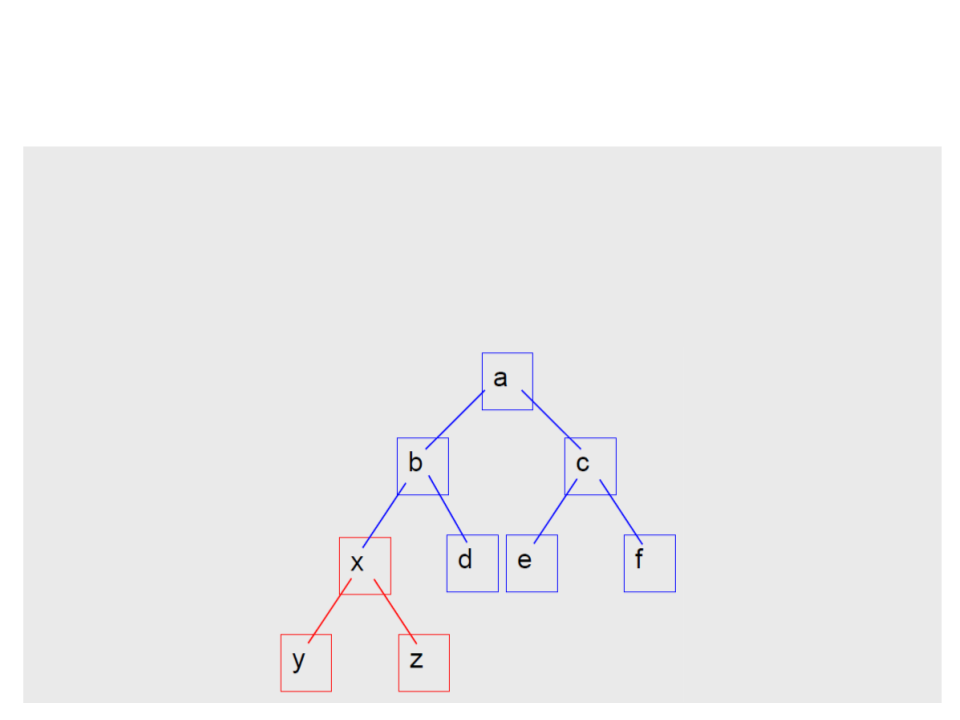
Árvores Binárias – Acrescentando Nós
a->esq->esq = arvore_cria('x',
arvore_cria('y',
arvore_criavazia(), arvore_criavazia()),
arvore_cria('z',
arvore_criavazia(), arvore_criavazia())
);
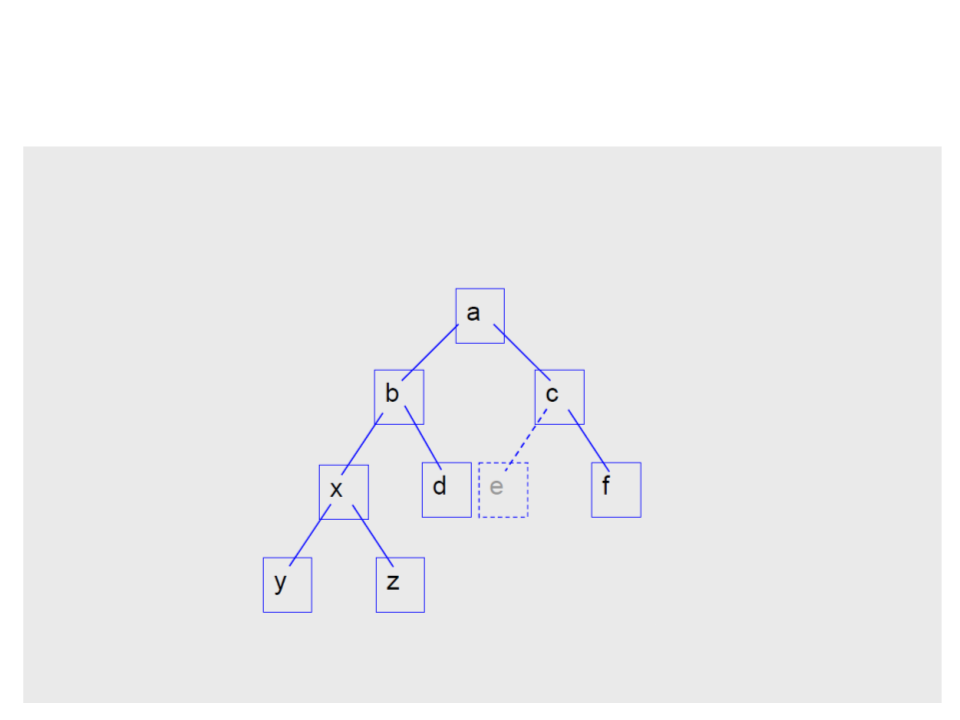
Árvores Binárias – Liberando Nós
a->dir->esq = libera(a->dir->esq);
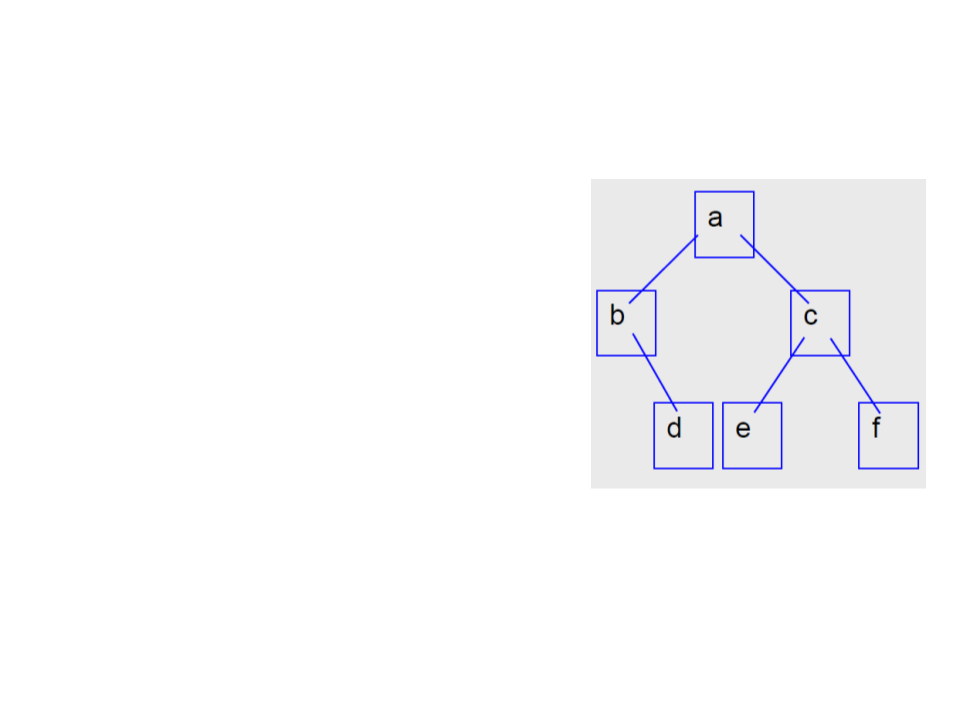
Árvores Binárias – Ordens de Percurso
•
Pré-ordem:
–
trata raiz, percorre sae, percorre sad;
–
exemplo: a b d c e f
•
•
Ordem simétrica:
–
percorre sae, trata raiz, percorre sad;
–
exemplo: b d a e c f
Pós-ordem:
–
percorre sae, percorre sad, trata raiz;
–
exemplo: d b e f c a
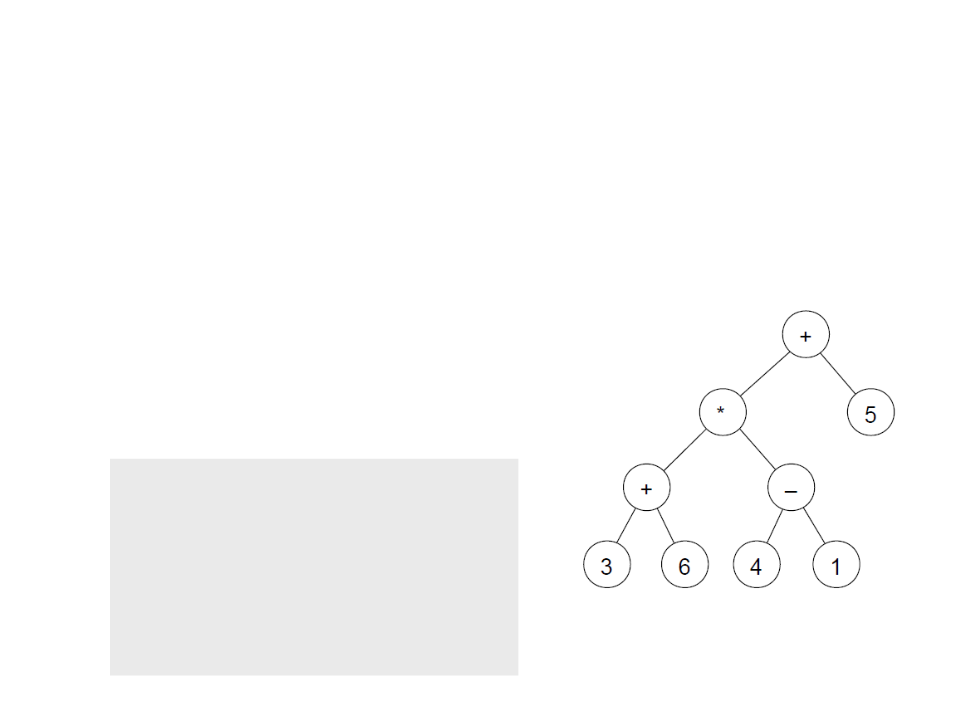
Árvores Binárias – Exercício
•
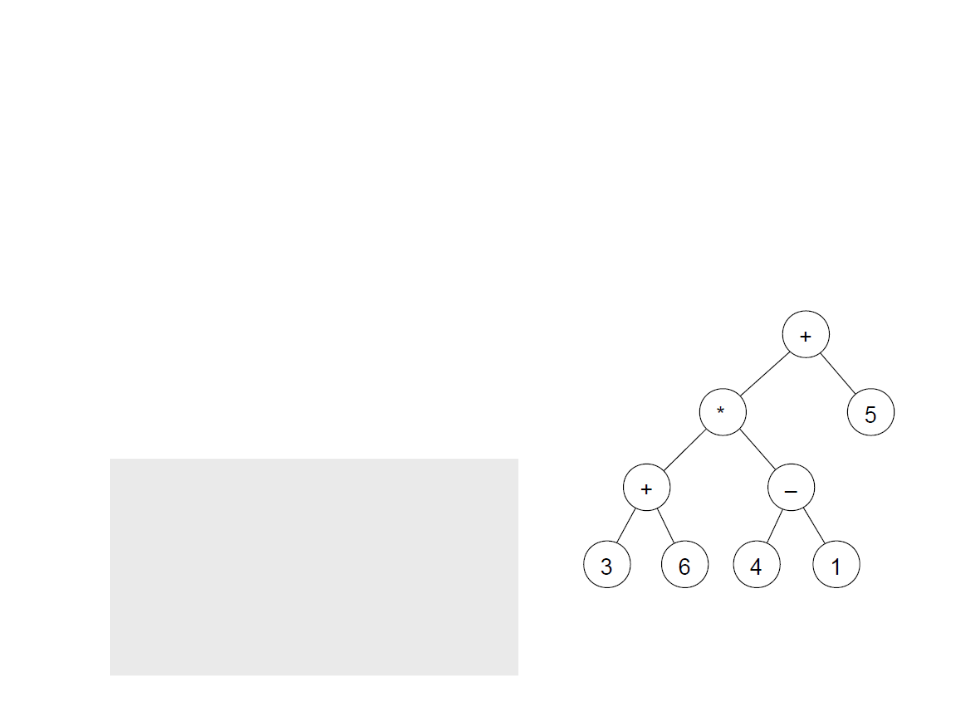
Considere uma árvore binária para representar expressões
aritméticas:
–
nós folhas representam operandos;
–
nós internos operadores;
–
Exemplo: (3+6)*(4-1)+5
struct noArvore {
int valor;
char op;
struct noArvore* esq;
struct noArvore* dir;
};
Árvores Binárias – Exercício
•
Considere uma árvore binária para representar expressões
aritméticas:
–
nós folhas representam operandos;
–
nós internos operadores;
–
Exemplo: (3+6)*(4-1)+5
struct noArvore {
int valor;
char op;
struct noArvore* esq;
struct noArvore* dir;
};
Árvores Binárias – Exercício 1
•
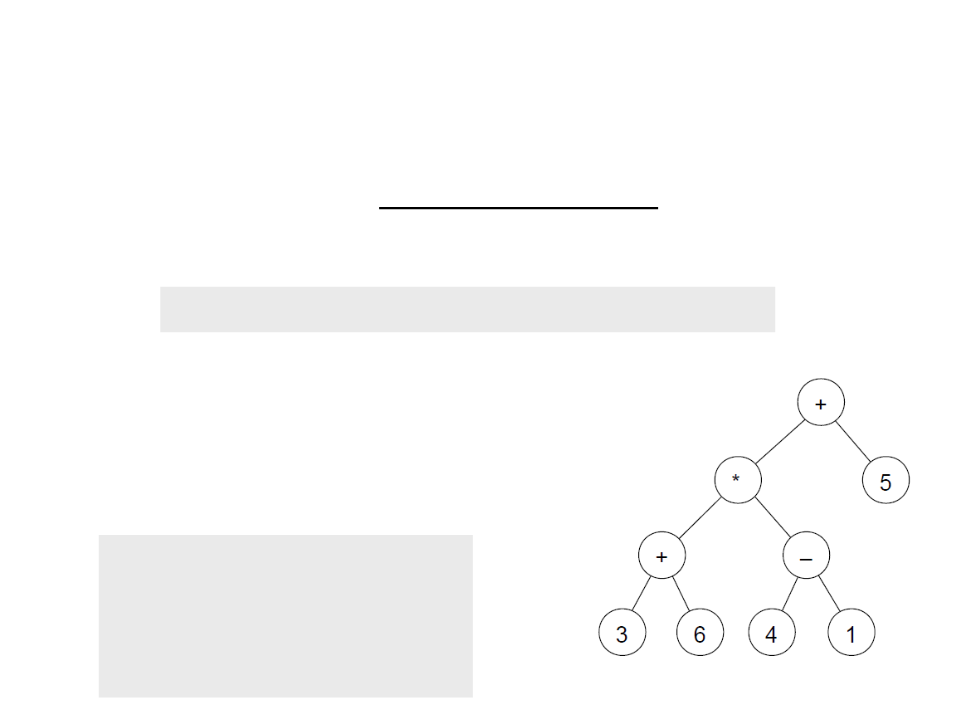
Crie uma função para imprimir a expressão codificada em um
árvore binária. A função deve seguir o seguinte protótipo:
void imprimeExp(NoArvore* a)
•
Para o exemplo ao lado, a função deve
imprimir a seguinte expressão:
(((3+6)*(4-1))+5)
struct noArvore {
int valor;
char op;
struct noArvore* esq;
struct noArvore* dir;
}
;

Árvores Binárias – Exercício 1
void imprimeExp(NoArvore* a)
{
if (!arvore_vazia(a))
{
if (arvore_vazia(a->dir) && arvore_vazia(a->esq))
printf("%d", a->valor);
else {
printf("(");
arvore_imprimeExp(a->esq);
printf("%c", a->op);
arvore_imprimeExp(a->dir);
printf(")");
}
}
}
Árvores Binárias – Exercício 2
•
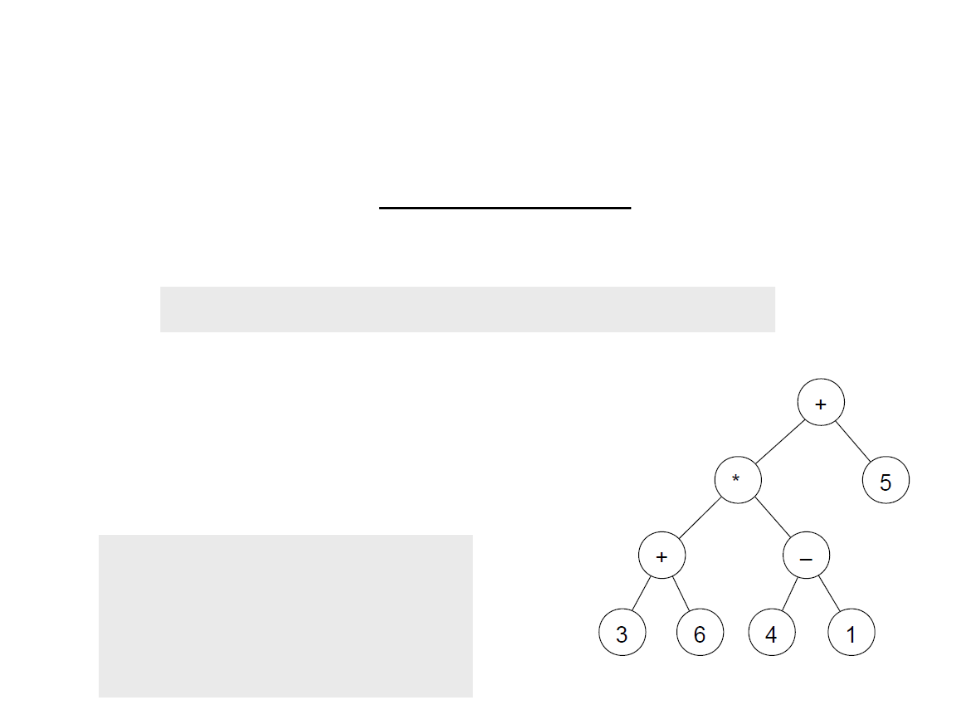
Crie uma função para avaliar a expressão codificada em um
árvore binária. A função deve seguir o seguinte protótipo:
float avalia(NoArvore* a)
•
Para o exemplo ao lado, o resultado da
expressão é: 20
struct noArvore {
int valor;
char op;
struct noArvore* esq;
struct noArvore* dir;
}
;

Árvores Binárias – Exercício 2
float avalia(NoArvore* a)
{
if (arvore_vazia(a->dir) && arvore_vazia(a->esq))
return a->valor;
else {
if(a->op == '+')
return avalia(a->esq) + avalia(a->dir);
if(a->op == '-')
return avalia(a->esq) - avalia(a->dir);
if(a->op == '*')
return avalia(a->esq) * avalia(a->dir);
if(a->op == '/')
return avalia(a->esq) / avalia(a->dir);
}
}

Exercícios
Lista de Exercícios 13 – Árvores Binárias
http://www.inf.puc-rio.br/~elima/prog2/
Árvore Binária de Busca (ABB)
•
•
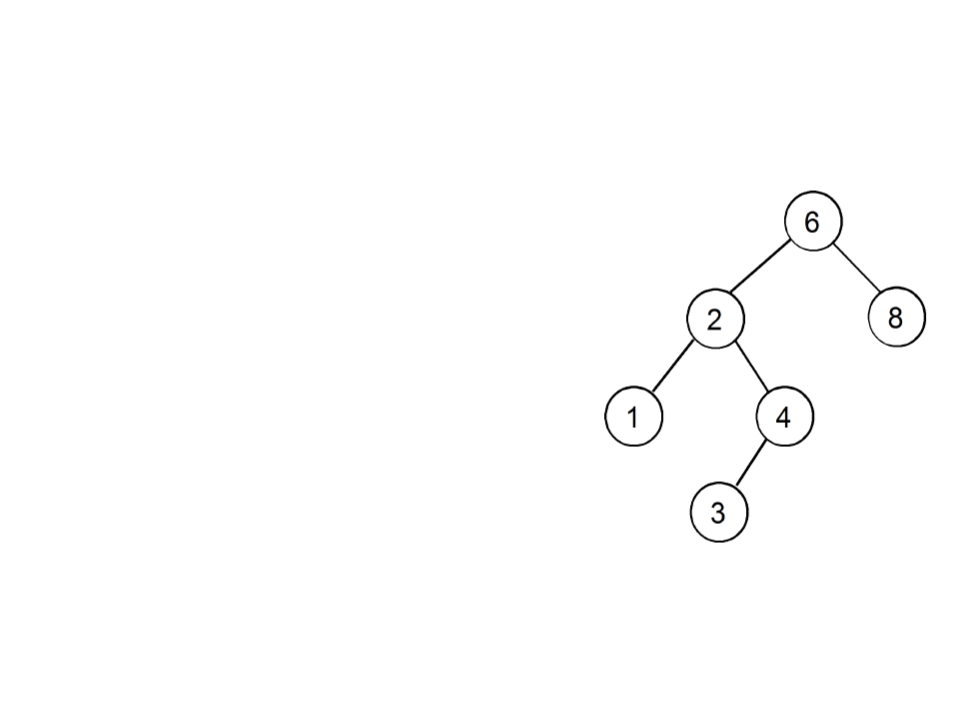
O valor associado à raiz é sempre maior
que o valor associado a qualquer nó da
sub-árvore à esquerda (sae);
O valor associado à raiz é sempre menor
ou igual (para permitir repetições) que o
valor associado a qualquer nó da sub-
árvore à direita (sad);
•
Quando a árvore é percorrida em ordem
simétrica (sae - raiz - sad), os valores são
encontrados em ordem crescente;
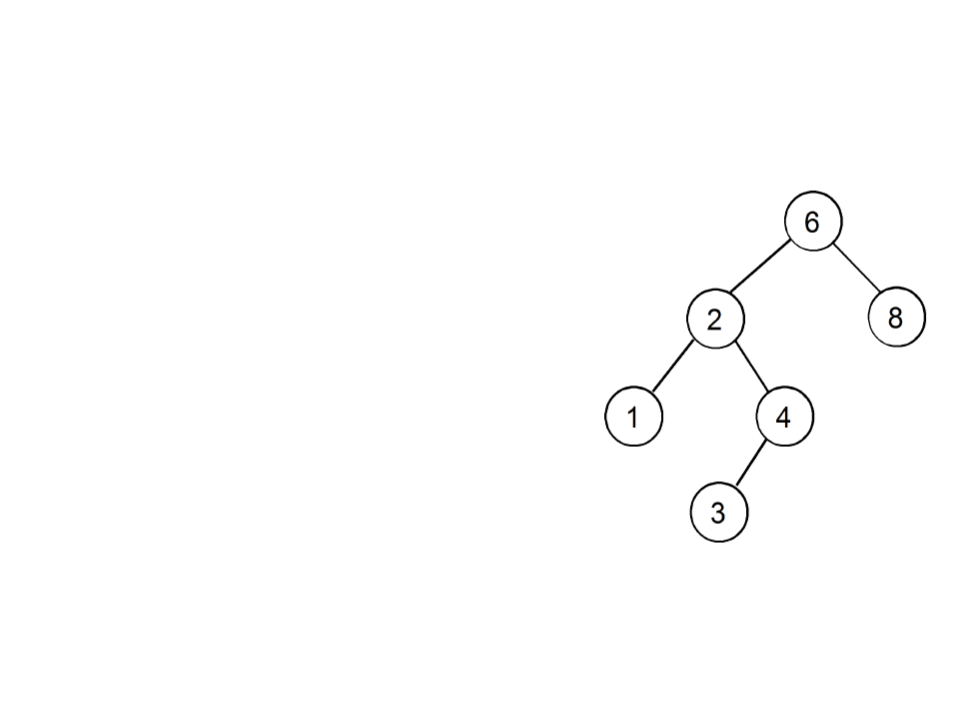
Pesquisa em Árvore Binária de Busca
•
Compare o valor dado com o valor
associado à raiz:
•
•
•
Se for igual, o valor foi encontrado;
Se for menor, a busca continua na sae;
Se for maior, a busca continua na sad;
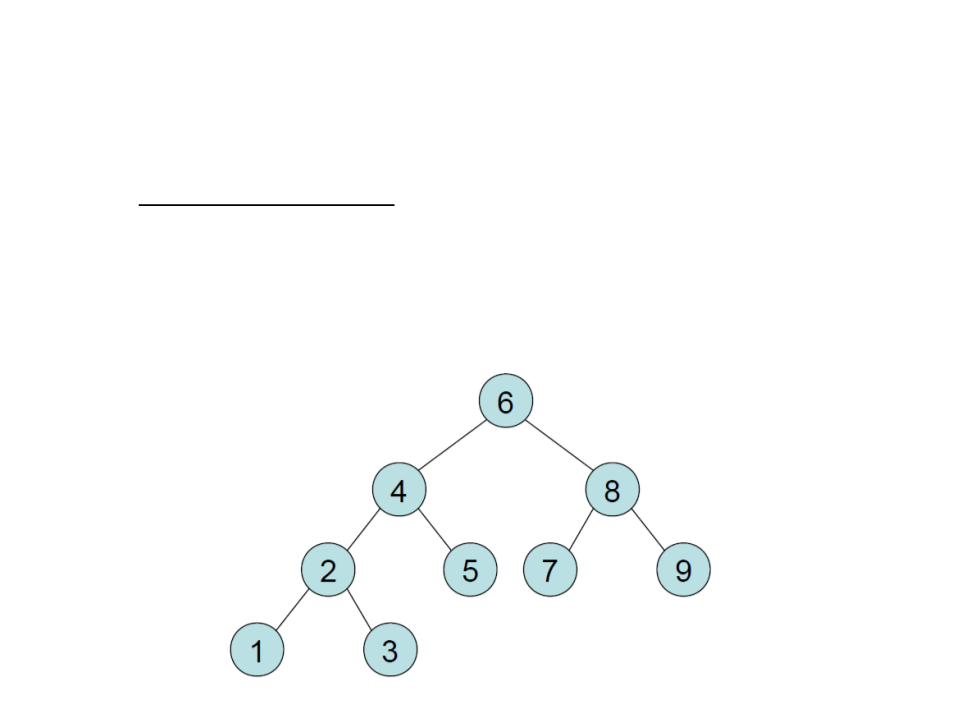
Pesquisa em Árvore Binária de Busca
•
•
Em árvores balanceadas os nós internos têm todos, ou quase
todos, 2 filhos;
Qualquer nó pode ser alcançado a partir da raiz em O(log n)
passos;
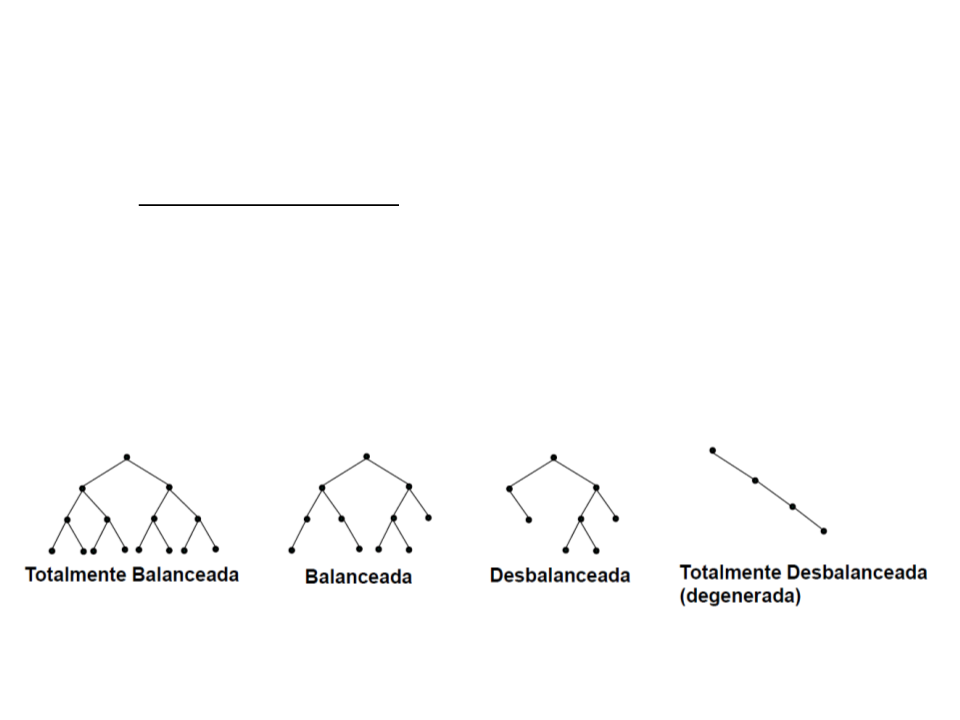
Pesquisa em Árvore Binária de Busca
•
•
Em árvores degeneradas todos os nós têm apenas 1 filho, com
exceção da (única) folha;
Qualquer nó pode ser alcançado a partir da raiz em O(n) passos;

Tipo Árvore Binária de Busca
•
A árvore é representada pelo ponteiro para o nó raiz:
struct noArvore {
int info;
struct noArvore* esq;
struct noArvore* dir;
};
typedef struct noArvore NoArvore;

Árvore Binária de Busca - Criação
•
Árvore vazia representada por NULL:
NoArvore* abb_cria(void)
{
return NULL;
}

Árvore Binária de Busca - Impressão
•
Imprime os valores da árvore em ordem crescente,
percorrendo os nós em ordem simétrica:
void abb_imprime(NoArvore* a)
{
if (a != NULL)
{
abb_imprime(a->esq);
printf("%d\n", a->info);
abb_imprime(a->dir);
}
}

Árvore Binária de Busca - Busca
•
•
Explora a propriedade de ordenação da árvore;
Possui desempenho computacional proporcional à altura da
árvore;
NoArvore* abb_busca(NoArvore* r, int v)
{
if (r == NULL)
return NULL;
else if (r->info > v)
return abb_busca(r->esq, v);
else if (r->info < v)
return abb_busca(r->dir, v);
else
return r;
}

Árvore Binária de Busca – Inserção
•
Recebe um valor v a ser inserido;
•
•
Retorna o eventual novo nó raiz da (sub-)árvore;
Para adicionar v na posição correta, faça:
–
se a (sub-)árvore for vazia:
• crie uma árvore cuja raiz contém v;
–
se a (sub-)árvore não for vazia:
•
compare v com o valor na raiz;
•
insira v na sae ou na sad, conforme o resultado da comparação;
Árvore Binária de Busca – Inserção
NoArvore* abb_insere(NoArvore* a, int v)
{
if (a == NULL)
{
a = (NoArvore*)malloc(sizeof(NoArvore));
a->info = v;
a->esq = NULL;
a->dir = NULL;
}
else if (v < a->info)
a->esq = abb_insere(a->esq, v);
else
a->dir = abb_insere(a->dir, v);
é necessário atualizar os ponteiros para as sub-árvores
à esquerda ou à direita ao chamar recursivamente a
return a;
função, pois a função de inserção pode alterar o valor
do ponteiro para a raiz da (sub-)árvore.
}
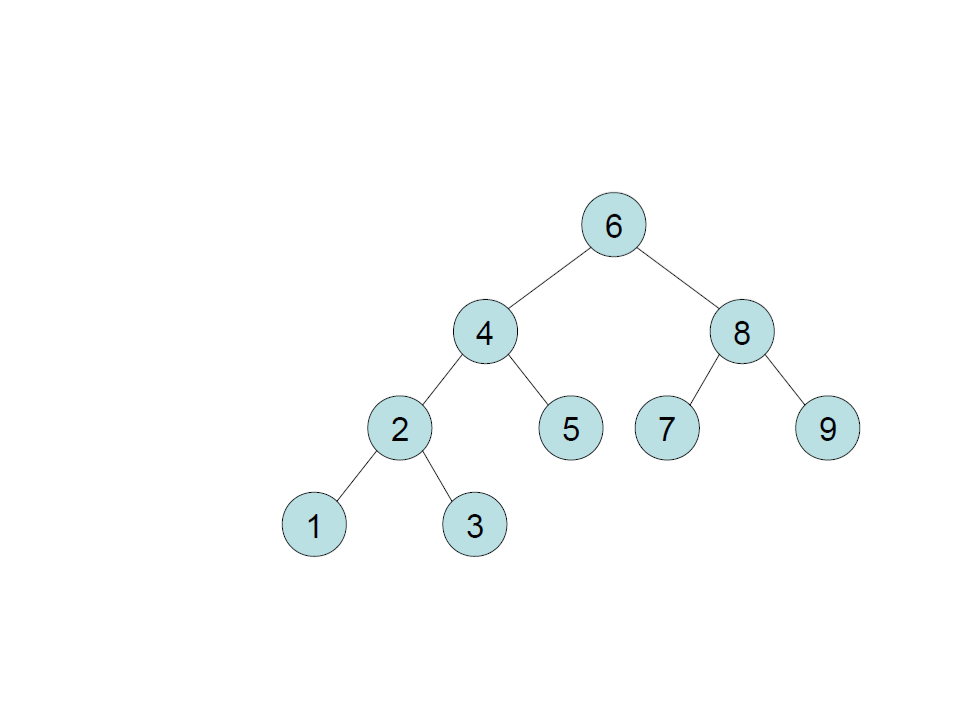
Árvore Binária de Busca – Inserção
cria
insere 6
insere 4
insere 8
insere 2
insere 5
insere 1
insere 3
insere 7
insere 9
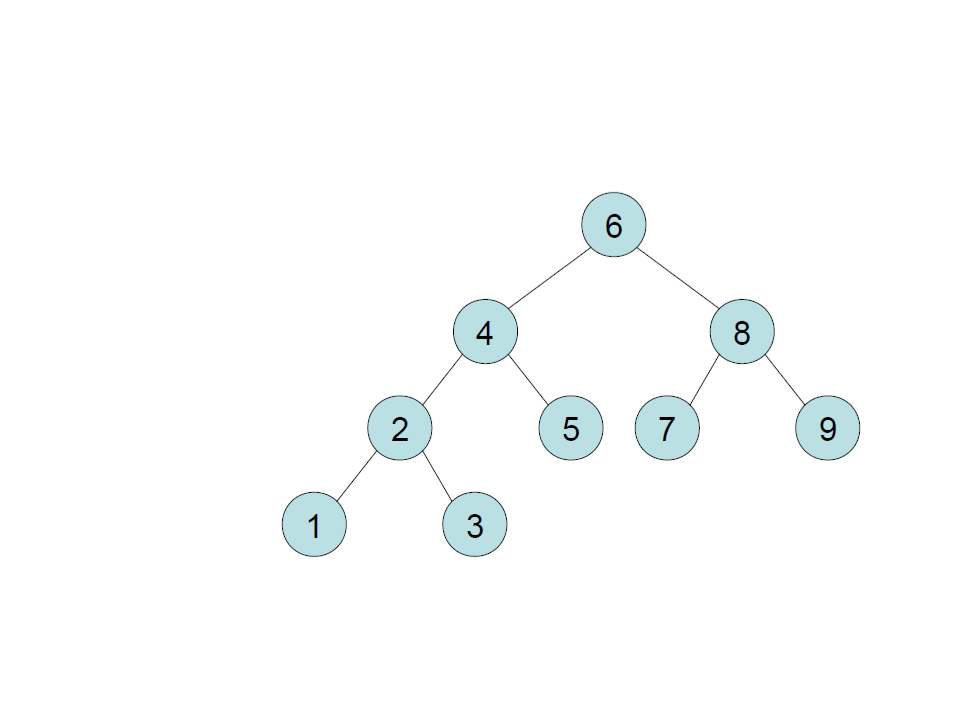
Árvore Binária de Busca – Inserção
cria
insere 6
insere 4
insere 8
insere 2
insere 5
insere 1
insere 3
insere 7
insere 9
insere 6
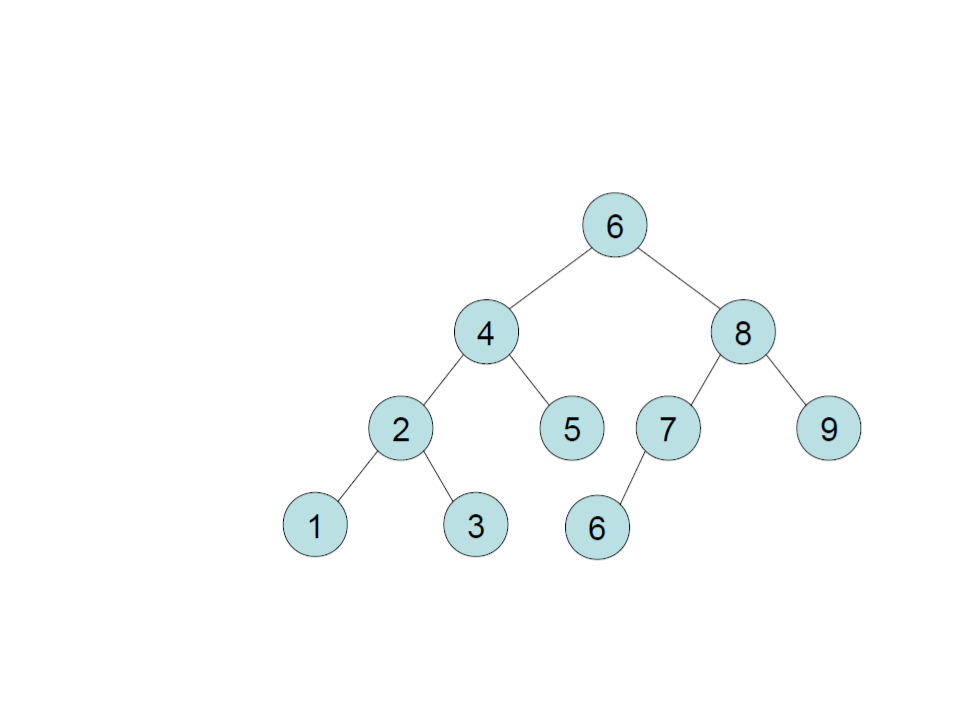
Árvore Binária de Busca – Inserção
cria
insere 6
insere 4
insere 8
insere 2
insere 5
insere 1
insere 3
insere 7
insere 9
insere 6

Árvore Binária de Busca – Inserção
NoArvore* abb_insere(NoArvore* a, int v)
{
if (a == NULL)
{
a = (NoArvore*)malloc(sizeof(NoArvore));
a->info = v;
a->esq = a->dir = NULL;
}
else if (v < a->info)
a->esq = abb_insere(a->esq, v);
else if (v > a->info)
a->dir = abb_insere(a->dir, v);
return a;
}

Árvore Binária de Busca – Remoção
•
•
Recebe um valor v a ser inserido;
Retorna a eventual nova raiz da árvore;
•
Para remover v, faça:
–
se a árvore for vazia:
•
nada tem que ser feito;
–
se a árvore não for vazia:
•
•
•
•
compare o valor armazenado no nó raiz com v:
se for maior que v, retire o elemento da sub-árvore à esquerda;
se for menor do que v, retire o elemento da sub-árvore à direita;
se for igual a v, retire a raiz da árvore;

Árvore Binária de Busca – Remoção
•
Para retirar a raiz da árvore, há 3 casos:
–
–
–
Caso 1: a raiz que é folha;
Caso 2: a raiz a ser retirada possui um único filho;
Caso 3: a raiz a ser retirada tem dois filhos;
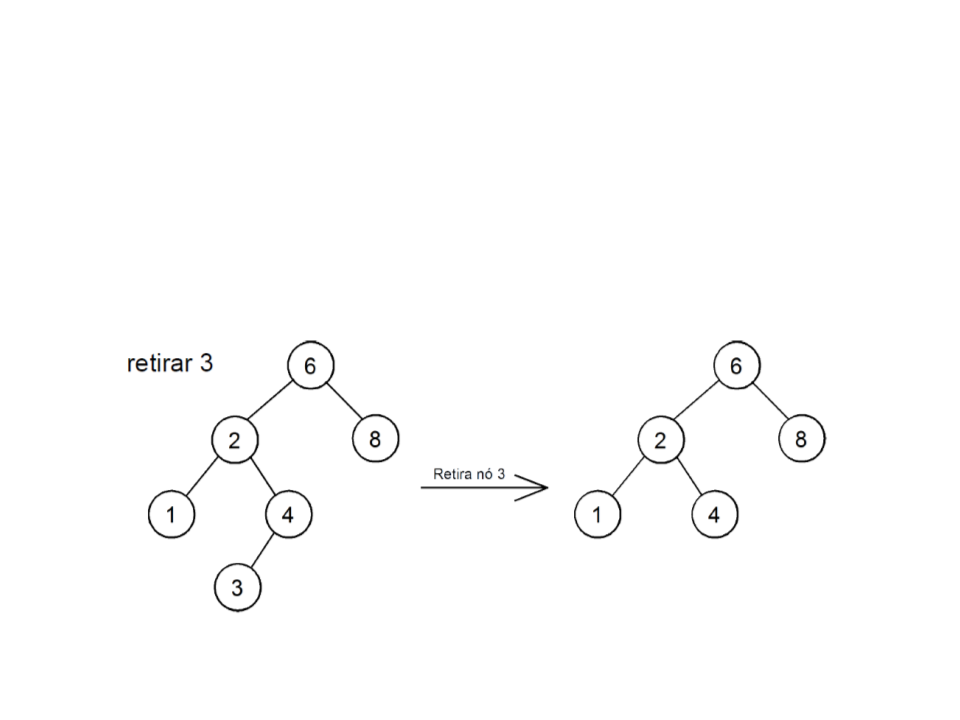
ABB – Remoção de Folha
•
Caso 1: a raiz da sub-árvore é folha da árvore original:
–
libere a memória alocada pela raiz
–
retorne a raiz atualizada, que passa a ser NULL
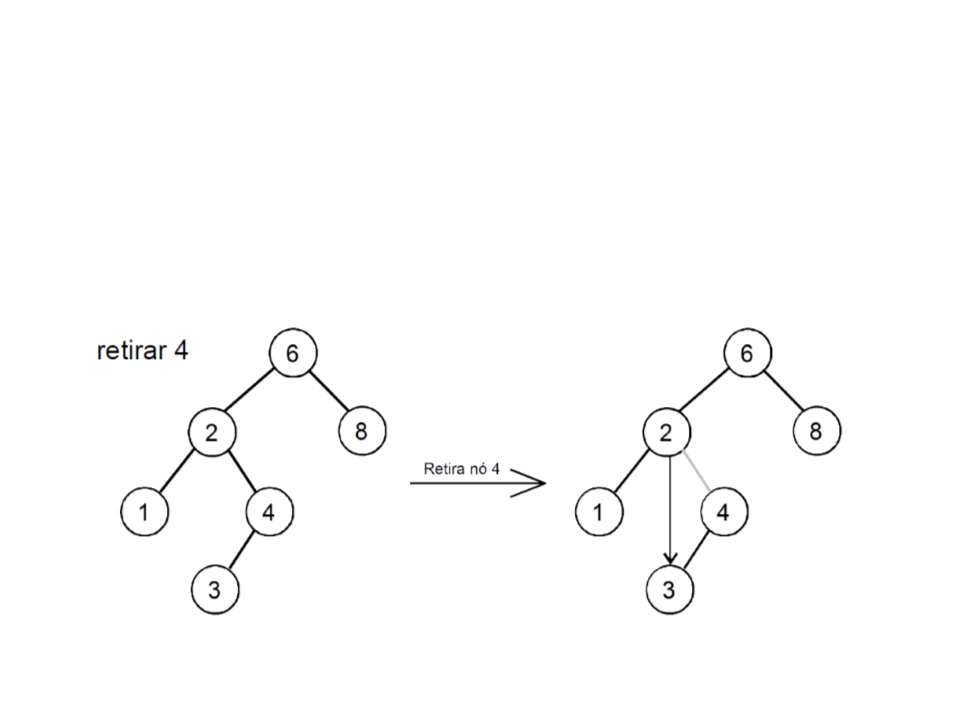
ABB – Remoção de pai de filho único
•
Caso 2: a raiz a ser retirada possui um único filho
–
libere a memória alocada pela raiz;
–
a raiz da árvore passa a ser o único filho da raiz;
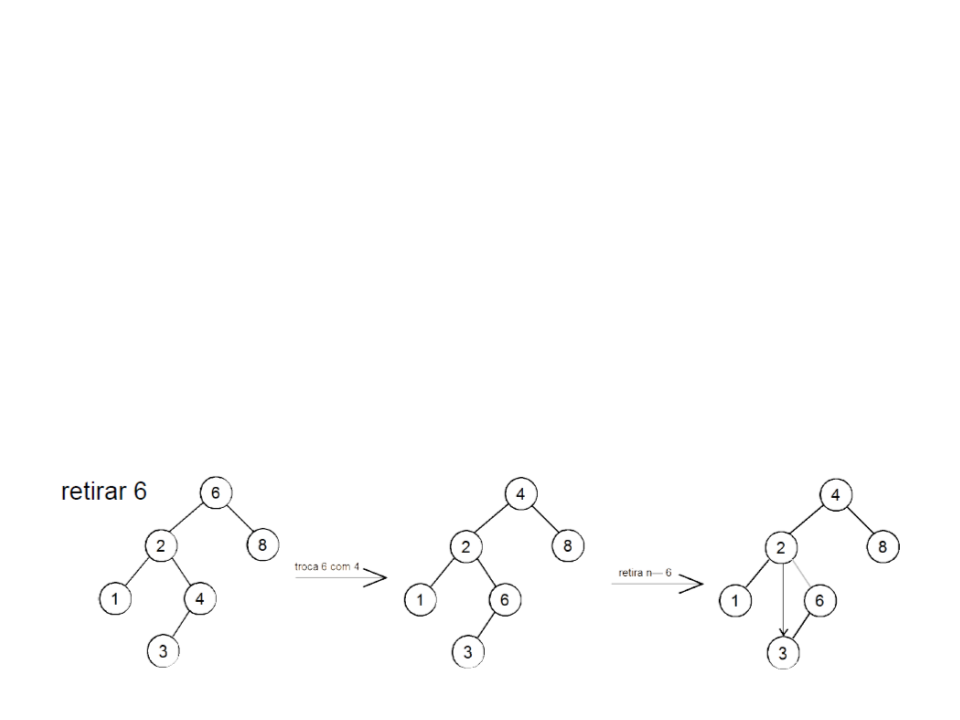
ABB – Remoção de pai de dois filhos
•
Caso 3: a raiz a ser retirada tem dois filhos
–
encontre o nó N que precede a raiz na ordenação (o elemento mais à
direita da sub-árvore à esquerda)
–
–
troque o dado da raiz com o dado de N
retire N da sub-árvore à esquerda (que agora contém o dado da raiz
que se deseja retirar)
•
retirar o nó N mais à direita é trivial, pois N é um nó folha ou N é um nó com um
único filho (no caso, o filho da direita nunca existe)

NoArvore* abb_retira(NoArvore* r, int v)
{
NoArvore *t, *f;
if (r == NULL)
return NULL;
else if (r->info > v)
r->esq = abb_retira(r->esq, v);
else if (r->info < v)
r->dir = abb_retira(r->dir, v);
else { /* achou o nó a remover */
if (r->esq == NULL && r->dir == NULL) /* nó sem filhos */
{
free(r);
r = NULL;
}
else if (r->esq == NULL) /* nó só tem filho à direita */
{
t = r;
r = r->dir;
free(t);
}
...

...
else if (r->dir == NULL) /* só tem filho à esquerda */
{
t = r;
r = r->esq;
free (t);
}
else { /* nó tem os dois filhos */
f = r->esq;
while (f->dir != NULL)
{
f = f->dir;
}
r->info = f->info; /* troca as informações */
f->info = v;
r->esq = abb_retira(r->esq, v);
}
}
return r;
}

Árvores Binárias de Busca – Exercício 1
•
Considerando a seguinte estrutura de uma árvore binária:
struct noArvore{
int info;
struct noArvore* esq;
struct noArvore* dir;
}
;
typedef struct noArvore NoArvore;
•
Implemente uma função que, dada uma árvore binária de busca, retorne a
quantidade de nós que guardam valores maiores que um determinado
valor x (também passado como parâmetro). Essa função tem o seguinte
protótipo:
int abb_maiores(NoArvore* a, int x);

Árvores Binárias de Busca – Exercício 1
int abb_maiores(NoABB* a, int x)
{
int n = 0;
if(a == NULL)
return 0;
if(a->info > x)
{
n++;
n = n + abb_maiores(a->esq, x);
n = n + abb_maiores(a->dir, x);
}
else{
n = n + abb_maiores(a->dir, x);
}
return n;
}

Leitura Complementar
•
Waldemar Celes, Renato Cerqueira, José Lucas
Rangel, Introdução a Estruturas de Dados, Editora
Campus (2004).
•
•
Capítulo 13 – Árvores
Capítulo 17 – Busca

Exercícios
Lista de Exercícios 14 – Árvores Binárias de Busca
http://www.inf.puc-rio.br/~elima/prog2/
