
INF 1007 – Programação II
Aula 09 – Ordenação de Vetores
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Ordenação de Vetores
•
Problema:
–
–
Entrada:
•
vetor com os elementos a serem ordenados;
Saída:
•
mesmo vetor com elementos na ordem especificada;
•
Algoritmos básicos de ordenação:
–
–
Ordenação Bolha (Bubble Sort);
Ordenação rápida (Quick Sort);
Bubble Sort
•
Algoritmo:
–
Quando dois elementos estão fora de ordem, troque-os de
posição até que o i-ésimo elemento de maior valor do
vetor seja levado para as posições finais do vetor;
–
Continue o processo até que todo o vetor esteja ordenado;
Bubble Sort
162 162 2124 12842 1128772 122722
6
12 11844 184 17 2222
Bubble Sort
6
6
6
6
12 14 8 17 22
12 8 14 17 22
182 11822 14 17 2222
8 1122 14 1177 2222

Bubble Sort - Exemplo
2
5 48 37 12 57 86 33 92
2
2
2
2
2
2
2
2
5 48 37 12 57 86 33 92
5 48 37 12 57 86 33 92
5 37 48 12 57 86 33 92
5 37 12 48 57 86 33 92
5 37 12 48 57 86 33 92
5 37 12 48 57 86 33 92
5 37 12 48 57 33 86 92
5 37 12 48 57 33 86 92
25x48
48x37
48x12
48x57
57x86
86x33
86x92
troca
troca
troca
Final do Passo 1
O maior elemento, 92, já está na sua posição final!

Bubble Sort - Exemplo
2
5 37 12 48 57 33 86 92
Final do Passo 1
2
2
2
2
2
2
2
5 37 12 48 57 33 86 92
5 37 12 48 57 33 86 92
5 12 37 48 57 33 86 92
5 12 37 48 57 33 86 92
5 12 37 48 57 33 86 92
5 12 37 48 33 57 86 92
5 12 37 48 33 57 86 92
25x37
37x12
37x48
48x57
troca
57x33 troca
57x86
Final do Passo 2
O segundo maior elemento, 86, já está na sua posição final!

Bubble Sort - Exemplo
2
5 12 37 48 33 57 86 92
Final do Passo 2
2
1
1
1
1
1
5 12 37 48 33 57 86 92
2 25 37 48 33 57 86 92
2 25 37 48 33 57 86 92
2 25 37 48 33 57 86 92
2 25 37 33 48 57 86 92
2 25 37 33 48 57 86 92
25x12 troca
25x37
37x48
48x33
48x57
troca
Final do Passo 3

Bubble Sort - Exemplo
2
5 12 37 48 33 57 86 92
Final do Passo 3
1
1
1
1
1
2 25 37 33 48 57 86 92
2 25 37 33 48 57 86 92
2 25 37 33 48 57 86 92
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
12x25
25x37
37x33 troca
37x48
Final do Passo 4
1
1
1
1
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
12x25
25x33
33x37
Final do Passo 5

Bubble Sort - Exemplo
2
5 12 33 37 48 57 86 92
Final do Passo 5
1
1
1
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
2 25 33 37 48 57 86 92
12x25
25x33
Final do Passo 6
1
2 25 33 37 48 57 86 92
12x25
1
2 25 33 37 48 57 86 92
Final do Passo 7
1
2 25 33 37 48 57 86 92
Fim da Ordenação

Bubble Sort - Implementação Iterativa (I)
void bolha(int n, int* v)
{
int fim, i, temp;
for (fim = n-1; fim > 0; fim--)
{
for (i=0; i<fim; i++)
{
if (v[i]>v[i+1])
{
temp = v[i];
v[i] = v[i+1];
v[i+1] = temp;
}
}
}
}
Bubble Sort - Implementação Iterativa (II)
void bolha(int n, int* v)
{
int i, fim, troca, temp;
for (fim = n-1; fim > 0; fim--){
troca = 0;
for (i=0; i<fim; i++){
if (v[i]>v[i+1]){
temp = v[i];
v[i] = v[i+1];
v[i+1] = temp;
troca = 1;
}
Implementação mais otimizada:
para a busca quando ocorre
uma passada sem trocas.
if (troca == 0)
return;
}
}
}

Bubble Sort - Complexidade
•
•
Esforço computacional ≅ número de comparações
≅
número máximo de trocas
–
–
–
primeira passada: n-1 comparações
segunda passada: n-2 comparações
terceira passada: n-3 comparações
Tempo total gasto pelo algoritmo:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) = n(n-1)/2 =
Algoritmo de ordem quadrática: O(n2)
ꢁ
Quick Sort
•
Algoritmo:
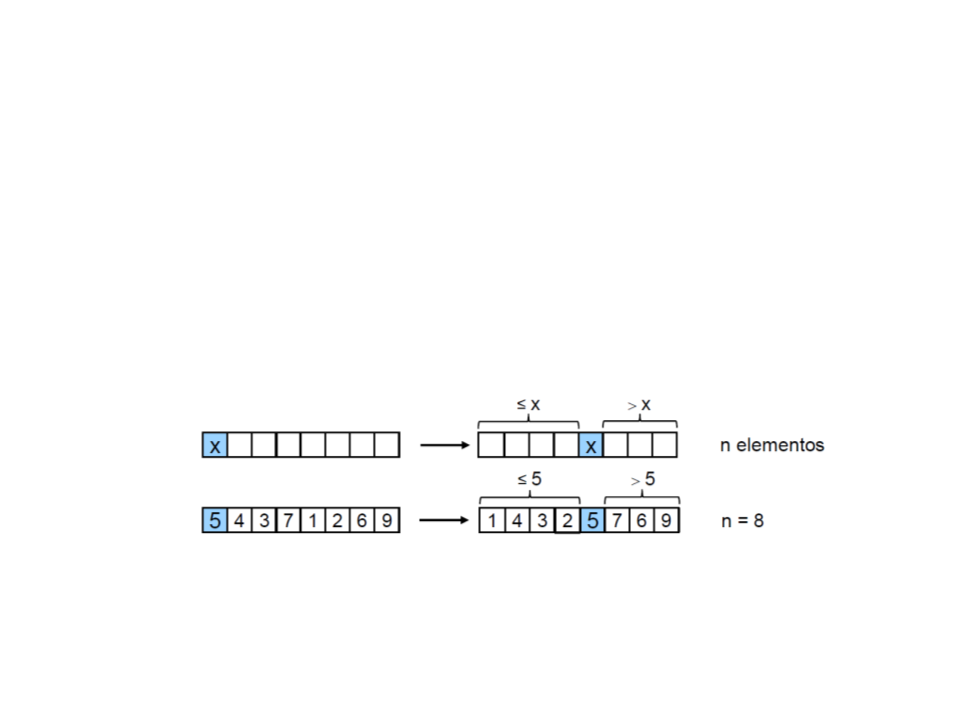
1. Escolha um elemento arbitrário x, o pivô;
2. Particione o vetor de tal forma que x fique na posição correta v[i]:
•
x deve ocupar a posição i do vetor sse:
todos os elementos v[0], … v[i-1] são menores que x;
todos os elementos v[i+1], …, v[n-1] são maiores que x;
3
. Chame recursivamente o algoritmo para ordenar os subvetores
v[0], … v[i-1] e v[i+1], …, v[n-1] (vetor da esquerda e vetor da direita)
•
continue até que os vetores que devem ser ordenados tenham 0 ou 1 elemento

Quick Sort
quicksort do vetor de tamanho n
se n > 1 então
PARTIÇÃO com pivô x
quicksort do subvetor à esquerda de x
quicksort do subvetor à direita de x
Quick Sort
•
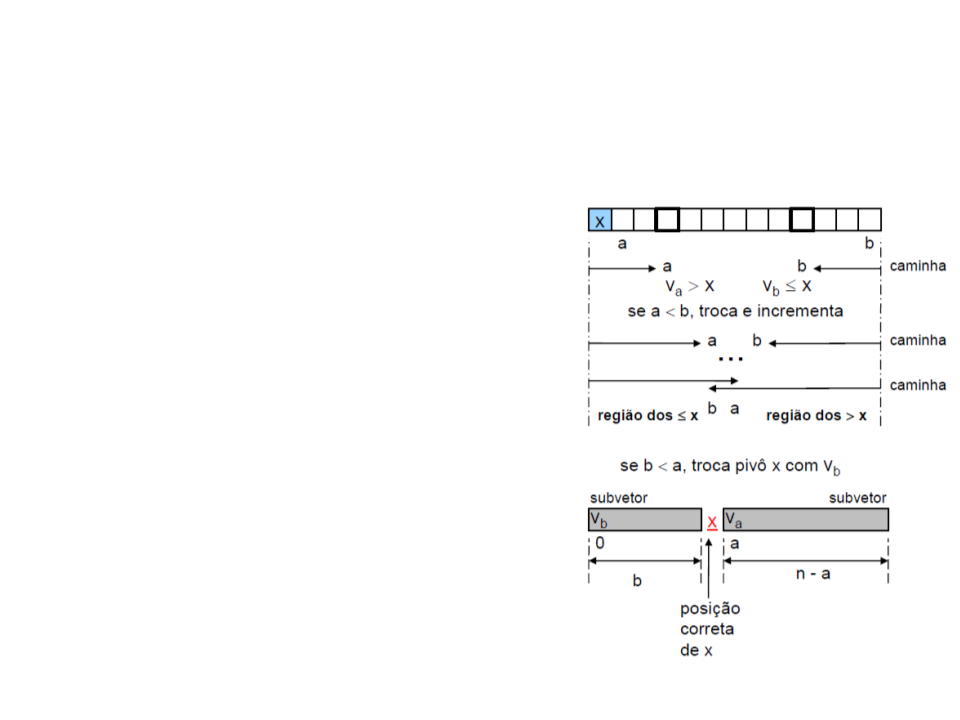
Processo de partição:
1. Caminhe com o índice a do início
para o final, comparando x com v[1],
v[2], … até encontrar v[a] > x
2
. Caminhe com o índice b do final para
o início, comparando x com v[n-1],
v[n-2], … até encontrar v[b] <= x
3. Troque v[a] e v[b]
4
. Continue para o final a partir de
v[a+1] e para o início a partir de
v[b-1]
5
. Termine quando os índices de busca
(a e b) se encontram (b < a)
•
A posição correta de x=v[0] é a posição
b, então v[0] e v[b] são trocados
Quick Sort
•
Processo de Partição:
–
Exemplo:
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
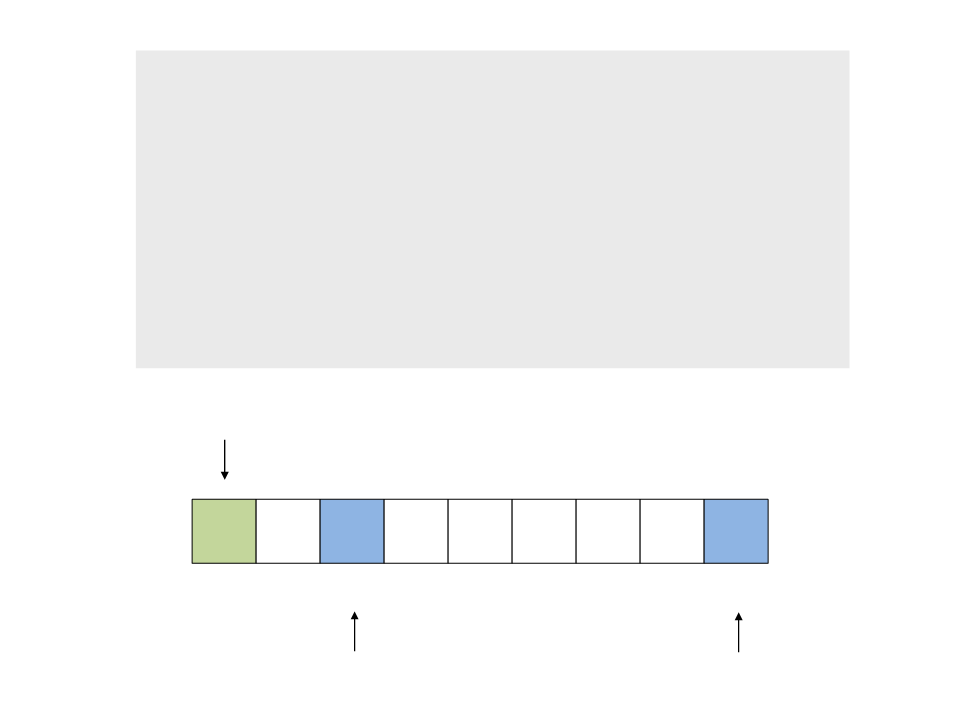
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
40
20
10
80
60
50 7 30 100
[
0]
[1] [2] [3] [4]
[5] [6] [7] [8]
a
b
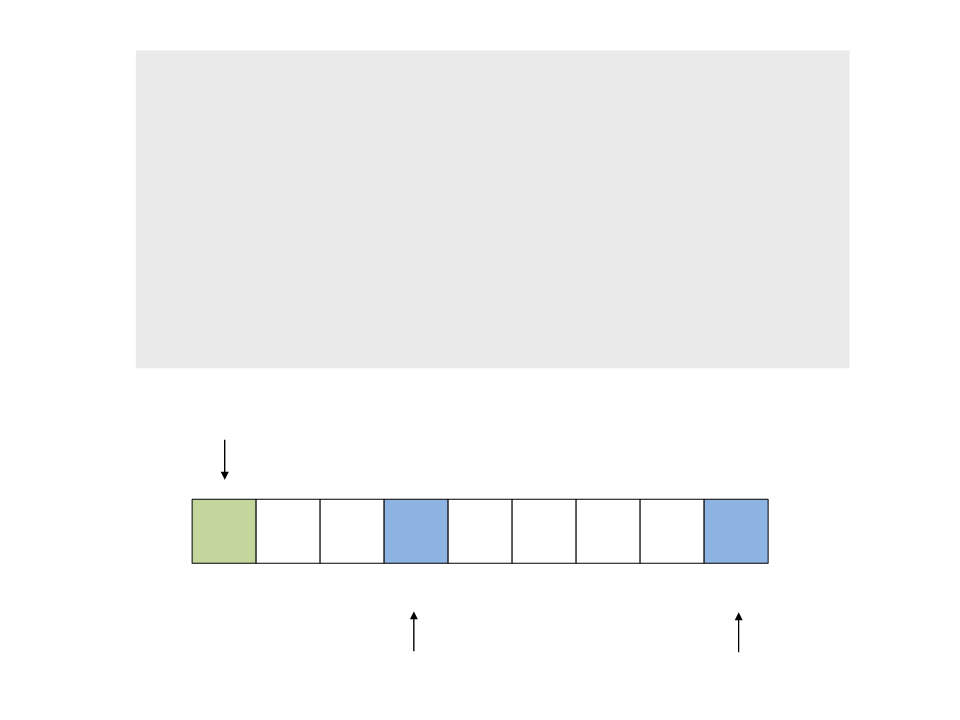
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
4
0 20 10
80
60 50
7
30 100
[7] [8]
[
0] [1] [2] [3] [4] [5]
[6]
a
b
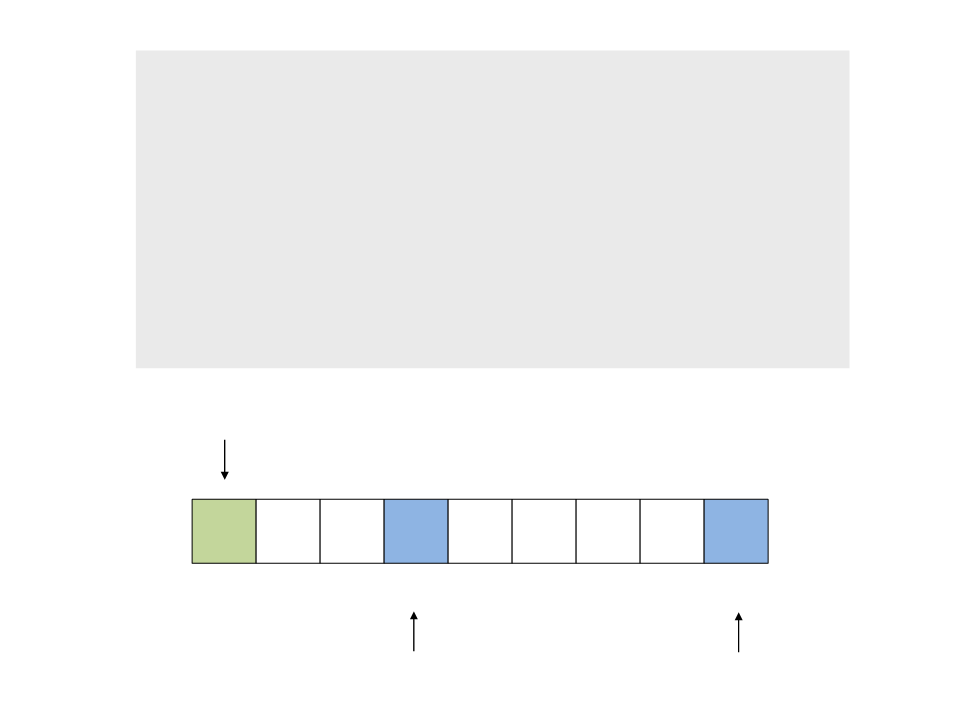
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
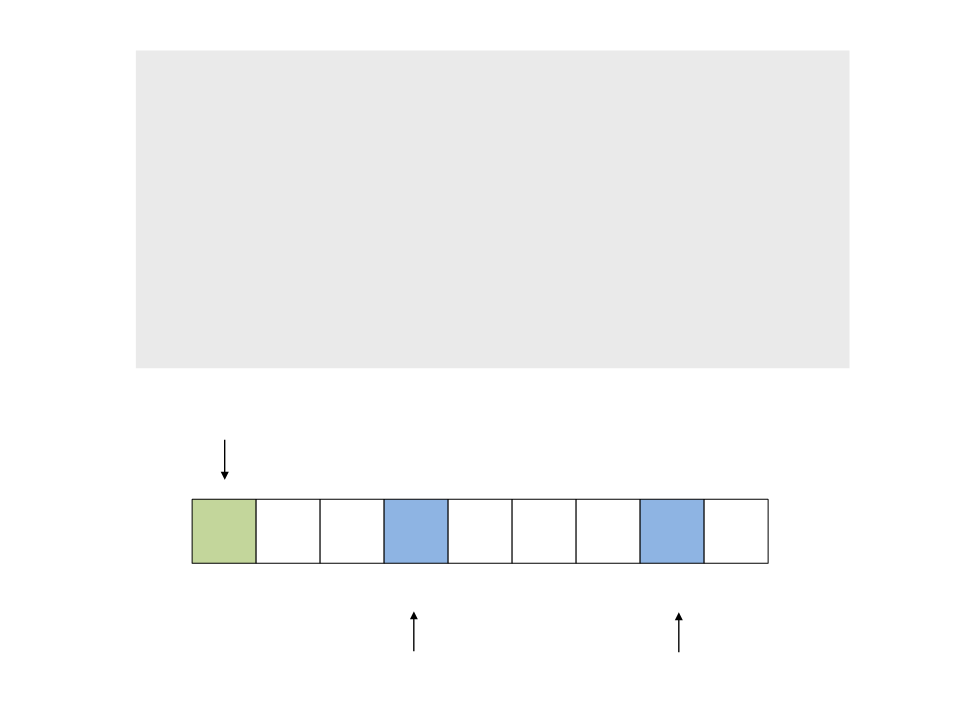
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
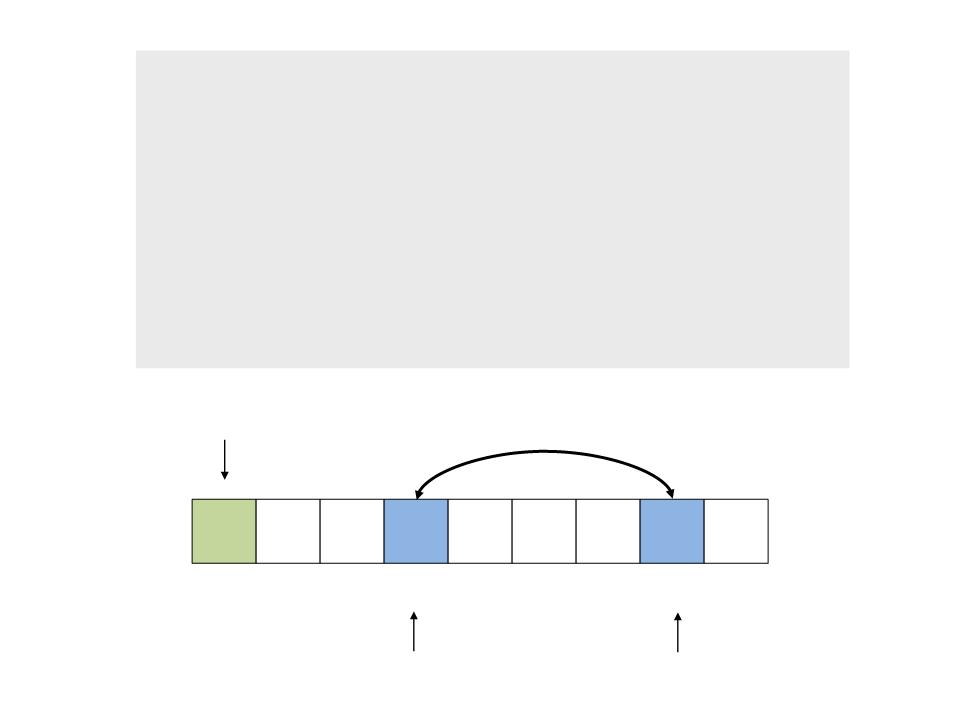
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
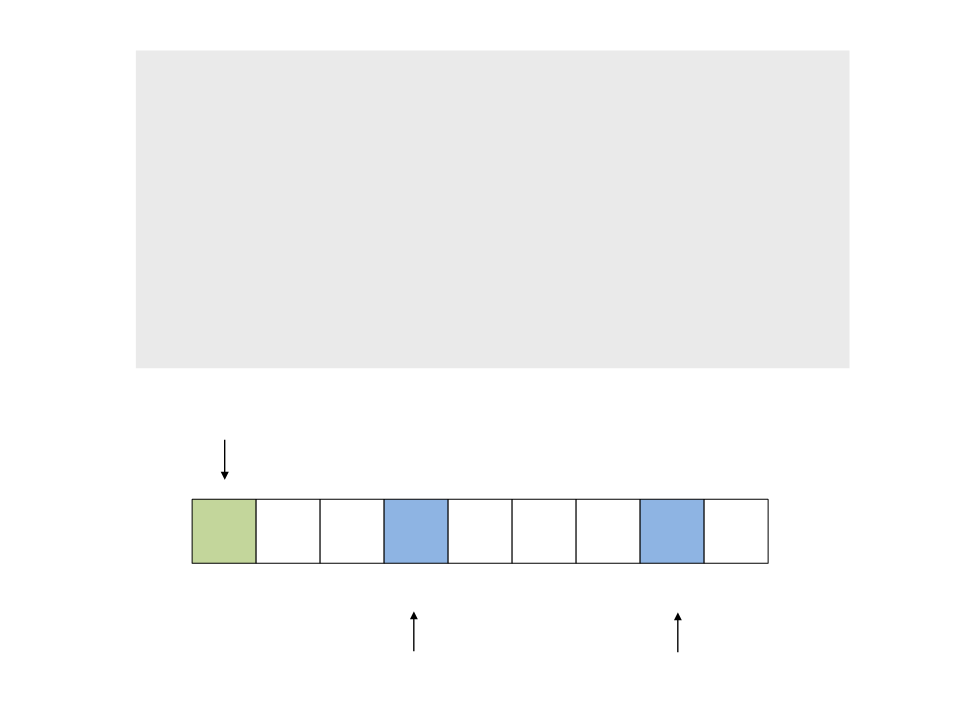
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
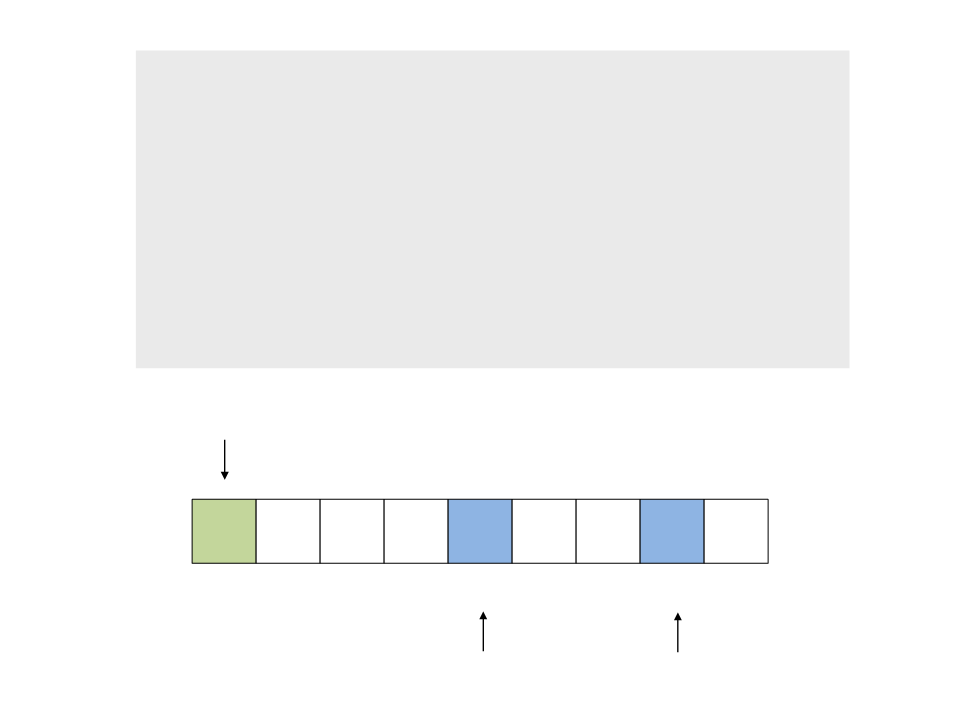
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10 30
[2] [3]
60
50
7
80 100
[7] [8]
[
0]
[1]
[4]
[5]
[6]
a
b
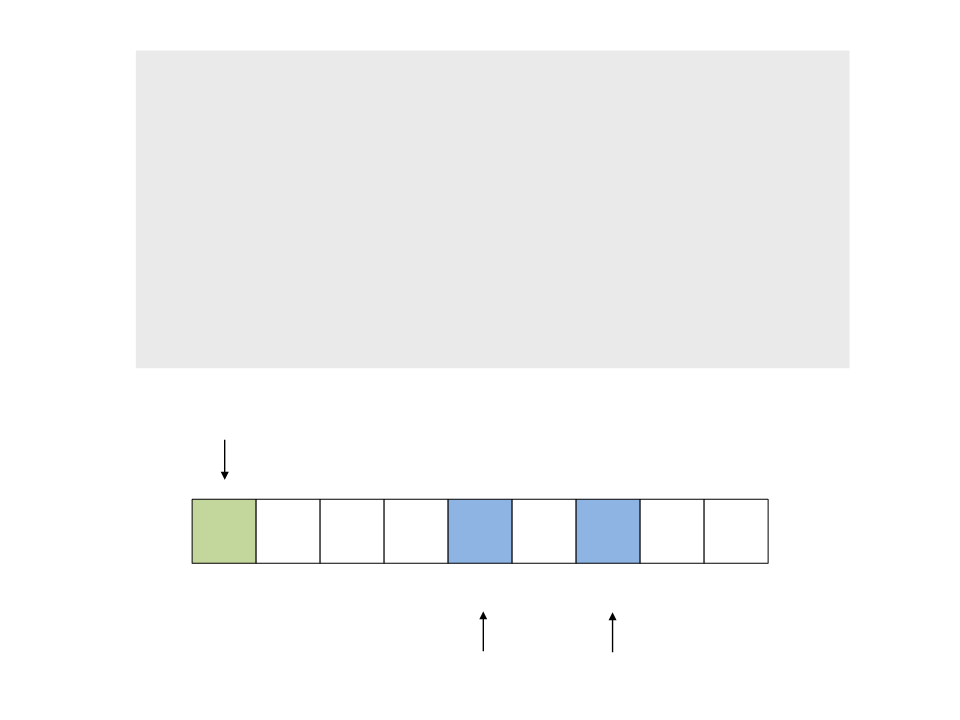
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
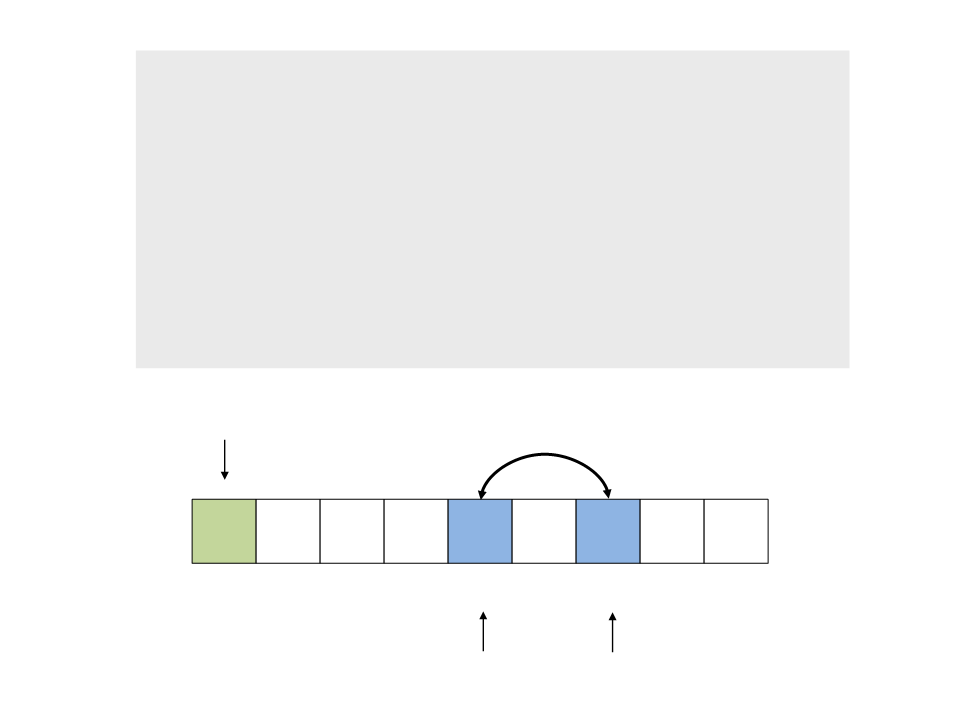
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0 20
[1]
10
30 60
50
7
80 100
[7] [8]
[
0]
[2] [3]
[4]
[5]
[6]
a
b
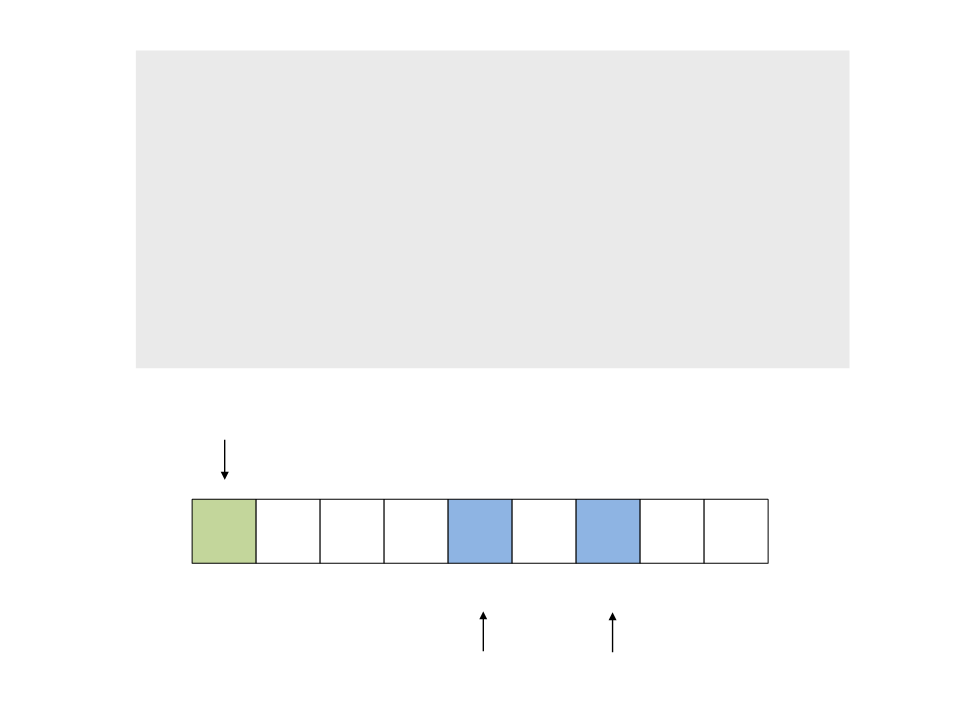
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
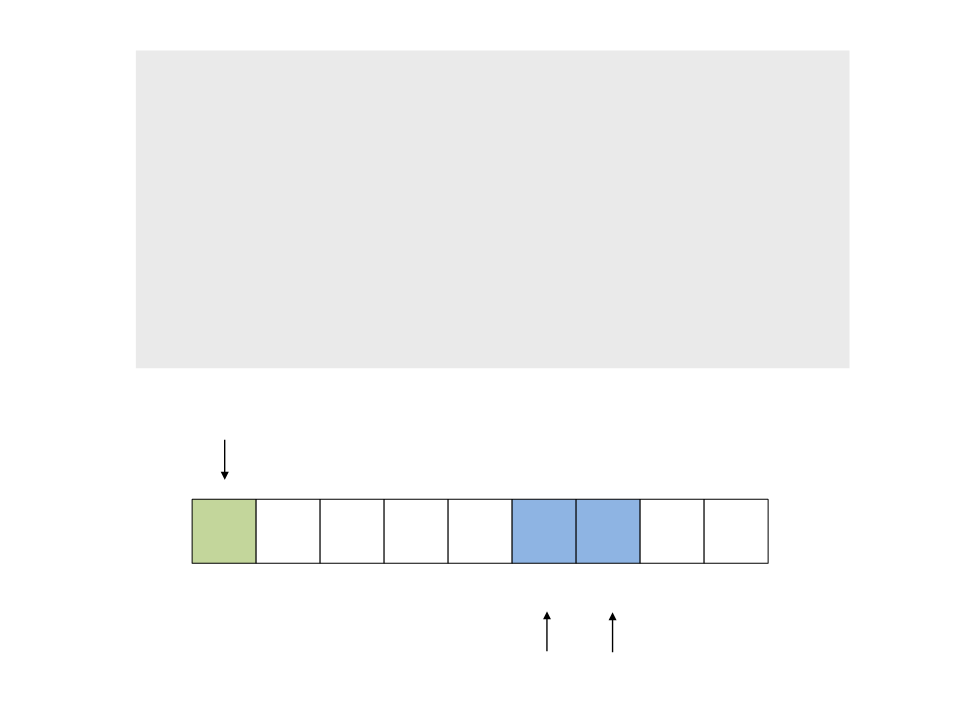
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5] [6]
a
b
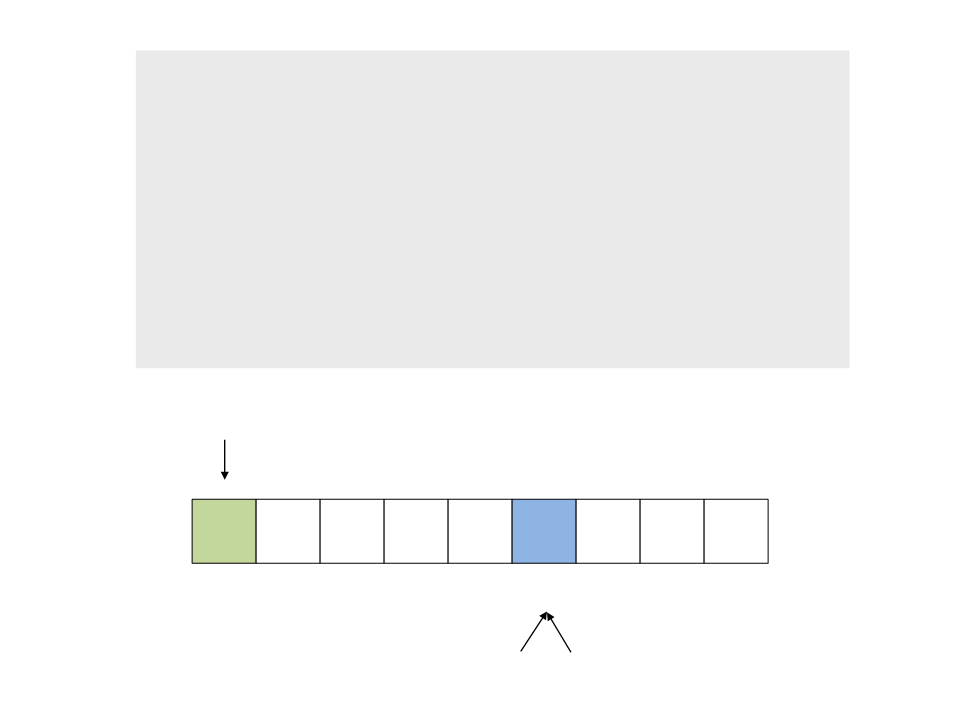
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
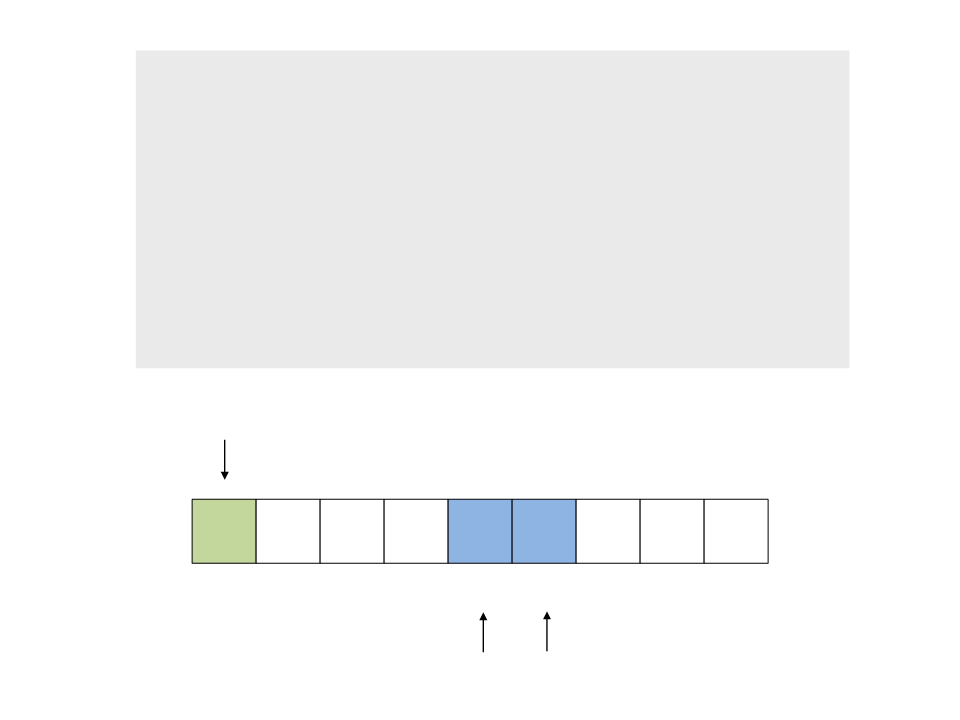
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
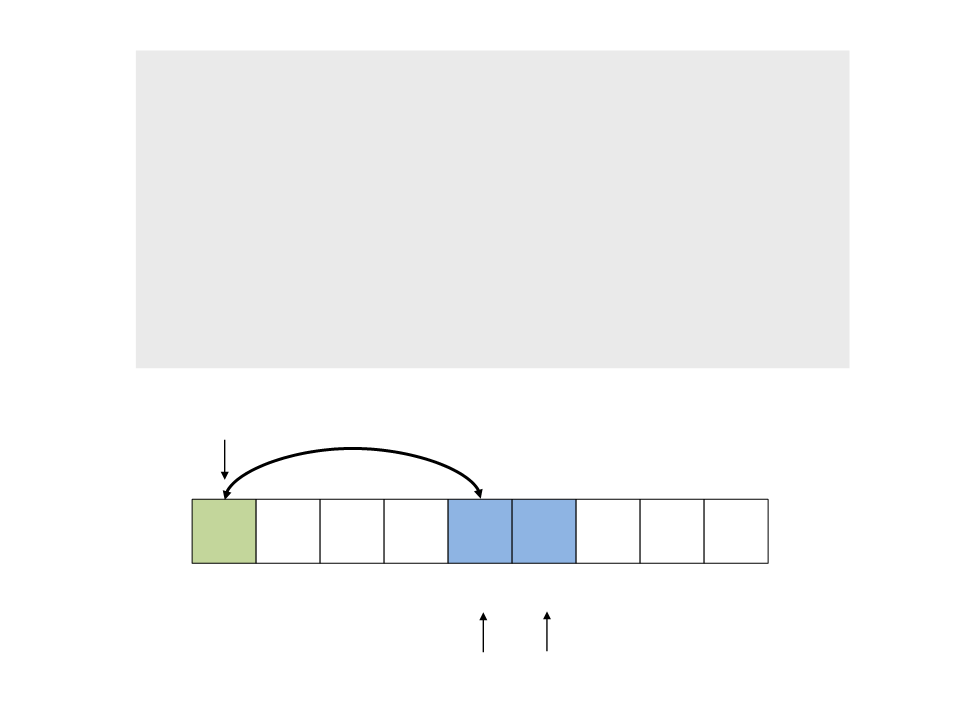
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
troca(&v[x], &v[b]);
x (pivô)
40
20
10
30
7
50 60 80 100
[
0] [1] [2] [3]
[4] [5] [6] [7] [8]
a
b
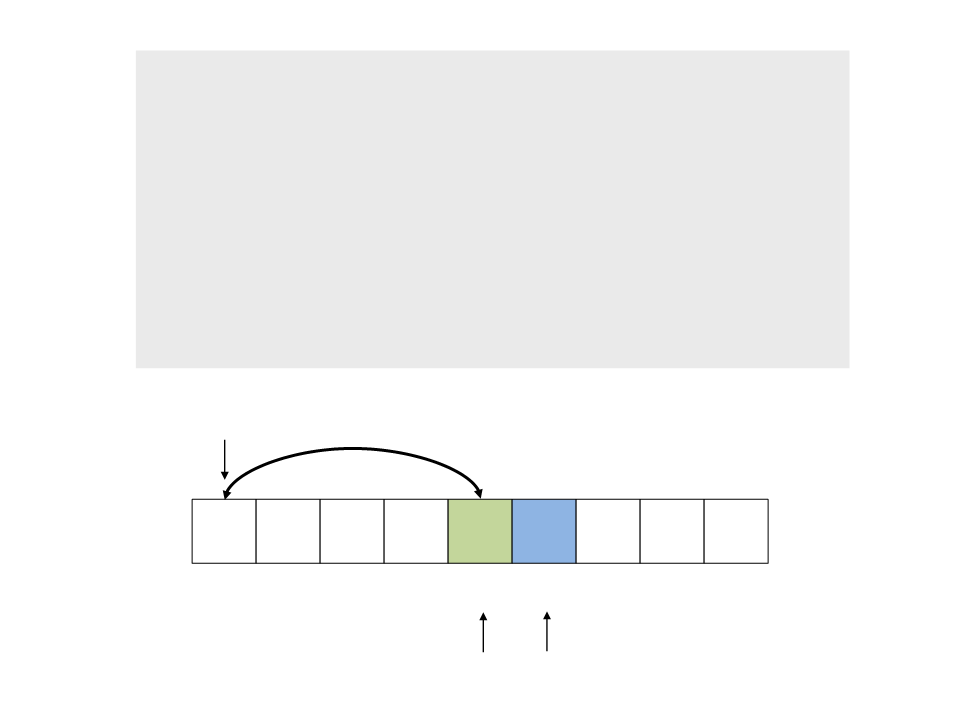
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
troca(&v[x], &v[b]);
x (pivô)
7
20 10
[1]
30 40
50
60 80 100
[6] [7] [8]
[
0]
[2] [3]
[4]
[5]
a
b
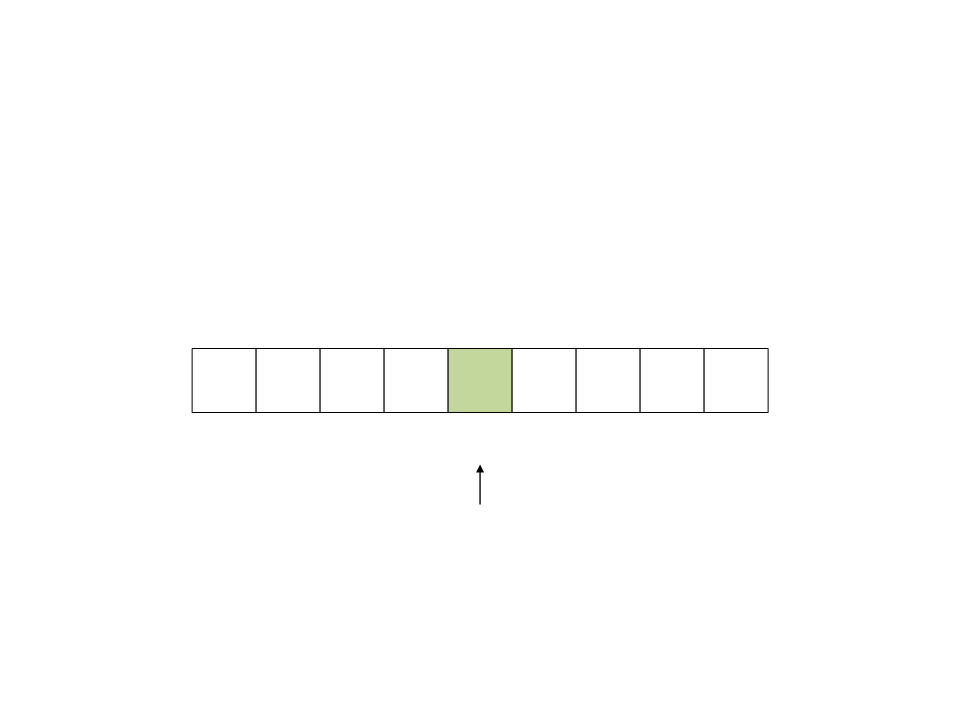
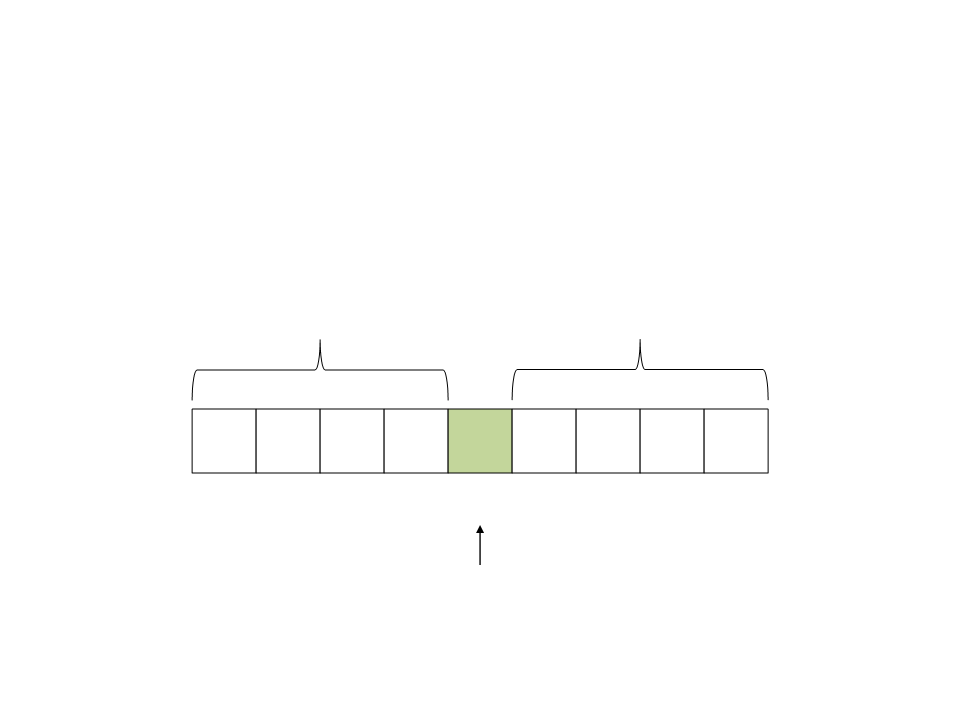
Quick Sort
•
Resultado da Partição:
7
20
10
30
40
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4] [5]
[6]
o pivô ocupa a sua posição
final na ordenação
Quick Sort
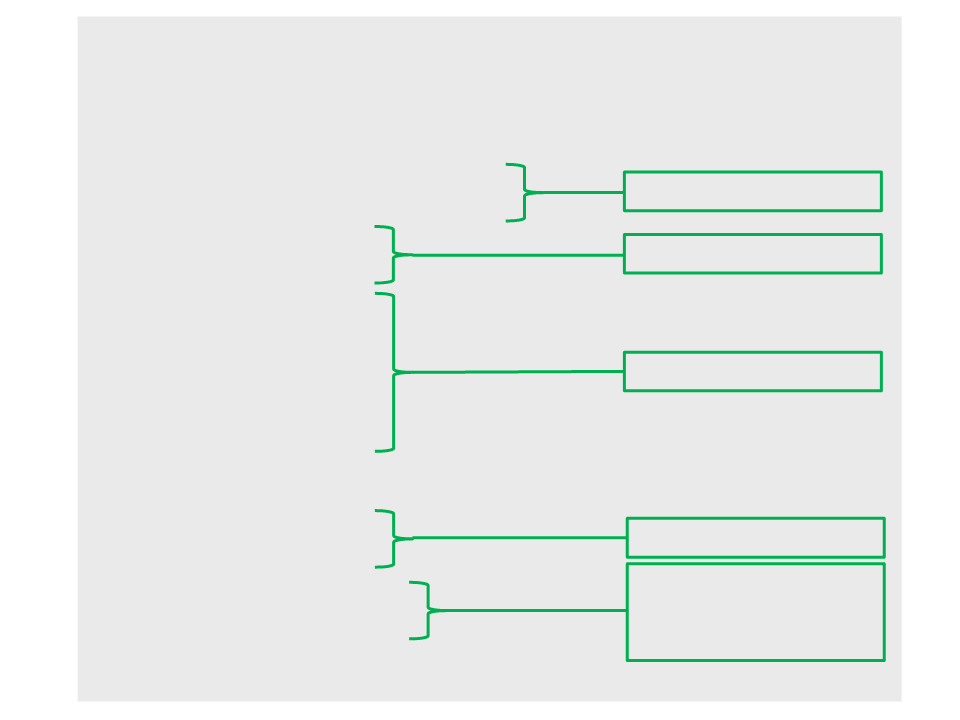
•
Chamada recursiva aos subvetores:
subvetor da esquerda
subvetor da direita
7
20 10 30
40 50
[5]
60 80 100
[6] [7] [8]
[
0]
[1] [2] [3] [4]
o pivô ocupa a sua posição
final na ordenação
void quicksort(int n, int* v){
int x, a, b, temp;
if (n > 1) {
x = v[0]; a = 1; b = n-1;
do {
while (a < n && v[a] <= x)
a++;
Caminha com o índice a
Caminha com o índice b
while (v[b] > x)
b--;
if (a < b) {
temp = v[a];
v[a] = v[b];
v[b] = temp;
a++; b--;
Faz a troca de a e b
}
}
while (a <= b);
v[0] = v[b];
Faz a troca do pivô e b
v[b] = x;
Chamada recursiva
para o subvetor da
esquerda e da direita
quicksort(b,v);
quicksort(n-a,&v[a]);
}
}
void quicksort(int n, int* v){
int x, a, b, temp;
if (n > 1) {
x = v[0]; a = 1; b = n-1;
do {
while(a<n && compInt(v[a],x) == 0)
a++;
while(compInt(v[b],x) == 1)
b--;
int compInt(int a, int b)
{
if (a < b) {
temp = v[a];
v[a] = v[b];
v[b] = temp;
a++; b--;
if (a > b)
return 1;
else
return 0;
}
}
}
while (a <= b);
v[0] = v[b];
v[b] = x;
quicksort(b,v);
quicksort(n-a,&v[a]);
}
}

Quick Sort
(1) Vetor para ser ordenado:
3
1
4
1
5
9
2
6
5
3
[
0] [1]
[2] [3]
[4] [5]
[6] [7] [8]
[9]
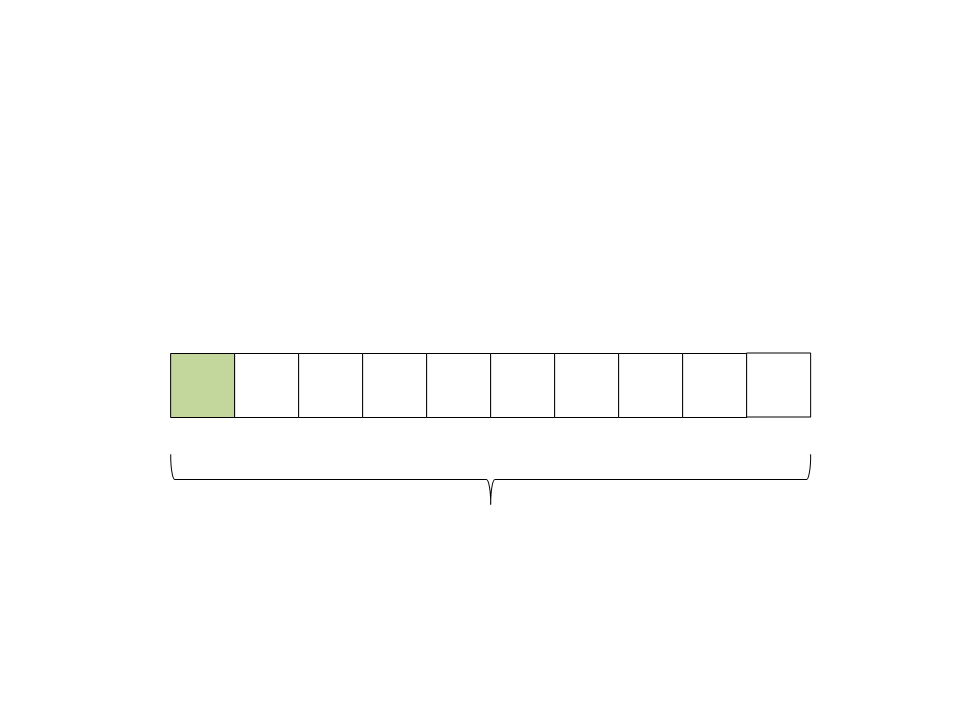
Quick Sort
(2) Selecione o pivô:
3
1
4
1
5
9
2
6
5
3
[
0]
[1]
[2] [3]
[4] [5]
[6]
[7] [8]
[9]
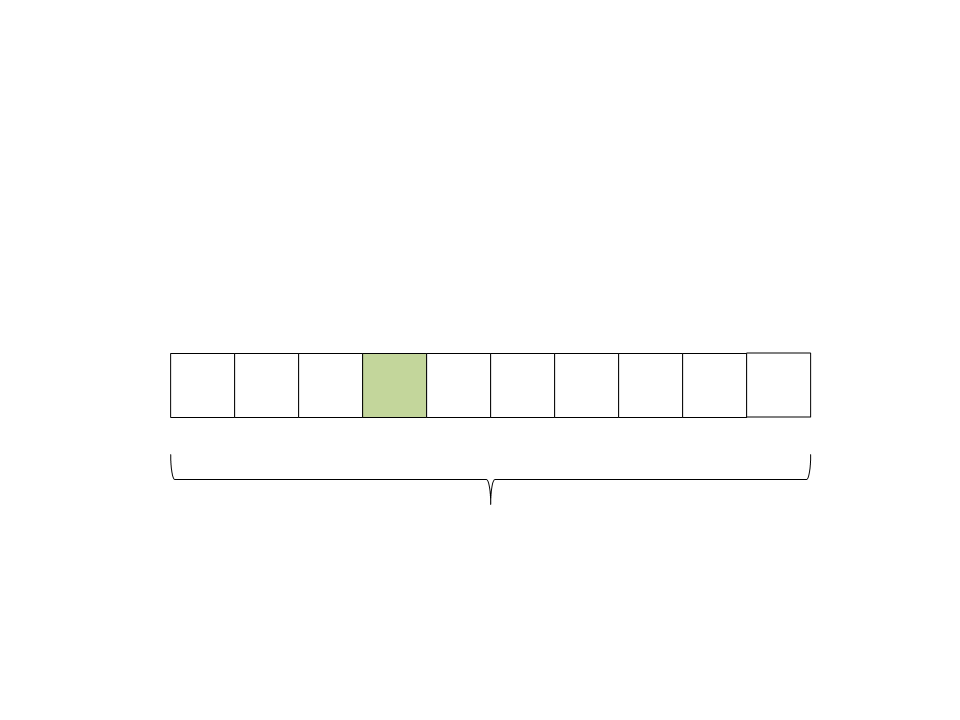
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
3) Particione o vetor. Todos os elementos maiores que o pivô
2
1
1
3
5
9
4
6
5
3
[
0] [1] [2] [3]
[4] [5]
[6]
[7] [8] [9]
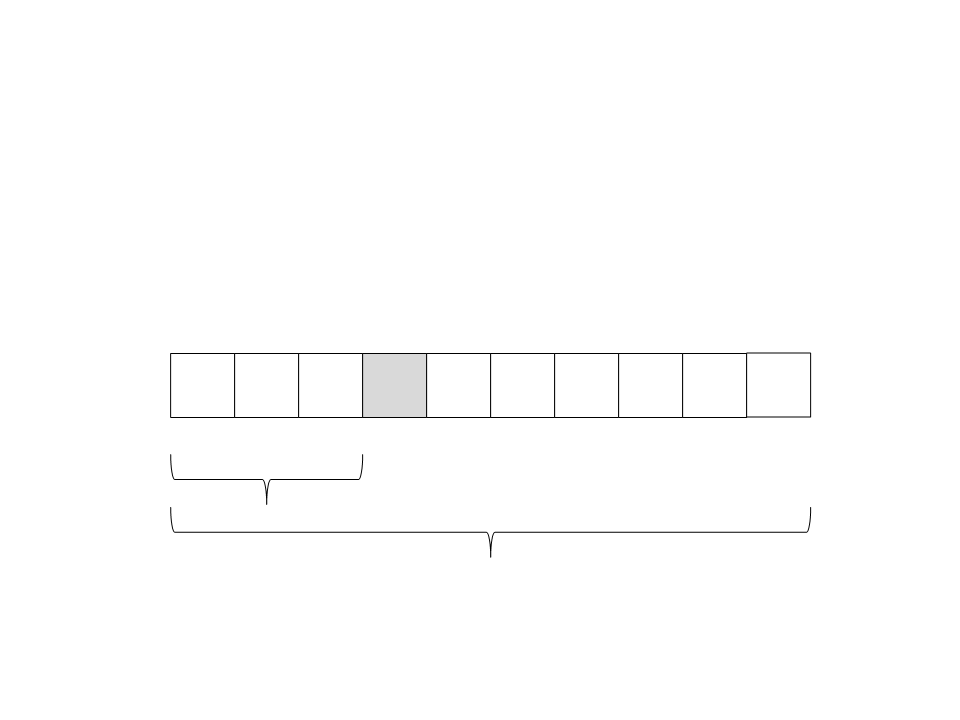
Quick Sort
(4) Chame recursivamente o quick sort para o subvetor da
esquerda:
2
1
1
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
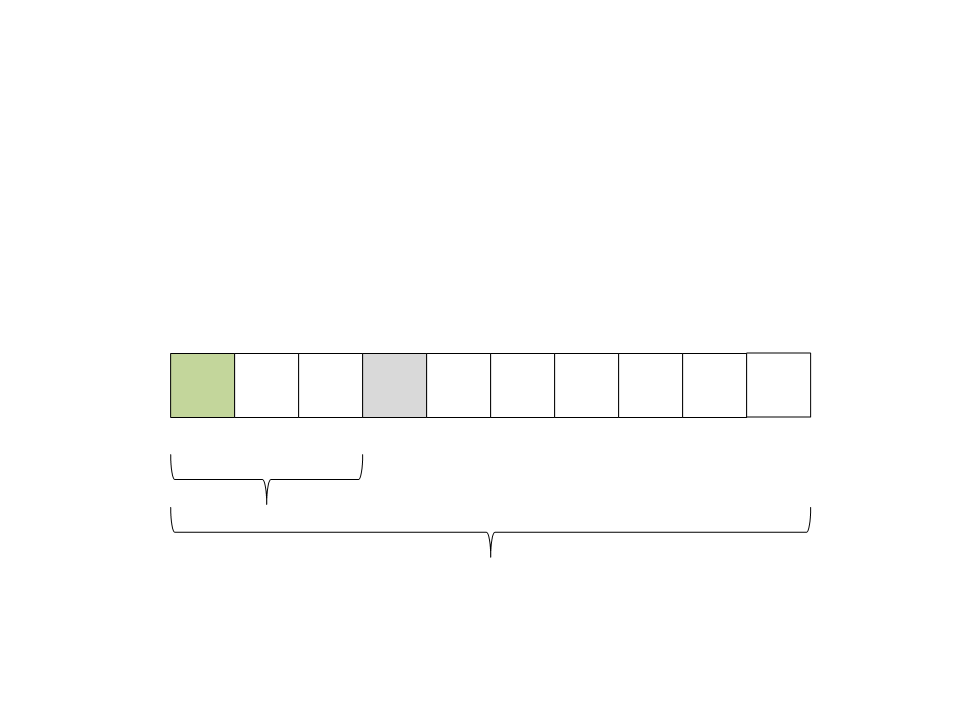
Quick Sort
(5) Selecione o pivô:
2
1
1
3
5
9
4
6
5
3
[
0] [1] [2] [3] [4]
[5] [6]
[7] [8] [9]
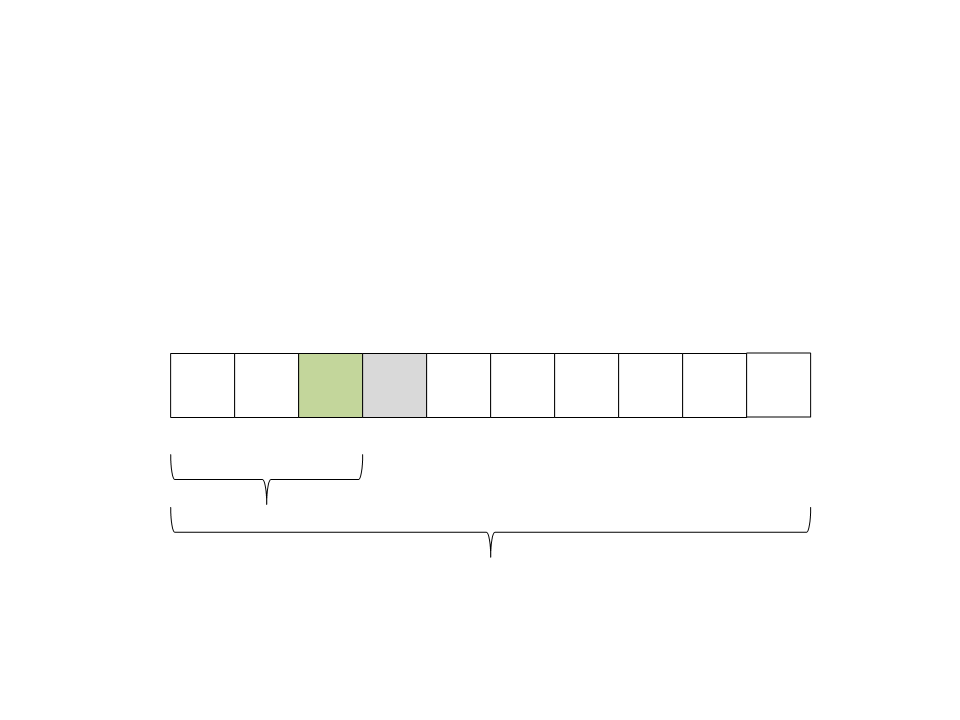
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
6) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5] [6]
[7] [8]
[9]
Quick Sort
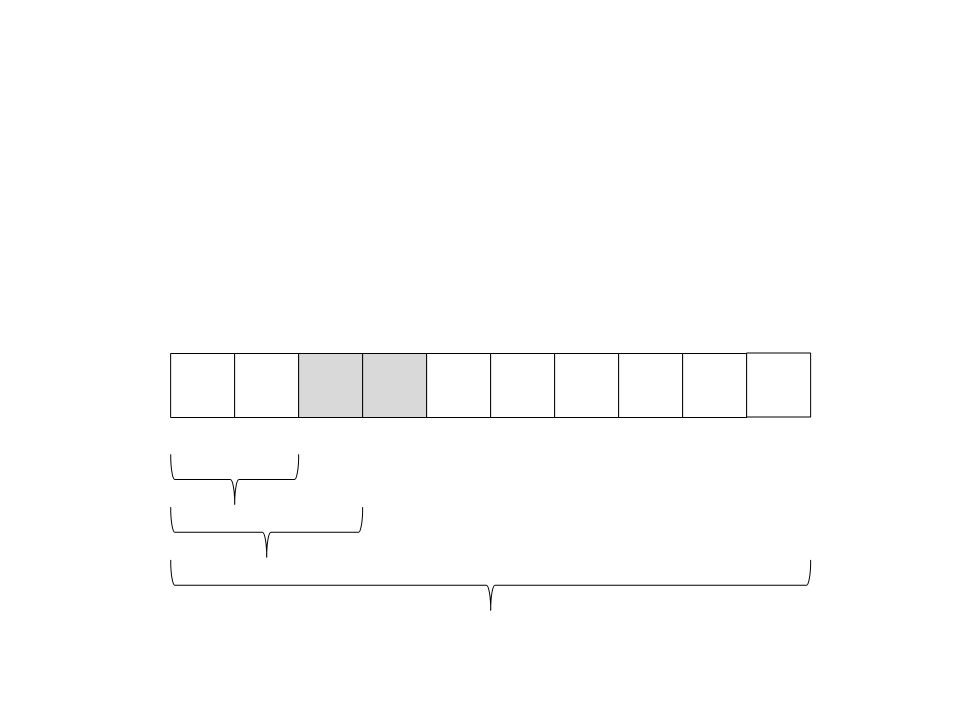
(7) Chame recursivamente o quick sort para o subvetor da
esquerda:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6] [7] [8]
[9]
Quick Sort
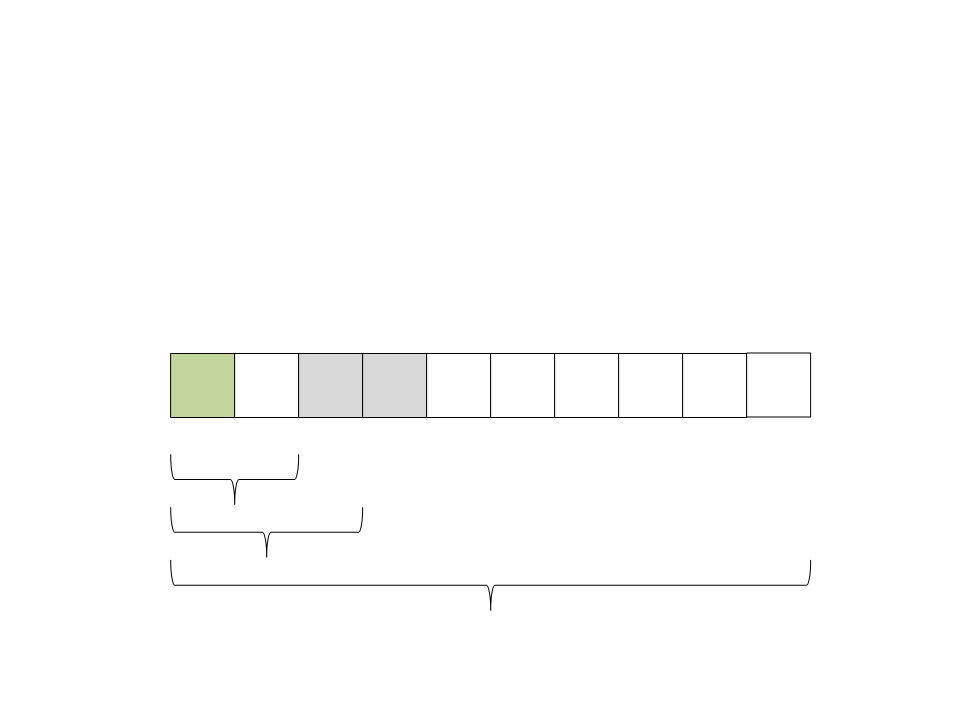
(8) Selecione o pivô:
1
1
2
3
5
9
4
6
5
3
[
0]
[1] [2] [3]
[4]
[5] [6]
[7] [8]
[9]
Quick Sort
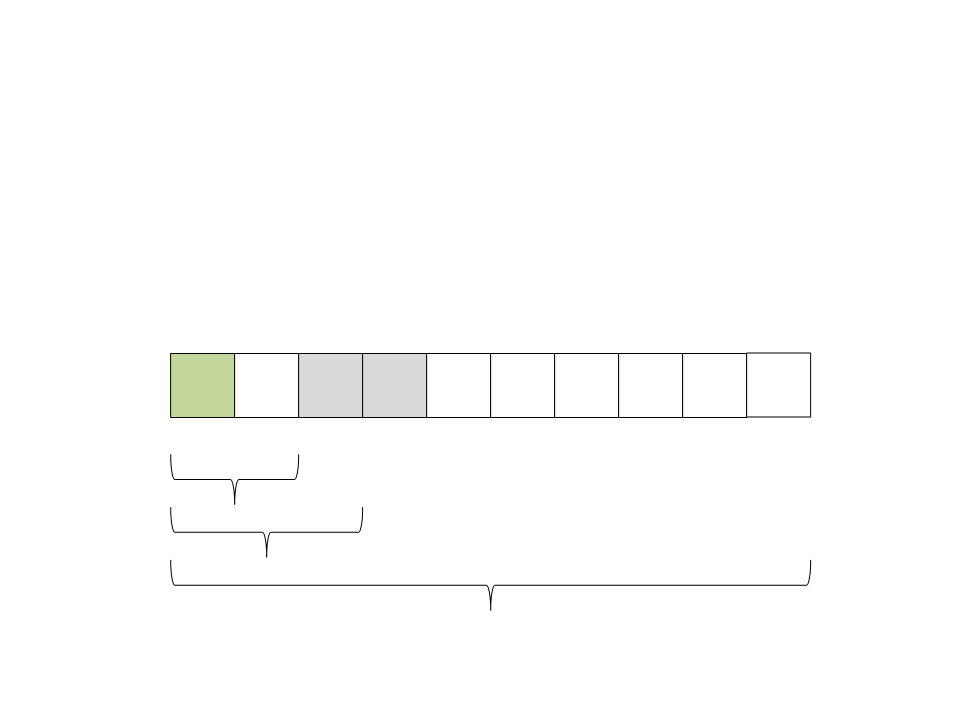
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
9) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
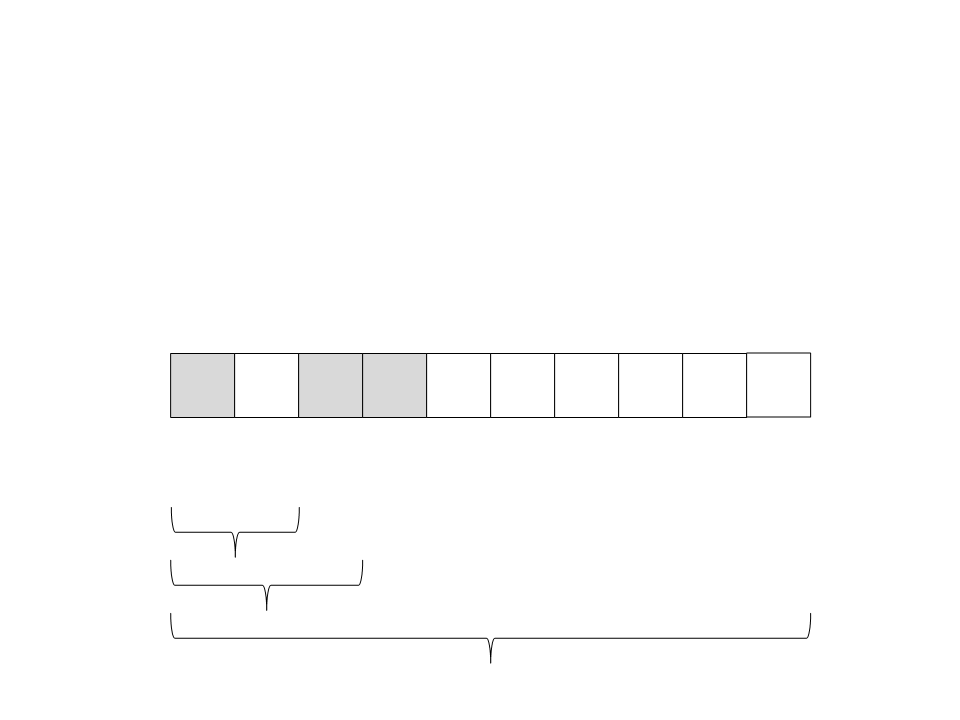
(
esquerda. O tamanho do vetor da esquerda é zero. A recursão
retorna.
10) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
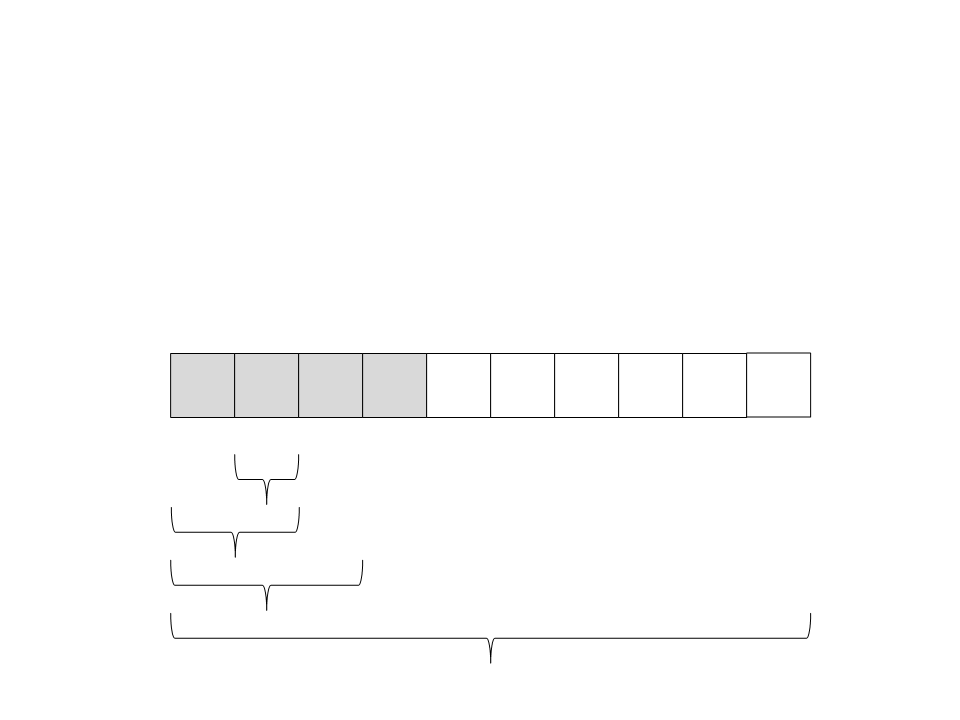
Quick Sort
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna.
11) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
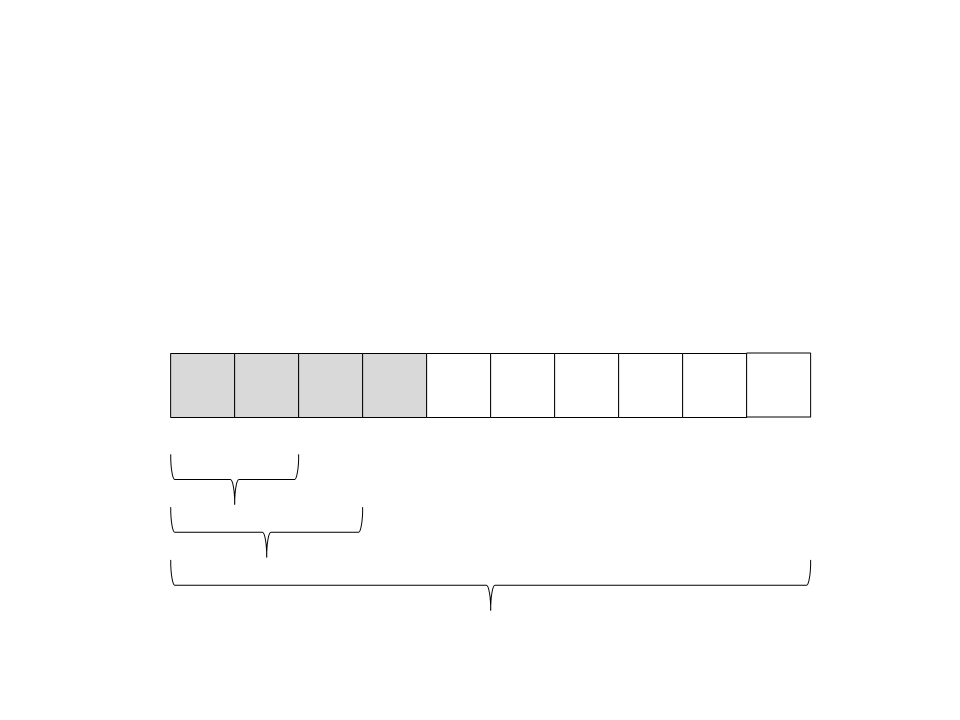
Quick Sort
(12) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
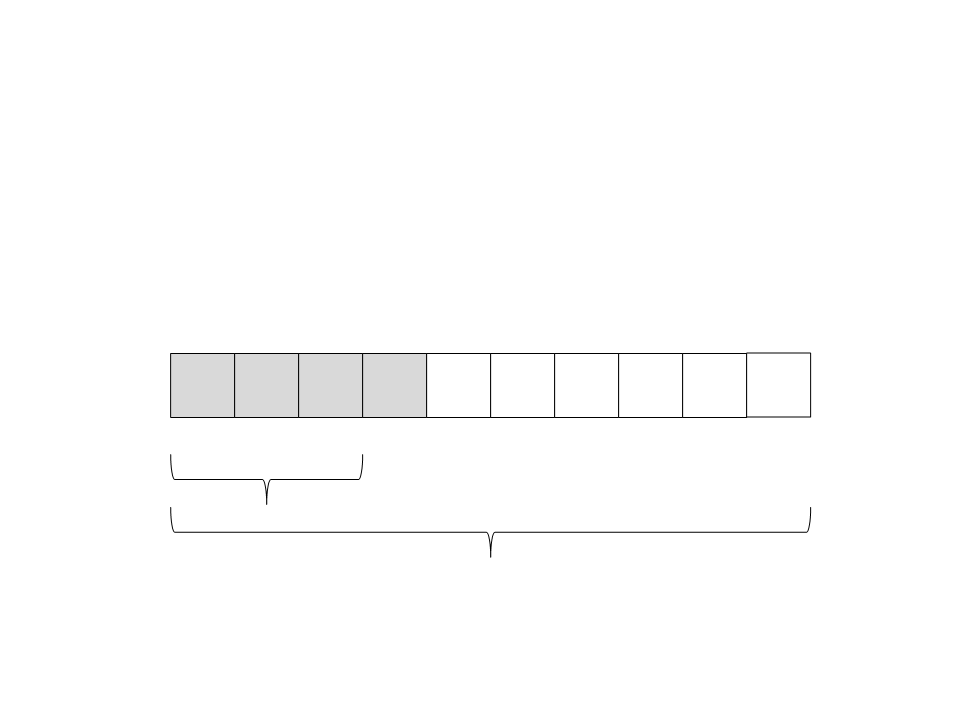
Quick Sort
(13) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6] [7] [8]
[9]
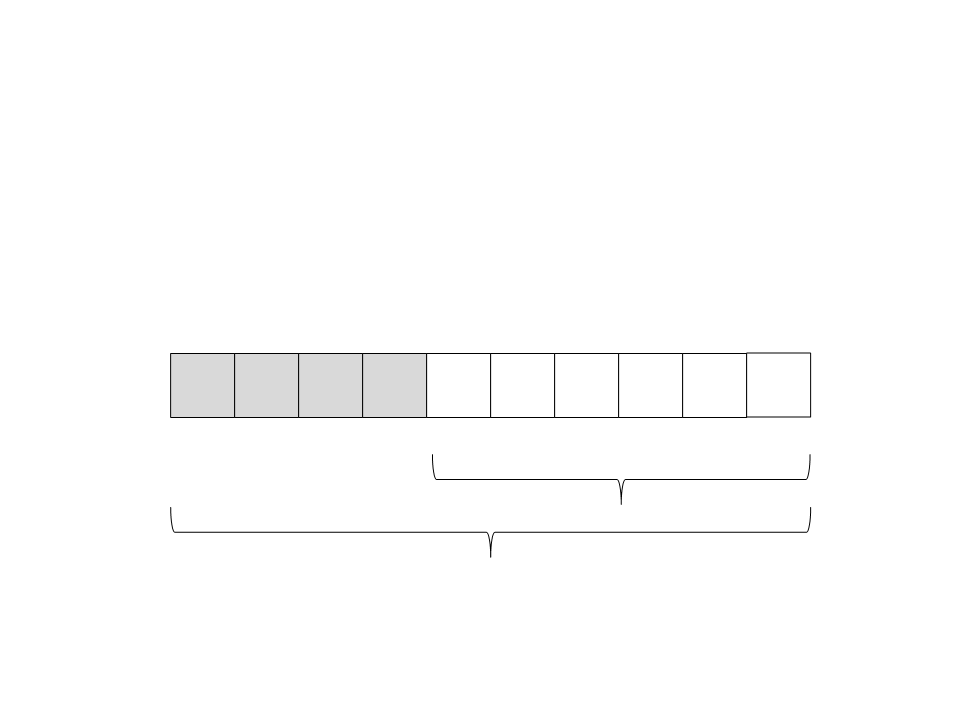
Quick Sort
(14) Chame recursivamente o quick sort para o subvetor da
direita:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
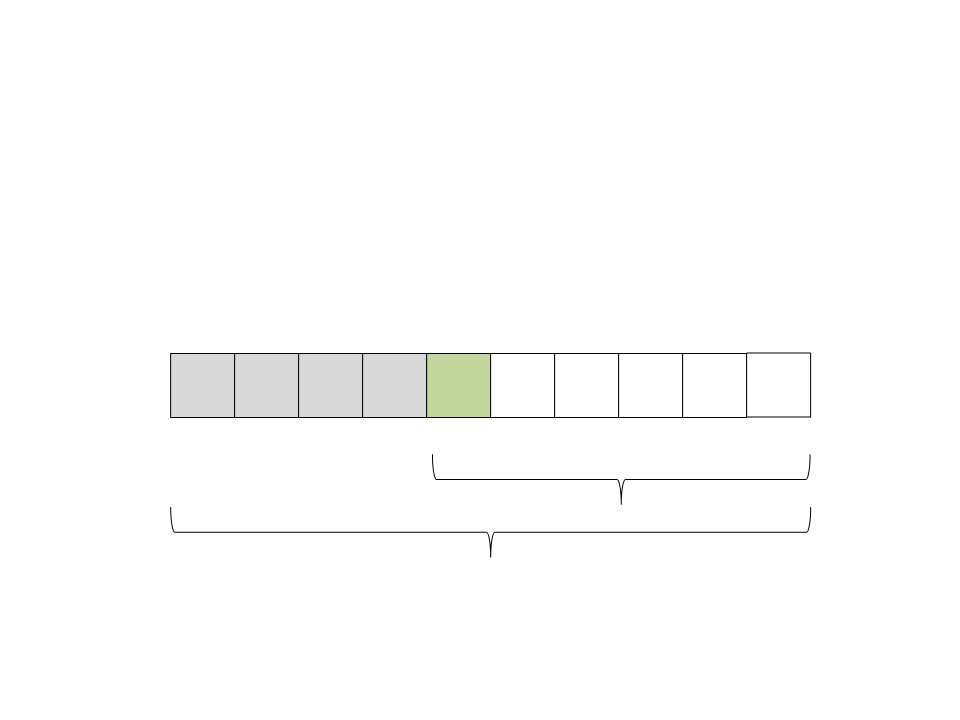
Quick Sort
(15) Selecione o pivô:
1
1
2
3
5
9
4
6
5
3
[
0] [1]
[2] [3] [4]
[5]
[6] [7] [8]
[9]
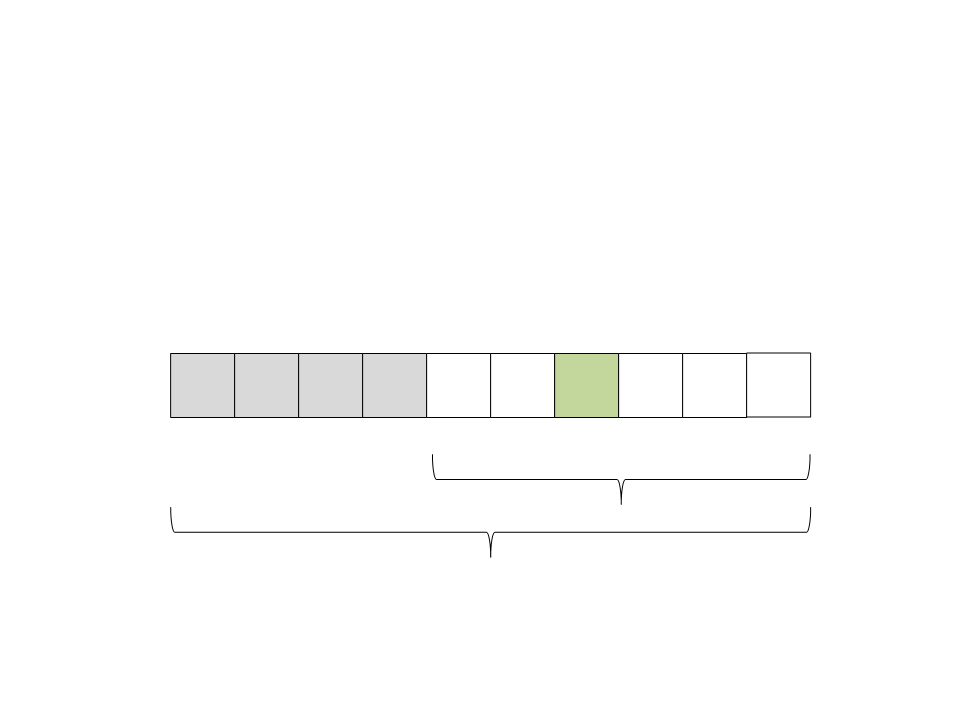
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
16) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
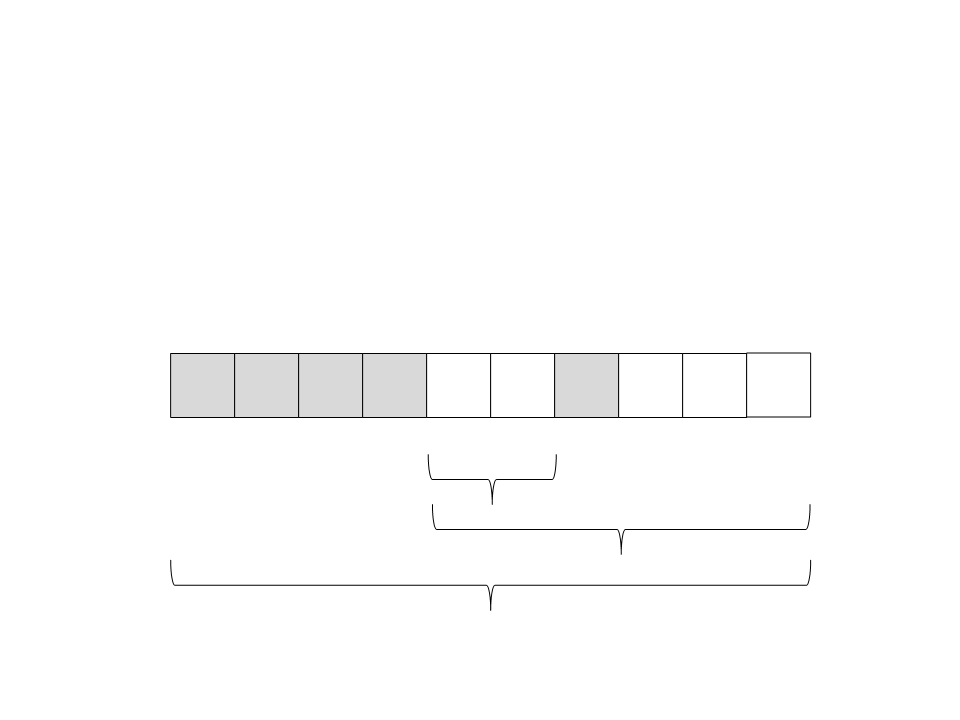
Quick Sort
(17) Chame recursivamente o quick sort para o subvetor da
esquerda:
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
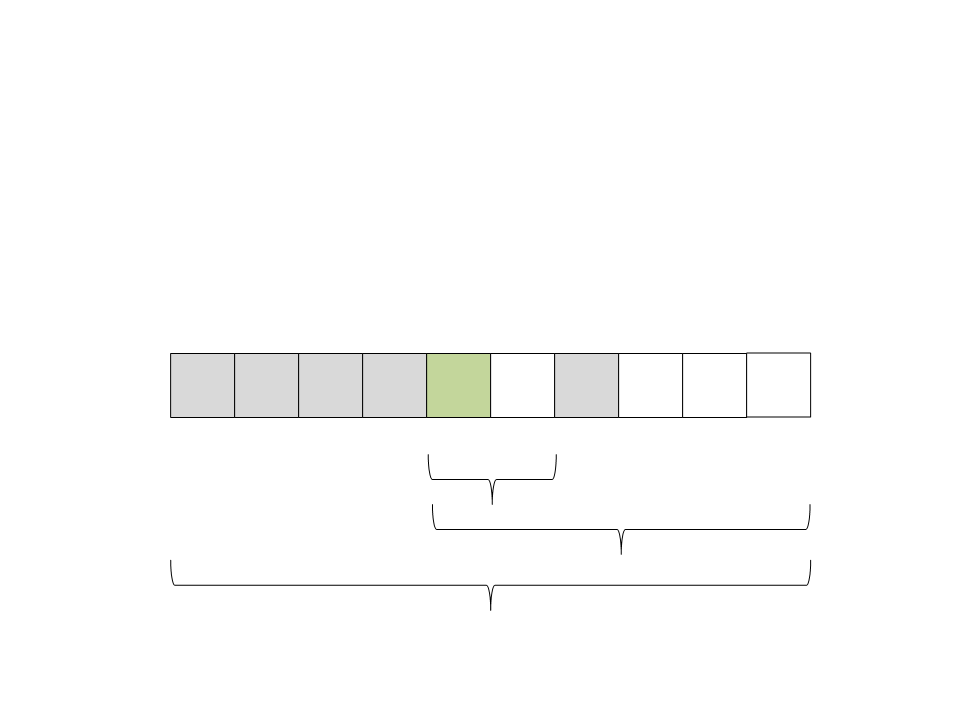
Quick Sort
(18) Selecione o pivô:
1
1
2
3
3
4
5
6
5
9
[
0]
[1] [2] [3]
[4]
[5]
[6]
[7] [8]
[9]
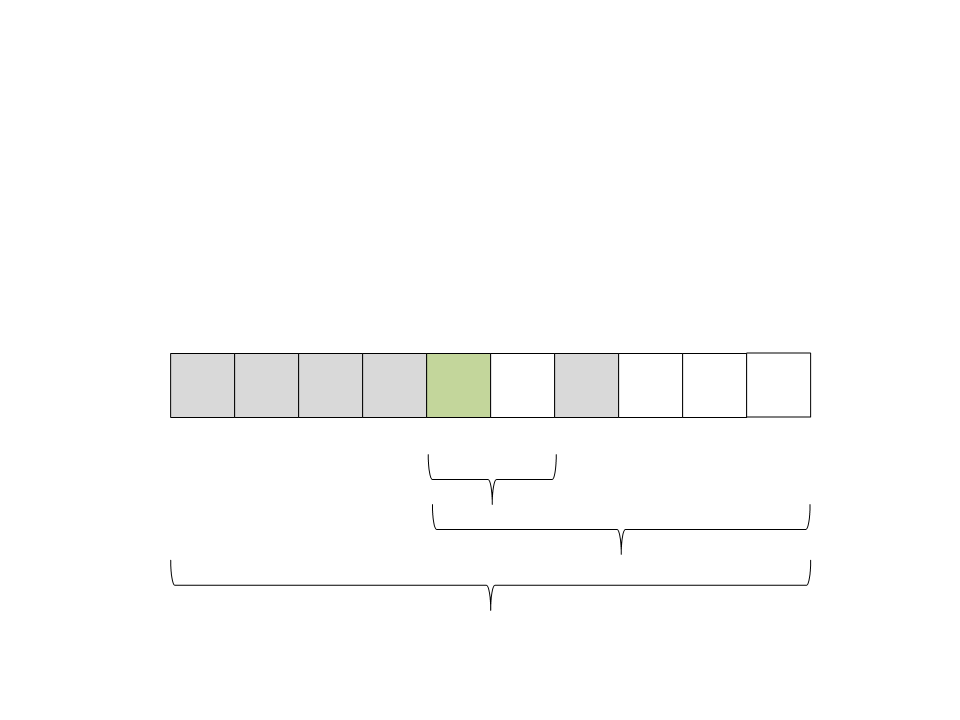
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
19) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4] [5] [6]
[7] [8]
[9]
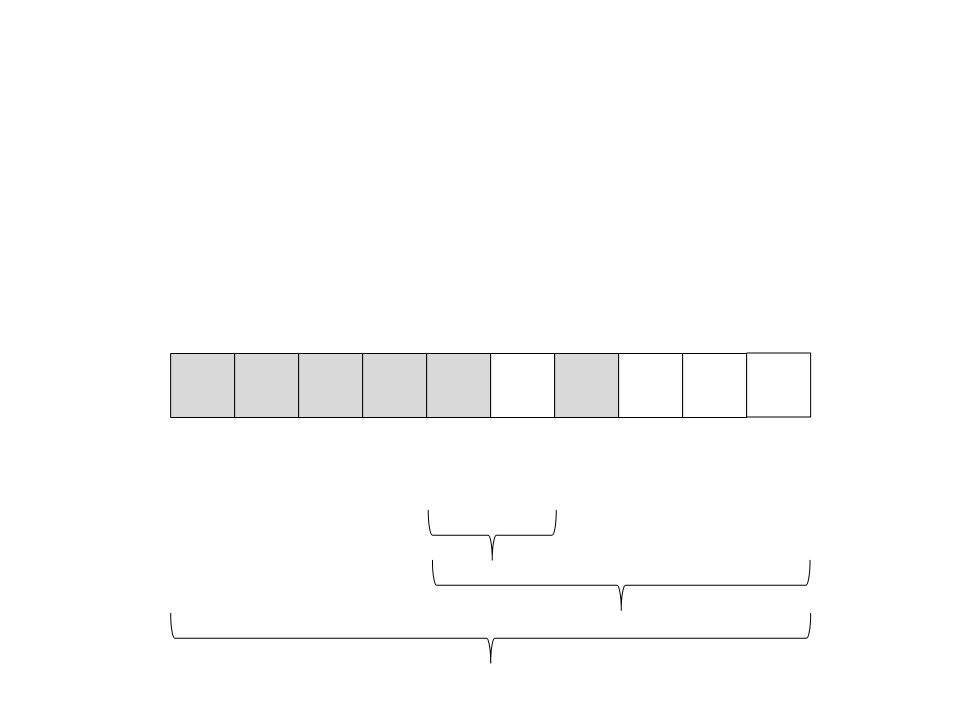
Quick Sort
(
esquerda. O tamanho do vetor da esquerda é zero. A recursão
retorna.
20) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
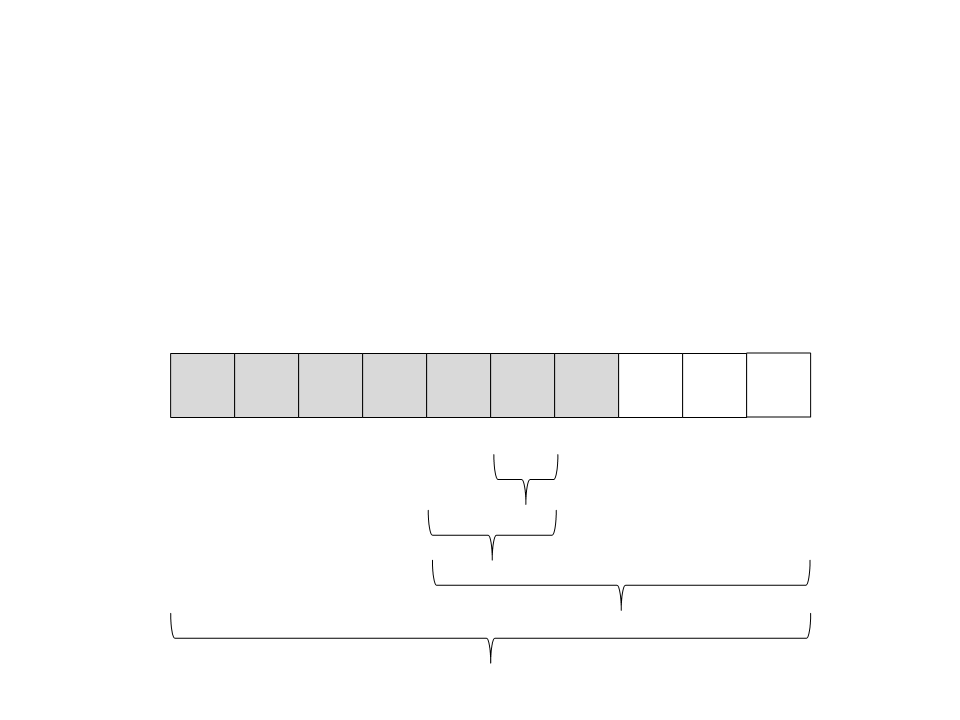
Quick Sort
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna.
21) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
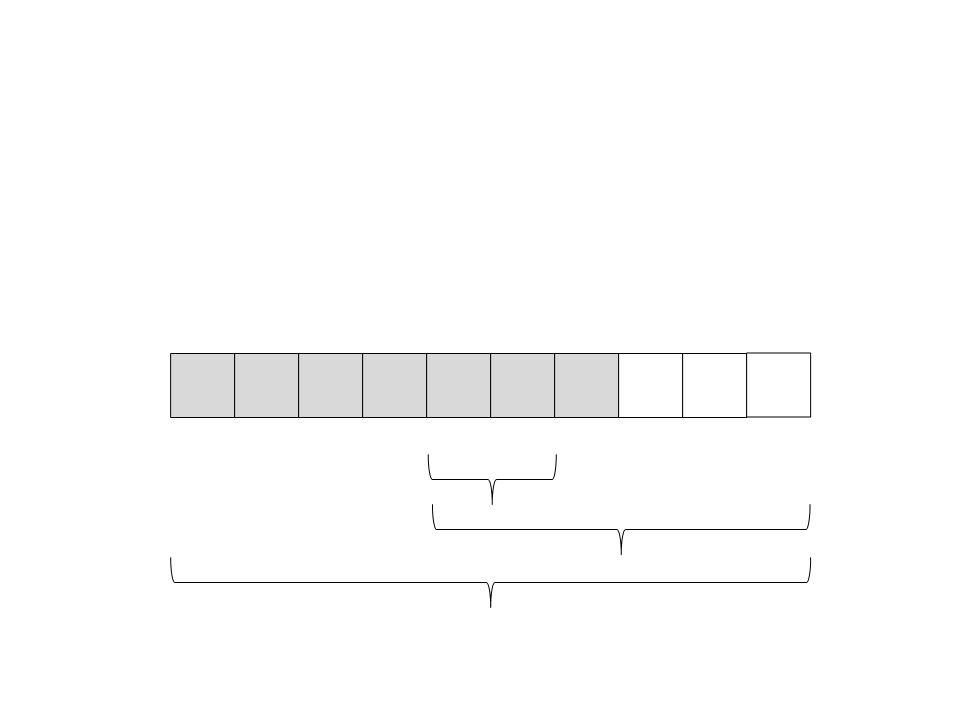
Quick Sort
(22) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
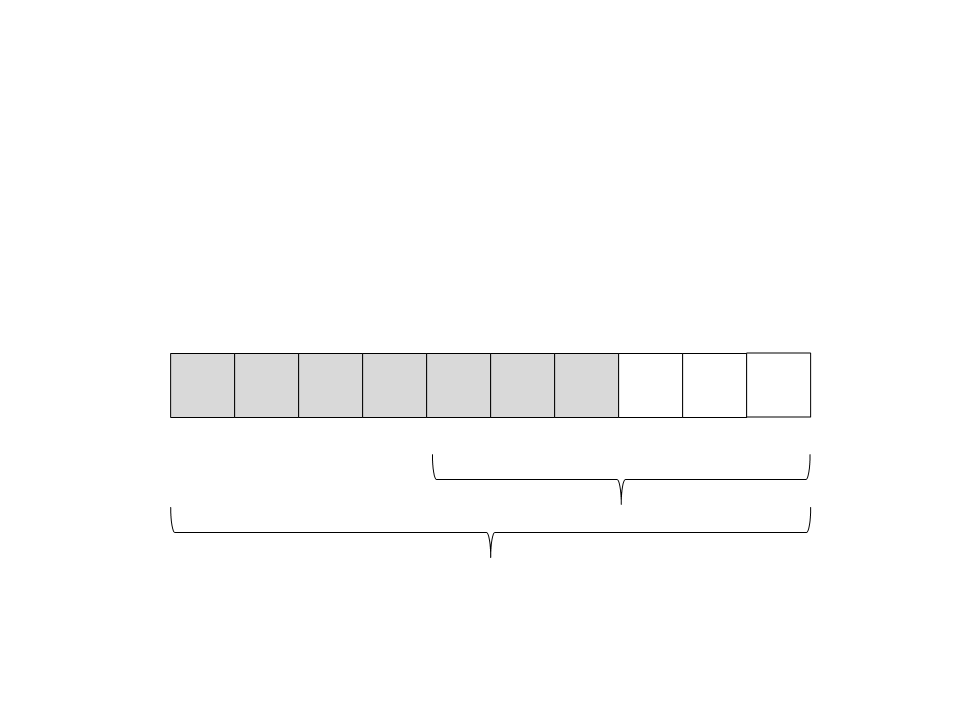
(23) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
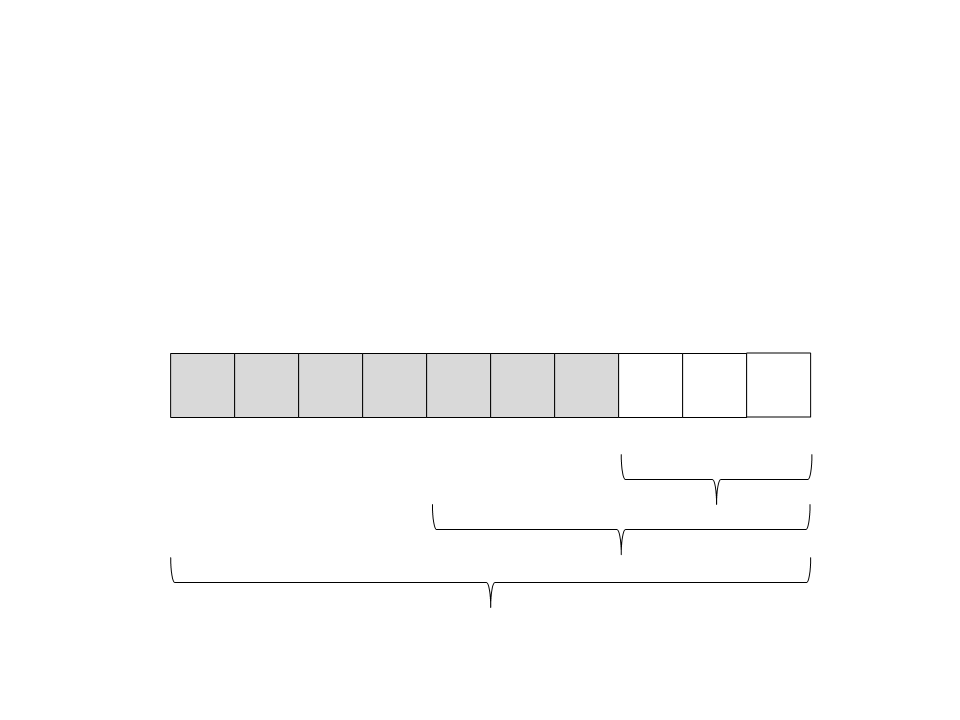
Quick Sort
(24) Chame recursivamente o quick sort para o subvetor da
direita:
1
1
2
3
3
4
5
6
5
9
[
0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
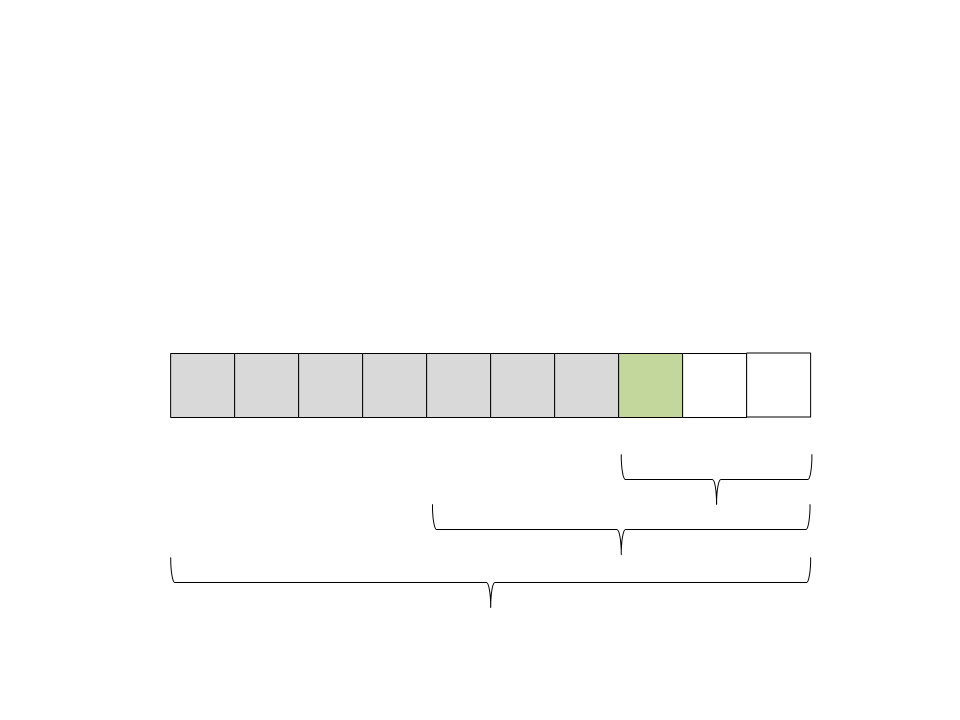
Quick Sort
(25) Selecione o pivô:
1
1
2
3
3
4
5
6
5
9
[
0] [1] [2] [3]
[4]
[5]
[6]
[7] [8]
[9]
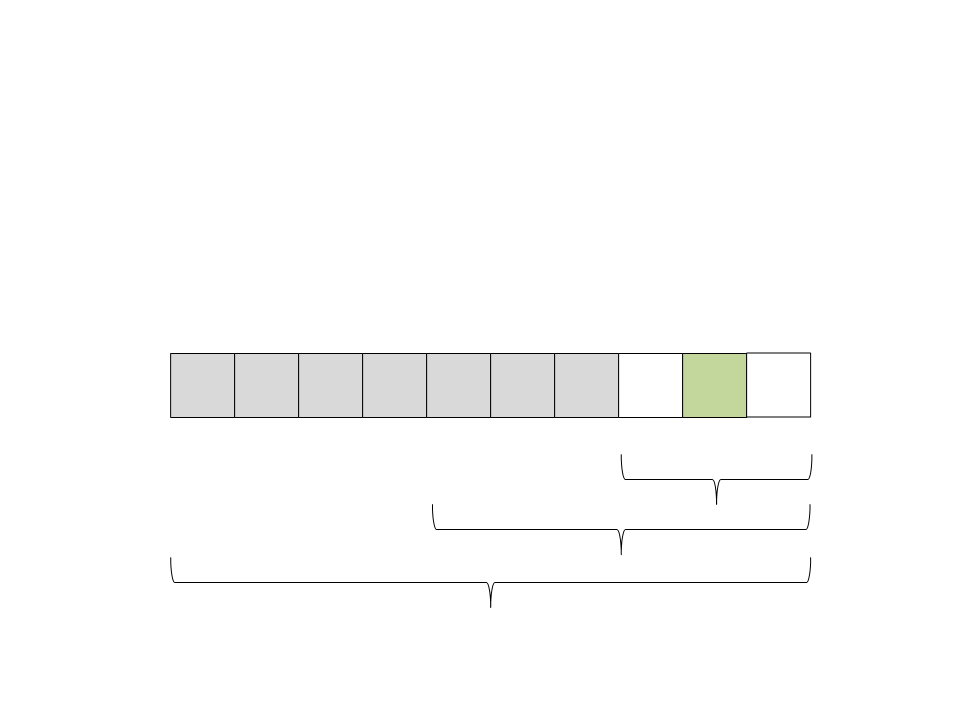
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
26) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
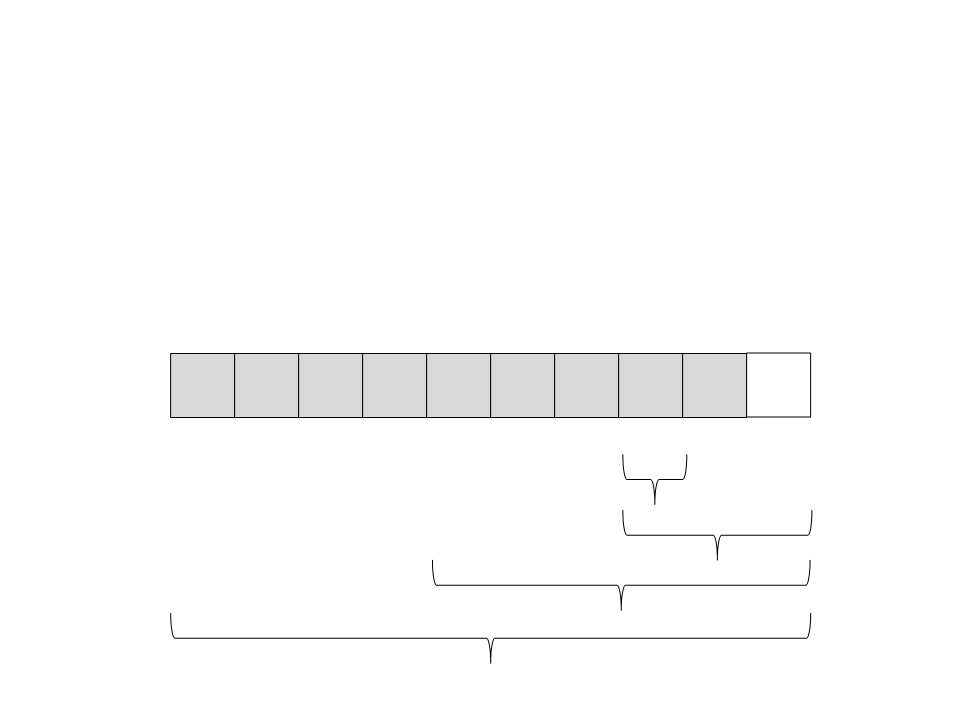
Quick Sort
(
esquerda. Só existe um elemento, então ele já está ordenado e a
recursão retorna:
27) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
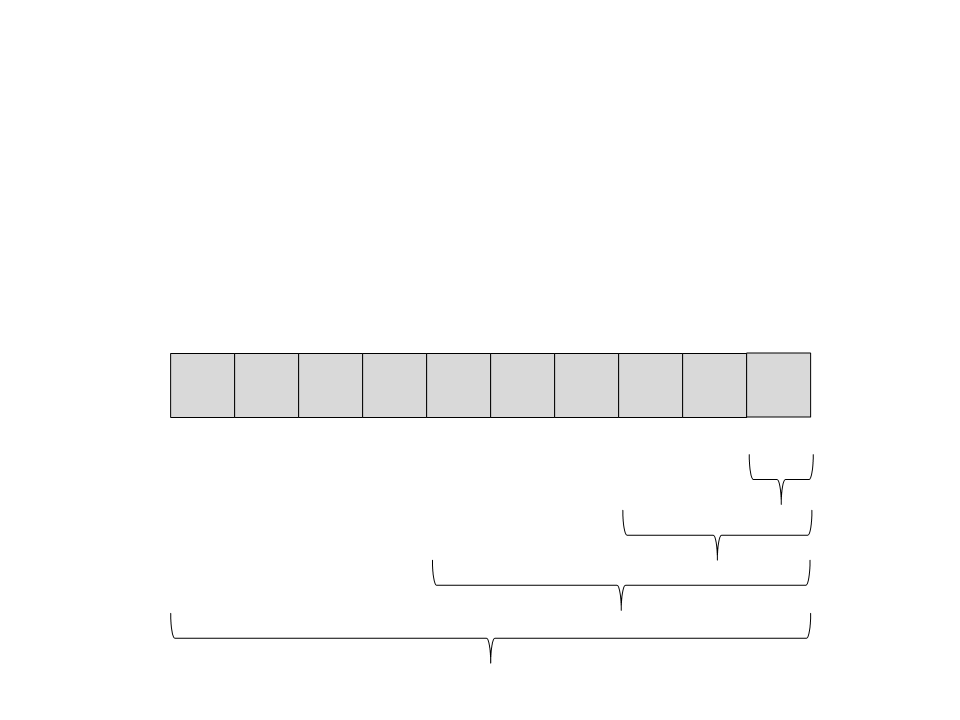
Quick Sort
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna:
28) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
5
6
9
[
0] [1] [2] [3]
[4] [5] [6]
[7] [8] [9]
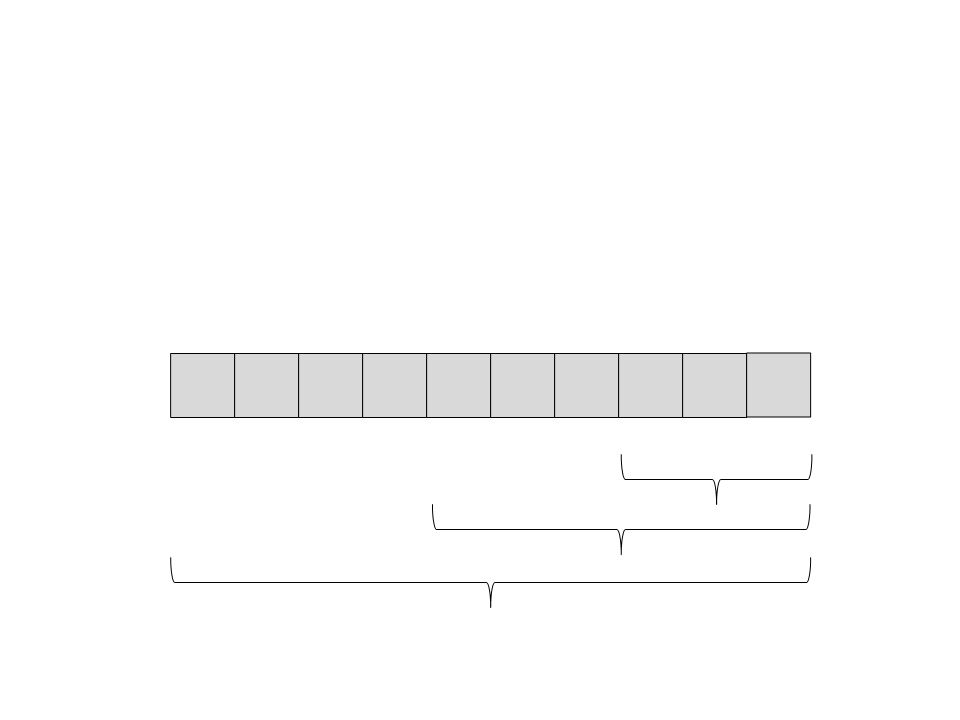
Quick Sort
(29) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
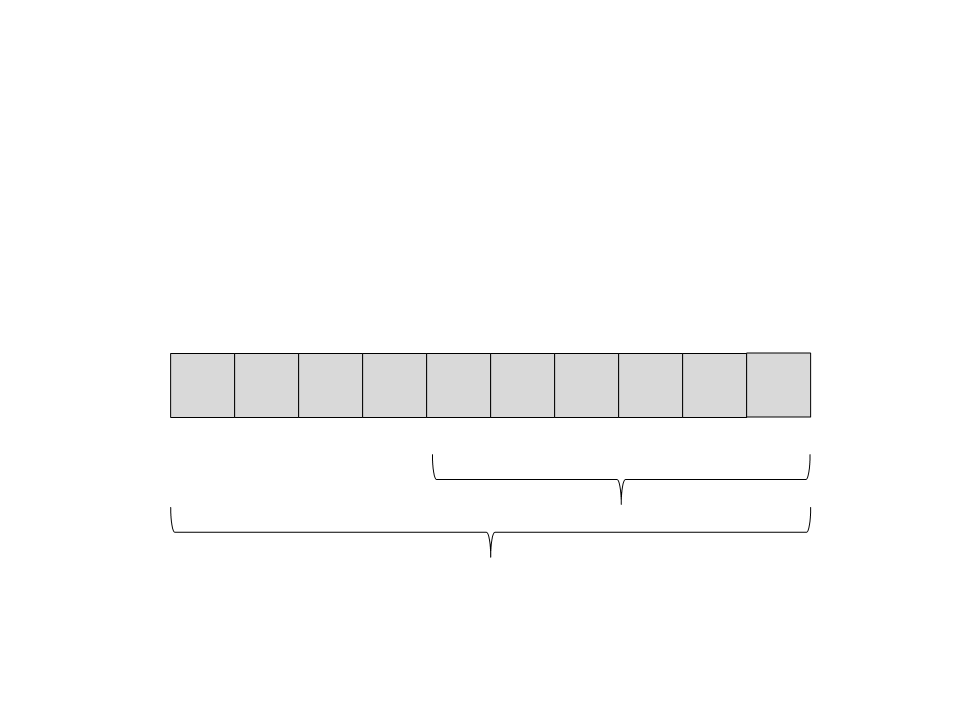
Quick Sort
(30) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
(
com o vetor completamente ordenado.
31) A recursão retorna para a primeira chamada do quick sort
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]

Quick Sort - Complexidade
•
Melhor caso:
–
pivô representa o valor mediano do conjunto dos elementos do vetor;
–
após mover o pivô para sua posição, restarão dois sub-vetores para
serem ordenados, ambos com o número de elementos reduzido à
metade, em relação ao vetor original;
–
complexidade: O(n log(n))
•
•
Pior caso:
–
pivô é o maior elemento e algoritmo recai em ordenação bolha;
Caso médio:
–
Complexidade: O(n log(n))

Quick Sort da stdlib.h
void qsort(void * v, int n, int tam,
int (*cmp)(const void *, const void *));
•
Parâmetros:
–
–
–
–
v: vetor de ponteiros genéricos
n: número de elementos do vetor
tam: tamanho em bytes de cada elemento (use sizeof para especificar)
cmp: ponteiro para a função que compara elementos genéricos. Ela deve
retornar < 0 se a < b, >0 se a > b e 0 se a == b:
int nome(const void * a, const void * b);
Quick Sort da stdlib.h
void qsort(void * v, int n, int tam,
int (*cmp)(const void *, const void *));
const é para garantir que
a função não modificará
os valores dos elementos
•
Exemplo de função de comparação:
static int compFloat(const void * a, const void * b)
{
float * aa = (float *)a; /* converte os ponteiros genericos */
float * bb = (float *)b;
if (*aa > *bb)
return 1;
else if (*aa < *bb)
return -1;
else
return 0;
}

Quick Sort da stdlib.h
void qsort(void * v, int n, int tam,
int (*cmp)(const void *, const void *));
•
Exemplo de chamada:
int main (void)
{
int i;
float v[8] = {25.6,48.3,37.7,12.1,57.4,86.6,33.3,92.8};
qsort(v, 8, sizeof(float), compFloat);
for (i=0; i<8; i++)
printf("%f \n", v[i]);
return 0;
}

qsort – Exemplo 2
struct aluno
{
int matricula;
char nome[41];
};
typedef struct aluno Aluno;
static int compPStructStr(const void * a, const void * b)
{
Aluno **aa = (Aluno **)a;
Aluno **bb = (Aluno **)b;
return strcmp((*aa)->nome, (*bb)->nome);
}
int main (void)
{
Aluno *alunos[6];
Aluno **p;
int i;
alunos[0] = (Aluno*)malloc(sizeof(Aluno));
alunos[0]->matricula = 82135123;
strcpy(alunos[0]->nome, "Julia");

alunos[1] = (Aluno*)malloc(sizeof(Aluno));
alunos[1]->matricula = 51364125;
strcpy(alunos[1]->nome, "Joao");
alunos[2] = (Aluno*)malloc(sizeof(Aluno));
alunos[2]->matricula = 62151578;
strcpy(alunos[2]->nome, "Bruno");
alunos[3] = (Aluno*)malloc(sizeof(Aluno));
alunos[3]->matricula = 35641215;
strcpy(alunos[3]->nome, "Pedro");
alunos[4] = (Aluno*)malloc(sizeof(Aluno));
alunos[4]->matricula = 45612681;
strcpy(alunos[4]->nome, "Maria");
alunos[5] = (Aluno*)malloc(sizeof(Aluno));
alunos[5]->matricula = 2654951;
strcpy(alunos[5]->nome, "Ana");
qsort(alunos, 6, sizeof(Aluno*), compPStructStr);
for (i = 0; i < 6; i++)
printf("%s - %d \n", alunos[i]->nome, alunos[i]->matricula);
return 0;
}

Leitura Complementar
•
Waldemar Celes, Renato Cerqueira, José Lucas
Rangel, Introdução a Estruturas de Dados, Editora
Campus (2004).
•
Capítulo 16 – Ordenação

Exercícios
Lista de Exercícios 08 – Ordenação
http://www.inf.puc-rio.br/~elima/prog2/
