
INF 1007 – Programação II
Aula 09 – Busca em Vetor
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Busca em Vetor
•
Problema:
–
–
Entrada:
•
vetor v com n elementos;
•
elemento d a procurar;
Saída:
•
m se o elemento procurado está em v[m];
•
-1 se o elemento procurado não está no vetor;
•
Tipos de Busca em Vetor:
–
Linear (ou sequencial);
–
Binária;

Busca Linear em Vetor
•
Algoritmo: Percorra o vetor vet, elemento a elemento,
verificando se elemé igual a um dos elementos de vet:
int busca(int n, int *vet, int elem)
{
int i;
for (i=0; i<n; i++)
{
if (elem == vet[i])
return i; /* encontrou */
}
/* não encontrou */
return -1;
}

Análise da Busca Linear em Vetor
•
Pior Caso: o elemento não está no vetor
–
Neste caso são necessárias n comparações
–
T(n) = n → O(n) - Linear!
•
•
Melhor Caso: o elemento é o primeiro
–
T(n) = O(1)
Complexidade de algoritmos:
Na análise de complexidade,
analisamos o “Pior Caso”, o
Caso Médio:
–
n/2 comparações
“Melhor Caso” e o “Caso Médio”
–
T(n) = n/2 → O(n) - Linear!

Busca Linear em Vetor Ordenado
•
E se o vetor estiver ordenado? Como ficaria o algoritmo?
int busca_ord(int n, int *vet, int elem)
{
int i;
for (i=0; i<n; i++)
{
if (elem == vet[i])
return i; /* encontrou */
else if (elem < vet[i])
return -1;/* interrompe busca */
}
/* não encontrou */
return -1;
}

Busca Linear em Vetor Ordenado
•
•
Qual a complexidade do algoritmo de busca linear em vetor
ordenado?
Melhor Caso:
Um algoritmo pode ter a mesma
–
T(n) = O(1)
complexidade de um outro, porém
pode ser mais, ou menos, eficiente.
Eficiência e Complexidade são coisas
diferentes!
•
Pior Caso:
–
T(n) = n → O(n) - Linear!

Busca Binária em Vetor Ordenado
•
•
•
Entrada:
–
vetor v com n elementos ordenados;
–
elemento d a procurar;
Saída:
–
m se o elemento procurado está em v[m];
–
-1 se o elemento procurado não está no vetor;
Procedimento:
–
–
–
–
–
Compare o elemento d com o elemento do meio de v;
Se o elemento d for menor, pesquise a primeira metade do vetor;
Se o elemento d for maior, pesquise a segunda parte do vetor;
Se o elemento d for igual, retorne a posição
Continue o procedimento subdividindo a parte de interesse até
encontrar o elemento d ou chegar ao fim;

int busca_bin(int n, int *vet, int elem)
{
/* no início consideramos todo o vetor */
int ini = 0;
int fim = n-1;
int meio;
/* enquanto a parte restante for maior que zero */
while(ini <= fim)
{
meio = (ini + fim) / 2;
if (elem < vet[meio])
fim = meio – 1; /* ajusta posição final */
else if (elem > vet[meio])
ini = meio + 1; /* ajusta posição inicial */
else
return meio; /* elemento encontrado */
}
return -1; /* não encontrou: restou tamanho zero */
}

Versão com Função para Comparação
int busca_bin(int n, int *vet, int elem)
{
int ini = 0;
int fim = n-1;
int comp_int(int a, int b)
int meio, cmp;
{
while(ini <= fim)
if (a < b)
{
return -1;
meio = (ini + fim) / 2;
else if (a > b)
cmp = comp_int(elem, vet[meio]);
return 1;
if (cmp < 0)
else
fim = meio - 1;
return 0;
else if (cmp > 0)
}
ini = meio + 1;
else
return meio;
}
return -1;
}
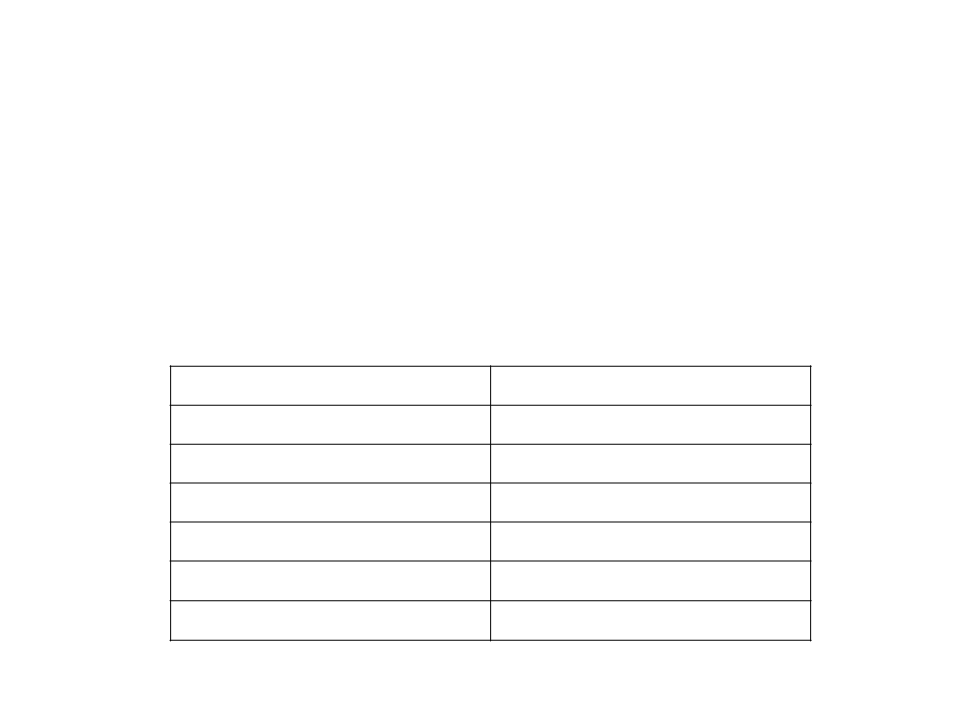
Busca Binária em Vetor Ordenado
•
Pior caso: elemento não está no vetor
–
–
–
2 comparações são realizadas a cada ciclo;
a cada repetição, a parte considerada na busca é dividida na metade;
T(n) = O(log n)
Repetição
Tamanho do Problema
1
2
n
n/2
n/4
n/8
…
3
4
…
log n
1

Analise de Algoritmos – Tipos de Crescimentos

Diferença entre O(n) e O(log n)
Tamanho
O(n)
10 seg
1 min
O(log n)
3 seg
10
0
6
6 seg
6
00
600
6 400
592 000
46 080 000
4 608 000 000
10 min
1 hora
1 dia
9 seg
3
12 seg
16 seg
21 seg
30 seg
36 seg
8
2
1 mês
1 ano
9
9
100 anos

Complexidade de Algoritmos
•
•
Em geral:
–
–
–
Uma única operação (ou comando) tem um tempo de execução de O(1);
Um loop que é repetido n vezes tem O(n);
Dois laços aninhados (nested loops) indo de 1 a n tem O(n2);
Se um algoritmo tem vários passos de complexidades
diferentes, a complexidade geral do algoritmo é dado pela
complexidade máxima:
–
Por exemplo, um algoritmo com 3 passos de O(n2), O(n2) e O(n), tem
2
complexidade O(n );

Busca Binária em Vetor Ordenado
•
O que pode variar no algoritmos da busca binária?
–
–
Critério de ordenação (primário e desempates);
A informação retornada:
•
•
•
•
•
O índice do elemento encontrado ou -1;
O valor de um campo específico;
O ponteiro para o elemento encontrado;
1 se encontrou, ou 0, caso contrário;
Outras...
–
Repetição ou não de valores (chaves).
Exercício 1 – Busca String
•
Escreva um programa que permita buscar um nome em um
vetor de strings ordenado alfabeticamente.
–
A função de busca deve seguir o seguinte protótipo:
int busca_bin(int n, char vet[][20], char *elem)
–
Dica: lembre-se que a função strcmp(a,b)já faz o trabalho de
retornar:
•
•
•
-1 se a < b;
+1 se a > b;
0 se a == b;

Exercício 1 - Solução
int busca_bin(int n, char vet[][20], char *elem)
{
int ini = 0;
int fim = n-1;
int meio, cmp;
while(ini <= fim)
{
meio = (ini + fim) / 2;
cmp = strcmp(elem, vet[meio]);
if (cmp < 0)
fim = meio - 1;
else if (cmp > 0)
ini = meio + 1;
else
return meio;
}
return -1;
}

Exercício 1 - Solução
int main (void)
{
char nomes[][20] = {{"Ana"},{"Joao"},{"Maria"},
{"Pedro"},{"Silvio"}};
char elem[] = "Silvio";
int res = busca_bin(5, nomes, elem);
printf("%d\n", res);
return 0;
}

Exercício 2 – Busca Estrutura
•
Escreva um programa que crie um vetor de ponteiros para a
estrutura Aluno (ordenado crescentemente por nome e
matricula) e permita realizar buscas por nomes nesse vetor.
struct aluno
{
char *nome;
int matricula;
};
typedef struct aluno Aluno;
–
A função de busca binária deve receber como parâmetros o número
de alunos, o vetor e o nome do aluno que se deseja buscar, e deve ter
como valor de retorno um ponteiro para o registro do aluno
procurado. Se não houver um aluno com o nome procurado, a função
deve retornar NULL.

Exercício 2 - Solução
Aluno* busca_bin(int n, Aluno *vet, char *elem)
{
int ini = 0;
int fim = n-1;
int meio, cmp;
while(ini <= fim)
{
meio = (ini + fim) / 2;
cmp = strcmp(elem, vet[meio].nome);
if (cmp < 0)
fim = meio - 1;
else if (cmp > 0)
ini = meio + 1;
else
return &vet[meio];
}
return NULL;
}

Exercício 2 - Solução
int main (void)
{
Aluno alunos[] = {{"Ana", 1},{"Joao", 2},{"Maria", 3},
{"Pedro", 4},{"Silvio", 5}};
char elem[] = "Silvio";
Aluno *res = busca_bin(5, alunos, elem);
printf("Nome: %s\nMatricula: %d \n", res->nome, res->matricula);
return 0;
}

Exercício 3 – Busca Critério de Ordenação
•
Considere a seguinte estrutura representando um registro de
um calendário de provas:
struct prova
{
char *disciplina;
Data dt_prova;
Data dt_seg_chamada;
};
typedef struct prova Prova;
struct data
{
int dia, mes, ano;
};
typedef struct data Data;

Exercício 3 – Busca Critério de Ordenação
•
Escreva uma função que faça uma busca binária em um vetor de
ponteiros para o tipo Prova, cujos elementos estão em ordem
cronológica, de acordo com a data da prova (dt_prova), com
desempate pela ordem alfabética de acordo com o nome da
disciplina.
–
–
–
Se existir mais de uma prova na data procurada, a função deve
retornar o índice da primeira delas;
Se não houver uma prova com a data procurada, a função deve
retornar -1;
Sua função deve ter o seguinte cabeçalho:
int busca(Prova **v, int n, Data d);

Exercício 3 - Solução
int datacmp(Data d1, Data d2)
{
if(d1.ano<d2.ano)
return -1;
if(d1.ano>d2.ano)
return 1;
if(d1.mes<d2.mes)
return -1;
if(d1.mes>d2.mes)
return 1;
if(d1.dia<d2.dia)
return -1;
if(d1.dia>d2.dia)
return 1;
return 0;
}

int busca_bin(Prova **v, int n, Data d)
{
int ini = 0;
int fim = n-1;
int meio, cmp;
while(ini <= fim)
{
meio = (ini + fim) / 2;
cmp = datacmp(d, v[meio]->dt_prova);
if (cmp == -1)
fim = meio - 1;
else if (cmp == 1)
ini = meio + 1;
else
{
while((meio > 0) && (datacmp(d, v[meio-1]->dt_prova)==0))
meio--;
return meio;
}
}
return -1;
}

Binary Search da stdlib.h
void * bsearch(void * info, void * v, int n, int tam,
int (*cmp)(const void *, const void *));
•
Parâmetros:
–
–
–
–
–
info: ponteiro para a informação que se deseja buscar;
v: vetor de ponteiros genéricos (ordenado);
n: número de elementos do vetor;
tam: tamanho em bytes de cada elemento (use sizeof para especificar);
cmp: ponteiro para função que compara elementos genéricos, sendo o
primeiro o endereço da informação e o segundo é o ponteiro para um dos
elementos do vetor. O critério de comparação deve ser o mesmo da
ordenação de v. A função deve retornar <0 se a<b, >0 se a>b e 0 se a == b;
Binary Search da stdlib.h
void * bsearch(void * info, void * v, int n, int tam,
int (*cmp)(const void *, const void *));
const é para garantir que
a função não modificará
os valores dos elementos
•
Exemplo de função de comparação:
static int compInt(const void * a, const void * b)
{
int * info = (int *)a; // converte o ponteiro genérico
int * bb = (int *)b; // converte o ponteiro genérico
if (*info < *bb)
return -1;
// faz as comparações
else if (*info > *bb)
return 1;
else
return 0;
}

Binary Search da stdlib.h
void * bsearch(void * info, void * v, int n, int tam,
int (*cmp)(const void *, const void *));
•
Exemplo de chamada:
int d = 23;
int *p;
p = (int *)bsearch(&d,v,N,sizeof(int),compInt); // N é o tamanho de v
i = p - v; // indice do elemento encontrado

static int compInt(const void * a, const void * b)
{
int * info = (int *)a;
int * bb = (int *)b;
if (*info < *bb)
return -1;
else if (*info > *bb)
return 1;
else
return 0;
}
int main (void)
{
int vet[6], elem = 16, *p;
vet[0] = 8;
vet[1] = 16;
vet[2] = 22;
vet[3] = 24;
vet[4] = 25;
vet[5] = 32;
p = (int *)bsearch(&elem, vet, 6, sizeof(int), compInt);
if (p != NULL)
printf("Valor: %d \nIndice: %d\n", *p, p - vet);
return 0;
}

struct aBlusnoearch – Exemplo 2
{
int matricula;
char nome[41];
};
typedef struct aluno Aluno;
static int compPStructStr(const void * a, const void * b)
{
char *info = (char *)a;
Aluno **bb = (Aluno **)b;
return strcmp(info, (*bb)->nome);
}
int main (void)
{
Aluno *alunos[6];
Aluno **p;
char elem[] = "Maria";
alunos[0] = (Aluno*)malloc(sizeof(Aluno));
alunos[0]->matricula = 2654951;
strcpy(alunos[0]->nome, "Ana");

alunos[1] = (Aluno*)malloc(sizeof(Aluno));
alunos[1]->matricula = 62151578;
strcpy(alunos[1]->nome, "Bruno");
alunos[2] = (Aluno*)malloc(sizeof(Aluno));
alunos[2]->matricula = 51364125;
strcpy(alunos[2]->nome, "Joao");
alunos[3] = (Aluno*)malloc(sizeof(Aluno));
alunos[3]->matricula = 82135123;
strcpy(alunos[3]->nome, "Julia");
alunos[4] = (Aluno*)malloc(sizeof(Aluno));
alunos[4]->matricula = 45612681;
strcpy(alunos[4]->nome, "Maria");
alunos[5] = (Aluno*)malloc(sizeof(Aluno));
alunos[5]->matricula = 35641215;
strcpy(alunos[5]->nome, "Pedro");
p = (Aluno **) bsearch(&elem, alunos, 6, sizeof(Aluno*),
compPStructStr);
if (p != NULL)
printf("%d\n", (*p)->matricula);
return 0;
}

Leitura Complementar
•
Waldemar Celes, Renato Cerqueira, José Lucas
Rangel, Introdução a Estruturas de Dados, Editora
Campus (2004).
•
Capítulo 17 – Busca

Exercícios
Lista de Exercícios 07 – Busca
http://www.inf.puc-rio.br/~elima/prog2/
