
Projeto e Análise de Algoritmos
Aula 14 – Distâncias Mínimas
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Distâncias Mínimas
•
Dado um grafo ponderado G = (V, E), um vértice s e um vértice g,
obter o caminho mais "curto" (de peso total mínimo) de s para g.
–
O problema pode incluir origens e destinos únicos ou múltiplos.
–
Caminho mais curto pode não ser único;
•
•
O caminho mais curto entre vértices de um grafo não ponderado é
aquele que possui o menor número de arestas.
O caminho mais curto entre os vértices de um grafo ponderado é
aquele cuja soma dos pesos das arestas possui o menor valor possível
dentre todos os caminhos existentes entre os referidos vértices.
–
Em grafos ponderados, o menor caminho pode não ser aquele com menor
número de arestas.

Algoritmo de Dijkstra
•
O algoritmo de Dijkstra assemelha-se a busca em largura, mas é um
algoritmo guloso, ou seja, toma a decisão que parece ótima no
momento.
•
•
O Dijkstra expande sempre o vértice de menor custo de caminho.
–
Se o custo de todos os passos for o mesmo, o algoritmo acaba realizando o
mesmo processo que a busca em largura.
A primeira solução encontrada é a solução ótima se custo do
caminho sempre aumentar ao logo do caminho, ou seja, não
existirem operadores com custo negativo.

Algoritmo de Dijkstra
DIJKSTRA(G, w, s, e)
for each u ∈ V[G]
g[u] ← ∞;
ꢀ[u] ← NULL;
g[s] ← 0;
Q ← CREATE-HEAP(g); //heap ordenado por g[v]
INSERT(Q, s);
C ← CREATE-HASHTABLE(); //hash table de nós já visitados
while Q ≠ ∅
v ← POP-MIN(Q);
if v = e
return ꢀ;
if (not CONTAINS(C, v))
INSERT(C, v);
for each u ∈ Adj[v]
if g[u] > g[v] + w(v, u)
g[u] ← g[v] + w(v, u);
ꢀ
[u] ← v
INSERT(Q, u);
return NULL;
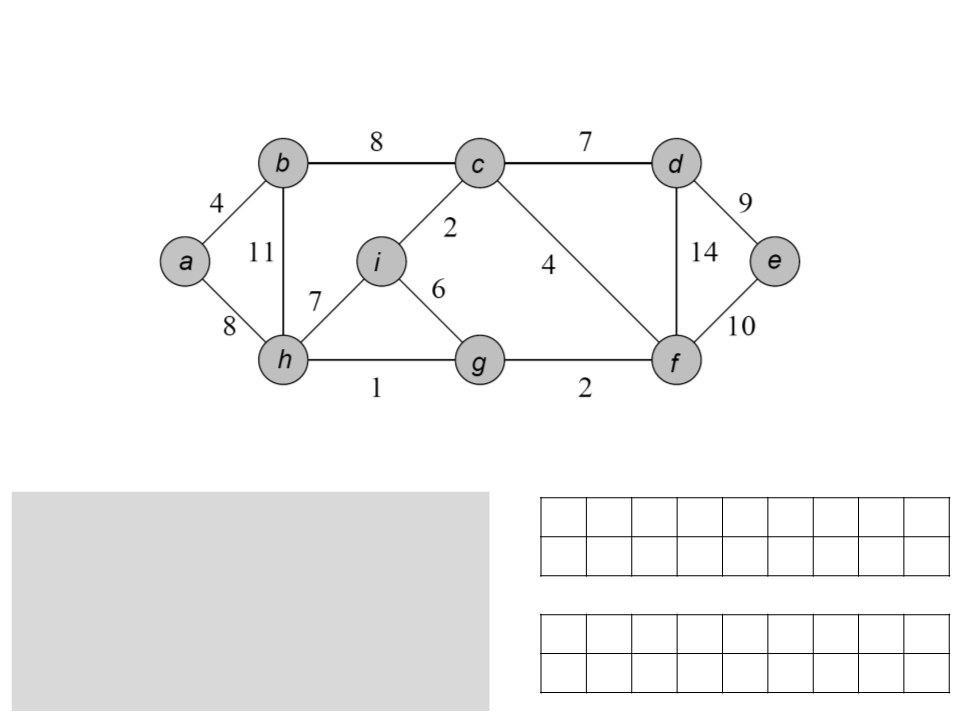
Algoritmo de Dijkstra
a b c d e f g h i
DIJKSTRA(G, w, s, e)
for each u ∈ V[G]
g[u] ← ∞;
ꢀ
g
ꢀ
[u] ← NULL;
g[s] ← 0;
Q ← CREATE-HEAP(g);
INSERT(Q, s);
C ← CREATE-HASHTABLE();
Q
C
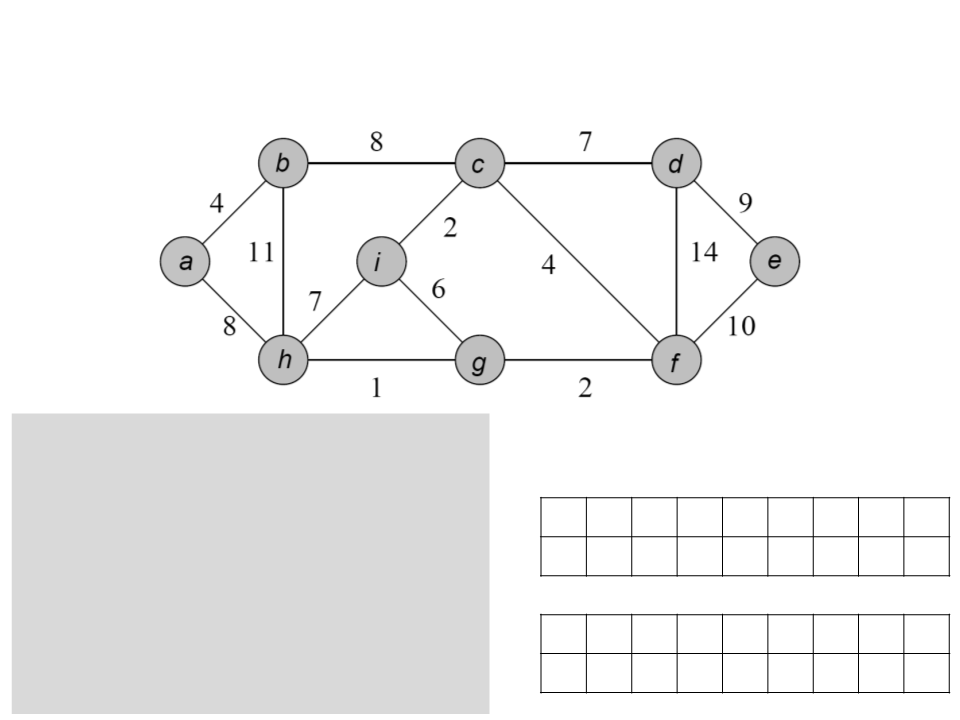
Algoritmo de Dijkstra
while Q ≠ ∅
v ← POP-MIN(Q);
if v = e
return ꢀ;
if (not CONTAINS(C, v))
INSERT(C, v);
a b c d e f g h i
ꢀ
g
for each u ∈ Adj[v]
if g[u] > g[v] + w(v, u)
g[u] ← g[v] + w(v, u);
Q
C
ꢀ
[u] ← v
INSERT(Q, u);
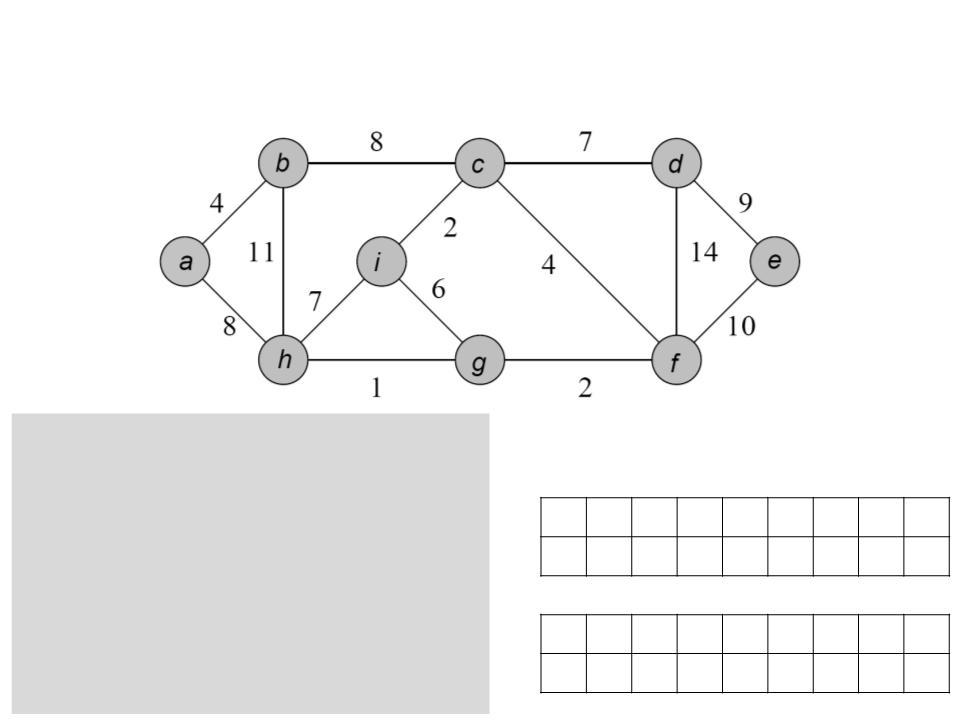
Algoritmo de Dijkstra
while Q ≠ ∅
v ← POP-MIN(Q);
if v = e
return ꢀ;
if (not CONTAINS(C, v))
INSERT(C, v);
a b c d e f g h i
/ a b c f g h a c
ꢀ
g 0 4 12 19 21 11 9 8 14
for each u ∈ Adj[v]
if g[u] > g[v] + w(v, u)
g[u] ← g[v] + w(v, u);
Q
ꢀ
[u] ← v
C a b h g f c i d e
INSERT(Q, u);

Algoritmo de Dijkstra - Análise
DIJKSTRA(G, w, s, e)
for each u ∈ V[G]
g[u] ← ∞;
• Inicializar g e ꢀ: O(V)
•
•
•
•
Criar Q e C: O(1)
ꢀ[u] ← NULL;
g[s] ← 0;
Q ← CREATE-HEAP(g);
INSERT(Q, s);
C ← CREATE-HASHTABLE();
while Q ≠ ∅
v ← POP-MIN(Q);
if v = e
Percorrer vértices em Q: O(V)
POP-MIN: O(1)
CONTAINS: O(1)
return ꢀ;
if (not CONTAINS(C, v))
INSERT(C, v);
• Percorrer vértices adjacentes:
O(A)
for each u ∈ Adj[v]
if g[u] > g[v] + w(v, u)
g[u] ← g[v] + w(v, u);
•
•
Atualizar heap Q: O(log V)
ꢀ
[u] ← v
INSERT(Q, u);
return NULL;
Complexidade:
O((V + A) log V)

Resolução de Problemas por Busca
•
Objetivo: Conjunto de estados que satisfazem o objetivo.
•
Tarefa de Busca: Encontrar a sequencia de ações que leva do
estado atual até um estado objetivo.
•
•
•
Quais são os estados?
Quais são as ações?
Nível de abstração?
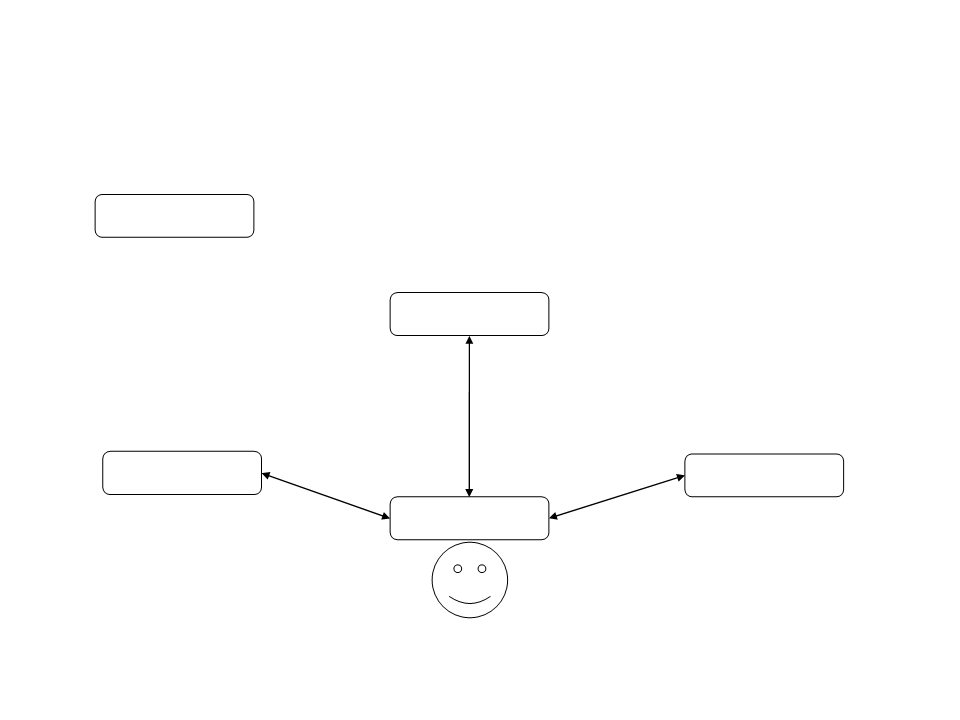
Problema de Busca
Bucharest
Timisoara
Sibiu
Zerind
Arad
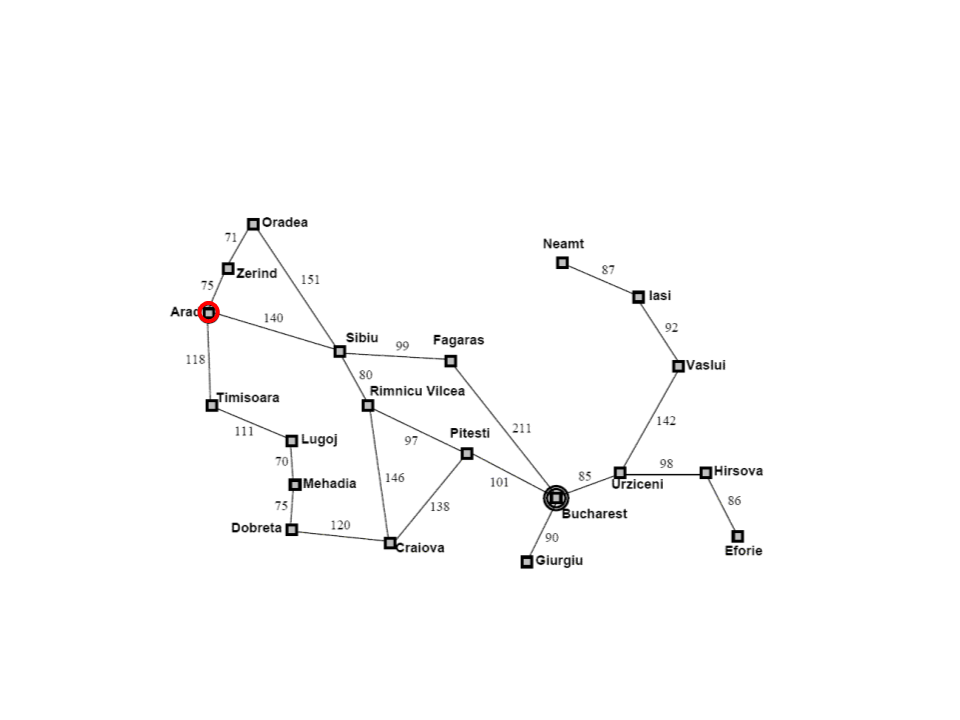
Problema de Busca

Definição de um Problema
•
•
•
•
Estado Inicial: Estado inicial do agente.
–
Ex: Em(Arad)
Estado Final: Estado buscado pelo agente.
–
Ex: Em(Bucharest)
Ações Possíveis: Conjunto de ações que o agente pode executar.
–
Ex: Ir(Cidade, PróximaCidade)
Espaço de Estados: Conjunto de estados que podem ser atingidos a partir do
estado inicial.
–
Ex: Mapa da Romênia.
•
Custo: Custo numérico de cada caminho.
–
Ex: Distância em KM entre as cidades.

Considerações em Relação ao Ambiente
•
Estático:
–
O Ambiente não pode mudar enquanto o agente está realizando a resolução
do problema.
•
•
Observável:
– O estado inicial do ambiente precisa ser conhecido previamente.
Determinístico:
–
O próximo estado do agente deve ser determinado pelo estado atual + ação. A
execução da ação não pode falhar.
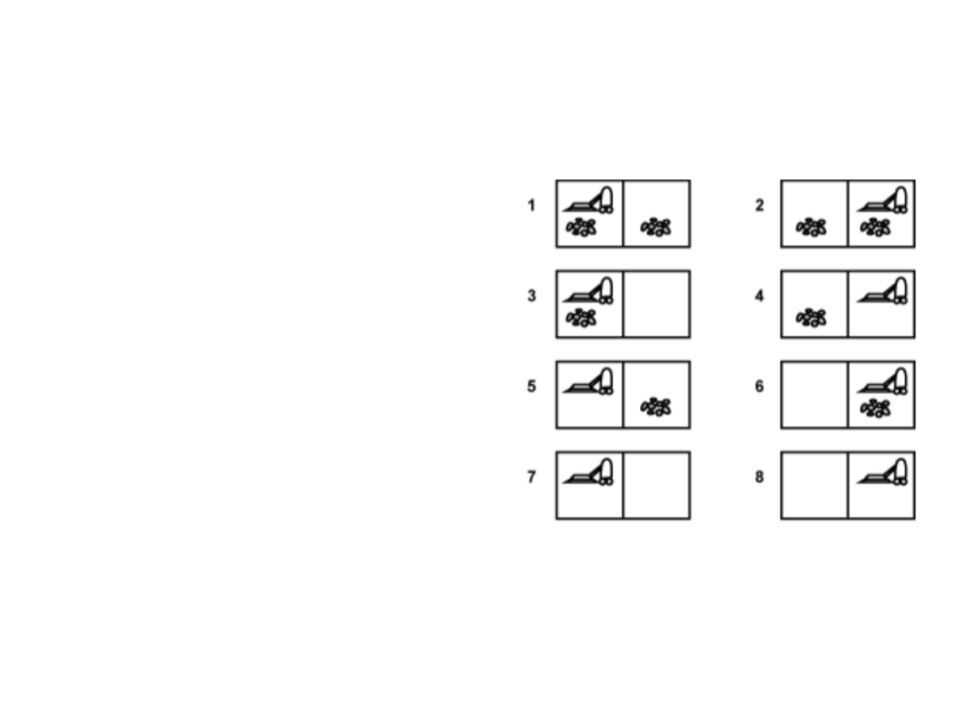
Exemplo: Aspirador de Pó
•
Espaço de Estados: 8 estados possíveis
(
figura ao lado);
•
•
Estado Inicial: Qualquer estado;
Estado Final: Estado 7 ou 8 (ambos
quadrados limpos);
•
•
Ações Possíveis: Mover para direita,
mover para esquerda e limpar;
Custo: Cada passo tem o custo 1, assim o
custo do caminho é definido pelo número
de passos;
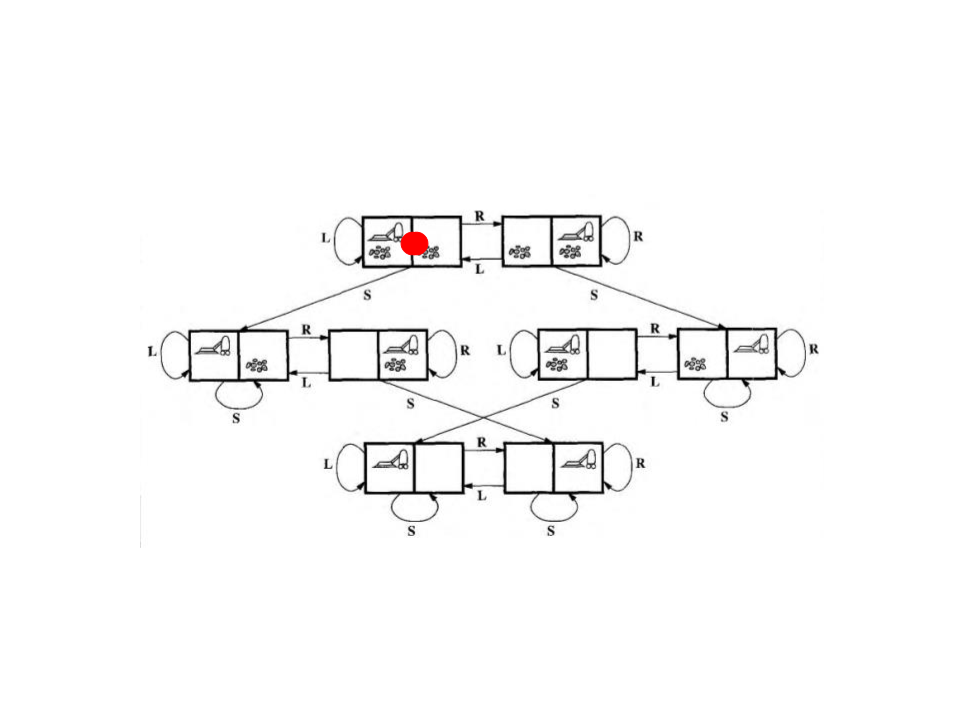
Exemplo: Aspirador de Pó

Exemplo: 8-Puzzle
•
•
•
•
Espaço de Estados: 181.440 possíveis estados;
Estado Inicial: Qualquer estado;
Estado Final: Figura ao lado – Goal State;
Ações Possíveis: Mover o quadrado vazio para
direita, para esquerda, para cima ou para baixo;
•
Custo: Cada passo tem o custo 1, assim o custo do
caminho é definido pelo número de passos;
•
•
15-puzzle (4x4) – 1.3 trilhões estados possíveis.
24-puzzle (5x5) – 10²⁵ estados possíveis.

Exemplo: Xadrez
4
0
•
•
•
Espaço de Estados: Aproximadamente 10
possíveis estados (Claude Shannon, 1950);
Estado Inicial: Posição inicial de um jogo de
xadrez;
Estado Final: Qualquer estado onde o rei
adversário está sendo atacado e o adversário
não possui movimentos válidos;
•
•
Ações Possíveis: Regras de movimentação de
cada peça do xadrez;
Custo: Quantidade de posições examinadas;

Exemplo: 8 Rainhas (Incremental)
•
Espaço de Estados: Qualquer disposição de 0
a 8 rainhas no tabuleiro (1.8 x 10¹⁴ possíveis
estados);
•
•
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8
rainhas estão no tabuleiro e nenhuma esta
sendo atacada;
•
•
Ações Possíveis: Colocar uma rainha em um
espaço vazio do tabuleiro;
Custo: Não importa nesse caso;
*
diferentes rotações e reflexões). E apenas 12 soluções únicas.
O jogo possui apenas 92 possíveis soluções (considerando

Exemplo: 8 Rainhas (Estados Completos)
•
Espaço de Estados: Tabuleiro com n rainhas,
uma por coluna, nas n colunas mais a esquerda
sem que nenhuma rainha ataque outra (2057
possíveis estados);
•
•
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8
rainhas estão no tabuleiro e nenhuma esta
sendo atacada;
•
•
Ações Possíveis: Adicionar uma rainha em
qualquer casa na coluna vazia mais à esquerda
de forma que não possa ser atacada;
Custo: Não importa nesse caso;

Aplicações em Problemas Reais
•
•
Cálculo de Rotas:
–
–
–
–
–
Planejamento de rotas de aviões;
Sistemas de planejamento de viagens;
Caixeiro viajante;
Rotas em redes de computadores;
Jogos de computadores (rotas dos personagens);
Alocação
–
Salas de aula;
–
Máquinas industriais;

Aplicações em Problemas Reais
•
•
Circuitos Eletrônicos:
–
Posicionamento de componentes;
–
Rotas de circuitos;
Robótica:
–
Navegação e busca de rotas em ambientes reais;
–
Montagem de objetos por robôs;

Métodos de Busca
•
Busca Cega ou Exaustiva:
–
Não sabe qual o melhor nó da fronteira a ser expandido. Apenas
distingue o estado objetivo dos não objetivos.
•
•
Busca Heurística:
–
Estima qual o melhor nó da fronteira a ser expandido com base em
funções heurísticas.
Busca Local:
–
Operam em um único estado e movem-se para a vizinhança deste
estado.

Busca Heurística
•
Algoritmos de Busca Heurística:
–
Busca Gulosa
–
A*
•
•
A busca heurística leva em conta o objetivo para decidir qual
caminho escolher.
Conhecimento extra sobre o problema é utilizado para guiar o
processo de busca.

Busca Heurística
•
Como encontrar um barco perdido?
–
–
Busca Cega -> Procura no oceano inteiro.
Busca Heurística -> Procura utilizando informações
relativas ao problema.
•
Exemplo: correntes marítimas, vento, etc.

Busca Heurística
•
•
Função Heurística (h)
–
Estima o custo do caminho mais barato do estado atual até
o estado final mais próximo.
–
São específicas para cada problema.
Exemplo:
–
Encontrar a rota mais curta entre duas cidades:
•
h(n) = distância em linha reta direta entre o nó n e o nó final.
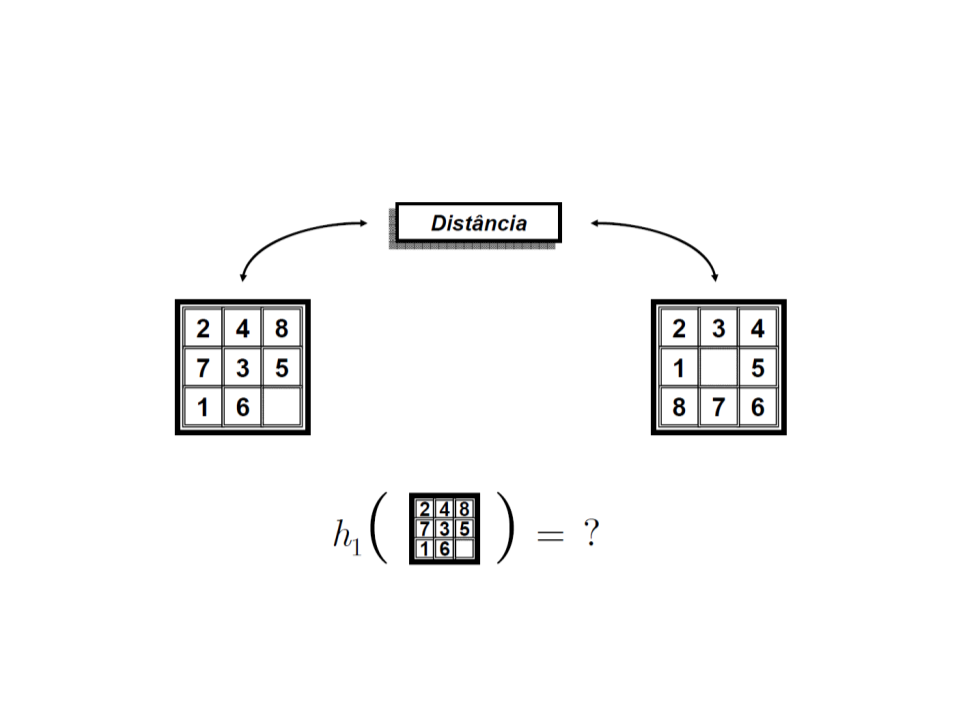
Função Heurística
Estado Atual
Estado Objetivo

Busca Heurística
•
Algoritmos de Busca Heurística:
–
–
Busca Gulosa
A*

Busca Gulosa
•
Estratégia:
–
Expande os nós que se encontram mais próximos do
objetivo (uma linha reta conectando os dois pontos no
caso de distancias), desta maneira é provável que a busca
encontre uma solução rapidamente.
•
A implementação do algoritmo se assemelha ao utilizado na
busca cega, entretanto utiliza-se uma função heurística para
decidir qual o nó deve ser expandido.
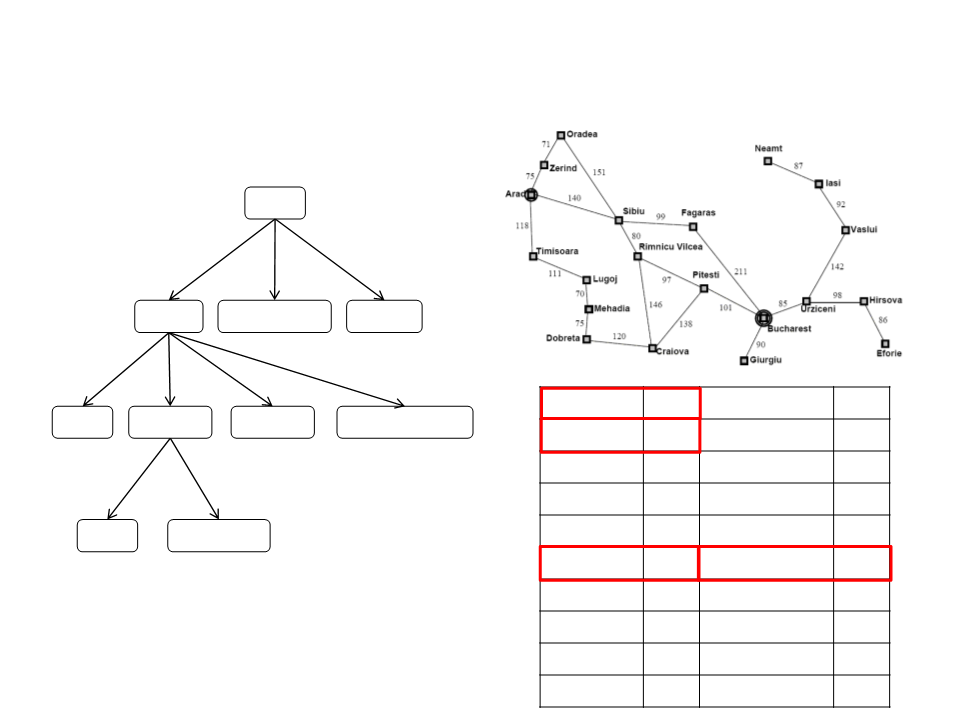
Busca Gulosa
Arad
366
Sibiu
253
Timissoara
329
Zerind
374
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Arad
66
Fagaras
176
Oradea
380
Rimnicu Vilcea
Bucharest
193
3
Craiova
Drobeta
Eforie
160
242
161
176
77
Rimnicu Vilcea 193
Sibiu
263
Bucharest
0
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
Timisoara
Vaslui
226
244
151
Função Heurística (h):
Distancia em linha reta
Lugoj
Zerind
Hirsova
Urziceni

Busca Gulosa
•
•
Custo de busca mínimo:
– No exemplo, não expande nós fora do caminho.
Não é ótima:
–
No exemplo, escolhe o caminho que é mais econômico à
primeira vista, via Fagaras.
–
Porém, existe um caminho mais curto via Rimnicu Vilcea.
•
Não é completa:
–
Pode entrar em loop se não detectar a expansão de
estados repetidos.
–
Pode tentar desenvolver um caminho infinito.
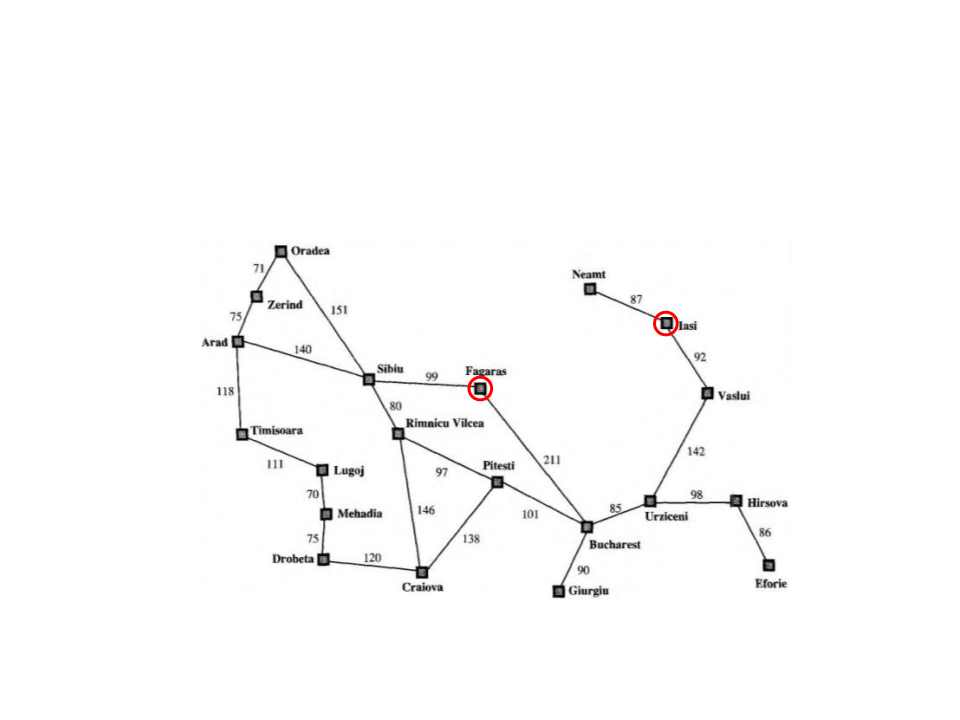
Busca Gulosa
•
Ir de Iasi para Fagaras?

Busca A*
•
Estratégia:
–
Combina o custo do caminho g(n) com o valor da
heurística h(n)
–
–
g(n) = custo do caminho do nó inicial até o nó n
h(n) = valor da heurística do nó n até um nó objetivo
(distancia em linha reta no caso de distancias espaciais)
–
f(n) = g(n) + h(n)
•
É a técnica de busca mais utilizada.
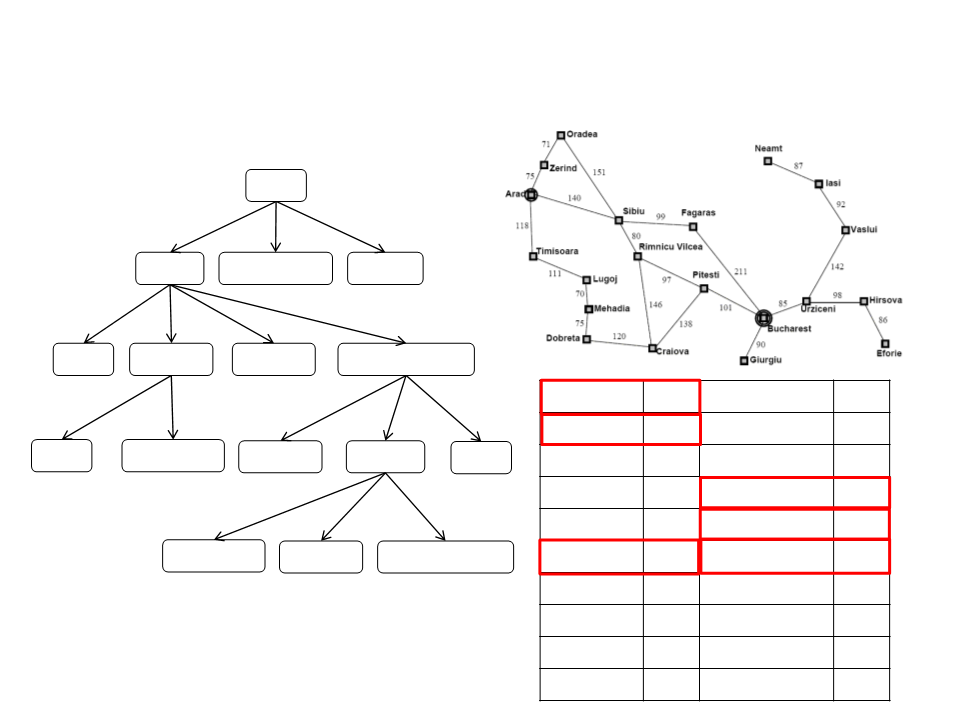
Busca A*
Arad
0+366=366
Sibiu
Timissoara
Zerind
1
40+253=393 118+329=447 75+374=449
Arad
Fagaras
Oradea
Rimnicu Vilcea
220+193=413
2
80+366=646 239+176=415 291+380=671
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
Sibiu
38+253=591
Bucharest
Craiova
Pitesti
Sibiu
160
242
161
176
77
3
450+0=450
366+160=526 317+100=417 300+253=553
Rimnicu Vilcea 193
Bucharest
418+0=418
Craiova
Rimnicu Vilcea
414+193=607
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
455+160=615
Timisoara
Vaslui
226
244
151
Lugoj
Zerind
Hirsova
Urziceni

Busca A*
•
•
A estratégia é completa e ótima.
Custo de tempo:
–
Exponencial com o comprimento da solução, porém boas funções heurísticas
diminuem significativamente esse custo.
•
•
Custo memória:
– Guarda todos os nós expandidos na memória.
Nenhum outro algoritmo ótimo garante expandir menos nós.

Exercícios
Lista de Exercícios 15 – Distâncias Mínimas
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Halim e Halim. Competitive Programming, 3rd
Edition, 2003.
Capítulo 4: Graph
•
•
Cormen, Leiserson, Rivest e Stein. Algoritmos –
Teoria e Prática, 2ª. Edição, Editora Campus,
2
002.
Capítulo 24: Caminhos mais curtos de única
origem
