
Projeto e Análise de Algoritmos
Aula 12 – Ordenação Topológica
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Problema
•
•
Um conjunto de N tarefas precisam ser executadas.
Tarefas são dependentes:
–
Exemplo: tarefa B só pode ser executada depois de A;
–
Podemos modelar o problema como um grafo direcionado.
•
Problema: Qual ordem de execução não viola as
dependências?
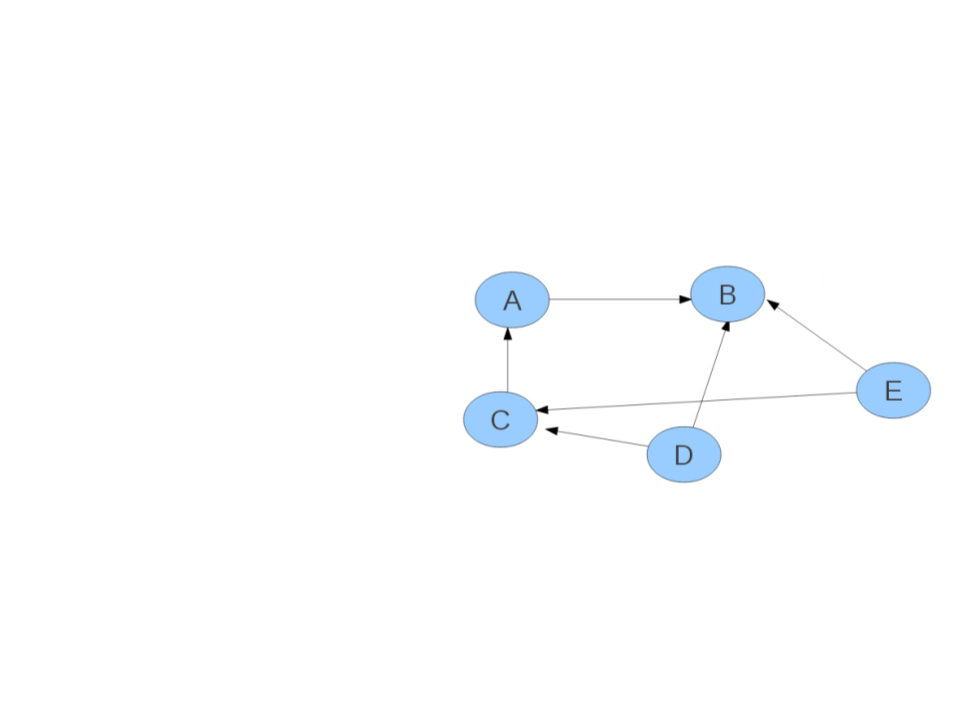
Problema – Exemplo
•
Exemplo:
–
–
–
–
–
–
B depende de A
A depende de C
C depende de D
B depende de E
B depende de D
C depende de E
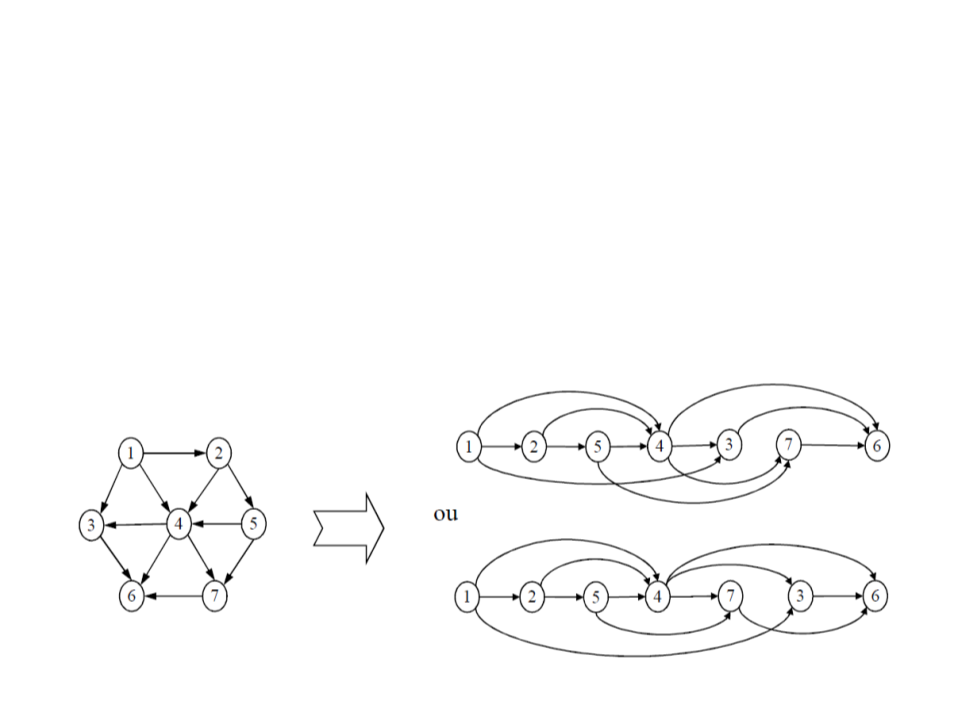
Ordenação Topológica
•
Ordenação linear dos vértices de um DAG (Grafo Acíclico
Dirigido) tal que, se existe uma aresta (u, v) no grafo, então u
aparece antes de v.
–
Impossível se o grafo for cíclico;
–
Não é necessariamente única.
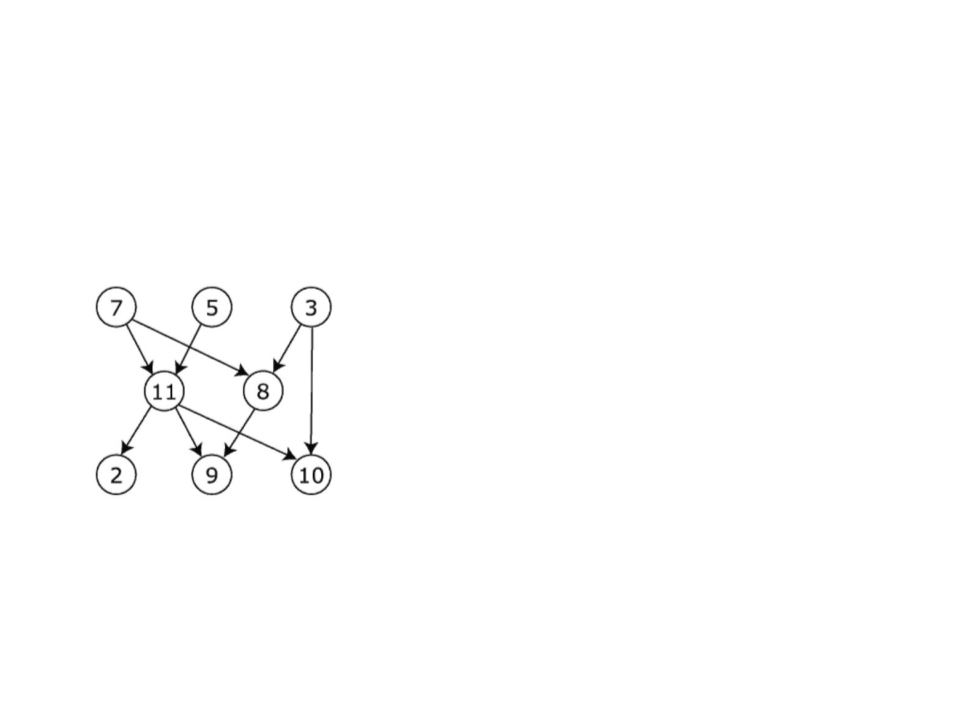
Ordenação Topológica
•
O grafo abaixo tem diversas ordenações topológicas possiveis:
•
•
•
•
•
•
7, 5, 3, 11, 8, 2, 9, 10
3, 5, 7, 8, 11, 2, 9, 10
3, 7, 8, 5, 11, 10, 2, 9
5, 7, 3, 8, 11, 10, 9, 2
7, 5, 11, 3, 10, 8, 9, 2
7, 5, 11, 2, 3, 8, 9, 10
•
Algoritmos:
–
Eliminação de vértices (algoritmo de Kahn);
–
Utilizando uma busca em profundidade;

Algoritmo de Kahn
OrdenacaoTopologicaKahn(G)
L ← ∅
for each uv ∈ A[G]
I[v] ← I[v] + 1
S ← vertices com grau de entrada zero (S = pilha)
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
return L
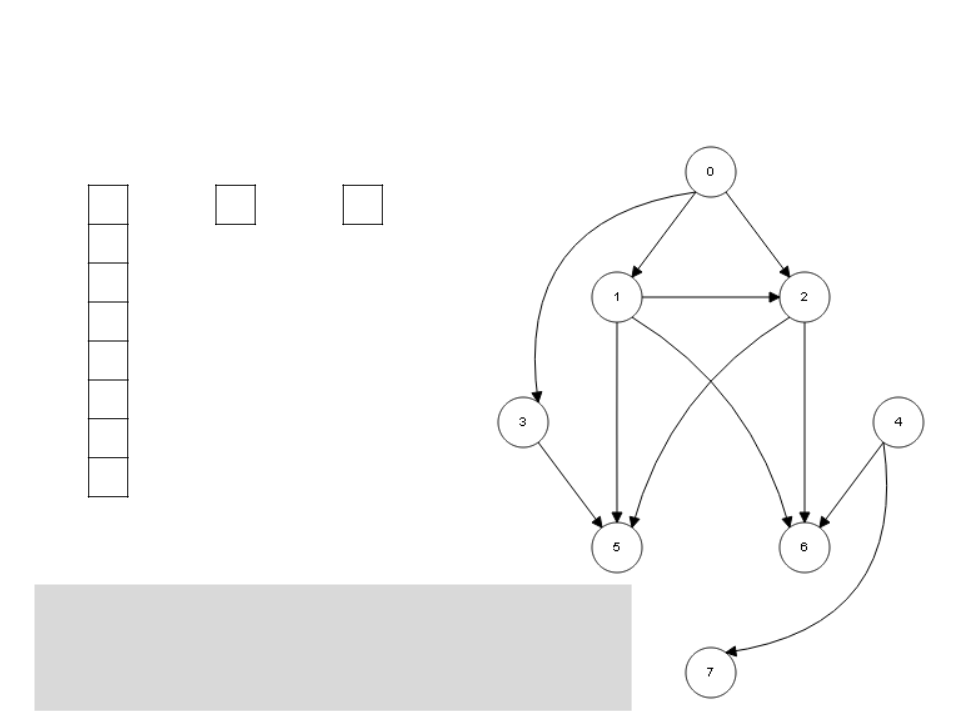
Algoritmo de Kahn
L
I
S
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
/
/
L ← ∅
for each uv ∈ A[G]
I[v] ← I[v] + 1
S ← vertices com grau de entrada zero
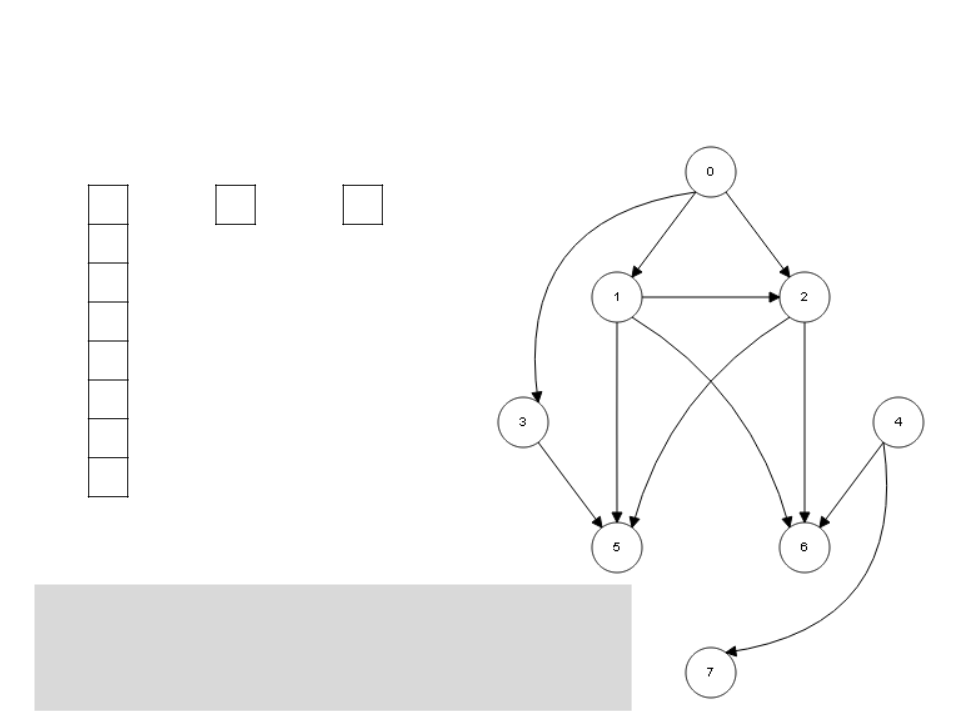
Algoritmo de Kahn
L
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
3
1
/
/
L ← ∅
for each uv ∈ A[G]
I[v] ← I[v] + 1
S ← vertices com grau de entrada zero
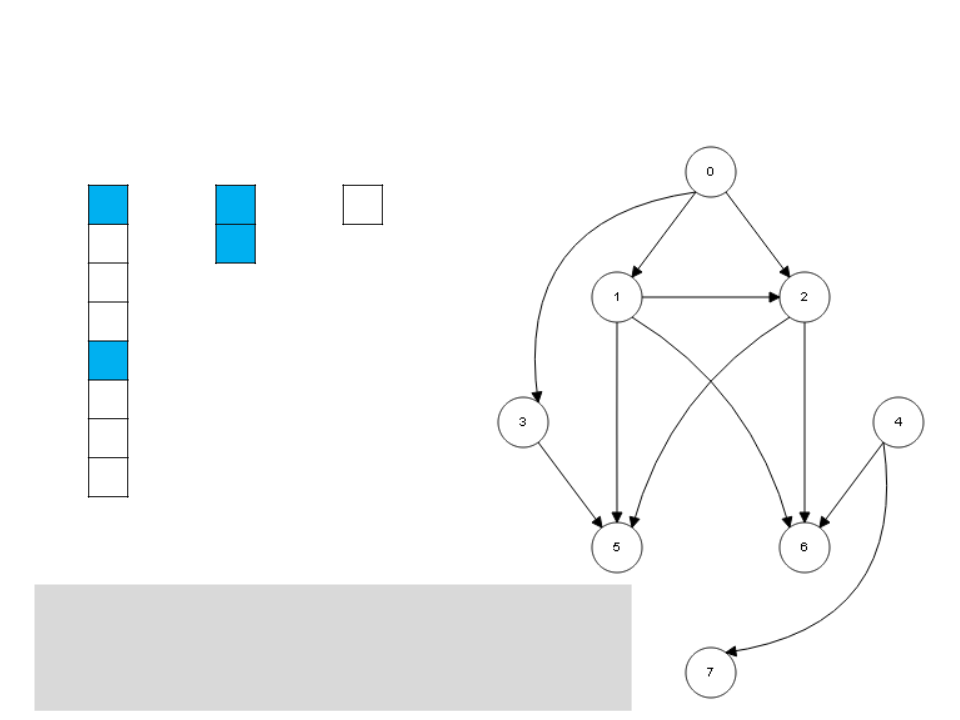
Algoritmo de Kahn
I
S
0
4
L
0
1
2
3
4
5
6
7
0
1
2
1
0
3
3
1
/
L ← ∅
for each uv ∈ A[G]
I[v] ← I[v] + 1
S ← vertices com grau de entrada zero
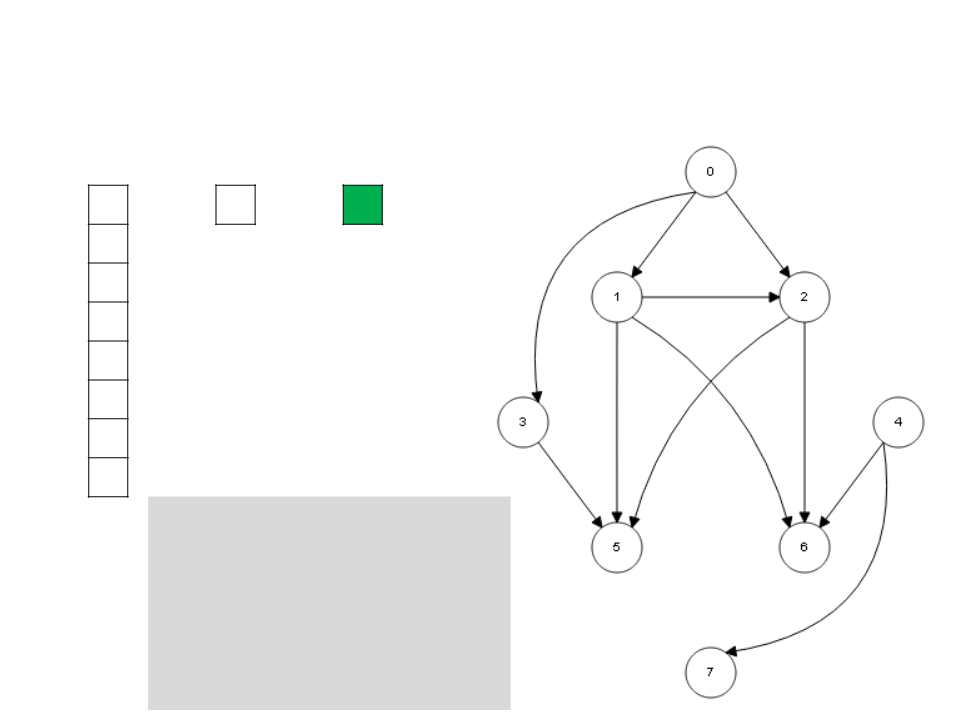
Algoritmo de Kahn
L
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
3
1
0
4
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
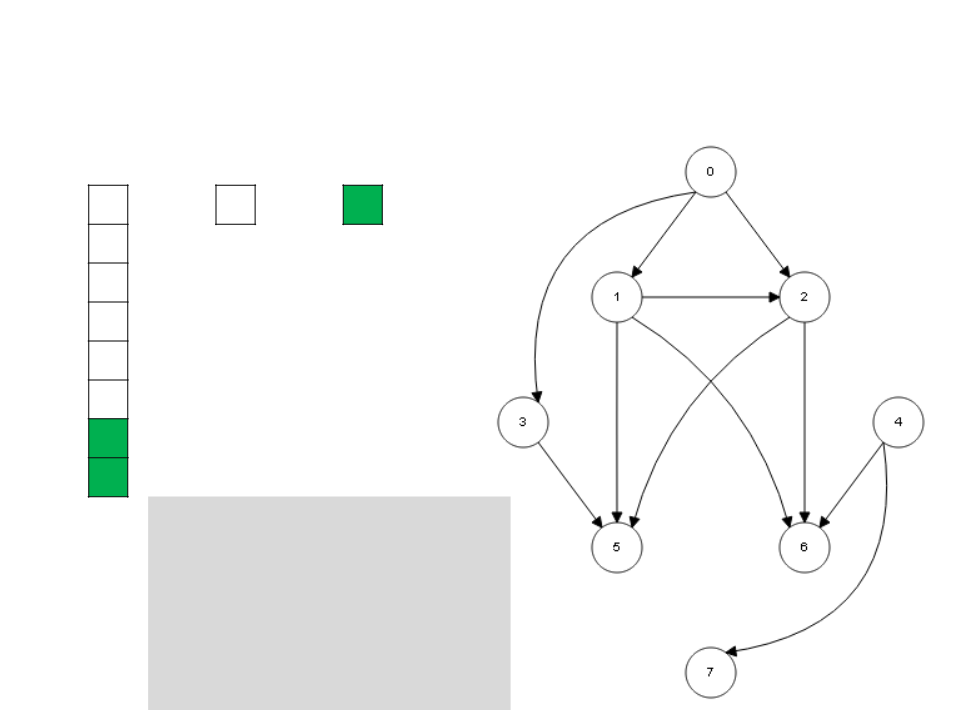
Algoritmo de Kahn
L
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
3
1
0
4
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
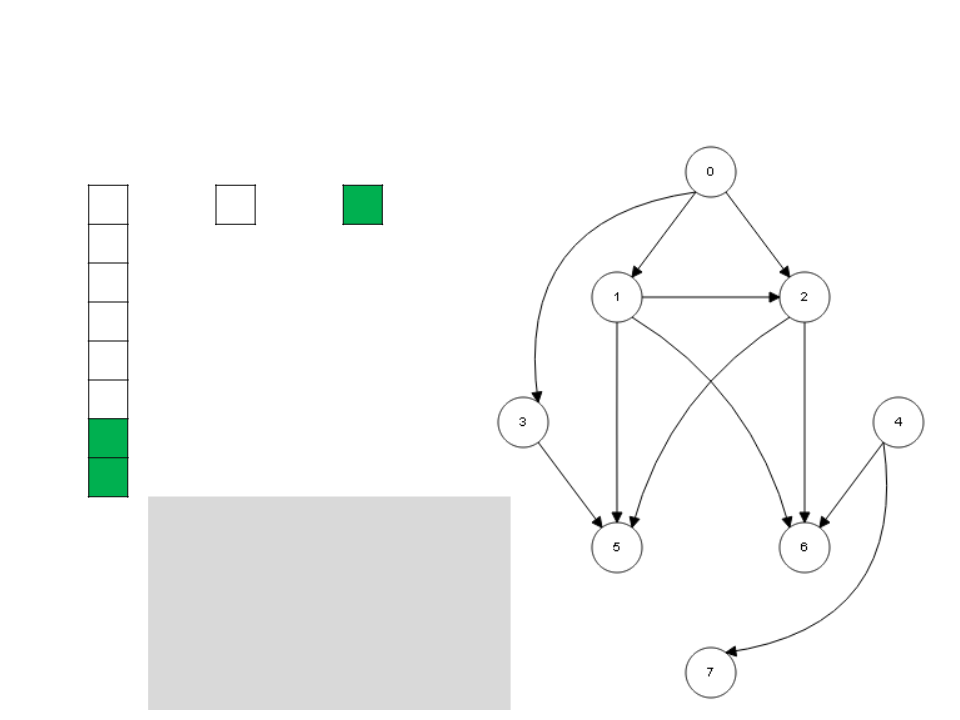
Algoritmo de Kahn
L
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
2
0
0
4
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
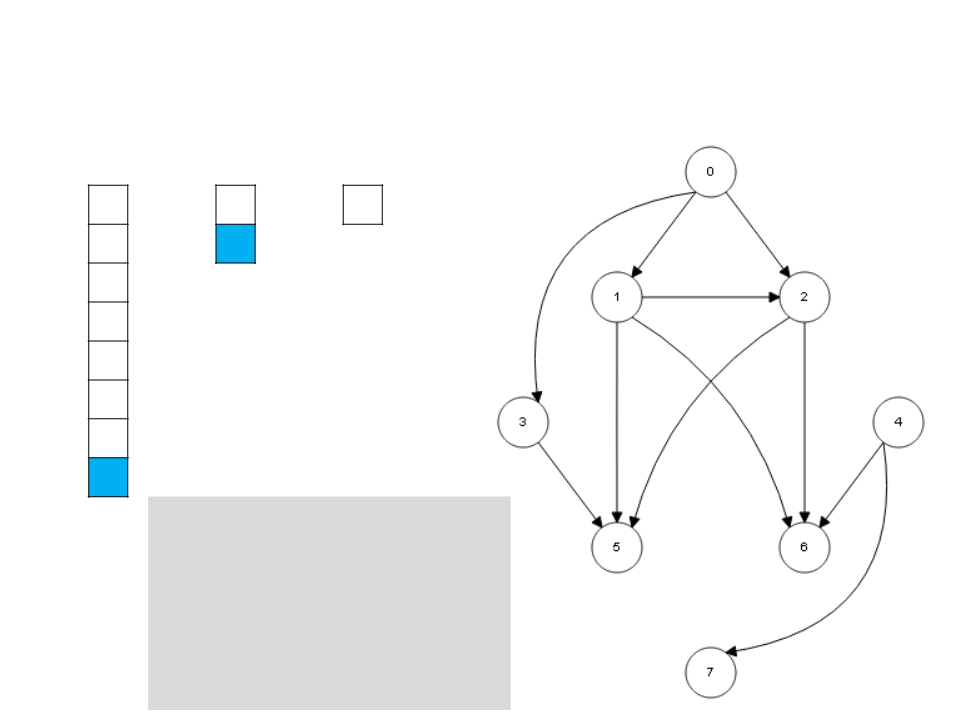
Algoritmo de Kahn
I
S
0
7
L
0
1
2
3
4
5
6
7
0
1
2
1
0
3
2
0
4
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
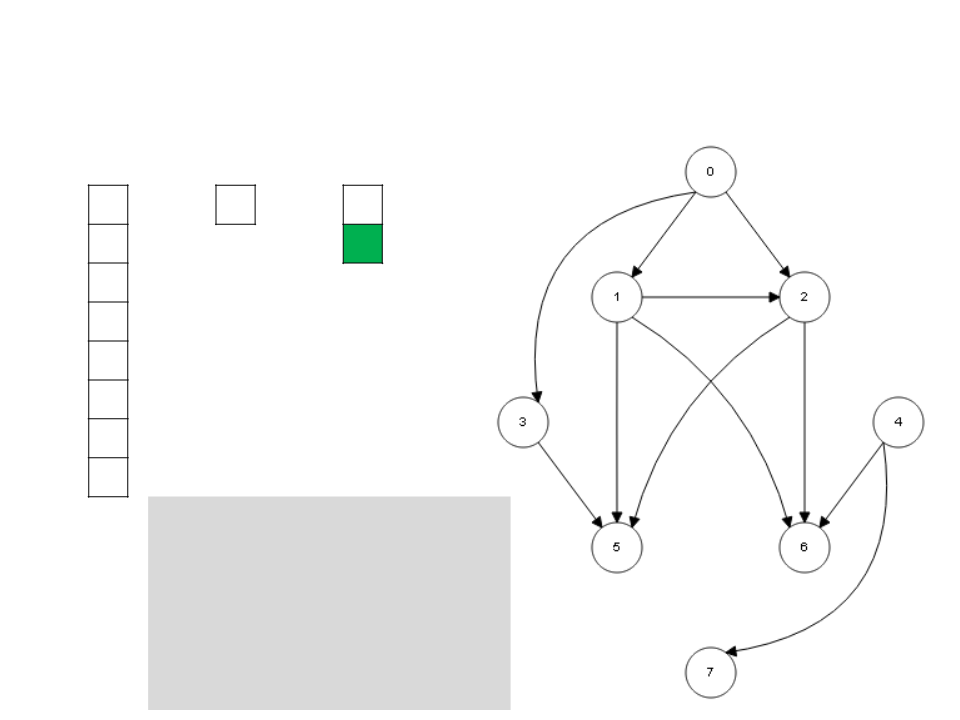
Algoritmo de Kahn
L
4
7
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
2
0
0
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
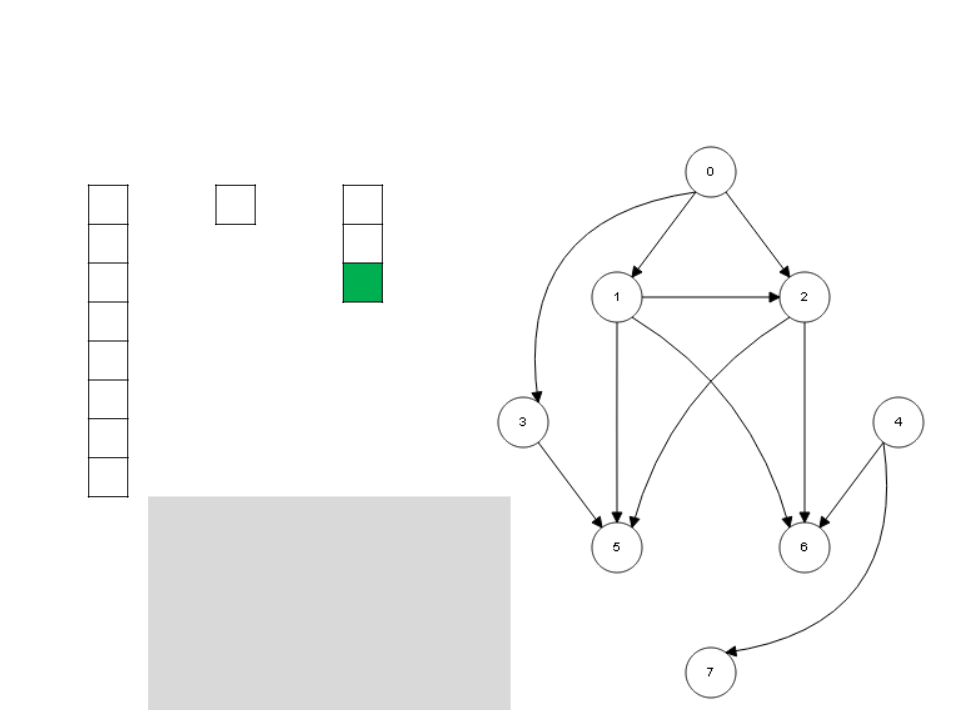
Algoritmo de Kahn
L
4
7
0
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
2
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
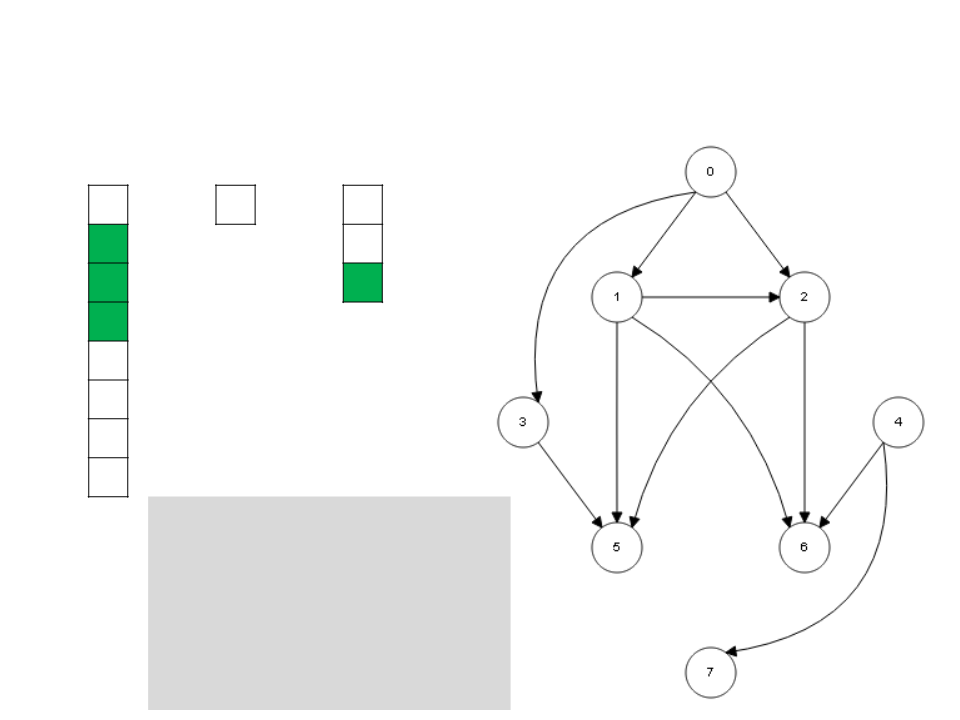
Algoritmo de Kahn
L
4
7
0
I
S
0
1
2
3
4
5
6
7
0
1
2
1
0
3
2
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
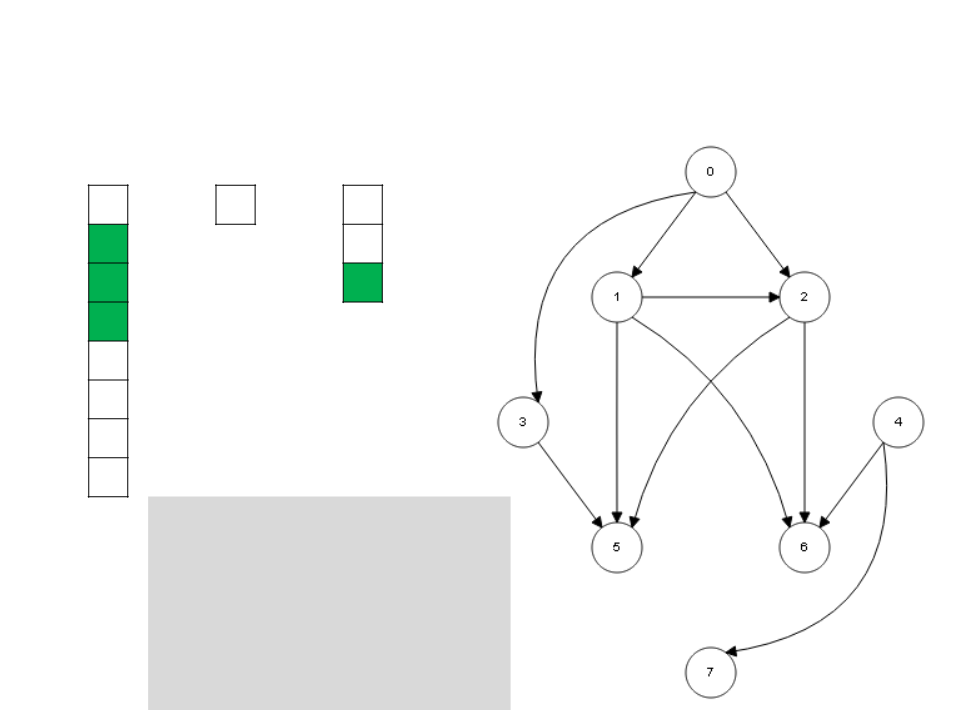
Algoritmo de Kahn
L
4
7
0
I
S
0
1
2
3
4
5
6
7
0
0
1
0
0
3
2
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
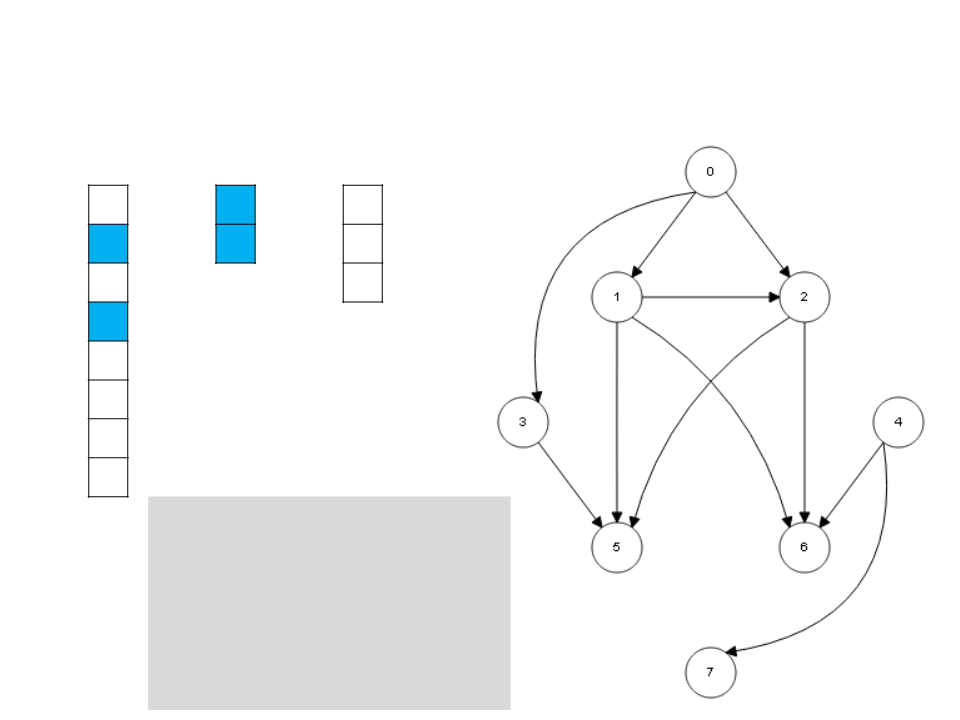
Algoritmo de Kahn
L
4
7
0
I
S
1
3
0
1
2
3
4
5
6
7
0
0
1
0
0
3
2
0
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
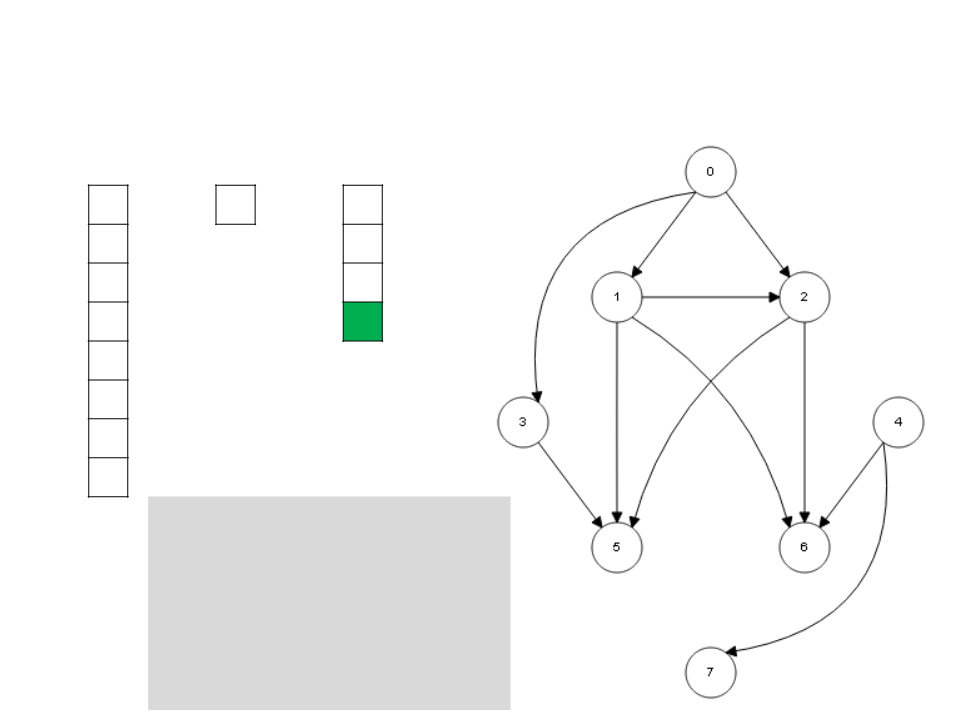
Algoritmo de Kahn
I
S
L
4
7
0
3
0
1
2
3
4
5
6
7
0
0
1
0
0
3
2
0
1
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
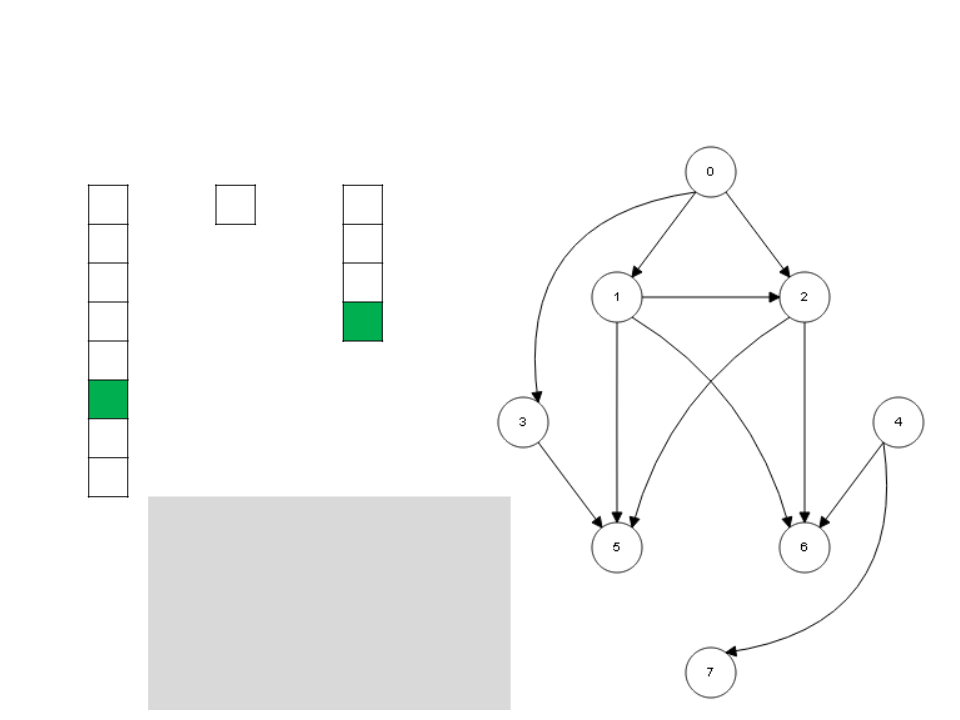
Algoritmo de Kahn
I
S
L
4
7
0
3
0
1
2
3
4
5
6
7
0
0
1
0
0
3
2
0
1
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
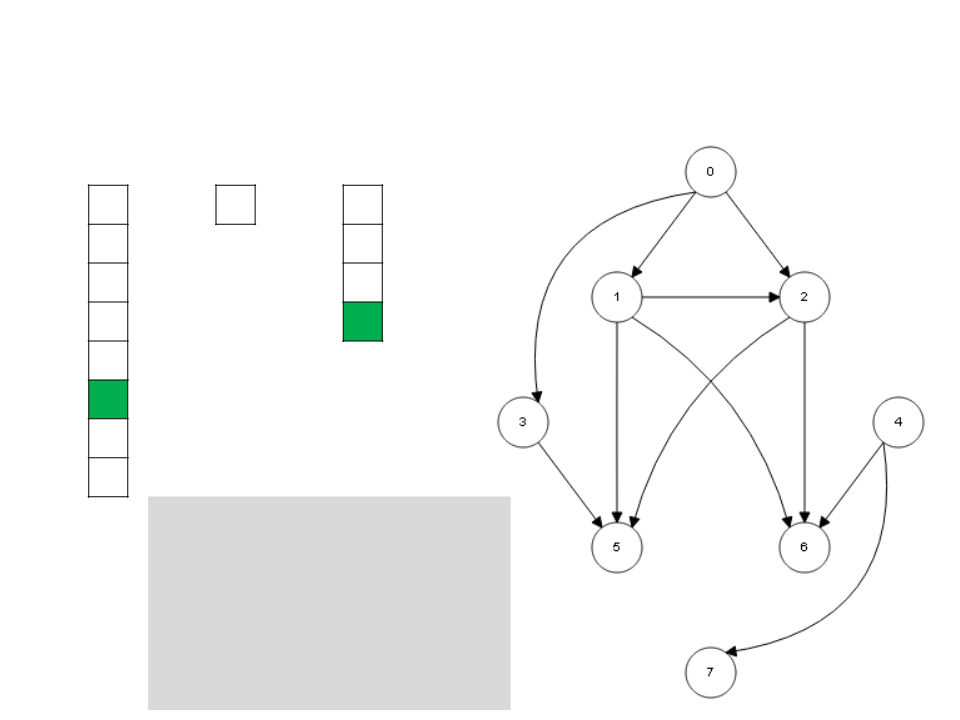
Algoritmo de Kahn
I
S
L
4
7
0
3
0
1
2
3
4
5
6
7
0
0
1
0
0
2
2
0
1
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
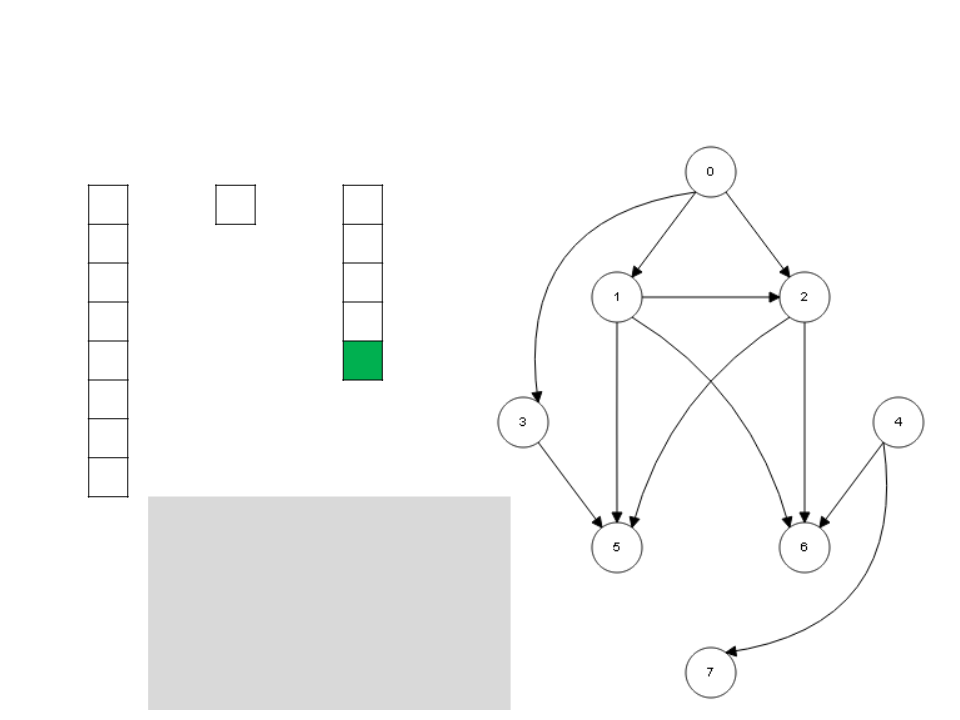
Algoritmo de Kahn
I
S
L
4
7
0
3
1
0
1
2
3
4
5
6
7
0
0
1
0
0
2
2
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
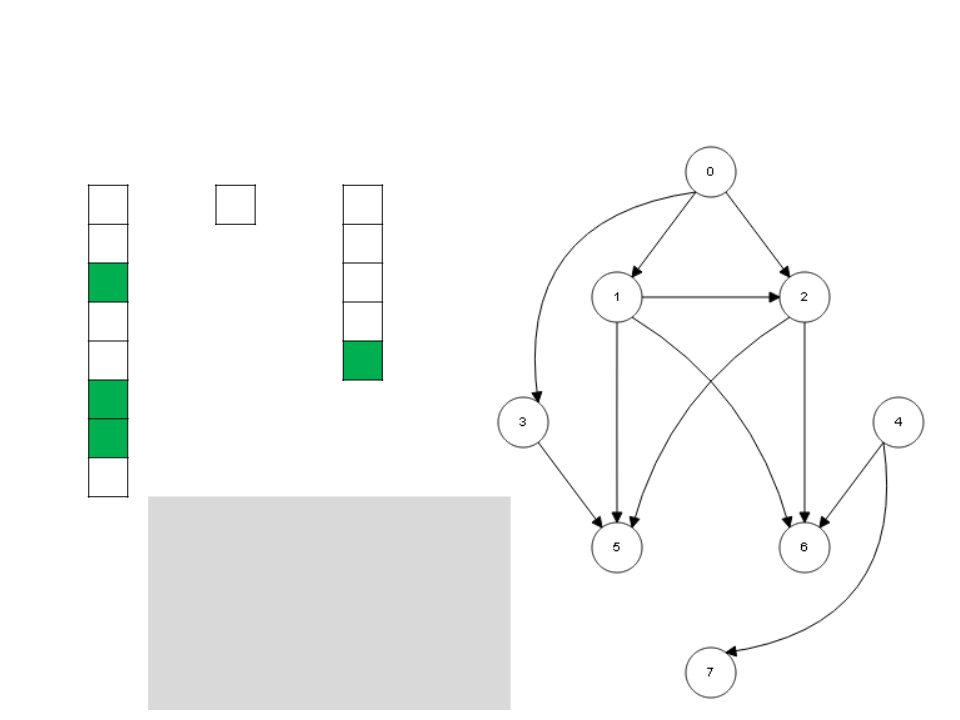
Algoritmo de Kahn
I
S
L
4
7
0
3
1
0
1
2
3
4
5
6
7
0
0
1
0
0
2
2
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
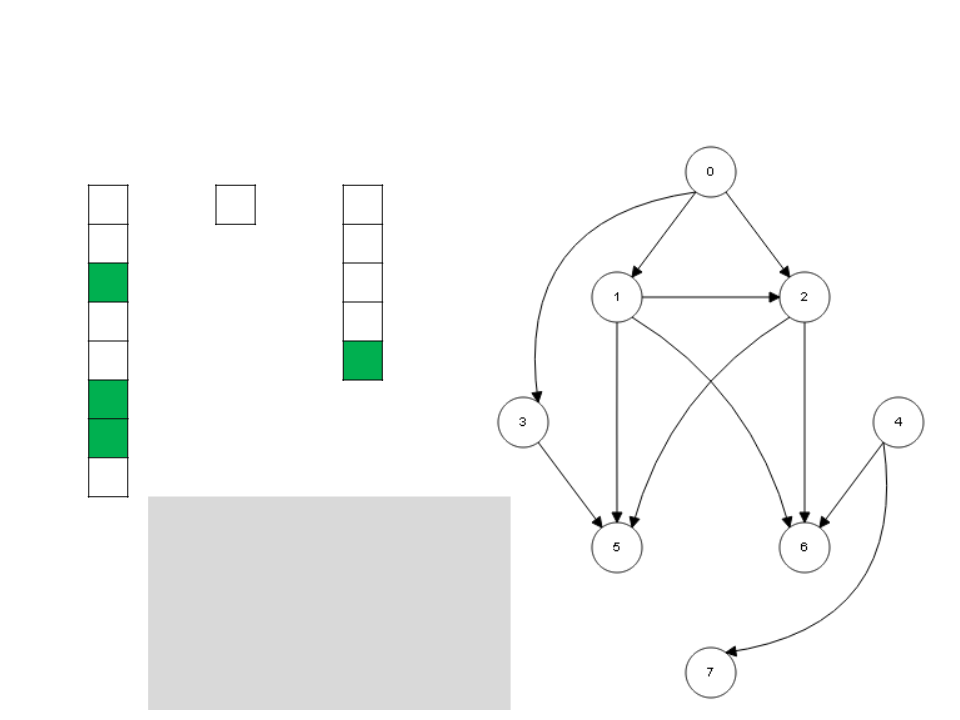
Algoritmo de Kahn
I
S
L
4
7
0
3
1
0
1
2
3
4
5
6
7
0
0
0
0
0
1
1
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
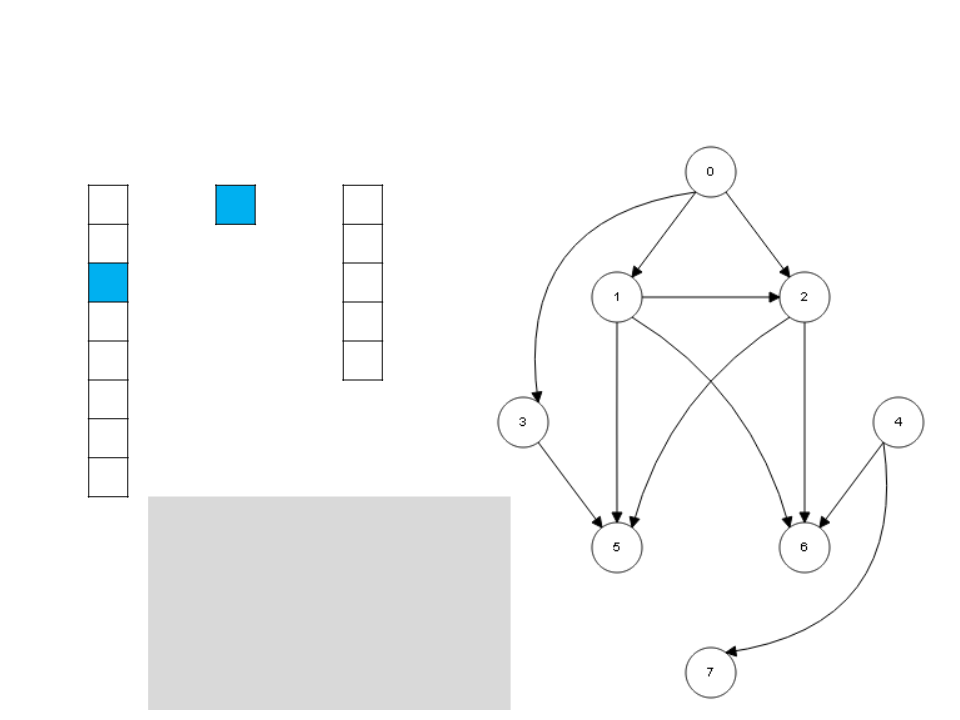
Algoritmo de Kahn
I
S
L
4
7
0
3
1
0
1
2
3
4
5
6
7
0
0
0
0
0
1
1
0
2
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
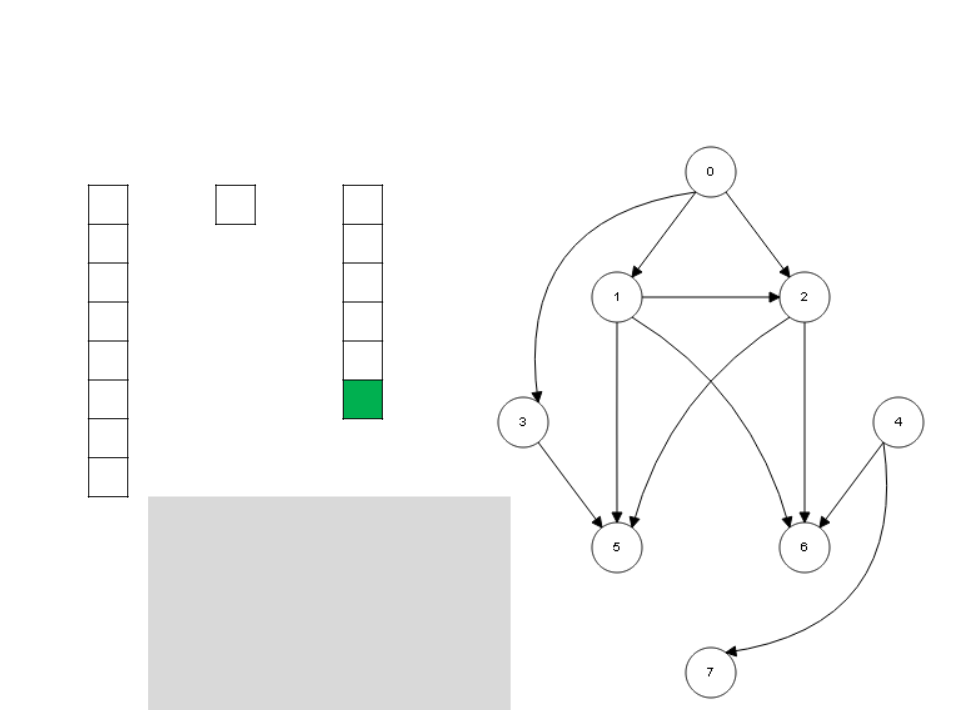
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
0
1
2
3
4
5
6
7
0
0
0
0
0
1
1
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
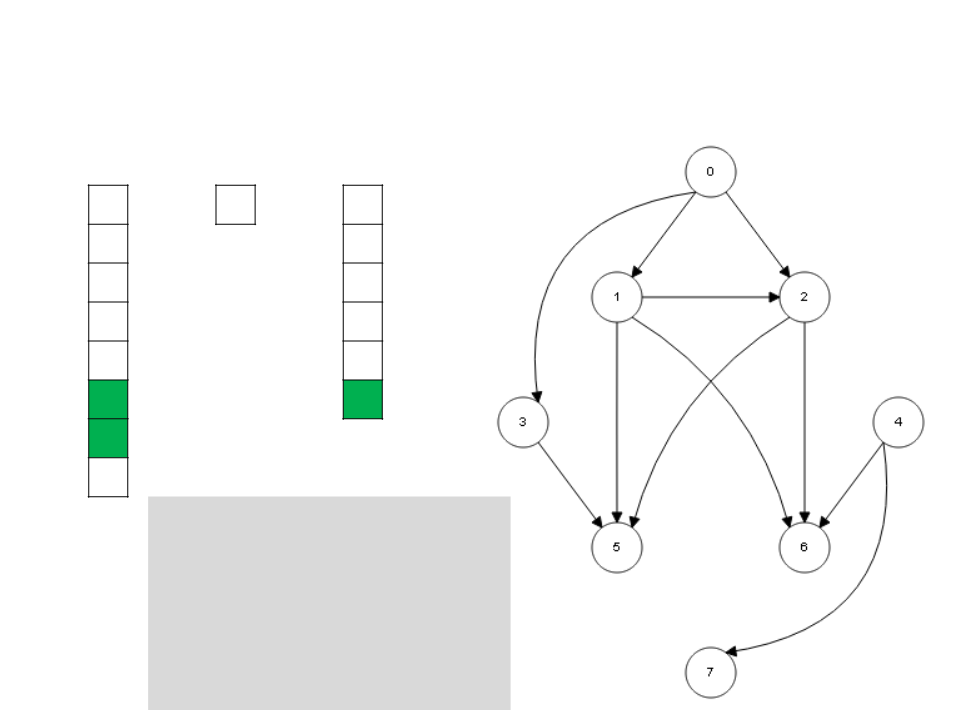
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
0
1
2
3
4
5
6
7
0
0
0
0
0
1
1
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
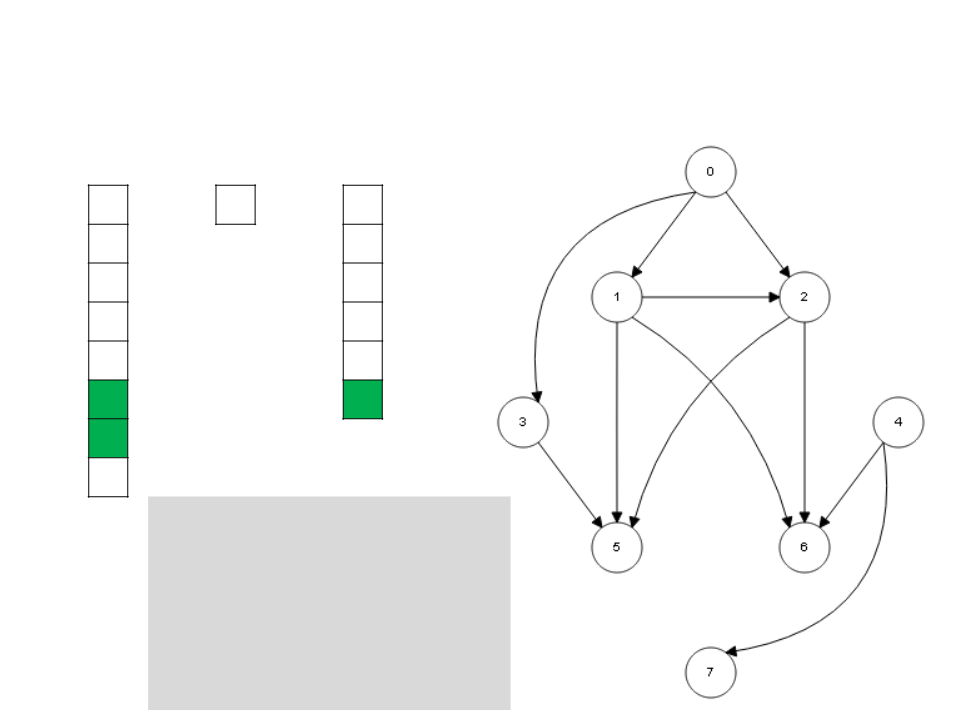
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
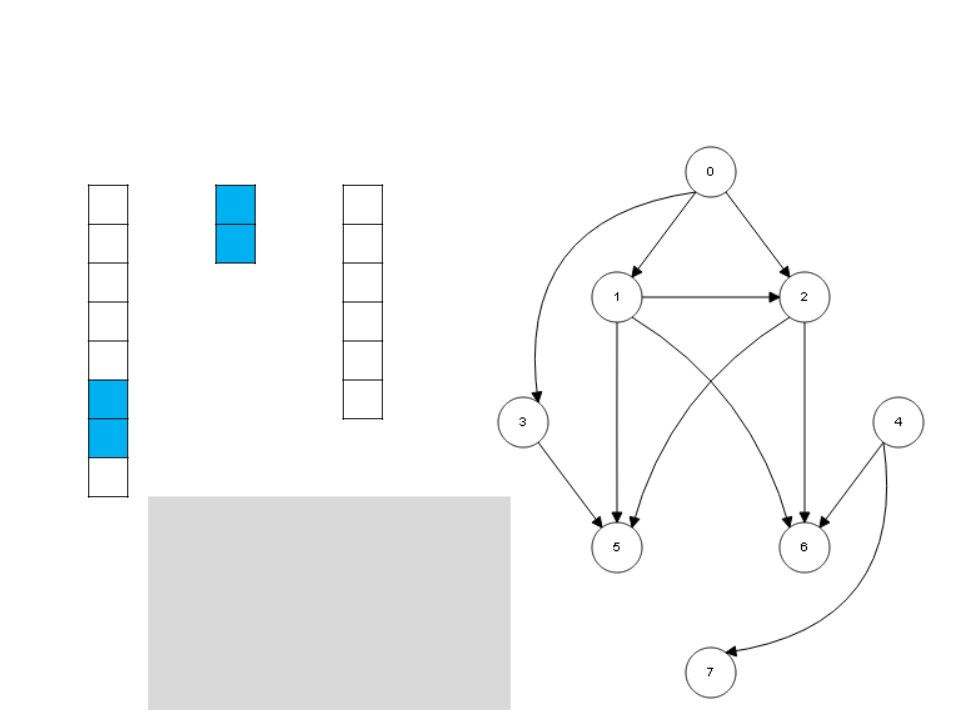
Algoritmo de Kahn
I
S
5
6
L
4
7
0
3
1
2
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
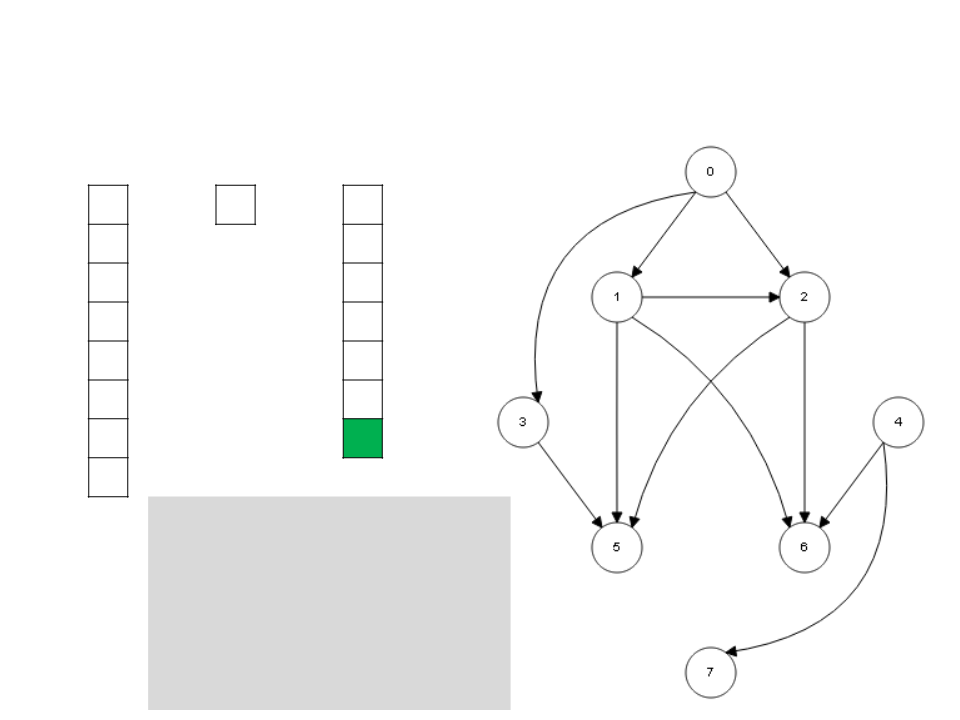
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
6
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
5
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
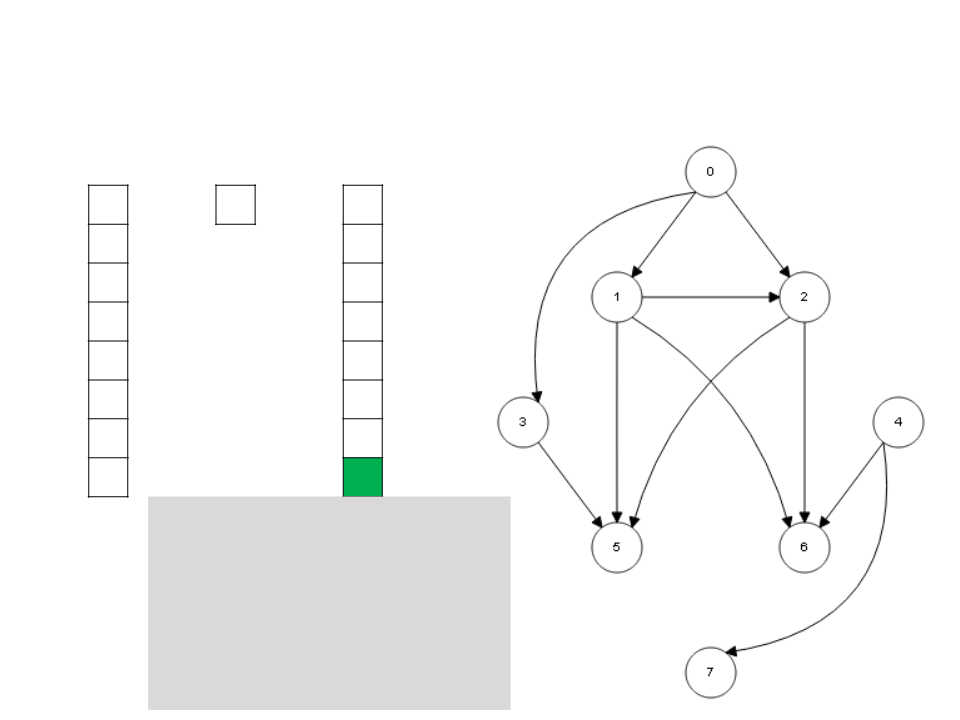
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
6
5
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
/
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
stack(u, S)
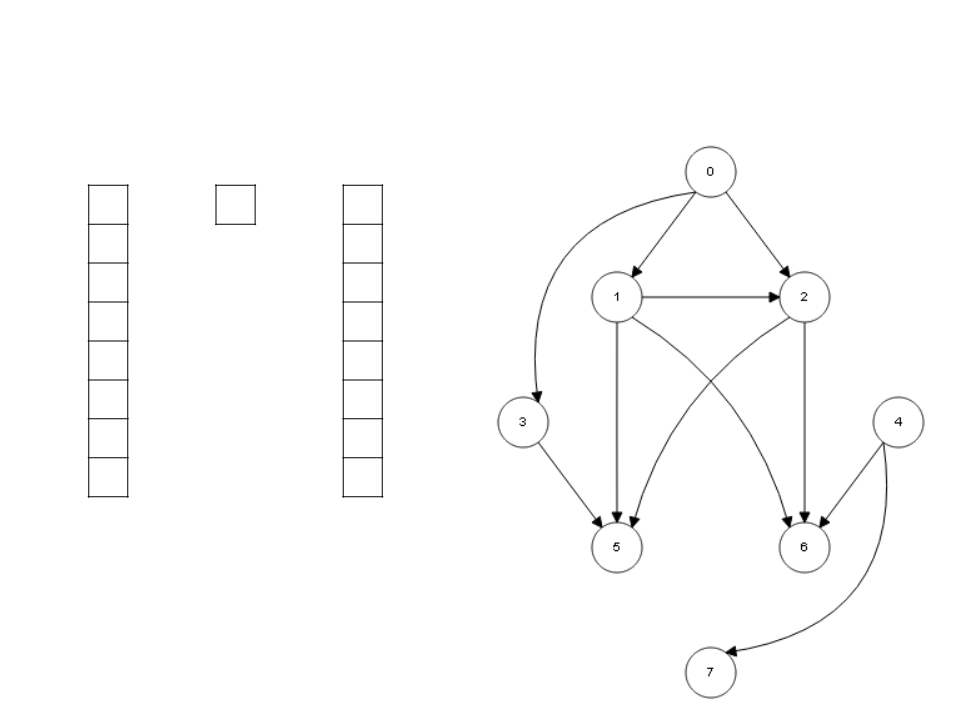
Algoritmo de Kahn
I
S
L
4
7
0
3
1
2
6
5
0
1
2
3
4
5
6
7
0
0
0
0
0
0
0
0
/

Algoritmo de Kahn – Análise
•
Inicializar o vetor I: O(A)
OrdenacaoTopologicaKahn(G)
L ← ∅
•
Inicializar a pilha S com os
vértices de entrada zero:
O(A)
for each uv ∈ A[G]
I[v] ← I[v] + 1
S ← vertices com grau de
entrada zero (S = pilha)
while S ≠ ∅
v ← unstack(S)
stack(v, L)
for each u ∈ Adj[v]
I[u] ← I[u] - 1
if I[u] = 0
•
Desempilhar e Empilhar
vértices: O(V) vertices, cada
um com tempo O(1)
•
•
Reduzir Ipara todos os
vértices adjacentes: O(V)
stack(u, S)
return L
Complexidade: O(V + A)

Algoritmo com Busca em
Profundidade
OrdenacaoTopologicaDFS(G)
L ← ∅
BuscaEmProfundidade(G)
return L
visita(u)
BuscaEmProfundidade(G)
for each u ∈ V[G]
c[u] ← white
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ[v] ← u
ꢀ
[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
visita(u)
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
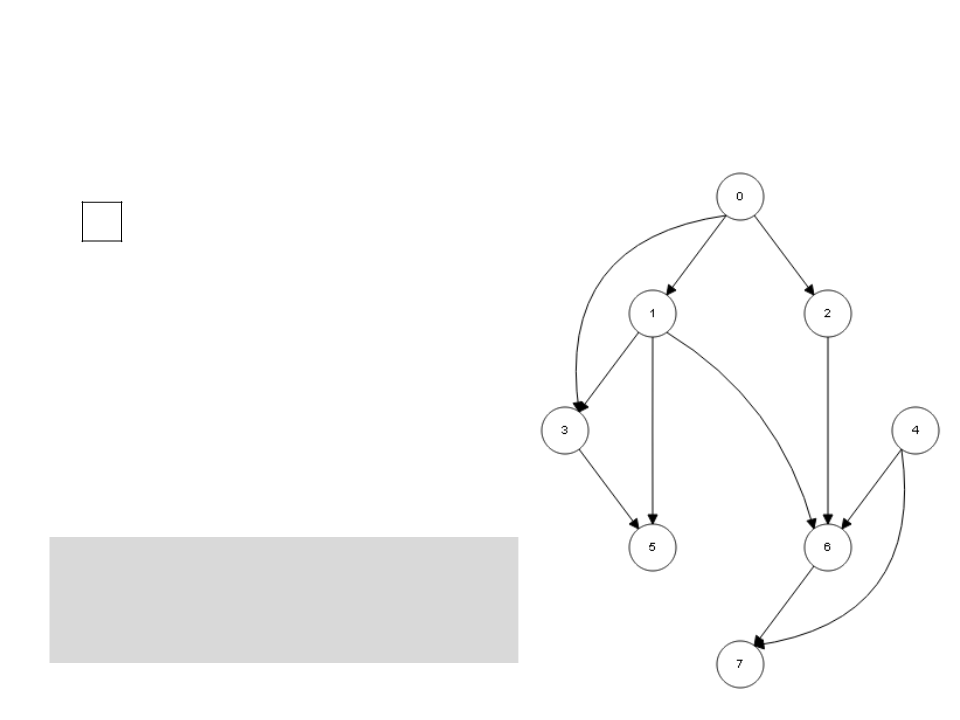
Ordenação Topológica – DFS
/
L
OrdenacaoTopologicaDFS(G)
L ← ∅
BuscaEmProfundidade(G)
return L
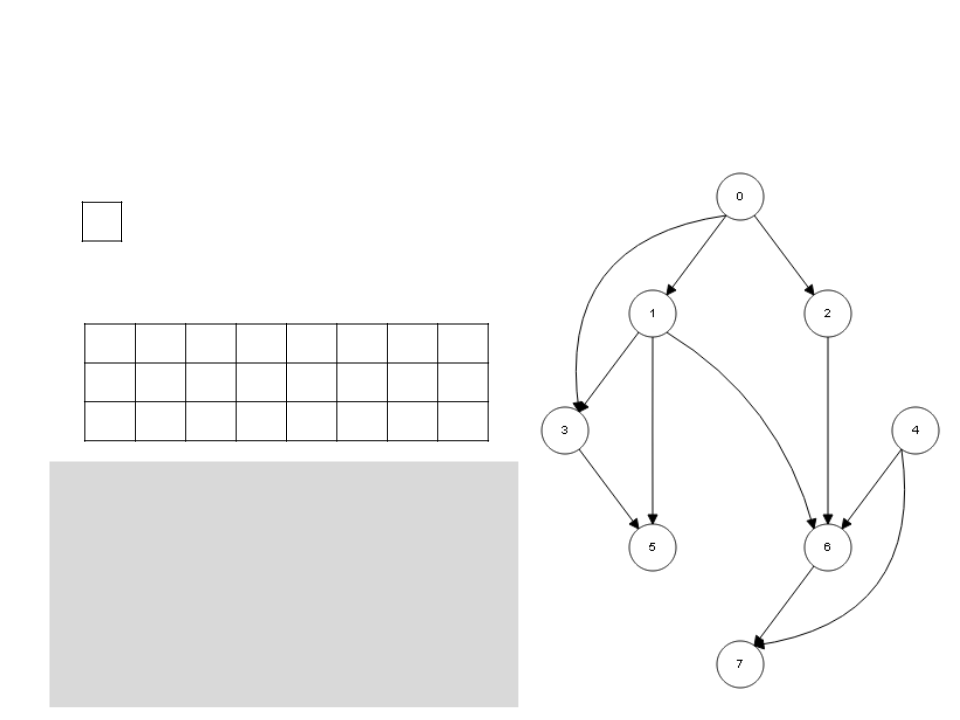
Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c w w w w w w w w
d
f
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
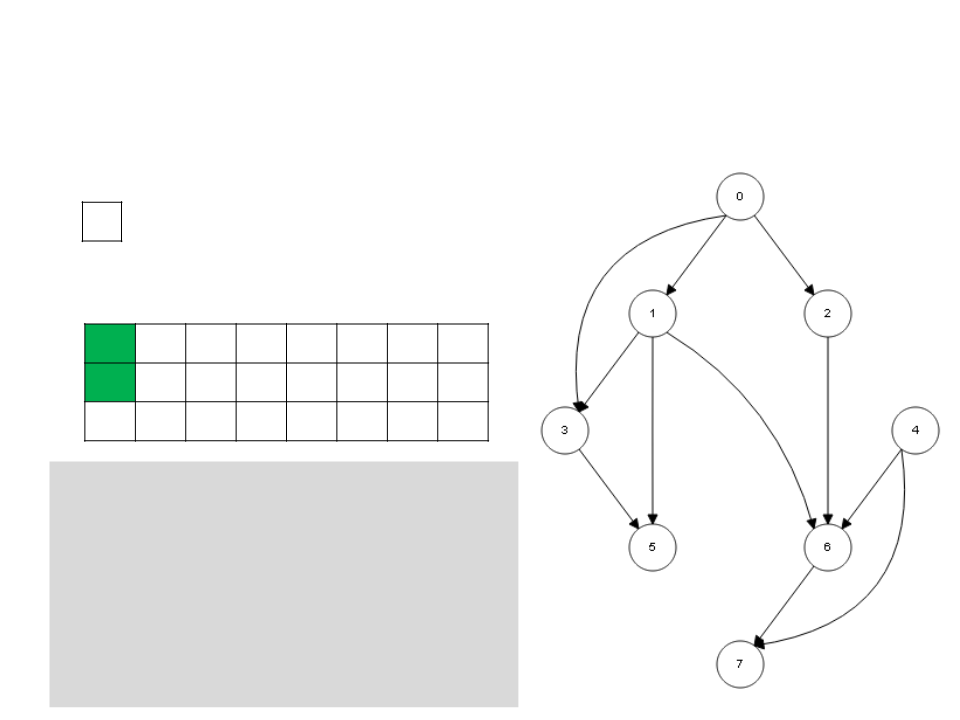
Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c g w w w w w w w
d 1
f
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
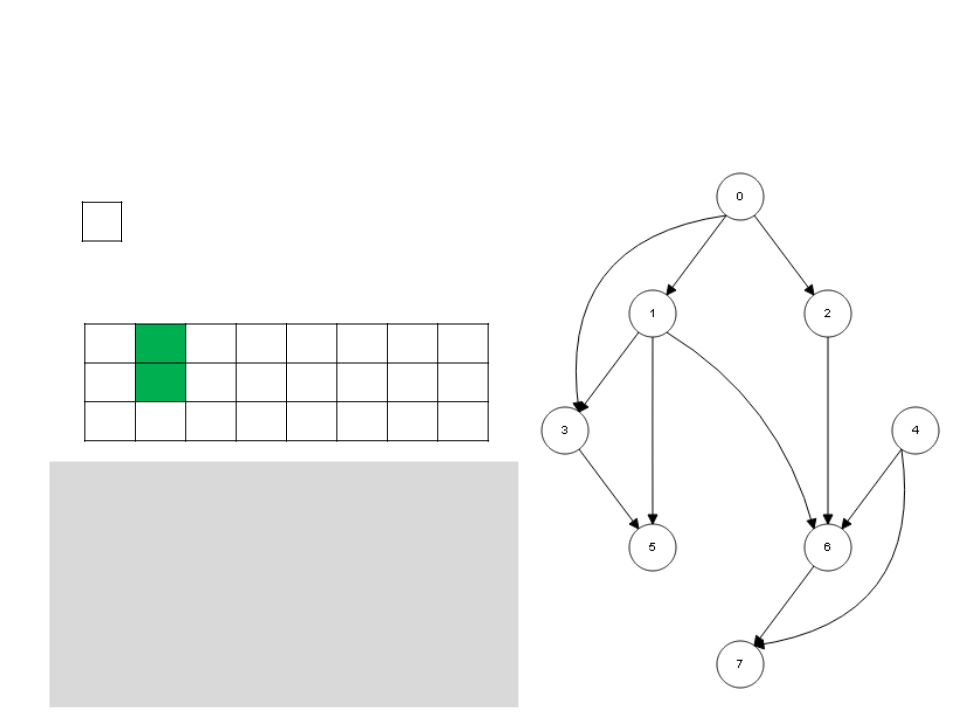
Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c g g w w w w w w
d 1 2
f
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
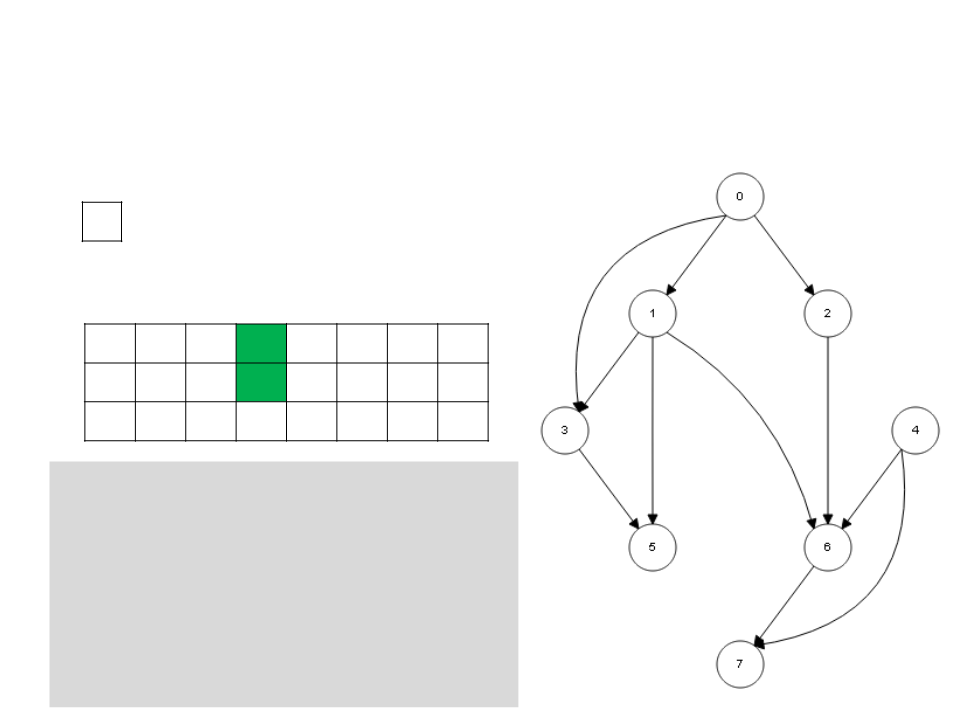
Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c g g w g w w w w
d 1 2
f
3
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
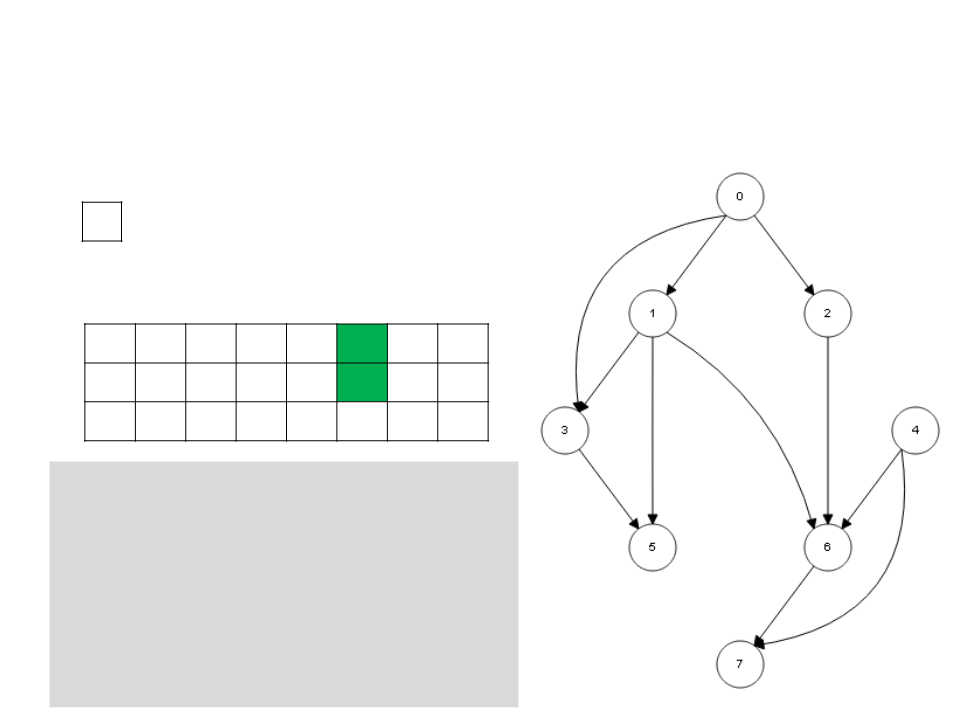
Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c g g w g w g w w
d 1 2
f
3
4
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)

Ordenação Topológica – DFS
/
L
0
1 2 3 4 5 6 7
c g g w g w b w w
d 1 2
f
3
4
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
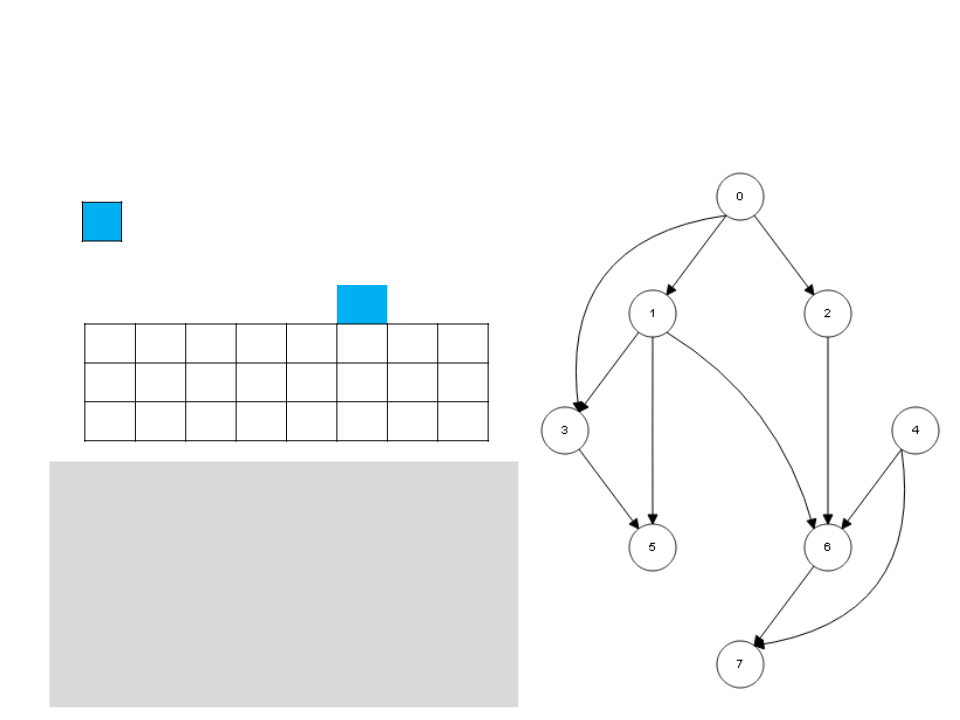
Ordenação Topológica – DFS
5
L
0
1 2 3 4 5 6 7
c g g w g w b w w
d 1 2
f
3
4
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
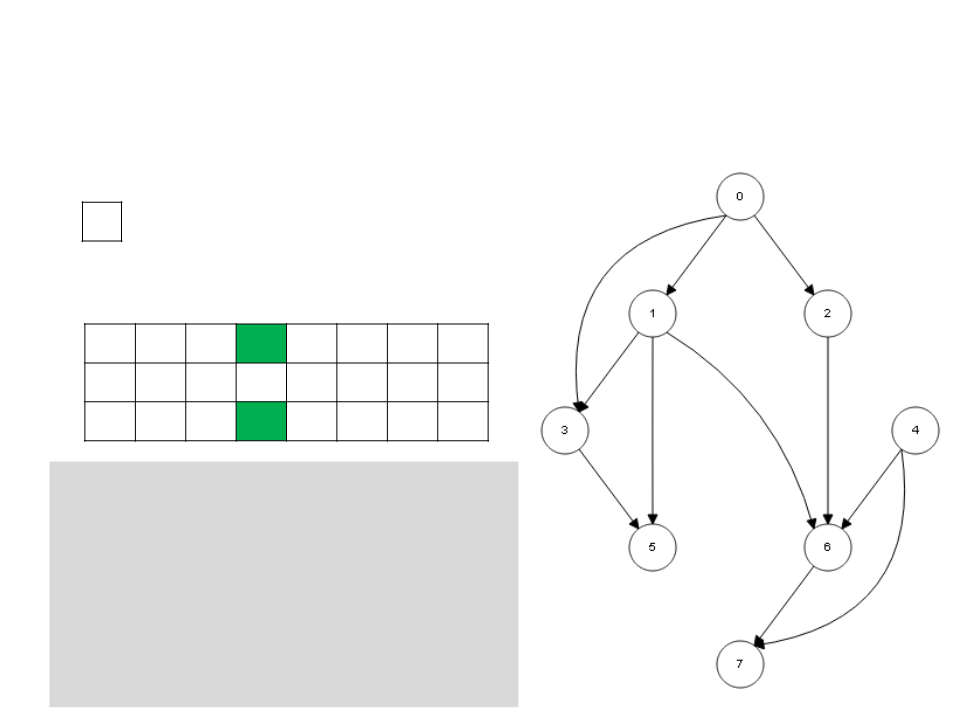
Ordenação Topológica – DFS
5
L
0
1 2 3 4 5 6 7
c g g w b w b w w
d 1 2
f
3
6
4
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
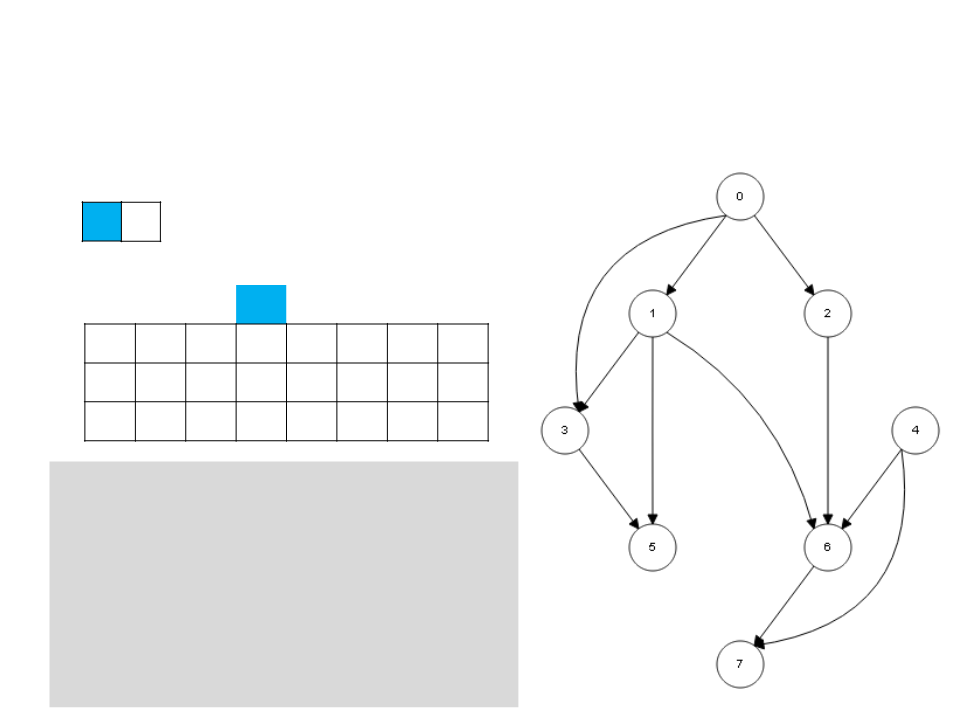
Ordenação Topológica – DFS
3
5
L
0
1 2 3 4 5 6 7
c g g w b w b w w
d 1 2
f
3
6
4
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
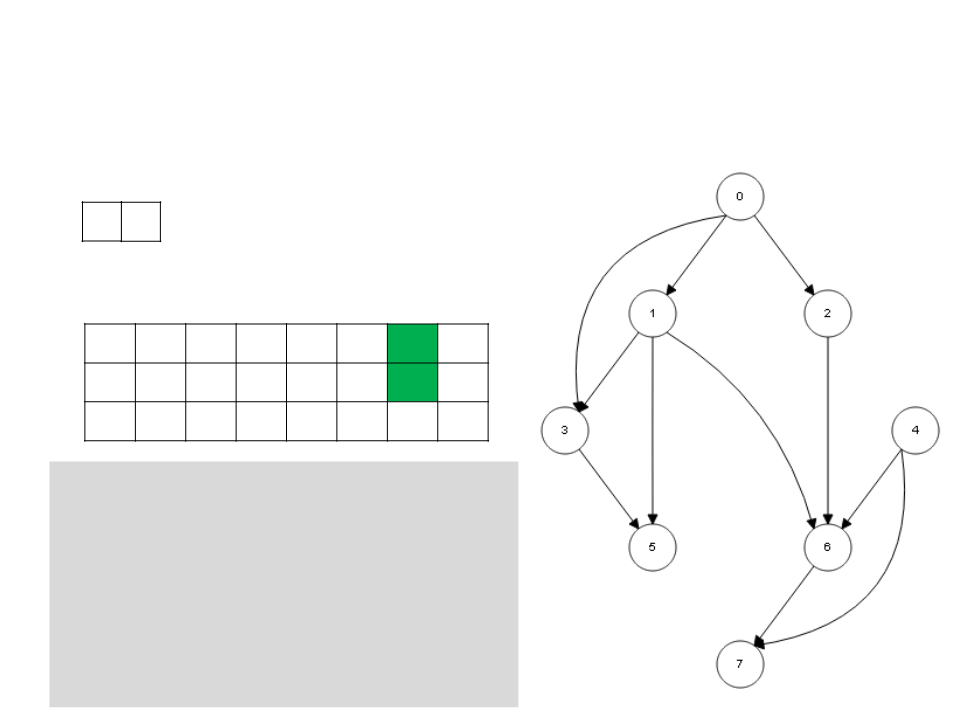
Ordenação Topológica – DFS
3
5
L
0
1 2 3 4 5 6 7
c g g w b w b g w
d 1 2
f
3
6
4 7
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
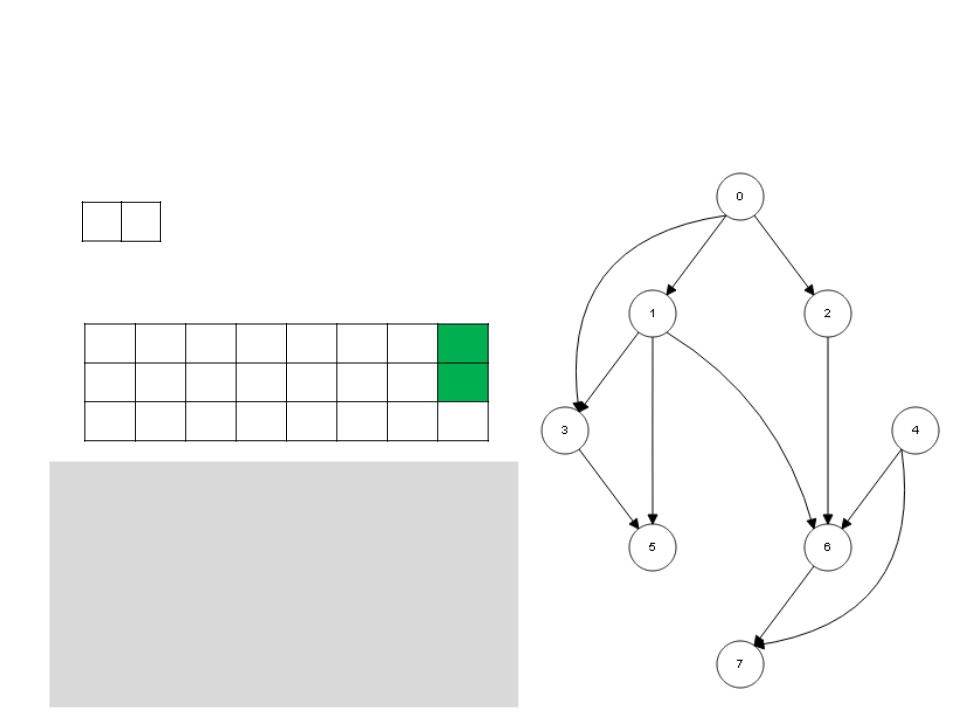
Ordenação Topológica – DFS
3
5
L
0
1 2 3 4 5 6 7
c g g w b w b g g
d 1 2
f
3
6
4 7 8
5
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
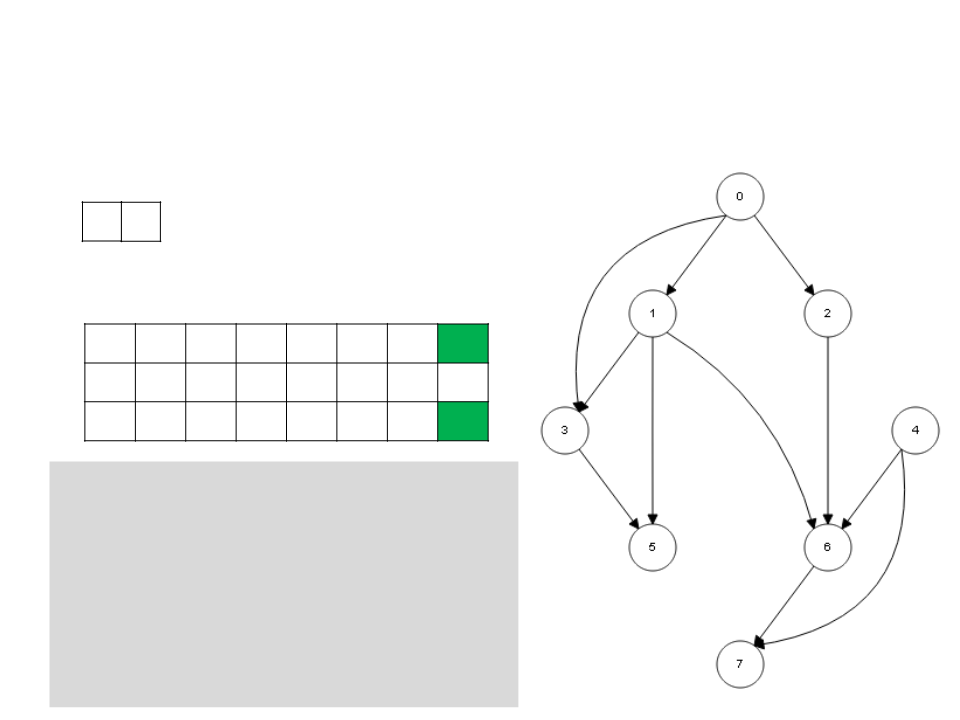
Ordenação Topológica – DFS
3
5
L
0
1 2 3 4 5 6 7
c g g w b w b g b
d 1 2
f
3
6
4 7 8
5
9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
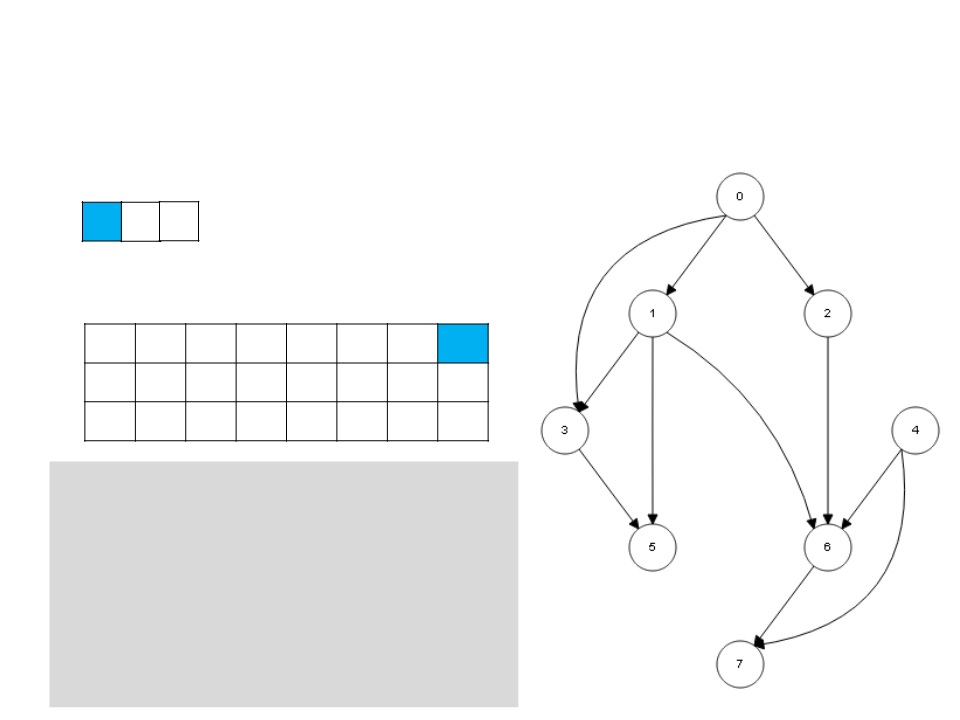
Ordenação Topológica – DFS
7
3 5
L
0
1 2 3 4 5 6 7
c g g w b w b g b
d 1 2
f
3
6
4 7 8
5
9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
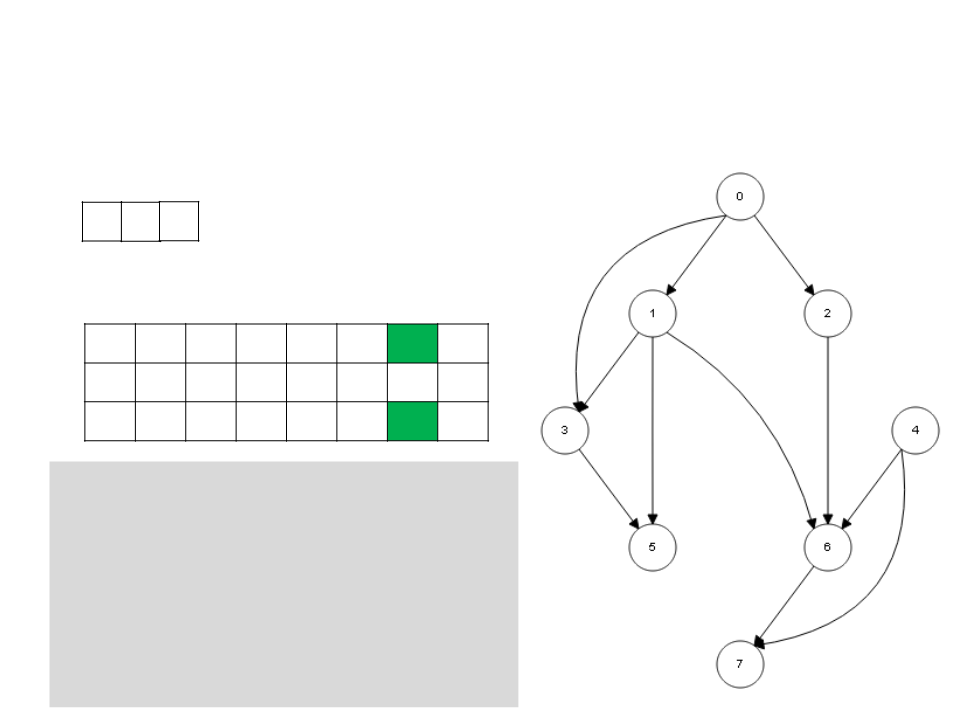
Ordenação Topológica – DFS
7
3 5
L
0
1 2 3 4 5 6 7
c g g w b w b b b
d 1 2
f
3
6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
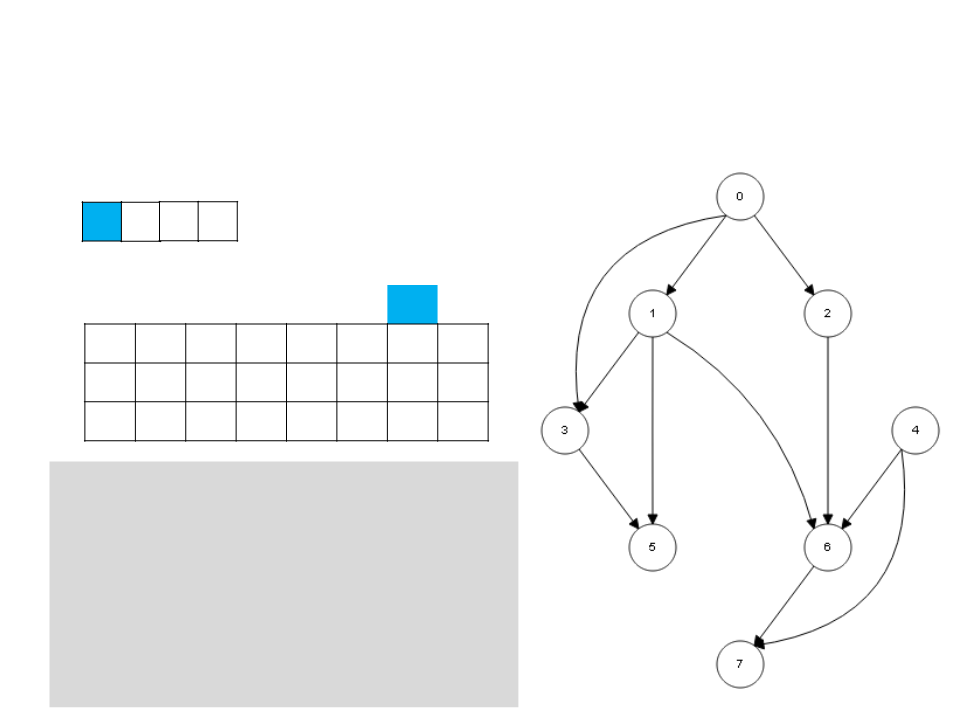
Ordenação Topológica – DFS
6
7 3 5
L
0
1 2 3 4 5 6 7
c g g w b w b b b
d 1 2
f
3
6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
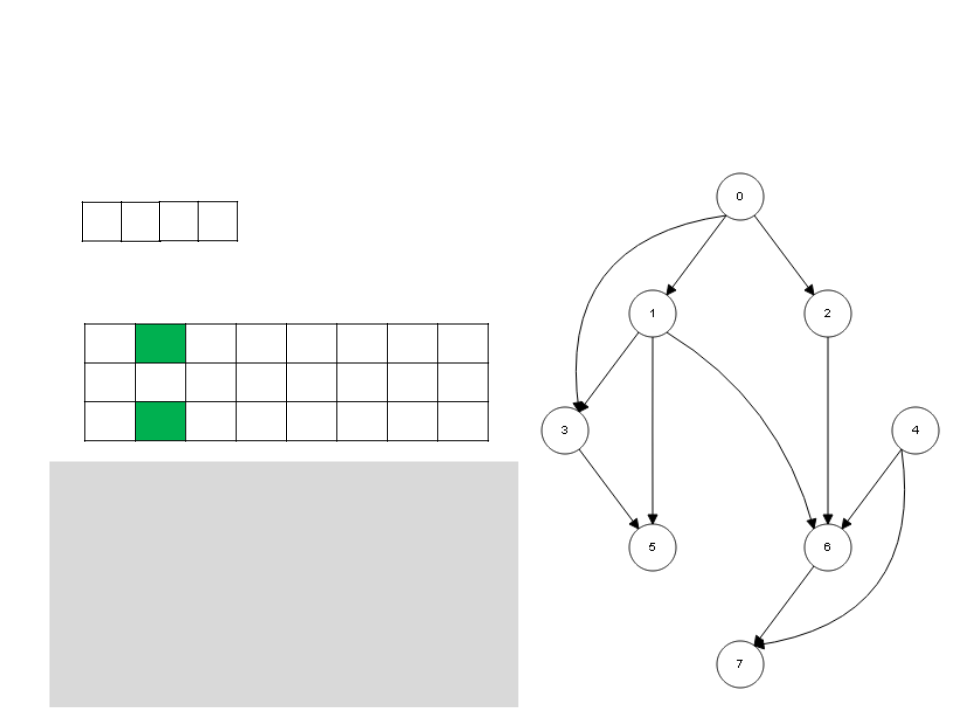
Ordenação Topológica – DFS
6
7 3 5
L
0
1 2 3 4 5 6 7
c g b w b w b b b
d 1 2
f 11
3
6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
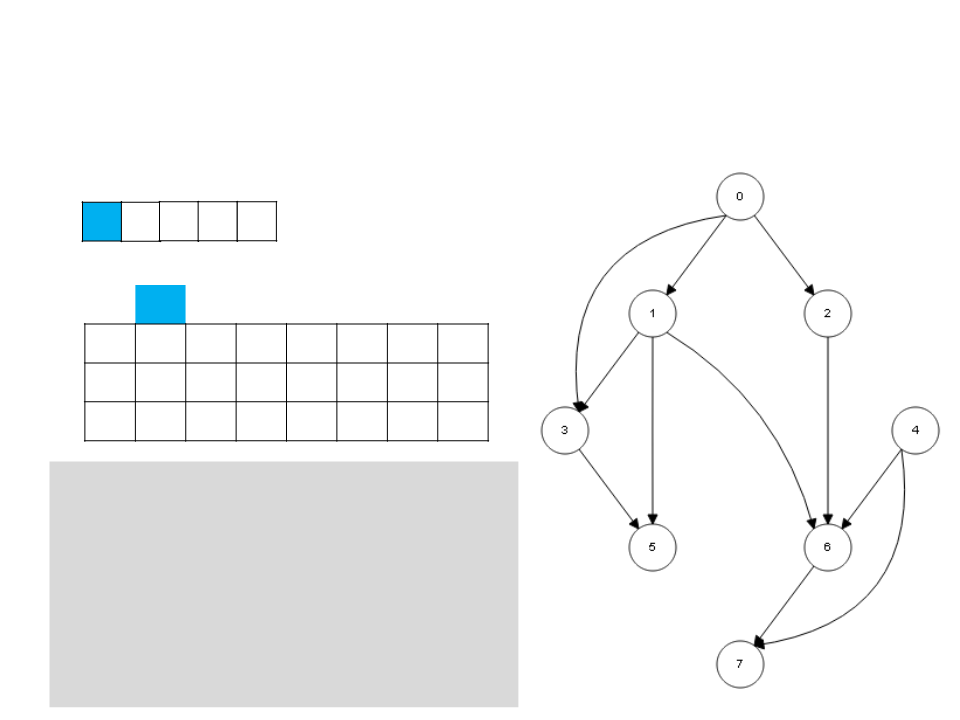
Ordenação Topológica – DFS
1
6 7 3 5
L
0
1 2 3 4 5 6 7
c g b w b w b b b
d 1 2
f 11
3
6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
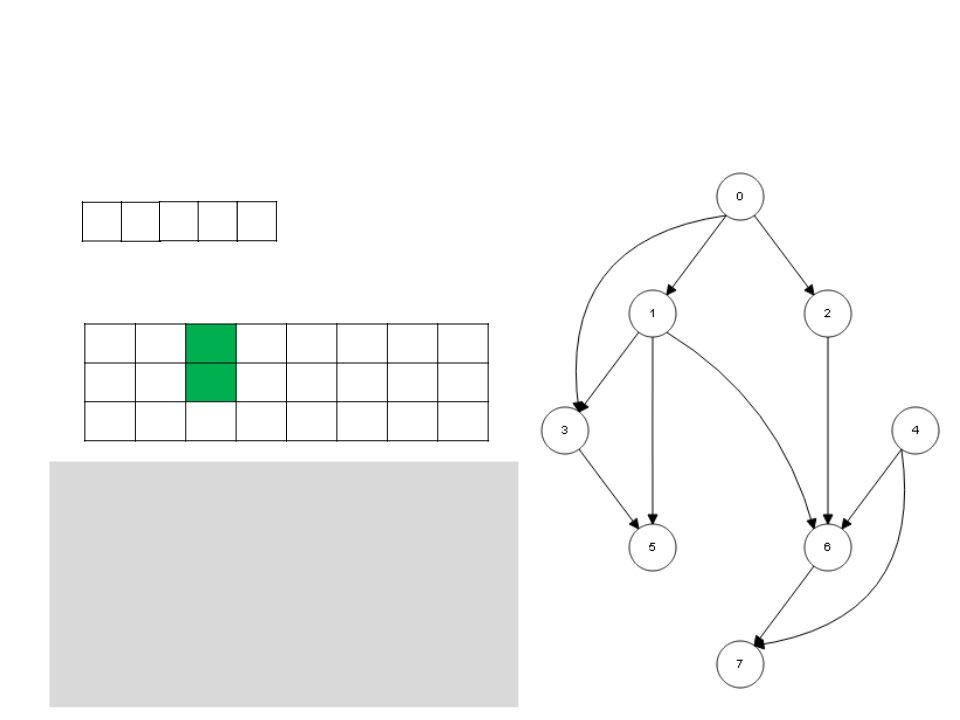
Ordenação Topológica – DFS
1
6 7 3 5
L
0
1 2 3 4 5 6 7
c g b g b w b b b
d 1 2 12 3
11
4 7 8
5 10 9
f
6
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
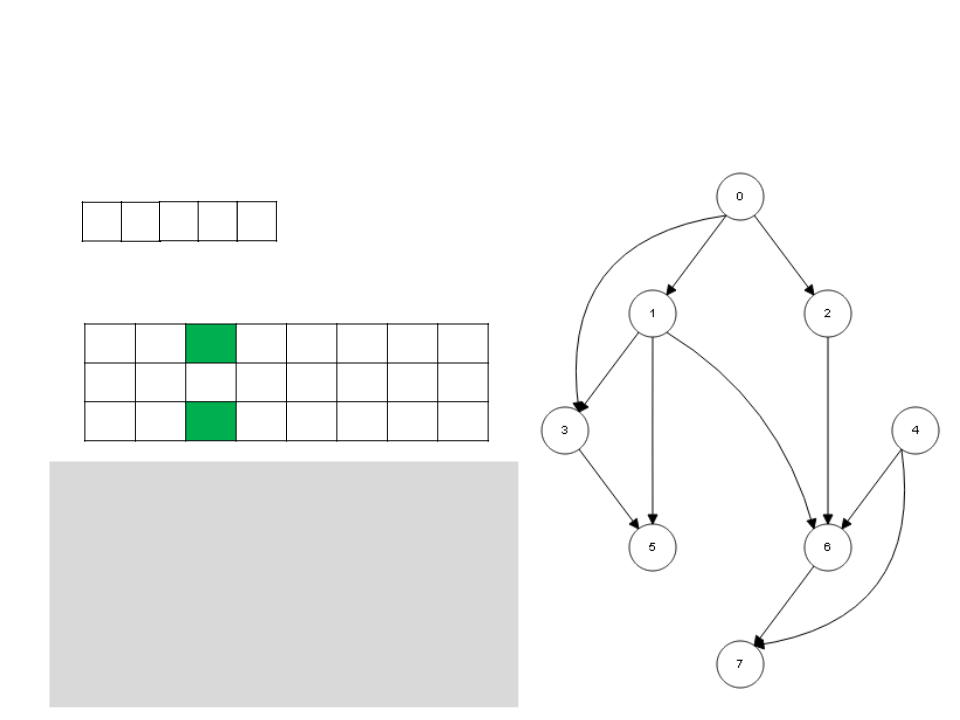
Ordenação Topológica – DFS
1
6 7 3 5
L
0
1 2 3 4 5 6 7
c g b b b w b b b
d 1 2 12 3
f 11 13 6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
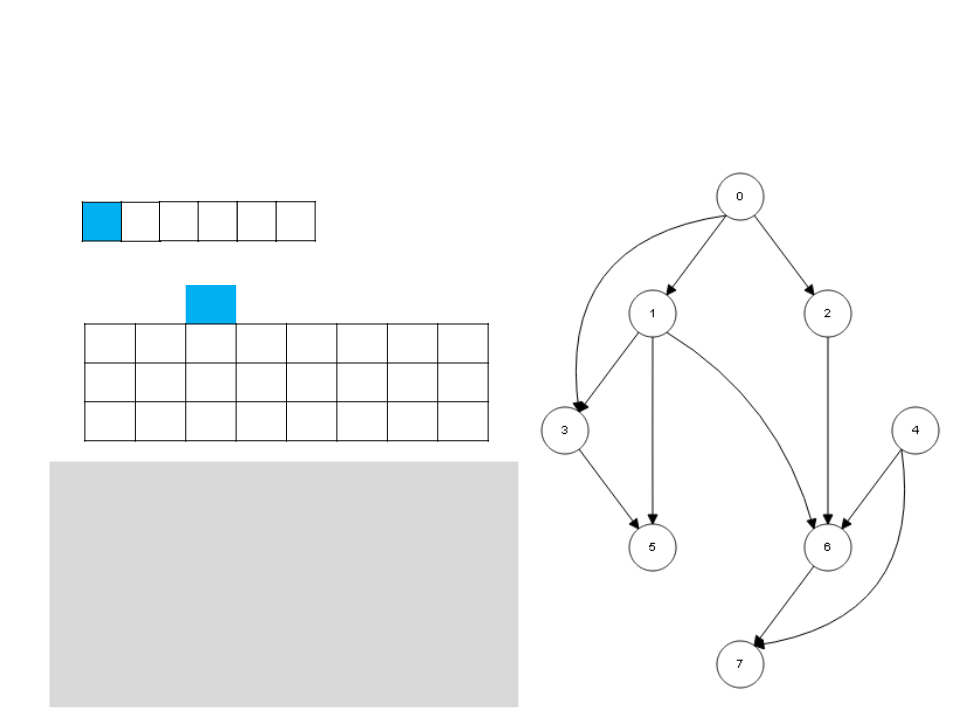
Ordenação Topológica – DFS
2
1 6 7 3 5
L
0
1 2 3 4 5 6 7
c g b b b w b b b
d 1 2 12 3
f 11 13 6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
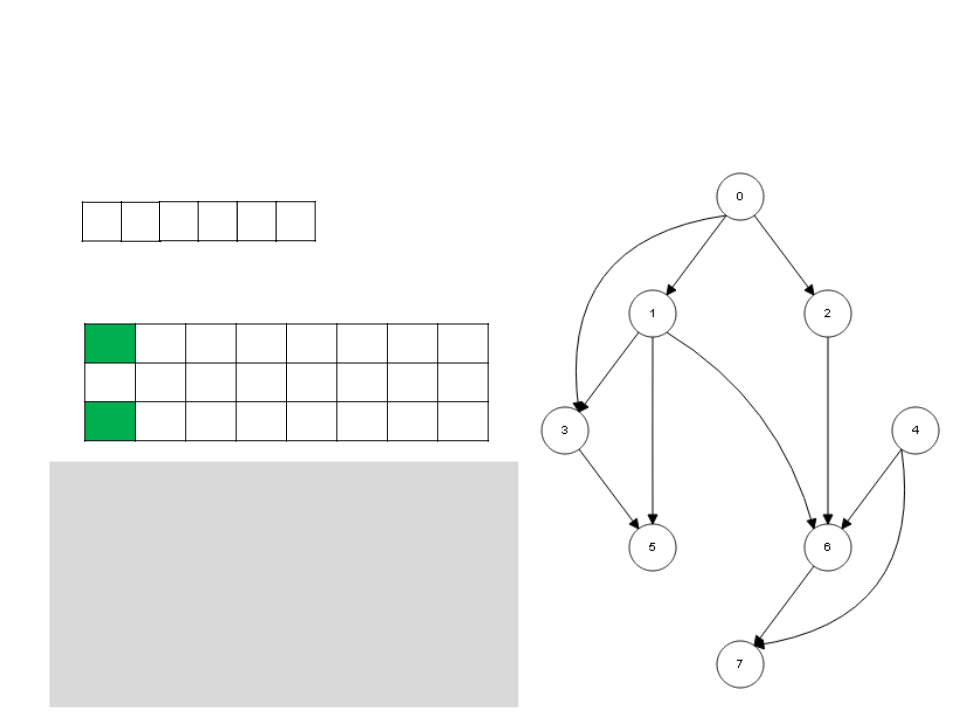
Ordenação Topológica – DFS
2
1 6 7 3 5
L
0
1 2 3 4 5 6 7
c b b b b w b b b
d 1 2 12 3
f 14 11 13 6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
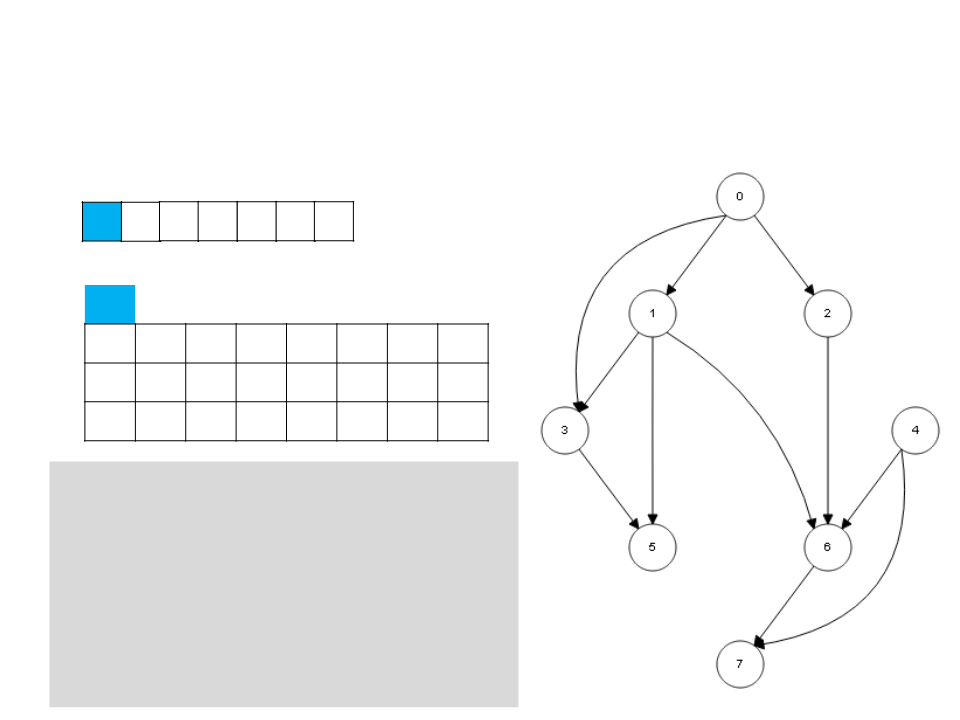
Ordenação Topológica – DFS
0
2 1 6 7 3 5
L
0
1 2 3 4 5 6 7
c b b b b w b b b
d 1 2 12 3
f 14 11 13 6
4 7 8
5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
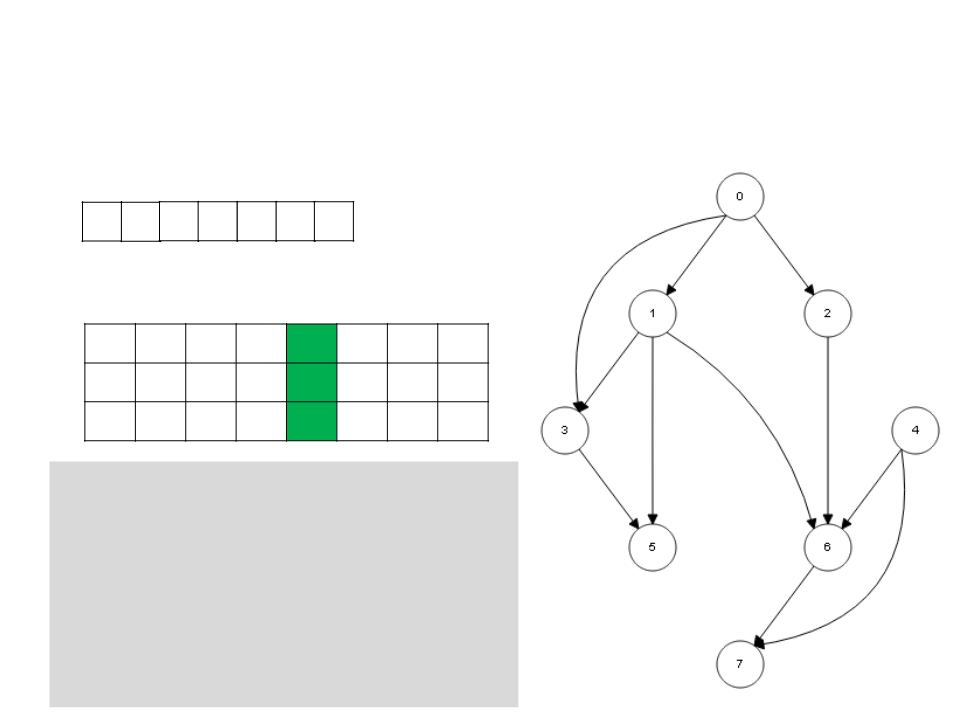
Ordenação Topológica – DFS
0
2 1 6 7 3 5
L
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 2 12 3 15 4 7 8
f 14 11 13 6 16 5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
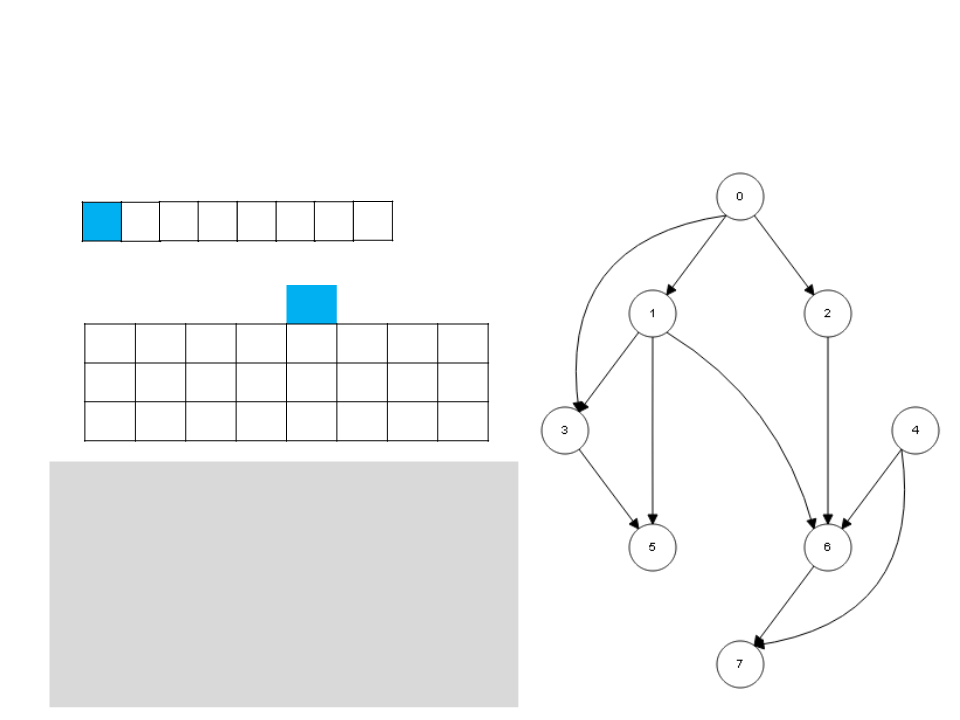
Ordenação Topológica – DFS
4
0 2 1 6 7 3 5
L
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 2 12 3 15 4 7 8
f 14 11 13 6 16 5 10 9
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢀ
[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
insertFront(L, u)
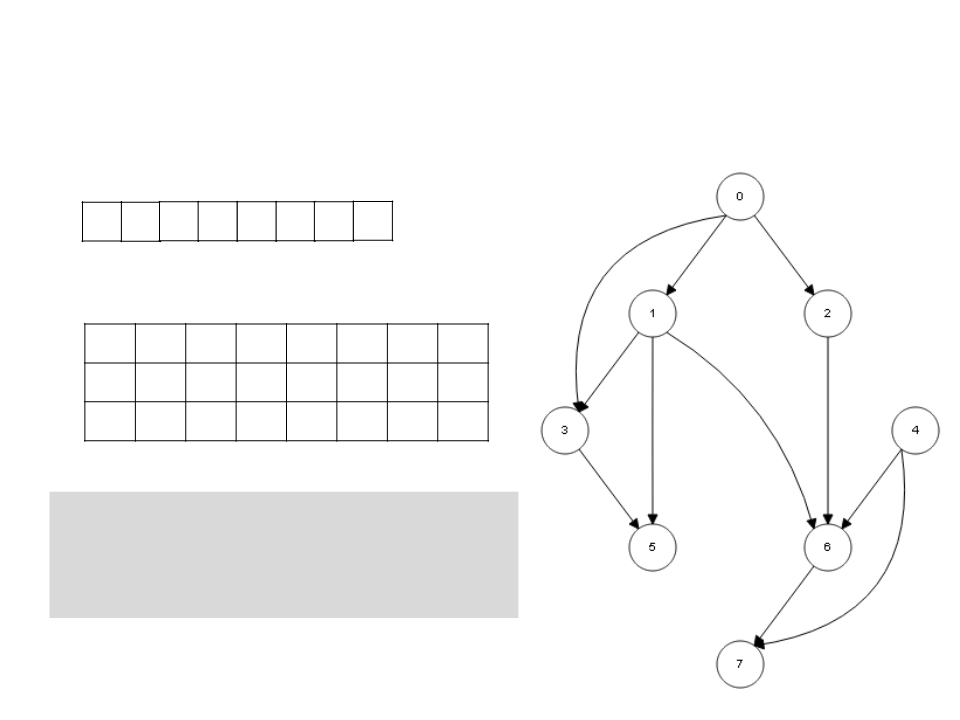
Ordenação Topológica – DFS
4
0 2 1 6 7 3 5
L
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 2 12 3 15 4 7 8
f 14 11 13 6 16 5 10 9
OrdenacaoTopologicaDFS(G)
L ← ∅
BuscaEmProfundidade(G)
return L
Ordenação Topológica (DFS) – Análise
OrdenacaoTopologicaDFS(G)
L ← ∅
• Complexidade: O(V + A)
BuscaEmProfundidade(G)
return L

Ordenação Topológica – Aplicações
•
Dependência entre tarefas: uma ordenação topológica é uma
sequência válida de tarefas;
•
•
•
Pré-requisitos de disciplinas: uma ordenação topológica é uma
sequência válida para se cursar as disciplinas;
Instalação de pacotes: uma ordenação topológica é uma
sequência válida para instalação de pacotes com dependências;
Compilação de sistemas: uma ordenação topológica é uma
sequência válida para compilar bibliotecas com dependências;

Exercícios
Lista de Exercícios 13 – Ordenação Topológica
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Halim e Halim. Competitive Programming, 3rd
Edition, 2003.
Capítulo 4: Graph
•
•
Cormen, Leiserson, Rivest e Stein. Algoritmos –
Teoria e Prática, 2ª. Edição, Editora Campus,
2
002.
Capítulo 22: Algoritmos Elementares de Grafos
