
Projeto e Análise de Algoritmos
Aula 10 – Métodos de Ordenação de
Complexidade Linear
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Ordenação
•
Problema:
–
Entrada: conjunto de itens a1, a2, . . . , an;
–
Saída: conjunto de itens permutados em uma ordem ak1,
ak2, . . . , akn, tal que, dada uma função de ordenação f,
tem-se a seguinte relação: f(ak1) < f(ak2) < . . . < f(akn).
•
•
Ordenar consiste no processo de rearranjar um conjunto de
objetos em uma ordem crescente ou descendente.
O objetivo principal da ordenação é facilitar a recuperação
posterior de itens do conjunto ordenado.

Métodos de Ordenação de
Complexidade Linear
O limite assintótico mínimo para algoritmos de ordenação
baseados em comparações é O(n log n), mas isso não quer
dizer que não seja possível existir um algoritmo de ordenação
melhor!
•
•
•
Existem algoritmos que não são baseados em comparações.
Porém, eles exigem algum outro tipo de conhecimento sobre
os dados a serem ordenados, portanto não são tão genéricos
como os algoritmos clássicos de ordenação por comparação.

Métodos de Ordenação de
Complexidade Linear
•
Algoritmos de ordenação de complexidade O(n):
–
–
–
Counting Sort: Os elementos a serem ordenados são números inteiros
pequenos, isto é, inteiros x onde x ∈ O(n);
Radix Sort: Os elementos a serem ordenados são números inteiros de
comprimento máximo constante, isto é, independente de n;
Bucket Sort: Os elementos são números uniformemente distribuídos
em um determinado intervalo (Exemplo: [0..1)).

Counting Sort
•
•
Suponha que um vetor A a ser ordenado contenha n números
inteiros, todos menores ou iguais a k (k ∈ O(n)).
Ideia básica:
–
Determinar, para cada elemento x da entrada A, o número de
elementos maiores que x;
–
Com esta informação, determinar a posição de cada elemento;
–
Exemplo: se 17 elementos forem menores que x então x ocupa a
posição 18 na saída.

Counting Sort
•
•
O algoritmo Counting Sort ordena estes n números em tempo
O(n + k) (equivalente a O(n)).
O algoritmo usa dois vetores auxiliares:
–
C, de tamanho k, que guarda em C[i] o número de ocorrências de
elementos i em A;
–
B, de tamanho n, onde se constrói o vetor ordenado;

Counting Sort
function couting_sort(int A[], n, k)
begin
for i ← 0 to k do
C[i] ← 0
for j ← 1 to n do
C[A[j]] ← C[A[j]] + 1
for i ← 1 to k do
C[i] ← C[i] + C[i − 1]
for j ← 1 to n do
begin
O(n + k)
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
end
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for i ← 0 to k do
C[i] ← 0
C 0 0 0 0 0
4
0
1
2
3
for j ← 1 to n do
C[A[j]] ← C[A[j]]+1
C 1 0 2 1 2
0
1
2
3
4
for i ← 1 to k do
C[i] ← C[i] + C[i−1]
C 1 1 3 4 6
0
1
2
3
4
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 1 1 3 4 6
0
1
2
3
4
B
4
6
1
2
3
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 1 1 3 4 5
0
1
2
3
4
B
4
6
1
2
3
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 1 1 3 4 5
0
1
2
3
4
B 0
1
4
6
2
3
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 3 4 5
0
1
2
3
4
B 0
1
4
6
2
3
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 3 4 5
0
1
2
3
4
B 0
1
2
3
4
6
2
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 2 4 5
0
1
2
3
4
B 0
1
2
3
4
6
2
4
5
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 2 4 5
0
1
2
3
4
B 0 2 2
4
6
1
2
3
4
5
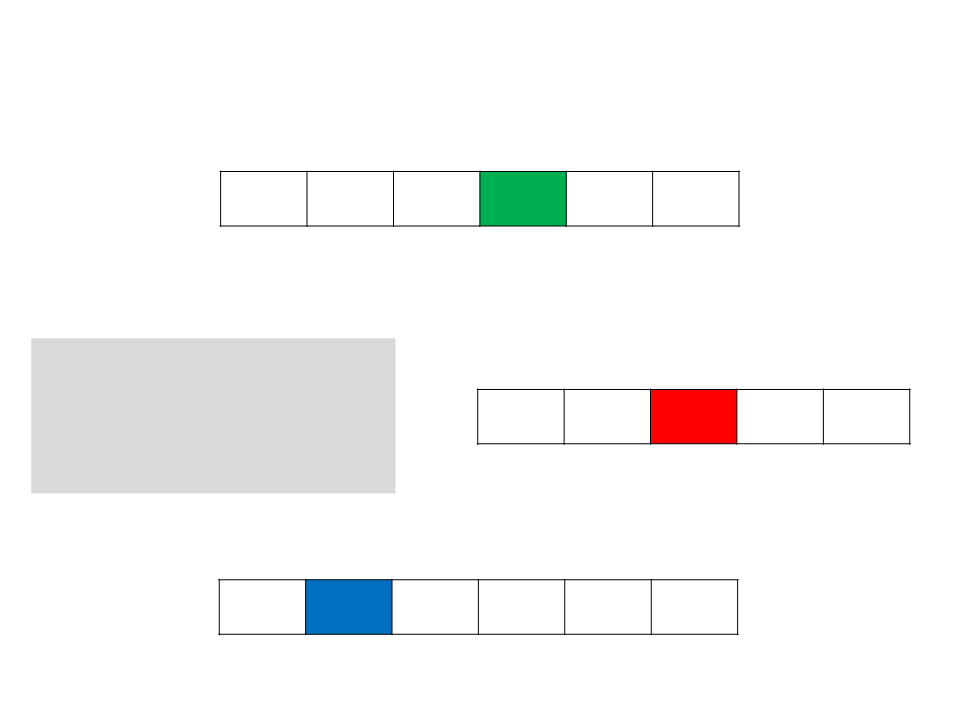
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 1 4 5
0
1
2
3
4
B 0 2 2
4
6
1
2
3
4
5
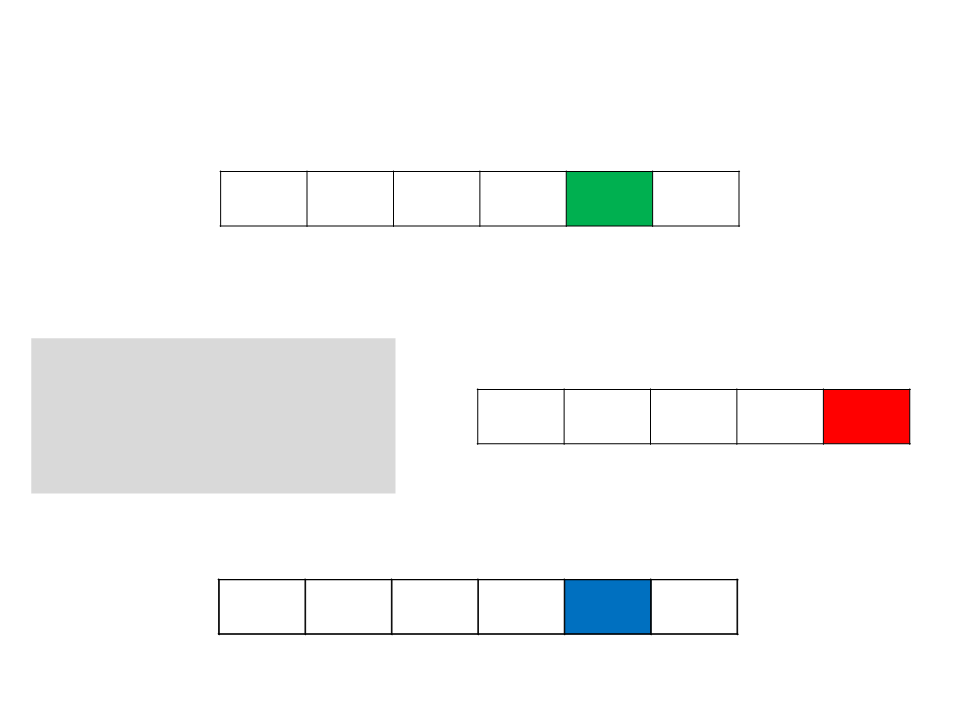
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 1 4 5
0
1
2
3
4
B 0 2 2
4 4
5 6
1
2
3
4
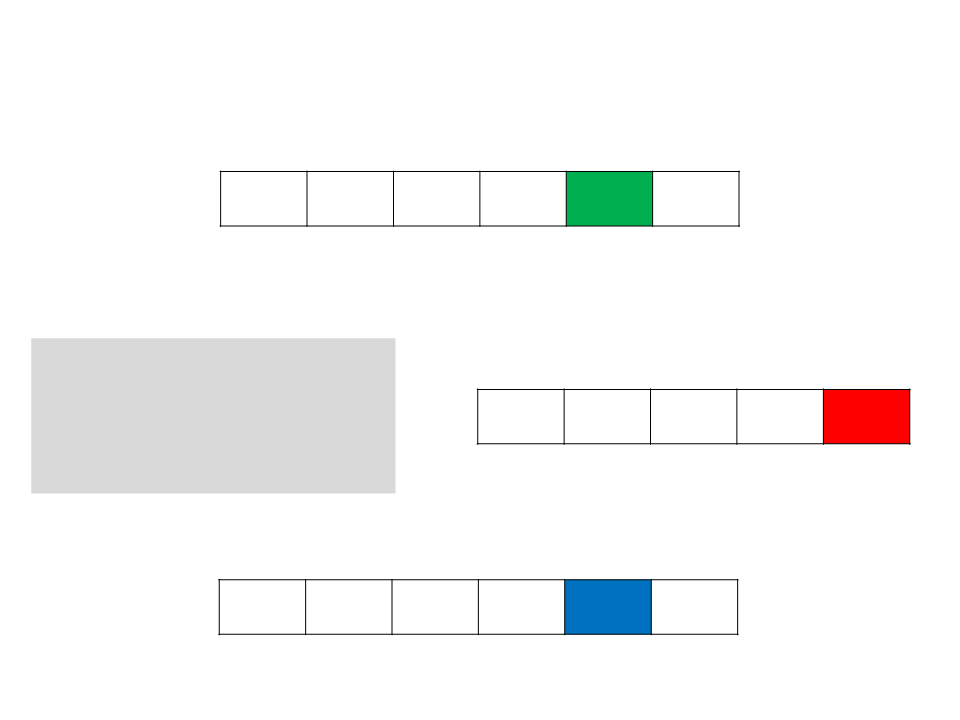
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 1 4 4
0
1
2
3
4
B 0 2 2
4 4
5 6
1
2
3
4
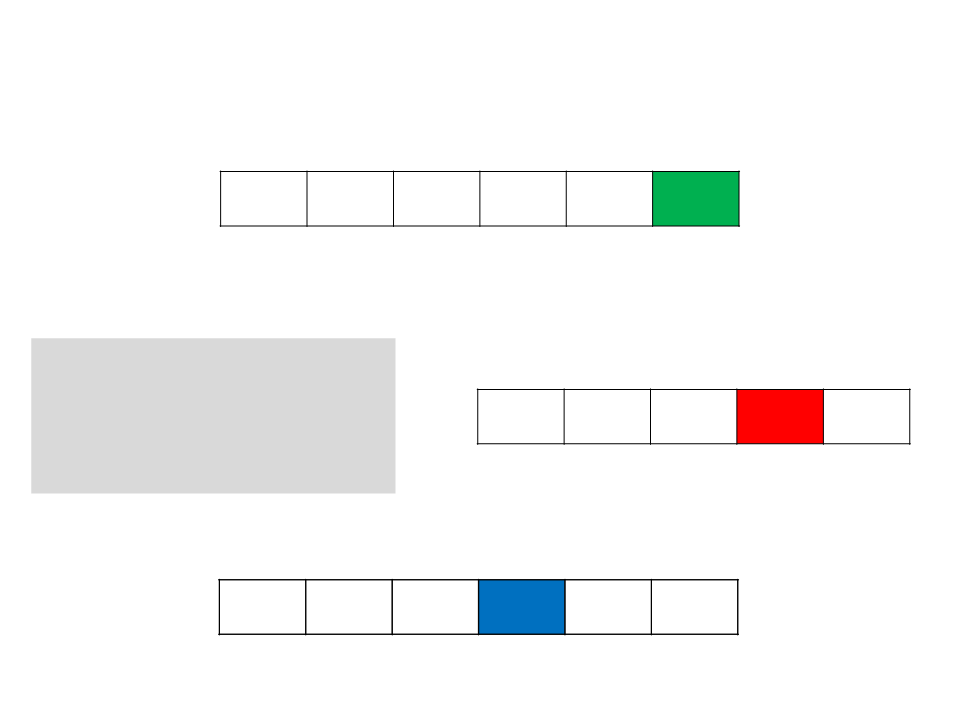
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 1 4 4
0
1
2
3
4
B 0 2 2 3 4 4
1
2
3
4
5
6
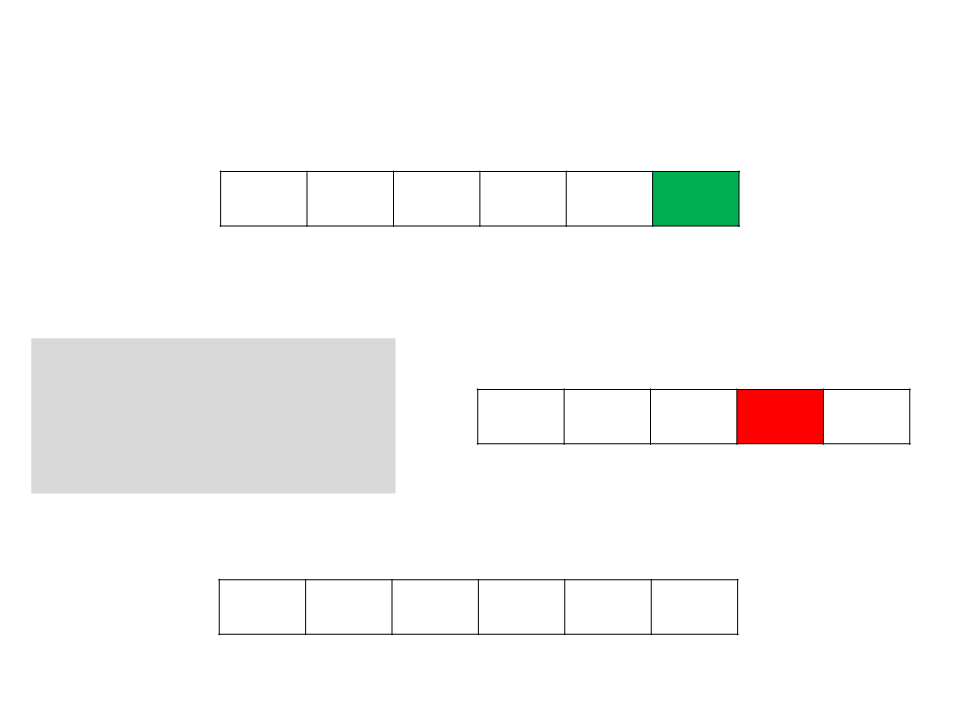
Counting Sort
A 4 0 2 2 4 3
1
2
3
4
5
6
for j ← 1 to n do
begin
B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]] − 1
end
C 0 1 1 3 4
0
1
2
3
4
B 0 2 2 3 4 4
1
2
3
4
5
6

Counting Sort – Complexidade
•
•
O algoritmo não faz comparações entre elementos de A.
Sua complexidade deve ser medida com base nas outras
operações (aritméticas, atribuições, etc.)
•
•
Claramente, o número de tais operações é uma função em
O(n + k), já que temos dois loops simples com n iterações e
dois com k iterações.
Assim, quando k ∈ O(n), este algoritmo tem complexidade
O(n).

Radix Sort
•
•
Pressupõe que as chaves de entrada possuem limite no valor
e no tamanho (quantidade de dígitos d);
Ordena em função dos dígitos (um de cada vez) a partir do
menos significativo;
–
É essencial utilizar um segundo algoritmo estável para realizar a
ordenação de cada dígito.
function radix_sort(int A[], n)
begin
for i ← 1 to n do
ordene os elementos de A pelo i-ésimo dígito usando
um metodo estável
end
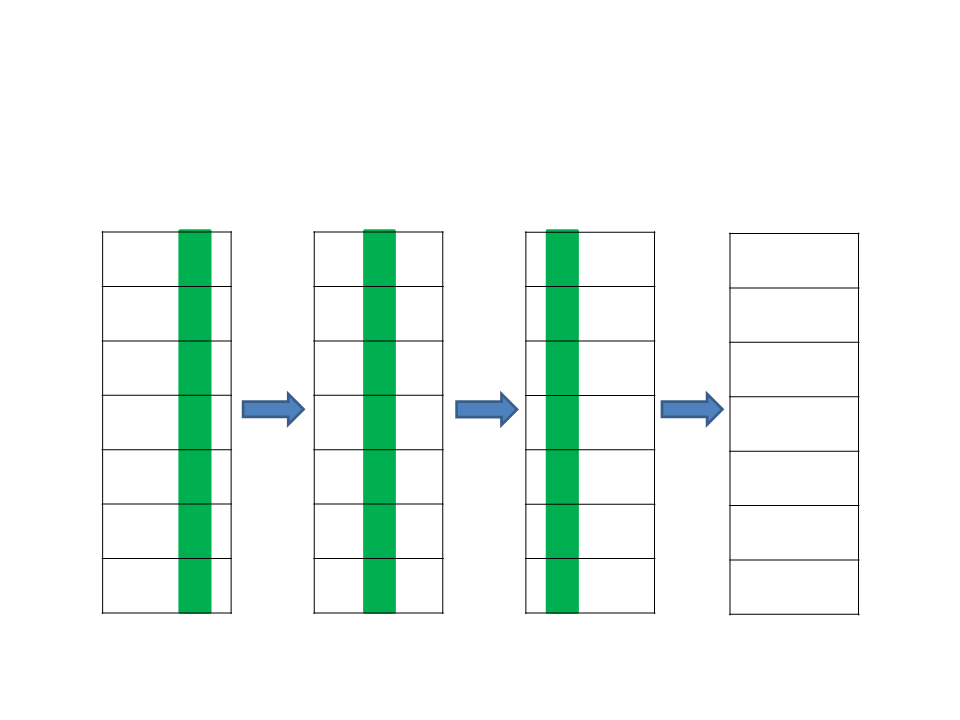
Radix Sort
3
4
6
8
4
7
3
2 9
5 7
5 7
3 9
3 6
2 0
5 5
7 2 0
3 5 5
4 3 6
4 5 7
6 5 7
3 2 9
8 3 9
7 2 0
3 2 9
3 5 5
4 3 6
4 5 7
6 5 7
7 2 0
8 3 9
3 2 9
4 3 6
8 3 9
3 5 5
4 5 7
6 5 7

Radix Sort – Complexidade
•
•
•
A complexidade do Radix Sort depende da complexidade do
algoritmo estável usado para ordenar cada dígito dos
elementos.
Se essa complexidade for O(n), obtemos uma complexidade
total de Θ(dn) para o Radix Sort.
–
Como supomos d constante, a complexidade reduz-se para O(n).
Se o algoritmo estável for, por exemplo, o Counting Sort,
obtemos a complexidade O(n + k).
–
Supondo k ∈ O(n), resulta numa complexidade O(n).

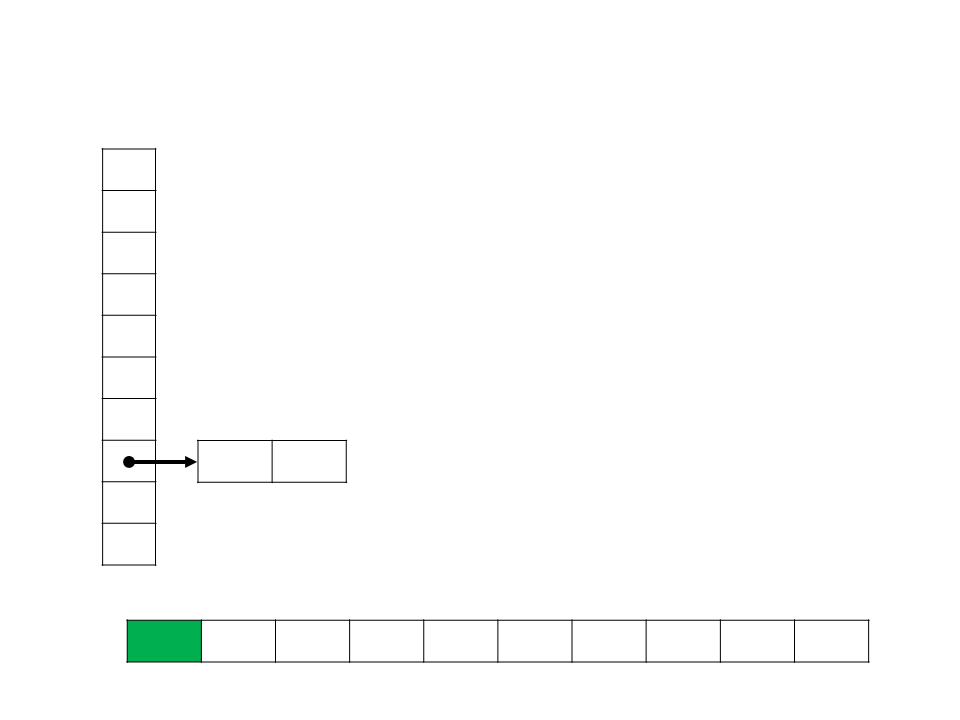
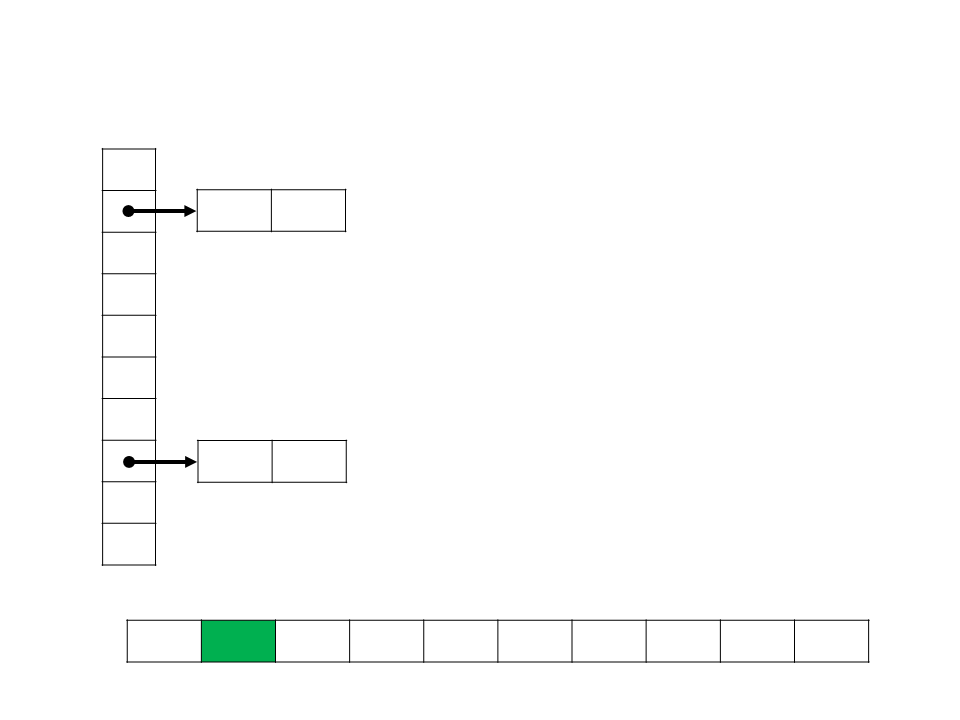
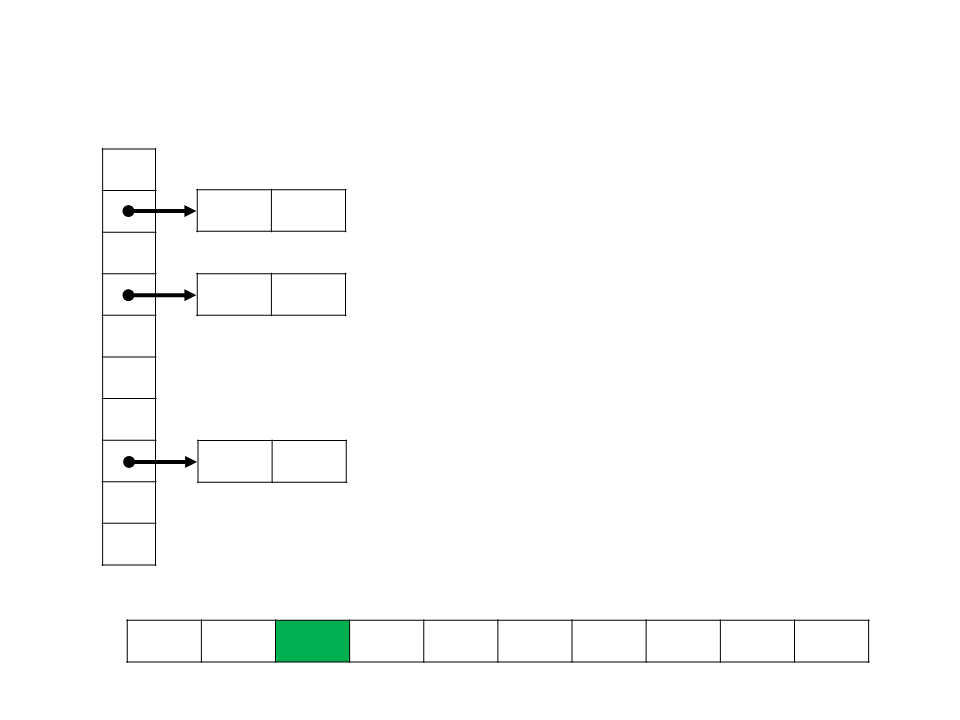
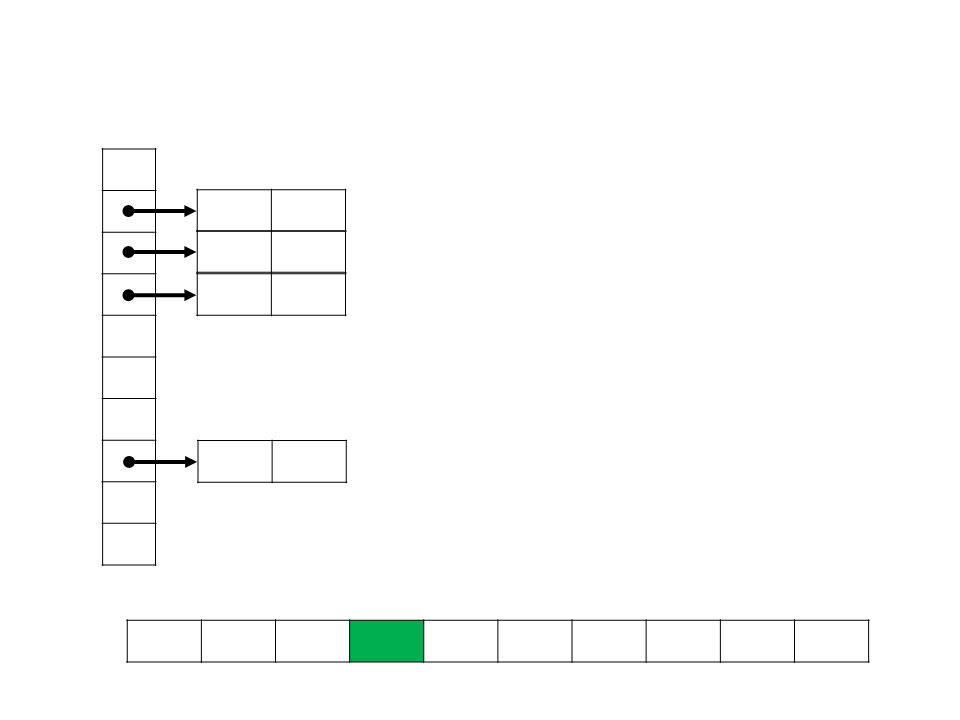
Bucket Sort
•
•
Assume que a entrada consiste em elementos distribuídos de
forma uniforme sobre uma determinado intervalo (exemplo:
[
0..1]);
A ideia do Bucket Sort é dividir o intervalo em n subintervalos
de mesmo tamanho (baldes), e então distribuir os n números
nos baldes;
•
•
Uma vez que as entradas são uniformemente distribuídas,
não se espera que muitos números caiam em cada balde;
Para produzir a saída ordenada, basta ordenar os números em
cada balde, e depois examinar os baldes em ordem, listando
seus elementos;

Bucket Sort
function bucket_sort(int A[], n, k)
begin
crie o vetor de baldes (listas) B de tamanho k
for i ← 1 to n do
insira A[i] no seu balde B[msbits(A[i])] na ordem
for i ← 1 to k do
concatene os baldes B[i]
end
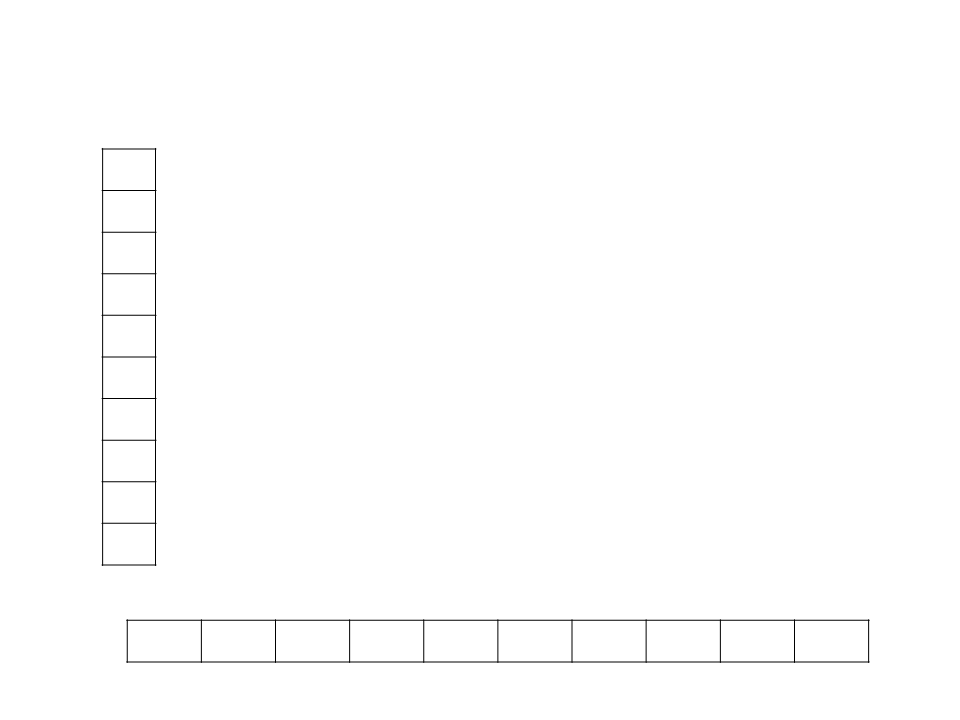
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
/
/
/
/
/
/
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
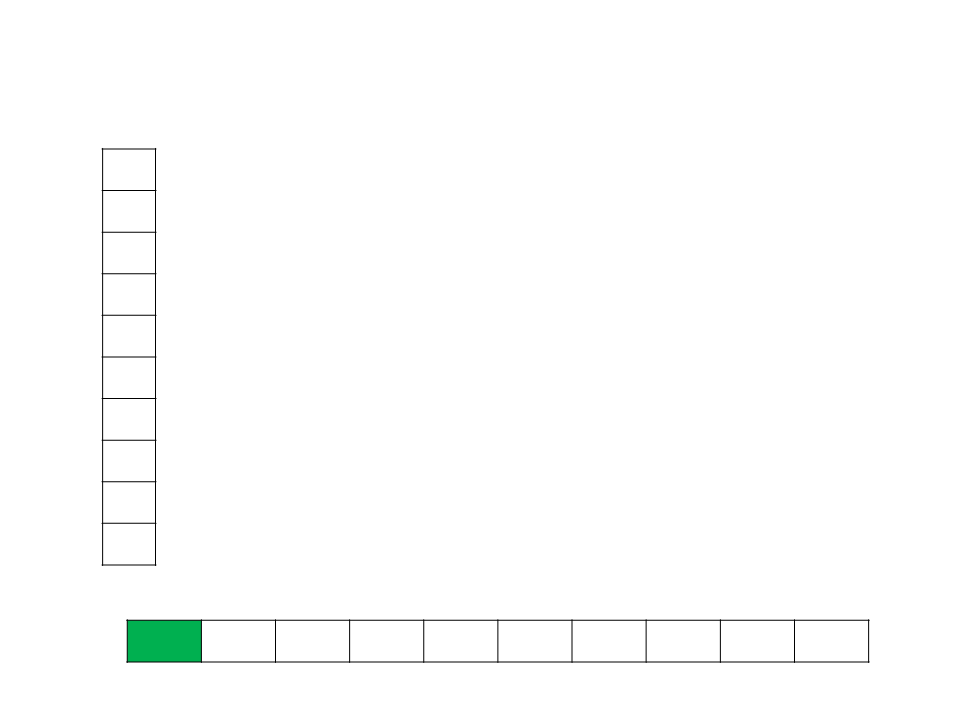
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
/
/
/
/
/
/
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
/
/
/
/
/
/
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,78
/
/
/
/
/
/
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,39
/
/
/
/
/
/
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,26
0,39
/
/
/
/
/
/
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
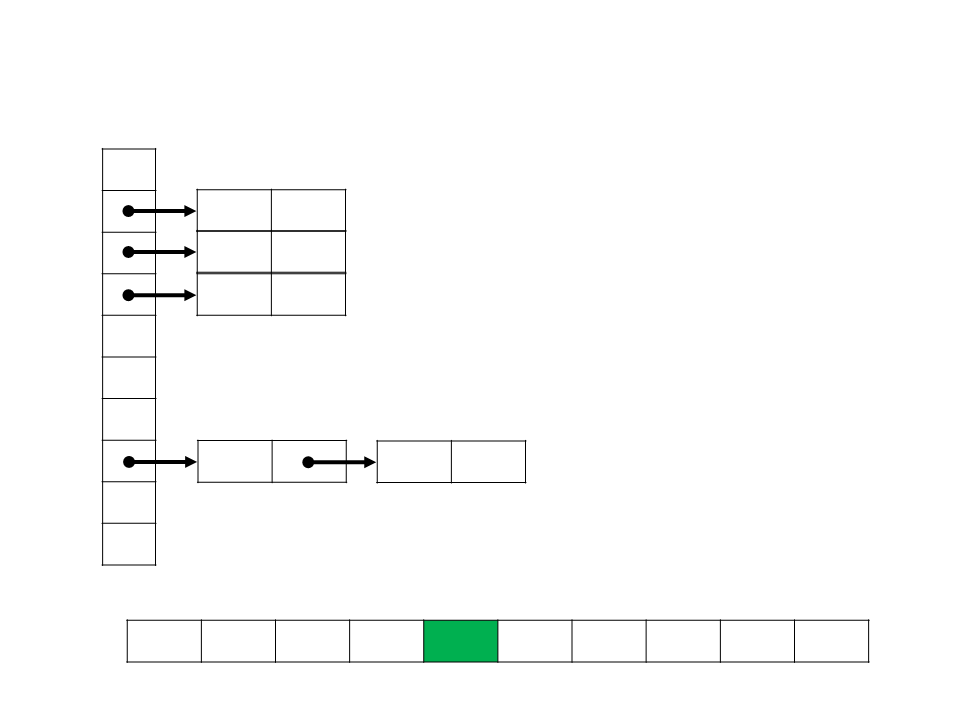
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,26
0,39
/
/
/
/
/
/
0,72
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
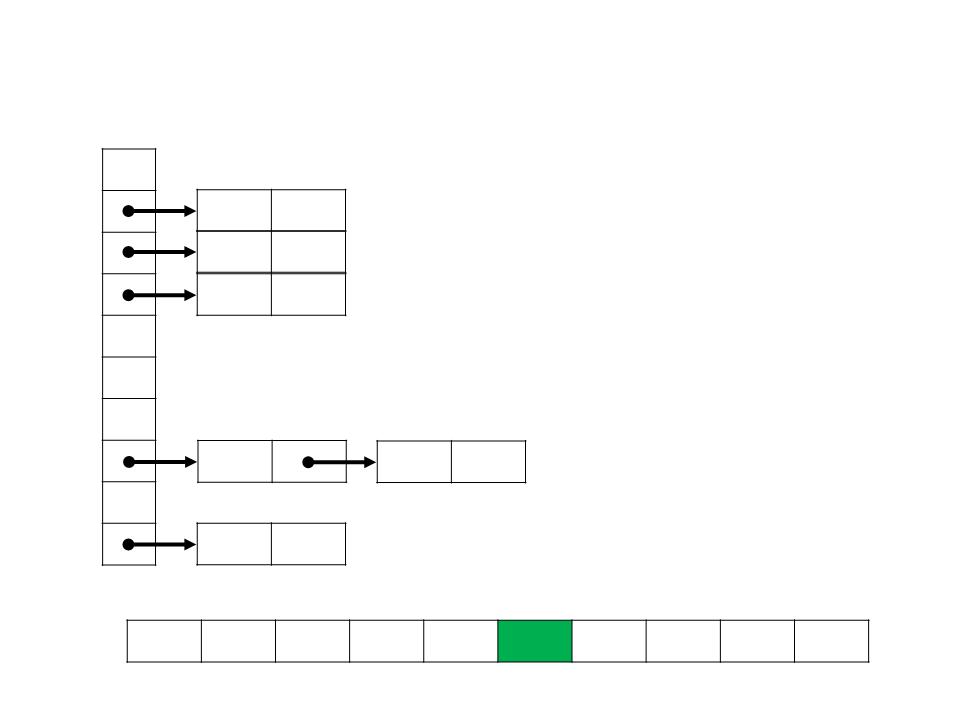
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,26
0,39
/
/
/
/
/
/
0,72
0,94
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
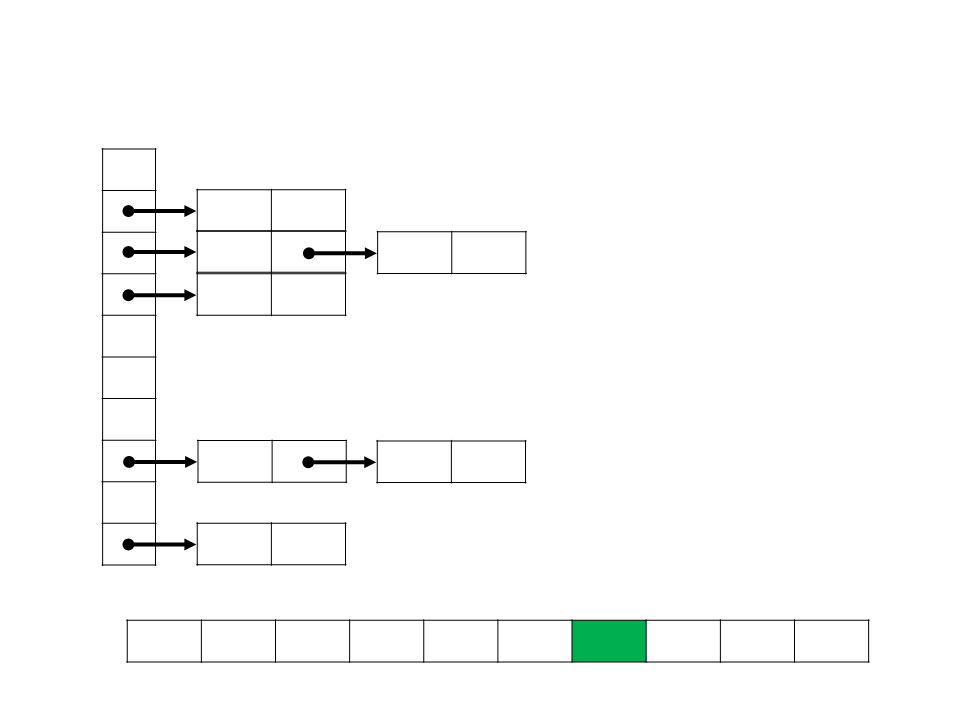
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,17
0,21
0,39
/
/
0,26
/
/
/
/
0,72
0,94
0,78
/
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
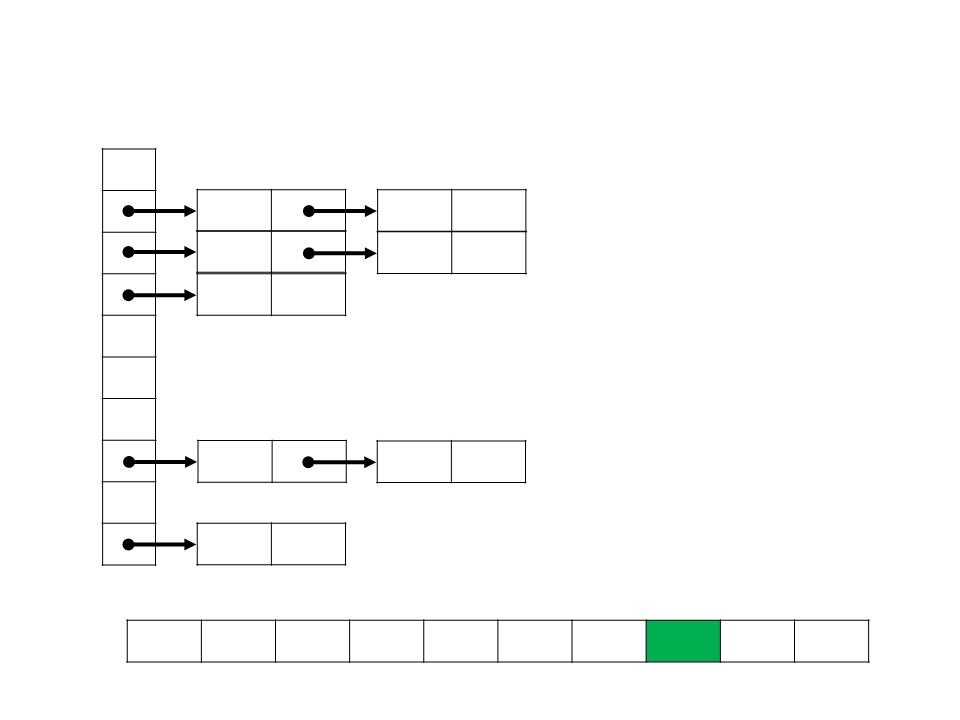
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,12
0,21
0,39
0,17
0,26
/
/
/
/
/
/
/
0,72
0,94
0,78
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
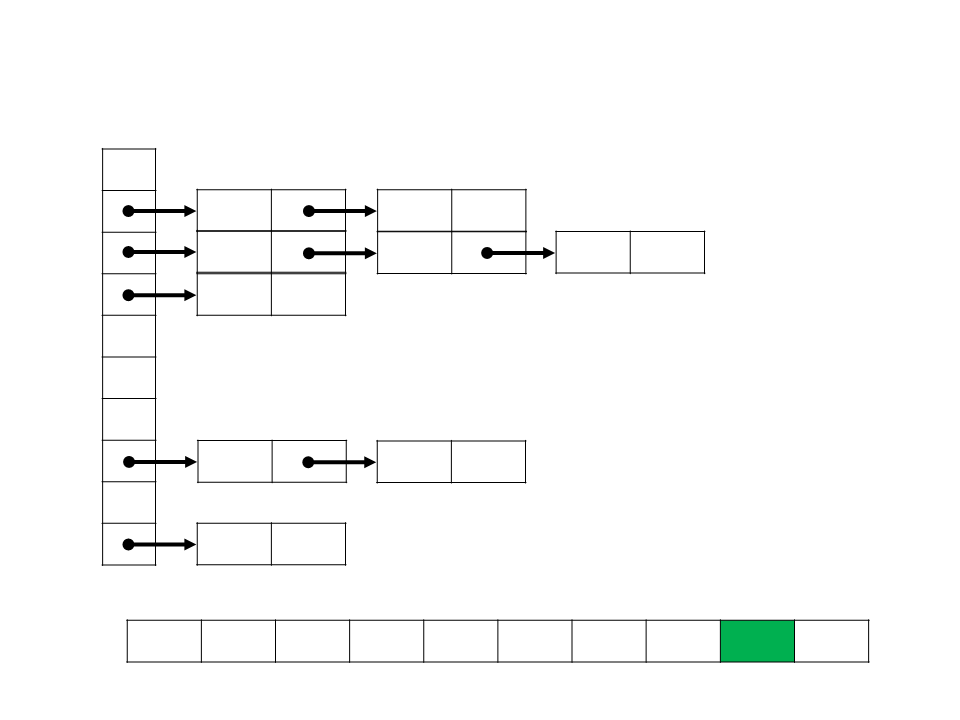
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,12
0,21
0,39
0,17
0,23
/
0,26
/
/
/
/
/
/
0,72
0,94
0,78
/
/
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68
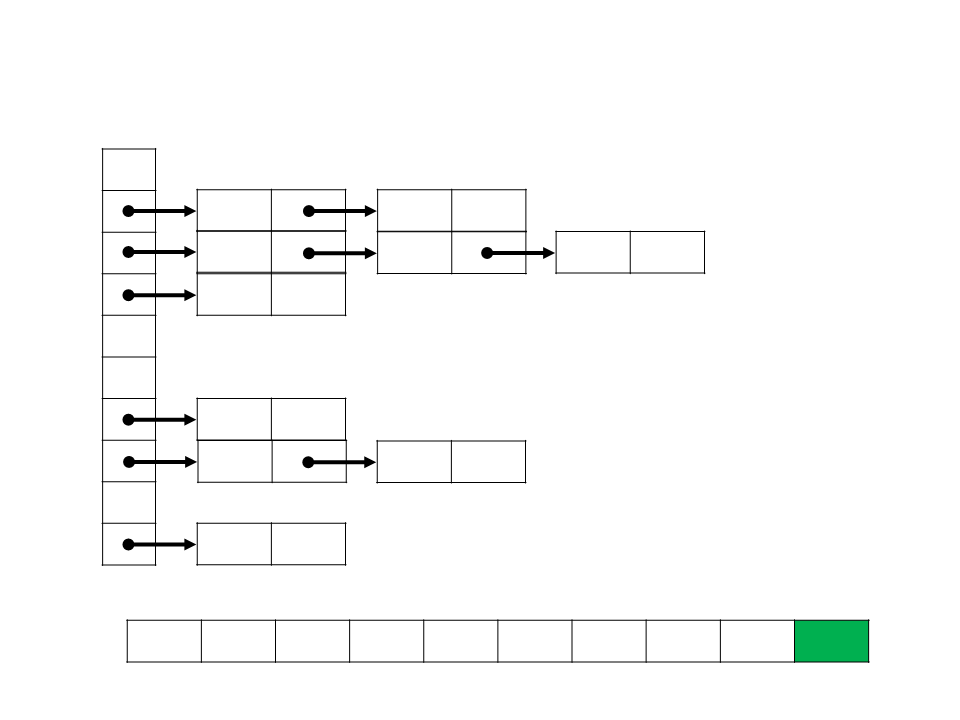
Bucket Sort
B
0
1
2
3
4
5
6
7
8
9
/
0,12
0,21
0,39
0,17
0,23
/
0,26
/
/
/
/
/
0,68
0,72
0,78
/
/
0,94
A 0,78 0,17 0,39 0,26 0,72 0,94 0,21 0,12 0,23 0,68

Bucket Sort – Complexidade
•
Se o vetor estiver uniformemente distribuído:
–
Caso médio: O(n + k)
•
•
Pior Caso: O(n2)
Bom quando o número de chaves é pequeno e há
em média poucos elementos por balde.

Exercício
1
armazenar o número de ocorrências de valores no vetor de
entrada. Considerando vetor de entrada A = {2, 1, 5, 2, 4, 4, 5, 4,
) O algoritmo Counting Sort utiliza um vetor auxiliar C para
3
, 4, 1, 3, 0, 1, 3, 0}, o conteúdo armazenado no vetor C após a
execução do Counting Sort é C = {0, 2, 5, 7, 11, 14}. Verdadeiro
ou Falso? Justifique sua resposta apresentando os valores do
vetor C durante as etapas do algoritmo.

Exercícios
Lista de Exercícios 11 – Algoritmos de
Ordenação de Complexidade Linear
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Cormen, T., Leiserson, C., Rivest, R., e Stein, C.
Algoritmos – Teoria e Prática (tradução da 2ª.
Edição americana), Editora Campus, 2002.
Capítulo 8: Ordenação em Tempo Linear
