
Projeto e Análise de Algoritmos
Aula 05 – Técnicas de Projeto de Algoritmos
(Programação Dinâmica)
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Estratégias de Projeto de Algoritmos
•
•
•
•
•
•
•
•
•
•
Força Bruta (Brute Force)
Dividir e Conquistar (Divide and Conquer)
Diminuir e Conquistar (Decrease and Conquer)
Transformar e Conquistar (Transform and Conquer)
Compromisso Tempo–Espaço (Space and Time Tradeoffs)
Estratégia Gulosa (Greedy)
Programação Dinâmica (Dynamic Programming)
Voltando Atrás (Backtracking)
Ramificar e Limitar (Branch and Bound)
Algoritmos Aproximados

Programação Dinâmica
•
A programação dinâmica tem como objetivo reduzir
o tempo de execução de um programa utilizando
soluções ótimas a partir de subproblemas
previamente calculados.
–
–
Resolvem-se os problemas de pequena dimensão e
guardam-se as soluções;
A solução de um problema é obtida combinando as de
problemas de menor dimensão.

Programação Dinâmica
•
•
Passos gerais de um algoritmo baseado em Programação
Dinâmica:
–
Dividir o problema em sub problemas;
–
Computar os valores de uma solução de forma bottom-up e
armazená-los (memorização);
–
Construir a solução ótima para cada subproblema utilizado os valores
computados.
Quando usar Programação Dinâmica?
–
Quando a solução ótima de um subproblema pode ser composta pelas
soluções ótimas dos subproblemas;
–
Quando o calculo da solução ótima implica muitas vezes no calculo do
mesmo subproblema.
Exemplo 1: Série de Fibonacci
•
•
Série de Fibonacci:
0
ꢁꢂ ꢃ = ቐ 1
ꢀ
ꢄꢅ ꢃ = 0
ꢄꢅ ꢃ = 1
ꢁꢂ ꢃ − 1 + ꢀꢁꢂ ꢃ − 2 ꢄꢅ ꢃ > 1
ꢀ
Algoritmo Simples:
1
2
3
4
5
. Fibonacci(n)
. se n < 2 então
. retorne n
. senão
O(2n)
. retorne fibonacci(n – 1) + fibonacci(n – 2)
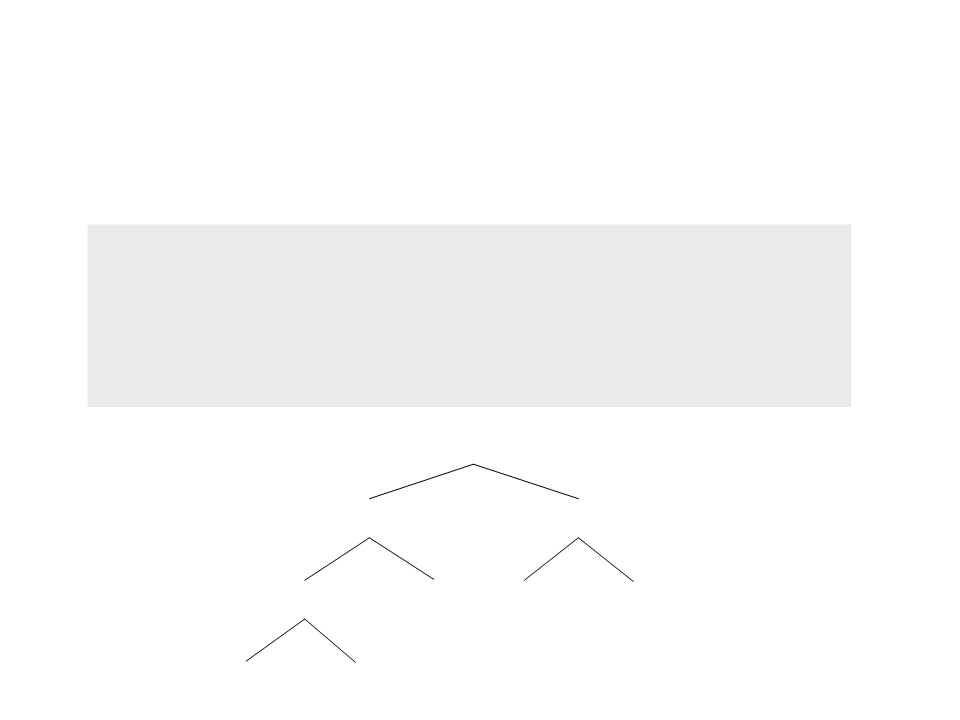
Exemplo 1: Série de Fibonacci
•
Algoritmo Simples:
1
2
3
4
5
. fib(n)
.
.
.
.
se n < 2 então
retorne n
senão
retorne fib(n – 1) + fib(n – 2)
fib(5)
fib(4)
fib(3)
fib(3)
fib(2) fib(2)
fib(1)
Problema: repetição de chamadas!
fib(2)
fib(1)

Exemplo 1: Série de Fibonacci
•
Algoritmo Baseado em Programação Dinâmica:
1
2
3
4
5
6
7
8
9
. fib(n)
O(n)
. se n < 2 então
.
.
retorne n
senão
. V[0] ← 0
. V[1] ← 1
. para i ← 2 até n faça
.
V[i] ← V[i-1] + V[i-2]
. retorne V[i]
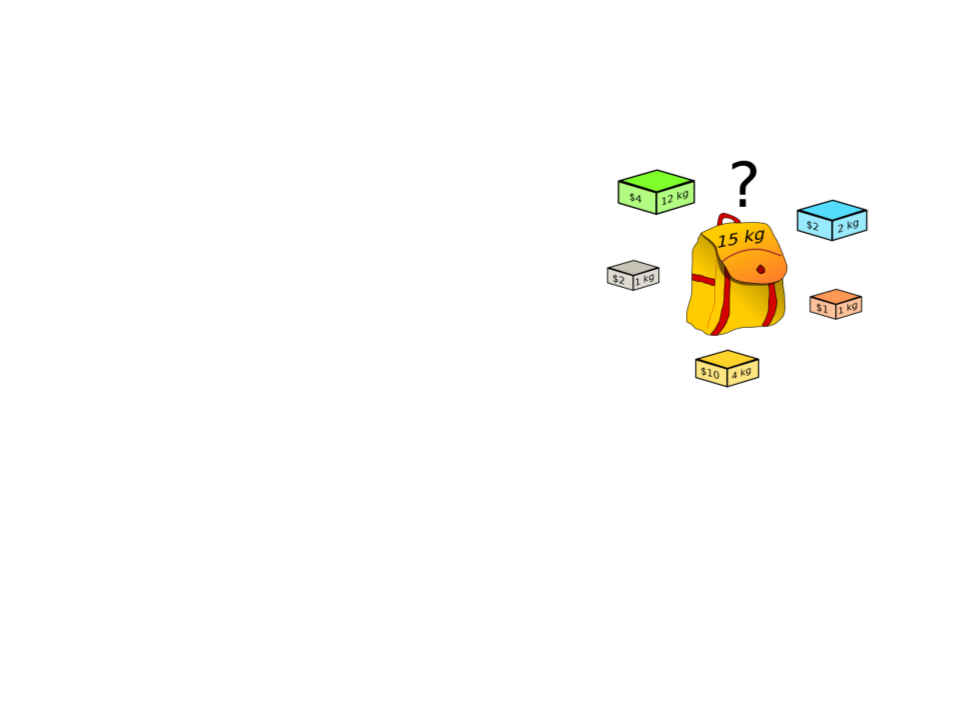
Exemplo 2: Problema da Mochila
•
•
Dados n itens:
–
–
–
Pesos: w1, w2, ..., wn
Valores: v1, v2, …, vn
Uma mochila de capacidade W
Problema: encontrar o subconjunto mais valioso de
itens que caibam dentro da mochila (Knapsack
Problem).

Exemplo 2: Problema da Mochila
•
•
Problema: encontrar o subconjunto mais valioso de
itens que caibam dentro da mochila (Knapsack
Problem).
Solução Baseada em Programação Dinâmica:
0
ꢆ[ꢁ, ꢇ] = ቐ ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ = 0 ꢈꢉ ꢇ = 0
ꢄꢅ ꢇꢊ > ꢇ
max ꢋꢊ + ꢆ ꢁ − 1, ꢇ − ꢇꢊ , ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ > 0 ꢅ ꢇꢊ ≤ ꢇ
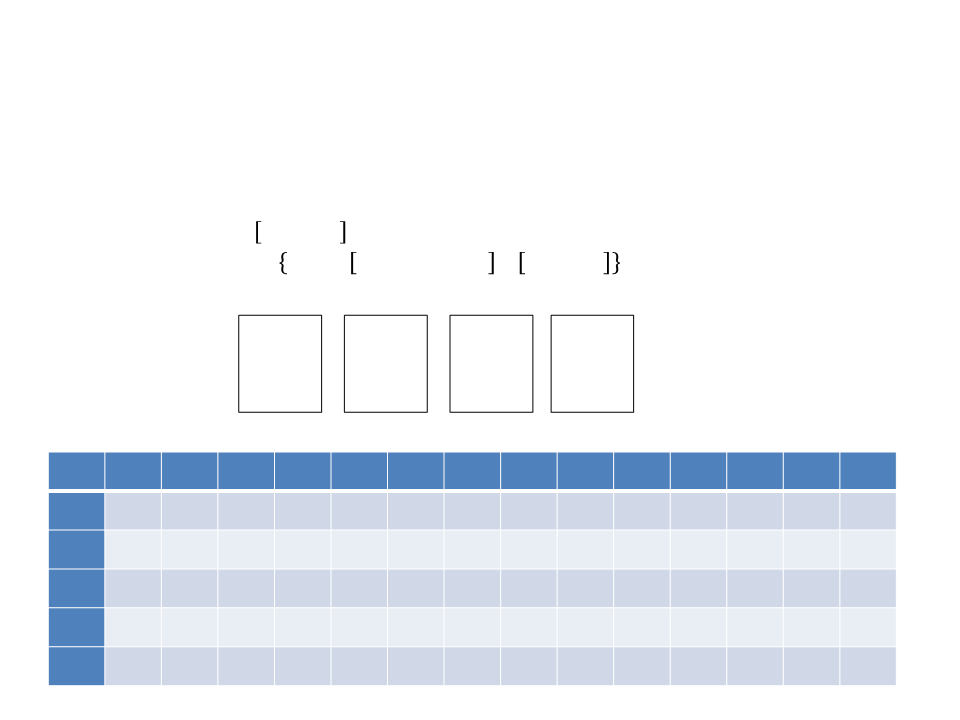
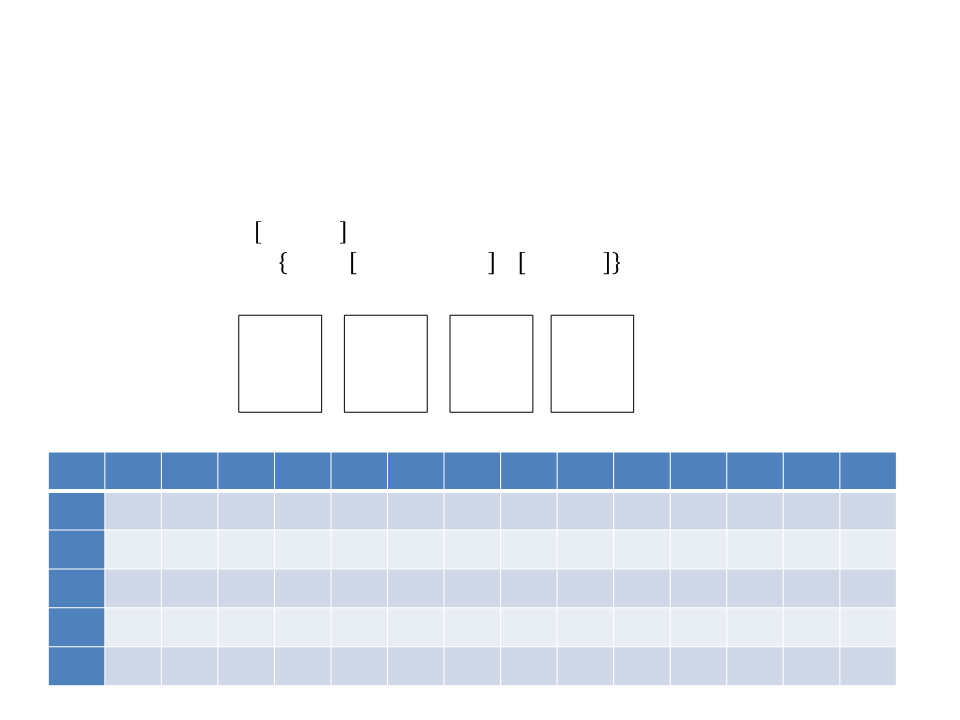
Exemplo 2: Problema da Mochila
0
ꢆ[ꢁ, ꢇ] = ቐ ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ = 0 ꢈꢉ ꢇ = 0
ꢄꢅ ꢇꢊ > ꢇ
max ꢋꢊ + ꢆ ꢁ − 1, ꢇ − ꢇꢊ , ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ > 0 ꢅ ꢇꢊ ≤ ꢇ
Item 1
V1 = 5
W1 = 5
Item 2
V2 = 4
W2 = 6
Item 3
V2 = 7
W2 = 8
Item 4
V2 = 7
W2 = 4
MAX = 13
w
0
1
2
3
4
5
6
7
8
9
10 11 12 13
0
1
2
3
4
i
Exemplo 2: Problema da Mochila
0
ꢆ[ꢁ, ꢇ] = ቐ ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ = 0 ꢈꢉ ꢇ = 0
ꢄꢅ ꢇꢊ > ꢇ
max ꢋꢊ + ꢆ ꢁ − 1, ꢇ − ꢇꢊ , ꢆ ꢁ − 1, ꢇ
ꢄꢅ ꢁ > 0 ꢅ ꢇꢊ ≤ ꢇ
Item 1
V1 = 5
W1 = 5
Item 2
V2 = 4
W2 = 6
Item 3
V2 = 7
W2 = 8
Item 4
V2 = 7
W2 = 4
MAX = 13
w
0
0
0
0
0
0
1
0
0
0
0
0
2
3
0
0
0
0
0
4
0
0
0
0
7
5
6
0
5
5
5
7
7
0
5
5
5
7
8
0
5
5
7
7
9
0
5
5
7
10 11 12 13
0
1
2
3
4
0
0
0
0
0
0
5
5
5
7
0
5
5
7
0
5
9
9
0
5
9
9
0
5
i
9
12
12 12 12 14 14

Exemplo 2: Problema da Mochila
1
2
3
4
5
6
7
8
9
1
1
1
1
1
1
. Mochila_DP(wi, vi, n, W)
.
.
.
para w ← 0 até W faça
V[0,w] ← 0
O(nW)
para i ← 1 até n faça
. V[i,0] ← 0
.
para i ← 1 até n faça
.
para w ← 0 até W faça
se wi ≤ w então
.
.
se vi + V[i-1, w-wi] > V[i-1, w] então
V[i,w] ← vi + V[i-1, w-wi]
senão
0.
1.
2.
V[i,w] ← V[i-1,w]
3. senão
4.
V[i,w] ← V[i-1,w]
5. retorna V[n, W]

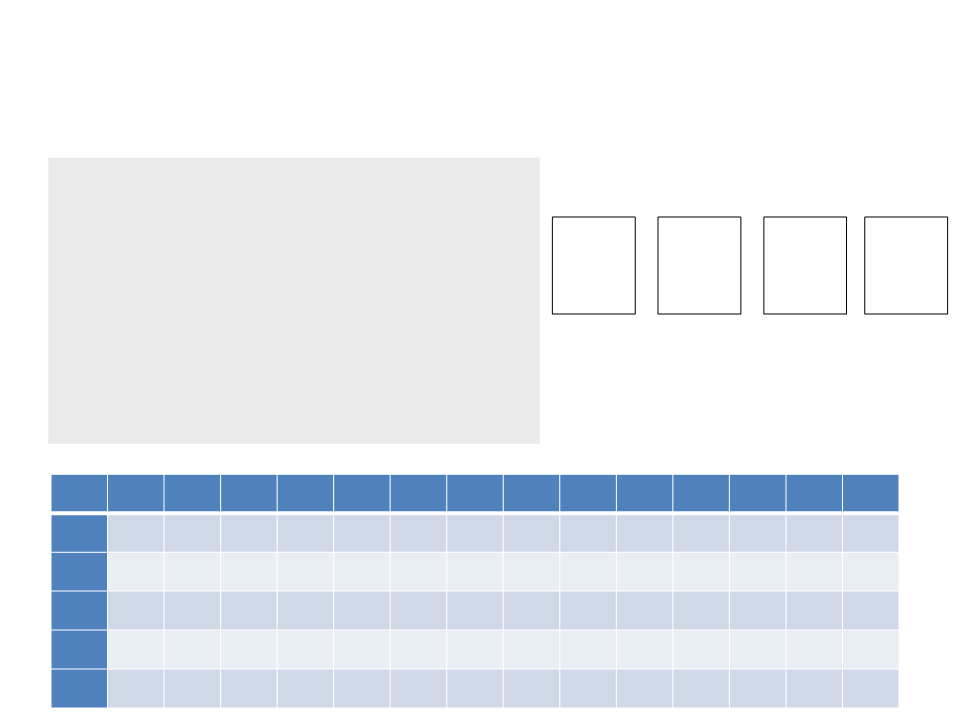
Exemplo 2: Problema da Mochila
•
O algoritmo encontra o máximo valor possível que pode ser
carregado na mochila. Como descobrir quais itens devem ser
carregados?
–
Toda a informação necessária para descobrir quais são os itens está na
tabela.
1. i ← n
2
3
4
5
6
7
8
9
. k ← W
. enquanto i > 0 e k > 0 faça
. se V[i, k] ≠ V[i-1, k] então
. coloque o item i na mochila
. i ← i - 1
. k ← k - wi
. senão
. i ← i-1
Exemplo 2: Problema da Mochila
1
2
3
4
5
6
7
8
9
. i ← n
. k ← W
. enquanto i > 0 e k > 0 faça
Item 1
V1 = 5
W1 = 5
Item 2
V2 = 4
W2 = 6
Item 3
V2 = 7
W2 = 8
Item 4
V2 = 7
W2 = 4
.
.
.
se V[i, k] ≠ V[i-1, k] então
coloque o item i na mochila
i ← i - 1
MAX = 13
. k ← k - wi
. senão
. i ← i-1
w
0
0
0
0
0
0
1
0
0
0
0
0
2
0
0
0
0
0
3
0
0
0
0
0
4
0
0
0
0
7
5
0
5
5
5
7
6
0
5
5
5
7
7
0
5
5
5
7
8
0
5
5
7
7
9
0
5
5
7
10 11 12 13
0
1
2
3
4
0
5
5
7
0
5
9
9
0
5
9
9
0
5
i
9
12
12 12 12 14 14
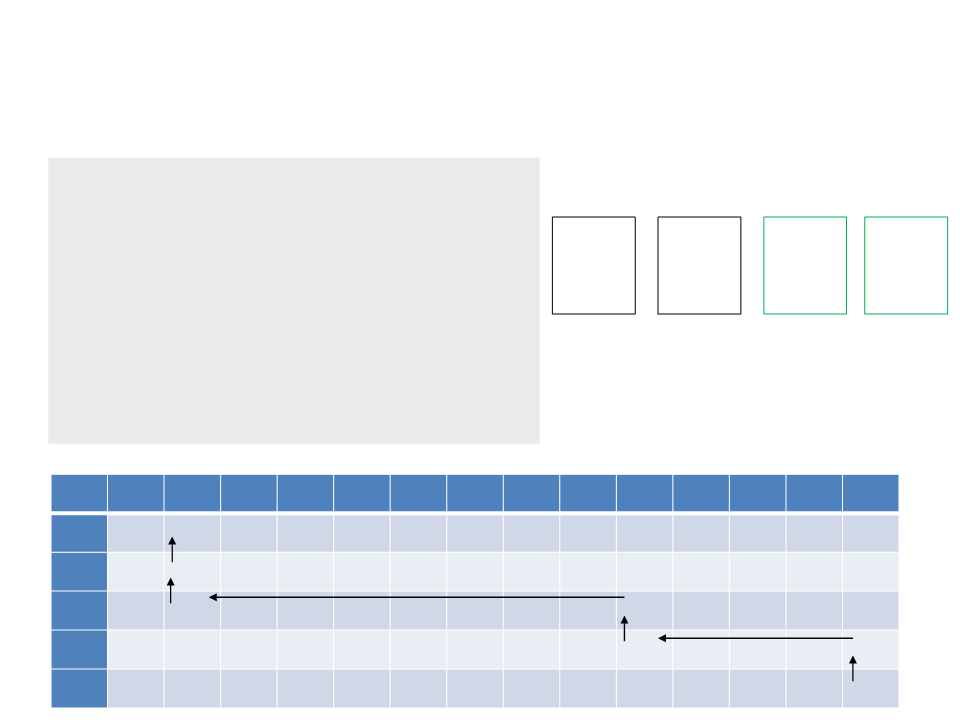
Exemplo 2: Problema da Mochila
1
2
3
4
5
6
7
8
9
. i ← n
. k ← W
. enquanto i > 0 e k > 0 faça
. se V[i, k] ≠ V[i-1, k] então
. coloque o item i na mochila
Item 1
V1 = 5
W1 = 5
Item 2
V2 = 4
W2 = 6
Item 3
V2 = 7
W2 = 8 W2 = 4
Item 4
V2 = 7
.
.
.
i ← i - 1
k ← k - wi
MAX = 13
Solução: {Item 3, Item 4}
senão
. i ← i-1
w
0
0
0
0
0
0
1
0
0
0
0
0
2
0
0
0
0
0
3
0
0
0
0
0
4
0
0
0
0
7
5
0
5
5
5
7
6
0
5
5
5
7
7
0
5
5
5
7
8
0
5
5
7
7
9
0
5
5
7
10 11 12 13
0
1
2
3
4
0
5
5
7
0
5
9
9
0
5
9
9
0
5
i
9
12
12 12 12 14 14

Programação Dinâmica
•
Outros algoritmos importantes baseados em
programação dinâmica que veremos ao longo do
curso:
–
Maior Subsequência Comum

Técnicas de Projeto de Algoritmos
•
•
•
Infelizmente, não existe uma técnica que seja a
melhor dentre todas.
Um problema pode ser resolvido de maneira mais
eficiente adotando-se uma técnica do que outra.
Uma técnica pode levar a um algoritmo O(2n) e outra
2
técnica a um algoritmo O(n ) na resolução de um
mesmo problema.

Exercícios
Lista de Exercícios 05 – Programação Dinâmica
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Levitin. Introduction to the Design and
Analysis of Algorithms, 3rd Edition, 2011.
Capítulo 8: Dynamic Programming
