
Projeto e Análise de Algoritmos
Aula 04 – Técnicas de Projeto de Algoritmos
(Método Guloso)
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Estratégias de Projeto de Algoritmos
•
•
•
•
•
•
•
•
•
•
Força Bruta (Brute Force)
Dividir e Conquistar (Divide and Conquer)
Diminuir e Conquistar (Decrease and Conquer)
Transformar e Conquistar (Transform and Conquer)
Compromisso Tempo–Espaço (Space and Time Tradeoffs)
Estratégia Gulosa (Greedy)
Programação Dinâmica (Dynamic Programming)
Voltando Atrás (Backtracking)
Ramificar e Limitar (Branch and Bound)
Algoritmos Aproximados

Método Guloso
•
•
Ideia: quando temos uma escolha a fazer, fazemos aquela que
pareça ser a melhor no momento.
–
Ou seja, fazemos uma escolha ótima local, na esperança de obter uma
solução ótima global.
O método guloso sugere construir uma solução através de
uma sequência de passos, cada um expandindo uma solução
parcialmente construída até o momento, até uma solução
completa para o problema ser obtida.
–
Métodos gulosos nem sempre garantem soluções ótimas, mas quando
eles garantem, geralmente são as soluções mais simples e eficientes.

Método Guloso
•
Em cada passo de um algoritmo guloso, a escolha
deve ser:
–
Possível: deve satisfazer as restrições do problema;
–
Localmente ótima: deve ser a melhor escolha local dentre
todas as escolhas disponíveis naquele passo;
–
Irreversível: uma vez feita, ele não pode ser alterada nos
passos subsequentes do algoritmo.
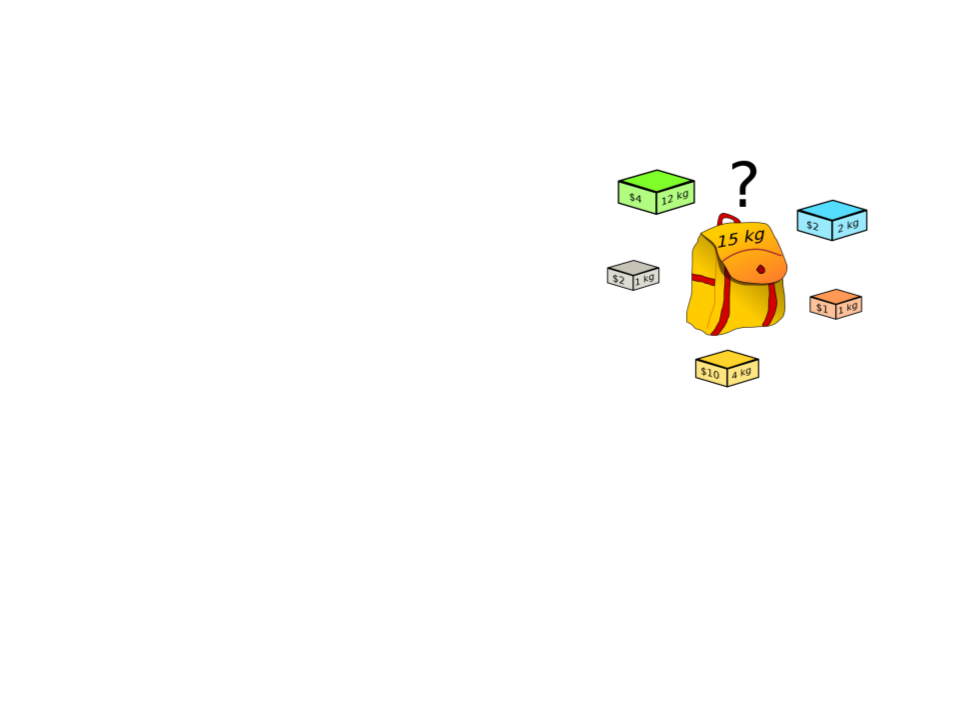
Exemplo 1: Problema da Mochila
•
•
Dados n itens:
–
–
–
Pesos: w1, w2, ..., wn
Valores: v1, v2, …, vn
Uma mochila de capacidade W
Problema: encontrar o subconjunto mais valioso de
itens que caibam dentro da mochila (Knapsack
Problem).

Exemplo 1: Problema da Mochila
•
•
Problema da Mochila 0-1:
–
Um ladrão rouba uma loja que contém n itens: o item i
tem peso wi e vale vi. Ele quer levar o maior valor possível
em uma mochila de carga máxima W. Quais itens escolher?
Problema da Mochila Fracionada:
–
Mesmo formulação anterior, mas agora ele pode carregar
frações dos itens, ao invés da escolha binária (0-1).
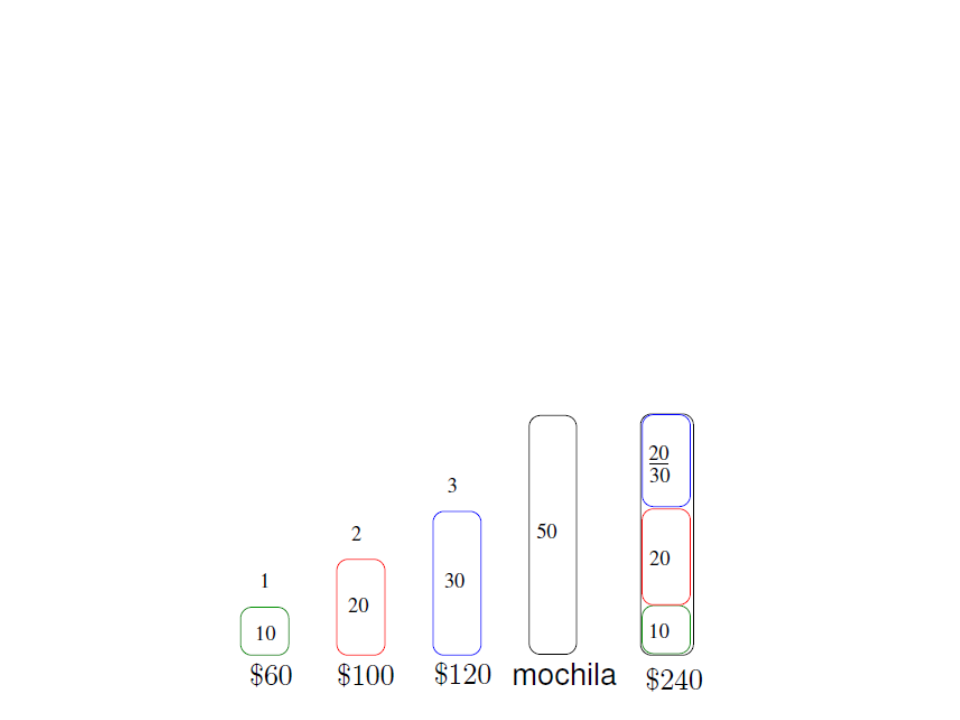
Exemplo 1: Problema da Mochila
Fracionada)
(
•
Algoritmo Guloso (ideia):
–
Ordene os itens por valor/peso (vi/wi);
–
Começando em i = 1, coloque na mochila o máximo
possível do item i que estiver disponível ;
–
Se puder levar mais, passe para o próximo item.

Exemplo 1: Problema da Mochila
Fracionada)
(
•
Algoritmo Guloso:
1
2
3
4
5
6
7
8
9
1
1
1
1
. Mochila_Fracionada(item, valor, peso, n, totalmochila)
. MergeSort(item, valor, peso, n)
.
.
.
.
.
.
carga ← 0
i ← 1
enquanto (carga < totalmochila) e (i <= n) faça
se (peso[i] ≤ totalmochila – carga) então
pegue todo o item[i]
carga ← carga + peso[i]
. senão
0.
1.
pegue (totalmochila - carga)/peso[i] do item[i]
carga ← carga + (totalmochila - carga)/peso[i]
2. i ← i + 1
3. retorne itens pegados
O(n log n)

Exemplo 2: Seleção de Atividades
•
Seja:
–
–
–
S = {a1, ... , an): conjunto de n atividades que podem ser executadas em
um mesmo local. Exemplo: palestras em um auditório.
Para todo i = 1, ..., n, a atividade ai começa no instante si e termina no
instante fi, com 0 < si < fi <∞.
As atividades ai e aj são ditas compatíveis se os intervalos [si,fi] e [sj, fj]
são disjuntos.
•
Problema: Encontre em S um subconjunto de atividades
mutuamente compatíveis que tenha tamanho máximo.

Exemplo 2: Seleção de Atividades
•
Exemplo:
i
1
1
4
2
3
5
3
0
6
4
5
7
5
3
8
6
5
9
7
8
9
10 11
12
si
fi
6
8
8
2
10 11 12 13 14
–
–
–
Pares de atividades incompatíveis: (a1, a2), (a1, a3)
Pares de atividades compatíveis: (a1, a4), (a4, a8)
Conjuntos máximos de atividades compatíveis:
(a1, a4, a8, a11) e (a2, a4, a9, a11)

Exemplo 2: Seleção de Atividades
•
Algoritmo Guloso:
1
2
3
4
5
6
7
8
9
. Seleciona_Atividade(a, s, f, n)
. MergeSort(a, s, f, n) //ordenação crescente por fi
. A ← {a1}
. i = 1
. Para m ← 2 até n faça
. se sm ≥ fi então
.
A ← A ∪ {am}
i ← m
.
O(n log n)
. retorne A

Método Guloso
•
Outros algoritmos gulosos que veremos ao longo do
curso:
–
–
–
Algoritmo de Prim (Árvores Geradoras Mínimas)
Algoritmo de Kruskal (Árvores Geradoras Mínimas)
Algoritmo de Dijkstra (Distâncias Mínimas)

Comentários sobre o Método Guloso
•
Vantagens:
–
–
–
Algoritmos simples;
Fácil implementação;
Quando garantem soluções ótimas, geralmente são os algoritmos mais
simples e eficientes;
•
Desvantagens:
–
–
–
Nem sempre garantem soluções ótimas locais;
Podem efetuar cálculos repetitivos;
Escolhe o caminho que, à primeira vista, é mais econômico;

Exercícios
Lista de Exercícios 04 – Método Guloso
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Levitin. Introduction to the Design and
Analysis of Algorithms, 3rd Edition, 2011.
Capítulo 9: Greedy Technique
