
Projeto e Análise de Algoritmos
Aula 03 – Técnicas de Projeto de Algoritmos
(Divisão e Conquista)
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Estratégias de Projeto de Algoritmos
•
•
•
•
•
•
•
•
•
•
Força Bruta (Brute Force)
Dividir e Conquistar (Divide and Conquer)
Diminuir e Conquistar (Decrease and Conquer)
Transformar e Conquistar (Transform and Conquer)
Compromisso Tempo–Espaço (Space and Time Tradeoffs)
Estratégia Gulosa (Greedy)
Programação Dinâmica (Dynamic Programming)
Voltando Atrás (Backtracking)
Ramificar e Limitar (Branch and Bound)
Algoritmos Aproximados

Divisão e Conquista
•
Ideia geral:
1
2
3
. Dividir a instância do problema em duas ou mais
instâncias menores;
. Resolver as instâncias menores (geralmente
recursivamente);
. Obter a solução para as instâncias originais (maiores)
através da combinação destas soluções.
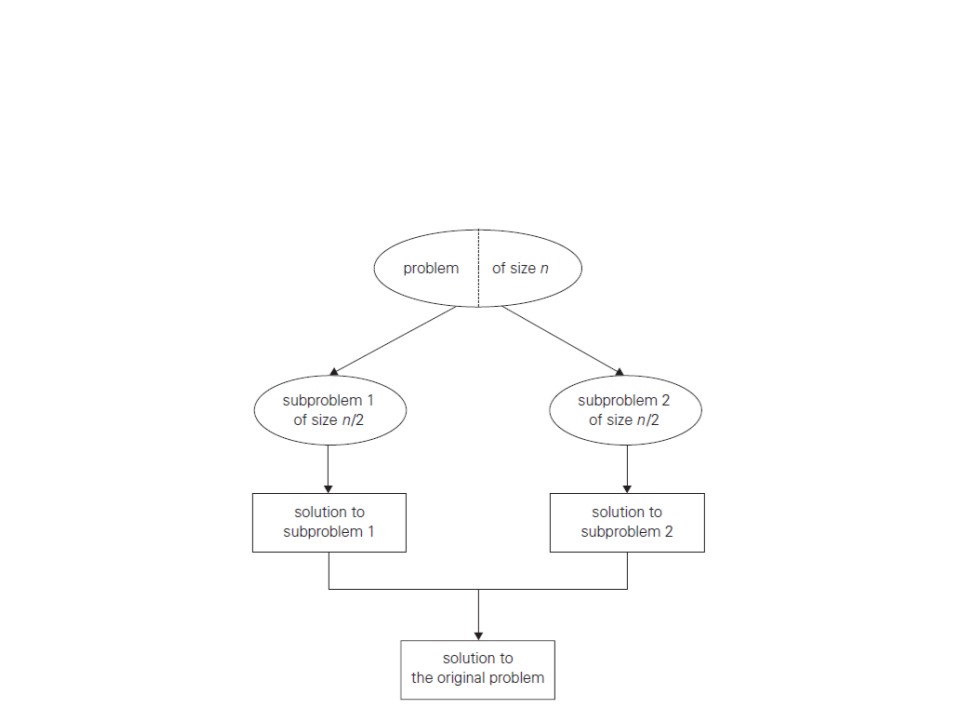
Divisão e Conquista
•
O paradigma de dividir e conquistar envolve 3 passos:
Dividir
Conquistar
Combinar

Divisão e Conquista
•
•
Exemplo: calcular a soma de n números ꢀ0 + … + ꢀꢁ−1
Se n > 1, podemos dividir o problema em duas
instâncias do mesmo problema:
–
Soma dos primeiros ꢂ/2 números;
–
Soma dos ꢂ/2 números restantes;
•
Uma vez estas duas somas computadas, adicionamos
seus valores para obter o resultado final:
ꢀ0
+ … + ꢀꢁ−1 = (ꢀ0 + … + ꢀ ꢁ/ꢃ −1) + (ꢀ0 + … + ꢀ ꢁ/ꢃ −1)

Divisão e Conquista
•
Esta é uma maneira eficiente de calcular a soma de n
números?
•
•
É mais eficiente do que uma adição força bruta?
Nem todos os algoritmos baseados na técnica de
dividir e conquistar são mais eficientes do que uma
solução força bruta.

Divisão e Conquista
•
•
•
Em geral, o tempo gasto na execução das três etapas
do algoritmo dividir e conquistar, é menor do que a
resolução por outros métodos.
A estratégia dividir e conquistar produz alguns dos
algoritmos mais importantes e eficientes da área da
computação.
Importante: a estratégia dividir e conquistar pode ser
facilmente adaptada a computação paralela.

Exemplo: Multiplicação de Inteiros Grandes
•
Problema: realizar a multiplicação de inteiros
grandes (da ordem de 100 dígitos decimais).
–
Ex: 358712253797428009 × 153461234908764388 = ?
Multiplicação Tradicional:
Algoritmo de Força Bruta:
-
-
multiplicação dígito a dígito;
soma dígito a dígito;
u
9
999
___7__7_7__7_ v
9993
9993
9993
9993
_
6
6
Complexidade: O(n2 + n) = O(n2)
6
6
_
_____________
7
7762223 u ×v

Exemplo: Multiplicação de Inteiros Grandes
•
Problema: realizar a multiplicação de inteiros
grandes (da ordem de 100 dígitos decimais).
–
Outra forma de multiplicar números grandes?
Passo 1 - Multiplicação dos Grandes
A = x1 × y1 A = 12 × 56 = 672
Passo 2 - Multiplicação dos Pequenos
B = x2 × y2 B = 34 × 78 = 2652
Passo 3 - Soma os dois grupos de x
C = x1 + x2 C = 12 + 34 = 46
Passo 4 - Soma os dois grupos de y
D = y1 + y2 D = 56 + 78 = 134
Passo 5 - Multiplique as somas dos grupos
E = C × D E = 46 × 134 = 6164
x1 x2
x 12 34
y
5
6 78
y1 y2

Exemplo: Multiplicação de Inteiros Grandes
•
Problema: realizar a multiplicação de inteiros
grandes (da ordem de 100 dígitos decimais).
–
Outra forma de multiplicar números grandes?
Passo 6 - Subtraia o produto da soma dos dois grupos (E),
o produto dos grandes (A) e o produto dos pequenos (B)
x1 x2
F = E - A - B
F = 6164 - 672 - 2652 = 2840
Passo 7 - Shift do produto dos grandes
x 12 34
G = A × ꢄꢅ 2
m
2x2
G = 672 × 10 = 6720000
y
5
6 78
Passo 8 - Shift do resultado das subtrações
y1 y2
H = F × ꢄꢅ m
H = 2840 × 10 = 284000
2
Passo 9 - Soma Final
I = G + B + H I = 6720000 + 2652 + 284000

Exemplo: Multiplicação de Inteiros Grandes
•
Algoritmo de Karatsuba
1
2
3
4
5
6
7
8
9
1
1
1
1
1
. KARATSUBA(u, v, n)
. se n < 3 então
. retorne u × v
O(ꢉꢊꢋꢌꢍꢎ) = O(n1.585)
.
senão
. m ← ꢂ/2
. a ← ꢆ/ꢄꢅꢇ
. b ← u mod 10m
. c ← ꢈ/ꢄꢅꢇ
.
d ← v mod 10m
0.
ac ← KARATSUBA(a, c, m)
1. bd ← KARATSUBA(b, d, m)
2. y ← KARATSUBA(a + b, c + d, m + 1)
3. x ← ac × 102m + (y - ac - bd)× 10m + bd
4. retorne x
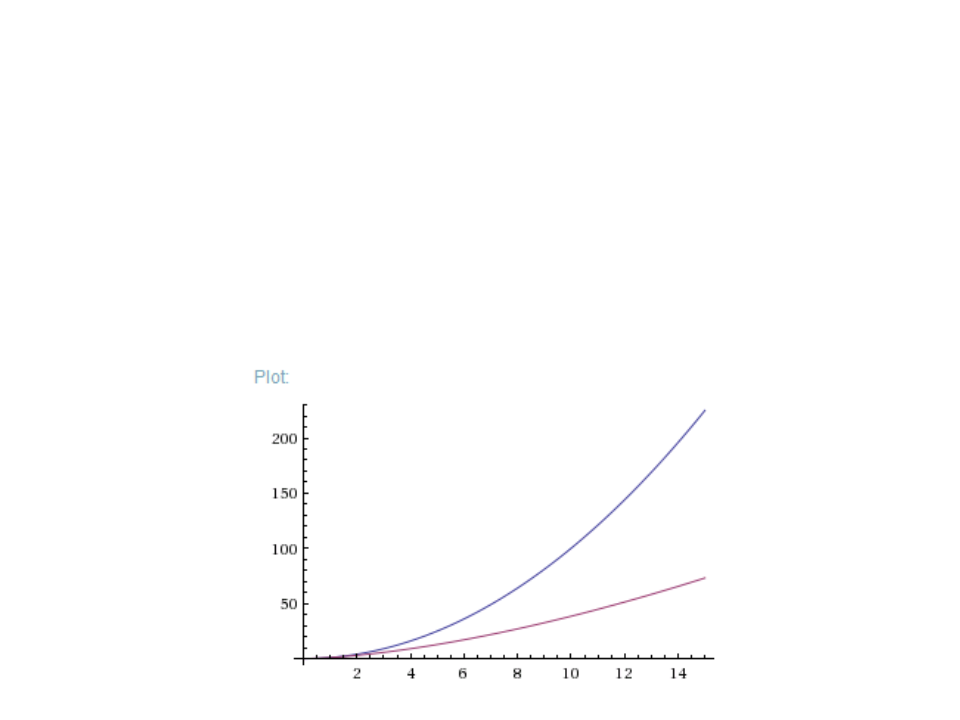
Exemplo: Multiplicação de Inteiros Grandes
•
•
Multiplicação Tradicional: O(ꢂꢃ)
ꢏꢐꢑ 3
ꢒ
Algoritmo de Karatsuba: O(ꢂ )
Wolfram Alpha:
plot n^2 from n=0 to 15, n ^ log base 2 of 3 from n=0 to 15

Divisão e Conquista
•
Outros algoritmos importantes baseados em divisão
e conquista que veremos ao longo do curso:
–
–
Merge Sort
Quick Sort

Quando Utilizar Divisão e Conquista?
•
Existem três condições que indicam que a estratégia
de divisão e conquista pode ser utilizada com
sucesso:
–
–
–
Deve ser possível decompor uma instância em sub-
instâncias.
A combinação dos resultados dever ser eficiente (trivial se
possível).
As sub-instâncias devem ser mais ou menos do mesmo
tamanho.

Comentários sobre a Divisão e Conquista
•
•
Muitos algoritmos eficientes são baseados nesta
técnica.
–
Contudo, ela pode ser inaplicável e inferior a soluções
algorítmicas mais simples.
Outras estratégias semelhantes:
–
Diminuir e Conquistar (Decrease and Conquer)
–
Transformar e Conquistar (Transform and Conquer)

Comentários sobre a Divisão e Conquista
•
Vantagens:
–
Pode gerar algoritmos eficientes com forte tendência a complexidade
logarítmica;
–
Facilmente paralelizável;
•
Desvantagens:
–
Geralmente são algoritmos recursivos (problema de estouro de pilha);
–
Repetição de sub-problemas;

Exercícios
Lista de Exercícios 03 – Divisão e Conquista
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Levitin. Introduction to the Design and
Analysis of Algorithms, 3rd Edition, 2011.
Capítulo 5: Divide-and-Conquer
