
Projeto e Análise de Algoritmos
Aula 02 – Técnicas de Projeto de Algoritmos
(Força Bruta)
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Tipos Importantes de Problemas
•
•
•
•
Problemas de Ordenação: Reorganizar os itens de uma dada
lista em ordem crescente.
Problemas de Busca: Encontrar um dado valor chamado de
chave de busca em um dado conjunto.
Processamento de Strings: Buscar uma dada palavra em um
texto, avaliar a similaridade entre cadeias de caracteres, etc.
Problemas de Grafos: Travessia de grafos (como visitar todos
os pontos de uma rede), caminho mais curto (qual a melhor
rota entre duas cidades), ordenação topológica.

Tipos Importantes de Problemas
•
Problemas Combinatoriais: Problemas onde é necessário
encontrar um objeto combinatorial (permutações,
combinações ou subconjuntos) que satisfaça certas restrições
e tenha certas propriedades (maximizar um valor, minimizar
um custo).
•
•
Problemas Geométricos: Envolvem objetos geométricos com
pontos, linhas e polígonos.
Problemas Numéricos: Envolvem objetos matemáticos de
natureza contínua: resolução de equações e sistemas de
equações, integrais definidas, etc.

Estratégias de Projeto de Algoritmos
•
•
•
•
•
•
•
•
•
•
Força Bruta (Brute Force)
Dividir e Conquistar (Divide and Conquer)
Diminuir e Conquistar (Decrease and Conquer)
Transformar e Conquistar (Transform and Conquer)
Compromisso Tempo–Espaço (Space and Time Tradeoffs)
Estratégia Gulosa (Greedy)
Programação Dinâmica (Dynamic Programming)
Voltando Atrás (Backtracking)
Ramificar e Limitar (Branch and Bound)
Algoritmos Aproximados

Força Bruta
•
•
A técnica de força bruta (também conhecida como a
busca exaustiva) é um método para resolver um
problema através de uma travessia completa (ou
parcial) no espaço de busca do problema para se
obter uma solução.
Durante a busca, é possível podar (optar por não
explorar) partes do espaço de busca, se for possível
determinar que estas partes não têm qualquer
possibilidade de conter a solução necessária.

Força Bruta
•
•
Geralmente, a força bruta é uma das estratégias mais
fáceis de aplicar.
Apesar de ser raramente uma fonte de algoritmos
eficientes ou brilhantes, é uma importante estratégia
de projeto de algoritmos.
•
É aplicável a uma ampla variedade de problemas.

Exemplo 1: Busca Sequencial
•
Comparar elementos sucessivos de uma dada lista com um
dada chave de busca até:
–
Encontrar um elemento similar (busca bem sucedida) ou;
–
A lista ser exaurida sem encontrar um elemento similar (busca mal
sucedida).
int busca(int n, int *vet, int elem)
{
int i;
for (i=0; i<n; i++){
if (elem == vet[i])
return i;
}
return -1;
}

Algoritmo Geral de Força Bruta
1
. Listar todas as soluções potenciais para o problema de uma
maneira sistemática.
–
Todas as soluções estão eventualmente listadas;
–
Nenhuma solução é repetida;
2
3
. Avaliar as soluções, uma a uma, talvez, desqualificando as
não práticas e mantendo a melhor encontrada até o
momento.
. Quando a busca terminar, retornar a solução encontrada.
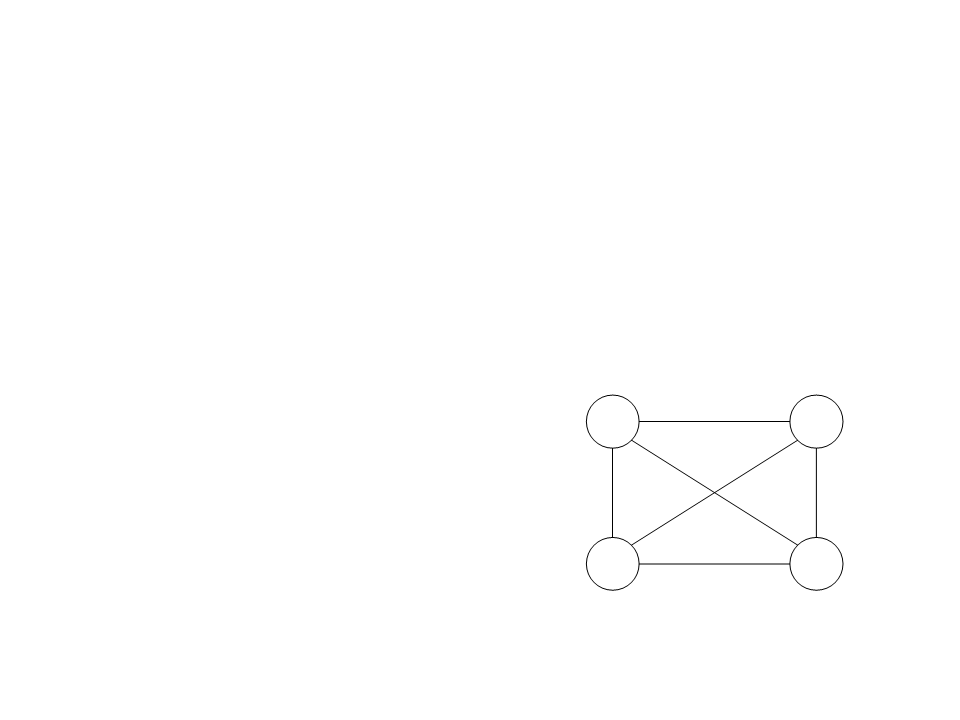
Exemplo 2: Caixeiro Viajante
•
Problema: dadas n cidades com distâncias conhecidas entre
cada par, encontrar o trajeto mais curto que passe por todas
as cidades exatamente uma vez antes de retornar a cidade de
origem (Traveling Salesman Problem (TSP)).
Trajeto:
Custo:
2
7
A
C
B
a → b → c → d → a
a → b → d → c → a
a → c → b → d → a
a → c → d → b → a
a → d → b → c → a
a → d → c → b → a
2+3+7+5 = 17
2+4+7+8 = 21
8+3+4+5 = 20
8+7+4+2 = 21
5+4+3+8 = 20
5+7+3+2 = 17
5
3
8
4
D
Hipóteses: (n-1)!
Complexidade: O(n!)
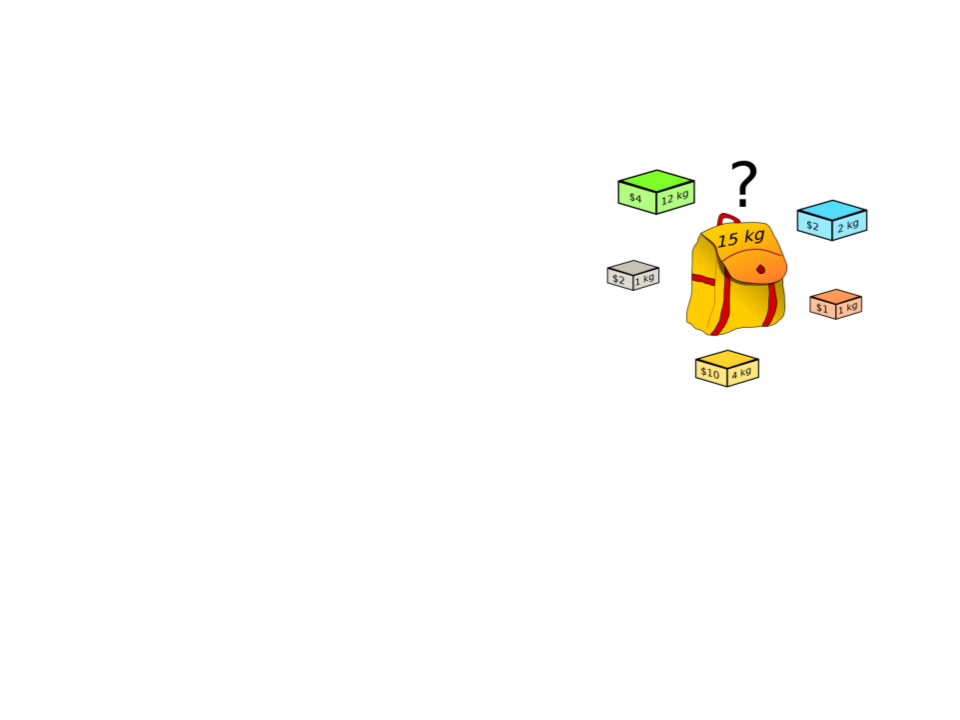
Exemplo 3: Problema da Mochila
•
•
Dados n itens:
–
–
–
Pesos: w1, w2, ..., wn
Valores: v1, v2, …, vn
Uma mochila de capacidade W
Problema: encontrar o subconjunto mais valioso de
itens que caibam dentro da mochila (Knapsack
Problem).
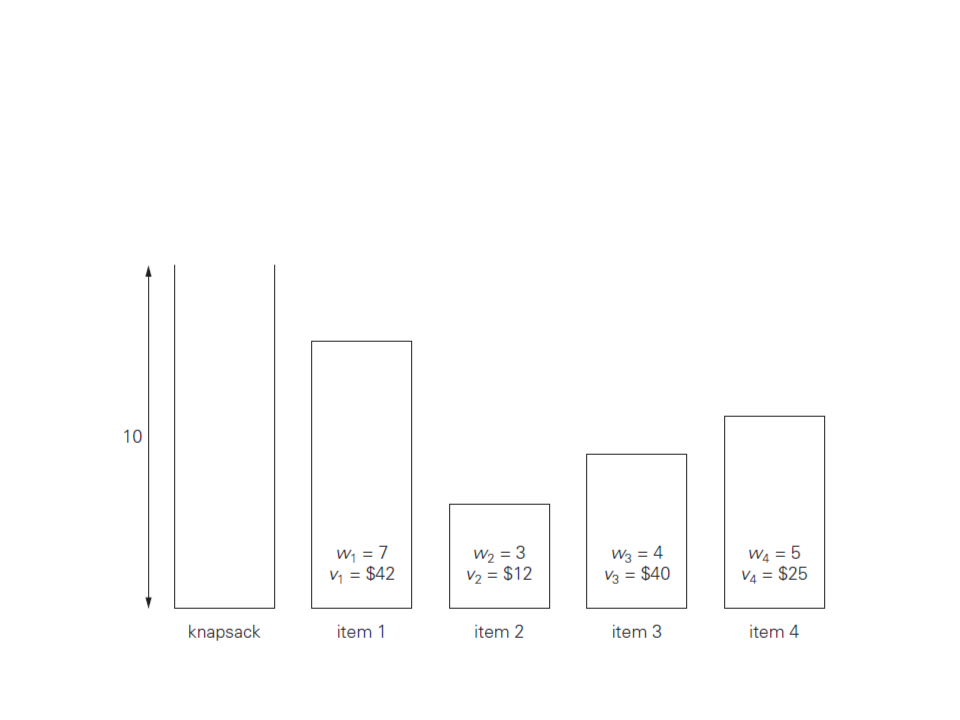
Exemplo 3: Problema da Mochila
•
Exemplo:
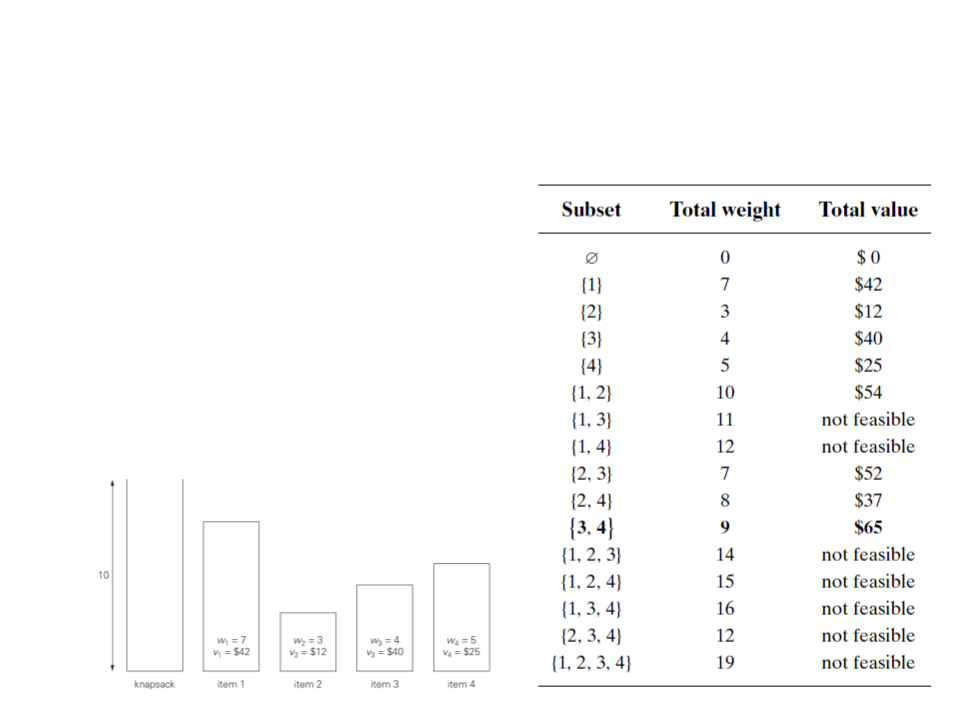
Exemplo 3: Problema da Mochila
•
Algoritmo de Força Bruta:
1. Identificar todos os subconjuntos
do conjunto de n itens dados;
2
. calcular o peso total de cada
subconjunto para identificar
subconjuntos praticáveis;
3
. encontrar um subconjunto com o
valor mais elevado entre eles.

Geração de Subconjuntos
void subsets(int vet[], int n)
{
int i, k;
for(i = 0; i < pow(2, n); i++)
{
printf("{ ");
for(k = 0; k < n; k++)
{
if((1 << k & i) != 0)
printf("%d ", vet[k]);
}
printf("}\n");
}
}

Exemplo 3: Problema da Mochila
•
•
•
Como o número de subconjuntos de um conjunto de
n
n elementos é 2 , a busca exaustiva leva a um
n
algoritmo O(2 ).
Assim, tanto para o problema do caixeiro viajante
quanto da mochila, a busca exaustiva leva a
algoritmos que são extremamente ineficientes.
Estes problemas são chamados de problemas NP-
hard.
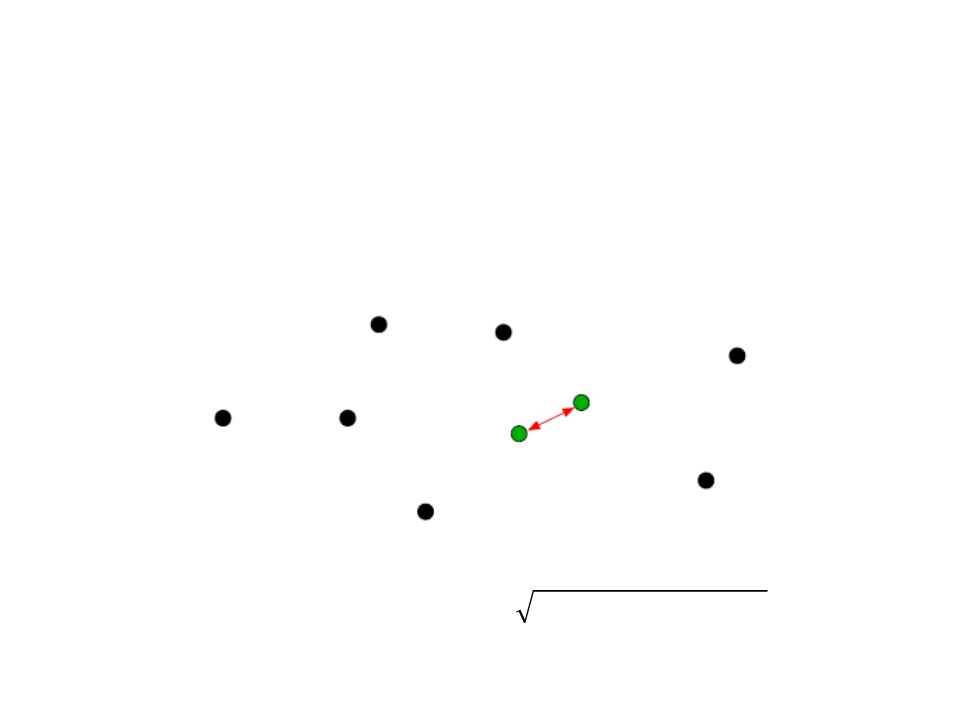
Exemplo 4: Par de Pontos mais Próximos
•
Problema: Dados n pontos no plano, determinar dois
deles que estão à distância mínima.
ꢀ
ꢁꢂꢃꢄꢅꢆꢁꢄ(ꢇ1, ꢈ1, ꢇ2, ꢈ2) = (ꢇ1−ꢇ2)2 + (ꢈ1−ꢈ2)

Exemplo 4: Par de Pontos mais Próximos
•
Problema: Dados n pontos no plano, determinar dois
deles que estão à distância mínima.
–
Entrada: coleção de n pontos (X[1 . . n] e Y[1 . . n]).
–
Saída: menor distância entre dois pontos da coleção.
1
2
3
4
5
6
7
. PAR-MAIS-PROXIMO(X, Y, n)
O(n2)
. d ← +∞
. para i ← 1 até n faça
. para j ← 1 até n faça
. se Distancia(X[i], Y[i], X[j], Y [j]) < d então
d ← Distancia(X[i], Y[i], X[j], Y [j])
. retorna d
.

Força Bruta
•
Outros algoritmos baseados em força bruta que
veremos ao longo do curso:
–
–
–
–
–
–
–
Multiplicação de Inteiros Grandes;
Busca de Padrões em String;
Maior Subsequência Comum;
Bubble Sort;
Selection Sort;
Busca em Profundidade;
Busca em Largura;

Comentários sobre a Força Bruta
•
•
Força bruta é uma estratégia direta para resolver um
problema, geralmente baseada diretamente no enunciado do
problema e definições dos conceitos envolvidos.
Algoritmos de busca exaustiva são executados em uma
quantidade de tempo realística somente para instâncias
muito pequenas.
–
Em muitos casos existem alternativas muito melhores!
•
Em alguns casos, busca exaustiva (ou variação) é a única
solução conhecida.

Comentários sobre a Força Bruta
•
•
Vantagens:
–
–
–
Ampla aplicabilidade;
Simplicidade;
Fornece algoritmos razoáveis para alguns problemas.
Desvantagens:
–
–
–
Raramente fornece algoritmos eficientes;
Alguns algoritmos força bruta são inaceitavelmente vagarosos;
Não tão construtivo/criativo quanto outras técnicas de projeto de
algoritmos.

Exercícios
Lista de Exercícios 02 – Força Bruta/Busca
Exaustiva
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Levitin. Introduction to the Design and
Analysis of Algorithms, 3rd Edition, 2011.
Capítulo 3: Brute Force and Exhaustive
Search
