
Projeto e Análise de Algoritmos
Aula 11 – Busca em Profundidade e
Busca em Largura
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>
Grafos (Revisão)
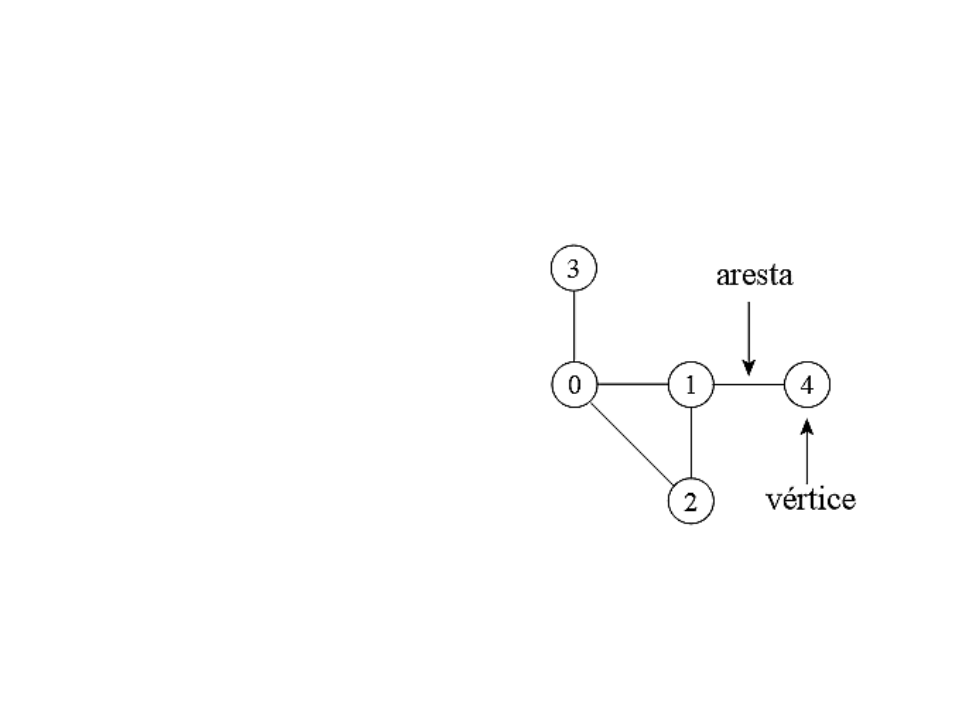
•
G = (V, A)
–
–
–
G: grafo;
V: conjunto de vértices;
A: conjunto de arestas;
Grafos (Revisão)
•
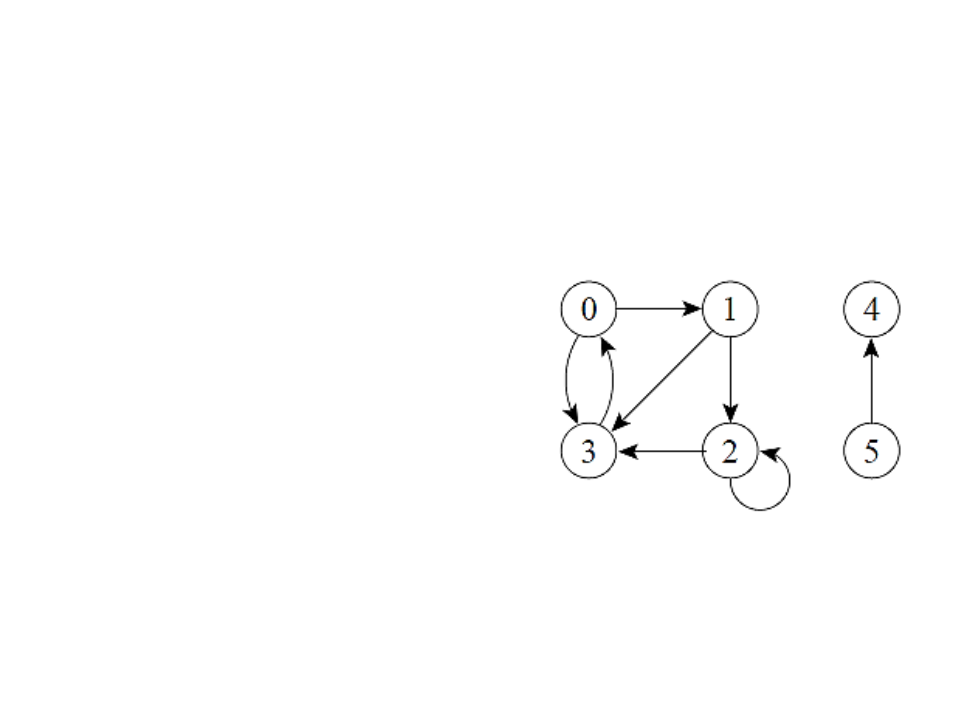
Grafos Direcionados
–
Uma aresta (u, v) sai do
vértice u e entra no vértice v.
•
O vértice v é adjacente ao
vértice u.
–
Podem existir arestas de um
vértice para ele mesmo,
chamadas de self-loops.
Grafos (Revisão)
•
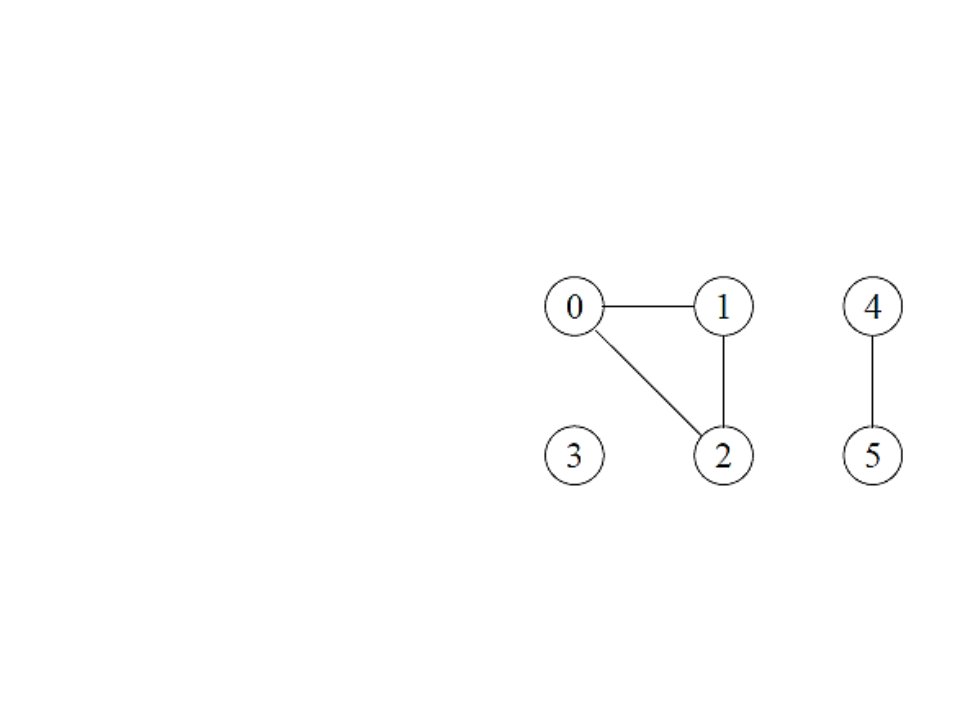
Grafos Não Direcionados
–
As arestas (u, v) e (v, u) são
consideradas como uma
única aresta. A relação de
adjacência é simétrica.
–
Self-loops não são
permitidos.
Grafos (Revisão)
•
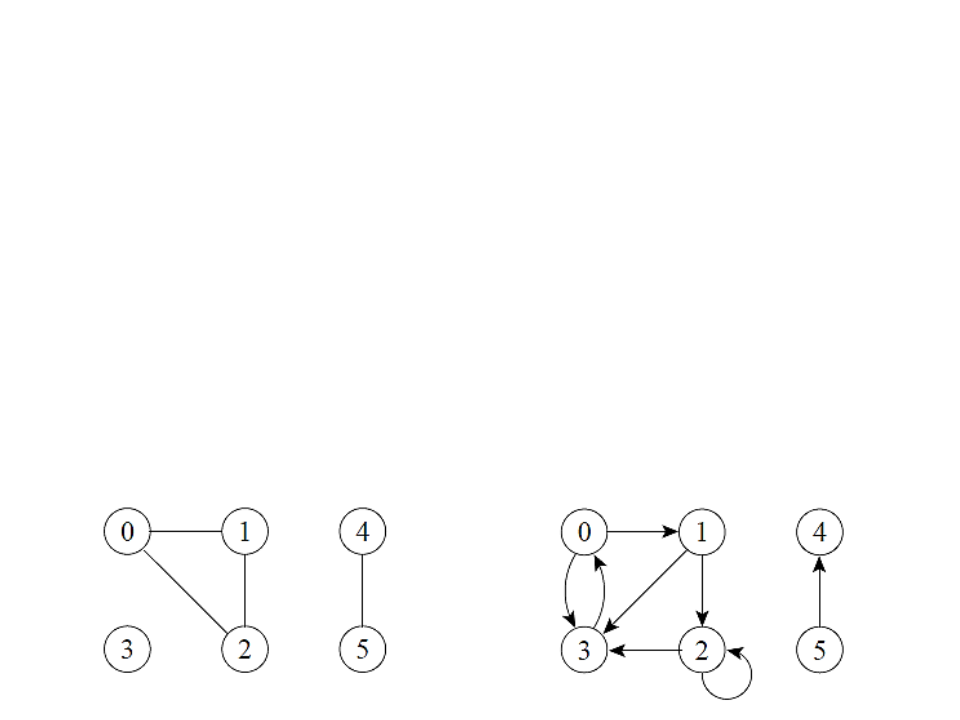
Grau de um Vértice
–
Em grafos não direcionados: é o número de arestas que
incidem nele.
–
Em grafos direcionados: é o número de arestas que saem
dele (out-degree) mais o número de arestas que chegam
nele (in-degree).
–
Um vérice de grau zero é dito isolado ou não conectado.

Grafos (Revisão)
•
Caminho entre Vértices
–
Um caminho de comprimento k de um vértice x a um
vértice y em um grafo G = (V, A) é uma sequência de
vértices (v0, v1, v2, ... , vk) tal que x = v0 e y = vk, e vi ∈ V para
i = 1, 2, ... , k.
–
–
O comprimento de um caminho é o número de arestas
nele, isto é, o caminho contém os vértices v0, v1, v2, ... , vk e
as arestas (v0, v1), (v1, v2), ... , (vk-1, vk).
Se existir um caminho c de x a y então y é alcançável a
partir de x via c.
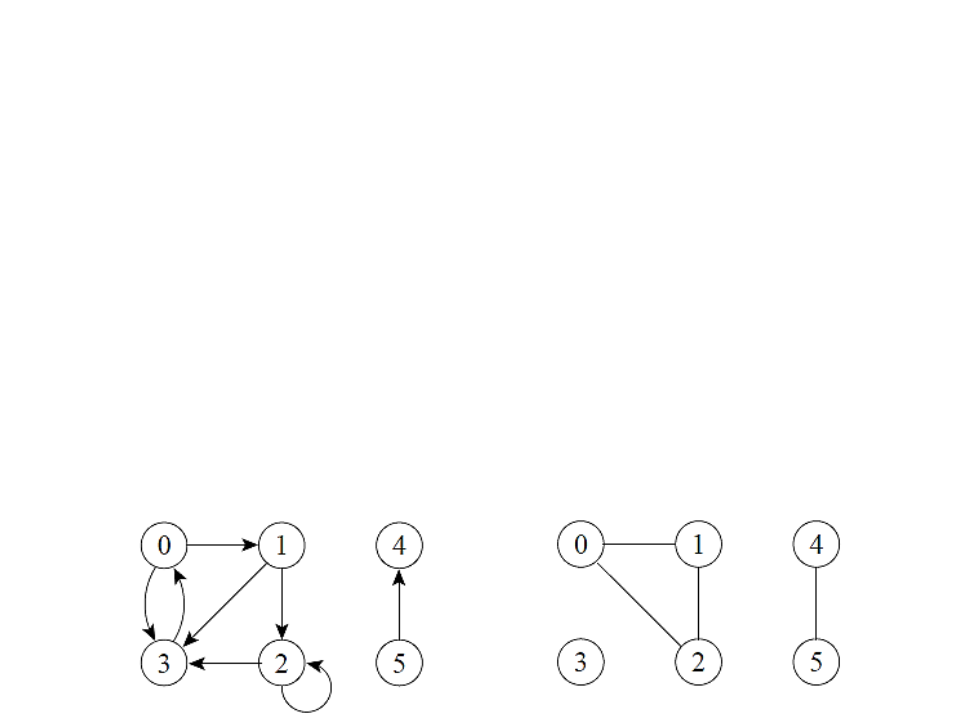
Grafos (Revisão)
•
Ciclos
–
Em um grafo direcionado: um caminho (v0, v1, ... , vk) forma
um ciclo se v0 = vk e o caminho contém pelo menos uma
aresta.
•
O self-loop é um ciclo de tamanho 1.
–
Em um grafo não direcionado: um caminho (v0, v1, ... , vk)
forma um ciclo se v0 = vk e o caminho contém pelo menos
três arestas.
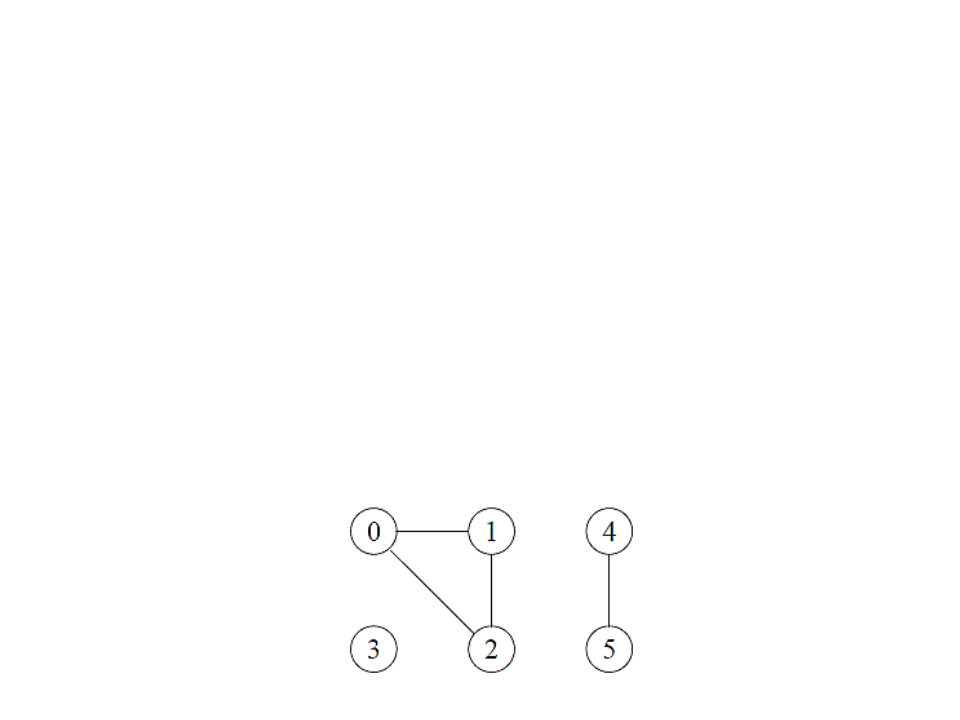
Grafos (Revisão)
•
Componentes Conectados
–
–
–
Um grafo não direcionado é conectado se cada par de
vértices está conectado por um caminho.
Os componentes conectados são as porções conectadas de
um grafo.
Um grafo não direcionado é conectado se ele tem
exatamente um componente conectado.
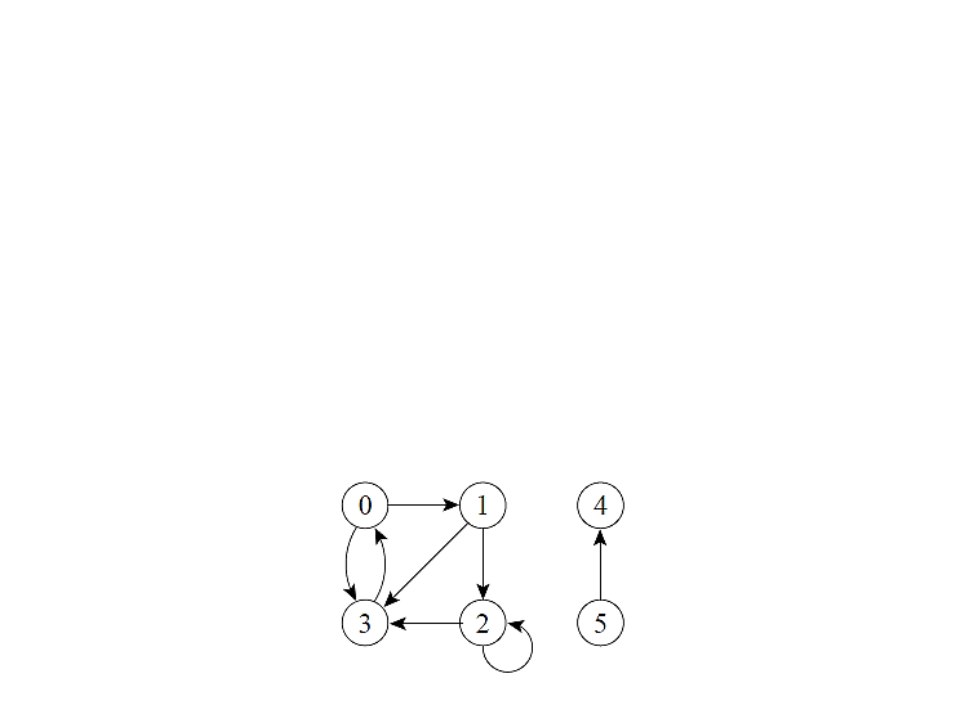
Grafos (Revisão)
•
Componentes Fortemente Conectados
–
–
–
Um grafo direcionado G = (V, A) é fortemente conectado se cada dois
vértices quaisquer são alcançáveis a partir um do outro.
Os componentes fortemente conectados de um grafo direcionado são
conjuntos de vértices sob a relação “são mutuamente alcançáveis”.
Um grafo direcionado fortemente conectado tem apenas um
componente fortemente conectado.
Grafos (Revisão)
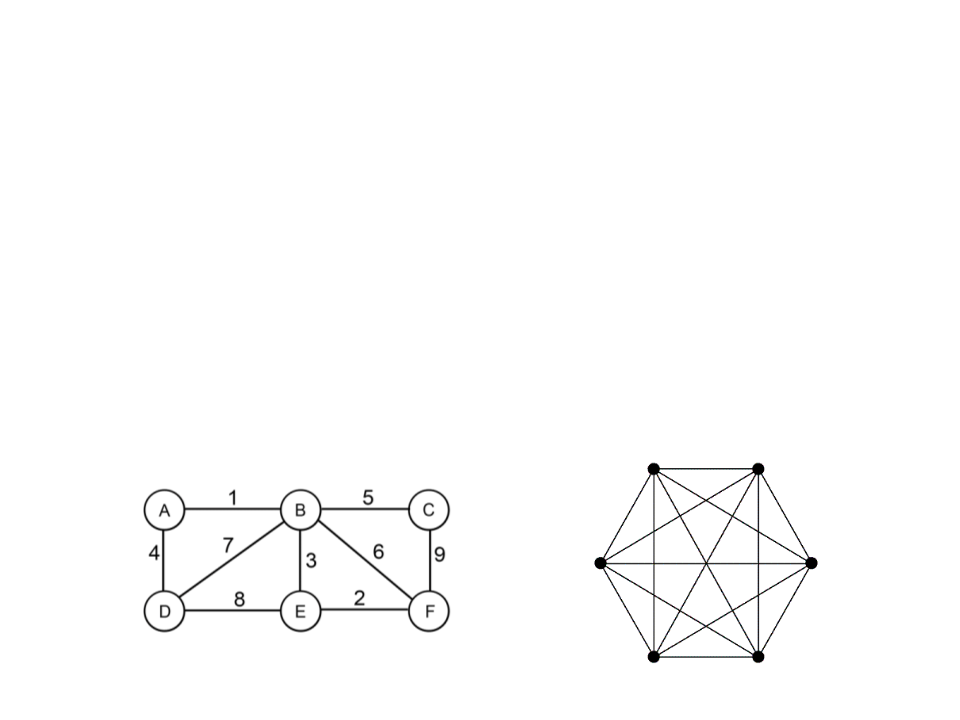
•
Outras Classificações de Grafos
–
Um grafo ponderado possui pesos associados às arestas.
–
Um grafo completo é um grafo não direcionado no qual
todos os pares de vértices são adjacentes.
Grafos (Revisão)
•
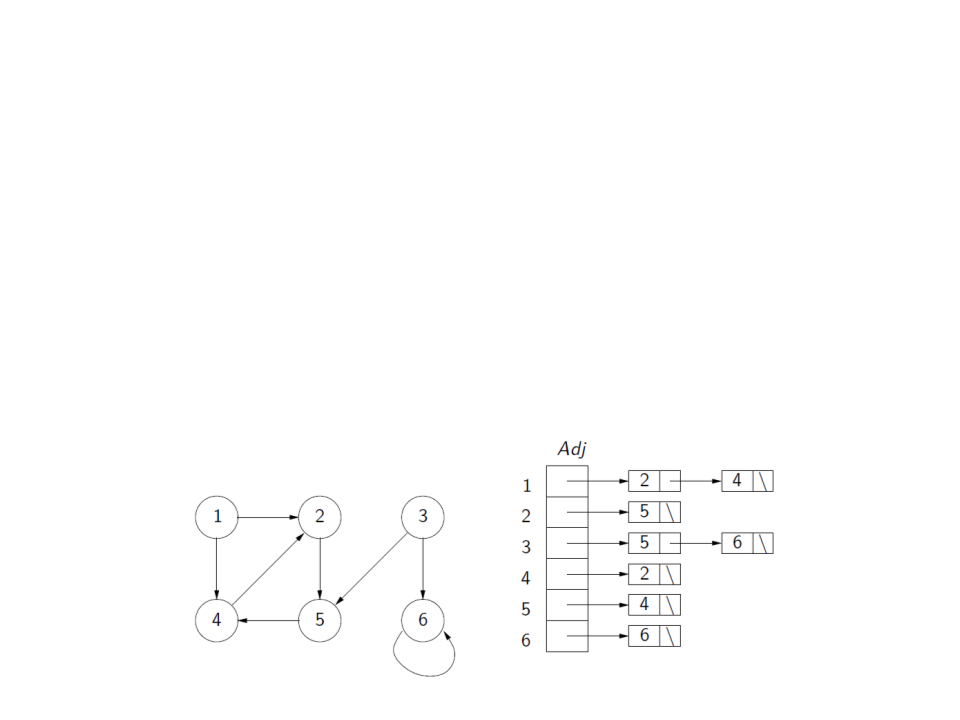
Representação de Grafos
–
Lista de Adjacências:
•
Consiste em um vetor Adj com |V| listas de adjacências, uma para
cada vértice v ∈ V.
•
Para cada u ∈ V, Adj[u] contém ponteiros para todos os vértices v tal
que (u, v) ∈ A. Ou seja, Adj[u] consiste de todos os vértices que são
adjacentes a u.
Grafos (Revisão)
•
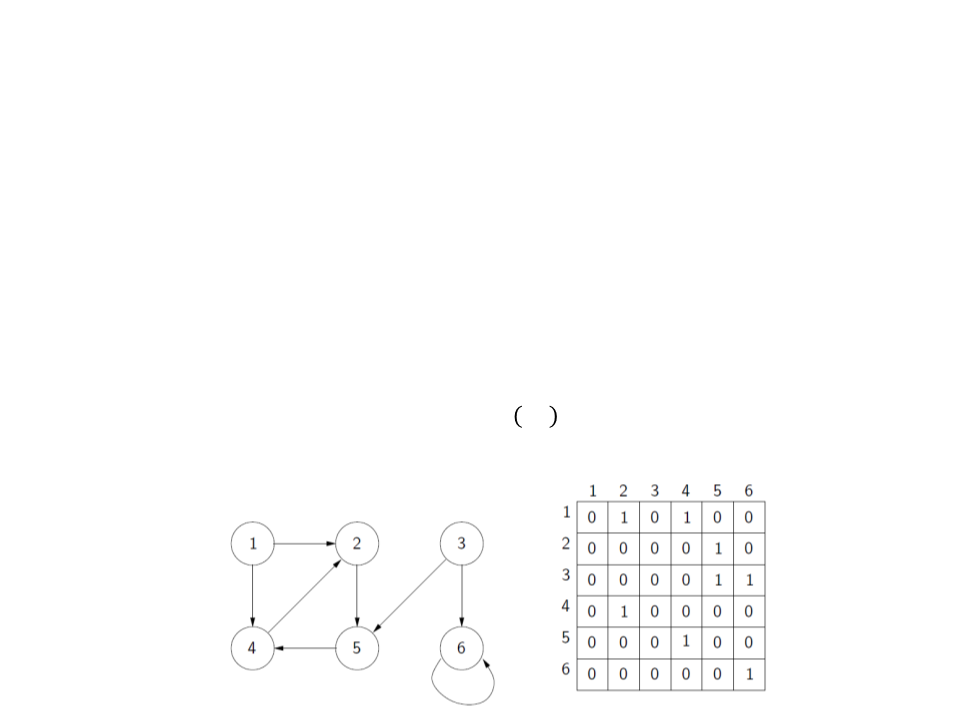
Representação de Grafos
–
Matriz de Adjacências:
•
Para um grafo G = (V, E), assumimos que os vértices são rotulados
com números 1, 2, . . . , |V|.
•
A representação consiste de uma matriz Aij de dimensões |V| × |V|,
onde:
1
0
ꢃꢄ ꢅ, ꢆ ∈ ꢇ
ꢀꢁꢂ
= ቊ
ꢈꢀꢃꢉ ꢈꢉꢊꢋꢌꢀꢌꢅꢉ

Busca em Largura
•
A busca em largura é um dos algoritmos mais simples para
exploração de um grafo.
–
Dados um grafo G = (V, E) e um vértice s, chamado de fonte, a busca
em largura sistematicamente explora as arestas de G de maneira a
visitar todos os vértices alcançáveis a partir de s.
•
•
Expande a fronteira entre vértices descobertos e não
descobertos uniformemente através da largura da fronteira.
–
O algoritmo descobre todos os vértices a uma distância k do vértice
origem antes de descobrir qualquer vértice a uma distância k + 1.
O grafo pode ser direcionado ou não direcionado.

Busca em Largura
•
Algoritmo:
–
Para controlar a busca, o algoritmo da Busca em Largura
pinta cada vértice na cor branca, cinza ou preto.
–
Todos os vértices iniciam com a cor branca e podem, mais
tarde, se tornar cinza e depois preto.
•
•
•
Branca: não visitado;
Cinza: visitado;
Preta: visitado e seus nós adjacentes visitados.

Busca em Largura
BuscaEmLargura(G, s)
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
Q ← {s} //Queue
while Q ≠ ∅
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
Busca em Largura
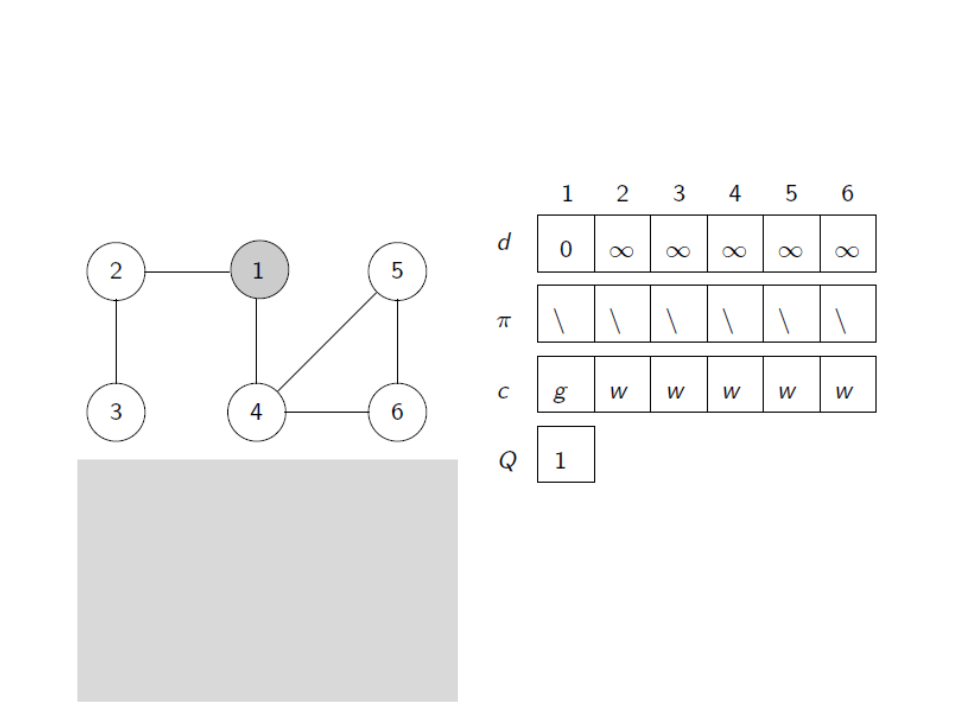
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
Q ← {s} //Queue
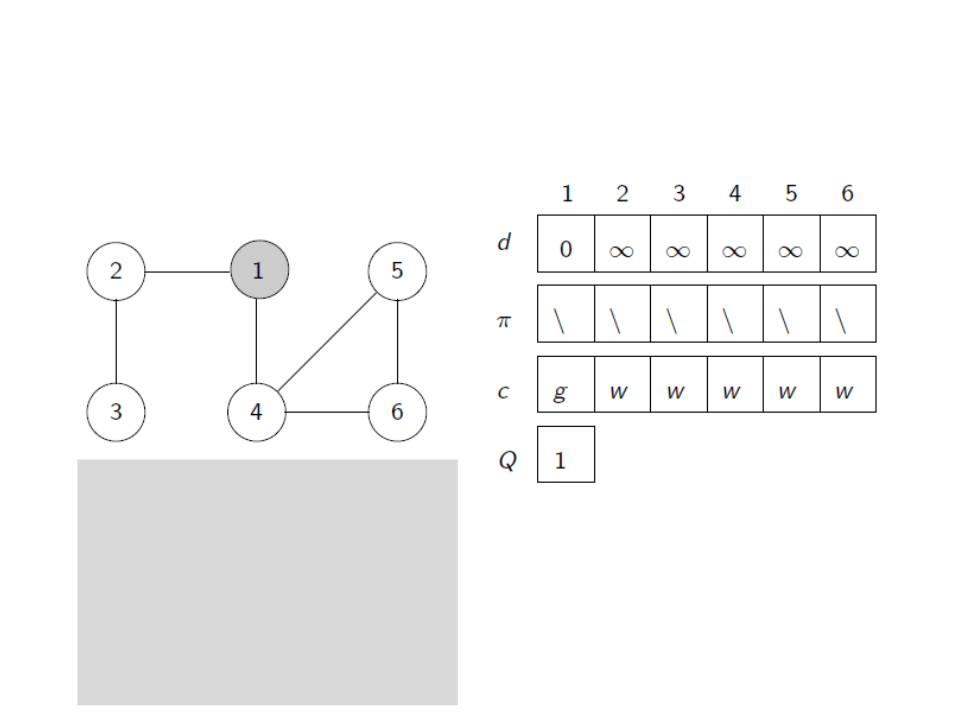
Busca em Largura
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
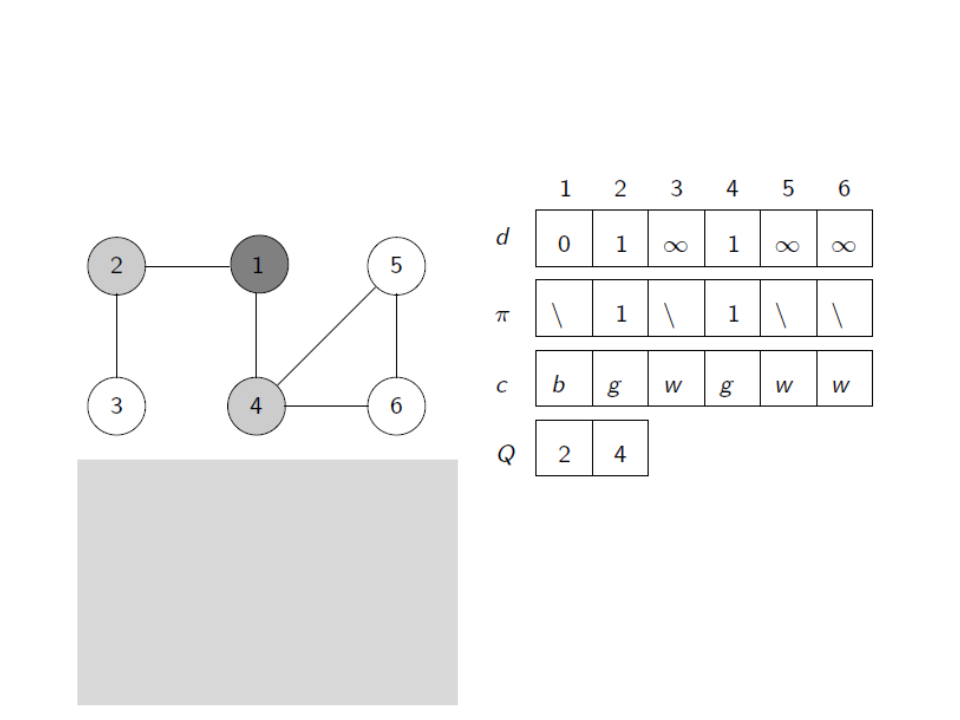
Busca em Largura
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
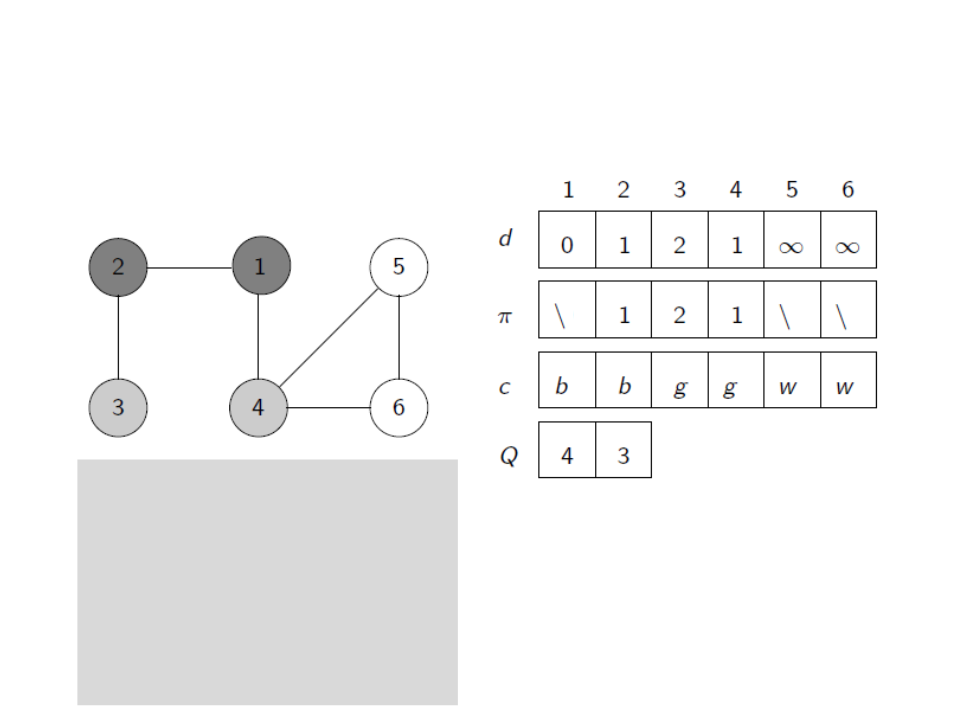
Busca em Largura
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
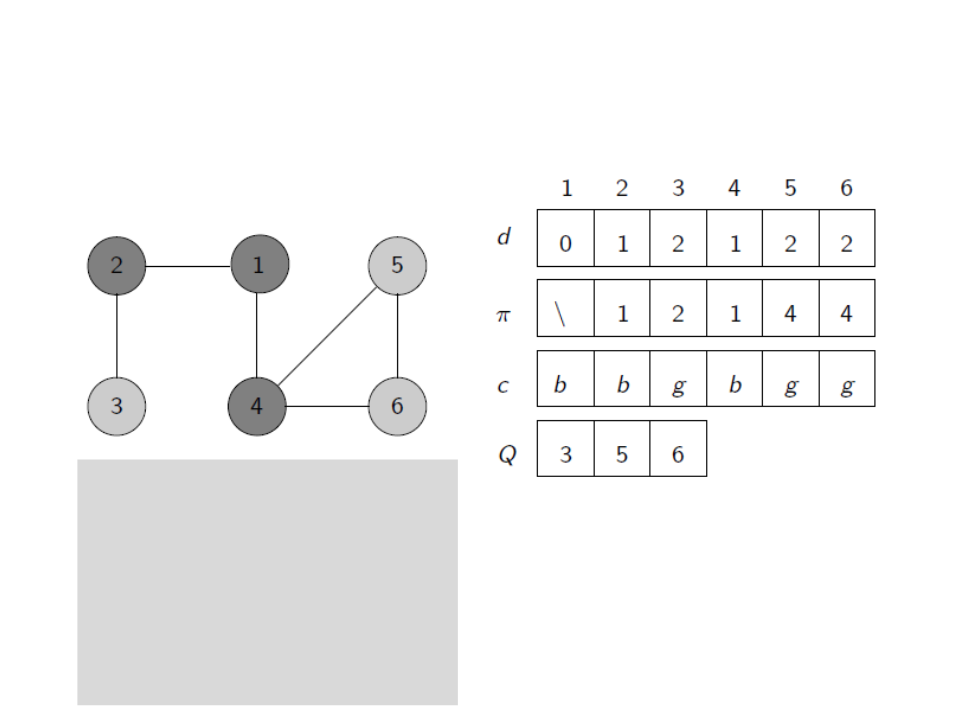
Busca em Largura
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black

Busca em Largura – Análise
BuscaEmLargura(G, s)
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
•
Cada vértice de V é colocado na fila Q
no máximo uma vez: O(V);
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
•
A lista de adjacência de um vértice
qualquer de u é percorrida somente
quando o vértice é removido da fila;
Q ← {s} //Queue
while Q ≠ ∅
u ← head[Q]
for each v ∈ Adj[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
•
A soma de todas as listas de adjacentes
é O(A), então o tempo total gasto com
as listas de adjacentes é O(A);
•
•
Enfileirar e desenfileirar tem custo O(1);
Complexidade: O(V + A)
c[u] ← black
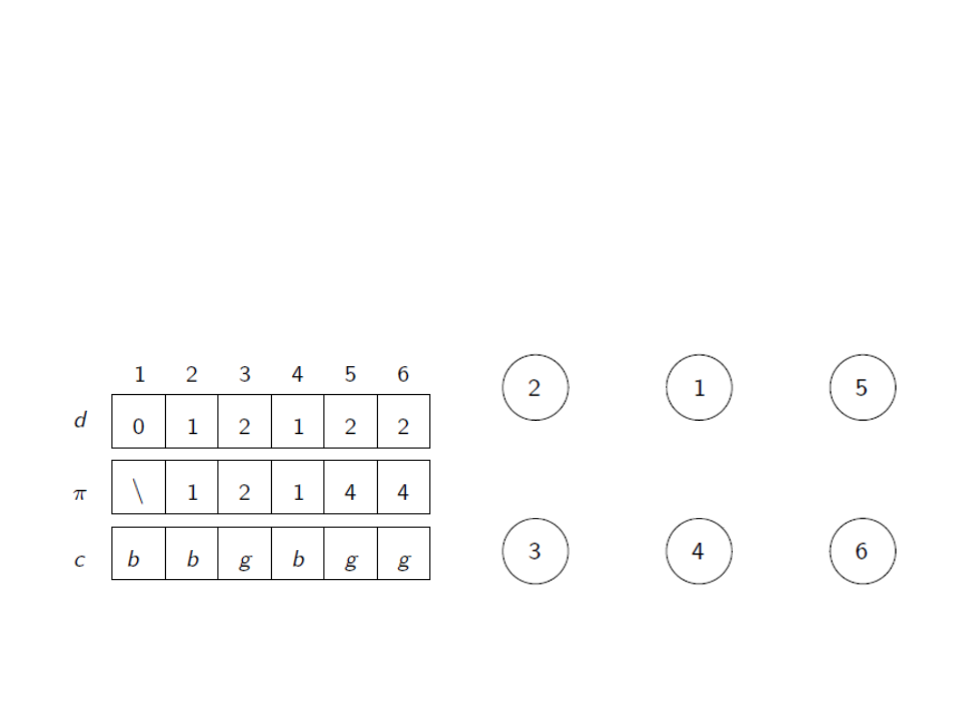
Busca em Largura
•
A partir de π é possível reconstruir a árvore da busca em
largura:
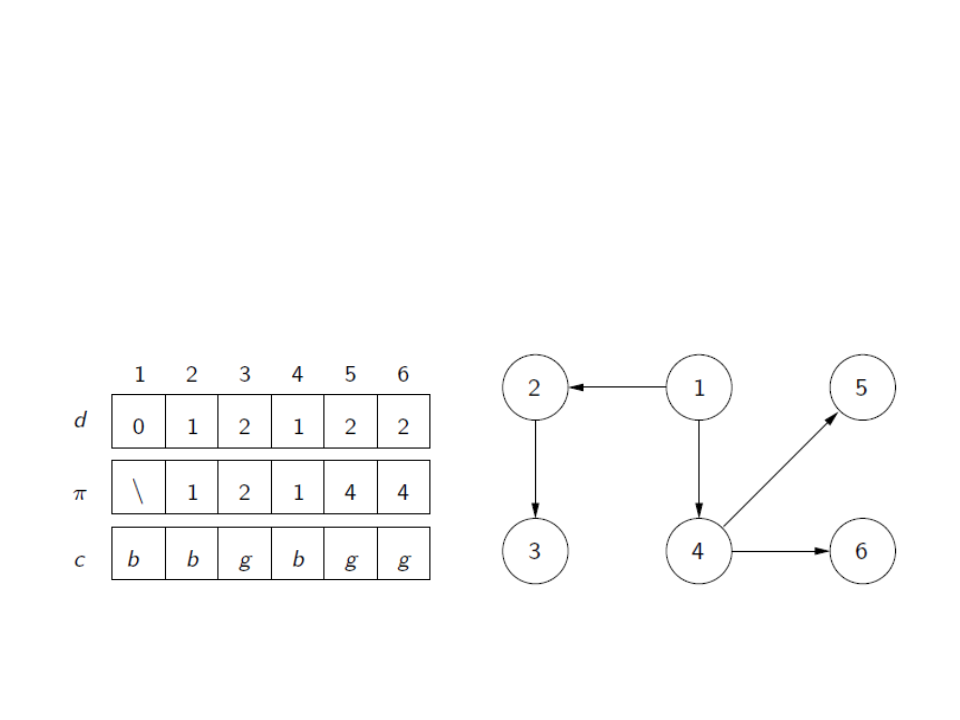
Busca em Largura
•
A partir de π é possível reconstruir a árvore da busca em
largura:

Busca em Profundidade
•
A estratégia é buscar o vértice mais profundo no grafo sempre
que possível:
–
As arestas são exploradas a partir do vértice v mais recentemente
descoberto que ainda possui arestas não exploradas saindo dele.
•
•
Quando todas as arestas adjacentes a v tiverem sido
exploradas a busca anda para trás para explorar vértices que
saem do vértice do qual v foi descoberto (backtraking).
O algoritmo é a base para muitos outros algoritmos
importantes, tais como verificação de grafos acíclicos,
ordenação topológica e componentes fortemente conectados.

Busca em Profundidade
•
Algoritmo:
–
Para controlar a busca, o algoritmo da Busca em
Profundidade pinta cada vértice na cor branca, cinza ou
preto.
–
Todos os vértices iniciam com a cor branca e podem, mais
tarde, se tornar cinza e depois preto.
•
•
•
Branca: não visitado;
Cinza: visitado;
Preta: visitado e seus nós adjacentes visitados.

Busca em Profundidade
•
Algoritmo:
–
A busca em profundidade também marca cada vértice com
um timestamp.
–
Cada vértice tem dois timestamps:
•
•
d[v]: indica o instante em que v foi visitado (pintado com cinza);
f[v]: indica o instante em que a busca pelos vértices na lista de
adjacência de v foi completada (pintado de preto).

Busca em Profundidade
BuscaEmProfundidade(G)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
visita(u)
visita(u)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
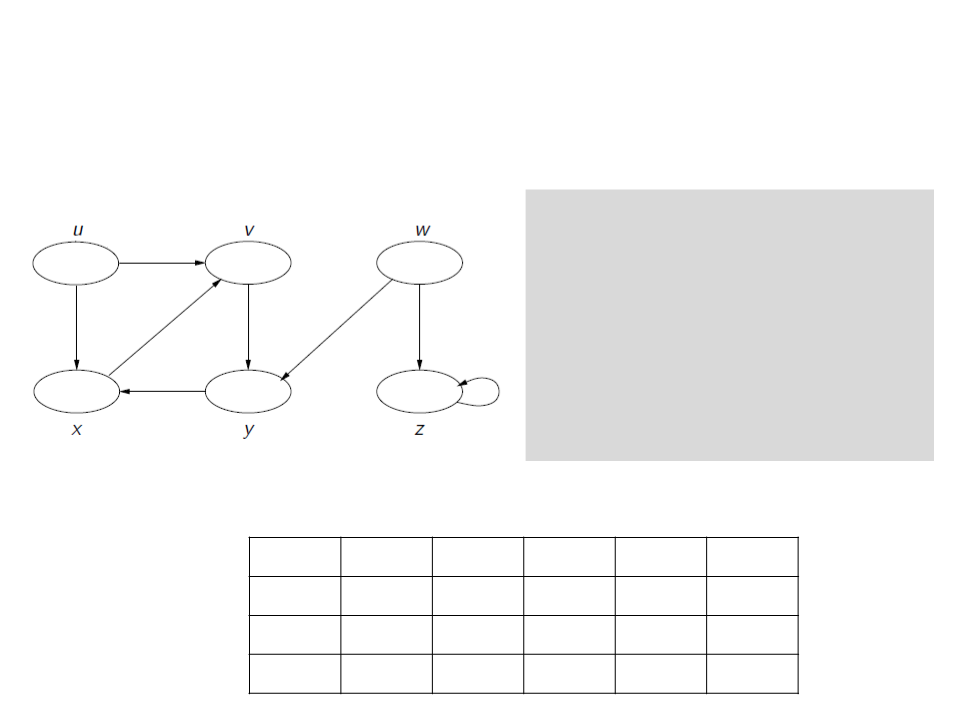
Busca em Profundidade
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
visita(u)
u
w
/
v
w
/
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
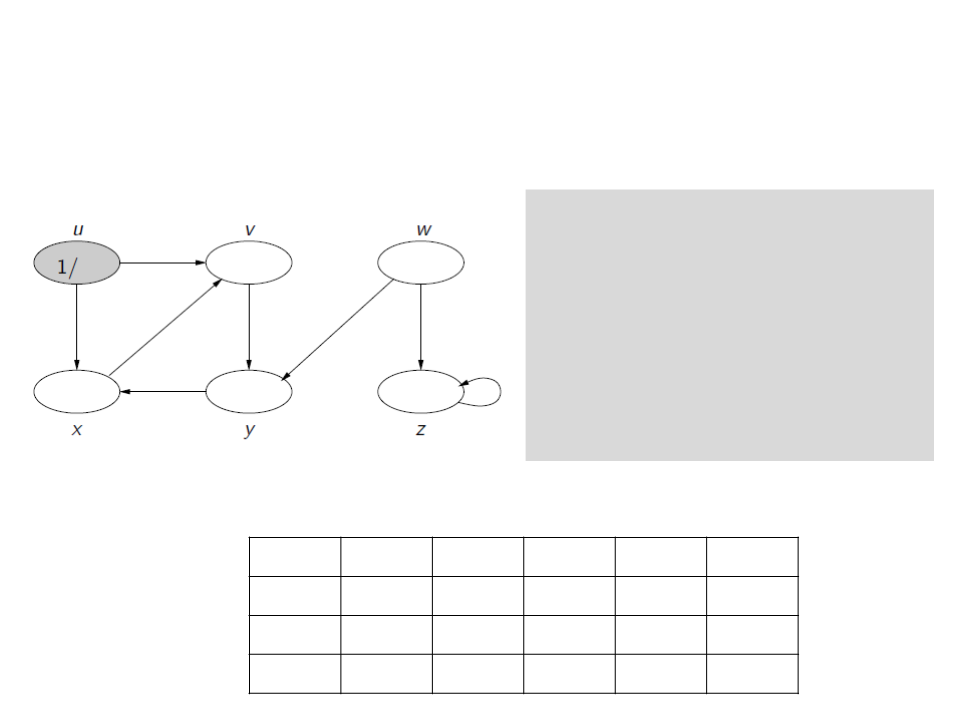
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
w
/
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1
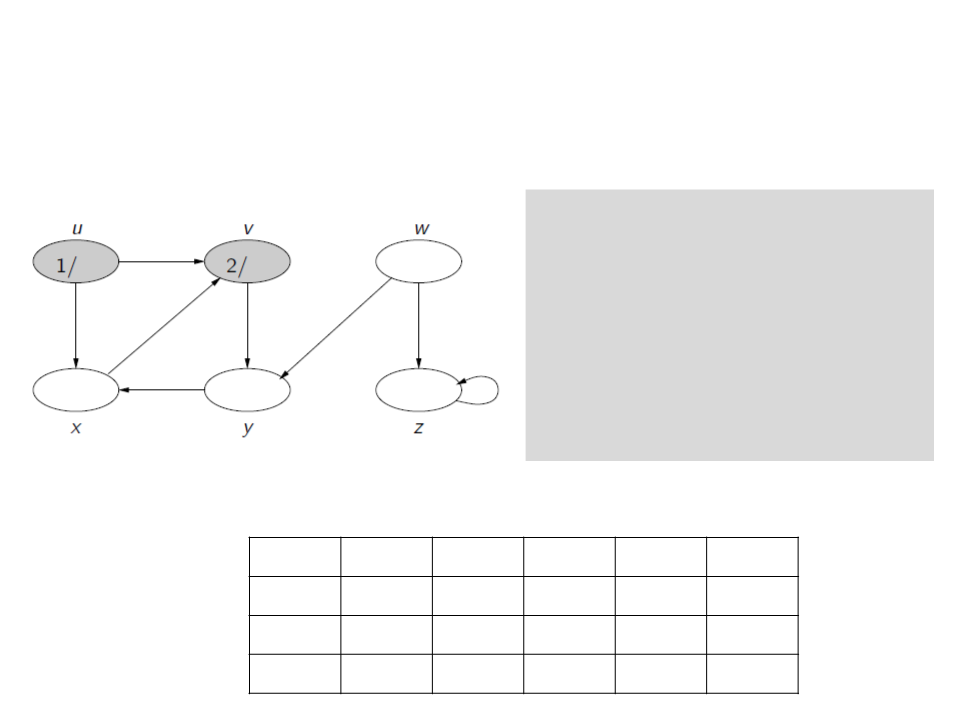
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1
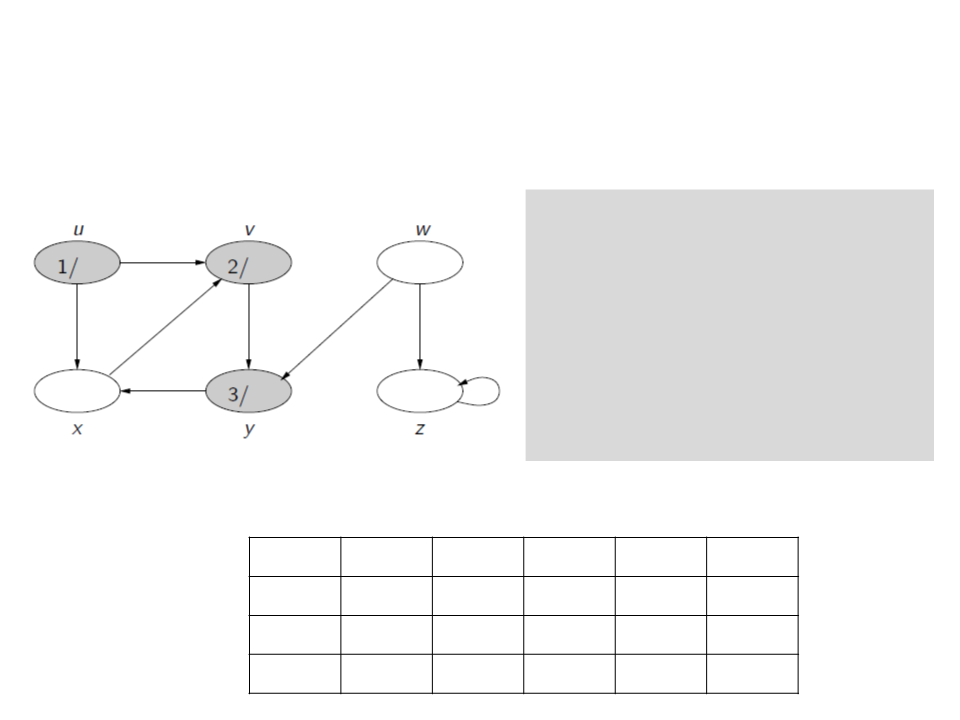
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
g
y
4
w
w
/
z
w
/
c
ꢍ
d
f
1
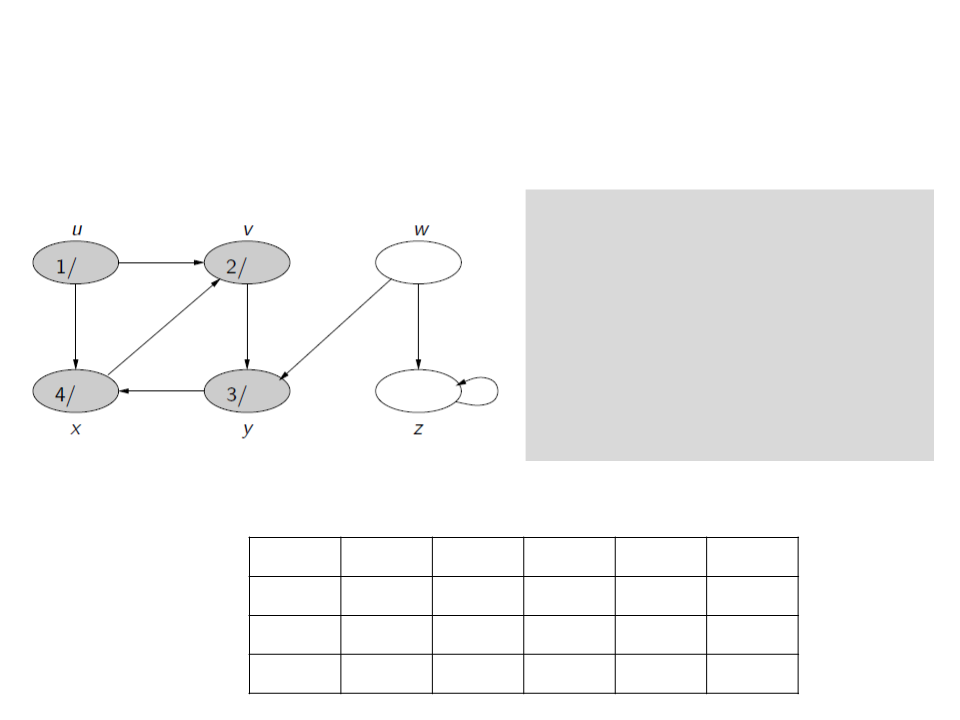
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
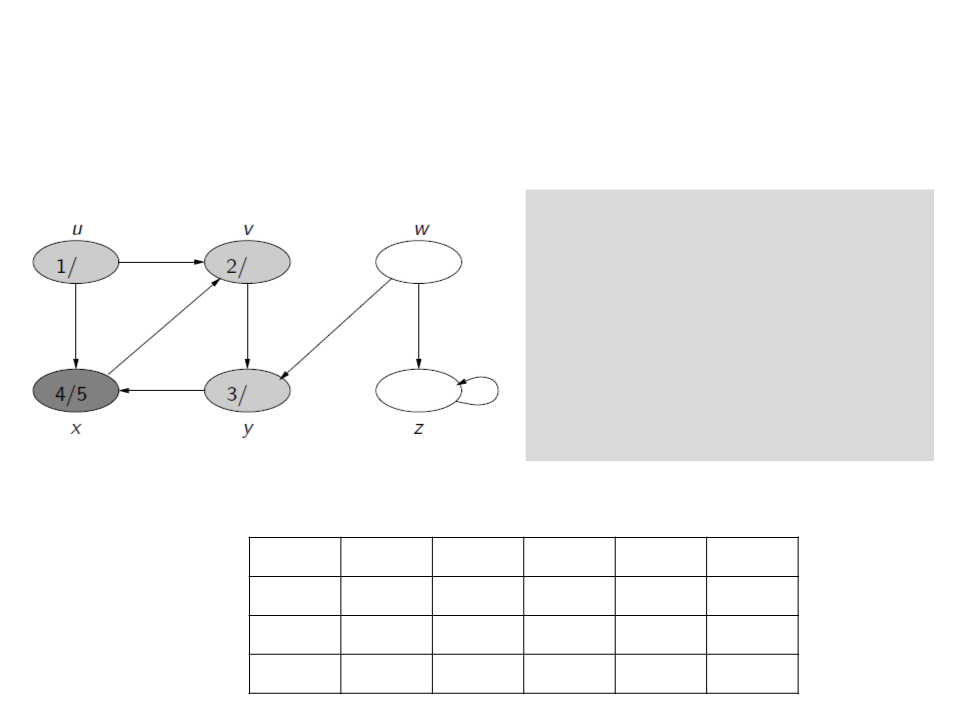
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
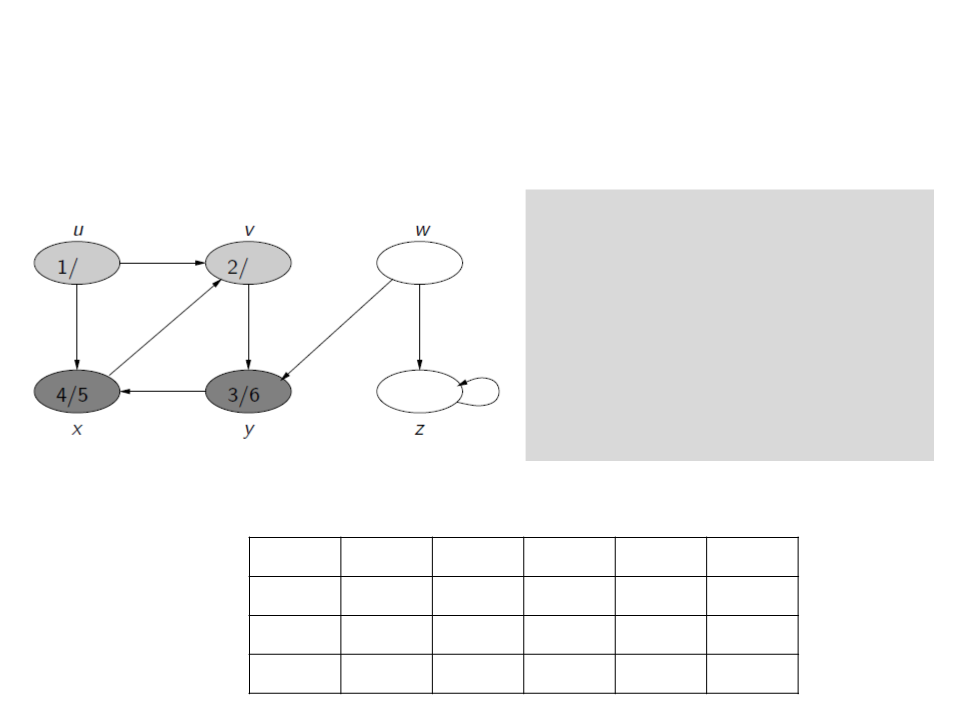
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
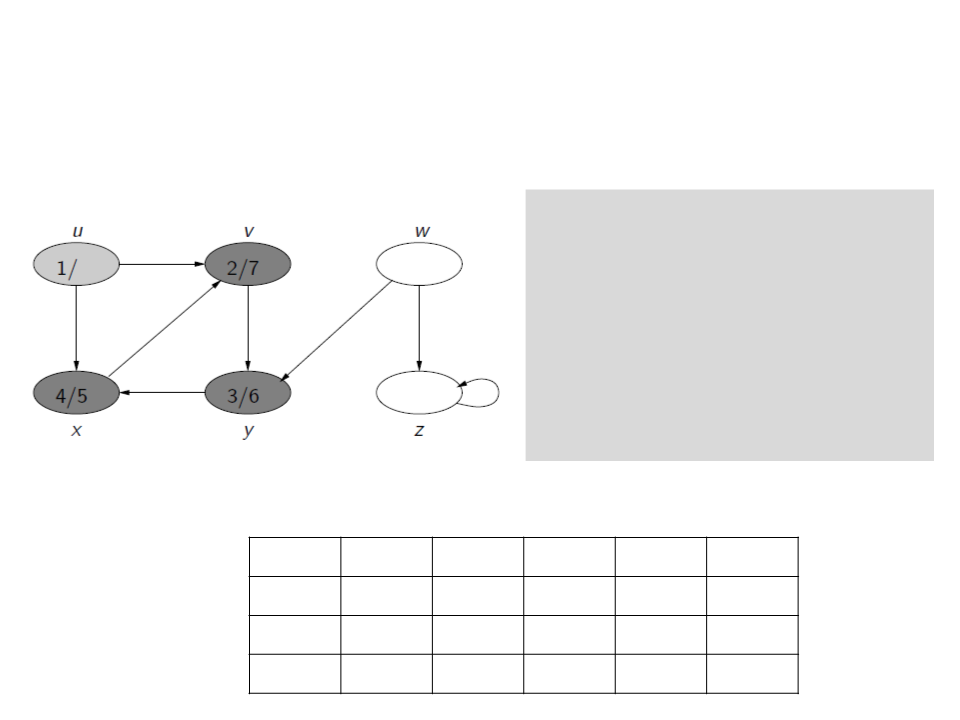
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
8
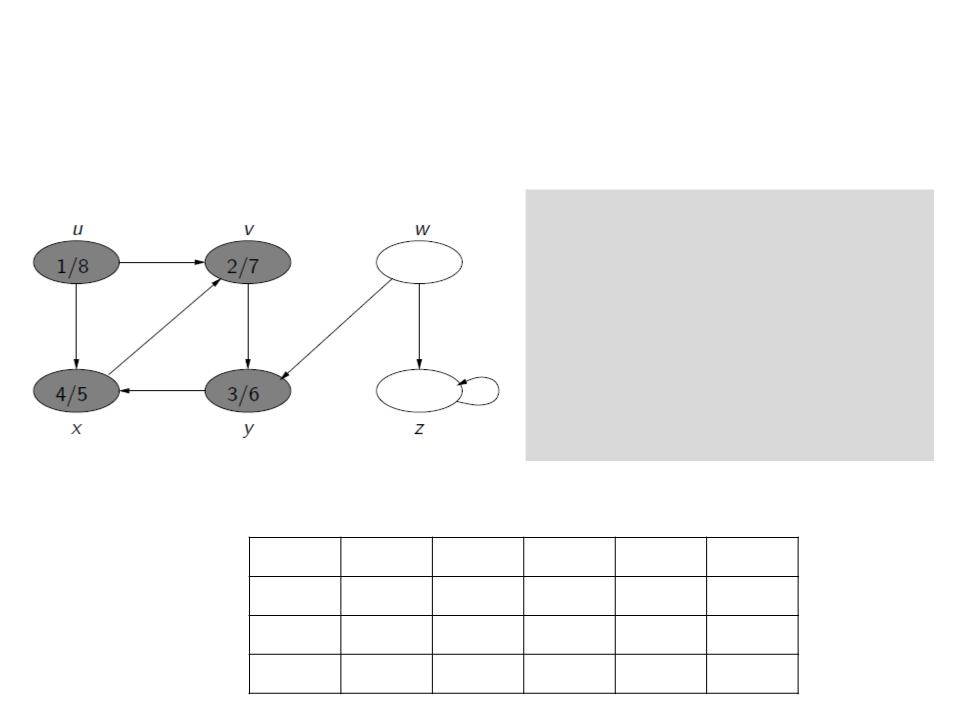
Busca em Profundidade
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
visita(u)
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
8
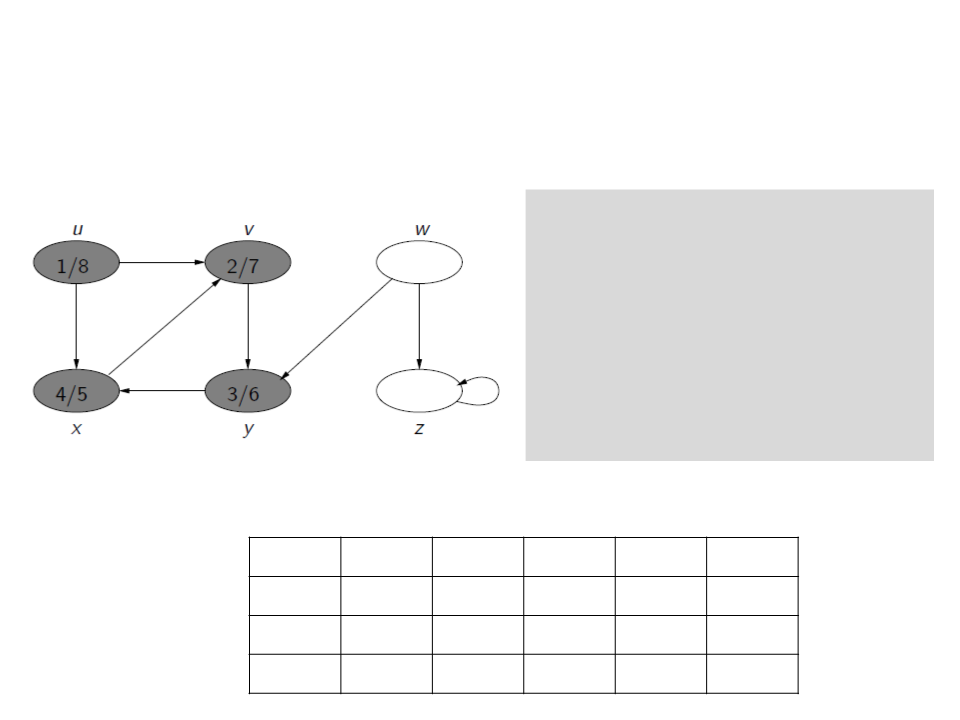
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
g
/
z
w
/
c
ꢍ
d
f
1
8
9
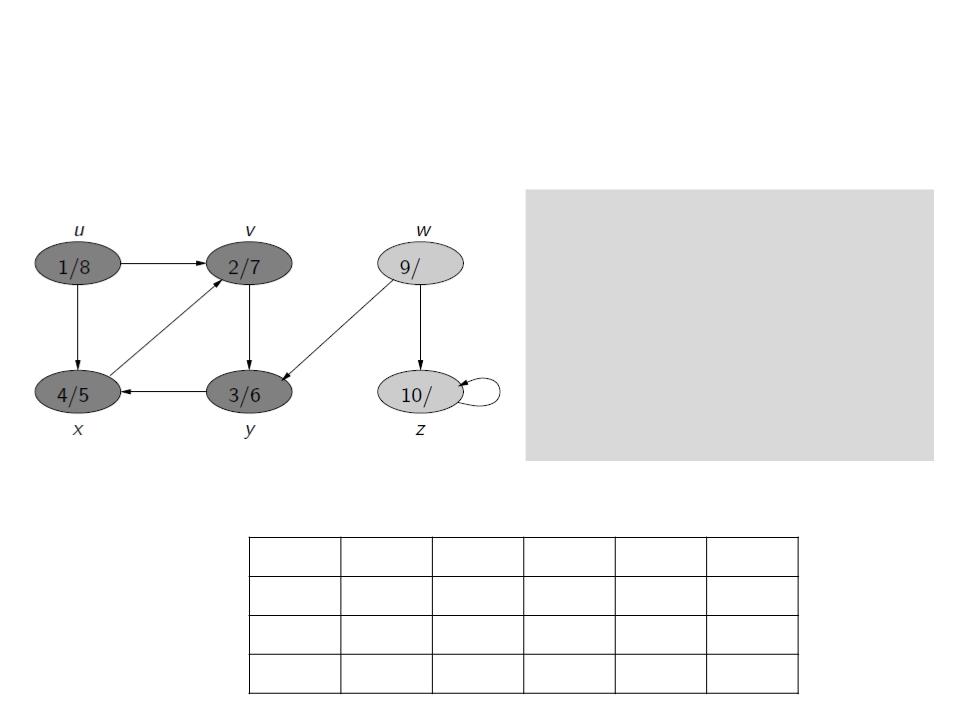
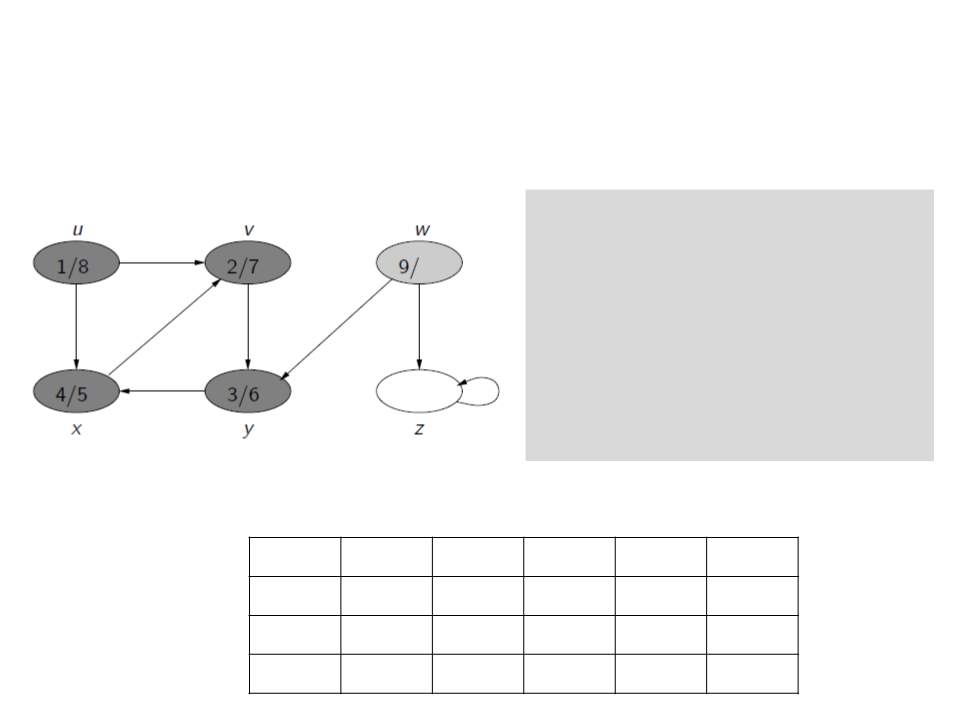
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
g
/
z
g
c
ꢍ
d
f
w
10
1
8
9
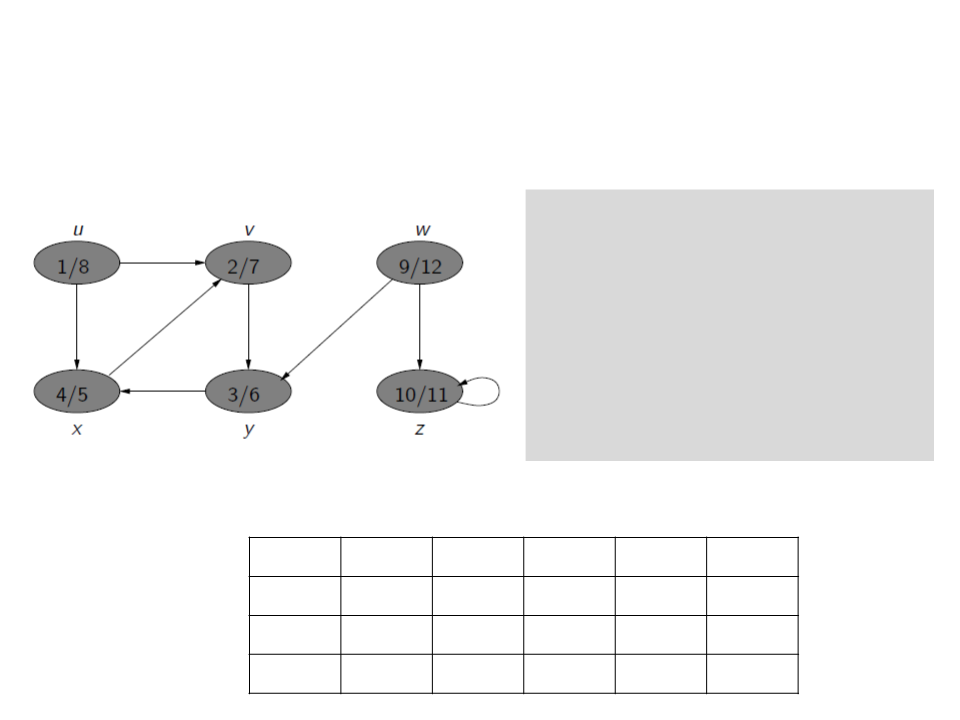
Busca em Profundidade
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
visita(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
b
z
b
c
ꢍ
d
f
/
w
10
12
1
8
9
11

Busca em Profundidade – Análise
BuscaEmProfundidade(G)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
•
O procedimento visitaé chamado
exatamente uma vez ara cada vértice u
V, isso porque visitaé chamado
apenas para vértices brancos e a
primeira ação é pintar o vértice de cinza:
O(V);
∈
time ← 0
for each u ∈ V[G]
if c[u] = white
visita(u)
•
•
O loop principal de visita(u)tem
complexidade O(A);
visita(u)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ Adj[u]
if c[v] = white
ꢍ[v] ← u
Complexidade: O(V + A)
visita(v)
c[u] ← black
f[u] ← time ← time + 1

Busca em Profundidade
•
Classificação de Arestas:
–
Arestas de árvore: são arestas de uma árvore de busca em
profundidade. A aresta (u, v) é uma aresta de árvore se v foi
descoberto pela primeira vez ao percorrer a aresta (u, v);
–
–
Arestas de retorno: conectam um vértice u com um antecessor v
em uma árvore de busca em profundidade (inclui self-loops);
Arestas de avanço: não pertencem à árvore de busca em
profundidade mas conectam um vértice a um descendente que
pertence à árvore de busca em profundidade;
–
Arestas de cruzamento: podem conectar vértices na mesma
árvore de busca em profundidade, ou em duas árvores diferentes.
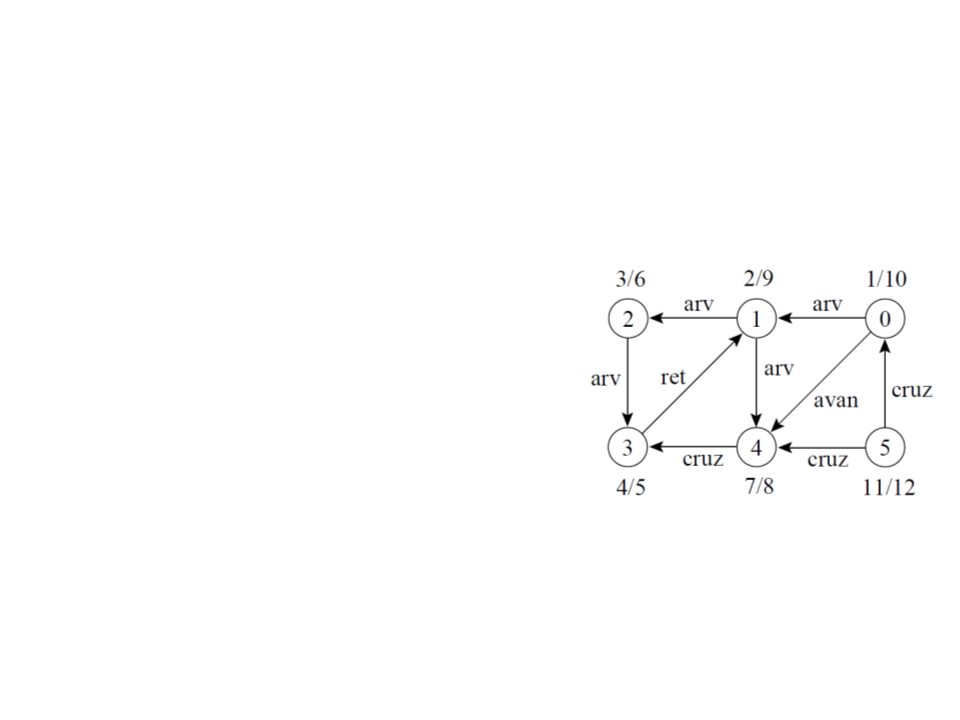
Busca em Profundidade
•
•
Classificação de arestas pode ser útil
para derivar outros algoritmos.
Na busca em profundidade cada
aresta pode ser classificada pela cor
do vértice que é alcançado pela
primeira vez:
–
–
–
Branco indica uma aresta de árvore.
Cinza indica uma aresta de retorno.
Preto indica uma aresta de avanço
quando u é descoberto antes de v ou uma
aresta de cruzamento caso contrário.

Exercícios
Lista de Exercícios 12 – Busca em Profundidade
e Busca em Largura
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Halim e Halim. Competitive Programming, 3rd
Edition, 2003.
Capítulo 4: Graph
•
•
Cormen, Leiserson, Rivest e Stein. Algoritmos –
Teoria e Prática, 2ª. Edição, Editora Campus,
2
002.
Capítulo 22: Algoritmos Elementares de Grafos
