
Projeto e Análise de Algoritmos
Aula 09 – Algoritmos de Ordenação
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Ordenação
•
Problema:
–
Entrada: conjunto de itens a1, a2, . . . , an;
–
Saída: conjunto de itens permutados em uma ordem ak1,
ak2, . . . , akn, tal que, dada uma função de ordenação f,
tem-se a seguinte relação: f(ak1) < f(ak2) < . . . < f(akn).
•
•
Ordenar consiste no processo de rearranjar um conjunto de
objetos em uma ordem crescente ou descendente.
O objetivo principal da ordenação é facilitar a recuperação
posterior de itens do conjunto ordenado.

Ordenação
•
•
Qualquer tipo de campo chave, sobre o qual exista uma
relação de ordem total <, para uma dada função de
ordenação, pode ser utilizado.
A relação < deve satisfazer as condições:
–
Apenas uma das seguintes expressões pode ser verdadeira: a < b, a =
b, a > b;
–
Se a < b e b < c então a < c;
•
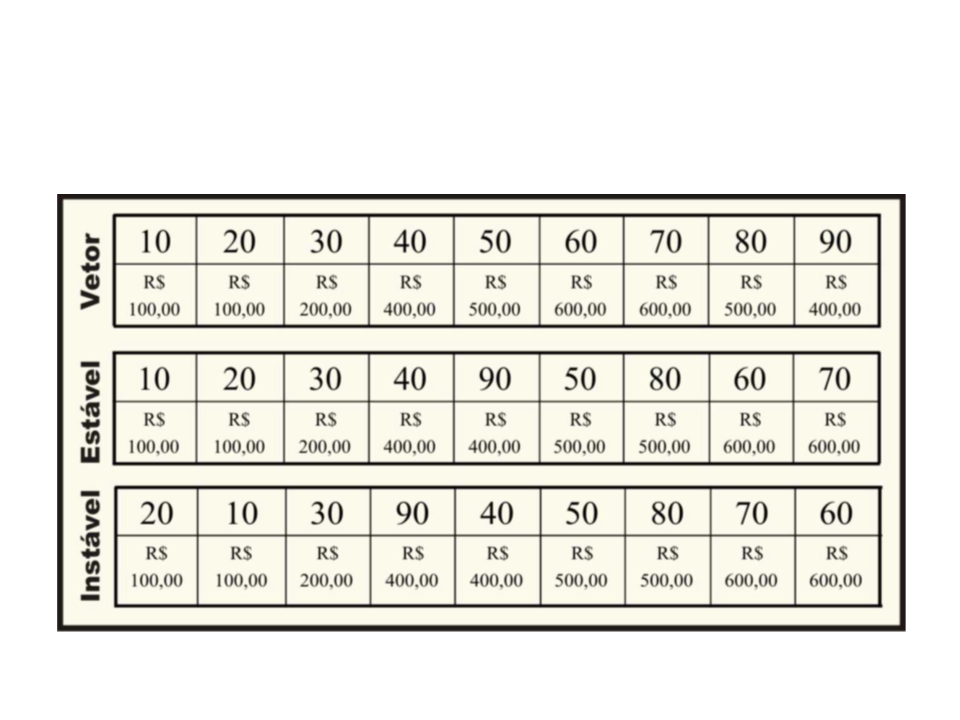
Um método de ordenação é dito estável se a ordem relativa
dos itens com chaves iguais mantém-se inalterada pelo
processo de ordenação.
Ordenação

Ordenação
•
Os métodos de ordenação são classificados em dois grandes
grupos:
–
Ordenação Interna: São os métodos que não necessitam de uma
memória secundária para o processo, a ordenação é feita na memória
principal do computador;
•
Qualquer registro pode ser acessado em tempo O(1);
–
Ordenação Externa: Quando o arquivo a ser ordenado não cabe na
memória principal e, por isso, tem de ser armazenado em disco.
•
Registros são acessados sequencialmente ou em grandes blocos;

Ordenação
•
•
Métodos de Ordenação:
–
–
–
–
–
Bubble Sort;
Selection Sort;
Insertion Sort;
Merge Sort;
Quick Sort;
Limite assintótico mínimo para algoritmos de ordenação
baseados em comparações:
O(n log n)
Bubble Sort
•
Algoritmo:
–
Quando dois elementos estão fora de ordem, troque-os de
posição até que o i-ésimo elemento de maior valor do
vetor seja levado para as posições finais do vetor;
–
Continue o processo até que todo o vetor esteja ordenado;
Bubble Sort
162 162 2124 12842 1128772 122722
6
12 11844 184 17 2222
Bubble Sort
6
6
6
6
12 14 8 17 22
12 8 14 17 22
182 11822 14 17 2222
8 1122 14 1177 2222

Bubble Sort - Implementação Iterativa (I)
void bubblesort(int n, int* v)
{
int fim, i, temp;
for (fim = n-1; fim > 0; fim--)
{
for (i=0; i<fim; i++)
{
if (v[i]>v[i+1])
{
temp = v[i];
v[i] = v[i+1];
v[i+1] = temp;
}
}
}
}
Bubble Sort - Implementação Iterativa (II)
void bubblesort(int n, int* v)
{
int i, fim, troca, temp;
for (fim = n-1; fim > 0; fim--){
troca = 0;
for (i=0; i<fim; i++){
if (v[i]>v[i+1]){
temp = v[i];
v[i] = v[i+1];
v[i+1] = temp;
troca = 1;
}
Implementação mais otimizada:
para a busca quando ocorre
uma passada sem trocas.
}
if (troca == 0)
return;
}
}

Bubble Sort - Complexidade
•
•
Esforço computacional ≅ número de comparações
≅
número máximo de trocas
–
–
–
primeira passada: n-1 comparações
segunda passada: n-2 comparações
terceira passada: n-3 comparações
Tempo total gasto pelo algoritmo:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Algoritmo de ordem quadrática: O(n2)
ꢁ

Bubble Sort
•
•
Complexidade: O(n2)
Vantagens:
–
–
Fácil Implementação;
É estável;
•
Desvantagens:
–
O fato do vetor já estar ordenado não ajuda em nada;
–
Ordem de complexidade quadrática;
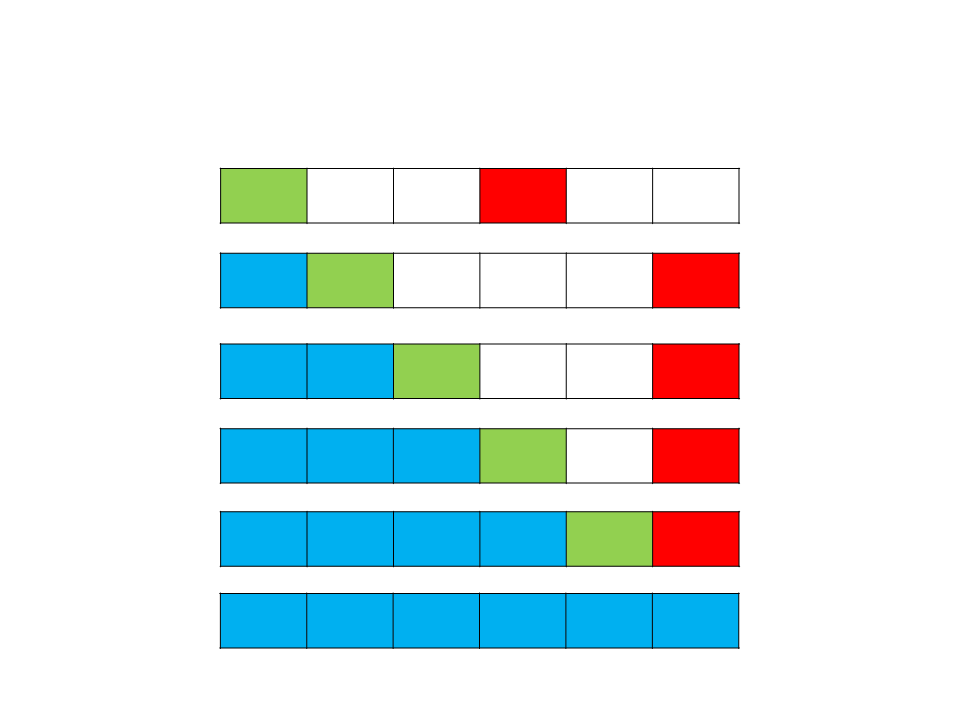
Selection Sort
•
Algoritmo:
–
Em cada etapa, em selecionar o maior (ou o menor)
elemento e alocá-lo em sua posição correta dentro da
futura lista ordenada.
Selection Sort
8
1
5 7 1 9 3
5 7 8 9 3
1
1
1
1
3 7 8 9 5
3 5 8 9 7
3 5 7 9 8
3 5 7 8 9

Selection Sort - Implementação
void selectSort(int arr[], int n)
{
int pos_min, temp, i, j;
for (i=0; i < n-1; i++){
pos_min = i;
for (j=i+1; j < n; j++){
if (arr[j] < arr[pos_min])
pos_min=j;
}
if (pos_min != i){
temp = arr[i];
arr[i] = arr[pos_min];
arr[pos_min] = temp;
}
}
}

Selection Sort – Complexidade
•
•
Esforço computacional ≅ número de comparações
≅
número máximo de trocas
Tempo total gasto pelo algoritmo:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Algoritmo de ordem quadrática: O(n2)
ꢁ

Selection Sort
•
•
Complexidade: O(n2)
Vantagens:
–
–
–
Fácil Implementação;
Pequeno número de movimentações;
Interessante para arquivos pequenos;
•
Desvantagens:
–
–
–
O fato de o arquivo já estar ordenado não influencia em nada;
Ordem de complexidade quadrática;
Algoritmo não estável;
Insertion Sort
•
Algoritmo:
–
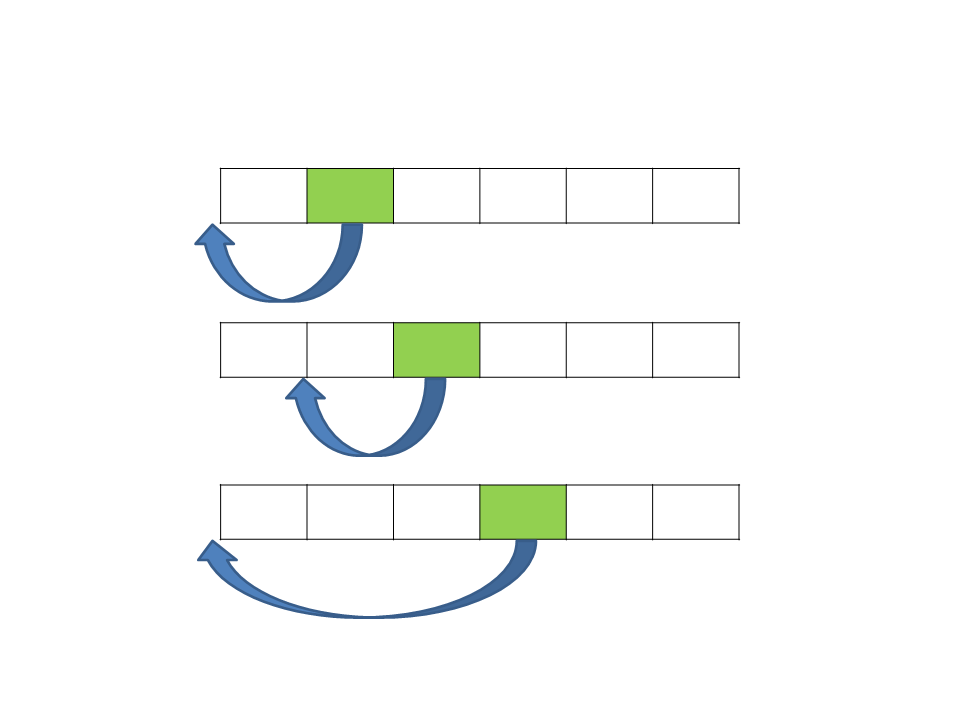
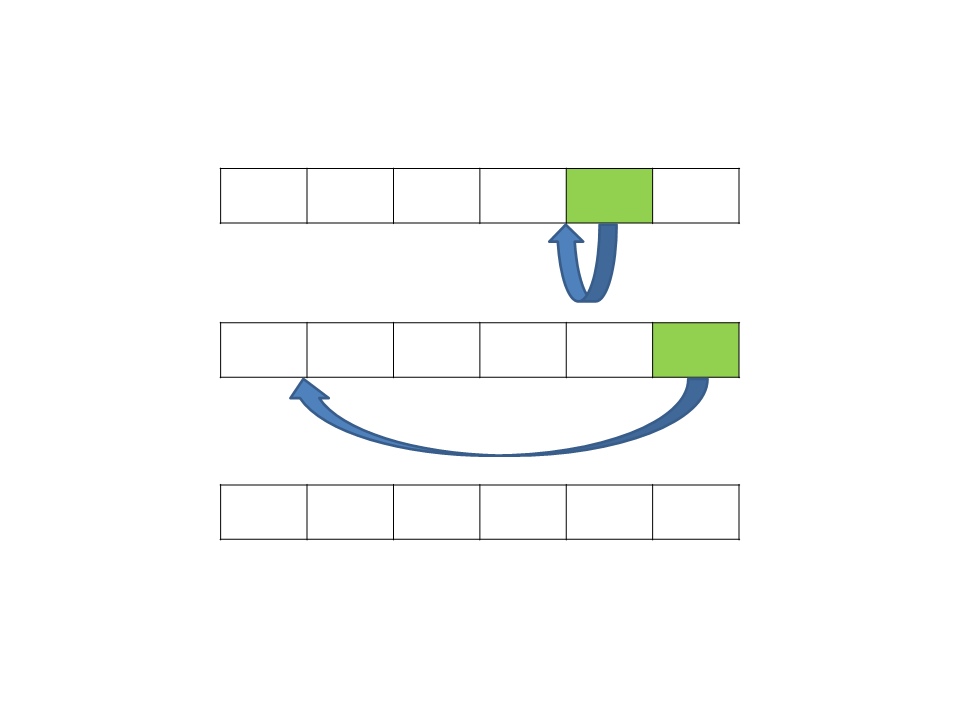
Em cada passo, a partir de i=2, o i-ésimo item da sequência
fonte é apanhado e transferido para a sequência destino,
sendo colocado na posição correta.
–
A inserção do elemento no lugar de destino é efetuado
movendo-se os itens com chave maiores para a direita e
então inserindo-o na posição que ficou vazia.
Insertion Sort
8
5
5 7 1 9 3
8 7 1 9 3
5
7 8 1 9 3
Insertion Sort
1
1
5 7 8 9 3
5 7 8 9 3
1
3 5 7 8 9

Insertion Sort – Implementação
void insertion_sort(int arr[], int length)
{
int j, i, temp;
for (i = 1; i < length; i++)
{
j = i;
while (j > 0 && arr[j] < arr[j-1])
{
temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
j--;
}
}
}

Insertion Sort – Complexidade
•
•
Esforço computacional ≅ número de comparações
≅
número máximo de trocas
Tempo total gasto pelo algoritmo:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Algoritmo de ordem quadrática: O(n2)
ꢁ

Insertion Sort
•
•
Complexidade: O(n2)
Vantagens:
–
–
–
Fácil Implementação;
Algoritmo estável;
O vetor já ordenado favorece a ordenação: O(n);
•
Desvantagens:
–
Ordem de complexidade quadrática;
–
Ineficiente quando o vetor está ordenado inversamente (algo natural
em um problema de ordenação);

Merge Sort
•
•
Algoritmo:
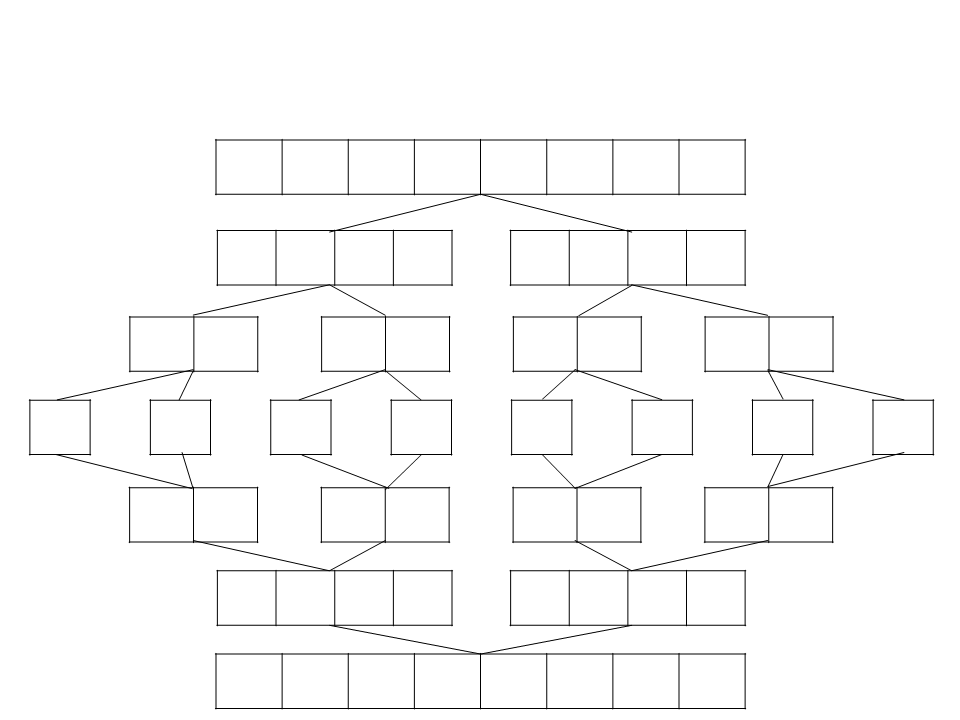
–
Criar uma sequência ordenada a partir de duas outras também
ordenadas.
–
Para isso, divide-se a sequência original em pares de dados, ordena-as;
depois as agrupa em sequências de quatro elementos, e assim por
diante, até ter toda a sequência dividida em apenas duas partes.
É um algoritmo de ordenação do tipo dividir para conquistar:
–
Dividir: Dividir os dados em subsequências pequenas;
–
Conquistar: Classificar as duas metades recursivamente aplicando o
merge sort;
–
Combinar: Juntar as duas metades em um único conjunto já
classificado.
Merge Sort
8
8
5 7 1 9 3 2 4
5 7 1
7 1
9 3 2 4
9 3
8
5
5
8
2 4
2
8
5
7
1
9
3
4
1 7
3 9
2 4
1
1
5 7 8 2 3 4 9
2 3 4 5 7 8 9

Merge Sort – Implementação
void mergeSort_ordena(int *v, int esq, int dir)
{
if (esq == dir)
return;
int meio = (esq+dir) / 2;
mergeSort_ordena(v, esq, meio);
mergeSort_ordena(v, meio+1, dir);
mergeSort_intercala(v, esq, meio, dir);
}

Merge Sort – Implementação
void mergeSort_intercala(int* v, int esq, int meio, int dir)
{
int i, j, k;
int a_tam = meio – esq + 1;
int b_tam = dir - meio;
int *a = (int*)malloc(sizeof(int) * a_tam);
int *b = (int*)malloc(sizeof(int) * b_tam);
for(i = 0; i < a_tam; i++)
{
a[i] = v[i+esq];
}
for(i = 0;i < b_tam; i++)
{
b[i] = v[i+meio+1];
}
[
continua…]

Merge Sort – Implementação
...
[
… continuação]
for(i = 0, j = 0, k = esq; k <= dir; k++)
{
if(i == a_tam)
v[k] = b[j++];
else if (j == b_tam)
v[k] = a[i++];
else if (a[i] < b[j])
v[k] = a[i++];
else
v[k] = b[j++];
}
free(a);
free(b);
}

Merge Sort – Complexidade
•
Tempo gasto para dividir: O(log n)
Repetição
Tamanho do Problema
1
2
n
n/2
n/4
…
3
…
log n
1
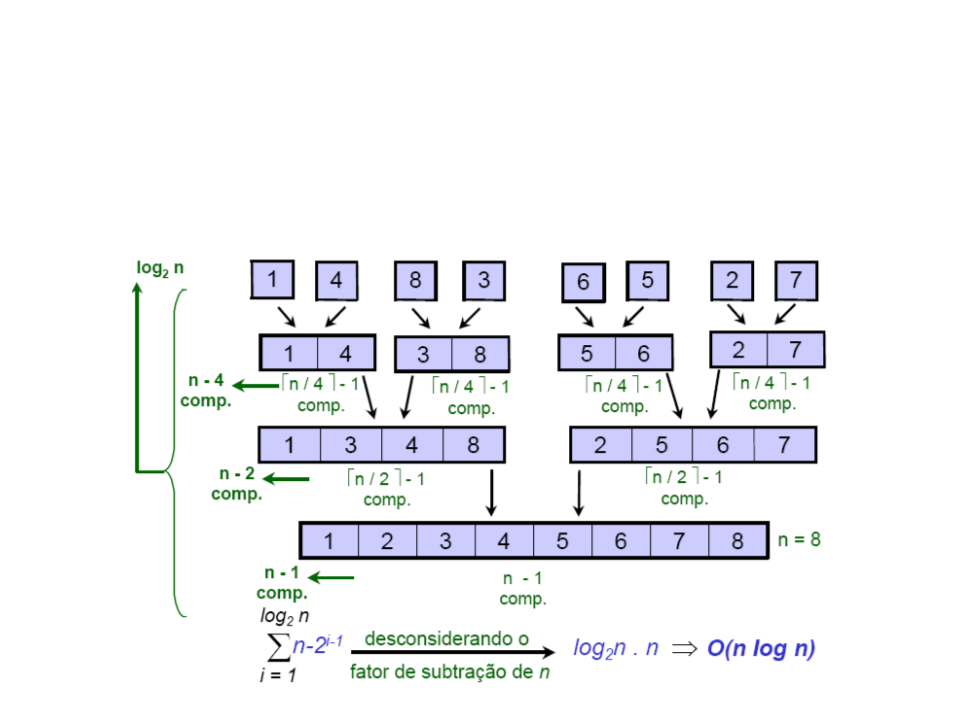
Merge Sort – Complexidade
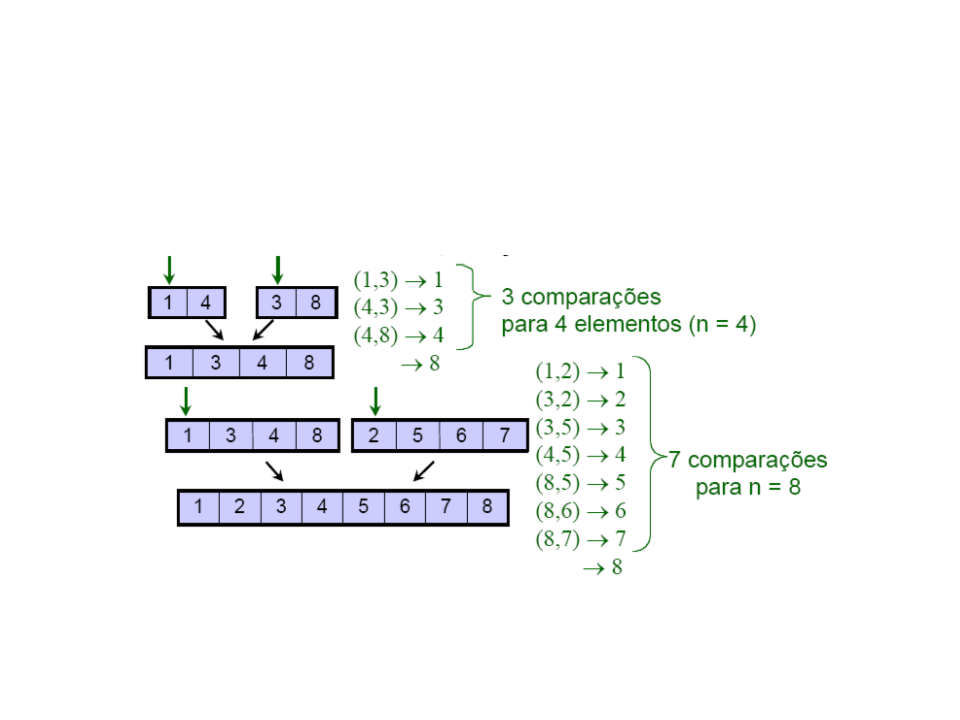
•
Tempo gasto para combinar: O(n)
Merge Sort – Complexidade
•
Tempo total gasto pelo algoritmo: O(n log n)

Merge Sort
•
•
Complexidade: O(n log n)
Vantagens:
–
–
Complexidade O(n log n);
É estável;
•
Desvantagens:
–
Tradicionalmente baseia-se em chamadas recursivas, mas é possível
implementa-lo sem utilizar recursão;
–
Utiliza memória auxiliar;
Quick Sort
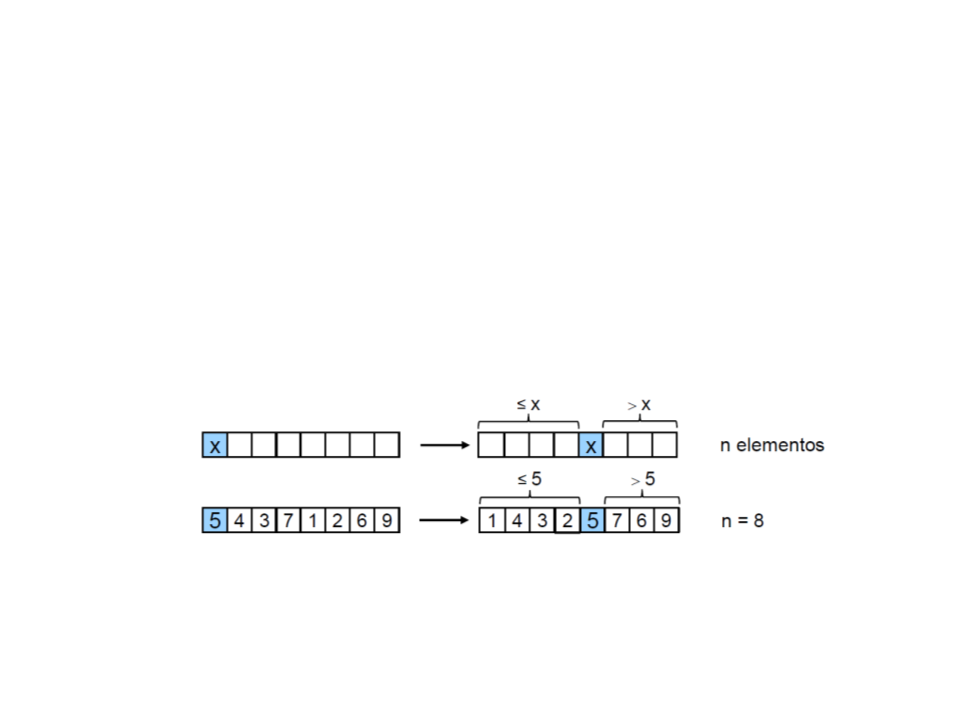
•
Algoritmo:
1. Escolha um elemento arbitrário x, o pivô;
2. Particione o vetor de tal forma que x fique na posição correta v[i]:
•
x deve ocupar a posição i do vetor sse:
todos os elementos v[0], … v[i-1] são menores que x;
todos os elementos v[i+1], …, v[n-1] são maiores que x;
3
. Chame recursivamente o algoritmo para ordenar os subvetores
v[0], … v[i-1] e v[i+1], …, v[n-1] (vetor da esquerda e vetor da direita)
•
continue até que os vetores que devem ser ordenados tenham 0 ou 1 elemento

Quick Sort
quicksort do vetor de tamanho n
se n > 1 então
PARTIÇÃO com pivô x
quicksort do subvetor à esquerda de x
quicksort do subvetor à direita de x
Quick Sort
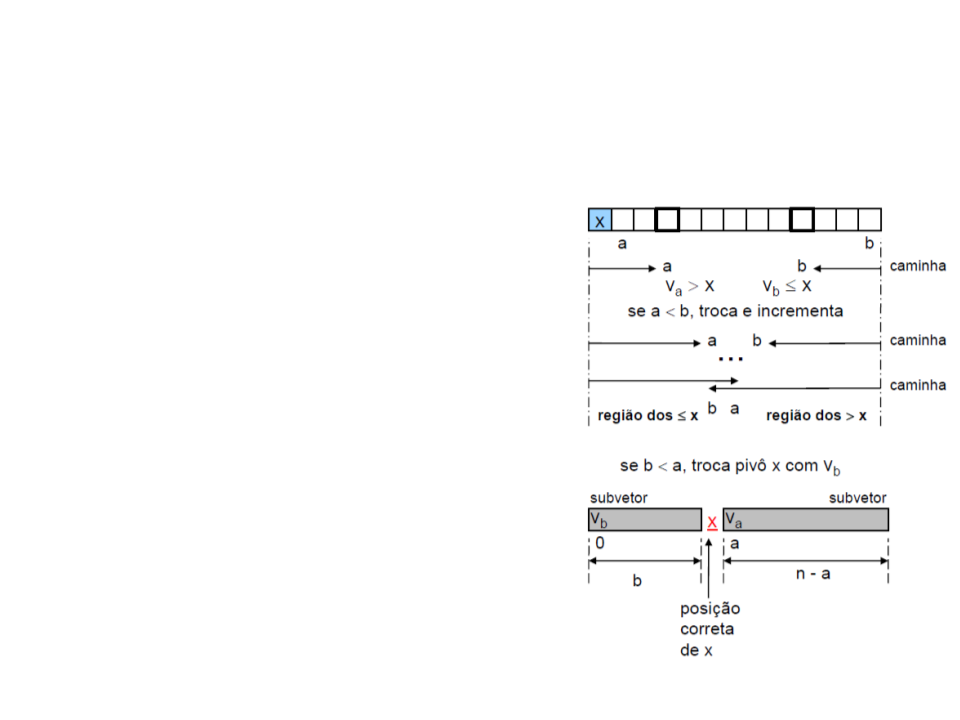
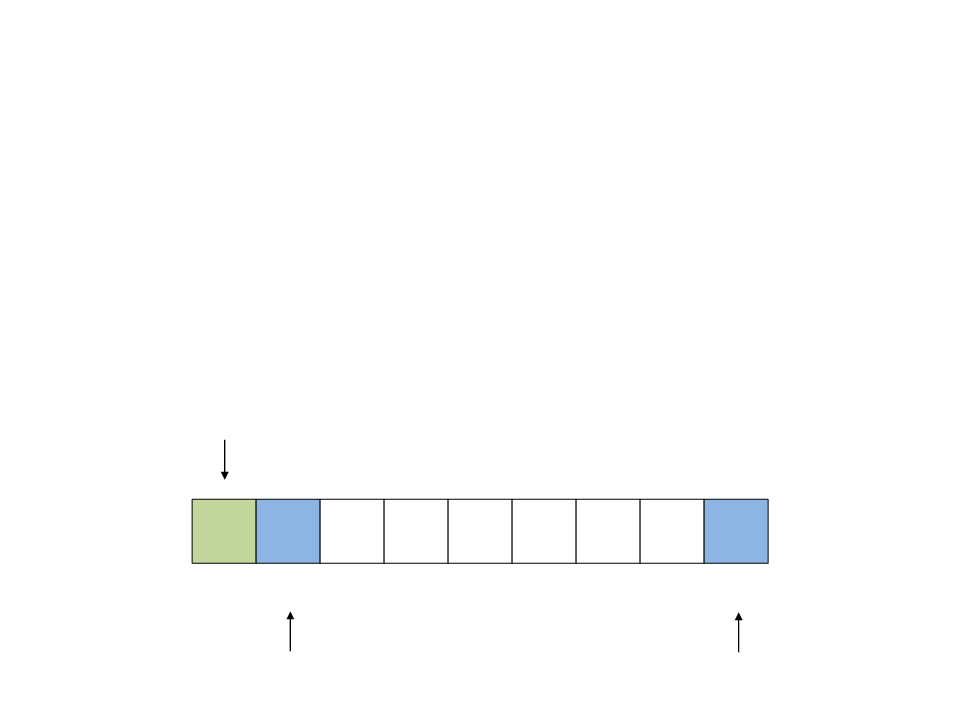
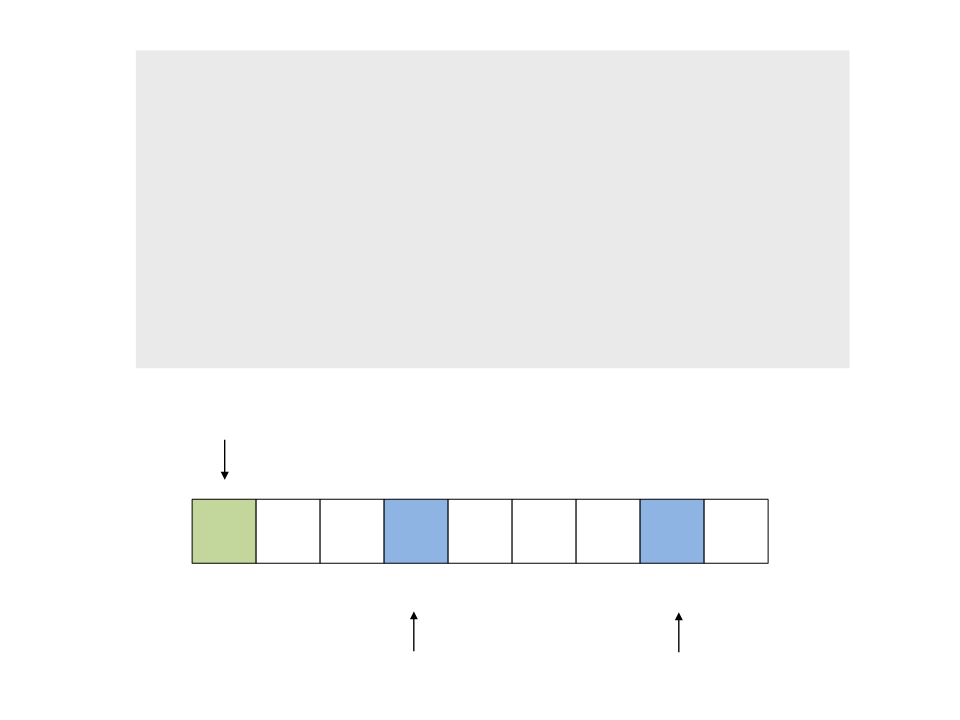
•
Processo de partição:
1. Caminhe com o índice a do início
para o final, comparando x com v[1],
v[2], … até encontrar v[a] > x
2
. Caminhe com o índice b do final para
o início, comparando x com v[n-1],
v[n-2], … até encontrar v[b] <= x
3. Troque v[a] e v[b]
4
. Continue para o final a partir de
v[a+1] e para o início a partir de
v[b-1]
5
. Termine quando os índices de busca
(a e b) se encontram (b < a)
•
A posição correta de x=v[0] é a posição
b, então v[0] e v[b] são trocados
Quick Sort
•
Processo de Partição:
–
Exemplo:
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
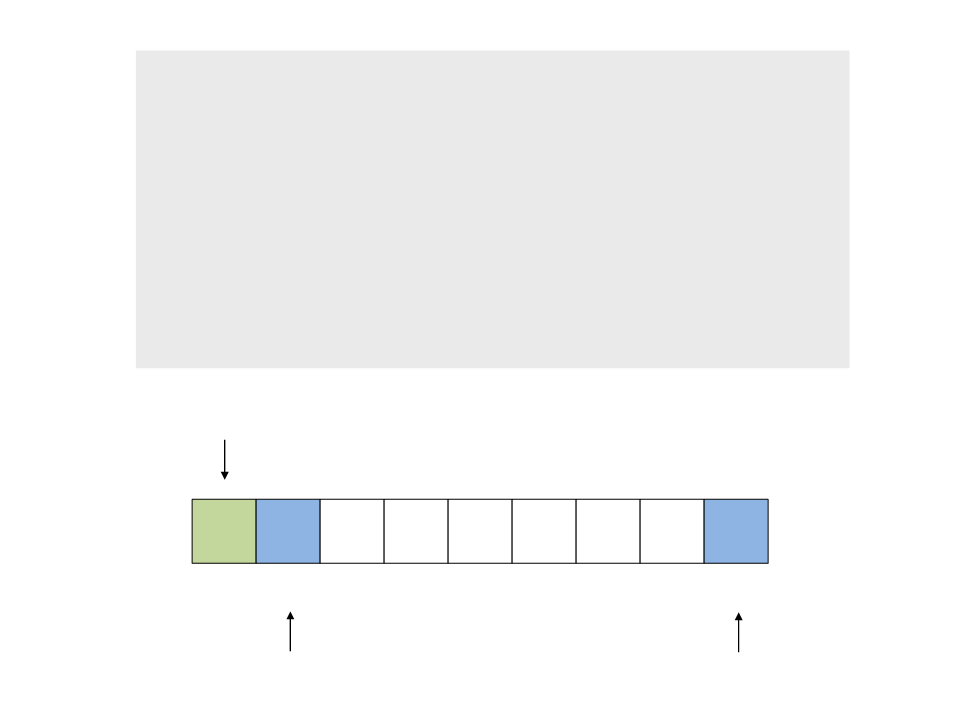
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
4
0
20 10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3] [4]
[5]
[6]
a
b
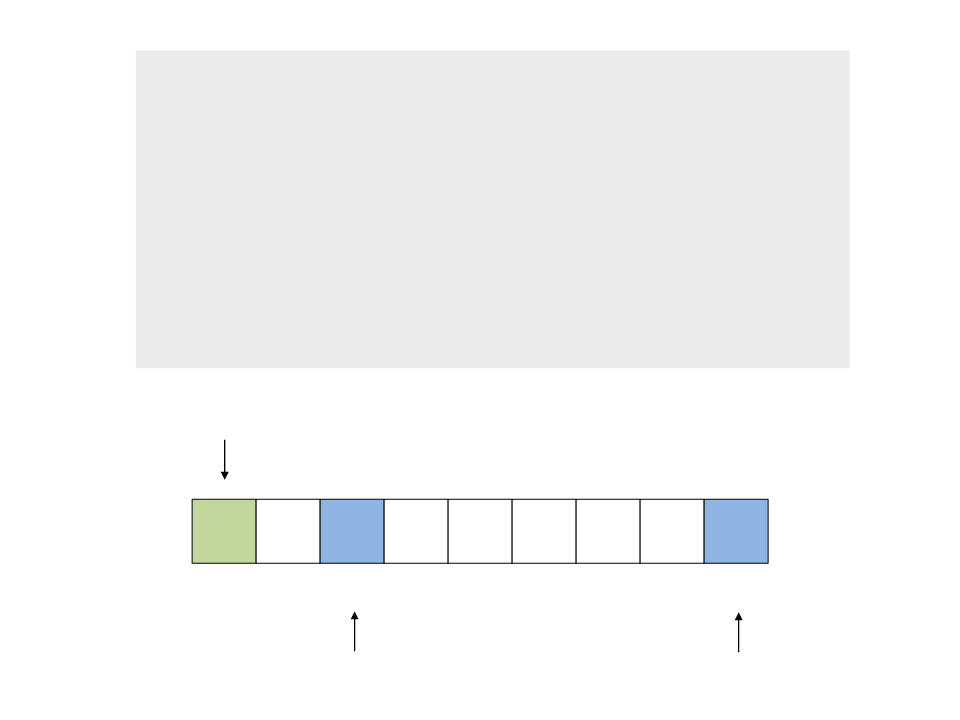
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1] [2] [3]
[4]
[5]
[6]
a
b
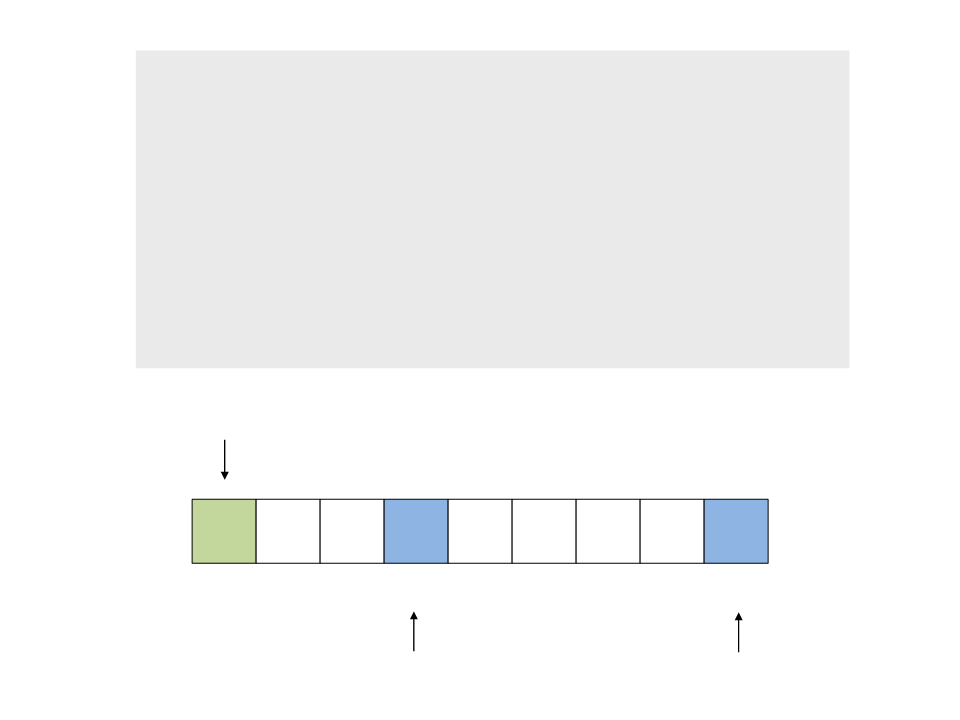
do{
while (a < n && v[a] <= x)
a++;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4] [5]
[6]
a
b
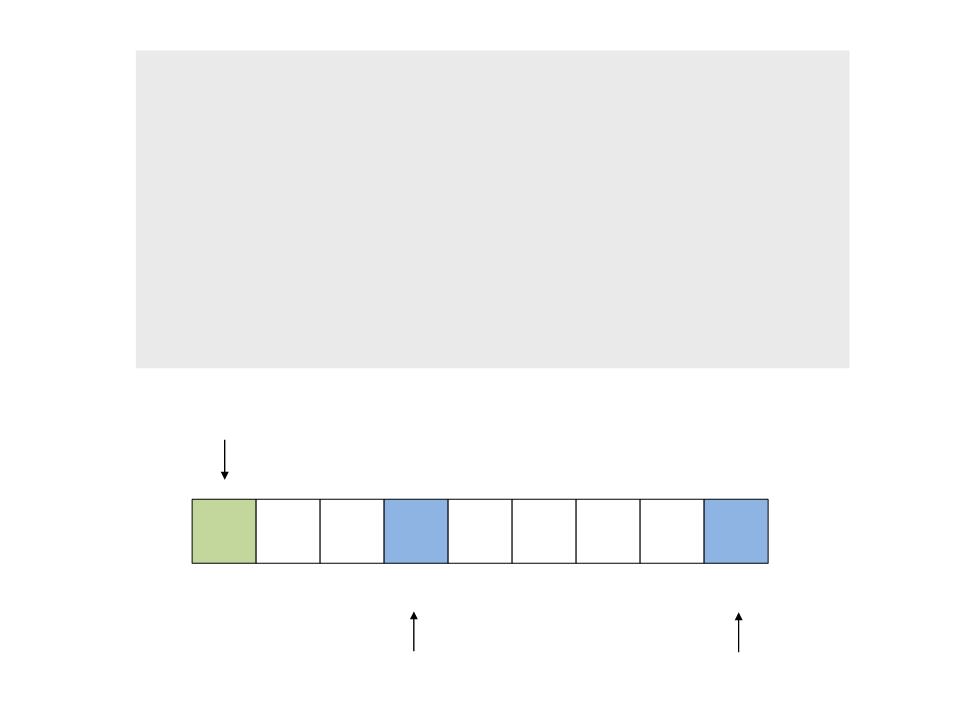
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
x (pivô)
40
20
10
80
60
50
7
30 100
[
0]
[1]
[2] [3]
[4]
[5]
[6] [7] [8]
a
b
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
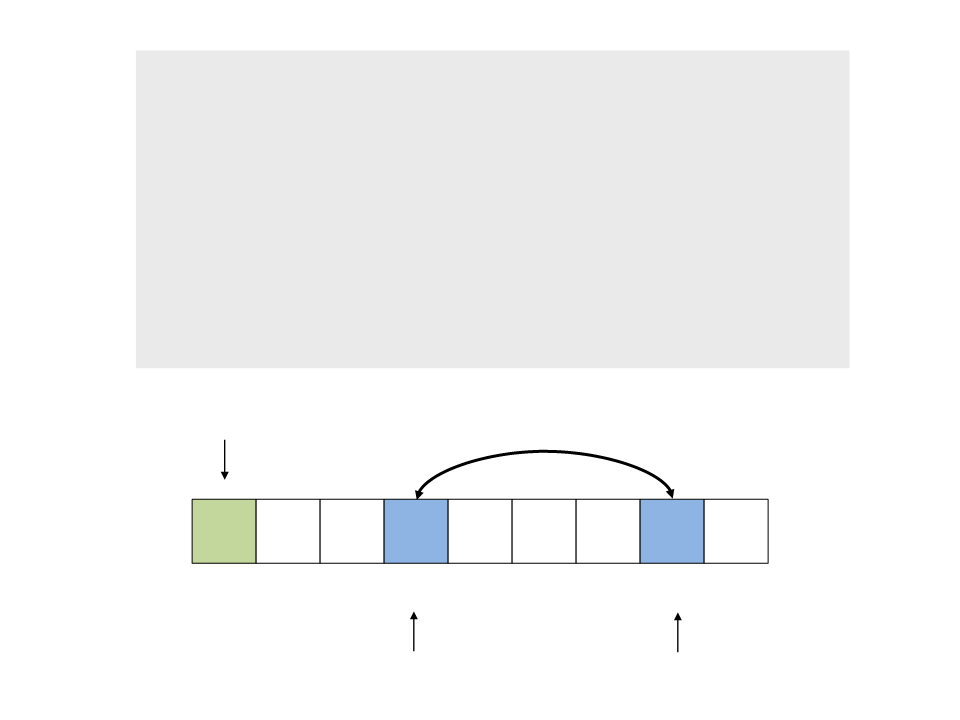
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
x (pivô)
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
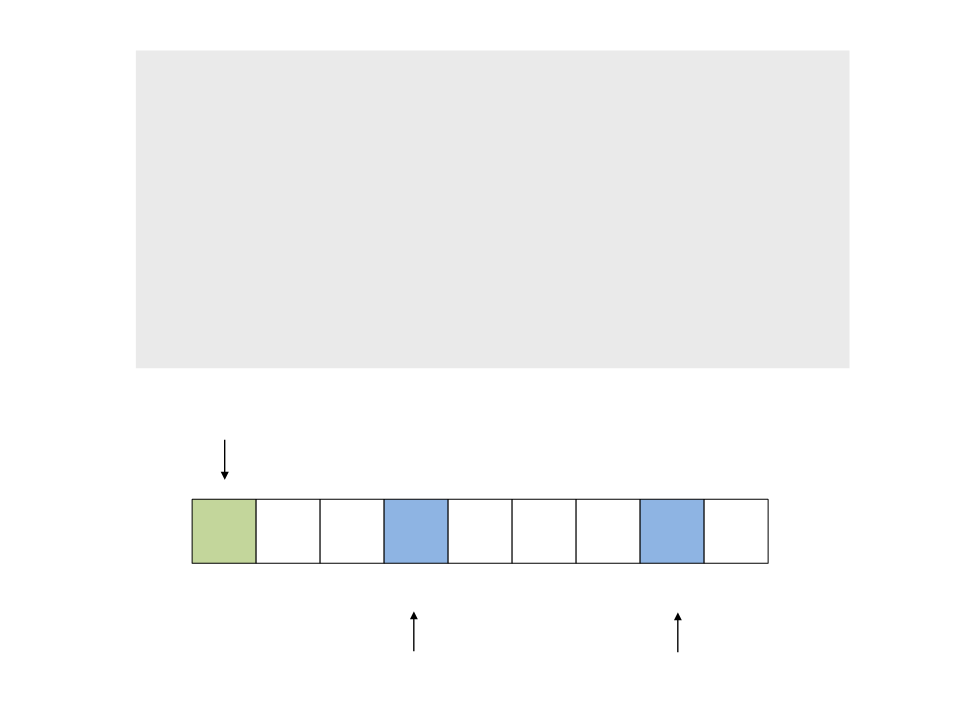
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
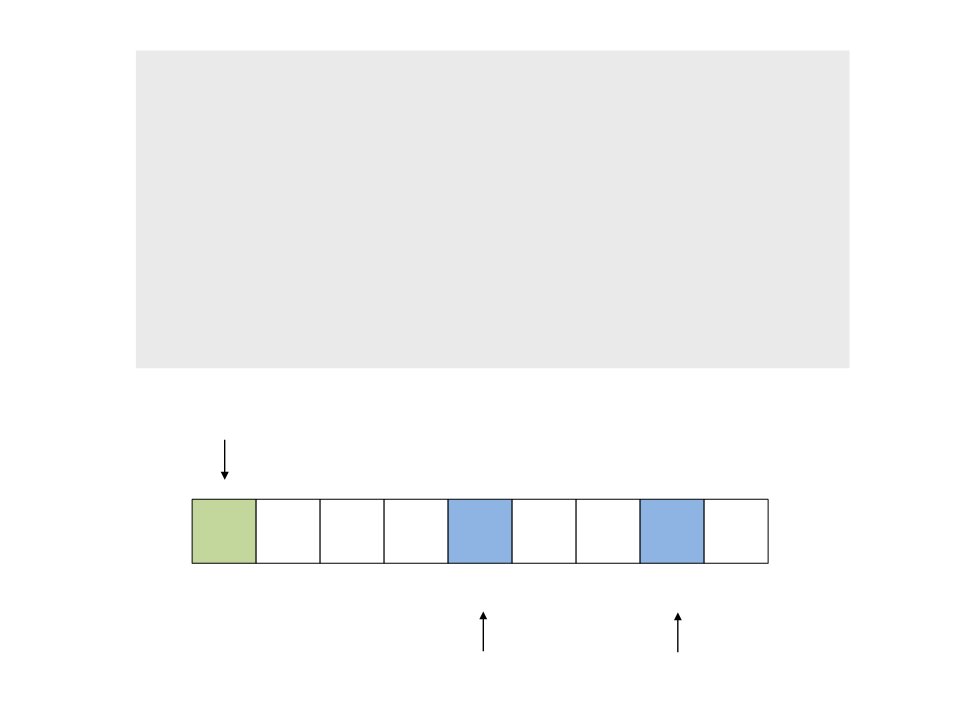
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3] [4]
[5]
[6]
a
b
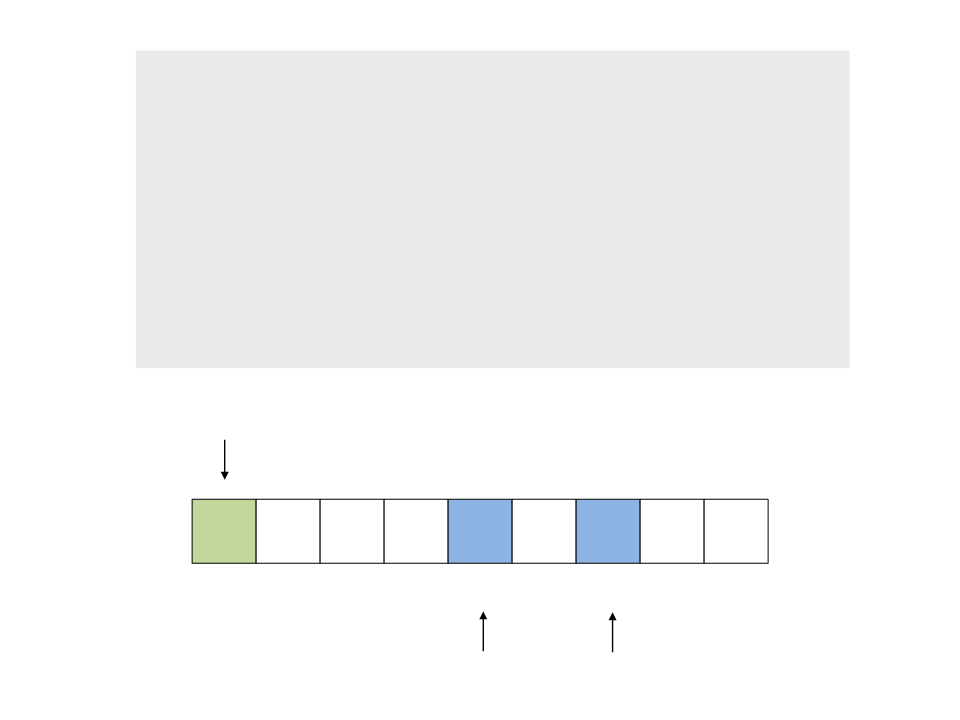
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
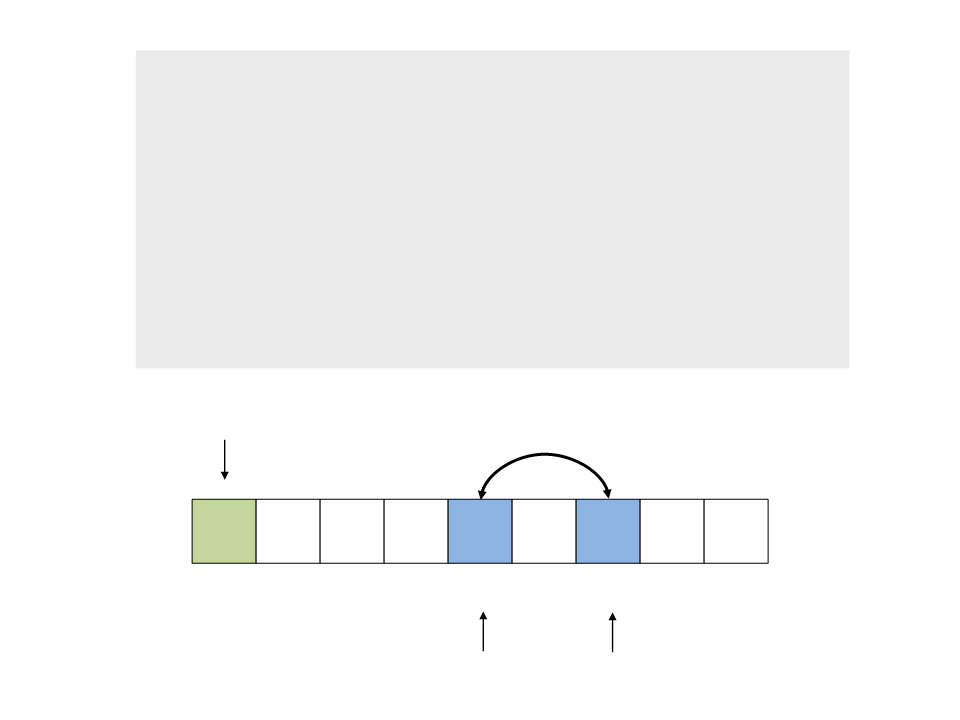
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
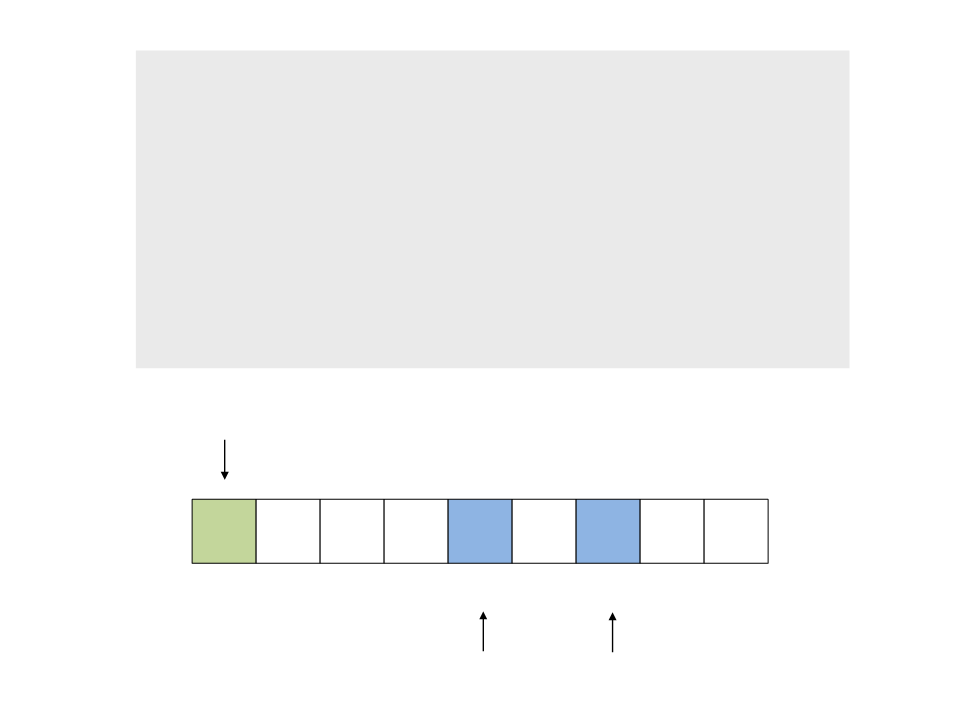
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
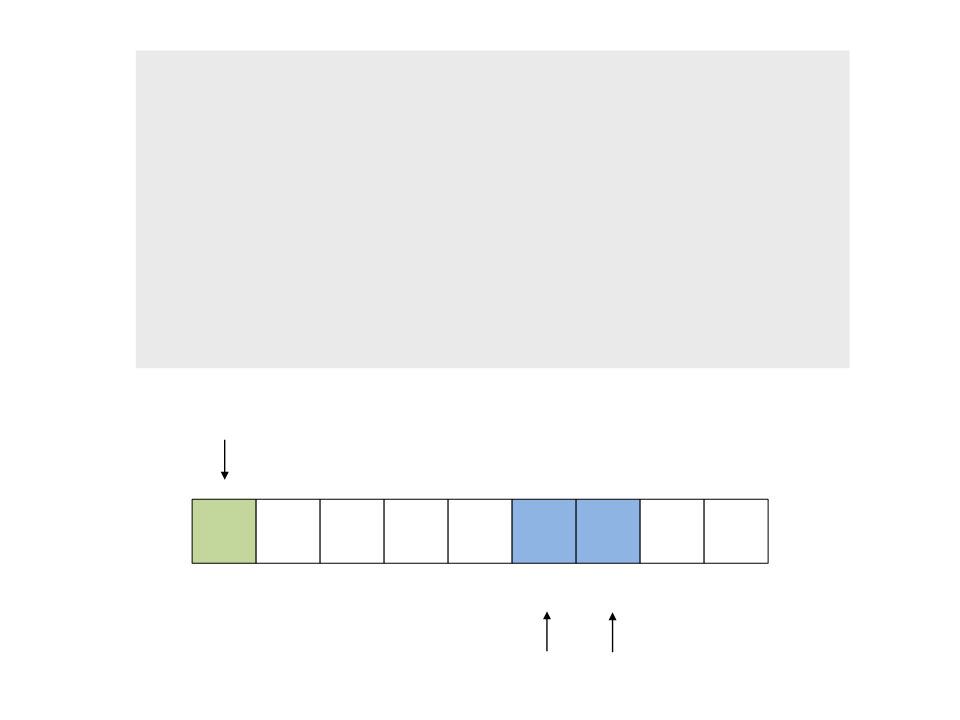
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
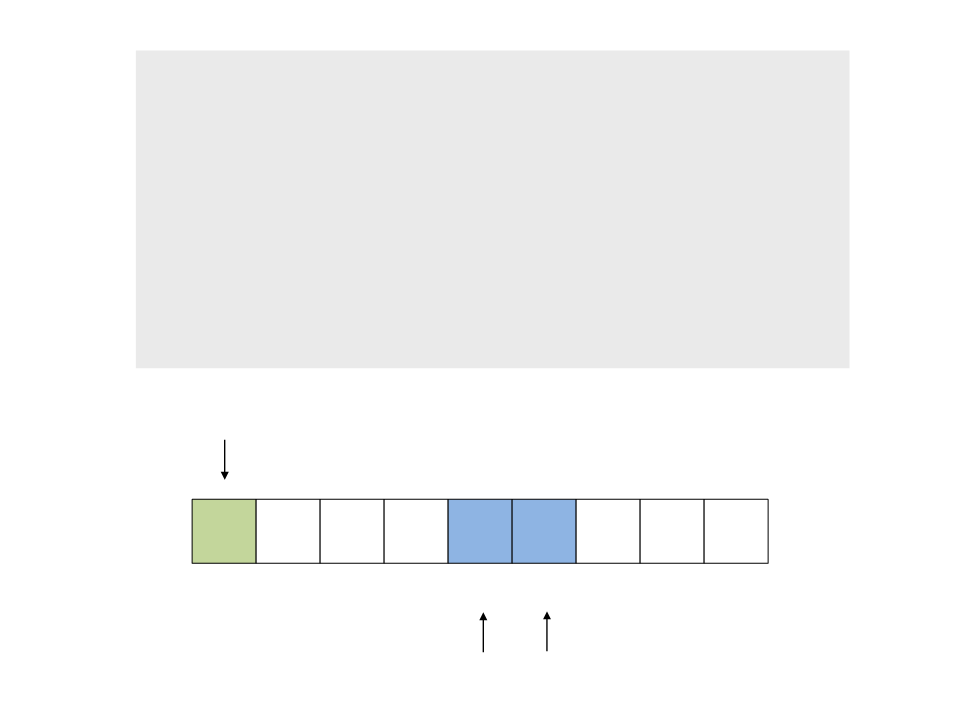
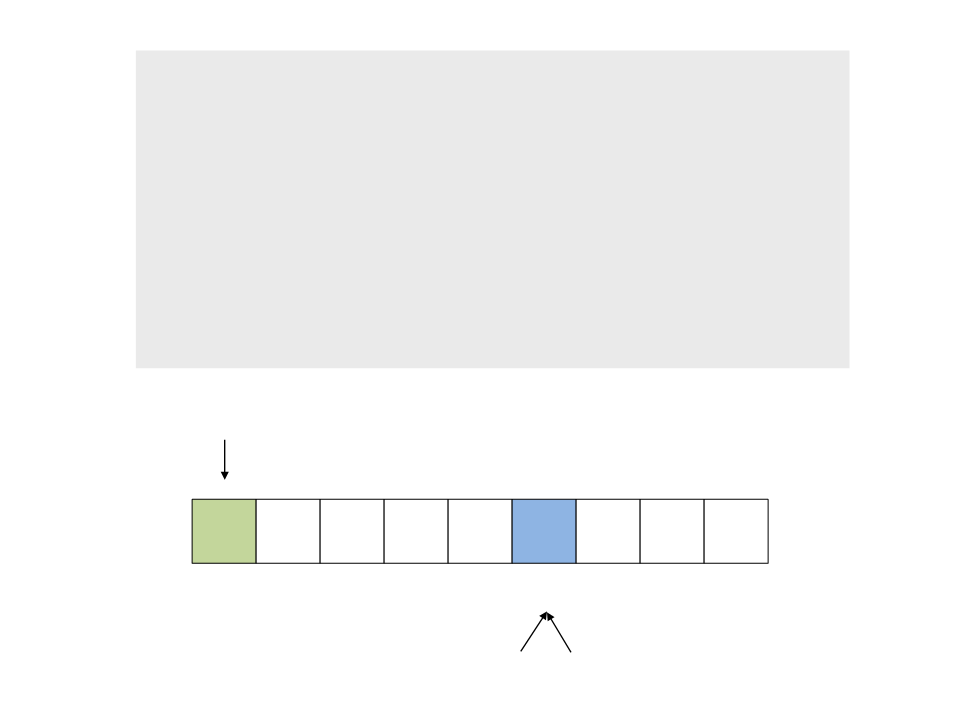
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
x (pivô)
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5] [6]
a
b
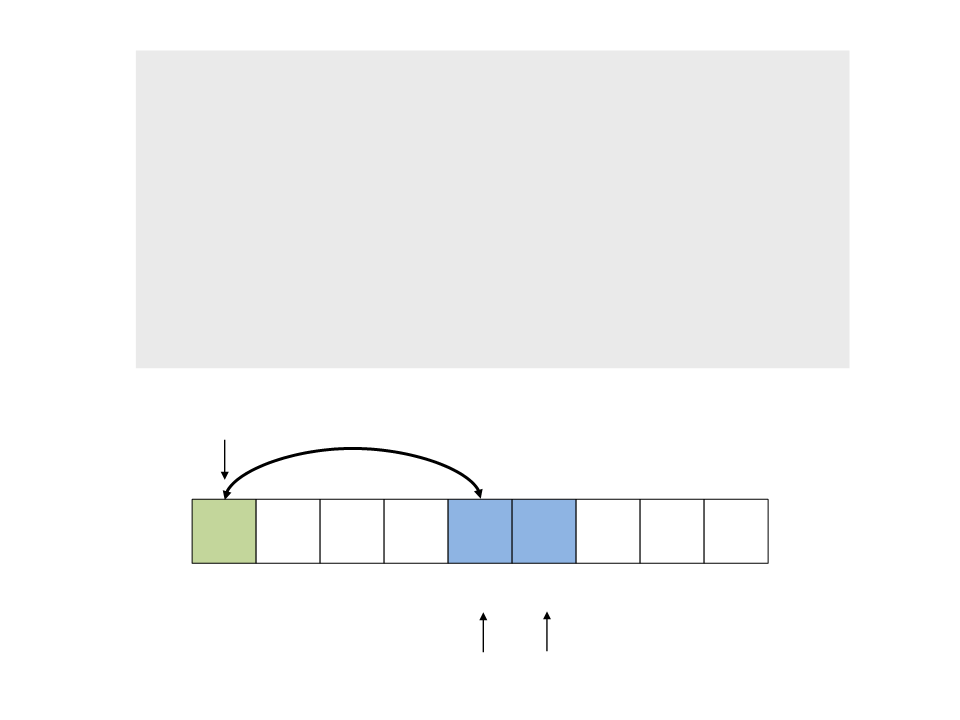
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
troca(&v[x], &v[b]);
x (pivô)
4
0
20
10
30
7
50
60 80 100
[6] [7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
a
b
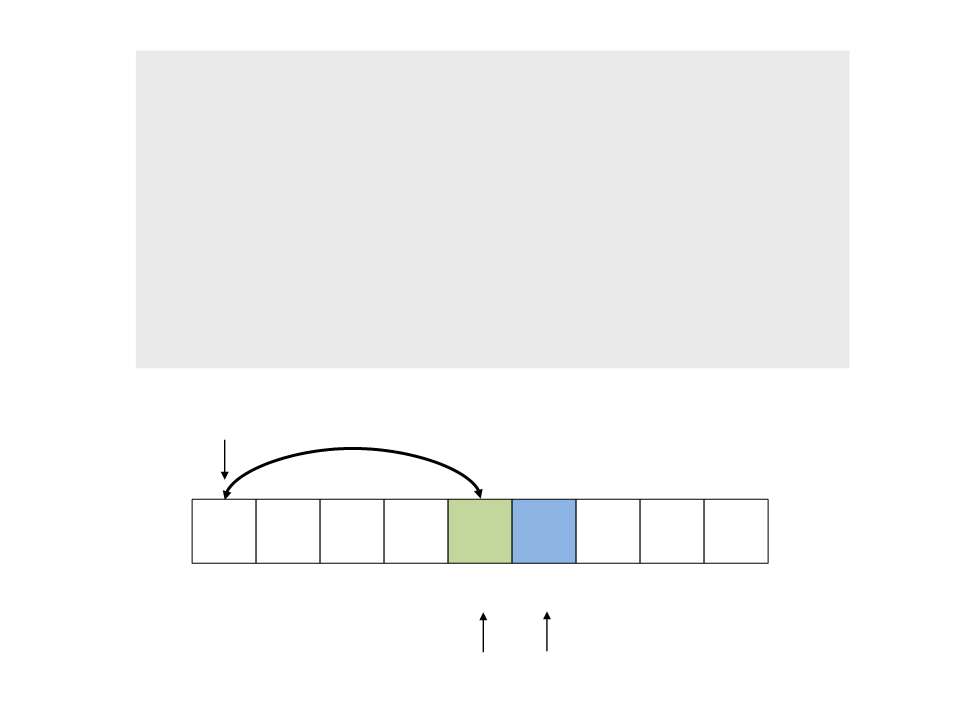
do{
while (a < n && v[a] <= x)
a++;
while (v[b] > x)
b--;
if (a < b)
troca(&v[a], &v[b]);
while (a <= b);
}
troca(&v[x], &v[b]);
x (pivô)
7
20
10
30
40 50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
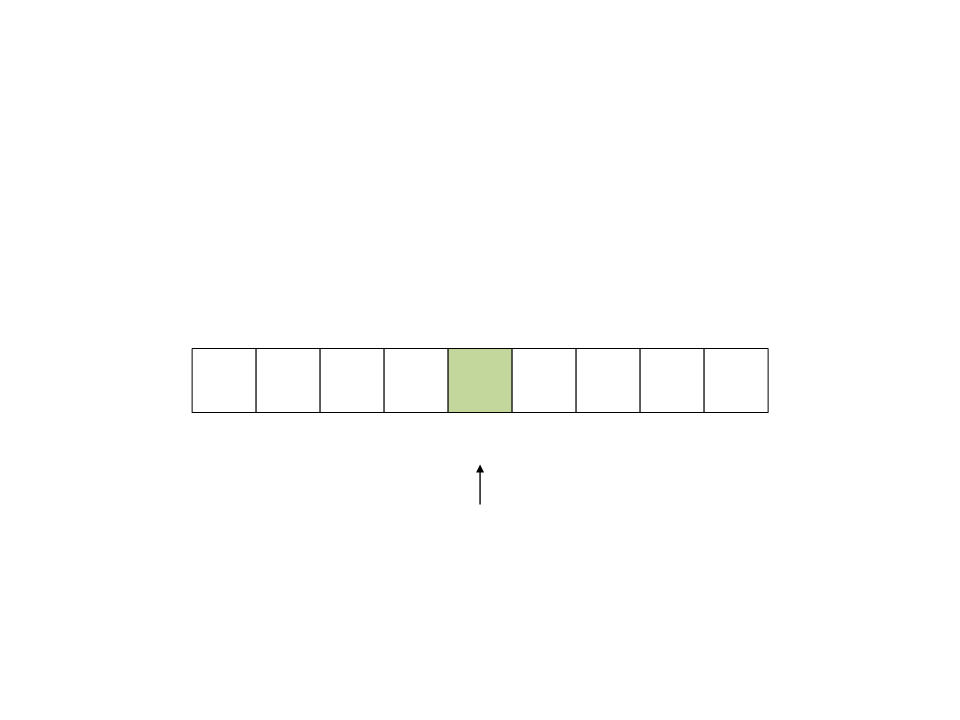
Quick Sort
•
Resultado da Partição:
7
20
10
30
40
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
o pivô ocupa a sua posição
final na ordenação
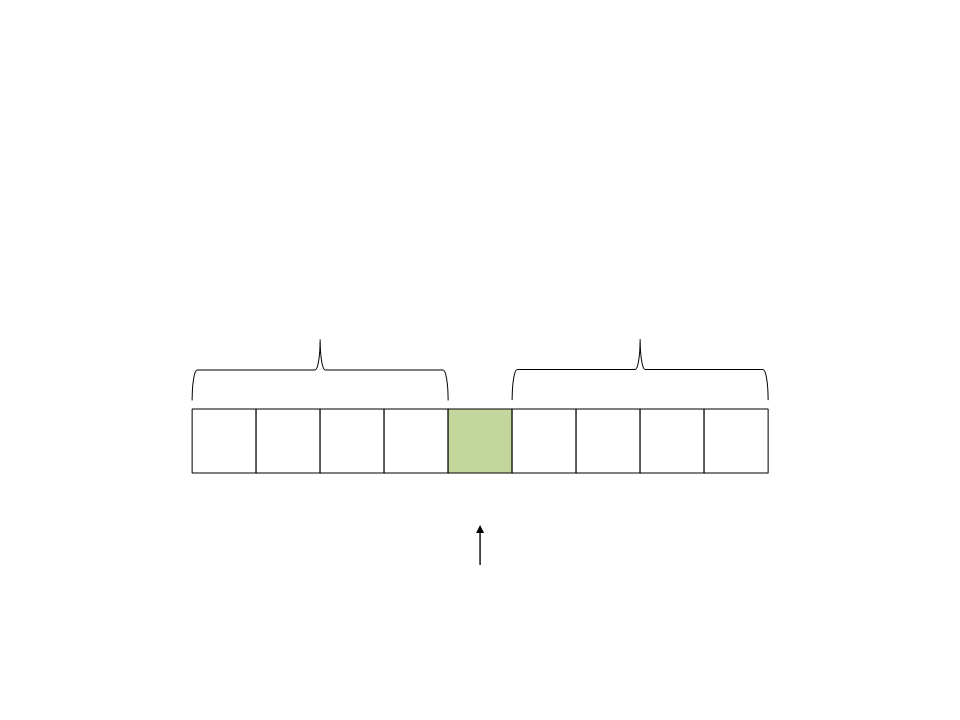
Quick Sort
•
Chamada recursiva aos subvetores:
subvetor da esquerda
subvetor da direita
7
20 10
[1]
30 40
[4]
50
60
80 100
[7] [8]
[
0]
[2] [3]
[5]
[6]
o pivô ocupa a sua posição
final na ordenação
void quicksort(int n, int* v){
int x, a, b, temp;
if (n > 1) {
x = v[0]; a = 1; b = n-1;
do {
while (a < n && v[a] <= x)
a++;
Caminha com o índice a
Caminha com o índice b
while (v[b] > x)
b--;
if (a < b) {
temp = v[a];
v[a] = v[b];
v[b] = temp;
a++; b--;
Faz a troca de a e b
}
}
while (a <= b);
v[0] = v[b];
Faz a troca do pivô e b
v[b] = x;
Chamada recursiva
para o subvetor da
esquerda e da direita
quicksort(b,v);
quicksort(n-a,&v[a]);
}
}

Quick Sort
(1) Vetor para ser ordenado:
3
1
4
1
5
9
2
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
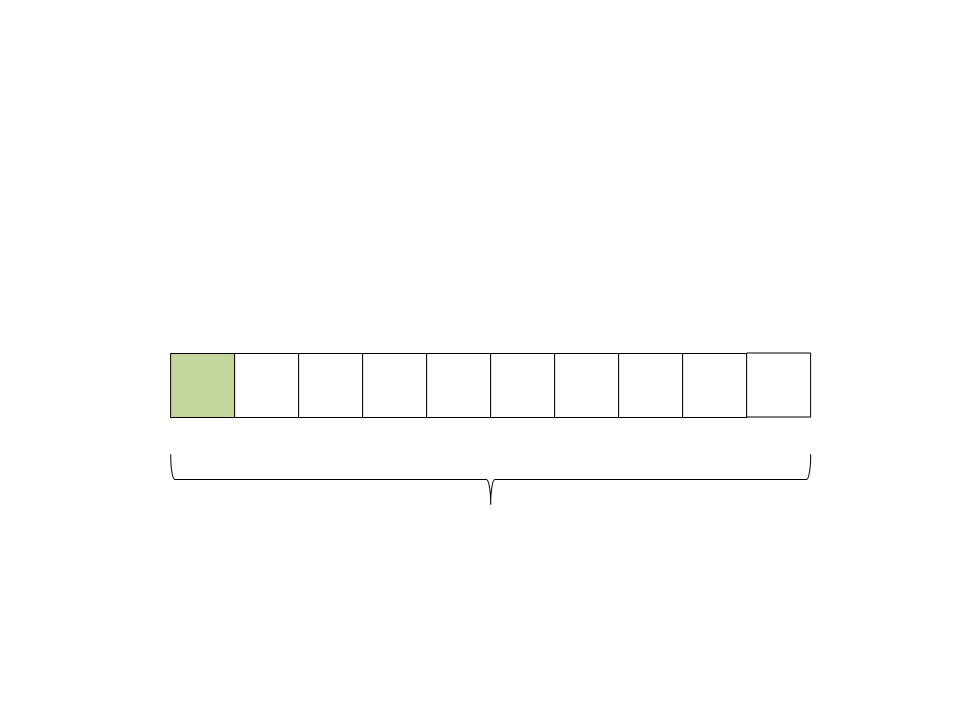
Quick Sort
(2) Selecione o pivô:
3
1
4
1
5
9
2
6
5
3
[
0] [1] [2] [3]
[4]
[5] [6]
[7] [8]
[9]
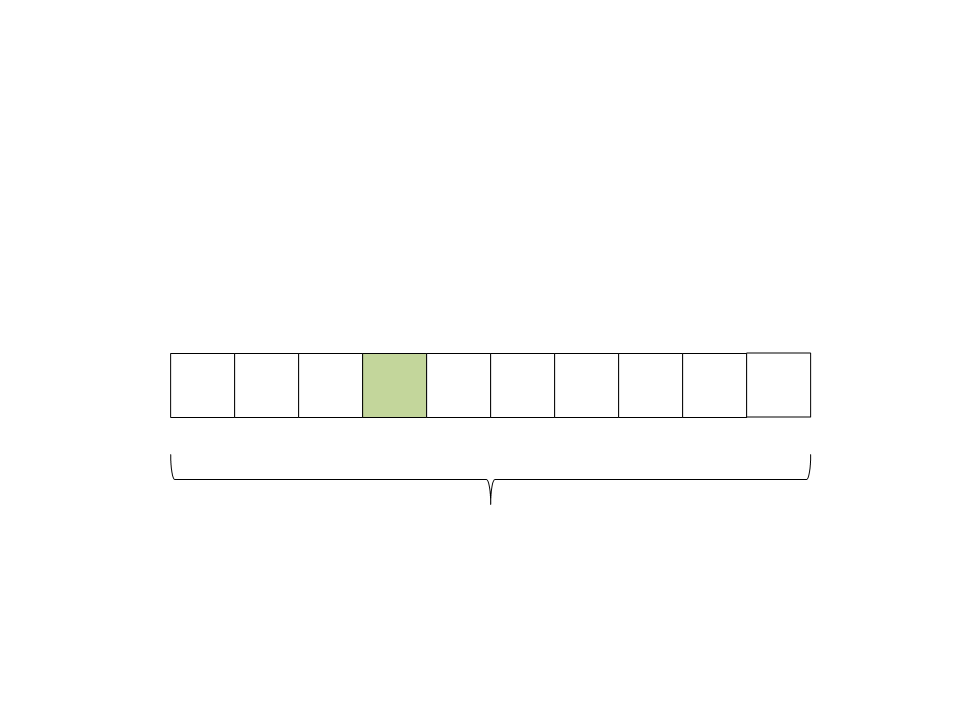
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
3) Particione o vetor. Todos os elementos maiores que o pivô
2
1
1
3
5
9
4
6
5
3
[
0]
[1]
[2] [3] [4]
[5]
[6]
[7] [8]
[9]
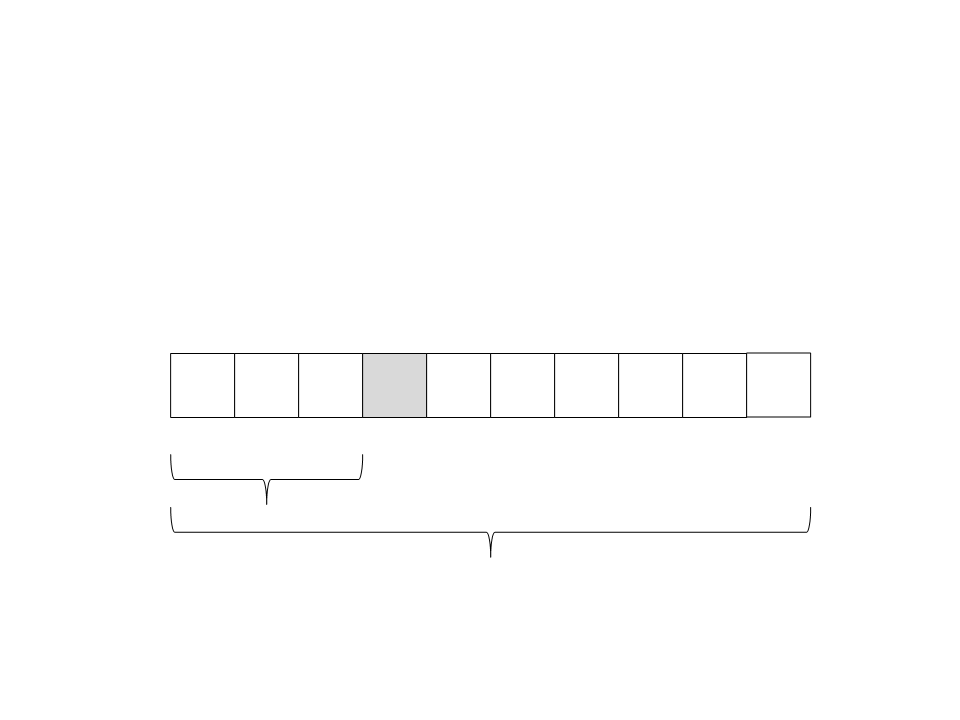
Quick Sort
(4) Chame recursivamente o quick sort para o subvetor da
esquerda:
2
1
1
3
5
9
4
6
5
3
[
0] [1] [2] [3] [4]
[5] [6] [7] [8]
[9]
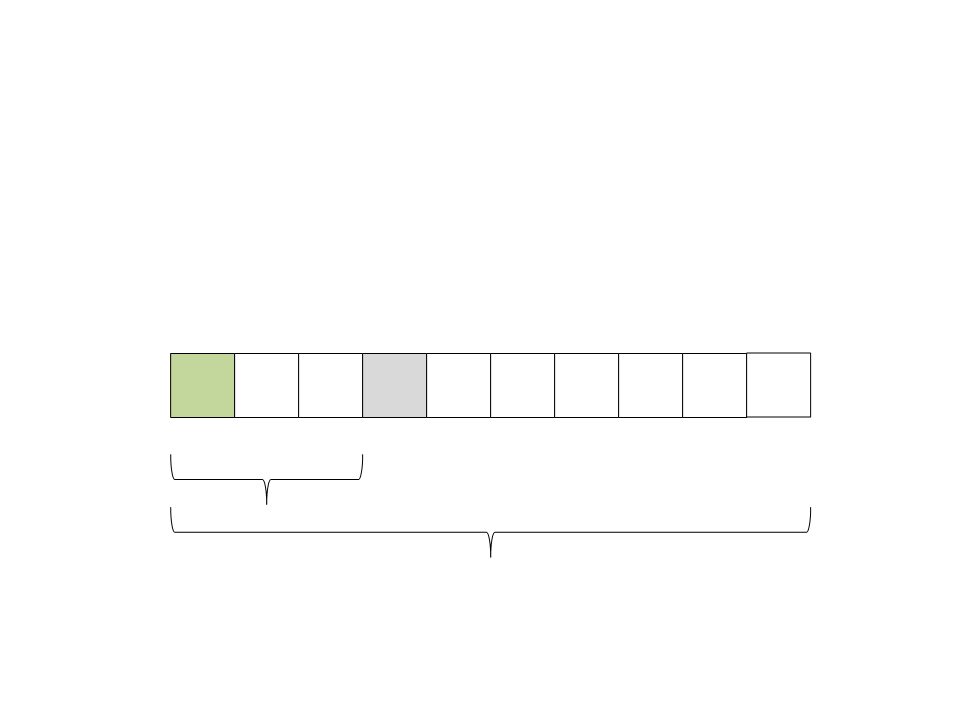
Quick Sort
(5) Selecione o pivô:
2
1
1
3
5
9
4
6
5
3
[
0] [1]
[2] [3] [4]
[5] [6]
[7] [8] [9]
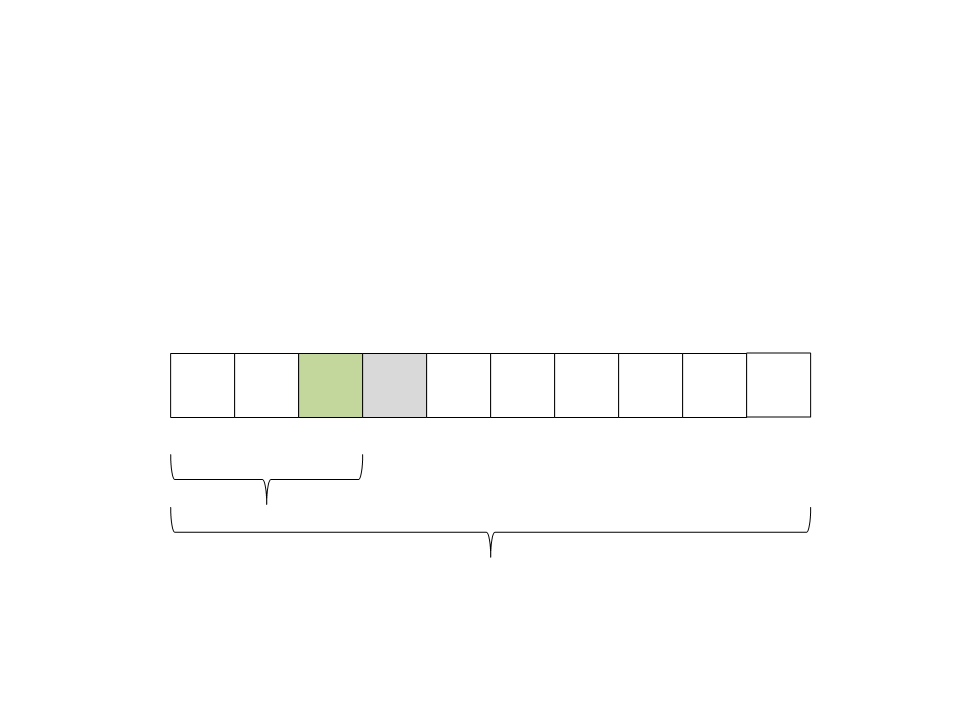
Quick Sort
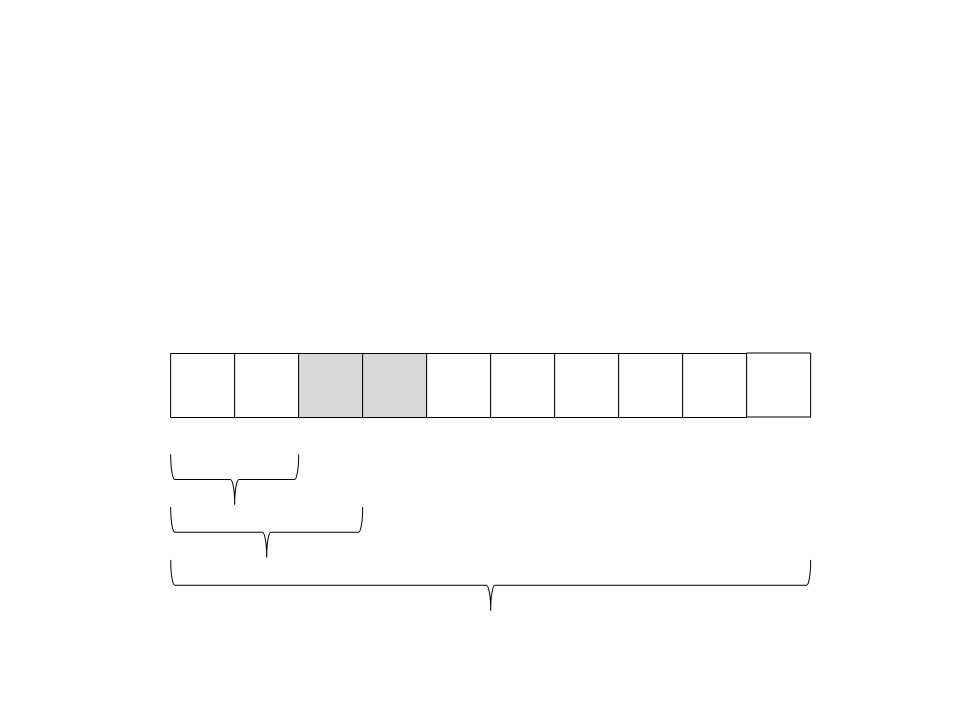
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
6) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
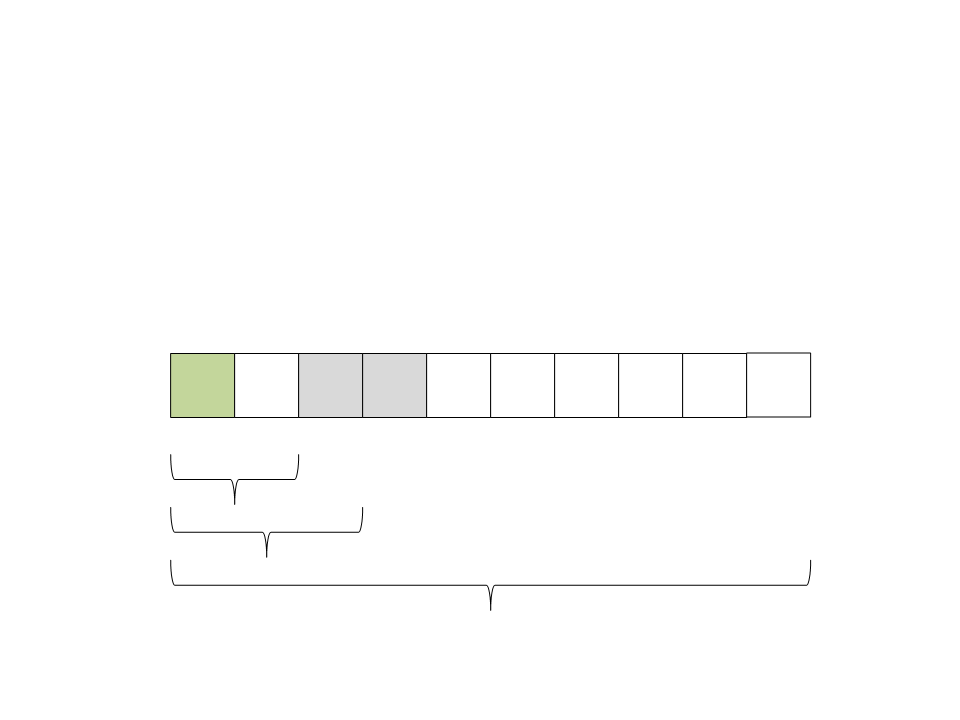
(7) Chame recursivamente o quick sort para o subvetor da
esquerda:
1
1
2
3
5
9
4
6
5
3
[
0] [1] [2] [3]
[4] [5] [6]
[7] [8] [9]
Quick Sort
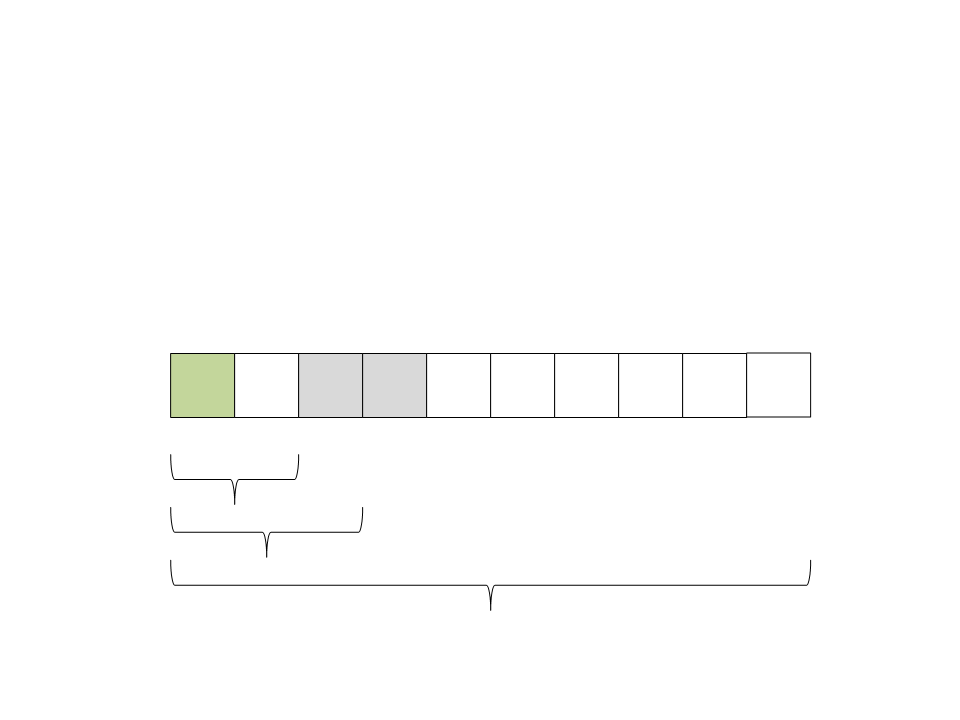
(8) Selecione o pivô:
1
1
2
3
5
9
4
6
5
3
[
0]
[1] [2] [3]
[4] [5]
[6]
[7] [8]
[9]
Quick Sort
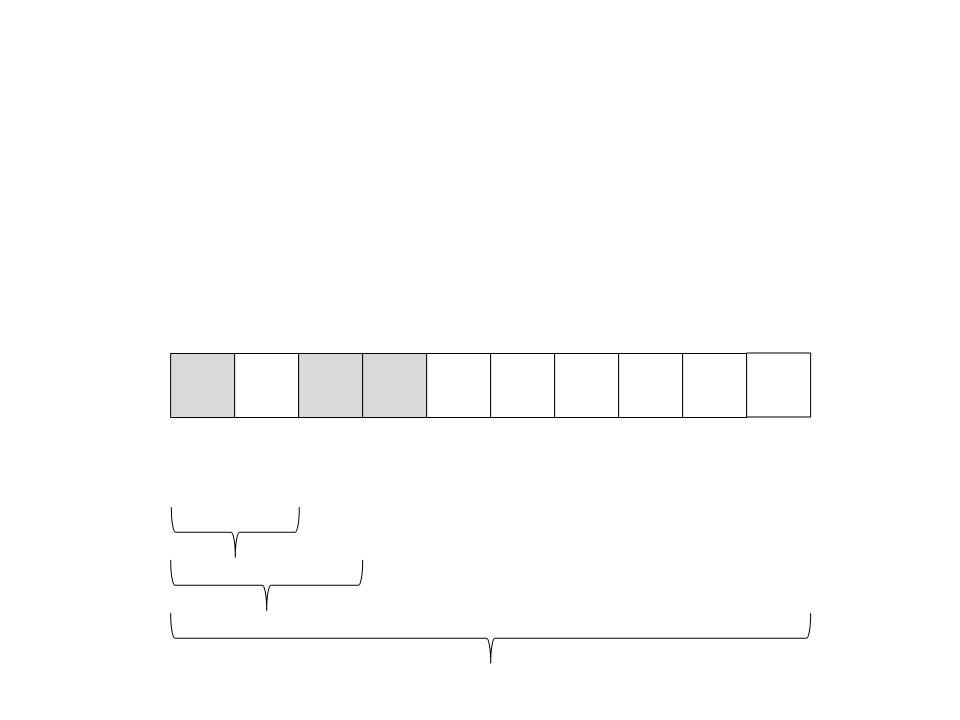
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
9) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
5
9
4
6
5
3
[
0] [1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
(
esquerda. O tamanho do vetor da esquerda é zero. A recursão
retorna.
10) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
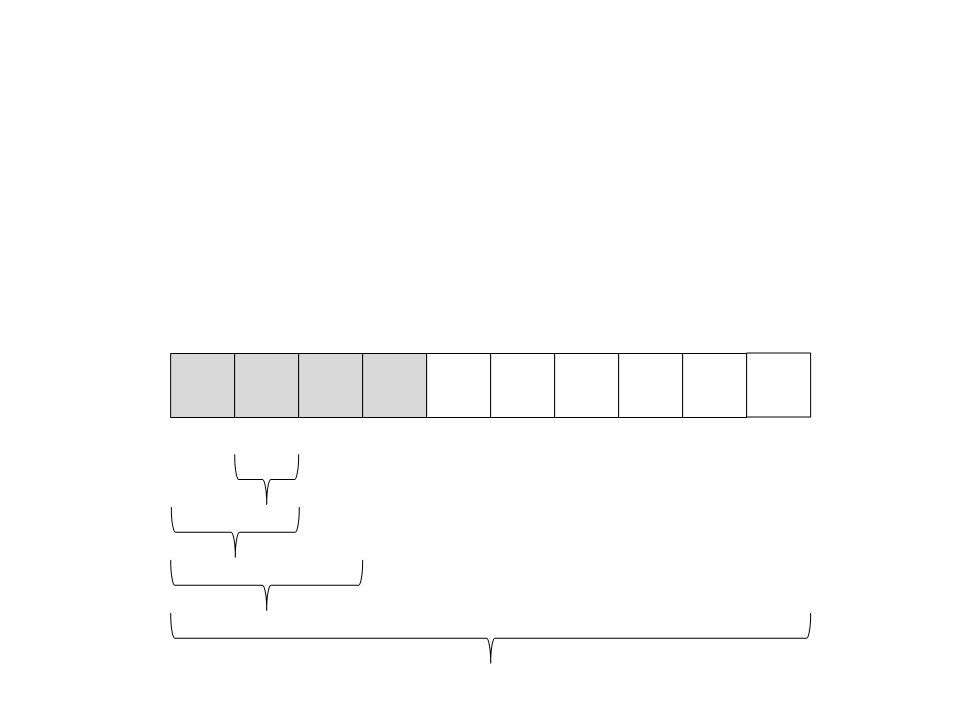
Quick Sort
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna.
11) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
5
9
4
6
5
3
[
0] [1] [2] [3]
[4] [5] [6]
[7] [8] [9]
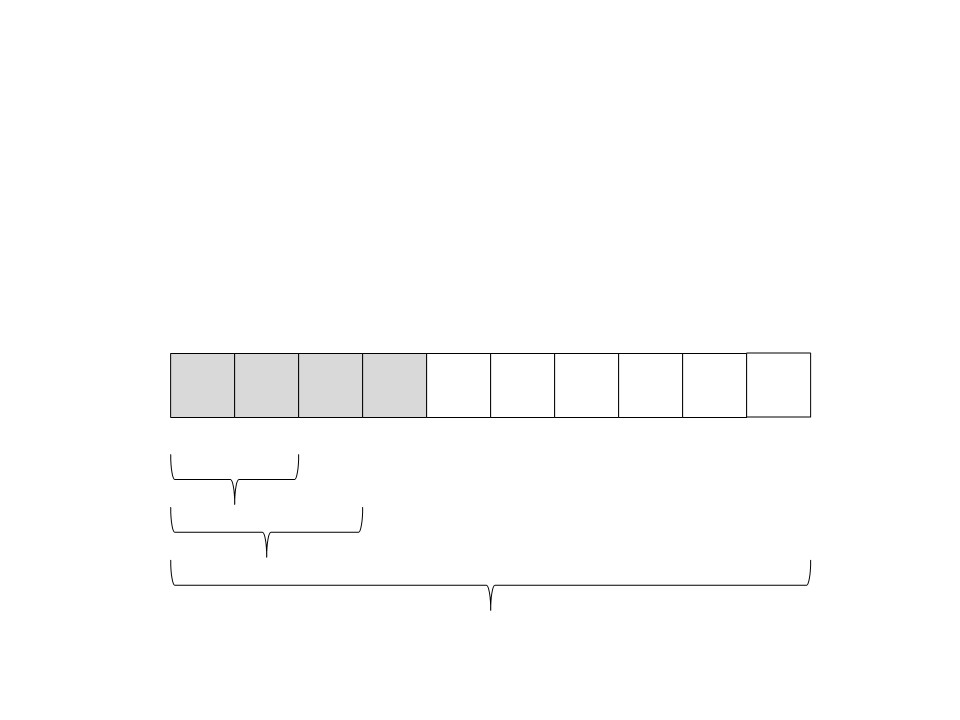
Quick Sort
(12) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
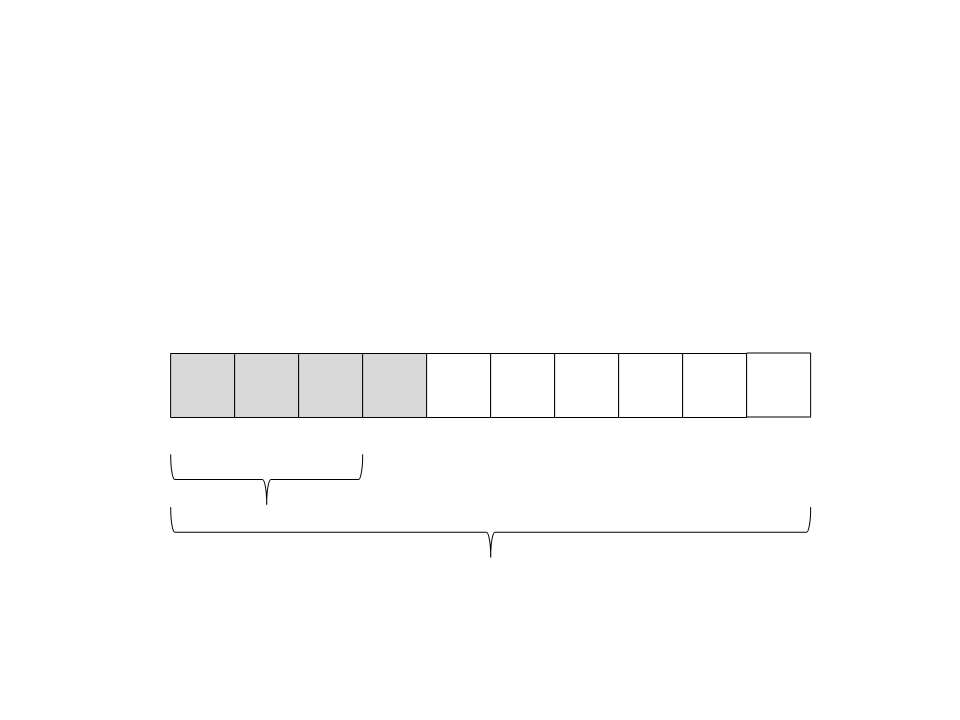
Quick Sort
(13) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor:
1
1
2
3
5
9
4
6
5
3
[
0]
[1] [2] [3] [4]
[5] [6]
[7] [8] [9]
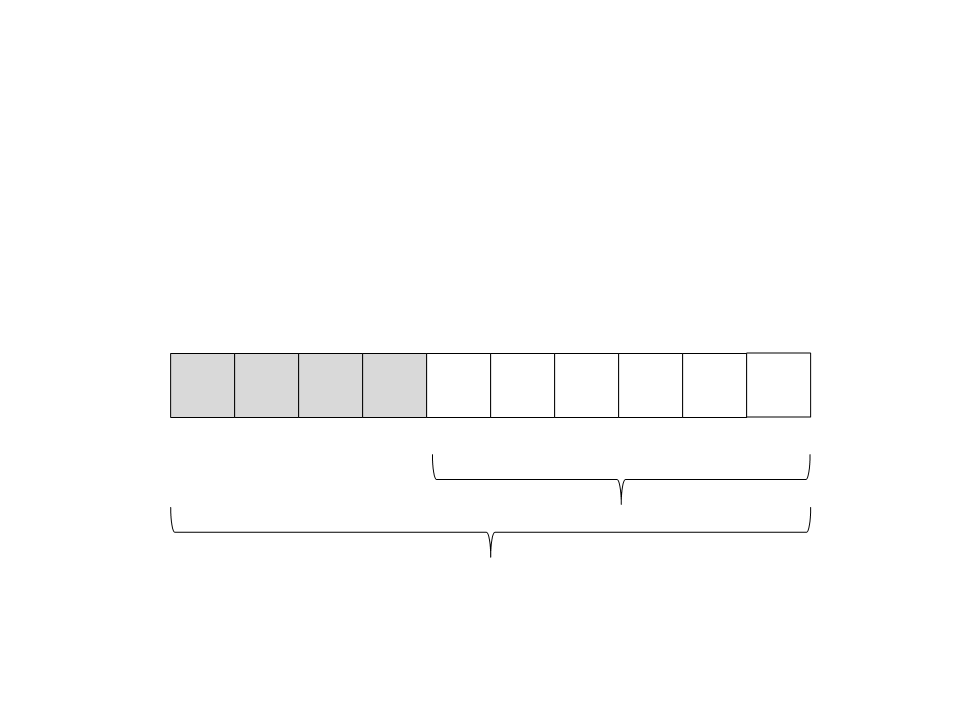
Quick Sort
(14) Chame recursivamente o quick sort para o subvetor da
direita:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4] [5]
[6] [7] [8]
[9]
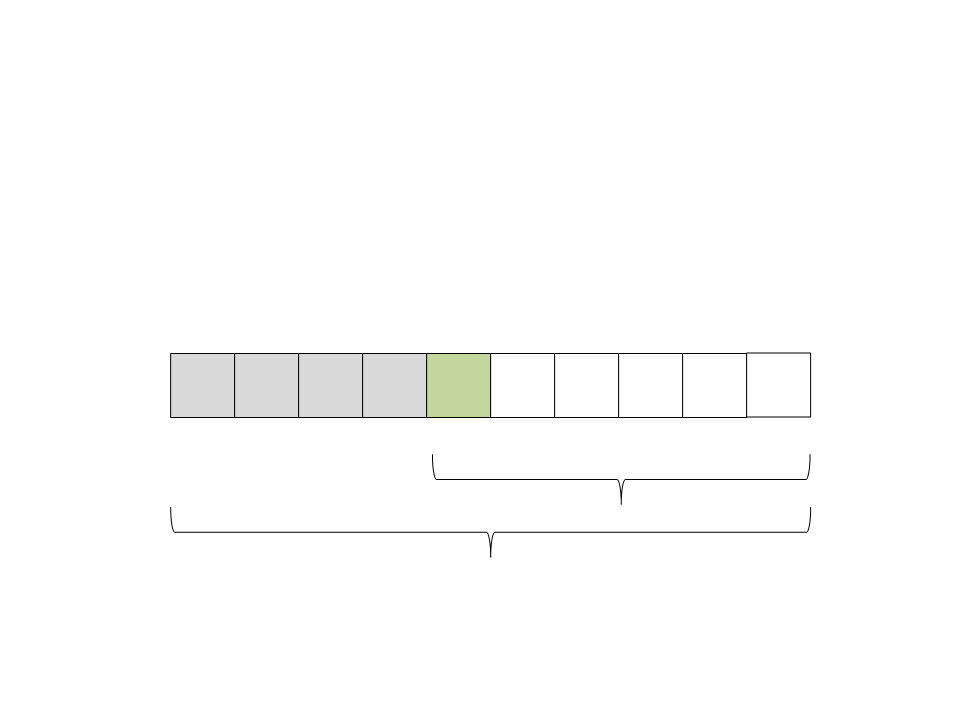
Quick Sort
(15) Selecione o pivô:
1
1
2
3
5
9
4
6
5
3
[
0]
[1]
[2] [3]
[4]
[5]
[6] [7] [8] [9]
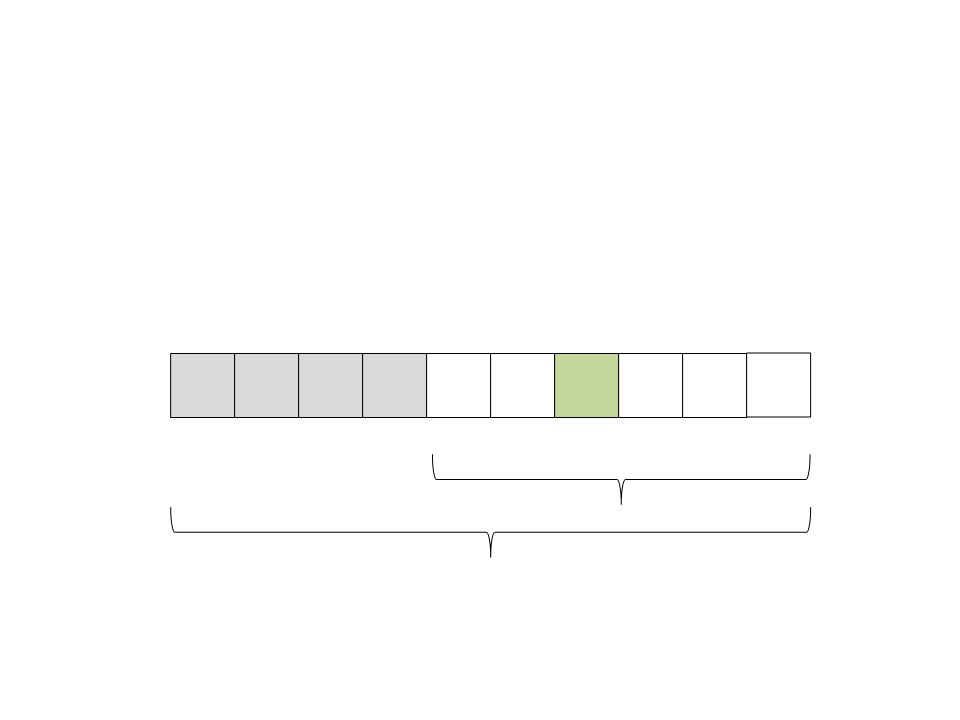
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
16) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
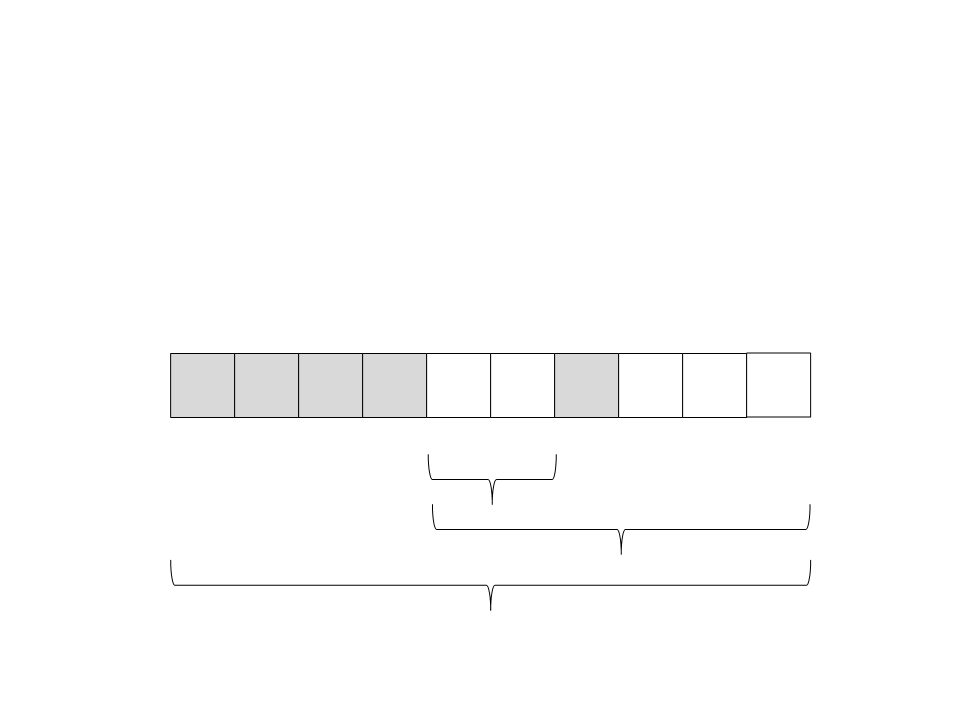
Quick Sort
(17) Chame recursivamente o quick sort para o subvetor da
esquerda:
1
1
2
3
3
4
5
6
5
9
[
0] [1] [2] [3]
[4] [5] [6] [7] [8]
[9]
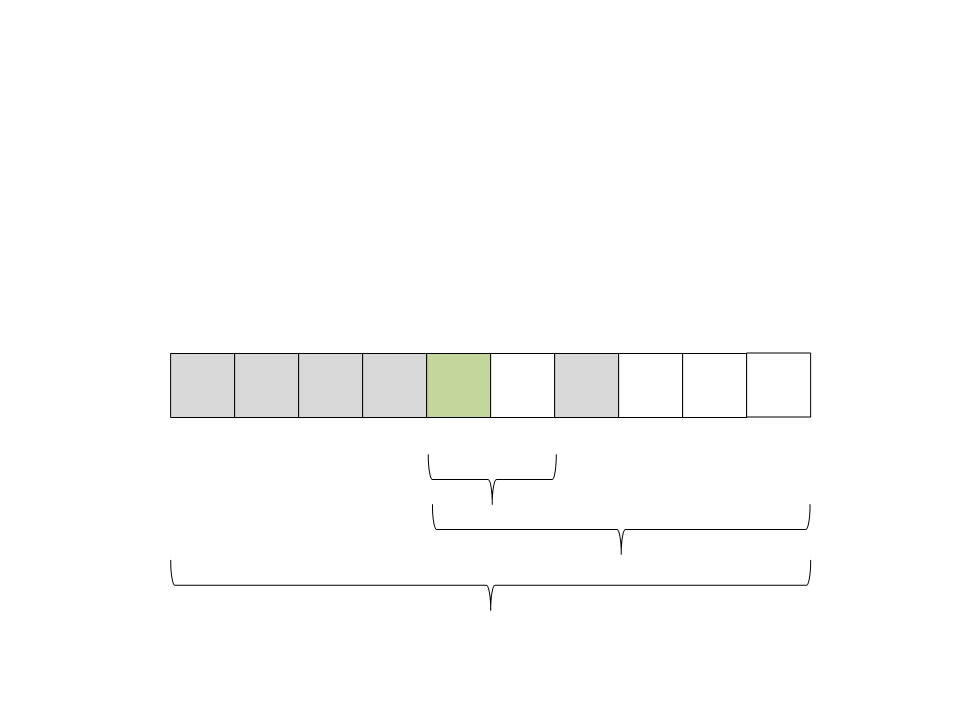
Quick Sort
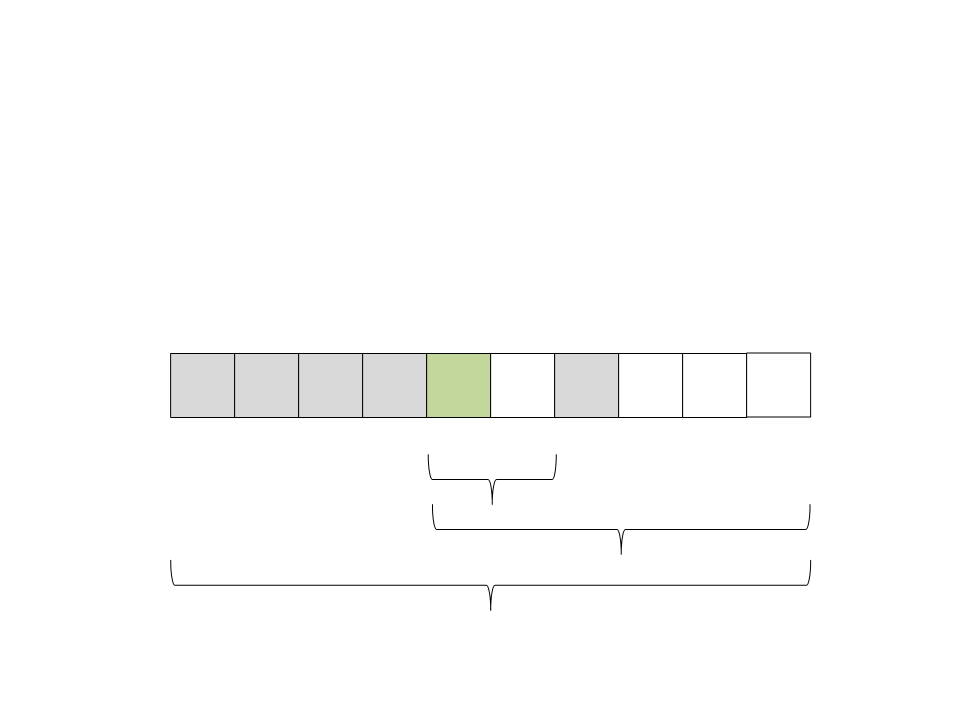
(18) Selecione o pivô:
1
1
2
3
3
4
5
6
5
9
[
0] [1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
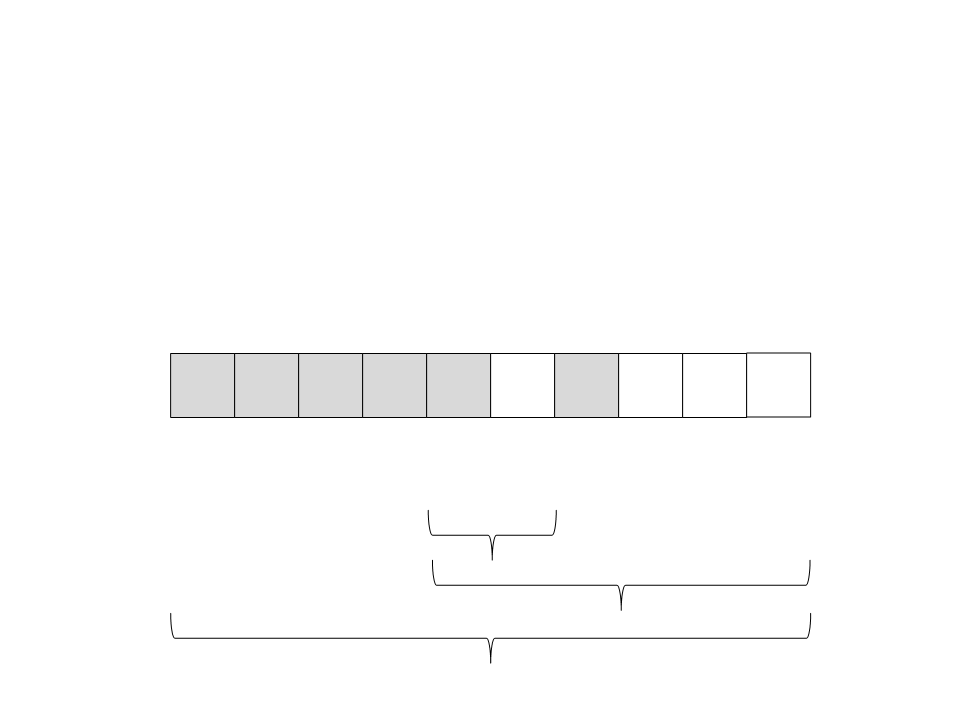
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
19) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
6
5
9
[
0] [1]
[2] [3]
[4]
[5]
[6]
[7] [8] [9]
Quick Sort
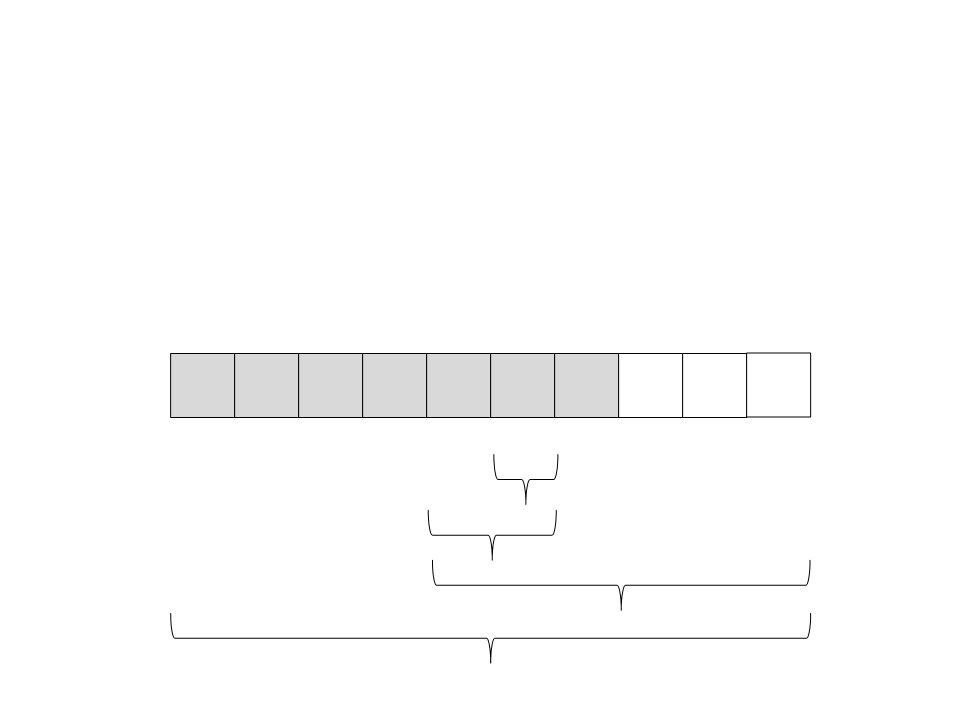
(
esquerda. O tamanho do vetor da esquerda é zero. A recursão
retorna.
20) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
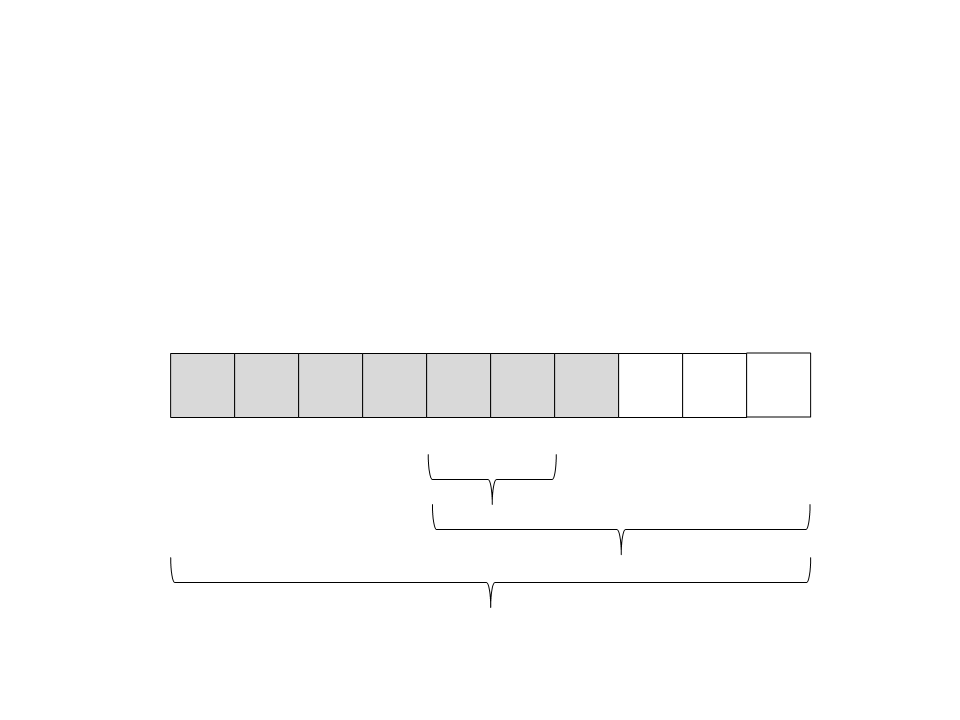
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna.
21) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
6
5
9
[
0]
[1] [2] [3]
[4] [5]
[6]
[7] [8] [9]
Quick Sort
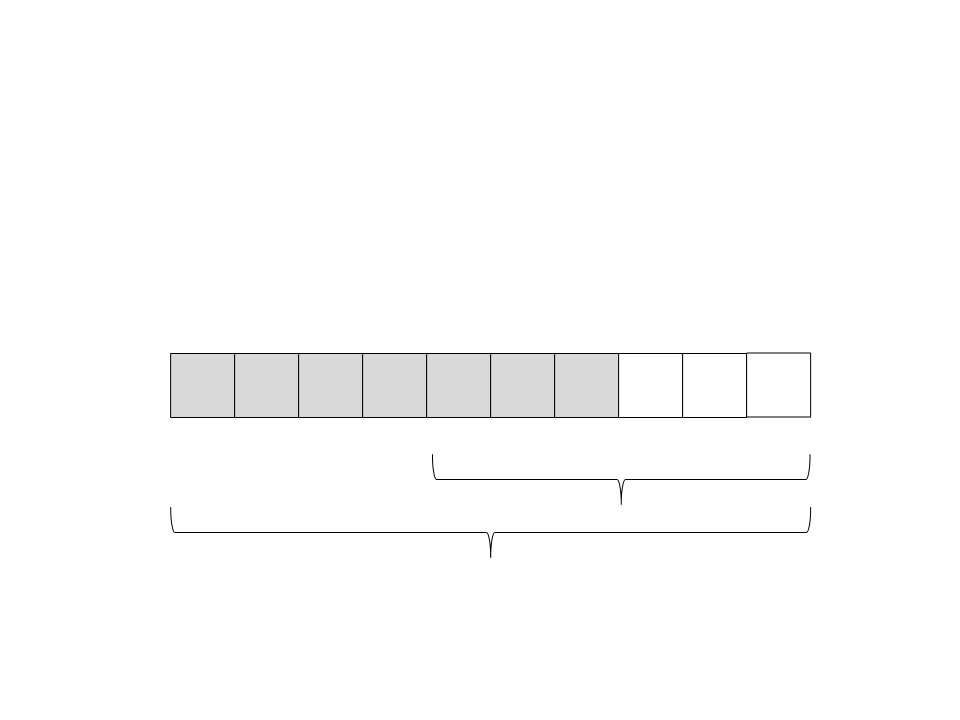
(22) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4] [5]
[6]
[7] [8]
[9]
Quick Sort
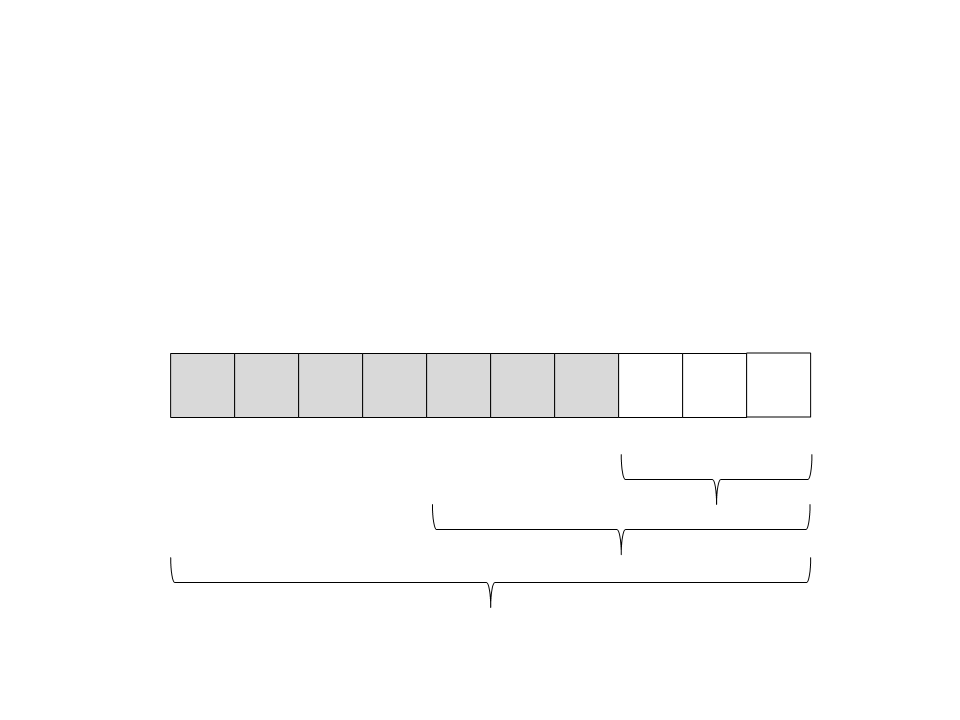
(23) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
6
5
9
[
0] [1] [2] [3]
[4]
[5]
[6] [7] [8]
[9]
Quick Sort
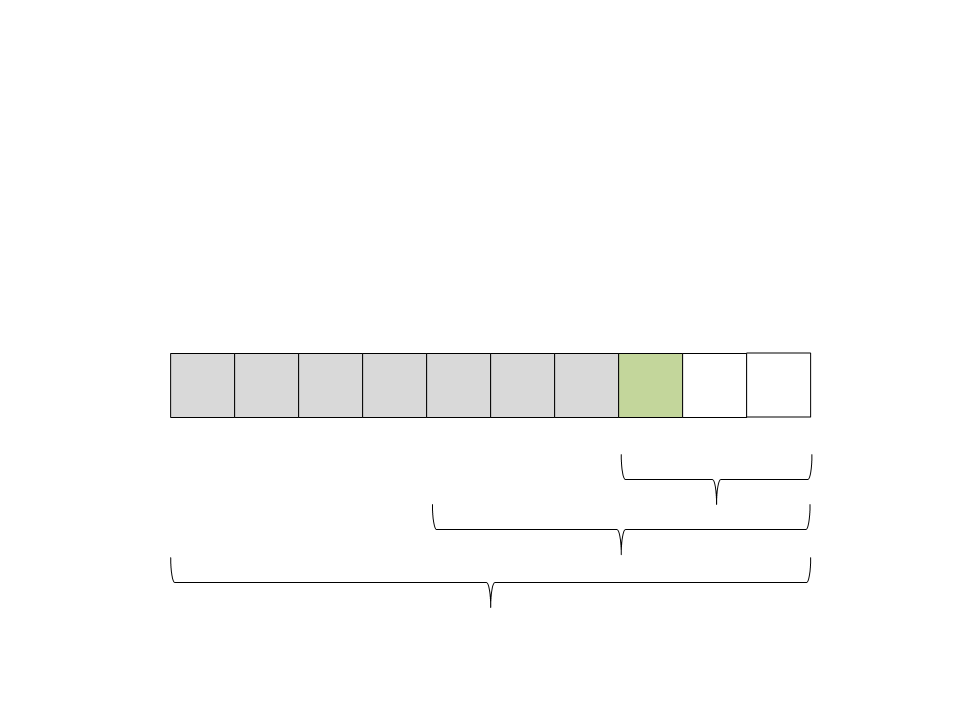
(24) Chame recursivamente o quick sort para o subvetor da
direita:
1
1
2
3
3
4
5
6
5
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
Quick Sort
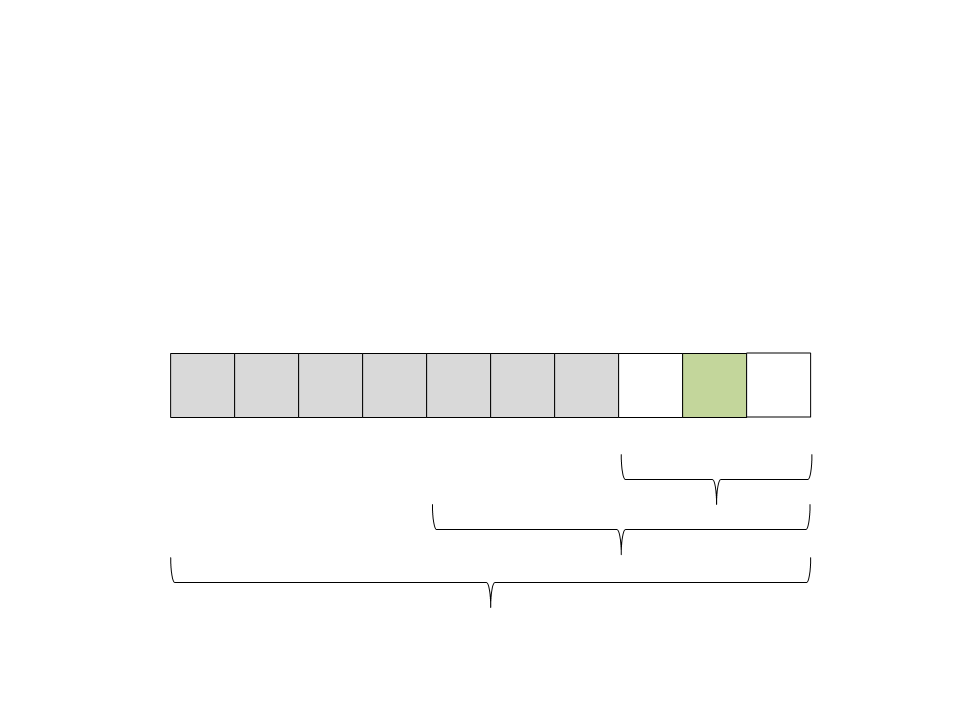
(25) Selecione o pivô:
1
1
2
3
3
4
5
6
5
9
[
0]
[1] [2] [3] [4] [5] [6] [7] [8]
[9]
Quick Sort
(
ficaram na direita e todos os elementos menores na esquerda. O
pivô já está ordenado:
26) Particione o vetor. Todos os elementos maiores que o pivô
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5] [6] [7] [8]
[9]
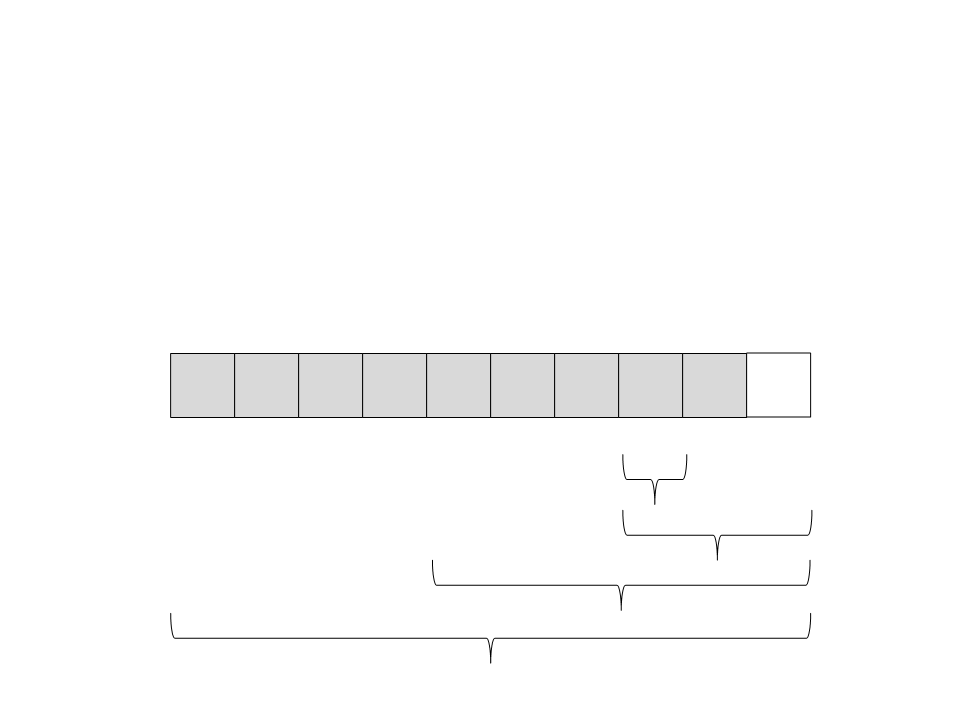
Quick Sort
(
esquerda. Só existe um elemento, então ele já está ordenado e a
recursão retorna:
27) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
5
6
9
[
0]
[1] [2] [3] [4]
[5] [6]
[7] [8] [9]
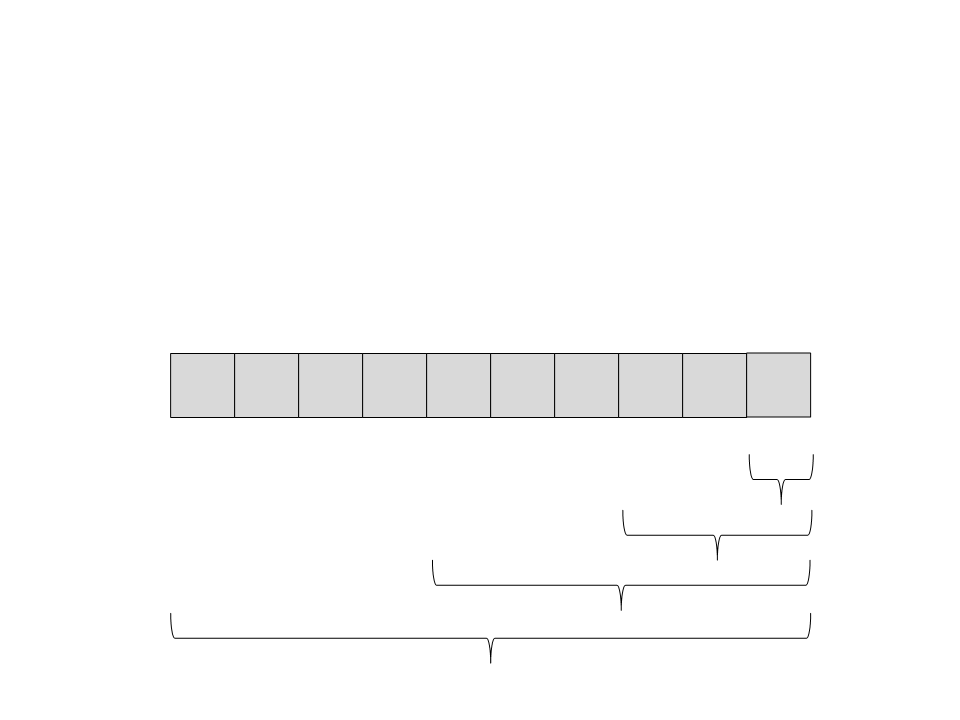
Quick Sort
(
direita. Só existe um elemento, então ele já está ordenado e a
recursão retorna:
28) Chame recursivamente o quick sort para o subvetor da
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5]
[6]
[7] [8]
[9]
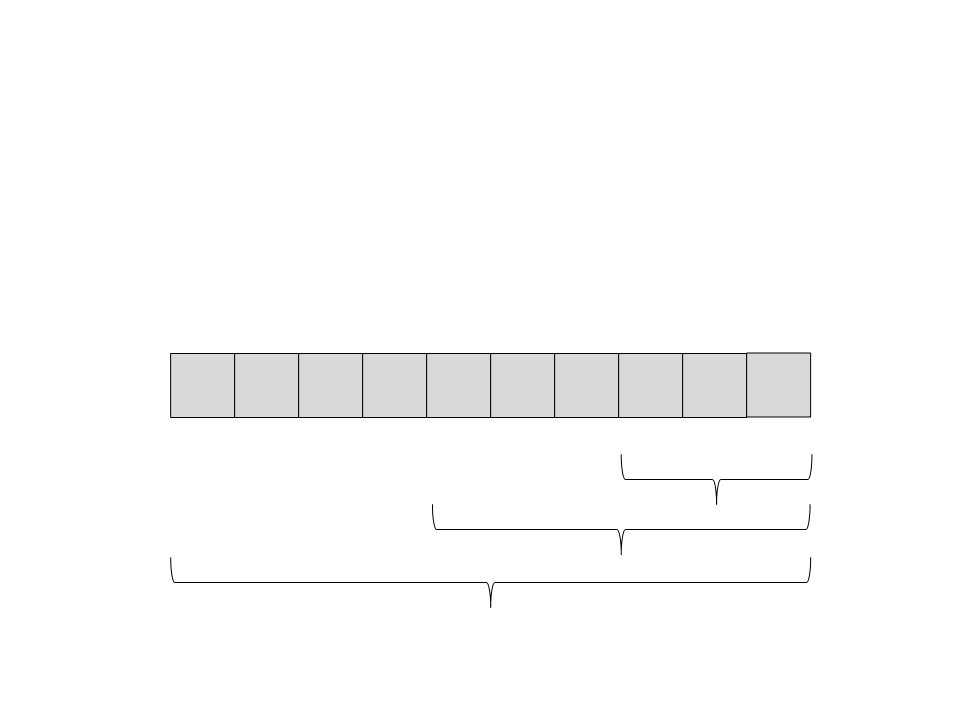
Quick Sort
(29) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
5
6
9
[
0]
[1]
[2] [3]
[4]
[5] [6] [7] [8]
[9]
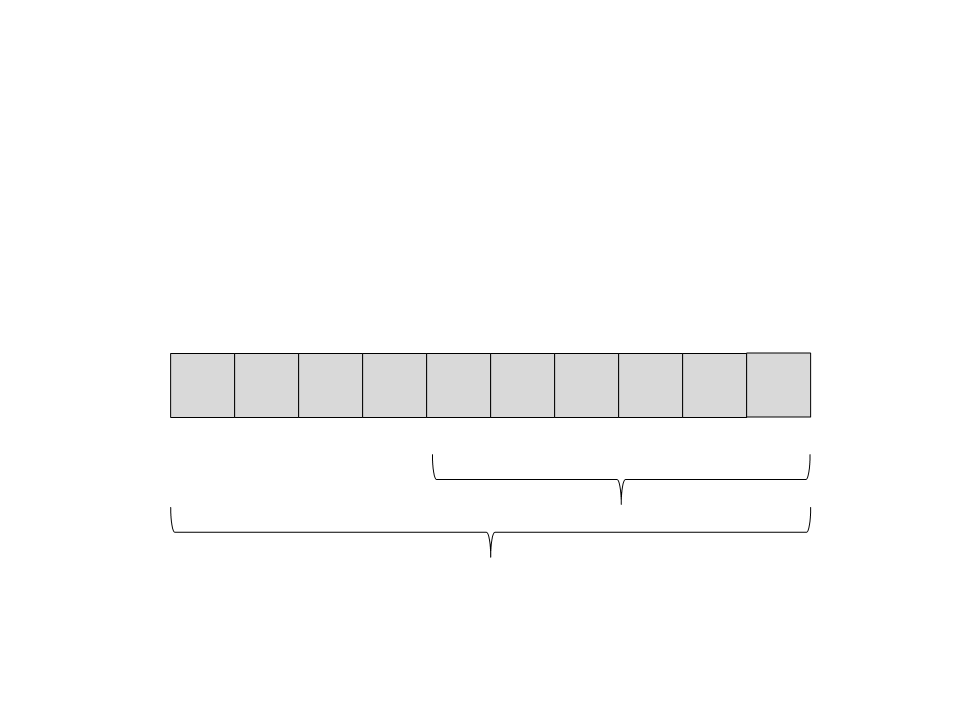
Quick Sort
(30) A recursão retorna. Não tem nada mais para ser feito nesse
subvetor.
1
1
2
3
3
4
5
5
6
9
[
0] [1]
[2] [3] [4]
[5]
[6] [7] [8] [9]
Quick Sort
(
com o vetor completamente ordenado.
31) A recursão retorna para a primeira chamada do quick sort
1
1
2
3
3
4
5
5
6
9
[
0] [1]
[2] [3] [4] [5] [6] [7] [8]
[9]

Quick Sort - Complexidade
•
Melhor caso:
–
Pivô representa o valor mediano do conjunto dos elementos do vetor;
–
Após mover o pivô para sua posição, restarão dois sub-vetores para
serem ordenados, ambos com o número de elementos reduzido à
metade, em relação ao vetor original;
–
Complexidade: T(n) = 2T(n/2)+n = n log n − n + 1 = O(n log n)

Quick Sort - Complexidade
•
Caso médio:
–
De acordo com Sedgewick e Flajolet (1996, p. 17), o número de
comparações é aproximadamente: T(n) ≈ 1.386 n log n − 0.846
–
Complexidade: T(n) = O(n log n)
Quick Sort - Complexidade
•
Pior caso:
–
Pivô é o maior elemento e algoritmo recai em ordenação bolha;
–
Complexidade: T(n) = O(n2)

Quick Sort
•
•
Melhorias:
–
Eliminação da recursão;
–
Melhor seleção do pivô: mediana de 3 partições evita pior caso em
conjuntos de dados ordenados;
–
–
Utilizar Insertion Sort conjuntos de dados pequenos;
Combinadas, essas melhorias fornecem um ganho de performance de
aproximadamente 20-25%.
O Quick Sort é considerado o melhor método para ordenação
interna de grandes conjuntos de dados (n ≥ 10.000).

Quick Sort
•
•
Complexidade O(n log n)
Vantagens:
–
Complexidade O(n log n)
•
Desvantagens:
–
Tradicionalmente baseia-se em chamadas recursivas, mas é possível
implementa-lo sem utilizar recursão;
–
Não é estável;

Exercícios
Lista de Exercícios 10 – Algoritmos de
Ordenação
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
Cormen, T., Leiserson, C., Rivest, R., e Stein, C.
Algoritmos – Teoria e Prática (tradução da 2ª.
Edição americana), Editora Campus, 2002.
•
•
Capítulo 4: Recorrências
Capítulo 7: Quick Sort
