
Projeto e Análise de Algoritmos
Aula 01 – Complexidade de Algoritmos
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

O que é um algoritmo?
•
Um conjunto de instruções executáveis para resolver um
problema (são as ideias por detrás dos programas)
–
O problema é a motivação para o algoritmo.
–
Geralmente existem vários algoritmos para um mesmo problema.
•
Como escolher?
–
–
Algoritmos são independentes da linguagem de programação, da
máquina, da plataforma, etc.
Algoritmos são representados através da descrição das instruções de
forma suficiente para que a audiência os entenda.

O que é um algoritmo?
•
•
Um problema é caracterizado pela descrição de uma entrada
e saída.
Exemplo: problema de ordenação
Entrada: uma sequência {a1; a2; ... ; an} de n números
Saída: uma permutação dos números {a'1; a'2; ... ; a'n}
tal que a'1 ≤ a'2 ≤ ... ≤ a'n
Entrada: 6 3 7 9 2 4
Saída: 2 3 4 6 7 9
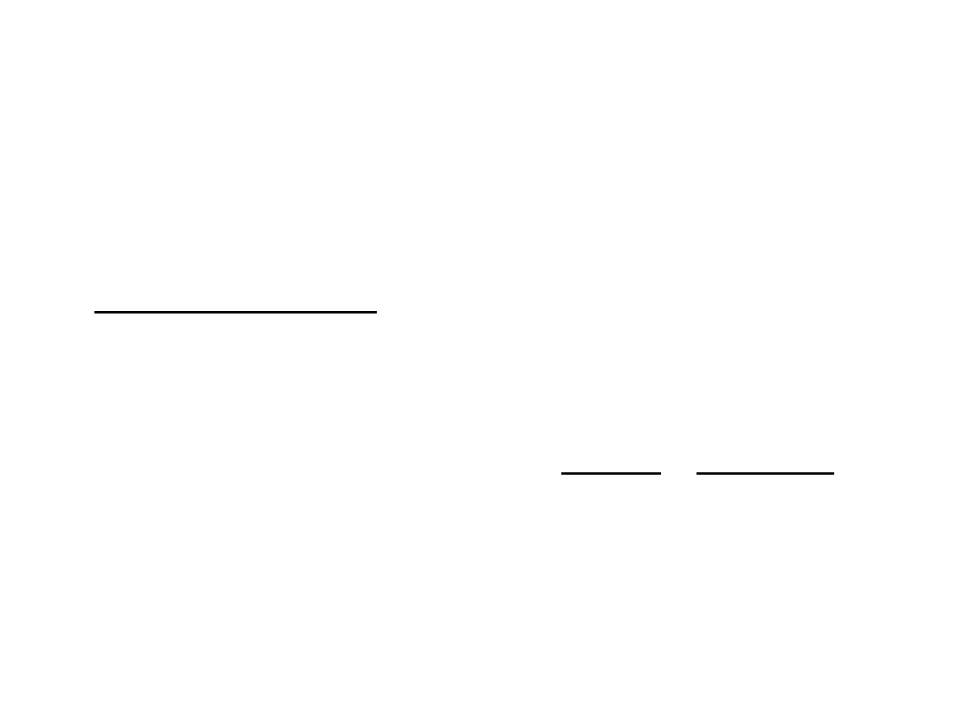
Propriedades Desejadas em um Algoritmo
•
•
Eficácia: deve ser capaz de resolver corretamente
todas as instâncias do problema.
Eficiência: a sua performance (tempo e memória)
tem de ser adequada.
Exemplo: Eficácia de um Algoritmo
•
Problema do Caixeiro Viajante:
Entrada: um conjunto S de n pontos no plano
Saída: o ciclo mais curto que visita todos os pontos de S
•
Exemplo:

Exemplo: Eficácia de um Algoritmo
•
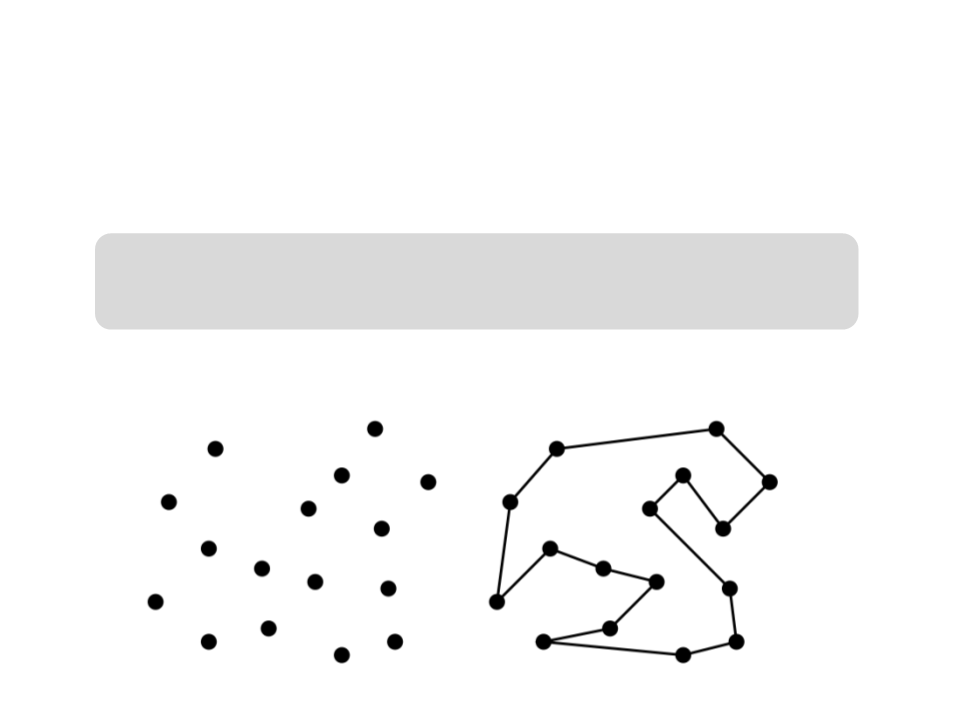
Problema do Caixeiro Viajante
–
Um primeiro possível algoritmo:
1. p1 ← ponto inicial escolhido aleatoriamente
2
3
4
5
6
. i ← 1
. enquanto (existirem pontos por visitar) fazer
. i ← i + 1
. pi ← vizinho não visitado mais próximo de pi-1
. retorna caminho p1 → p2 → ... → pn → p1
Exemplo: Eficácia de um Algoritmo
•
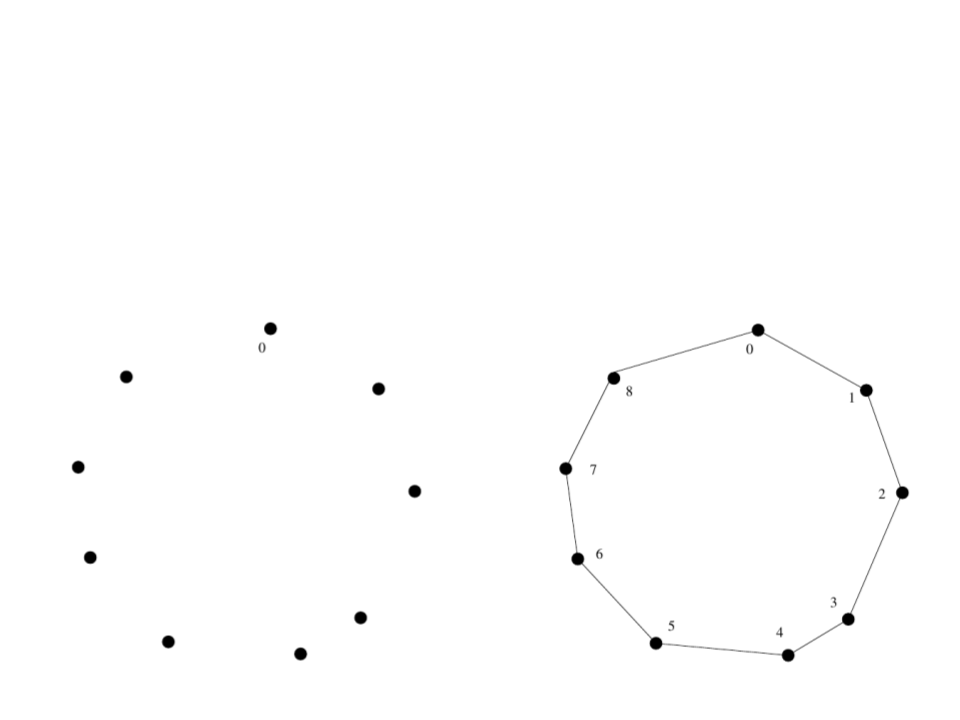
Problema do Caixeiro Viajante
–
Parece funcionar…
→
Exemplo: Eficácia de um Algoritmo
•
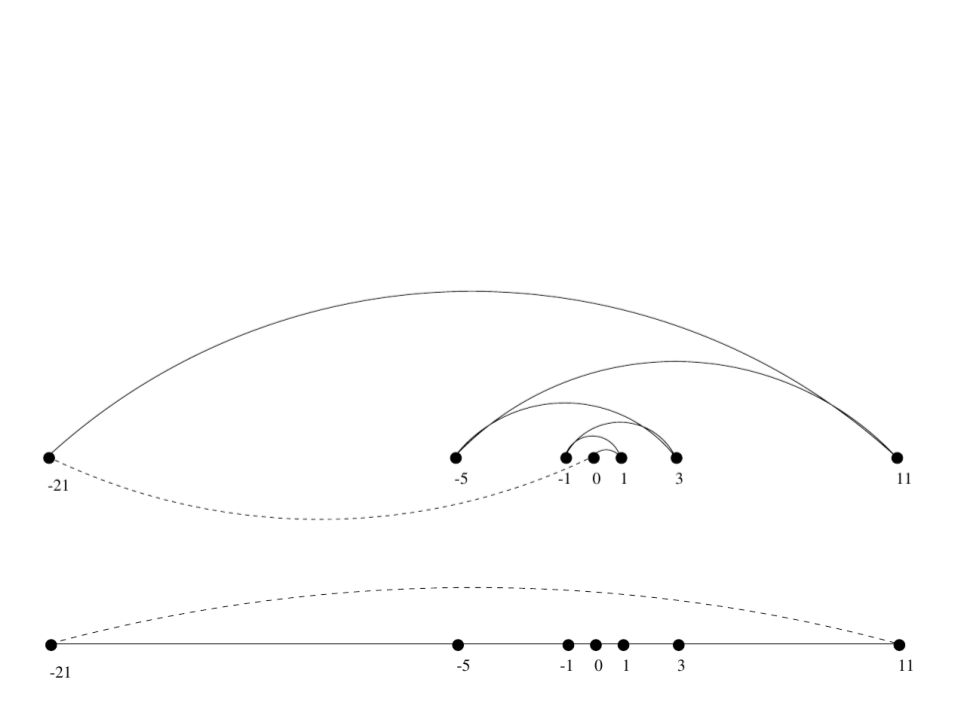
Problema do Caixeiro Viajante
–
Mas não funciona para todas as instâncias do problema!

Exemplo: Eficácia de um Algoritmo
•
Problema do Caixeiro Viajante
–
Um segundo possível algoritmo:
1. Para i ← 1 até (n - 1) fazer
2.
Adiciona ligação ao par de pontos mais próximo tal
que os pontos estão em componentes conexas (cadeias
de pontos) diferentes
3. Adiciona ligação entre dois pontos dos extremos da
cadeia ligada
4. retorna o ciclo que formou com os pontos

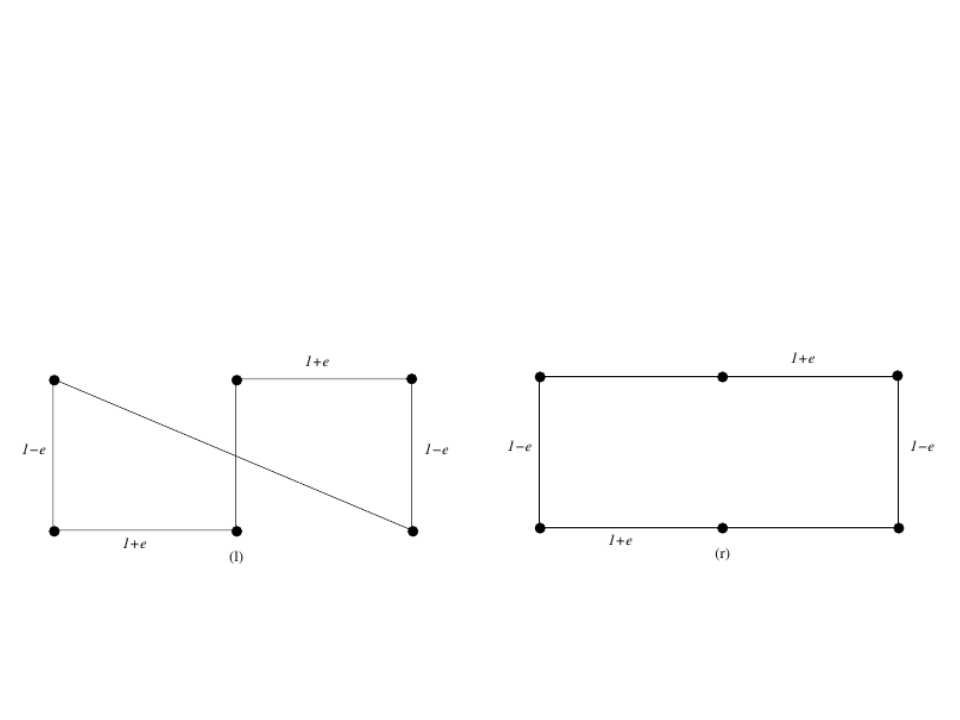
Exemplo: Eficácia de um Algoritmo
•
Problema do Caixeiro Viajante
–
Parece funcionar…
Exemplo: Eficácia de um Algoritmo
•
Problema do Caixeiro Viajante
–
Mas não funciona para todas as instâncias do problema!

Exemplo: Eficácia de um Algoritmo
•
Problema do Caixeiro Viajante
–
Um terceiro possível algoritmo (força bruta):
1
2
3
4
5
. Pmin ← uma qualquer permutação dos pontos de S
. Para Pi ← cada uma das permutações de pontos de S
. Se (custo(Pi) < custo(Pmin)) Então
. Pmin ← Pi
. retorna caminho formado por Pmin
–
O algoritmo é eficaz/correto, mas extremamente lento!
•
P(n) = n! = n × (n - 1) × ... × 1 (n fatorial)
•
Exemplo: P(20) = 2,432,902,008,176,640,000

Exemplo: Eficácia de um Algoritmo
•
•
•
O problema apresentado é uma versão restrita (euclidiana) de um dos
problemas mais "clássicos": Travelling Salesman Problem (TSP).
Este problema tem inúmeras aplicações (mesmo na forma "pura")
–
Exemplos: produção industrial, rotas de veículos, análise genômica...
Não é conhecida nenhuma solução eficiente para este problema (que
gere resultados ótimos, e não apenas "aproximados")
•
•
A solução apresentada tem complexidade temporal: O(n!)
O TSP pertence a classe dos problemas NP-hard
–
A versão de decisão pertence à classes dos problemas NP-completos

Eficiência de um Algoritmo
•
•
Quantas operações simples um computador pode realizar por
segundo? (aproximação em ordem de grandeza)
Assumindo que um computador realizar 1 milhão de
operações simples por segundo, quanto tempo demorariam
as seguintes quantidades de instruções?
Quantidade
100
< 1 seg
< 1 seg
1 seg
1,000
< 1 seg
1 seg
10,000
< 1 seg
2 min
100,000
< 1 seg
3 horas
32 anos
1,000,000
1 seg
N
N2
N3
2N
N!
12 dias
18 min
12 dias
31,710 anos
1017 anos
muito tempo muito tempo muito tempo muito tempo
muito tempo muito tempo muito tempo muito tempo muito tempo
muito tempo > 1025 anos

Eficiência de um Algoritmo
•
Voltando as permutações do algoritmo para o problema do
caixeiro viajante:
–
P(n) = n! = n × (n - 1) × ... × 1
Exemplo de 6 permutações de {1, 2, 3}:
2 3
3 2
1
1
2
2
3
3
1 3
3 1
1 2
2 1

Eficiência de um Algoritmo
•
Quanto tempo demora um programa que passa por todas as
permutações de n números? (tempos aproximados
considerando cerca de 10 permutações por segundo)
7
n = 8: 0,003s
n = 9: 0,026s
n = 10: 0,236s
n = 11: 2,655s
n = 12: 33,923s
…
n = 20: 5000 anos !

Eficiência de um Algoritmo
•
Um computador mais rápido adiantaria alguma
coisa?
•
Se n = 20 = 5000 anos, hipoteticamente:
–
–
–
10x mais rápido ainda demoraria 500 anos;
5,000x mais rápido ainda demoraria 1 ano;
1,000,000x mais rápido demoraria quase dois dias mas:
•
n = 21 já demoraria mais de um mês;
•
n = 22 já demoraria mais de dois anos!
•
A taxa de crescimento do algoritmo é muito importante!

Eficiência de um Algoritmo
•
•
Como conseguir prever o tempo que um algoritmo
demora?
Como conseguir comparar dois algoritmos diferentes?

Random Access Machine (RAM)
•
•
Precisamos de um modelo que seja genérico e independente
da máquina/linguagem usada.
Vamos considerar uma Random Access Machine (RAM)
–
–
–
Cada operação simples (+, -, / , *) demora 1 passo;
Cada acesso á memória custa também 1 passo;
Tempo de execução: número de passos executados em relação ao
tamanho da entrada (T(n)).
•
As operações são simplificadas, mas mesmo assim isto é útil
(somar dois inteiros não custa o mesmo que dividir dois reais,
mas veremos que esses valores não são importantes em uma
visão global)

Exemplo de Contagem de Operações
•
Um programa simples:
int count = 0;
int i;
for (i=0; i<n; i++)
if (v[i] == 0)
count++;
•
Número de operações simples:
Declarações de variáveis
Atribuições
2
2
Comparação “menor que”
Comparação “igual a”
Acesso ao vetor
n + 1
n
n
Incremento
Entre n e 2n (dependendo dos zeros)

Exemplo de Contagem de Operações
•
Um programa simples:
int count = 0;
int i;
for (i=0; i<n; i++)
if (v[i] == 0)
count++;
•
Total de operações no pior caso:
T(n) = 2 + 2 + (n + 1) + n + n + 2n = 5 + 5n
•
Total de operações no melhor caso:
T(n) = 2 + 2 + (n + 1) + n + n + n = 5 + 4n

Tipos de Análises de um Algoritmo
•
Análise do Pior Caso:
–
T(n) = tempo máximo do algoritmo para uma entrada
qualquer de tamanho n.
•
•
Análise Caso Médio:
–
T(n) = tempo médio do algoritmo para todos as entradas
de tamanho n.
•
Implica conhecer a distribuição estatística das entradas.
Análise do Melhor Caso:
–
T(n) = avaliação ingênua de um algoritmo que é rápido
para algumas entradas.
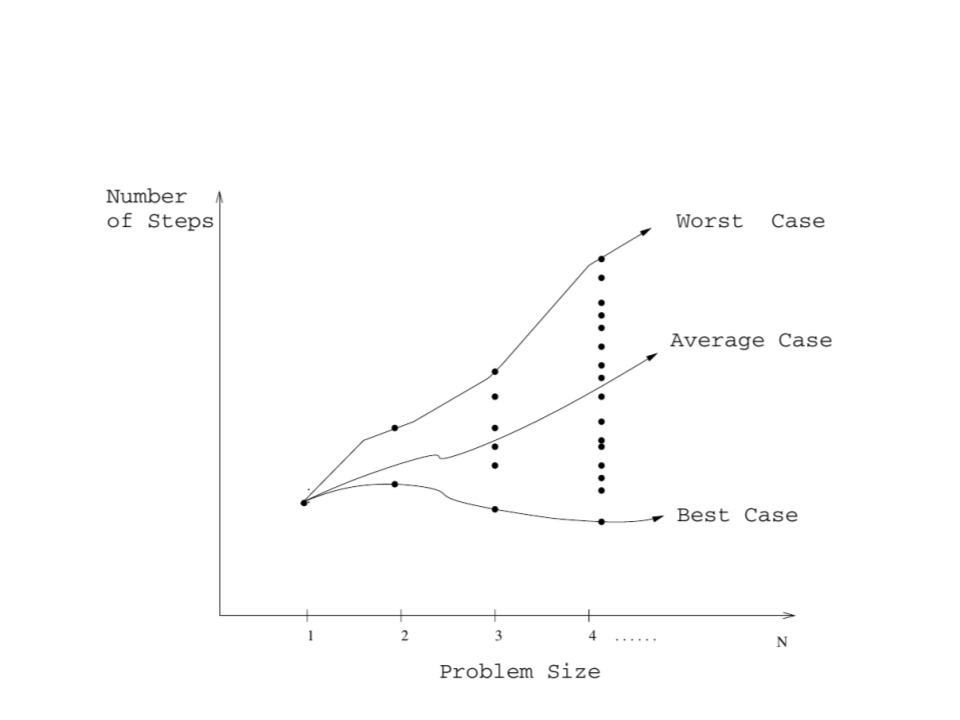
Tipos de Análises de um Algoritmo

Análise Assintótica
•
•
Precisamos de ferramenta matemática para comparar funções
Na análise de algoritmos usa-se a Análise Assintótica
–
Estudo do comportamento de algoritmos para entradas arbitrariamente
grandes ou a "descrição" da taxa de crescimento.
•
•
Usa-se uma notação especifica: O, ꢀ, ꢁ (big O, omega, theta)
Permite "simplificar" expressões como a mostrada
anteriormente focando apenas nas ordens de grandeza.

Análise Assintótica – Notação
•
•
•
f(n) = O(g(n))
–
Significa que C × g(n) é um limite superior de f(n)
f(n) = ꢂ(g(n))
–
Significa que C × g(n) é um limite inferior de f(n)
f(n) = ꢃ(g(n))
–
Significa que C1 × g(n) é um limite inferior de f(n) e
C2 × g(n) é um limite superior de f(n)
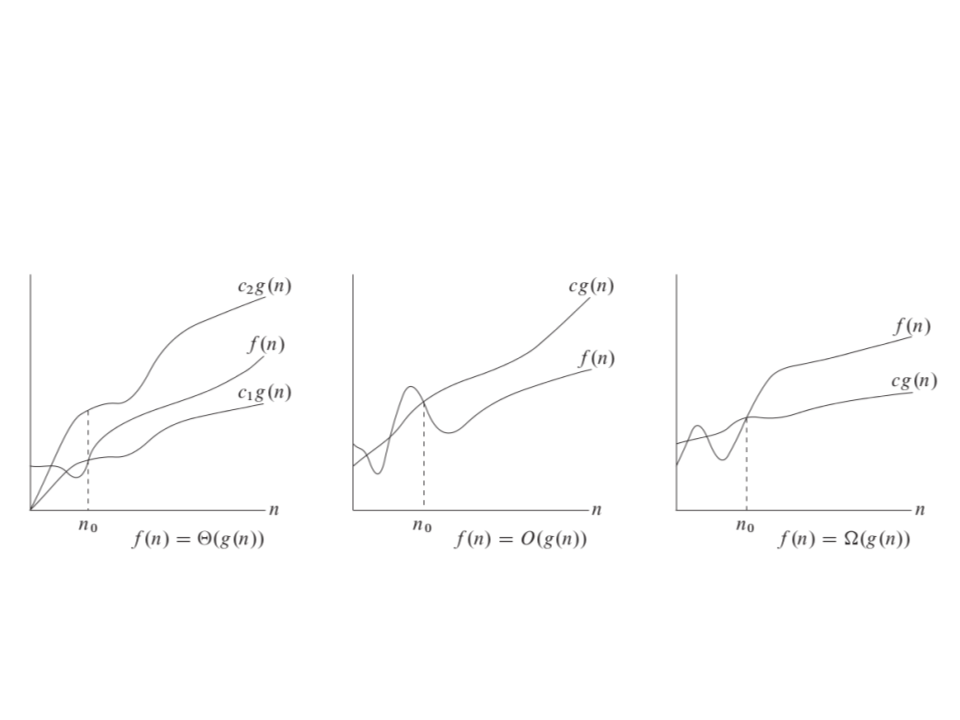
Análise Assintótica – Notação
ꢃ
O
ꢂ

Análise Assintótica – Formalização
•
•
f(n) = O(g(n)) se existem constantes positivas n0 e c
tal que f(n) ≤ c × g(n) para todo o n ≥ n0
f(n) = 3n2 - 100n + 6
2
–
–
–
f(n) = O(n )
f(n) = O(n3)
f(n) ≠ O(n)

Análise Assintótica – Formalização
•
•
f(n) = ꢂ(g(n)) se existem constantes positivas n0 e c
tal que f(n) ≥ c × g(n) para todo o n ≥ n0
f(n) = 3n2 - 100n + 6
2
–
–
–
f(n) = Ω(n )
f(n) ≠ Ω(n3)
f(n) = Ω(n)

Análise Assintótica – Formalização
•
•
f(n) = ꢃ(g(n)) se existem constantes positivas n0, c1 e
c2 tal que c1 × g(n) ≤ f(n) ≤ c2 × g(n) para todo o n ≥
n0
f(n) = 3n2 - 100n + 6
2
–
–
–
f(n) = Θ(n )
f(n) ≠ Θ(n3)
f(n) ≠ Θ(n)
•
f(n) = Θ(g(n)) implica que f(n) = O(g(n)) e f (n) = Ω(g(n))

Análise Assintótica
•
•
O estudo assintótico nos permite ignorar constantes e termos
que não são dominantes.
Considerando a função f(n) = 3n2 + 10n + 50

Análise Assintótica – Regras Praticas
•
•
Multiplicação por uma constante não altera o comportamento:
–
–
Θ(c × f (n)) = Θ(f(n))
2 2
99 × n = Θ(n )
Em um polinômio a n + a n + ... + a n2 + a1n + a0 podemos nos
x
x-1
x
x-1
2
focar na parcela com o maior expoente:
3 2 3
3n - 5n + 100 = Θ(n )
4 2 4
6n - 20 = Θ(n )
0.8n + 224 = Θ(n)
–
–
–
•
Em uma soma/subtração podemos nos focar na parcela dominante:
n
3
n
–
–
–
2 + 6n = Θ(2 )
2
n! - 3n = Θ(n!)
n log n + 3n = Θ(n2)
2

Análise Assintótica – Exercício
•
•
T(n) = 32n2 + 17n + 32
Responda se T(n) é
2
–
–
–
–
–
–
–
–
–
O(n )? Sim
3
O(n )? Sim
Ω(n)? Sim
2
Ω(n )? Sim
O(n)? Não
2
Θ(n )? Sim
3
Ω(n )? Não
Θ(n)? Não
4
Θ(n )? Não
Crescimento Assintótico
Função
Nome
Exemplos
1
log n
n
constante
logarítmica
linear
Somar dois números
Pesquisa binária, inserir um número em uma heap
1 ciclo para buscar o valor máximo em um vetor
Ordenação (merge sort, heap sort)
2 ciclos (bubble sort, selection sort)
3 ciclos (Floyd-Warshall)
n log n linearítimica
n2
n3
2n
n!
quadrática
cúbica
exponencial
fatorial
Pesquisa exaustiva (subconjuntos)
Todas as permutações
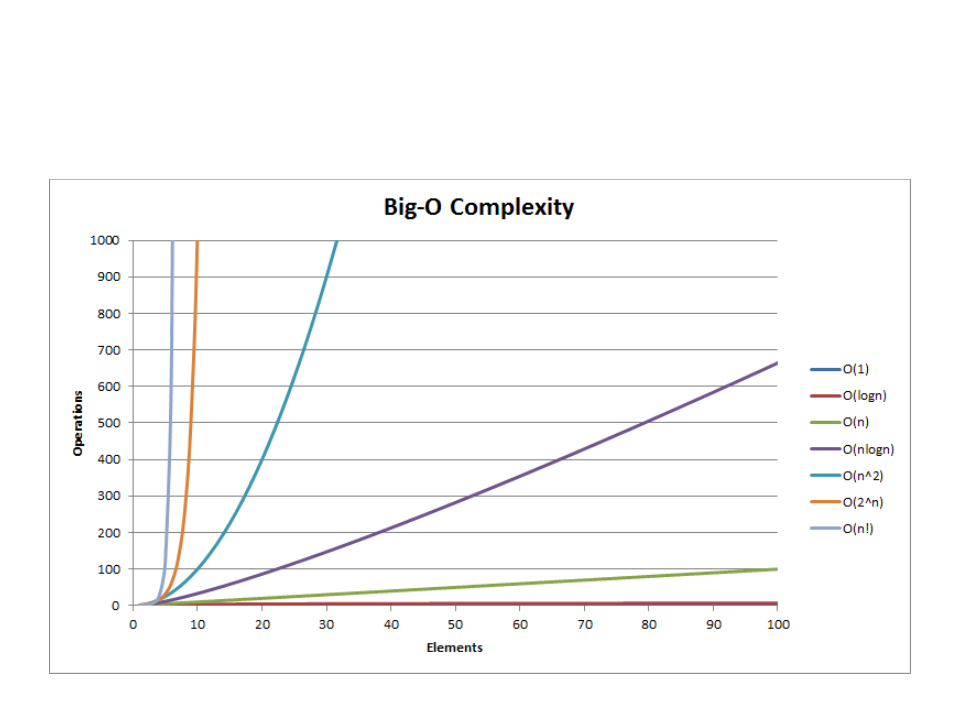
Crescimento Assintótico

Análise Assintótica – Exemplos Praticos
•
•
•
•
Um programa tem dois pedaços de código A e B, executados um a seguir
2
ao outro, sendo que A corre em O(n log n) e B em O(n ).
2 2
O programa corre em O(n ), porque n > n log n
–
Um programa chama n vezes uma função O(log n), e em seguida volta a
chamar novamente n vezes outra função O(log n)
–
O programa corre em O(n log n)
Um programa tem 5 ciclos, chamados sequencialmente, cada um deles
com complexidade O(n)
–
O programa corre em O(n)
Um programa P tem tempo de execução proporcional a 100 × n log n.
1
2
Um outro programa P tem 2 × n . Qual é o programa mais eficiente?
1
2
2
–
P é mais eficiente porque n > n log n. No entanto, para um n pequeno, P2 é
mais rápido e pode fazer sentido ter um programa que chama P ou P de
1
2
acordo com o valor de n.

Exercícios
1
) Escreva um algoritmo para verificar se um vetor contêm pelo
menos dois valores duplicados (em qualquer lugar do vetor).
Em seguida, analise a complexidade do algoritmo proposto.
bool hasDuplicate(int *vet, int n){
int i, j;
bool duplicate = false;
for (i = 0; i < n; i++){
for (j = 0; j < n; j++){
if (i != j && A[i] == A[j])
return true;
}
}
return false;
O(n2)
}
Exercícios
) Qual a complexidade do seguinte algoritmo?
2
int i, j, k, x, result = 0;
for (i = 0; i < N; i++){
for (j = i; j < N; j++){
for (k = 0; k < M; k++){
x = 0;
while (x < N){
m
m
result++;
x += 3;
n
n2
}
}
for (k = 0; k < 2 * M; k++)
if (k % 7 == 4)
result++;
}
O(n2mn) = O(mn3)
}
Exercícios
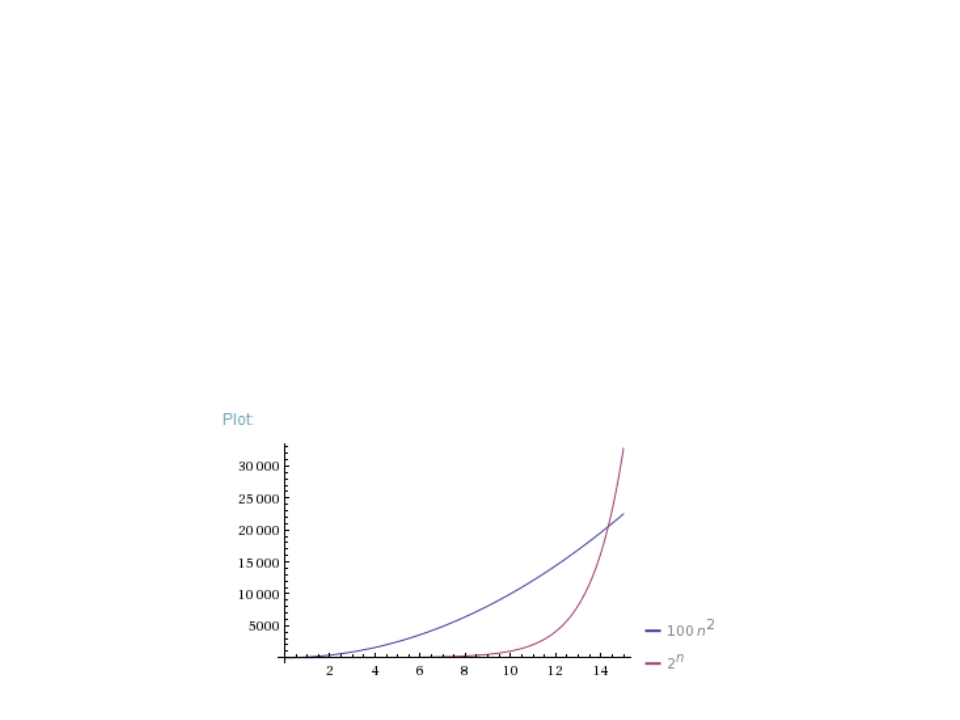
3
) Qual o menor valor de n tal que um algoritmo cujo tempo de
2
execução é 100n funciona mais rápido que um algoritmo
n
cujo tempo de execução é 2 na mesma máquina?
Wolfram Alpha:
plot 100*n^2 from n=0 to 15, 2^n from n=0 to 15

Exercícios
Lista de Exercícios 01 – Complexidade de
Algoritmos
http://www.inf.puc-rio.br/~elima/paa/

Leitura Complementar
•
•
Cormen, T., Leiserson, C., Rivest, R., e Stein, C.
Algoritmos – Teoria e Prática (tradução da 2ª.
Edição americana), Editora Campus, 2002.
Capítulo 1: A função dos Algoritmos na
Computação
•
•
Capítulo 2: Conceitos Básicos
Capítulo 3: Crescimento de Funções
