
Projeto e Análise de Algoritmos
Aula 09 – Árvore Geradora Mínima
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Árvore Geradora Mínima
•
•
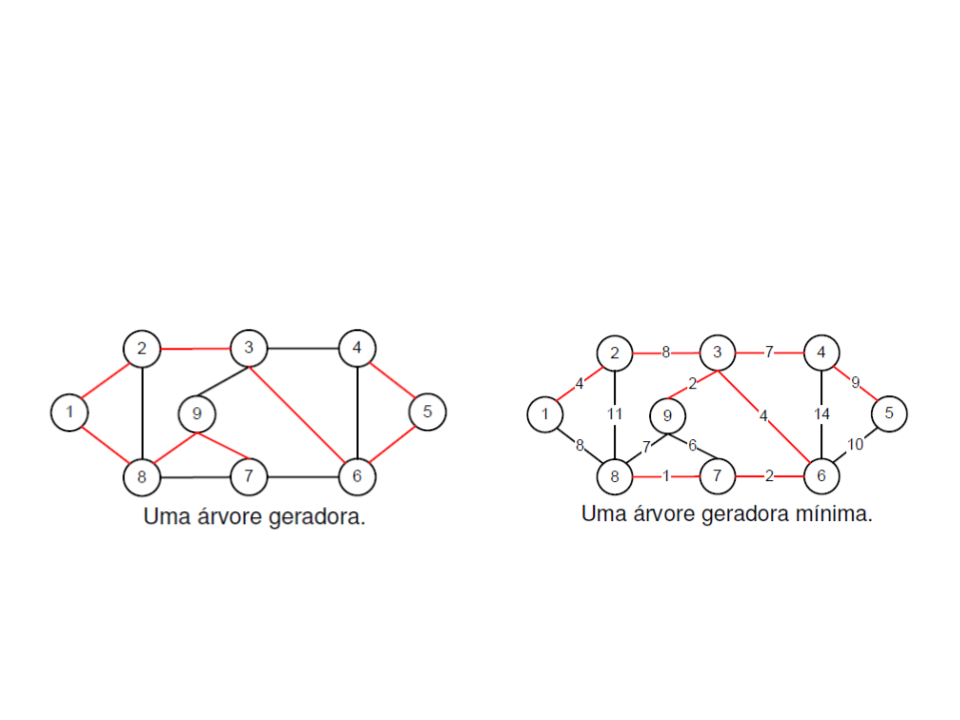
Dado um grafo não direcionado conectado G, uma árvore T é
chamada de árvore geradora de G se T é um subgrafo de G que
possui todos os vértices de G.
Uma árvore geradora mínima é uma árvore geradora com peso
menor ou igual a cada uma das outras árvores geradoras possíveis.
–
Também conhecida como árvore de extensão mínima ou árvore de extensão de
peso mínimo;
•
Aplicações:
–
–
–
Projeto de redes de telecomunicação;
Projeto de rodovias, ferrovias, etc;
Projeto de redes de transmissão de energia;
Árvore Geradora Mínima
•
Exemplo:

Árvore Geradora Mínima
•
Existem dois algoritmos clássicos para resolver o problema da
árvore geradora mínima:
–
Algoritmo de Prim;
–
Algoritmo de Kruskal;
•
•
Ambos são considerados algoritmos gulosos:
– A estratégia gulosa defende que a menor escolha a cada passo deve ser feita,
mesmo que tal escolha não nos leve a uma solução ótima ao final da
execução.
Diferente de alguns algoritmos gulosos, os algoritmos de árvore
geradora mínima sempre encontram a solução ótima.
Algoritmo Guloso – Caminho Mínimo
•
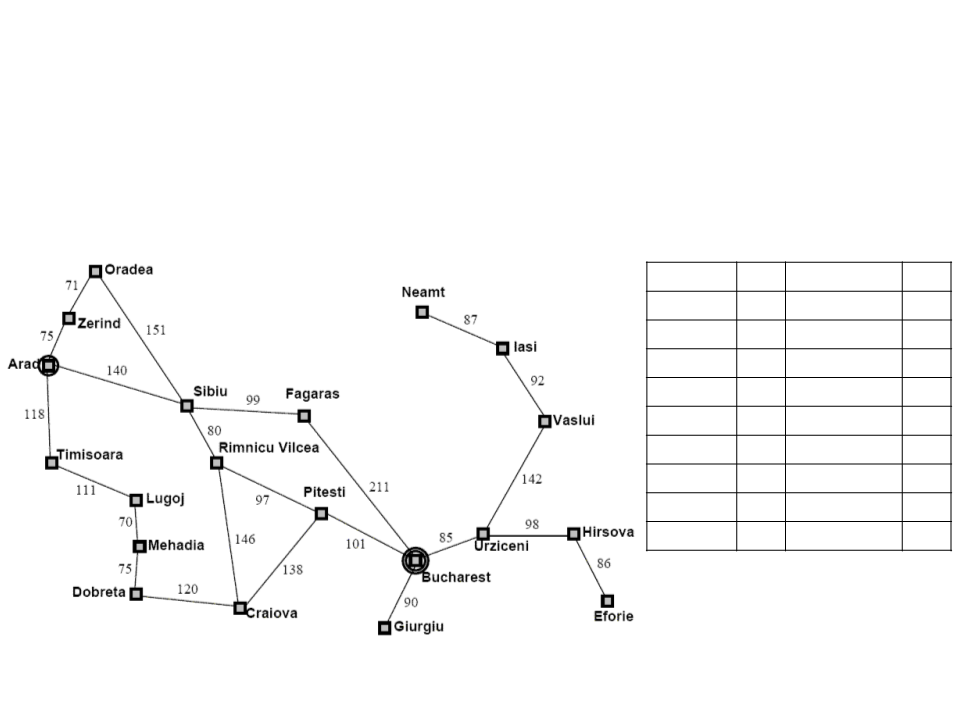
Como ir de Arad a Bucharest?
Distâncias em linha reta até Bucharest:
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
160
242
161
176
77
Rimnicu Vilcea 193
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
Timisoara
Vaslui
226
244
151
Lugoj
Zerind
Hirsova
Urziceni
Algoritmo de Prim
•
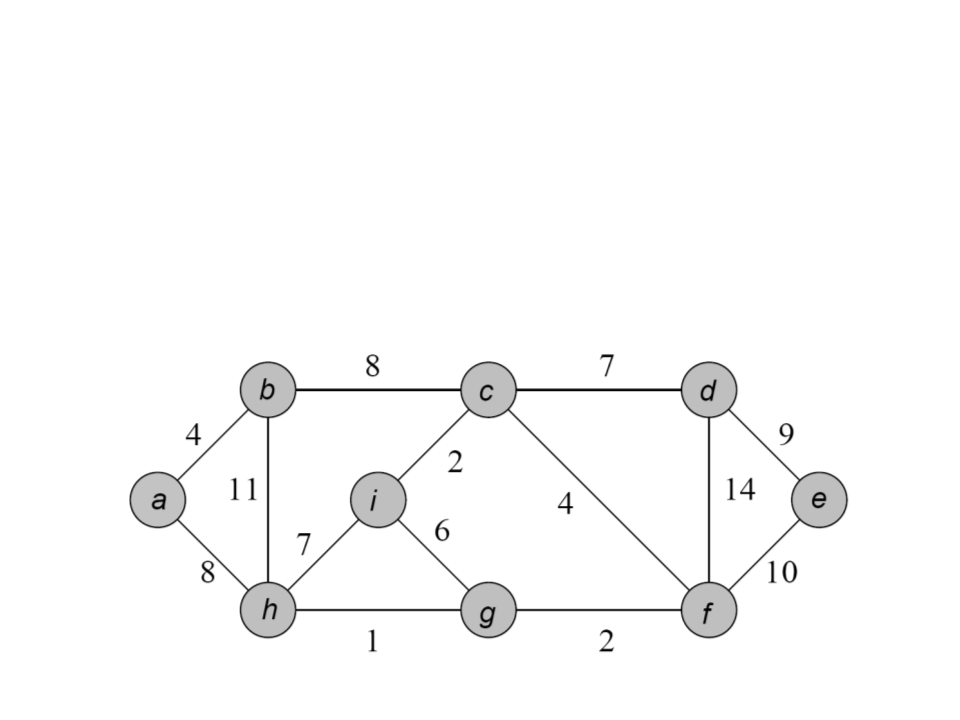
Ideia: a partir de um vértice inicial, selecione as arestas de
menor peso disponíveis a cada vértice não visitado.
–
Sem ciclos, pois só visita novos vertices.

Algoritmo de Prim
AGM-PRIM(G, w, r)
for each u ∈ V[G]
key[u] ← ∞;
ꢀ
[u] ← NULL;
key[r] ← 0;
Q ← V[G];
//heap ordenado por key[v]
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v) < key[v])
ꢀ
[v] ← u;
key[v] ← w(u, v);
return ꢀ;
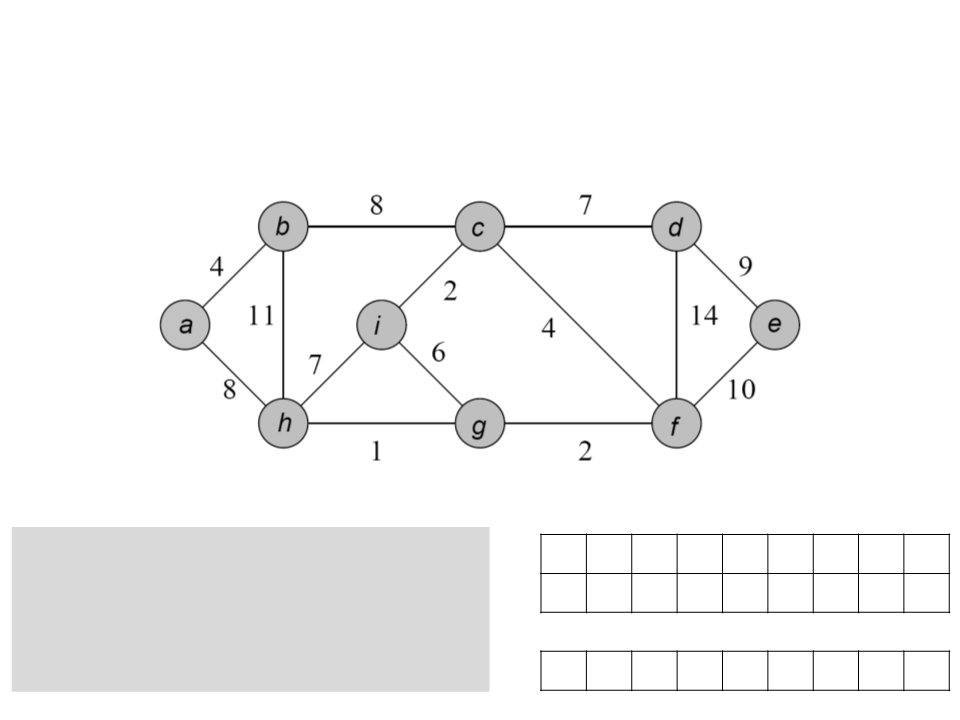
Algoritmo de Prim
a b c d e f g h i
AGM-PRIM(G, w, r)
for each u ∈ V[G]
key[u] ← ∞;
ꢀ
key
ꢀ
[u] ← NULL;
key[r] ← 0;
Q ← V[G];
Q
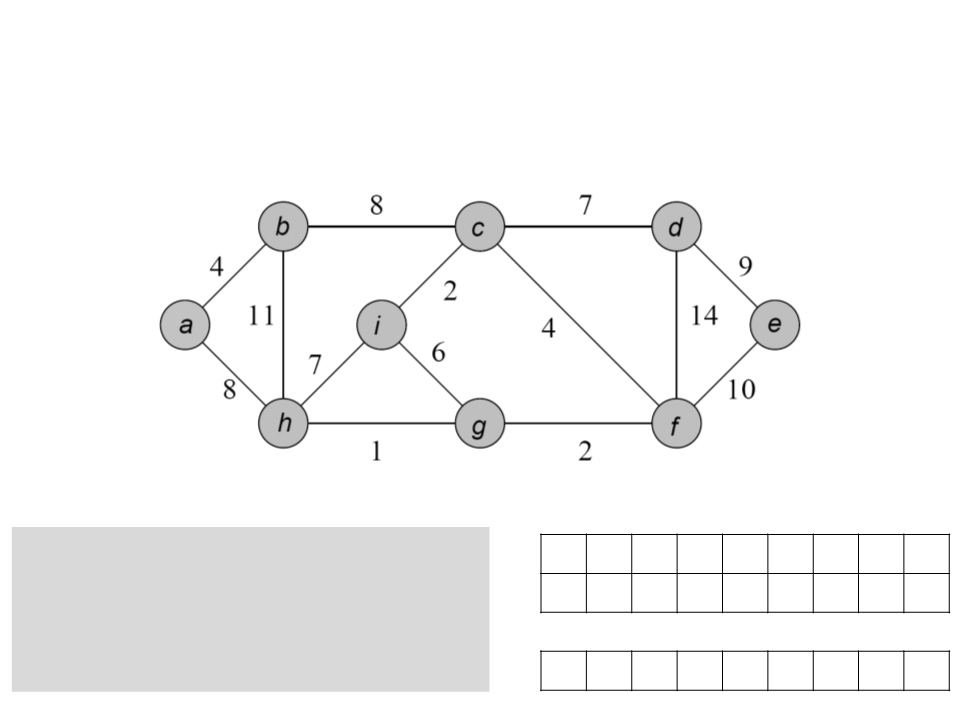
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
ꢀ
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
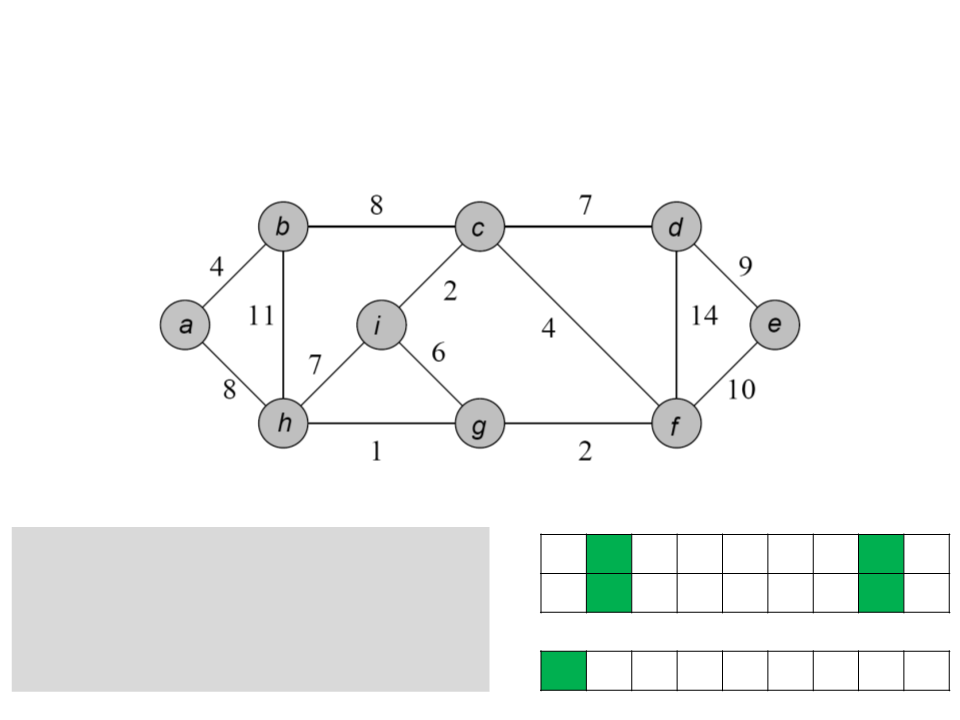
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
ꢀ
/ a / / / / / a /
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
0 4 ∞ ∞ ∞ ∞ ∞ 8 ∞
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q a b c d e f g h i
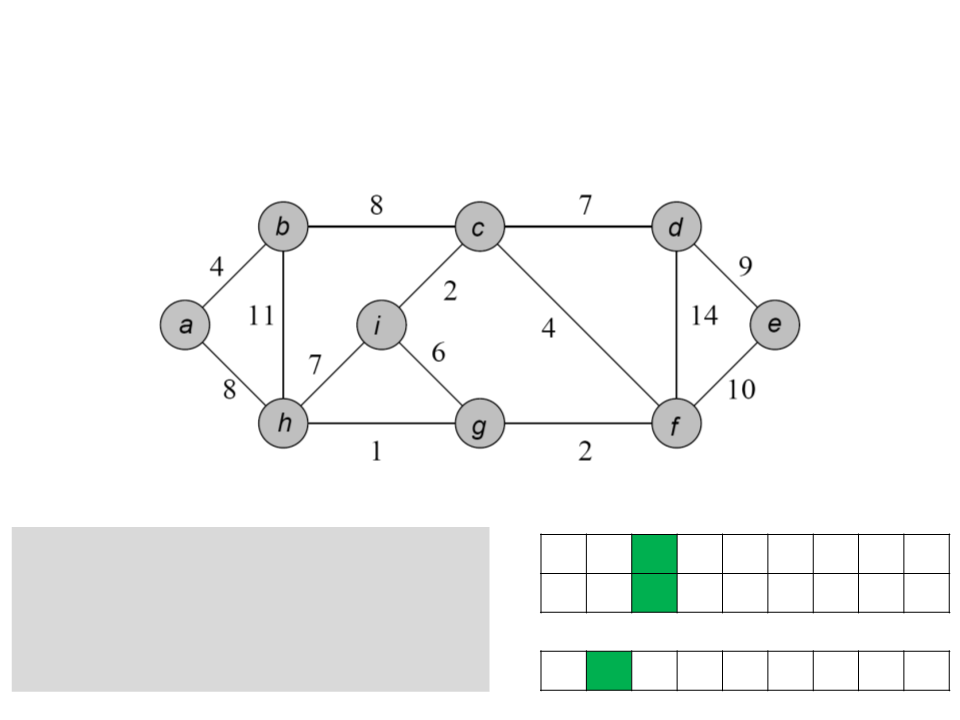
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
ꢀ
/ a b / / / / a /
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
0 4 8 ∞ ∞ ∞ ∞ 8 ∞
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
b h c d e f g i
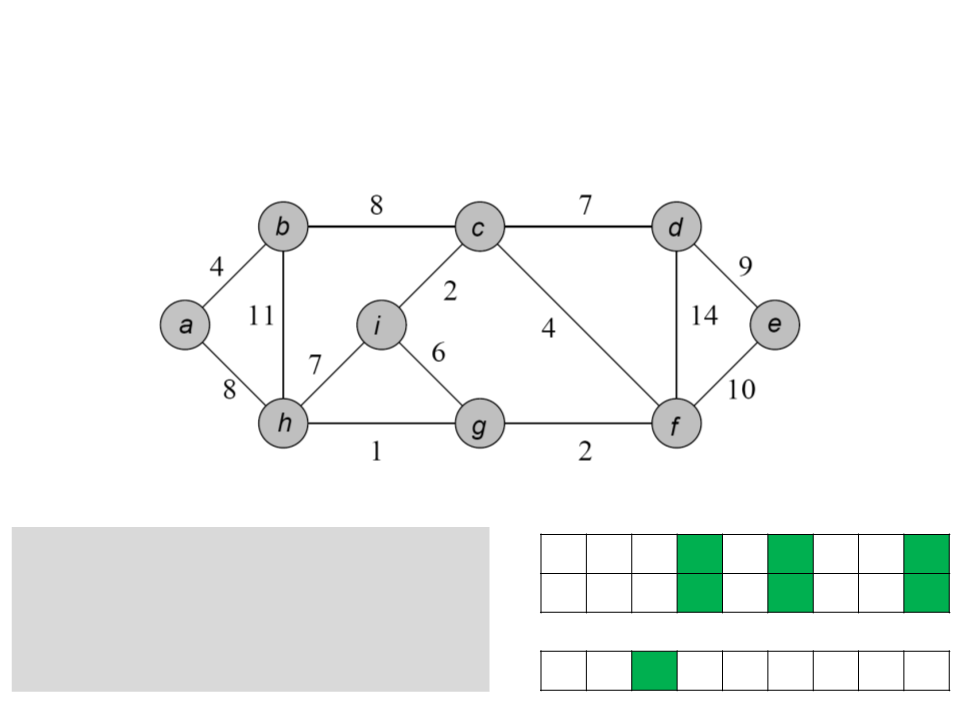
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
ꢀ
/ a b c / c / a c
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
0 4 8 7 ∞ 4 ∞ 8 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
c h d e f g i
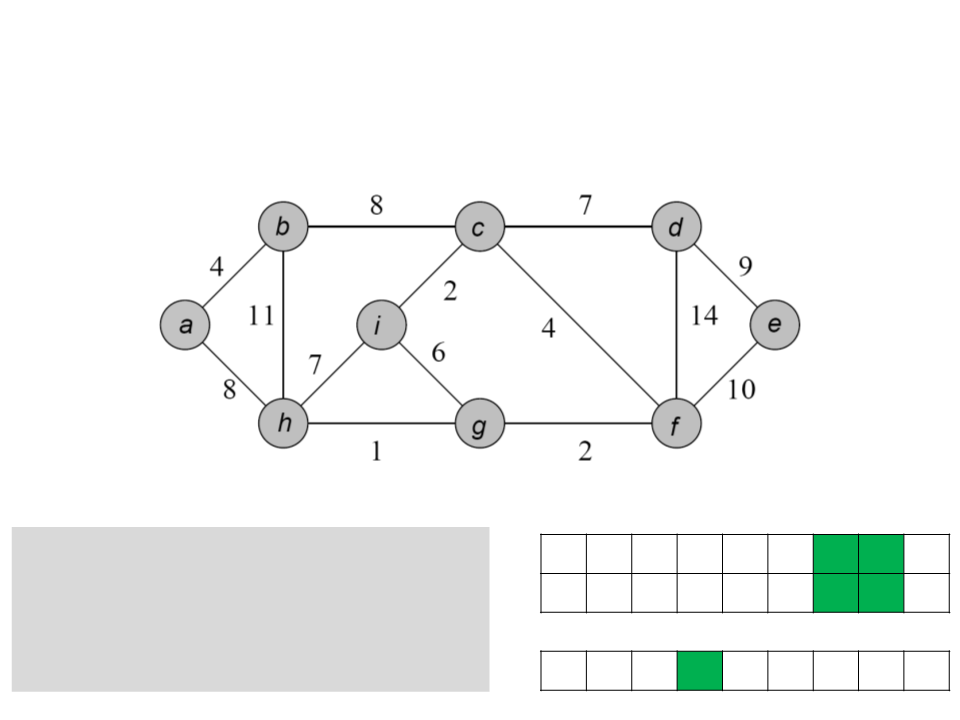
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
ꢀ
/ a b c / c i i c
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
0 4 8 7 ∞ 4 6 7 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
i f d h e g
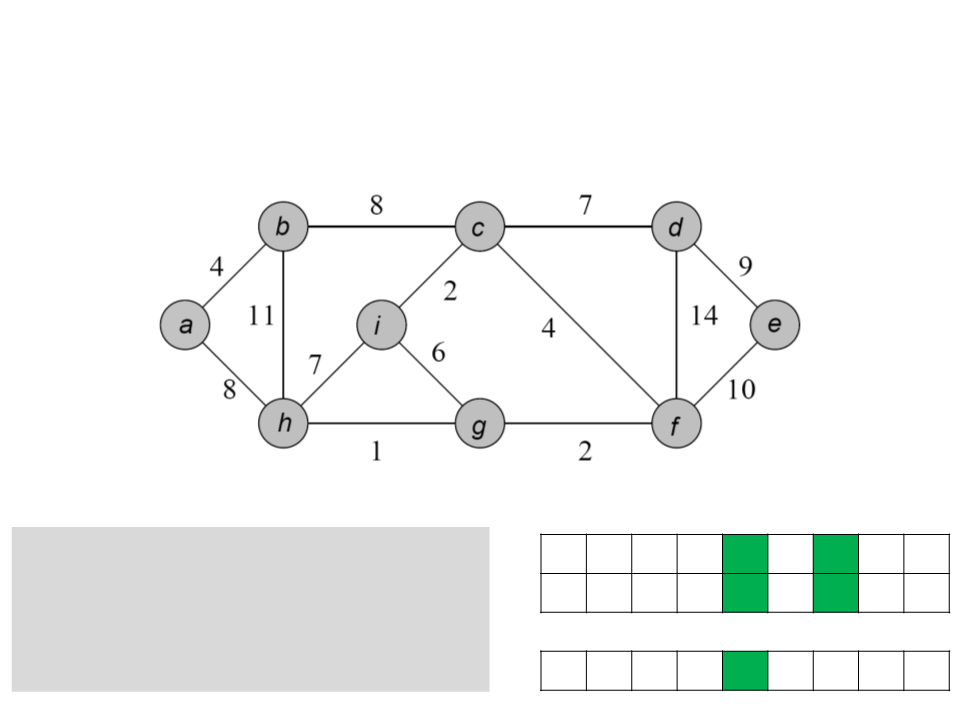
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
ꢀ
/ a b c f c f i c
0 4 8 7 10 4 2 7 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
f g d h e
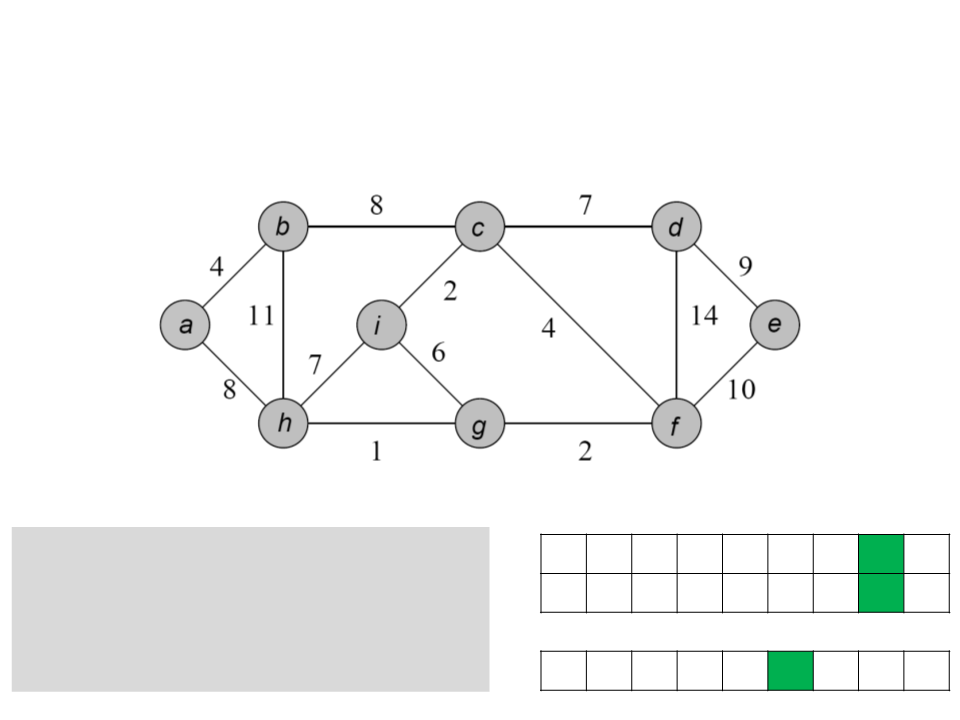
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
ꢀ
/ a b c f c f g c
0 4 8 7 10 4 2 1 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
g d h e
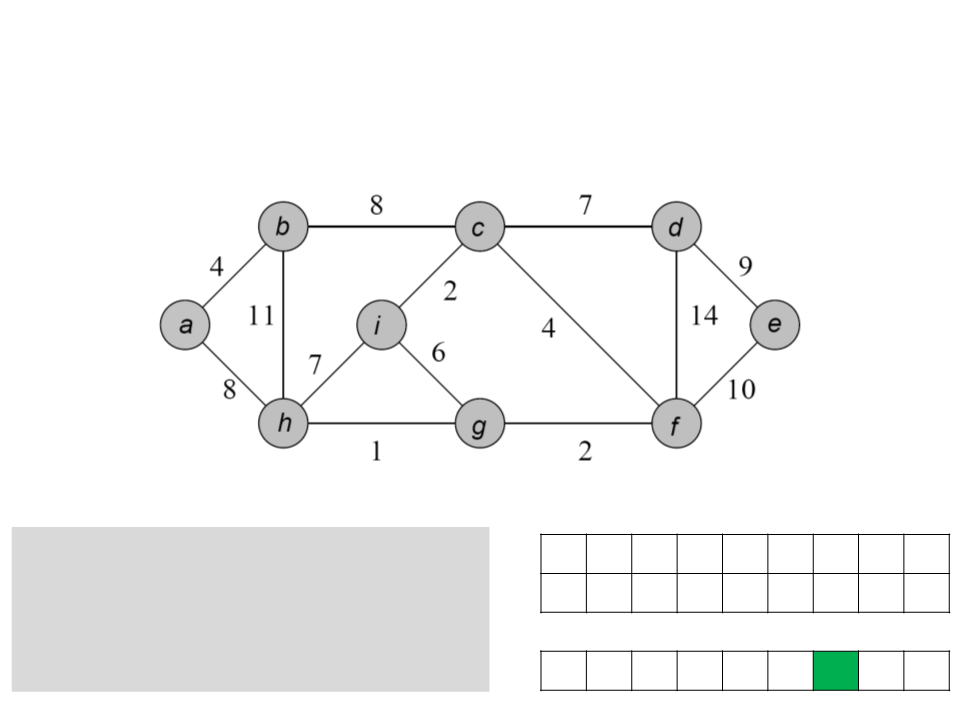
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
ꢀ
/ a b c f c f g c
0 4 8 7 10 4 2 1 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
h d e
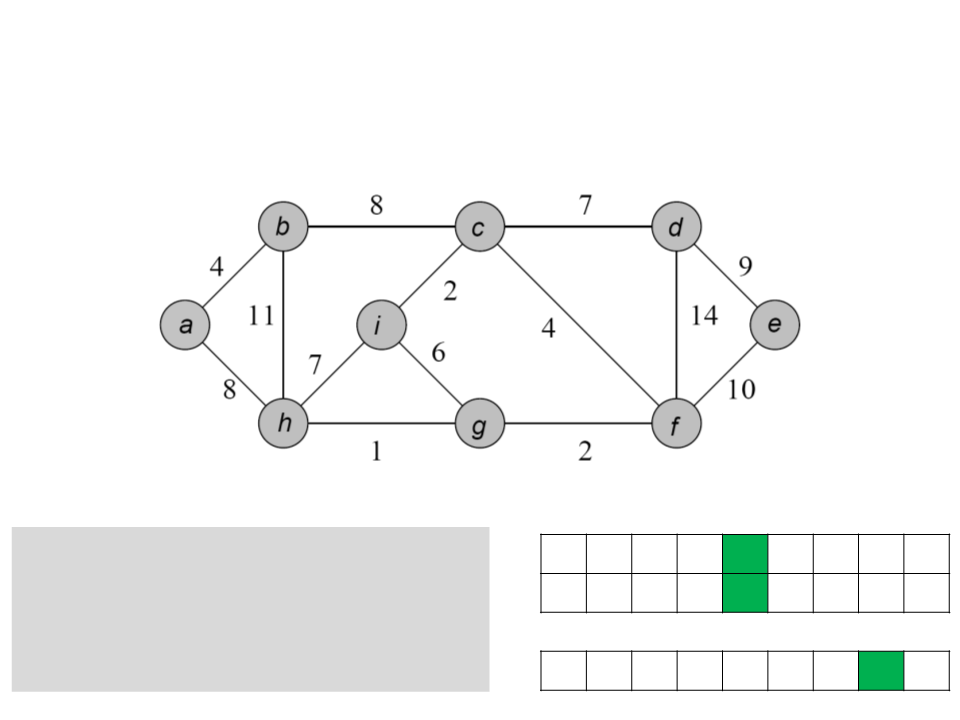
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
ꢀ
/ a b c d c f g c
0 4 8 7 9 4 2 1 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
d e
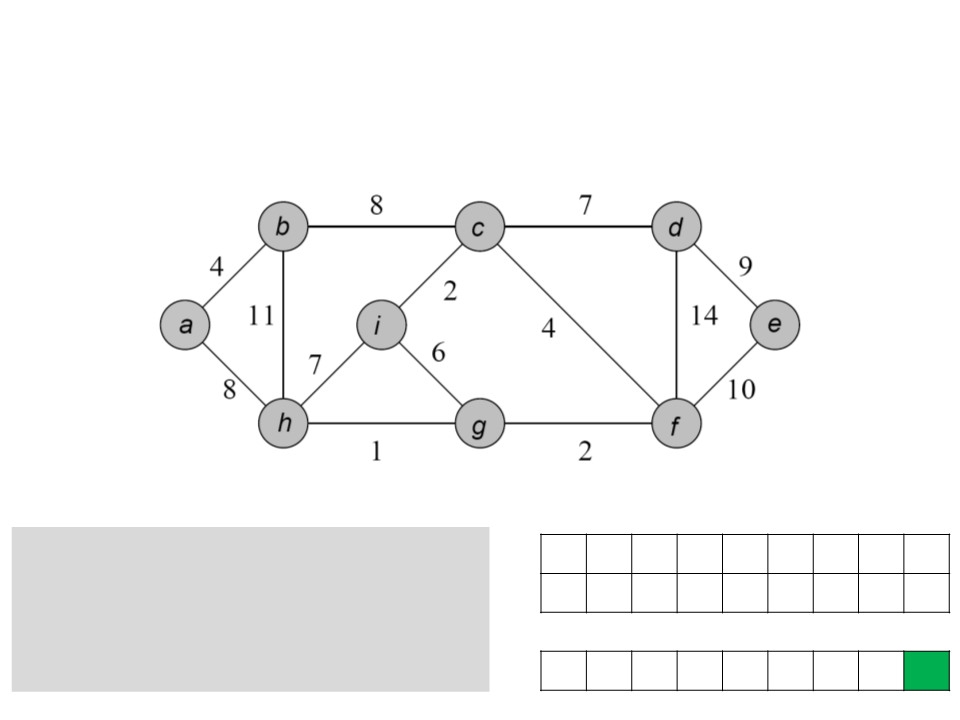
Algoritmo de Prim
a b c d e f g h i
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
if (v ∈ Q) and (w(u, v)<key[v])
ꢀ
/ a b c d c f g c
0 4 8 7 9 4 2 1 2
key
ꢀ
[v] ← u;
key[v] ← w(u, v);
Q
e
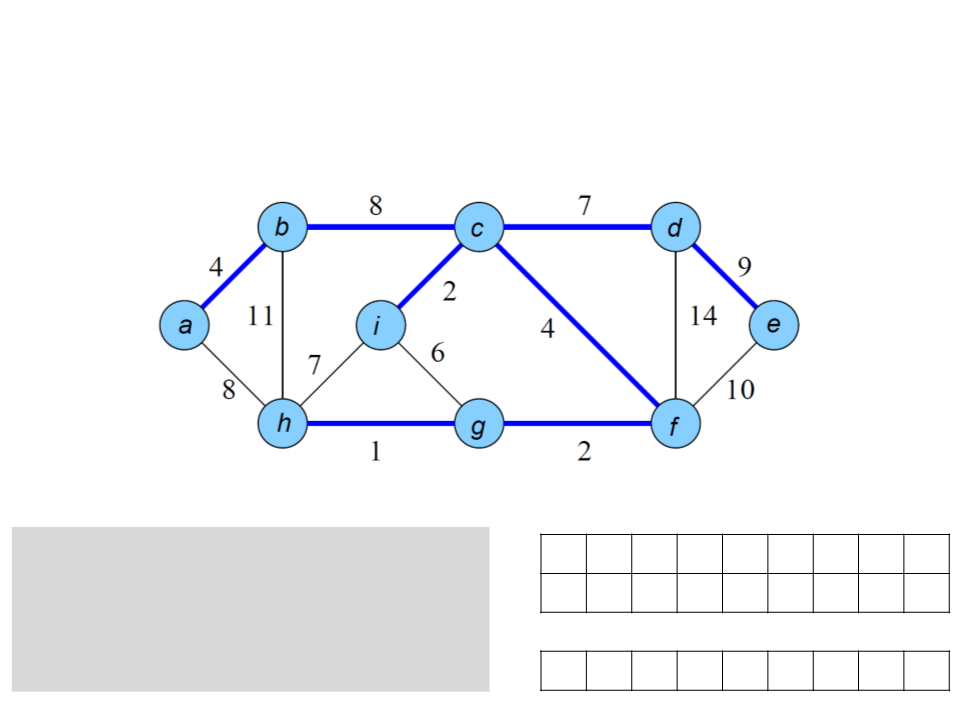
Algoritmo de Prim
a b c d e f g h i
/ a b c d c f g c
4 8 7 9 4 2 1 2
return ꢀ;
ꢀ
0
key
Q

Algoritmo de Prim – Análise
•
•
•
•
•
Inicializar key e ꢀ: O(V)
AGM-PRIM(G, w, r)
for each u ∈ V[G]
key[u] ← ∞;
Inicializar heap Q: O(V)
Percorrer vértices em Q: O(V)
POP-MIN: O(log V)
ꢀ
[u] ← NULL;
key[r] ← 0;
Q ← V[G]; //heap ordenado por key[v]
while Q ≠ ∅
u ← POP-MIN(Q);
for each v ∈ Adj[u]
Percorrer vértices adjacentes:
O(A)
if (v ∈ Q) and (w(u, v) < key[v])
ꢀ
[v] ← u;
key[v] ← w(u, v);
return ꢀ;
•
•
Atualizar key e heap Q: O(log V)
Complexidade:
O((V + A) log V)
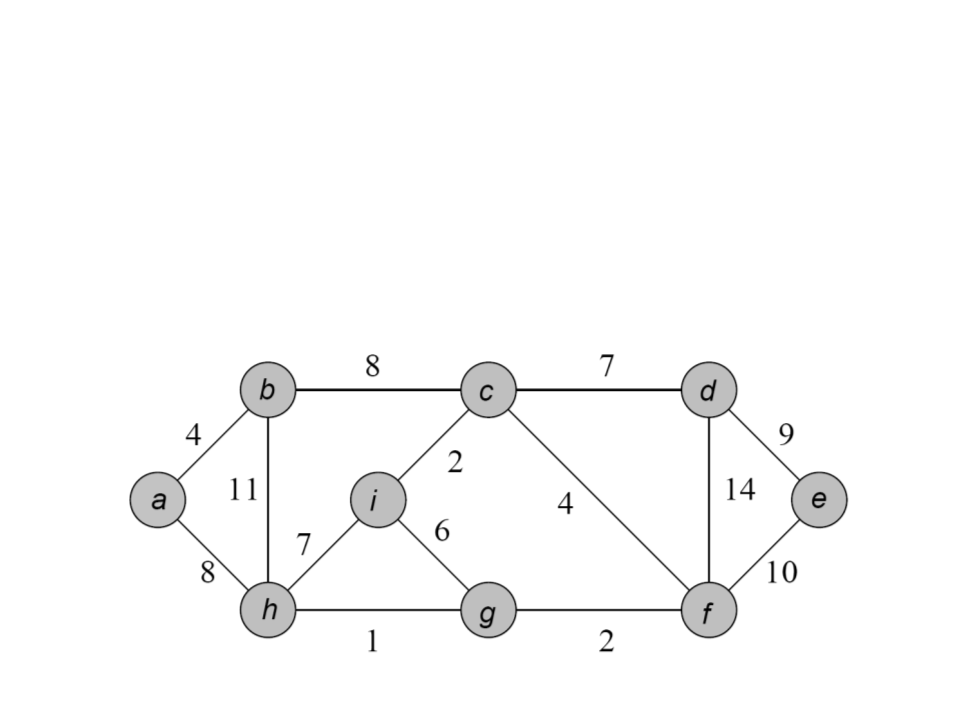
Algoritmo de Kruskal
•
Ideia: selecionar arestas de menor peso sucessivamente até
que uma árvore geradora seja obtida
–
Como as arestas são as de menor peso, é seguro adicioná-las à arvore
geradora mínima.

Algoritmo de Kruskal
•
Versão Inicial:
KRUSKAL(G)
A = ∅;
sort G[E] by weight(u, v);
for each (u, v) ∈ G[E]
if (u, v) est˜ao em componentes distintos de GA
A ← A ∪ {(u, v)};
return A
•
Problema: como verificar eficientemente se u e v estão no mesmo
componente da floresta GA = (V, A)?

Algoritmo de Kruskal
•
•
•
Inicialmente GA = (V, ∅), ou seja, GA corresponde à floresta
onde cada componente é um vértice isolado.
Ao longo do algoritmo, esses componentes são modificados
pela inclusão de arestas em A.
Uma estrutura de dados para representar GA = (V, A) deve ser
capaz de executar eficientemente as seguintes operações:
–
Dado um vértice u, determinar o componente de GA que contém u;
–
Dados dois vértices u e v em componentes distintos C e C’, fazer a
união desses em um novo componente.

Conjuntos Disjuntos
•
•
Uma estrutura de dados para conjuntos disjuntos mantém
uma coleção {S1, S2, . . . , Sk} de conjuntos disjuntos dinâmicos
(isto é, eles mudam ao longo do tempo).
Cada conjunto é identificado por um representante que é um
elemento do conjunto.
–
Quem é o representante é irrelevante, mas se o conjunto não for
modificado, então o representante não pode ser alterado.

Conjuntos Disjuntos
•
Uma estrutura de dados para conjuntos disjuntos deve ser
capaz de executar as seguintes operações:
–
–
MAKE-SET(x): cria um novo conjunto contendo somente o elmento {x}.
UNION(x, y): une os conjuntos (disjuntos) que contém x e y, digamos
Sx e Sy, em um novo conjunto Sx ∪ Sy . Os conjuntos Sx e Sy são
descartados da coleção.
–
FIND-SET(x): devolve um apontador para o representante do (único)
conjunto que contém x.

Algoritmo de Kruskal
KRUSKAL(G)
A = ∅;
for each v ∈ G[V]
MAKE-SET(v);
sort G[A] by weight(u, v);
for each (u, v) ∈ G[A]
if FIND-SET(u) ≠ FIND-SET(v)
A ← A ∪ {(u, v)};
UNION(u, v);
return A

Algoritmo de Kruskal – Análise
KRUSKAL(G)
A = ∅;
for each v ∈ G[V]
MAKE-SET(v);
•
•
•
•
Ordenação: O(A log A)
V chamadas a MAKE-SET
2 A chamadas a FIND-SET
V − 1 chamadas a UNION
sort G[A] by weight(u, v);
for each (u, v) ∈ G[A]
if FIND-SET(u) ≠ FIND-SET(v)
A ← A ∪ {(u, v)};
UNION(u, v);
•
A complexidade depende de como
as operações são implementadas.
return A
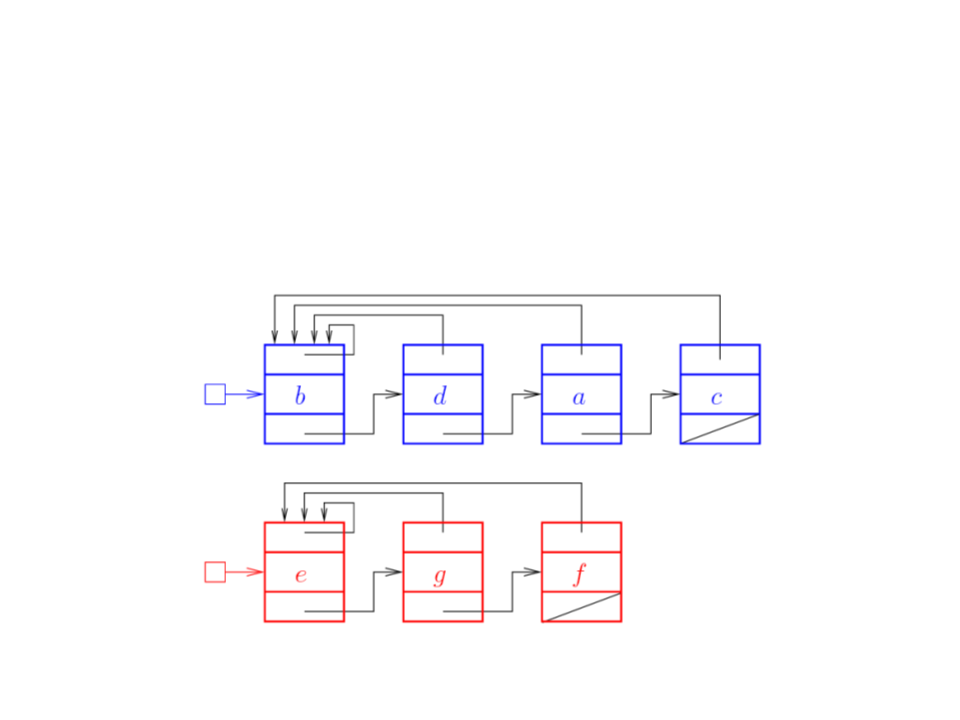
Conjuntos Disjuntos com
Listas Encadeadas
•
•
Cada conjunto tem um representante (início da lista);
Cada nó tem um campo que aponta para o representante;
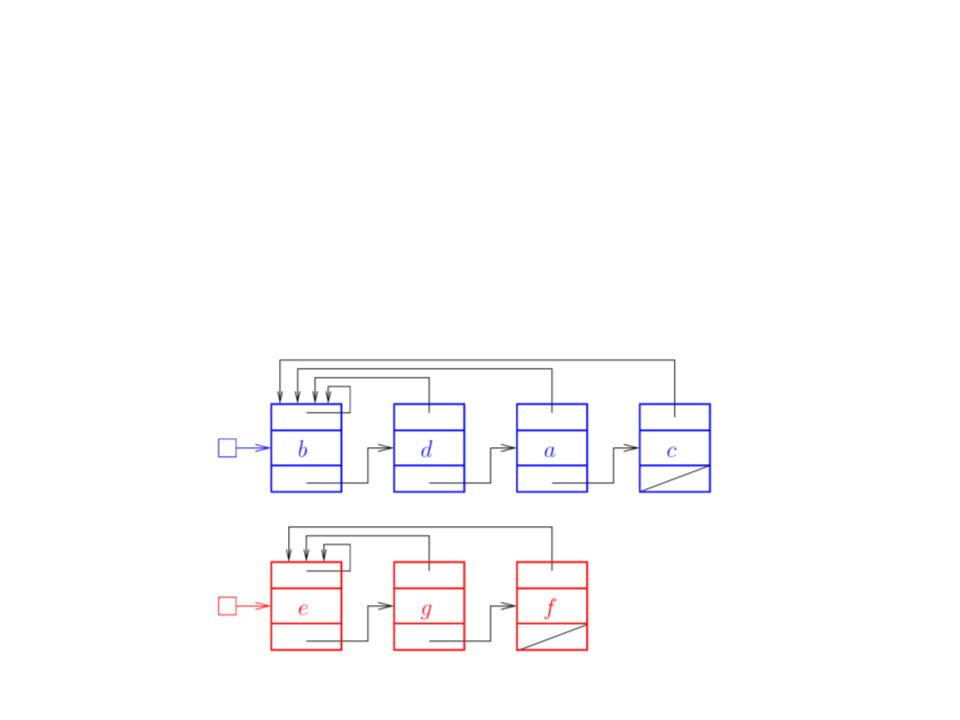
Conjuntos Disjuntos com
Listas Encadeadas
Complexidade:
MAKE-SET(x): O(1)
•
–
–
–
FIND-SET(x): O(1)
UNION(x, y): O(n)
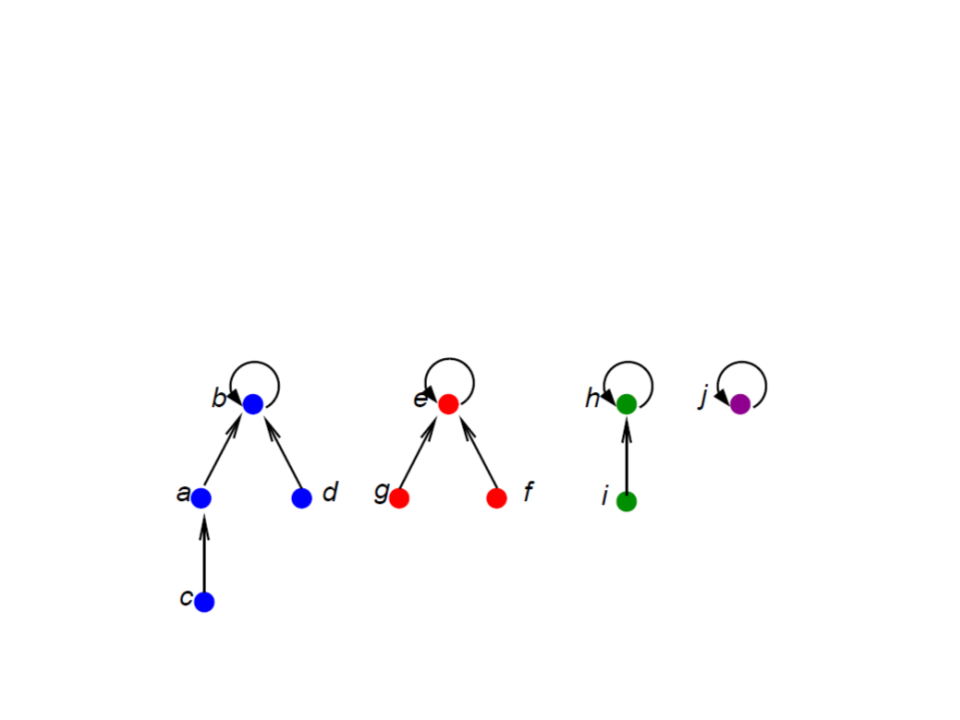
Conjuntos Disjuntos com Florestas
•
•
•
Cada conjunto corresponde a uma árvore;
Cada elemento aponta para seu pai;
A raiz é o representante do conjunto e aponta para si mesma.
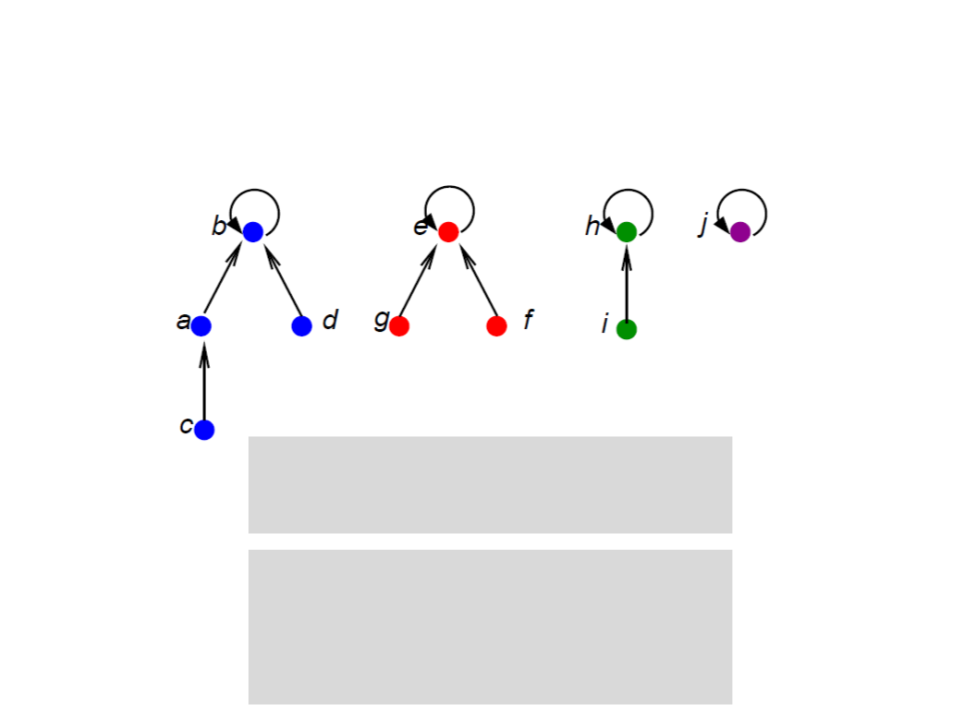
Conjuntos Disjuntos com Florestas
MAKE-SET(x)
pai[x] ← x;
FIND-SET(x)
if x = pai[x]
return x;
else
return FIND-SET(pai[x]);
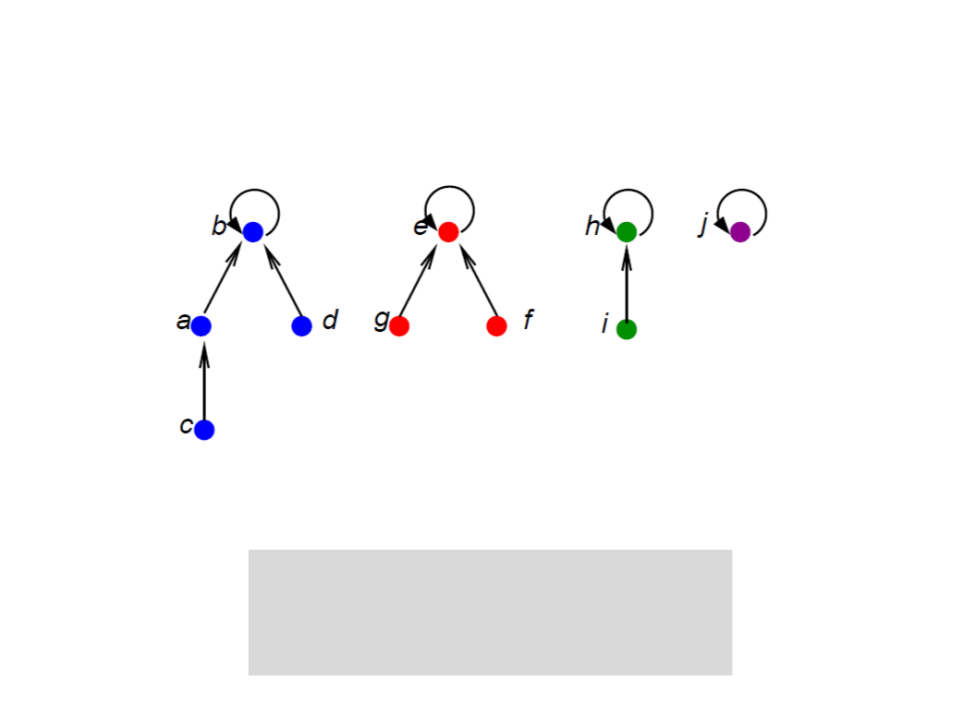
Conjuntos Disjuntos com Florestas
UNION(x, y)
x' ← FIND-SET(x);
y' ← FIND-SET(y);
pai[y'] ← x'
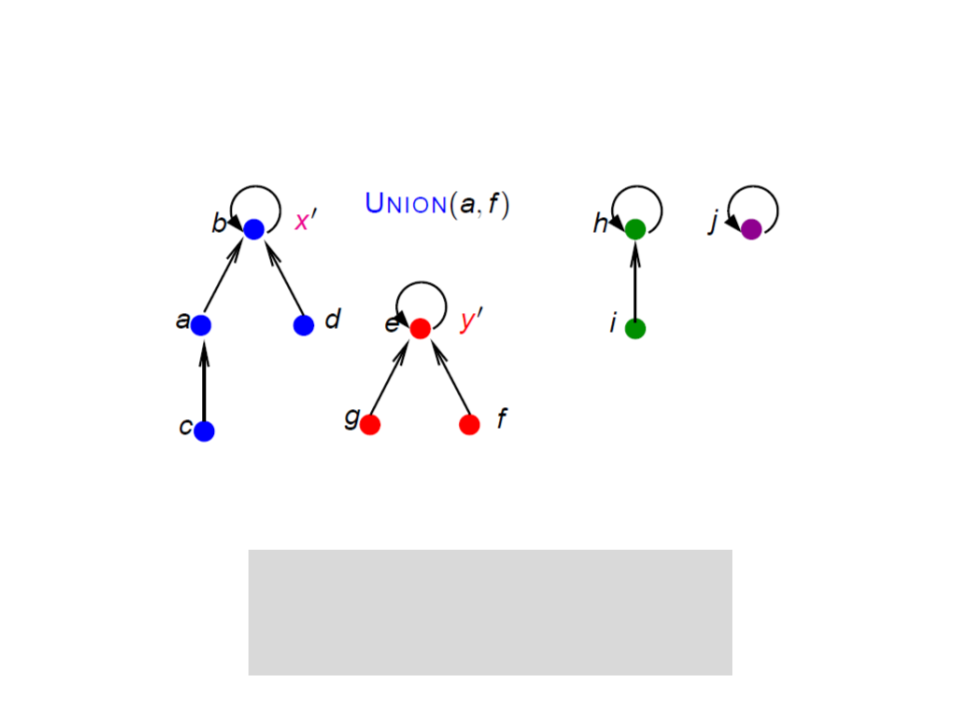
Conjuntos Disjuntos com Florestas
UNION(x, y)
x' ← FIND-SET(x);
y' ← FIND-SET(y);
pai[y'] ← x'
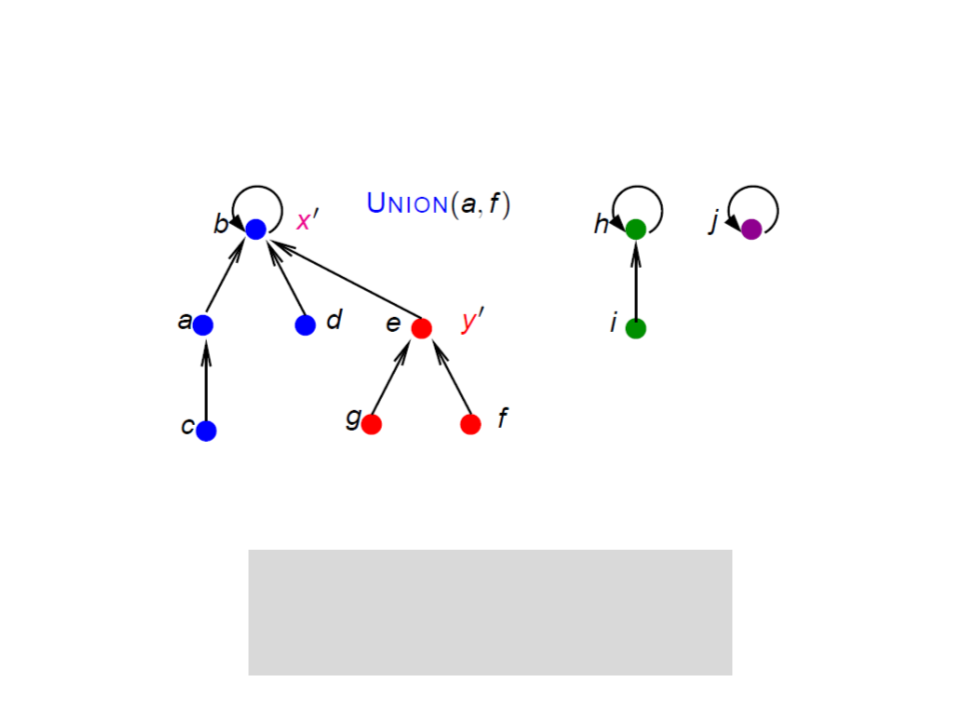
Conjuntos Disjuntos com Florestas
UNION(x, y)
x' ← FIND-SET(x);
y' ← FIND-SET(y);
pai[y'] ← x'

Conjuntos Disjuntos com Florestas
•
•
Complexidade?
–
–
–
MAKESET: (1)
UNION: O(n)
FINDSET: O(n)
Melhorias?
–
Union by rank;
–
Path compression;
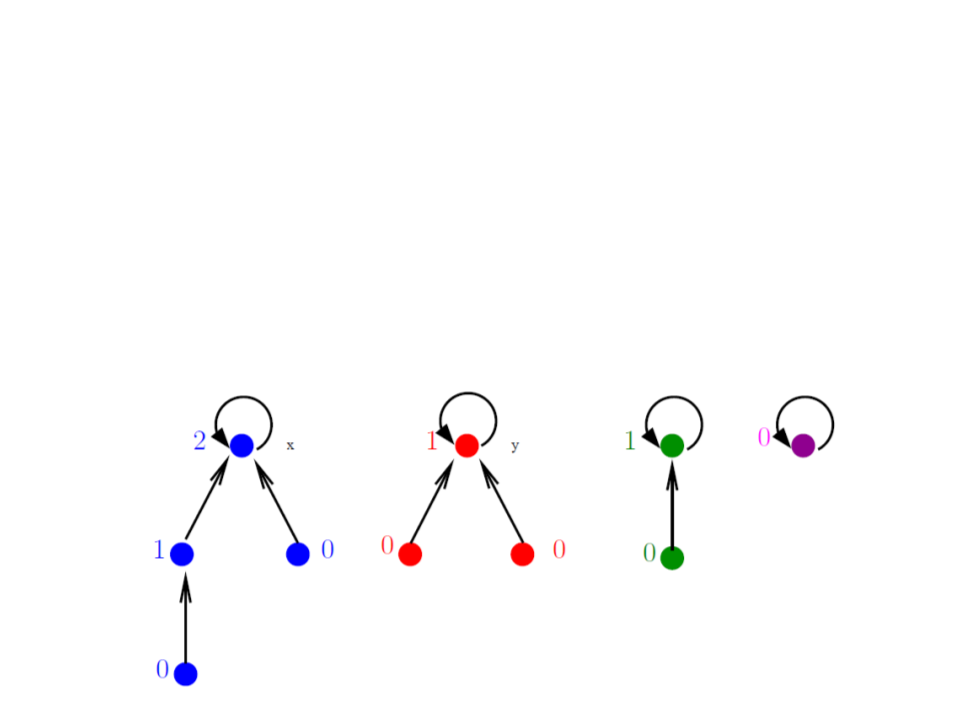
Conjuntos Disjuntos com Florestas
•
Union by rank:
–
Objetivo: sempre unir a menor árvore a raiz da maior;
–
Cada nó x possui um "posto" rank[x] que é um limitante superior para
a altura de x;
–
A raiz com menor rank aponta para a raiz com maior rank;
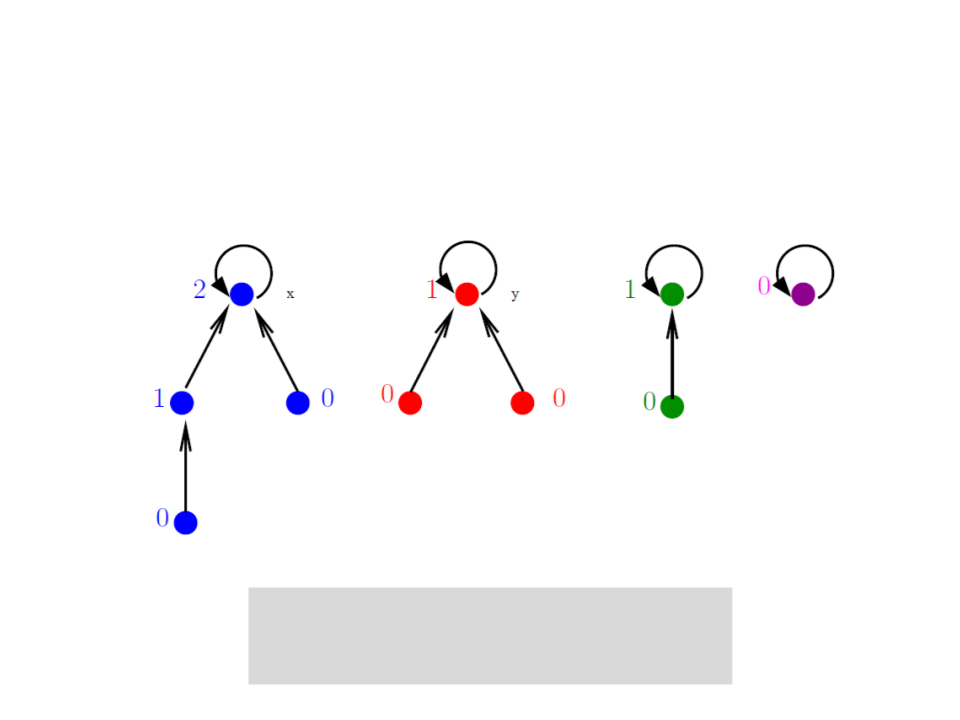
Conjuntos Disjuntos com Florestas
•
Union by rank:
MAKE-SET(x)
pai[x] ← x;
rank[x] ← 0;
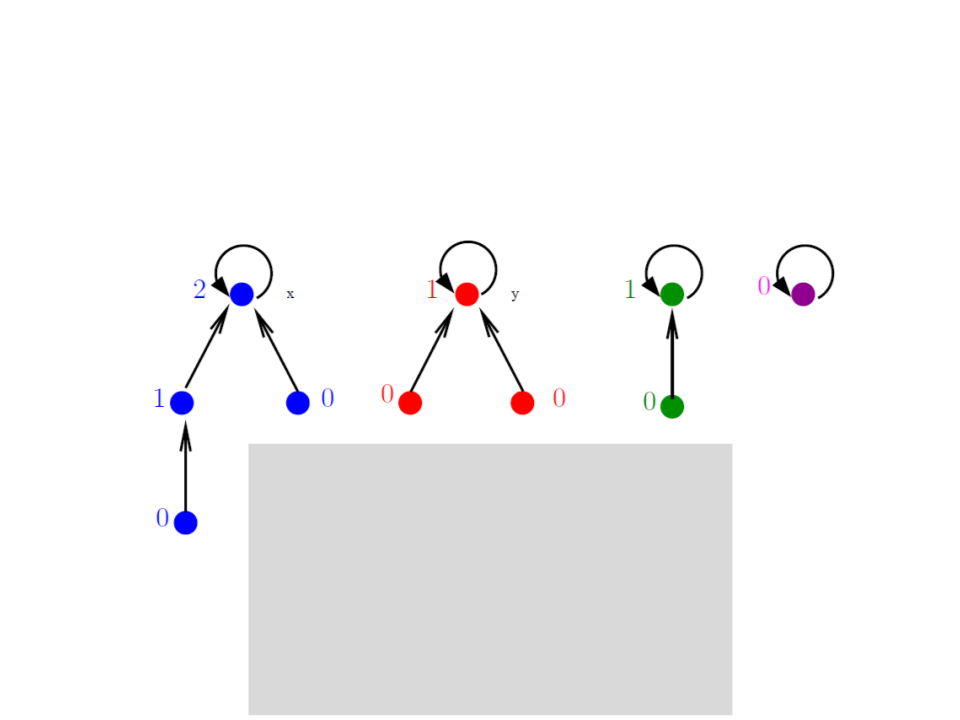
Conjuntos Disjuntos com Florestas
•
Union by rank:
UNION(x, y)
x' ← FIND-SET(x);
y' ← FIND-SET(y);
if rank[x'] < rank[y']
pai[y'] ← x'
else
pai[x'] ← y'
if rank[x'] = rank[y']
rank[y'] ← rank[y'] + 1

Conjuntos Disjuntos com Florestas
•
Complexidade com o union by rank:
–
–
–
MAKESET: (1)
UNION: O(log n)
FINDSET: O(log n)
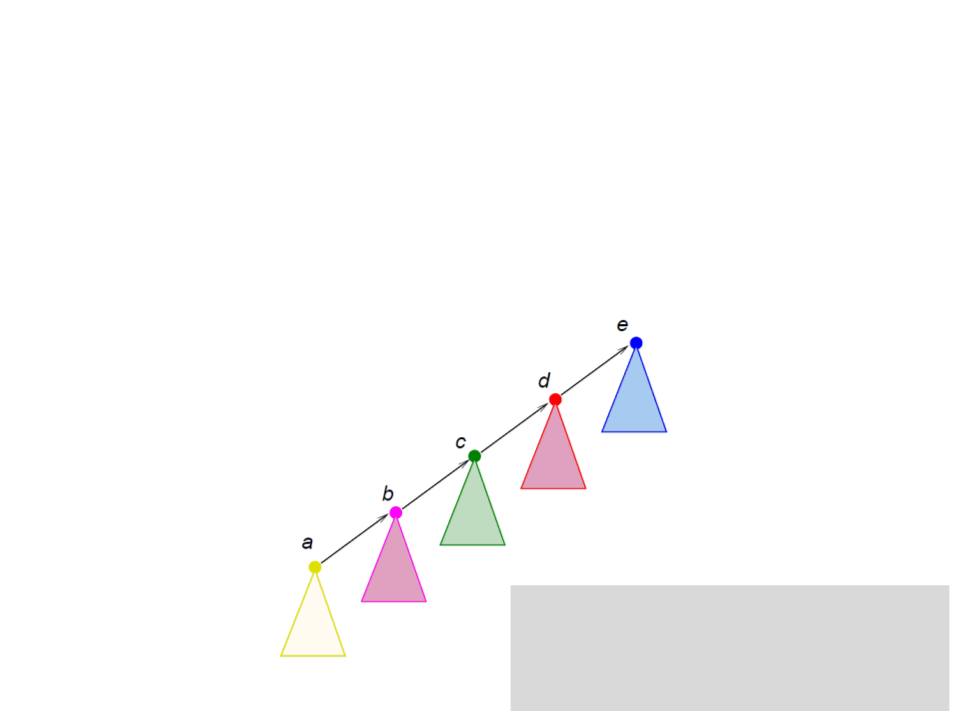
Conjuntos Disjuntos com Florestas
•
Path compression:
–
Ao tentar determinar o representante (raiz da árvore) de um nó
fazemos com que todos os nós no caminho apontem para a raiz.
FIND-SET(x)
if x ≠ pai[x]
pai[x] ← FIND-SET(pai[x])
return pai[x]
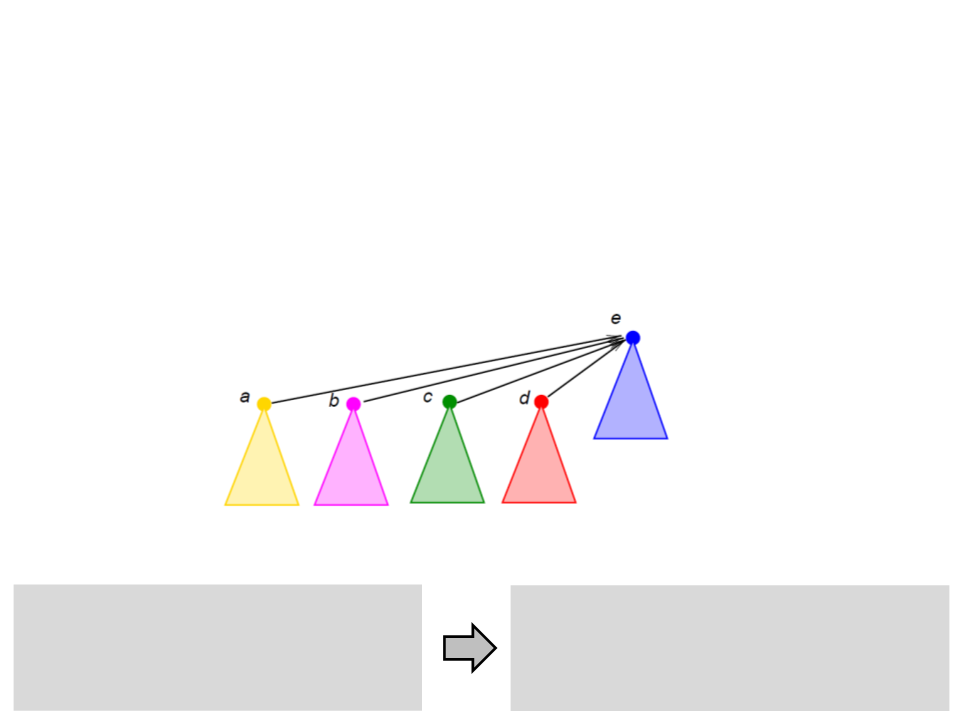
Conjuntos Disjuntos com Florestas
•
Path compression:
–
Ao tentar determinar o representante (raiz da árvore) de um nó
fazemos com que todos os nós no caminho apontem para a raiz.
FIND-SET(x)
FIND-SET(x)
if x = pai[x]
return x;
return FIND-SET(pai[x]);
if x ≠ pai[x]
pai[x] ← FIND-SET(pai[x])
return pai[x]

Conjuntos Disjuntos com Florestas
•
Complexidade com o union by rank e Path compression:
–
–
–
MAKESET: (1)
UNION: O(ꢁ(n))
FINDSET: O(ꢁ(n))
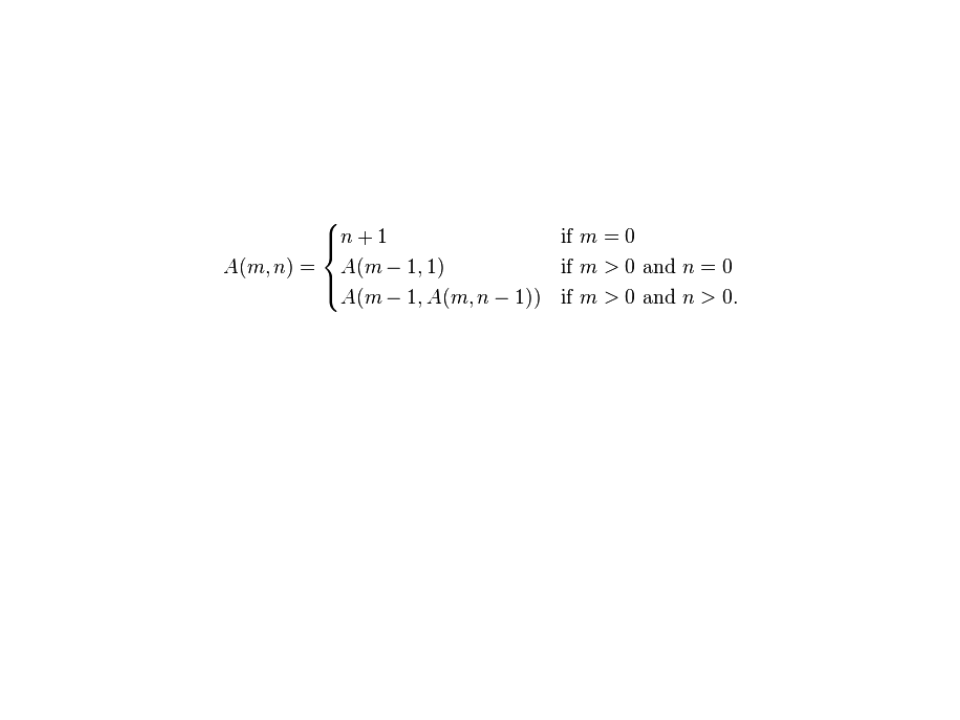
Conjuntos Disjuntos com Florestas
•
•
Função de Ackermann:
A complexidade cresce muito rapidamente:
–
–
–
–
–
A(1, 0) = 2
A(1, 1) = 3
A(2, 2) = 7
A(3, 2) = 29
A(4, 2) = 265536 − 3 (mais que o número estimado de atomos do universo!)
•
ꢁ(n) → Inverso da função de Ackermann → (ꢁ(n) ≤ 4)

De Volta ao Algoritmo de Kruskal
KRUSKAL(G)
• Ordenação: O(A log A)
A = ∅;
for each v ∈ G[V]
MAKE-SET(v);
•
•
Chamadas a MAKE-SET: O(V)
Chamadas a FIND-SET e
UNION: O(A)
sort G[E] by weight(u, v);
for each (u, v) ∈ G[E]
if FIND-SET(u) ≠ FIND-SET(v)
A ← A ∪ {(u, v)};
•
Complexidade:
O(A log A)
UNION(u, v);
return A

Exercícios
Lista de Exercícios 09 – Árvore Geradora
Mínima
http://www.inf.puc-rio.br/~elima/paa/
