
Projeto e Análise de Algoritmos
Aula 08 – Componentes Fortemente
Conectados
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Componentes Fortemente Conectados
•
Um componente fortemente conectado (Strongly Connected
Component - SCC) de um grafo orientado G= (V, A) é um conjunto
máximo de vértices C ⊆ V, tal que, para todo par de vértice u e v:
–
u ⇝ v
–
v ⇝ u
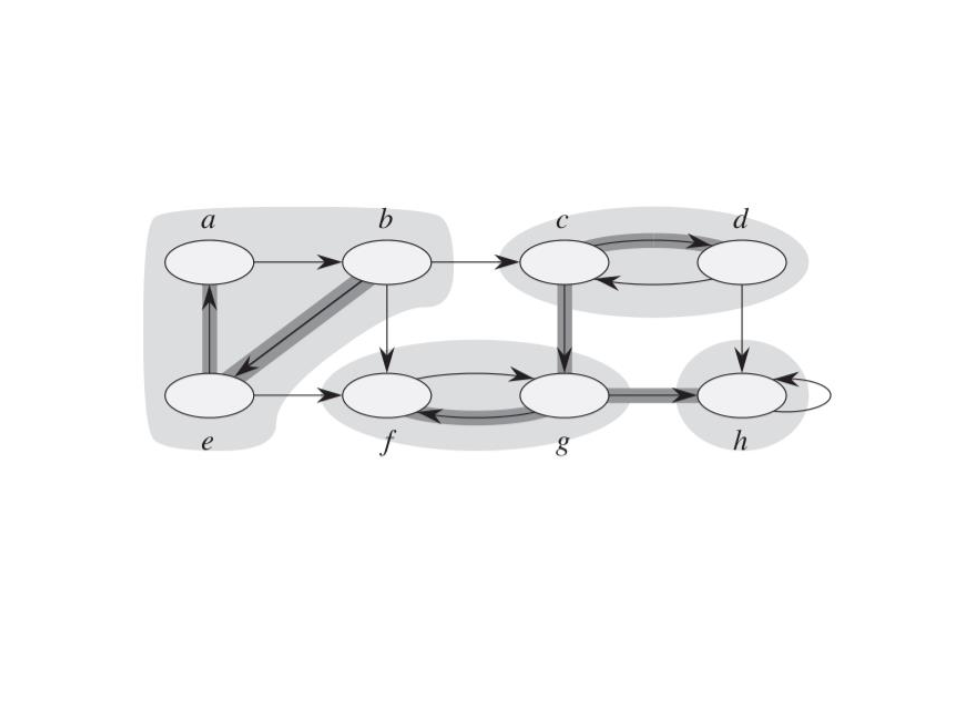
Componentes Fortemente Conectados
•
Algoritmos:
–
Algoritmo de Kosaraju;
–
Algoritmo de Tarjan;

Algoritmo de Kosaraju
1. Chama BuscaEmProfundidade(G) para obter os tempos de
término t[u] para cada vértice u.
2
. Obtem GT (G transposto).
3
. Chama BuscaEmProfundidade(GT), realizando a busca a partir
do vértice de maior t[u] obtido pela BuscaEmProfundidade(G).
4
em profundidade em G a partir do vértice de maior t[u]
dentre os vértices restantes.
. Enquanto houver vértices restantes, inicie uma nova busca
T
5. Retorne os vértices de cada árvore da floresta obtida como
um componente fortemente conectado separado.
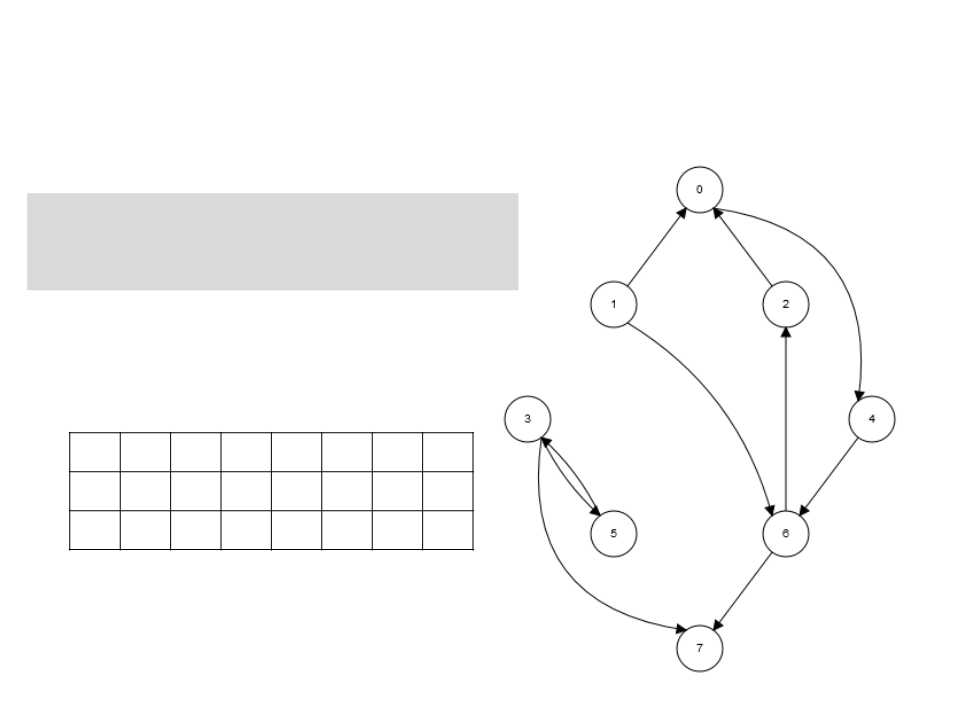
Algoritmo de Kosaraju
1. Chama BuscaEmProfundidade(G)
para obter os tempos de término
t[u] para cada vértice u.
0
1 2 3 4 5 6 7
c
d
f
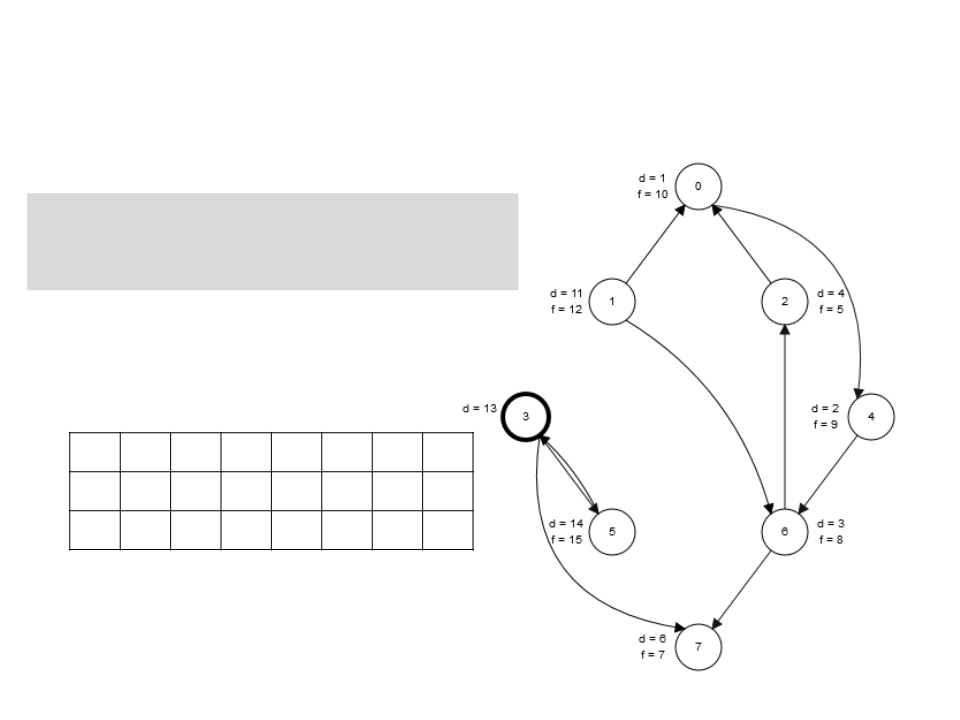
Algoritmo de Kosaraju
1. Chama BuscaEmProfundidade(G)
para obter os tempos de término
t[u] para cada vértice u.
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 11 4 13 2 14 3 6
f 10 12 5 16 9 15 8 7
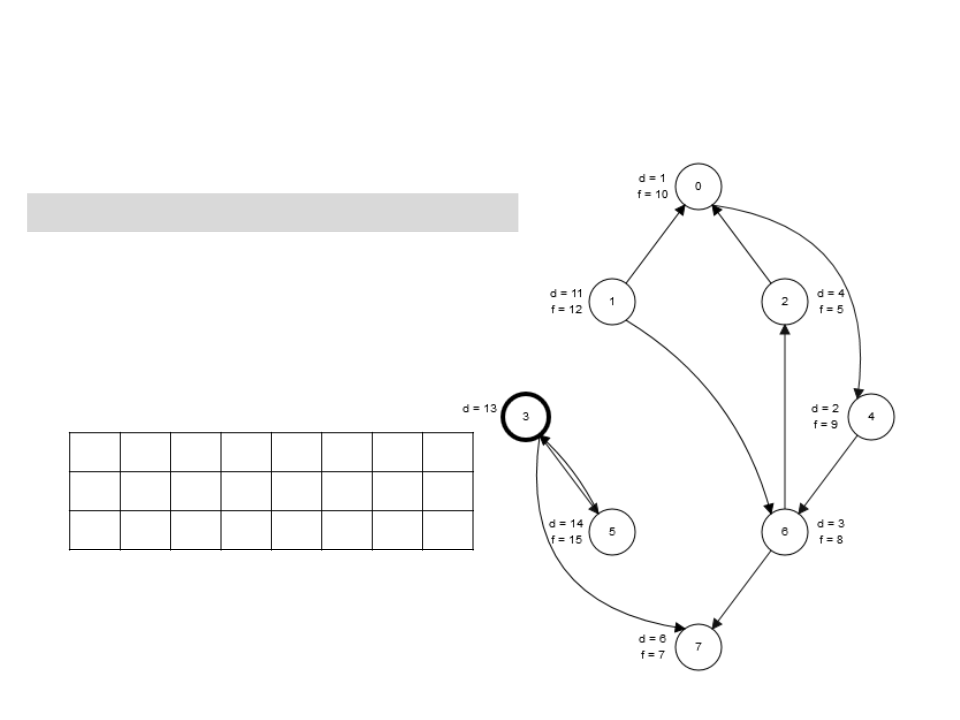
Algoritmo de Kosaraju
2
. Obtem GT (G transposto).
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 11 4 13 2 14 3 6
f 10 12 5 16 9 15 8 7
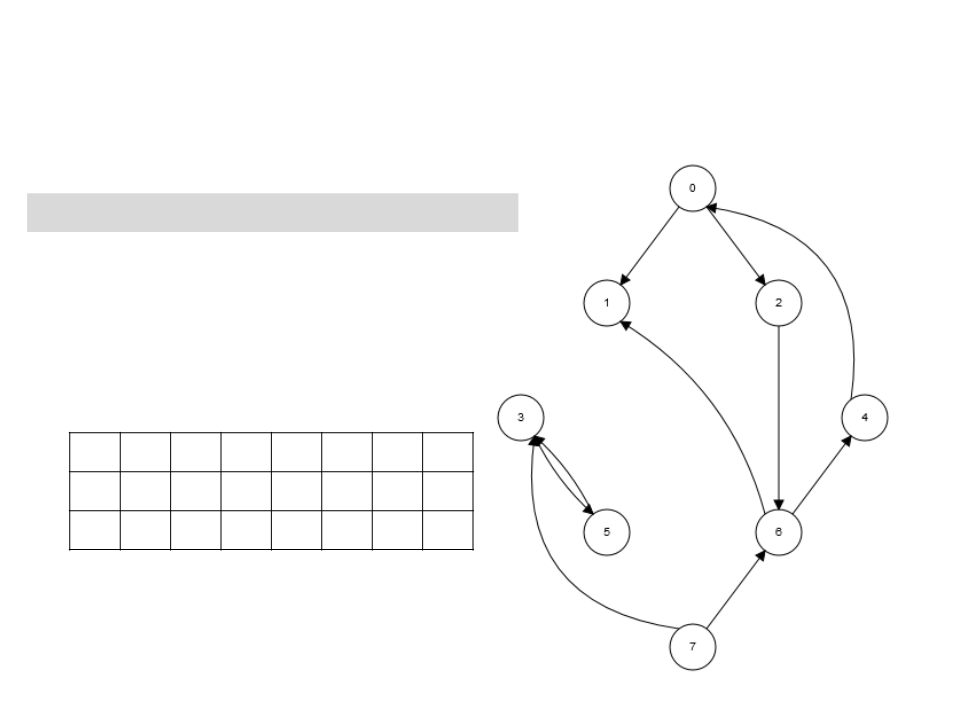
Algoritmo de Kosaraju
2
. Obtem GT (G transposto).
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 11 4 13 2 14 3 6
f 10 12 5 16 9 15 8 7
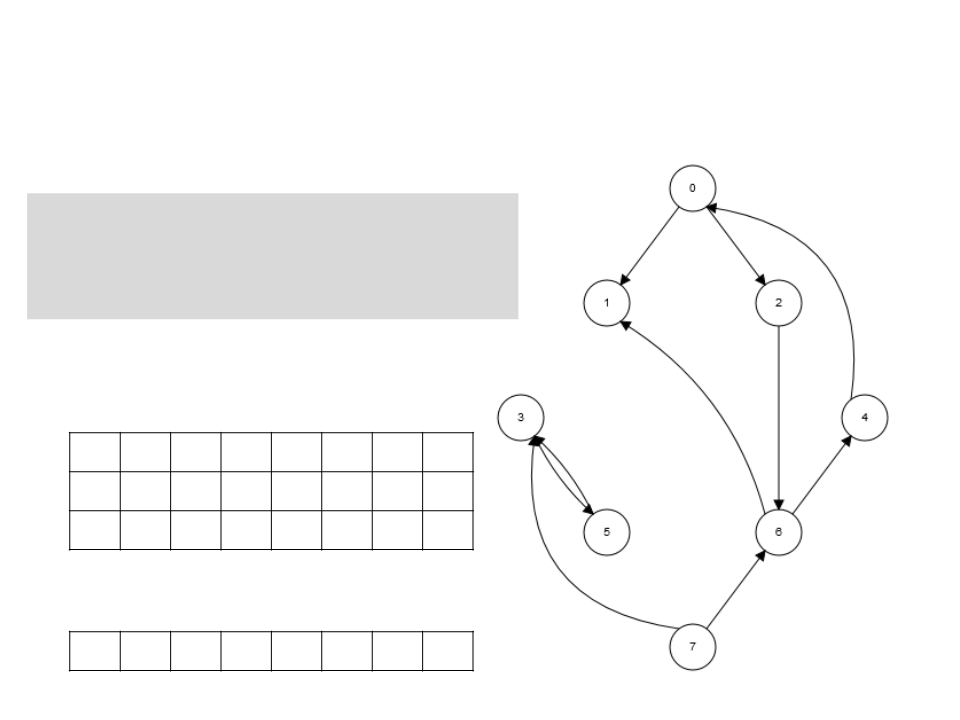
Algoritmo de Kosaraju
3
. Chama BuscaEmProfundidade(GT),
realizando a busca a partir do
vértice de maior t[u] obtido
pela BuscaEmProfundidade(G).
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 11 4 13 2 14 3 6
f 10 12 5 16 9 15 8 7
f
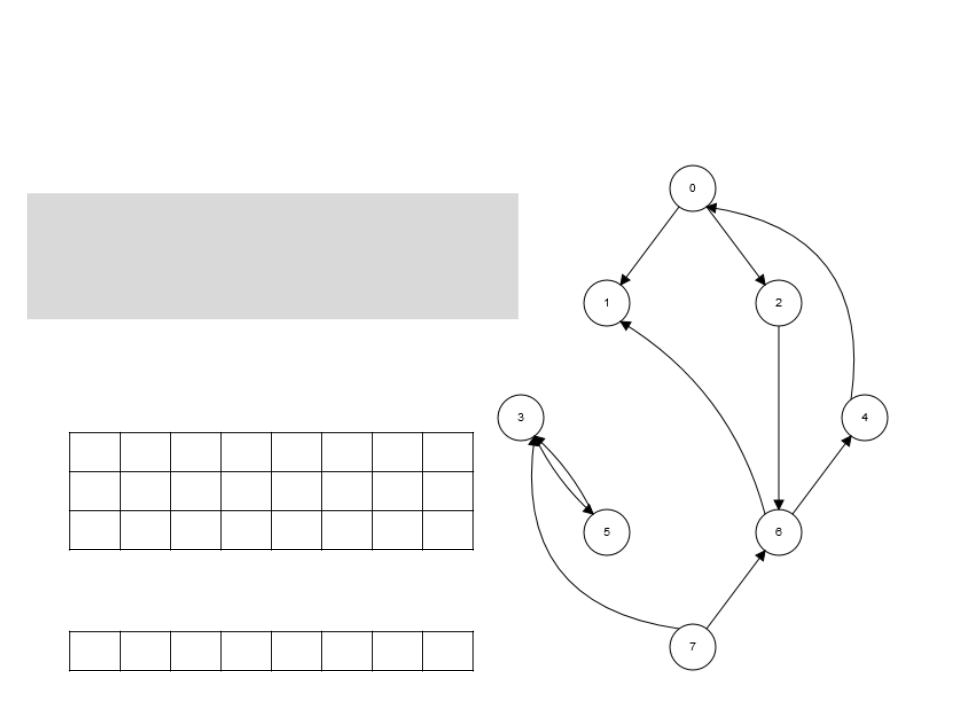
Algoritmo de Kosaraju
3
. Chama BuscaEmProfundidade(GT),
realizando a busca a partir do
vértice de maior t[u] obtido
pela BuscaEmProfundidade(G).
0
1 2 3 4 5 6 7
c b b b b b b b b
d 1 11 4 13 2 14 3 6
f 10 12 5 16 9 15 8 7
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5
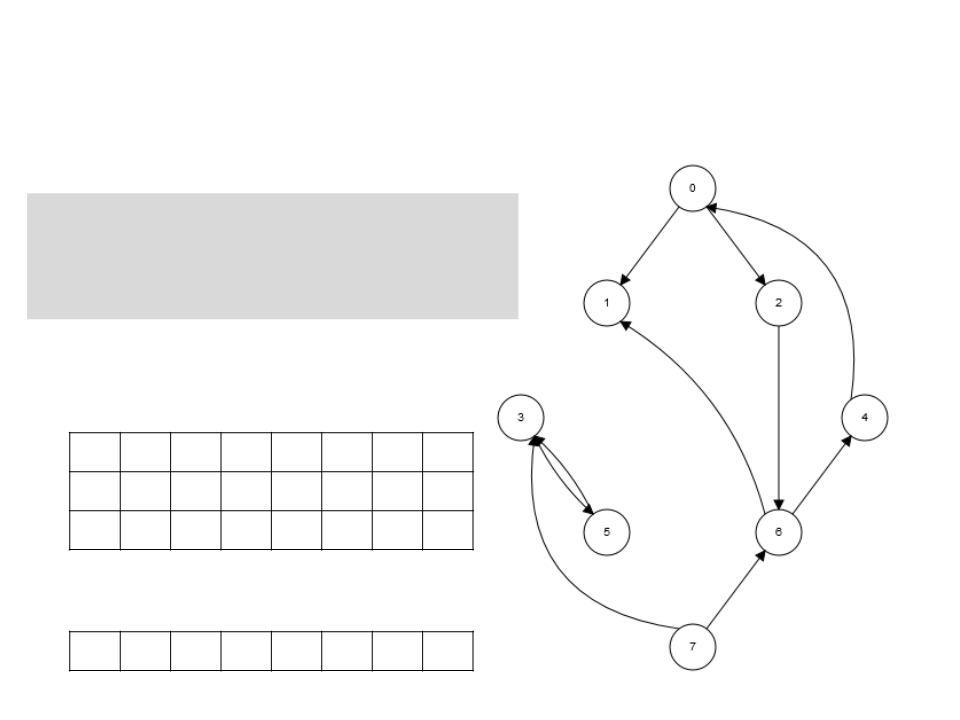
Algoritmo de Kosaraju
3
. Chama BuscaEmProfundidade(GT),
realizando a busca a partir do
vértice de maior t[u] obtido
pela BuscaEmProfundidade(G).
0
1 2 3 4 5 6 7
c
d
f
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5
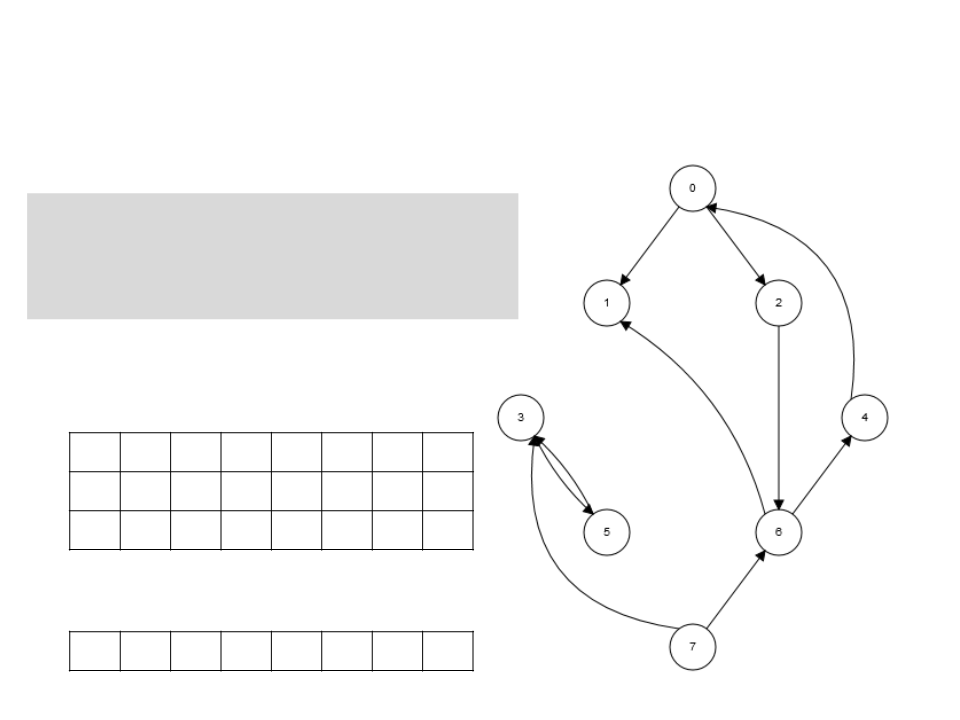
Algoritmo de Kosaraju
3
. Chama BuscaEmProfundidade(GT),
realizando a busca a partir do
vértice de maior t[u] obtido
pela BuscaEmProfundidade(G).
0
1 2 3 4 5 6 7
c
d
f
b
1
4
b
2
3
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5
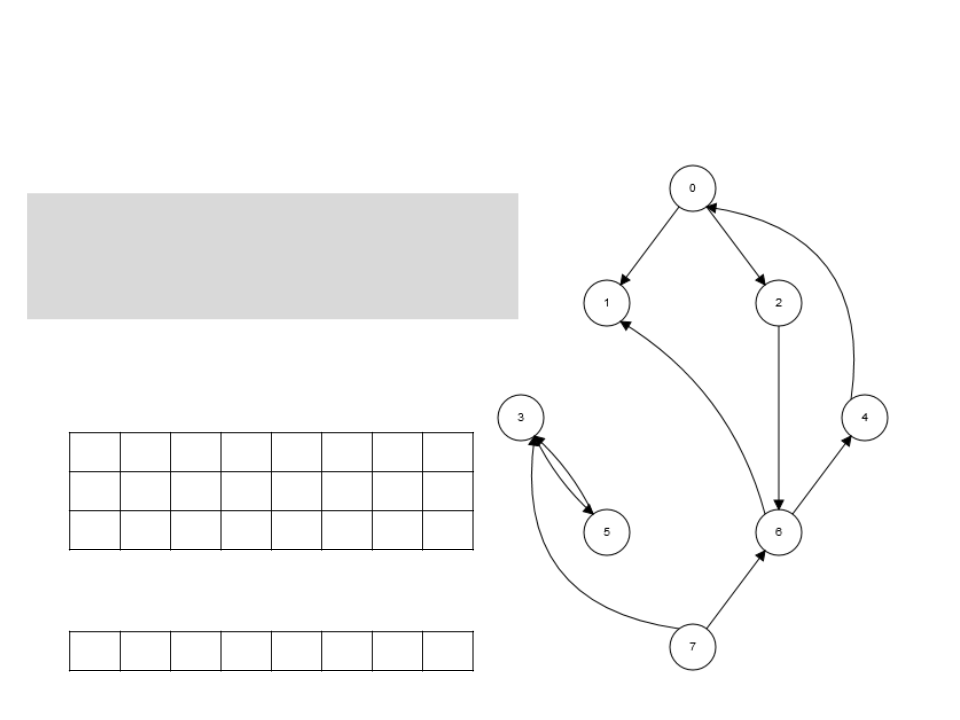
Algoritmo de Kosaraju
5. Retorne os vértices de cada
árvore da floresta obtida como
um componente fortemente
conectado separado.
0
1 2 3 4 5 6 7
c
d
f
b
1
4
b
2
3
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5
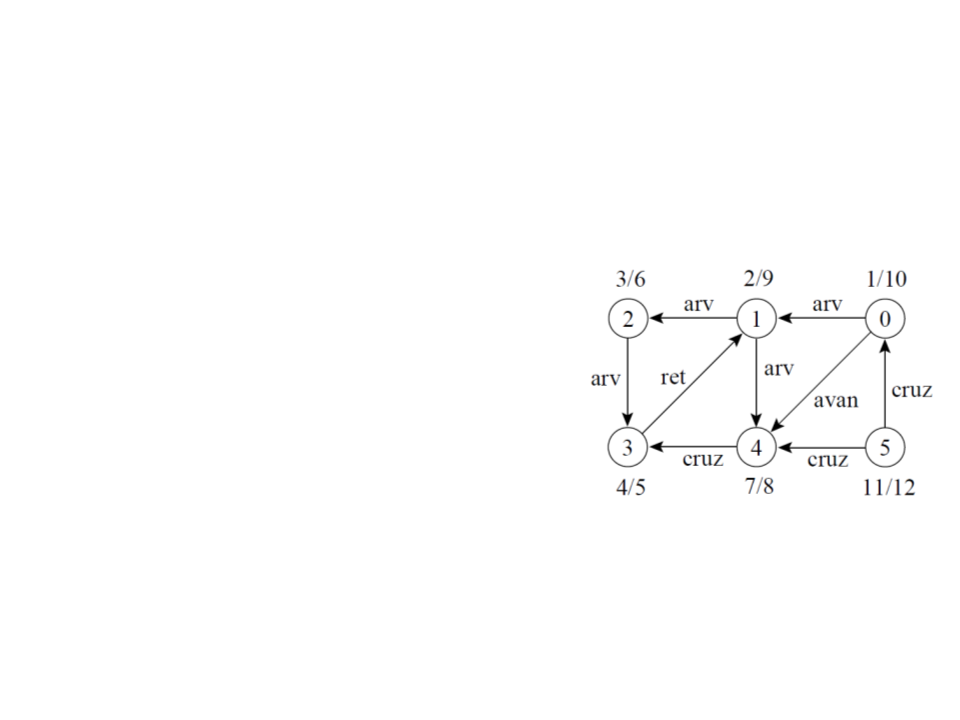
Classificação de Arestas
•
•
Classificação de arestas pode ser útil
para derivar outros algoritmos.
Na busca em profundidade cada
aresta pode ser classificada pela cor
do vértice que é alcançado pela
primeira vez:
–
–
–
Branco indica uma aresta de árvore.
Cinza indica uma aresta de retorno.
Preto indica uma aresta de avanço
quando u é descoberto antes de v ou uma
aresta de cruzamento caso contrário.
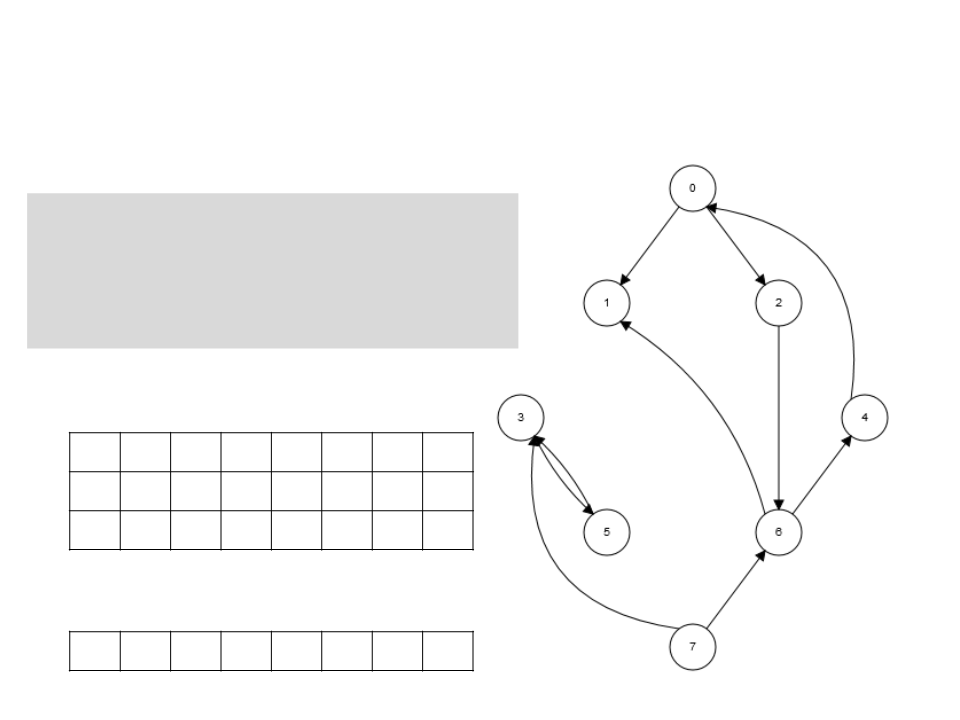
Algoritmo de Kosaraju
4. Enquanto houver vértices
restantes, inicie uma nova busca
T
em profundidade em G a partir do
vértice de maior t[u] dentre os
vértices restantes.
0
1 2 3 4 5 6 7
c
d
f
b
1
4
b
2
3
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5
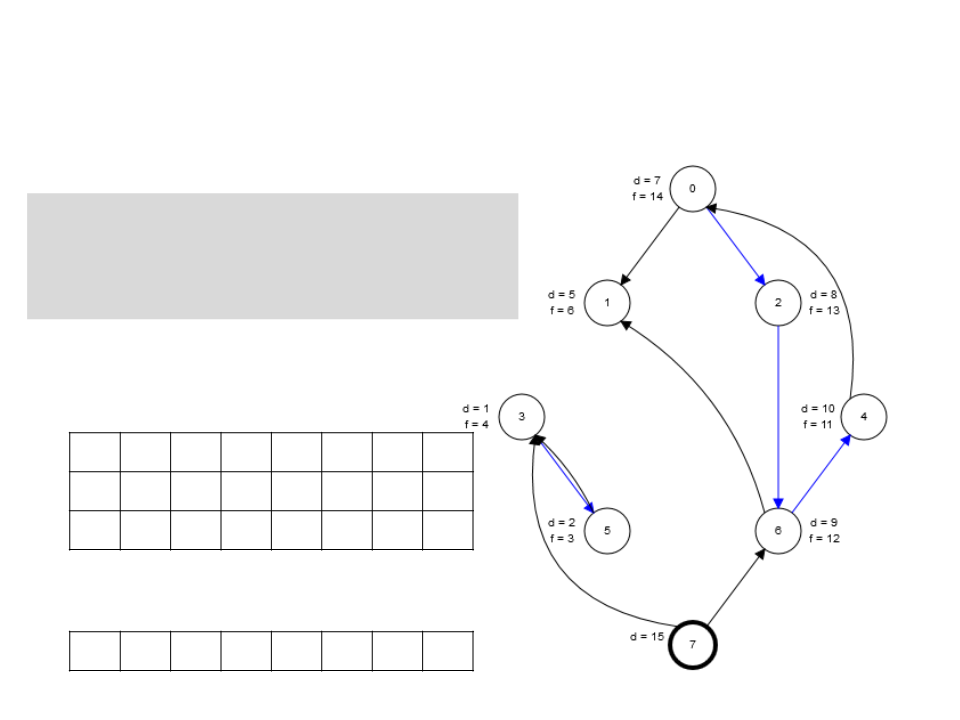
Algoritmo de Kosaraju
5. Retorne os vértices de cada
árvore da floresta obtida como
um componente fortemente
conectado separado.
0
1 2 3 4 5 6 7
c b b b b b b b b
d 7 5 8 1 10 2 9 15
f 14 6 13 4 11 3 12 16
3
5 1 0 4 6 7 2
f 16 15 12 10 9 8 7 5

Algoritmo de Kosaraju – Análise
1. Chama BuscaEmProfundidade(G) para obter os
tempos de término t[u] para cada vértice u.
2
. Obtem GT (G transposto).
3
. Chama BuscaEmProfundidade(GT), realizando
a busca a partir do vértice de maior t[u]
obtido pela BuscaEmProfundidade(G).
O(V + A)
4
. Enquanto houver vértices restantes, inicie
T
uma nova busca em profundidade em G a partir
do vértice de maior t[u] dentre os vértices
restantes.
5. Retorne os vértices de cada árvore da
floresta obtida como um componente fortemente
conectado separado.

Algoritmo de Tarjan
1. Chamar BuscaEmProfundidade(G).
2
. Ao visitar um vértice v, coloca-lo em uma pilha S;
. Calcular e guardar os valores de d[v] e low[v];
d[v]: Número de vértices visitados quando v é descoberto;
3
low[v]: O menor valor de d[] ou low[] atingível por uma
aresta de retorno na árvore de v;
4
. Se ao concluir a exploração de um vértice v d[v] = low[v],
então v é "raíz" de um componente fortemente conectado.
Nesse caso retirar tudo o que está na pilha S até v e
reportar esses elementos como um componente fortemente
conectado;
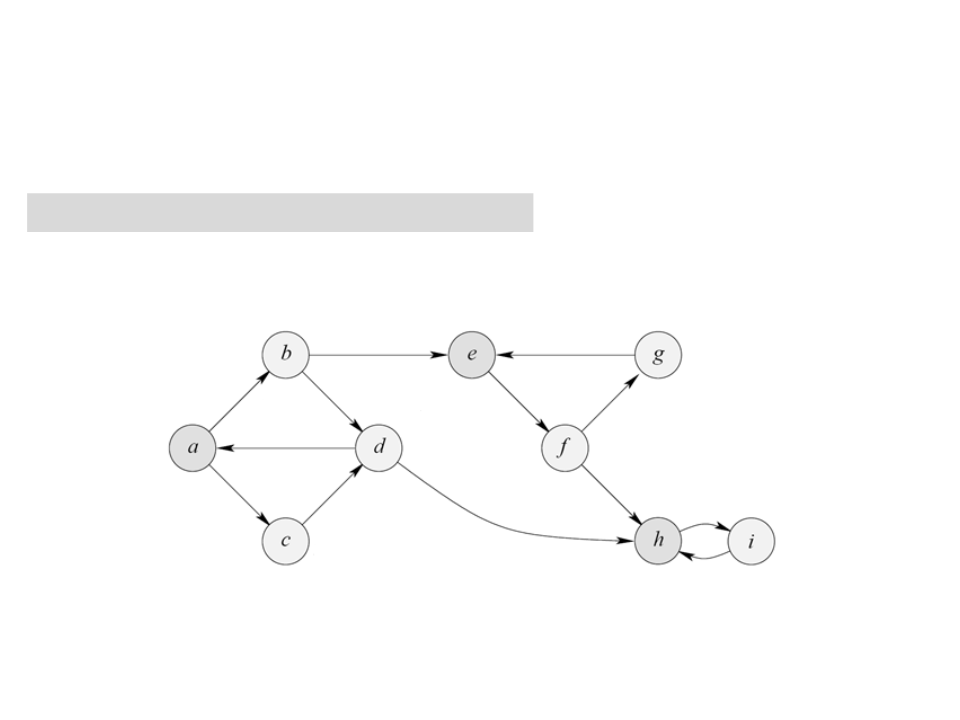
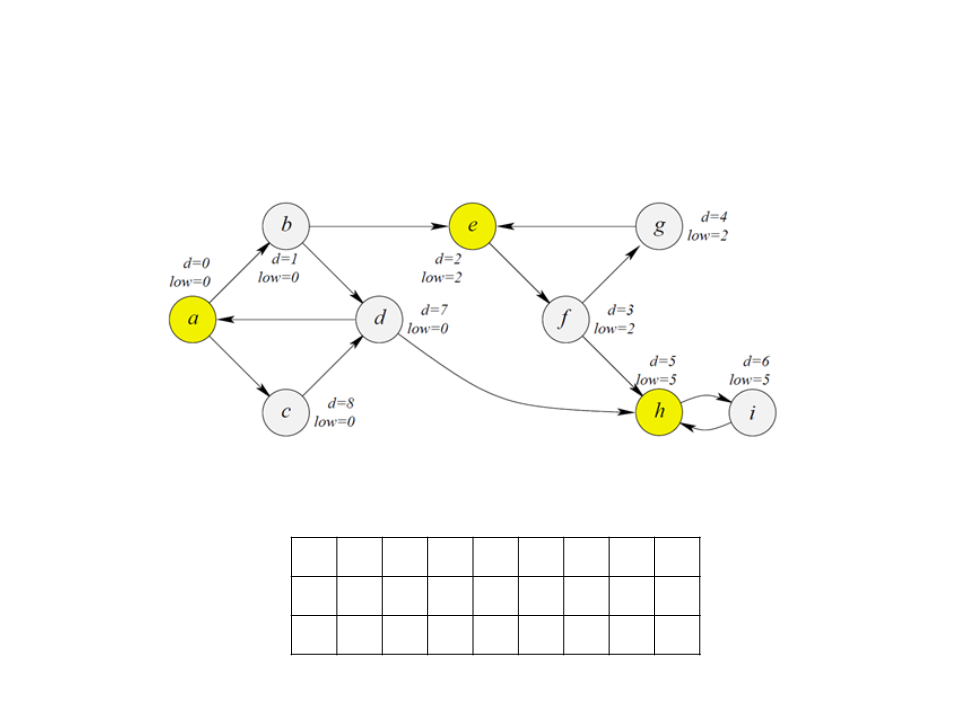
Algoritmo de Tarjan
1. Chamar BuscaEmProfundidade(G).
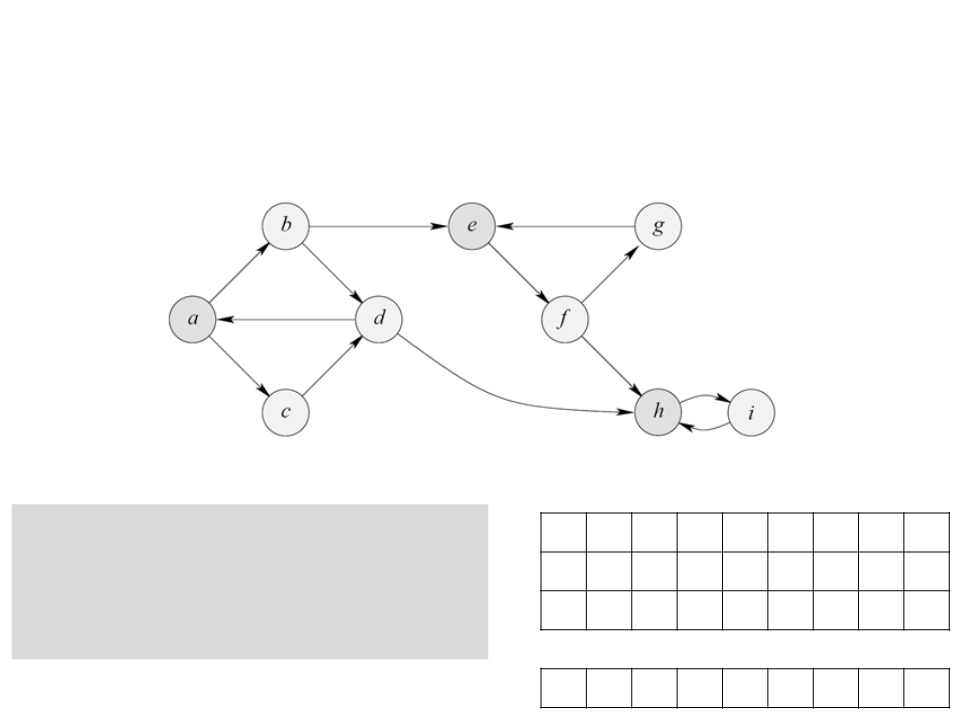
Algoritmo de Tarjan
a b c d e f g h i
2
coloca-lo em uma pilha S;
. Ao visitar um vértice v,
c
d
3. Calcular e guardar os
low
valores de d[v] e low[v];
S
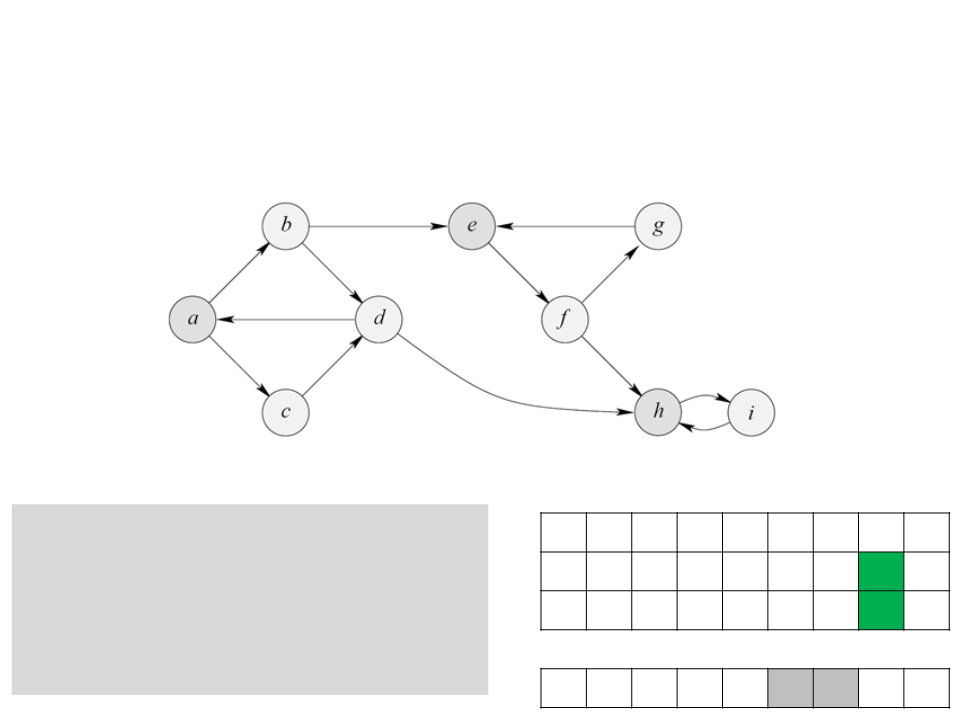
Algoritmo de Tarjan
a b c d e f g h i
c g g w w g g b b b
4
. Se ao concluir a exploração de
um vértice v d[v] = low[v], então v
é raíz de um componente fortemente
conectado. Nesse caso retirar tudo
o que está na pilha S até v e
d 0 1
low
2 3 4 5 6
2 5 5
reportar esses elementos como um
componente fortemente conectado;
S a b e f g h i
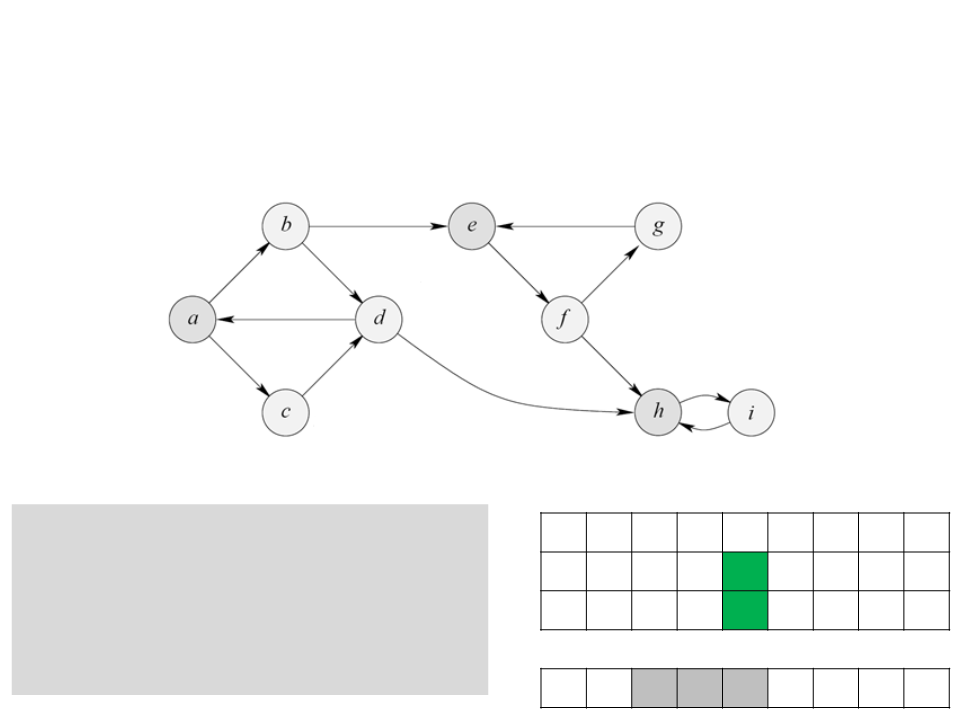
Algoritmo de Tarjan
a b c d e f g h i
c g g w w b b b b b
4
. Se ao concluir a exploração de
um vértice v d[v] = low[v], então v
é raíz de um componente fortemente
conectado. Nesse caso retirar tudo
o que está na pilha S até v e
d 0 1
low
2 3 4 5 6
2 2 2 5 5
reportar esses elementos como um
componente fortemente conectado;
S a b e f g
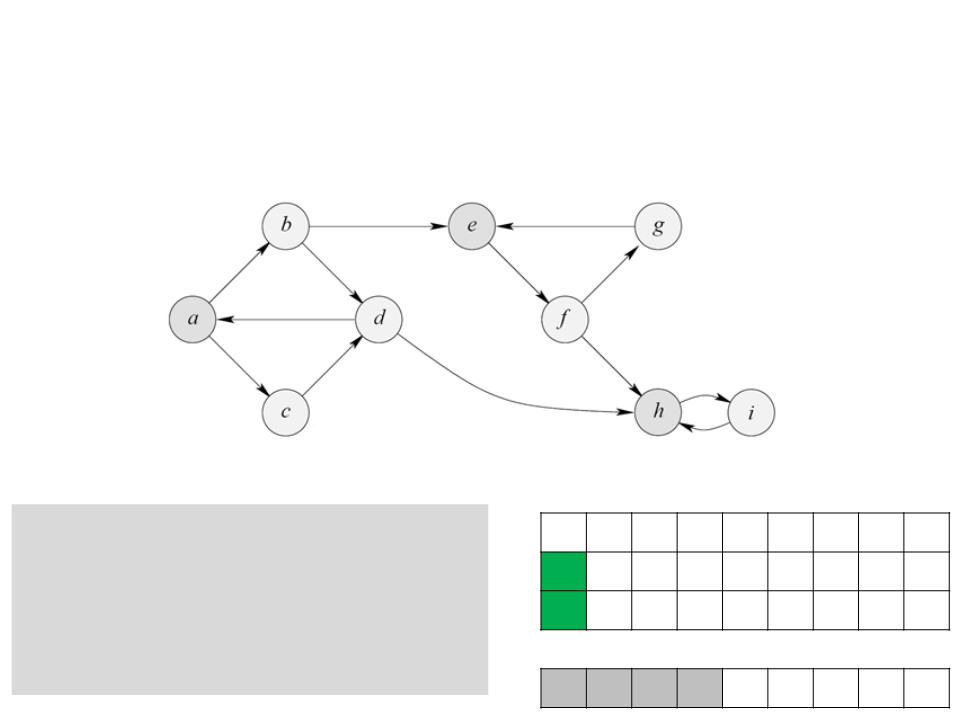
Algoritmo de Tarjan
a b c d e f g h i
4
. Se ao concluir a exploração de
c b b b b b b b b b
d 0 1 8 7 2 3 4 5 6
low 0 0 0 0 2 2 2 5 5
um vértice v d[v] = low[v], então v
é raíz de um componente fortemente
conectado. Nesse caso retirar tudo
o que está na pilha S até v e
reportar esses elementos como um
componente fortemente conectado;
S a b d c
Algoritmo de Tarjan
a b c d e f g h i
c b b b b b b b b b
d 0 1 8 7 2 3 4 5 6
low 0 0 0 0 2 2 2 5 5

Algoritmo de Tarjan – Análise
1. Chamar BuscaEmProfundidade(G).
2
3
4
. Ao visitar um vértice v, coloca-lo em
uma pilha S;
. Calcular e guardar os valores de d[v]
e low[v];
O(V + A)
. Se ao concluir a exploração de um
vértice v d[v] = low[v], então v é
"
raíz" de um componente fortemente
conectado. Nesse caso retirar tudo o
que está na pilha S até v e reportar
esses elementos como um componente
fortemente conectado;

Aplicações
•
Encontrar grupos de pessoas relacionadas em redes sociais;
–
Sistemas de recomendação;
•
•
Resolver problemas de 2-satisfiability (2-SAT);
Algoritmo de model checking;

Exercícios
Lista de Exercícios 08 – Componentes
Fortemente Conectados
http://www.inf.puc-rio.br/~elima/paa/
