
Projeto e Análise de Algoritmos
Aula 04 – Maior Subsequência Comum (LCS)
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Problema
•
•
Subsequência: sequência de caracteres não
necessariamente contíguos, retirados de uma cadeia
em ordem.
–
Exemplo: AAAG é subsequência da cadeia CGATAATTGAGA
Problema: Dadas duas sequências X = {x1, x2, . . . , xm}
e Y = {y1, y2, . . . , yn}, encontrar uma subsequência de
maior tamanho (LCS(X, Y))

Problema
•
•
Problema: Dadas duas sequências X = {x1, x2, . . . , xm}
e Y = {y1, y2, . . . , yn}, encontrar uma subsequência de
maior tamanho (LCS(X, Y))
Exemplo:
–
X = {A, B, C, B, D, A, B}
–
Y = {B, D, C, A, B, A}
–
LCS(X, Y) = {B, C, B, A} ou {B, D, A, B}

Problema
•
Exemplo de Aplicação: análise do DNA de dois ou
mais organismos distintos.
–
Um DNA é composto por uma sequência de moléculas,
chamadas de bases:
•
Adenina (A); Timina (T); Citosina (C); Guanina (G).
–
–
Exemplo: ACGGGTAGTCGCAA
Computacionalmente, um DNA pode ser visto como um
vetor de caracteres, com o alfabeto {A, T, G, C}

Problema
•
•
Dado os DNAs de dois organismos:
–
S1 = ACCGTGGAAAAGGTTAAGGCCAGGATTTAACCGCGGGC
–
S2 = ACCGCGGTTTAATCCGGATAGGTTGAAATGGTTGAAAC
É possível questionar:
–
–
–
Quão semelhantes são estes dois organismos?
Estes organismos são da mesma espécie?
Um destes organismos é ancestral do outro organismo?
•
As respostas vão depender de semelhanças.

Como Resolver?
•
•
Problema: Dadas duas sequências X = {x1, x2, . . . , xm}
e Y = {y1, y2, . . . , yn}, encontrar uma subsequência de
maior tamanho (LCS(X, Y))
Exemplo:
–
X = {A, B, C, B, D, A, B}
–
Y = {B, D, C, A, B, A}
–
LCS(X, Y) = {B, C, B, A} ou {B, D, A, B}

LCS – Força Bruta
•
•
Algoritmo: Enumera-se todas as possíveis
subsequências de X. Checa-se se cada uma destas
subsequências também é subsequências de Y,
guardando a de maior comprimento.
Complexidade?
m
–
–
–
Existem 2 subsequências diferentes de X;
Tempo linear para verificar se a subsequência de X está em Y;
O(2m n) = O(2m) → INEFICIENTE!

LCS – Força Bruta
•
Outras soluções?

LCS – Programação Dinâmica
•
•
Solução: Programação Dinâmica!
Idéia: quebrar o problema em subproblemas, com
estrutura semelhante ao problema geral. Armazena-
se a solução para cada um desses subproblemas para
utiliza-las para a solução geral.

LCS – Programação Dinâmica
•
•
Dada uma sequência X = {x1, x2, . . . , xm}, define-se o
i-ésimo prefixo de X, para i = 0, 1, 2, . . . , m como Xi =
{
x1, x2, . . . , xi}
Por exemplo, dada a sequência X = {A, B, C, B,D, A, B}
–
–
–
X0 = {}
X3 = {A, B, C}
X4 = {A, B, C, B}

LCS – Programação Dinâmica
•
Uma LCS(X, Y) pode ser obtida recurivamente da
seguinte forma:
–
–
Se xm = yn deve-se procurar uma LCS(Xm−1, Yn−1) e depois
acrescentar xm ou yn.
Se xm ≠ yn, então deve-se resolver 2 subproblemas:
•
•
•
Encontrar uma LCS(Xm−1, Yn);
Encontrar uma LCS(Xm, Yn−1);
Sendo a LCS mais longa destas duas.
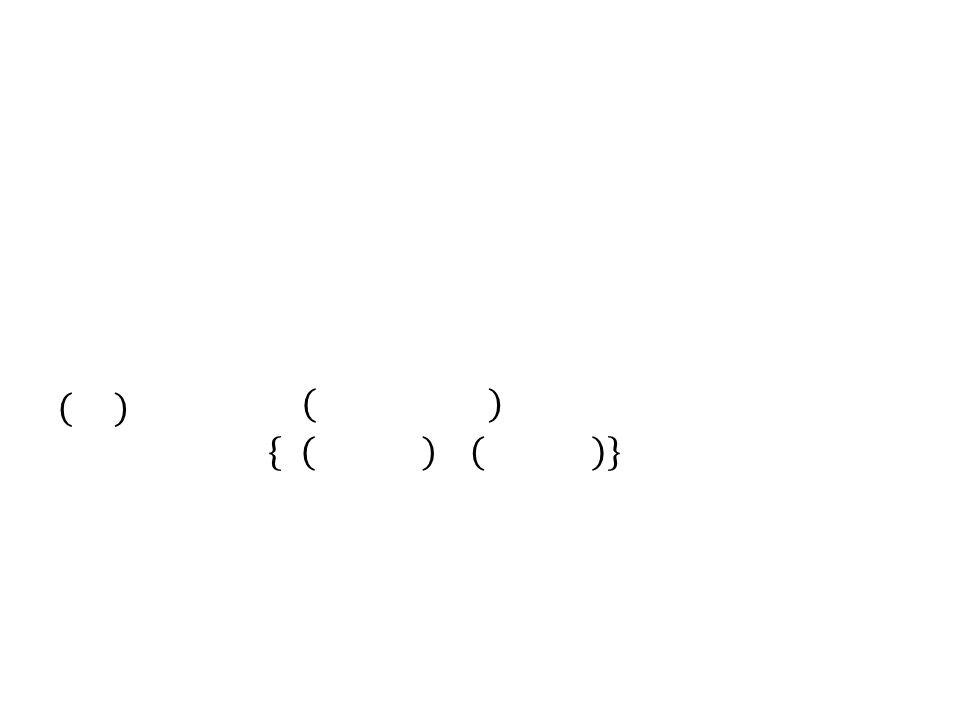
LCS – Programação Dinâmica
•
Defina c(i, j) como o tamanho da LCS(Xi, Yj):
0
ꢄꢅ ꢁ = 0 ꢆꢇ ꢂ = 0
ꢃ ꢁ − 1, ꢂ − 1 + 1
ꢁ, ꢂ = ቐ
max ꢀ ꢁ − 1, ꢂ , ꢀ ꢁ, ꢂ − 1
ꢄꢅ ꢁ = ꢂ
ꢄꢅ ꢁ ≠ ꢂ
ꢀ

LCS – Programação Dinâmica
•
Ideia do Algoritmo:
–
Considere duas sequências como entrada, X = {x1, x2, . . . ,
xm} e Y = {y1, y2, . . . , yn};
–
Os valore c(i, j) são armazenados em uma tabela c[0..m,
0
..n], onde os valores são computados linha a linha,
esquerda para direita;
–
Também há uma tabela b[1..m, 1..n] tal que são
armazenados as entradas para a escolha da solução ótima
dos subproblemas quando está se computando c(i , j).
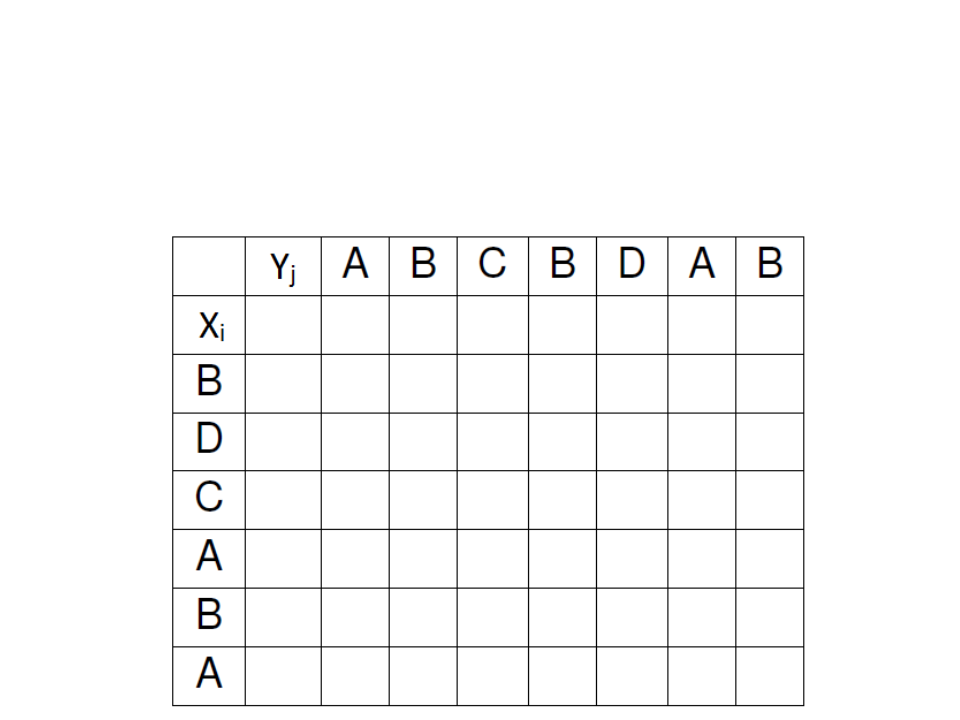
LCS – Exemplo
•
X=BDCABA e Y=ABCBDAB
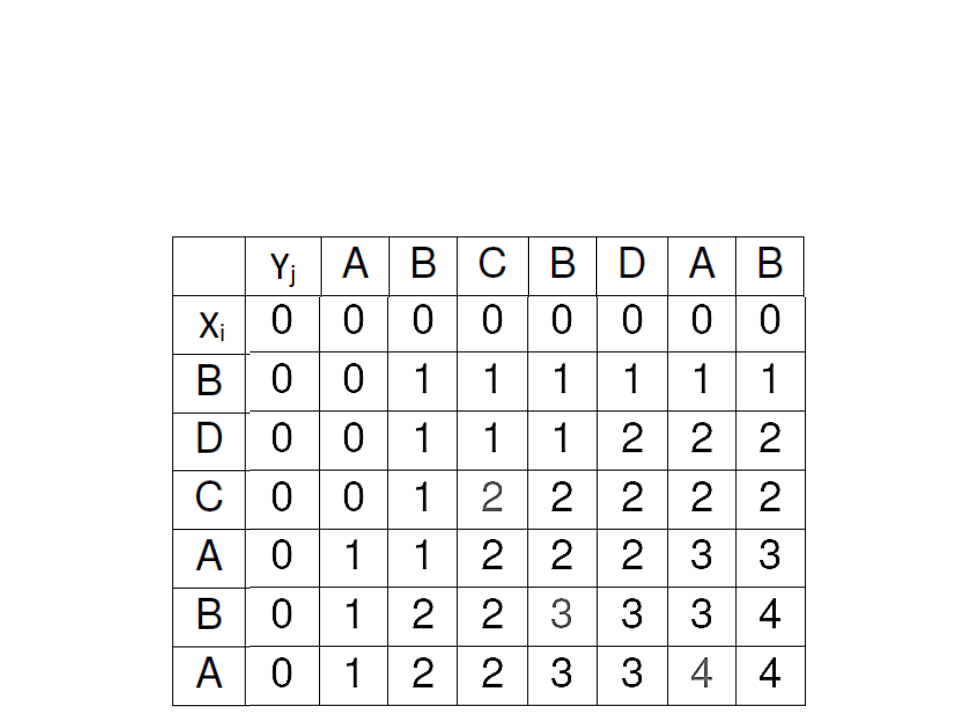
LCS – Exemplo
•
X=BDCABA e Y=ABCBDAB

LCS – Algoritmo
O(mn)

LCS – Algoritmo
•
Algoritmo para imprimir a LCS na ordem correta:

Exercícios
1
2
3
) Determine a LCS(X, Y) para X = {1, 0, 0, 1, 0, 1,
0, 1} e Y = {0, 1, 0, 1, 1, 0, 1, 1, 0}.
) É possível implementar o algoritmo sem a
tabela b?
) Implemente o algoritmo para encontrar e
exibir uma LCS para duas sequências de
entrada.
