IPRJ – PROJETO E ANÁLISE DE ALGORITMOS
LISTA DE EXERCÍCIOS 10
1
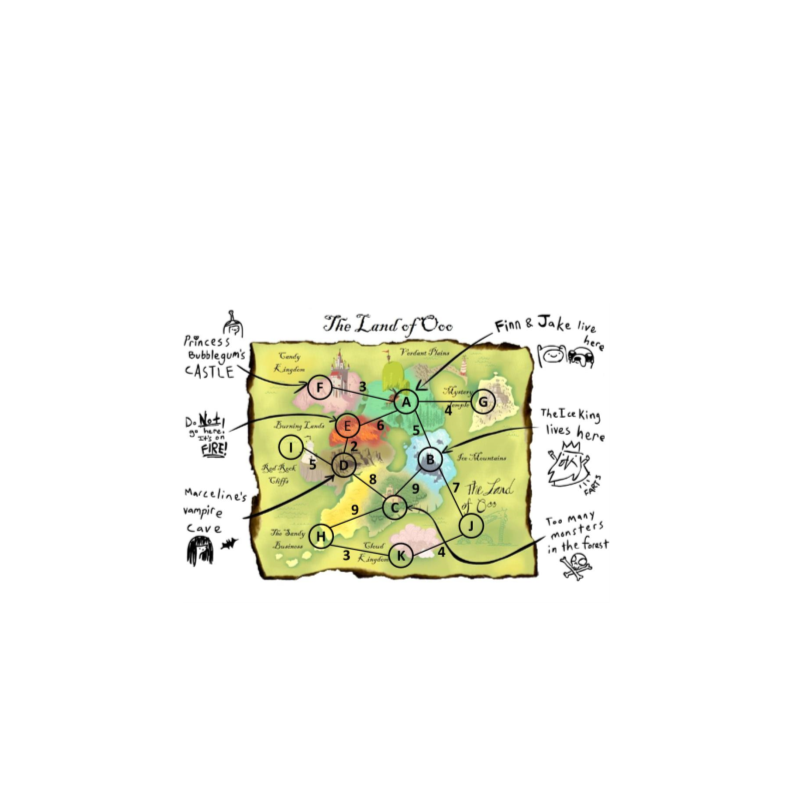
) Uma grande festa vai acontecer no Reino das Nuvens! Finn e Jake estão no castelo
da Princesa Jujuba planejando qual seria a melhor rota para chegar até a festa.
A figura abaixo ilustra o mapa da Terra de Ooo:
Responda as questões abaixo considerando "F" como o vértice inicial. Vértices
sucessores devem ser dispostos em ordem alfabética.
a) Realize uma busca em largura no grafo e apresente os valores de π e d
gerados pelo algoritmo.
b) Realize uma busca em profundidade no grafo e apresente os valores de π, d
e f gerados pelo algoritmo.
c) Construa as árvores de busca geradas pelos algoritmos de busca em
largura e busca em profundidade.
d) Considerando "K" como vértice objetivo, realize uma busca de caminho
mínimo utilizando o algoritmo de Dijkstra e apresente os valores de π e g
gerados pelo algoritmo. Em seguida apresenta o caminho mínimo
encontrado.
2
3
) Em uma busca em largura, o valor d[u] atribuído a um vértice u é independente da
ordem na qual são dados os vértices em cada lista de adjacências. Verdadeiro ou
Falso? Justifique sua resposta.
) Após muitos anos pedalando, Geovane já não têm a mesma disposição para
encarar as diversas subidas de Nova Friburgo. Como sabemos, Nova Friburgo é
extremamente montanhosa. Por razões sentimentais, ele não quer mudar para
uma cidade mais plana. Resolveu, então, que tentaria evitar grandes altitudes em
seus caminhos.
Para isso, Geovane obteve com o serviço topográfico da prefeitura um mapa de
Nova Friburgo, em que cada rua do mapa possui a informação da maior altitude
encontrada quando trafegada. Tudo que ele precisa fazer agora é implementar um
programa para determinar rotas que minimizem a altura percorrida entre pares
(
origem, destino).
a) Defina e ilustre uma estrutura de dados para armazenar e representar o
mapa fornecido pela prefeitura.
b) Apresente o pseudocódigo de um algoritmo que receba como parâmetro
uma origem e um destino. O algoritmo deve retornar um caminho entre a
origem e o destino que evite passar por grandes altitudes.
4
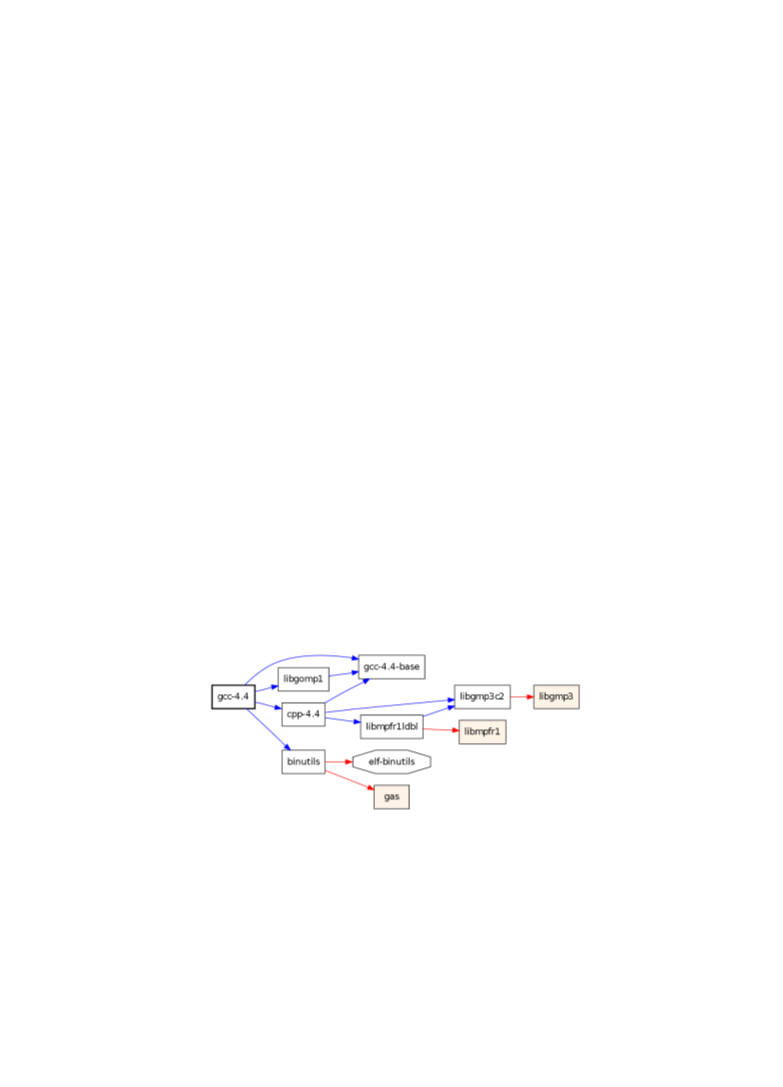
) Para instalar o gcc-4.4 é necessário instalar um conjunto de dependências. A figura
abaixo ilustra estas dependências:
a) Utilizando o algoritmo de Kahn, apresente uma ordenação topológica
definindo uma sequência valida para a instalação do gcc-4.4 e suas
dependências. Justifique sua resposta apresentando o conteúdo do vetor I e
da pilha L em todas as iterações do algoritmo.
b) Utilizando
o algoritmo de ordenação topológica com busca em
profundidade, apresente uma ordenação topológica definindo uma
sequência valida para a instalação do gcc-4.4 e suas dependências.
Justifique sua resposta apresentando o conteúdo do vetor d e f e da lista L
no final da execução do algoritmo.
5
6
) Se existe um caminho de u para v em um grafo orientado F, então qualquer busca
em profundidade deve resultar em d[v] ≤ f[u]. Verdadeiro ou Falso? Justifique sua
resposta.
) Durante sua campanha eleitoral, o prefeito de Nova Friburgo prometeu que, até o
fim de seu mandato, os cidadãos conseguiriam se locomover entre os principais
pontos do município sem passar por nenhum trecho de estrada de terra (quando
assumiu o cargo, não era possível ir à nenhum lugar sem passar pelo barro).
A primeira providência que tomou foi finalizar as diversas vias de ligação que
haviam sido parcialmente construídas, mas não terminadas. Assim que concluiu
esta etapa, já com o orçamento reduzido, o prefeito precisa determinar se a
promessa já fora cumprida ou não.
a) Defina e ilustre uma estrutura de dados para representar este problema.
b) Apresente o pseudocódigo de um algoritmo que determine se a promessa
do prefeito já foi cumprida ou não.
7
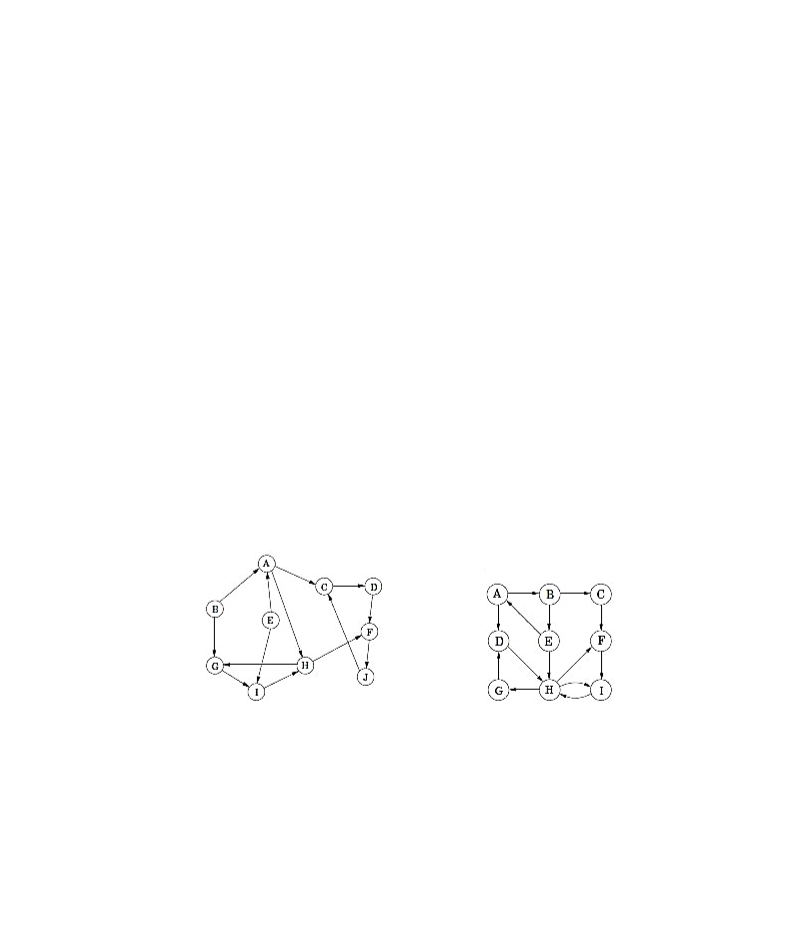
) Considerando os seguintes grafos:
(
a)
(b)
Responda as questões a seguir iniciando os algoritmos pelo vértice "A" e dispondo
os vértices sucessores em ordem alfabética.
a) Utilizando o algoritmo de Kosaraju, apresente os componentes fortemente
conectados de cada um dos grafos na ordem em que eles são encontrados
pelo algoritmo.
b) Utilizando o algoritmo de Tarjan, apresente os componentes fortemente
conectados de cada um dos grafos na ordem em que eles são encontrados
pelo algoritmo.
8
9
) Dado um grafo orientado representado por uma lista de adjacências, qual a
complexidade do processo de calcular o grau de saída de um vértice? Justifique sua
resposta descrevendo o processo.
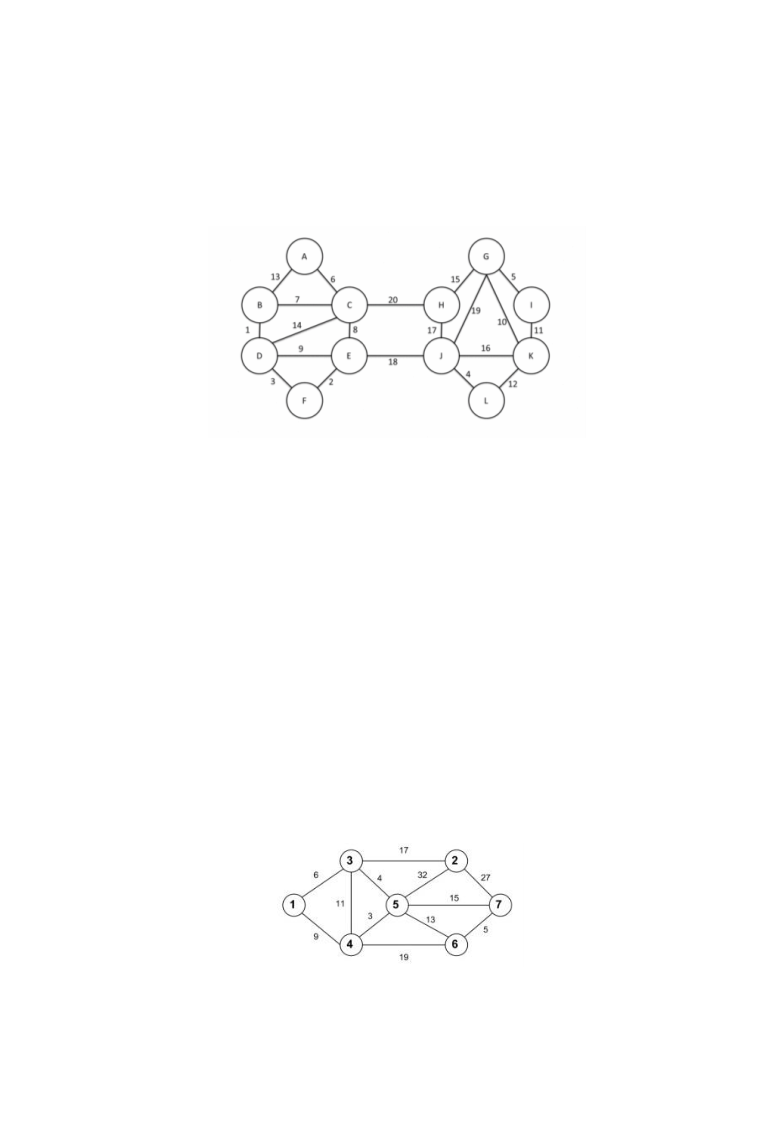
) Considerando o seguinte grafo:
Responda as questões a seguir iniciando os algoritmos pelo vértice "A" e dispondo
os vértices sucessores em ordem alfabética.
a) Utilize o algoritmo de Prim para encontrar uma árvore geradora mínima
para o grafo. Justifique sua resposta apresentando os valores de π e key
gerados pelo algoritmo.
b) Utilize o algoritmo de Kruskal com Conjuntos Disjuntos com Florestas para
encontrar uma árvore geradora mínima para o grafo. Justifique sua
resposta apresentando a árvore final presente conjunto disjunto.
1
0) Você é o responsável por substituir e otimizar a rede e os roteadores de uma
empresa. Os roteadores transmitem os dados entre si através de cabos de rede e os
dados transmitidos podem trafegar por uma ou mais rotas para serem entregues
ao destinatário. Considerando o alto preço dos cabos de rede, você deve projetar a
nova infraestrutura da rede da empresa de forma com que todos os roteadores
consigam transmitir dados entre si economizando o máximo possível de cabos de
rede. A figura abaixo mostra a atual infraestrutura de rede da empresa:
Apresente o pseudocódigo de um algoritmo para otimizar a infraestrutura de rede
da empresa e descobrir qual será o custo total gasto com cabos de rede.
1
1) A transposta de um grafo orientado G = (V, A) é o grafo GT = (V, AT), onde AT={(v,u)
∈
V×V|(u,v) ∈ A}. Desse modo, GT é G com todas as suas arestas invertidas.
a) Considerando que G é representado por uma lista de adjacências, descreva
um algoritmo para calcular GT a partir de G. Em seguida, análise a
complexidade do algoritmo proposto.
b) Considerando que G é representado por uma matriz de adjacências,
descreva um algoritmo para calcular GT a partir de G. Em seguida, análise a
complexidade do algoritmo proposto.
1
2) Um grafo orientado G=(V, A) é dito "semiconectado" se, para todos os pares de
vértices u, v ∈ V, temos u ⇝ v ou v ⇝ u. Forneça um algoritmo eficiente para
determinar se G é ou não "semiconectado". Análise a complexidade do algoritmo
proposto.
