
INTRODUÇÃO À PROGRAMAÇÃO
LISTA DE EXERCÍCIOS 12
1
. Faça um programa para ler uma matriz digitada pelo usuário (tamanho 3x3) e exibir uma
mensagem dizendo se a mesma é uma matriz identidade ou não. O seu programa deve
implementar e utilizar a função matriz_identidade, que recebe como parâmetro
uma matriz quadrada de inteiros de dimensão n, e retorna 1 se a matriz for uma matriz
identidade, e 0 caso contrario. A função deve obedecer ao seguinte protótipo:
int matriz_identidade(int mat[][N], int n);
Lembre-se que uma matriz é considerada identidade quando os elementos da diagonal
principal são todos iguais a 1 e os elementos restantes são iguais a zero.
2
3
. Faça um programa para ler uma matriz (tamanho 5x5), e em seguida calcular e exibir
produto dos elementos da diagonal principal da matriz. O seu programa deve
implementar e utilizar a função produto_diagonal, que recebe como parâmetro uma
matriz quadrada de float de dimensão n, e retorna o produto da diagonal principal. A
função deve obedecer ao seguinte protótipo:
float produto_diagonal(float mat[][N], int n);
. Escreva um programa para ler uma matriz contendo as 3 notas obtidas por cada aluno em
uma disciplina, onde cada linha representa um aluno e cada coluna indica uma das notas
do aluno. Exemplo:
O programa deve armazenar as notas dos alunos em uma matriz, e implementar e utilizar
as funções aprovadose reprovados, que recebem como parâmetro a matriz com as
notas dos alunos e retornam o número de alunos aprovados/reprovados. As funções
devem obedecer aos seguintes protótipos:
int aprovados(int n, float notas [][3])
int reprovados(int n, float notas [][3])
O seu programa também deve implementar e utilizar a função media_alunos, que
recebe como parâmetro a matriz de notas e um vetor para ser preenchido com a media
dos alunos. A função deve obedecer ao seguinte protótipo:
void media_alunos(int n, float notas [][3], float media[])

4
. Faça um programa para ler uma matriz (tamanho 5x5) e exibir uma mensagem dizendo se
a mesma é uma matriz triangular superior, uma matriz triangular inferior ou nenhum dos
casos.
O
seu
programa
deve
implementar
e
utilizar
a
função
triangular_superior_inferior, que recebe como parâmetro uma matriz
quadrada de inteiros de dimensão n, e retorna 1 se a matriz for uma matriz triangular
superior, 2 se a matriz for uma matriz triangular inferior, e 0 caso contrario. A função deve
obedecer ao seguinte protótipo:
int triangular_superior_inferior(int mat[][N], int n);
Lembre-se que uma matriz é considerada triangular superior quando todos os elementos
abaixo da diagonal principal são iguais a zero, e triangular inferior quando todos os
elementos acima da diagonal principal são iguais a zero.
5
. Faça um programa para ler uma matriz (tamanho 5x5), e em seguida calcular e exibir a
soma dos elementos acima e abaixo da diagonal principal da matriz. O seu programa deve
implementar e utilizar as funções soma_superior e soma_inferior, que recebem
como parâmetro uma matriz quadrada de float de dimensão n, e retornam a soma dos
elementos acima/abaixo da diagonal principal. As funções devem obedecer aos seguintes
protótipos:
float soma_superior(float mat[][N], int n);
float soma_inferior(float mat[][N], int n);
6
. Considere uma tabela com os resultados de um campeonato de futebol, onde os
resultados dos times são dispostos numa ordem qualquer. Como ilustrado a seguir, para
cada time registrasse total de pontos ganhos (PG), número de vitórias (V), número de
empates (E), número de derrotas (D), número de gols pró (GP) e número de gols contra
(GC).
Considere ainda que os números da tabela são representados em uma matriz de valores
inteiros. Cada linha da matriz representa os resultados de um determinado time. Na
primeira coluna da matriz armazena-se o número de pontos ganhos, na segunda o número
de vitórias e assim por diante.
a) Escreva uma função que retorne o número do time com o melhor saldo de gols. A
função deve receber como parâmetros o número de times, n, e a tabela com os
resultados, tab, e deve obedecer ao seguinte protótipo:
int melhorsaldo(int n, int tab[][6]);
b) Escreva uma função que retorne o número do time que está na liderança. A
liderança é determinada pelo time que tiver maior número de pontos ganhos. Se
um ou mais times tiverem o mesmo número de pontos, e usado o seguinte
critério de desempate: número de vitórias e saldo de gols, nesta ordem. Se,
mesmo assim, dois ou mais times empatarem, deve-se retornar o número de um
dos times líderes. A função deve receber como parâmetros o número de times, n,
e a tabela com os resultados, tab, e deve obedecer ao seguinte protótipo:
int lider(int n, int tab[][6]);
c) Escreva uma função que retorne o número do time que está em ultimo lugar na
classificação, obedecendo o mesmo critério de classificação do item anterior. Se
dois ou mais times empatarem em todos os critérios, deve-se retornar um dos
times que está em último lugar. A função deve receber como parâmetros o
número de times, n, e a tabela com os resultados, tab, e deve obedecer ao
seguinte protótipo:
int ultimo(int n, int tab[][6]);
d) Escreva um programa que leia os dados da tabela de resultados e teste suas
funções.
7
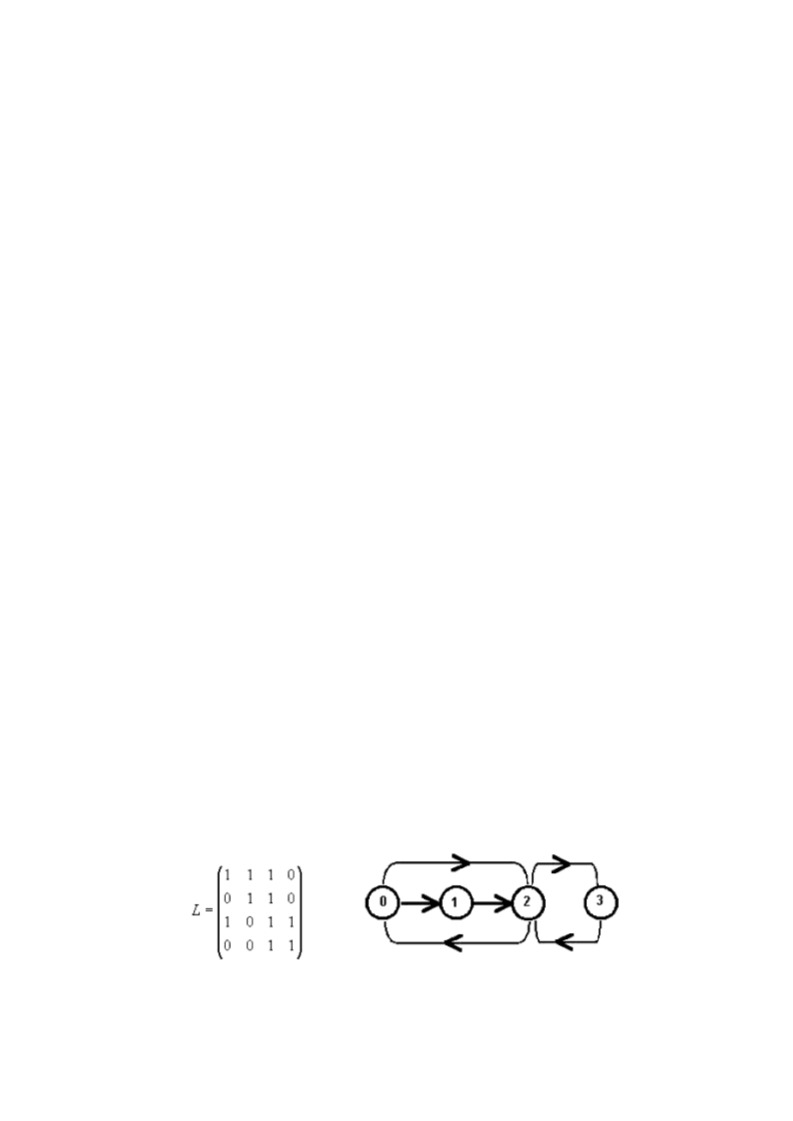
. Considere n cidades numeradas de 0 a n-1 que estão interligadas por uma série de
estradas de mão única. As ligações entre as cidades são representadas pelos elementos de
uma matriz quadrada Lnxn, cujos elementos lij assumem o valor 1 ou 0, conforme exista ou
não estrada direta que saia da cidade i e chegue à cidade j.
Assim, os elementos da linha i indicam as estradas que saem da cidade i, e os elementos
da coluna j indicam as estradas que chegam à cidade j. Por convenção lii = 1, mas atenção,
uma ligação da cidade para ela mesma não deve ser contada como saída nem entrada da
cidade. A figura abaixo mostra um exemplo para n = 4 e seu código pode considerar uma
matriz L de tamanho 4x4.
Para cada uma das questões abaixo, você deve desenvolver a função solicitada e também
testa-la através de chamadas na função principal do programa.
a) Escreva uma função que recebe a matriz de ligações L e um índice de cidade k, e
escreve na tela quantas estradas saem e quantas chegam à cidade k (só considerar
estradas e saídas diretas).
Exemplo de saída para k=0:
Existe 1 estrada(s) que chega(m) na cidade 0 e 2
estrada(s) para sair.
b) Escreva uma função que recebe a matriz de ligações L e retorne o índice da cidade
onde chegam o maior número de estradas.
c) Escreva uma função que recebe a matriz de ligações L e um índice de cidade k, e
testa se todas as ligações diretas entre a cidade k e outras são de mão dupla. Caso
seja de mão dupla a função retorna 1, ou retorna 0 para o caso contrário.
d) Escreva uma função que recebe a matriz de ligações L e um vetor C de tamanho
igual ao número de cidades. A função escreve no vetor C para cada cidade se ela é
(1) ou não é (0) isolada, isto é, se não têm ligação com nenhuma outra. Os índices
das posições no interior de C representam as respectivas cidades. Exemplo: C[5]
deve ser preenchido avaliando se a sexta cidade é ou não isolada.
e) Escreva uma função que recebe a matriz de ligações L e escreva em um arquivo
chamado “avisos.txt” uma mensagem alertando cada uma das cidades que são fim
de linha, ou seja, as cidades das quais não há saída, apesar de haver entrada. Sua
função deve escrever no arquivo a seguinte mensagem para cada cidade fim de
linha encontrada em L: “Atenção a cidade XXX é fim de linha, não há saídas dela!”
f) Escreva uma função que recebe a matriz L e um vetor com uma sequência de m
inteiros cujos valores estão entre 0 e o número de cidades –1. A sequência de
inteiros no vetor representa um roteiro percorrendo as cidades de destino em
destino. Sua função deve verificar se é possível realizar o roteiro correspondente e
nesse caso retornar 1 ou se não é possível, por não haver estradas ligando as
cidades desejadas na ordem do roteiro. No exemplo dado, o roteiro representado
pela sequência (m=5) 2 3 2 1 0 é impossível.
