
Introdução à Programação
Aula 10 – Matrizes
Edirlei Soares de Lima
<edirlei@iprj.uerj.br>

Conjuntos Bidimensionais
•
•
Uma matriz representa um conjunto bidimensional de valores.
Exemplo de matriz de inteiros:
3
7
1
5
6
1 8 6 1
2 5 4 9
9 3 1 2
8 6 7 3
4 9 2 1
•
Similar a variáveis simples e vetores, matrizes devem ser
declaradas para que o espaço de memória seja reservado.

Matrizes
•
•
Como a matriz representa um conjunto bidimensional,
devemos especificar as duas dimensões na declaração:
–
o número de linhas e o número de colunas:
tipo nome_matriz[numero_linhas][numero_colunas];
Exemplo:
int minha_matriz[3][3];
?
?
?
? ?
? ?
? ?

Matrizes
•
É possível acessar os valores da matriz através de seu índice
bidimensional.
int minha_matriz[3][3];
0
1 2
0
1
2
5
? ?1
?
?
? ?8 ?
? ?
minha_matriz[0][0] = 5;
minha_matriz[2][1] = 8;
minha_matriz[0][2] = 1;

Matrizes
•
•
Exemplos de Declaração:
int a[10][10];
float matriz1[20][20];
int mapa[100][100];
Declaração e Inicialização:
int teste[3][3] =
{{2,5,1},{3,7,2},{9,1,5}};

Matrizes - Exemplo 1
•
•
Notas obtidas por alunos de uma disciplina:
Entrada: arquivo com as três notas obtidas por cada aluno.
•
O objetivo é ler as notas do arquivo e armazená-las na memória
para que, posteriormente, seja possível processarmos as notas:
calcular a média dos alunos, a média da disciplina, verificar
quantos alunos foram aprovados , etc.
Matrizes - Exemplo 1
•
•
Usando vetores: precisamos declarar três vetores, um para
cada nota:
float p1[50];
float p2[50];
float p3[50];
Outra alternativa é usar apenas uma estrutura para armazenar
todas as notas de todos os alunos. Usando matrizes, teríamos:
float notas[50][3];
–
Dessa forma as notas do i-ésimo aluno são representadas por
notas[i][0], notas[i][1] e notas[i][2]

#
include <stdio.h>
int main (void)
{
int i = 0, j, nalunos;
float media = 0.0;
float notas[50][3];
FILE *f = fopen("notas.txt","r");
if(f == NULL)
{
printf("Erro na leitura do arquivo.\n");
return 0;
}
/
* lê valores do arquivo */
while((fscanf(f,"%f %f %f", ¬as[i][0], ¬as[i][1],
notas[i][2])==3) && (i<50))
&
{
i++;
}
nalunos = i;
fclose(f);
[Continua...]

/
* calcula média */
for (i=0; i<nalunos; i++)
{
for (j=0; j<3; j++)
{
media = media + notas[i][j];
}
}
media = media / (3*nalunos);
/
* exibe média calculada */
printf("Media da disciplina: %.2f\n", media);
return 0;
}

Passagem de Matrizes para Funções
•
•
É possível que funções auxiliares recebam como parâmetro
uma matriz.
–
Passar uma matriz para uma função é análogo a passar um vetor ->
Passa-se na verdade uma referência para a matriz.
Uma diferença importante com relação a vetores é que o
parâmetro que representa a matriz deve ter especificado o
número de colunas da matriz.
–
Isso é necessário pois o compilador precisa conhecer o número de
colunas da matriz para fazer a conta de endereçamento.

Matrizes – Exemplo 1 (com funções)
•
Função auxiliar que ler valores de um arquivo e armazena em
uma matriz:
int le_valores (float mat[][3])
{
int i = 0;
FILE *f = fopen("notas.txt", "r");
while (fscanf(f, "%f %f %f", &mat[i][0],&mat[i][1],
&
mat[i][2]) == 3 && i < 50)
{
i++;
}
fclose(f);
return i;
}

Matrizes – Exemplo 1 (com funções)
•
Função auxiliar para calcular a média:
float media(int n, float mat[][3])
{
int i, j;
float soma = 0.0;
for (i=0; i<n; i++)
{
for (j=0; j<QTD_COL; j++)
{
soma = soma + mat[i][j];
}
}
return soma /(QTD_COL*n);
}

Matrizes – Exemplo 1 (com funções)
•
Função principal:
int main (void)
{
int n;
float m;
float notas[50][3];
n = le_valores(notas);
m = media(n,notas);
printf("Media da disciplina: %f", m);
return 0;
}

Funções Algébricas
•
•
Em muitas aplicações computacionais, fazemos uso de
matrizes quadradas, isto é, matrizes em que o número de
linhas é igual ao número de colunas.
Podemos assumir que a dimensão das matrizes é N x N, onde
N é uma constante simbólica.
–
Por exemplo, se quisermos que nosso código seja usado para matrizes
4
x 4, fazemos:
#
define N 4

Funções Algébricas – Exemplo 1
•
Verificar se uma matriz é simétrica: retorna 1 se verdadeiro e 0 se falso:
–
Uma matriz é simétrica se ela for igual a sua transposta;
–
Uma matriz transposta é o resultado da troca de linhas por colunas da matriz original;
int simetrica(double A[][N])
{
int i, j;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
if (A[i][j] != A[j][i])
return 0;
}
}
return 1;
}

Funções Algébricas – Exemplo 2
•
Calcular a transposta de uma matriz:
–
Uma matriz transposta é o resultado da troca de linhas por colunas da matriz original;
void cria_transposta(double A[][N], double T[][N])
{
int i, j;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
T[j][i] = A[i][j];
}
}
}

Funções Algébricas – Exemplo 3
•
Transpor uma matriz:
–
Uma matriz transposta é o resultado da troca de linhas por colunas da matriz original;
void transpoe(double A[][N])
{
int i, j;
for (i=0; i<N; i++)
{
for (j=0; j<i; j++)
{
double t = A[i][j];
A[i][j] = A[j][i];
A[j][i] = t;
}
}
}

Funções Algébricas – Exemplo 4
•
Multiplicar uma matriz por um escalar:
void mult_matriz_escalar(double A[][N], double s,
double B[][N])
{
int i, j;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
B[i][j] = s * A[i][j];
}
}
}

Funções Algébricas – Exemplo 5
Multiplicação de matrizes:
•
void mult_matriz_matriz(double A[][N], double B[][N],
double C[][N])
{
int i, j, k;
for (i=0; i<N; i++)
{
for (j=0; j<N; j++)
{
C[i][j] = 0.0;
for (k=0; k<N; k++)
{
C[i][j] = C[i][j] + A[i][k] * B[k][j];
}
}
}
}
Representação de Tabelas
•
•
Muitas aplicações precisam organizar informações na forma
de tabelas, e matrizes são naturalmente estruturas de dados
adequadas para representação de tabelas.
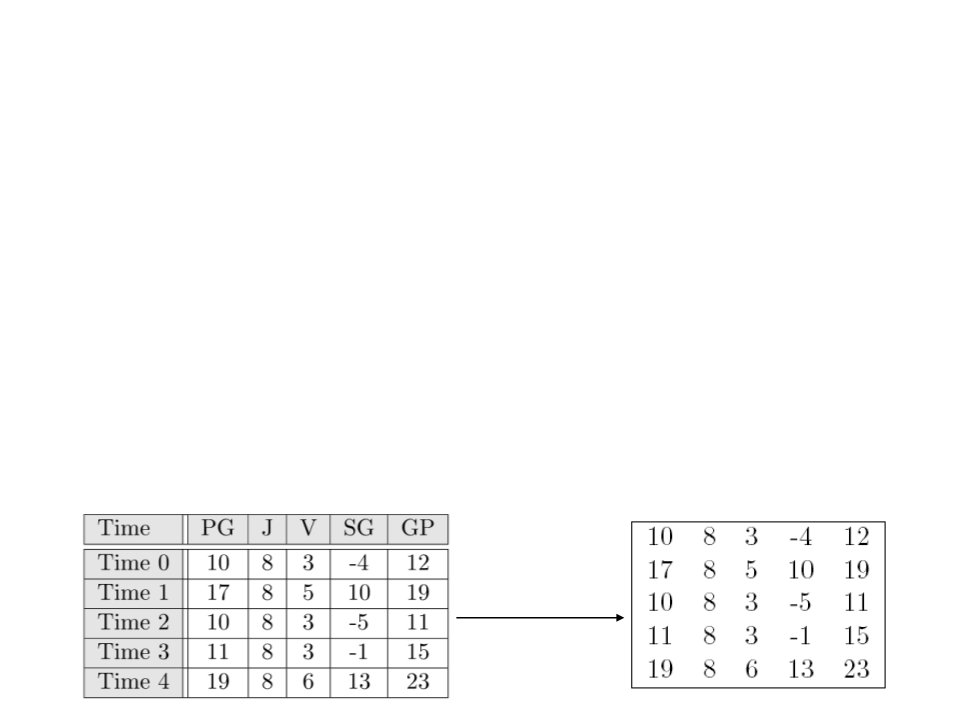
Para exemplificar, vamos considerar uma tabela de um
campeonato de futebol.
–
Cada linha armazena as informações de um determinado time do
campeonato: número de pontos ganhos (PG), número de jogos (J),
número de vitorias (V), saldo de gols (SG) e gols próprios (GP).
gerando a matriz

Representação de Tabelas
•
Um critério usualmente usado para classificação dos times é:
número de pontos ganhos, número de vitórias, saldo de gols
e, finalmente, número de gols próprios.
•
•
Assim, o líder do campeonato é o time que tem o maior
número de pontos.
Se dois times tem o mesmo número de pontos, usa-se o
maior número de vitórias como critério de desempate; se o
número de vitórias também for igual, usa-se o saldo de gols;
por fim, usa-se o número de gols próprios.

Representação de Tabelas
•
•
Podemos então codificar uma função que recebe como
parâmetros o número de times e a matriz representando a
tabela do campeonato e retorna o número do time que é
líder.
Para o código ficar mais legível, podemos definir constantes
simbólicas como:
#
#
#
#
#
define PG 0
define J 1
define V 2
define SG 3
define GC 4

int lider(int n, int t[][5])
{
int l = 0; /* assume inicialmente time 0 como líder */
for (i = 1; i < n; i++)
{
if (t[i][PG] > t[l][PG])
{
l = i;
}
else if (t[i][PG] == t[l][PG])
{
if (t[i][V] > t[l][V])
{
l = i;
}
else if (t[i][V] == t[l][V])
{
[Continua...]

if (t[i][SG] > t[l][SG])
{
l = i;
}
else if (t[i][SG] == t[l][SG] &&
t[i][GP] > t[l][GP])
{
l = i;
}
}
}
}
return l;
}

Exercícios
Lista de Exercícios 12 – Matrizes
http://www.inf.puc-rio.br/~elima/prog1/
