
Introdução a Computação
Aula 01 – Resolução de Problemas Lógicos
Edirlei Soares de Lima
<elima@inf.puc-rio.br>
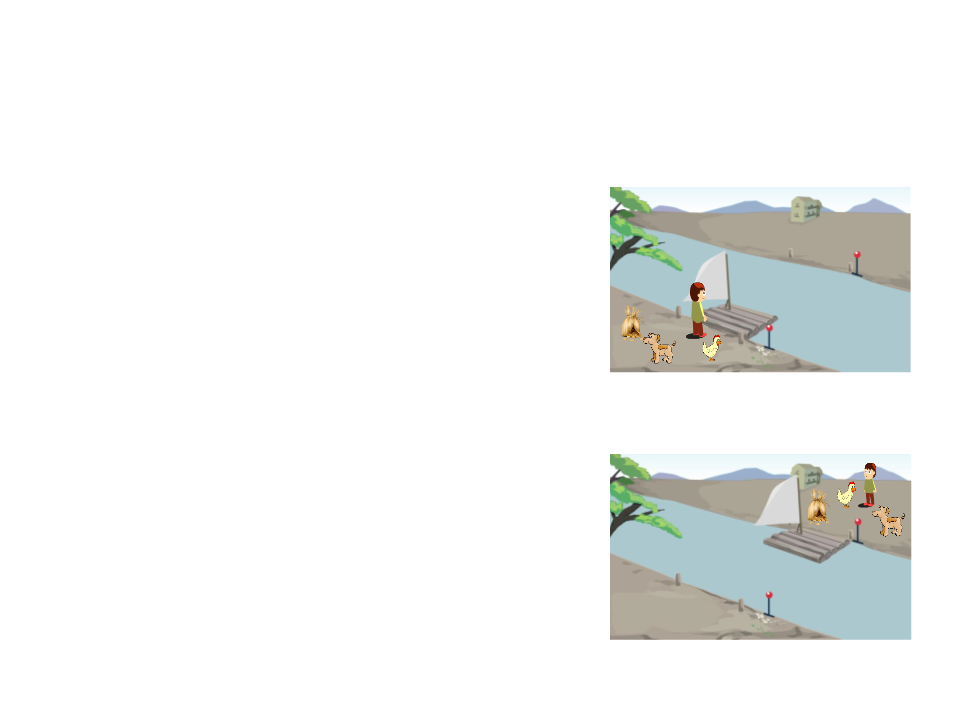
Desafio 1
•
•
•
Um senhor está em uma das margens de um
rio com uma raposa, uma galinha e um saco
de milho.
Ele pretende atravessar o rio com suas cargas
em um barco que só comporta ele e uma das
cargas.
Ele não pode deixar em uma das margens
sozinhos, a raposa e a galinha, nem a galinha
e o milho.

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução

Desafio 1 - Solução
(
(
(
(
(
(
(
1) Atravessar a galinha.
2) Retornar sozinho.
3) Atravessar a raposa.
4) Retornar com a galinha.
5) Atravessar o milho.
6) Retornar sozinho.
7) Atravessar a galinha.
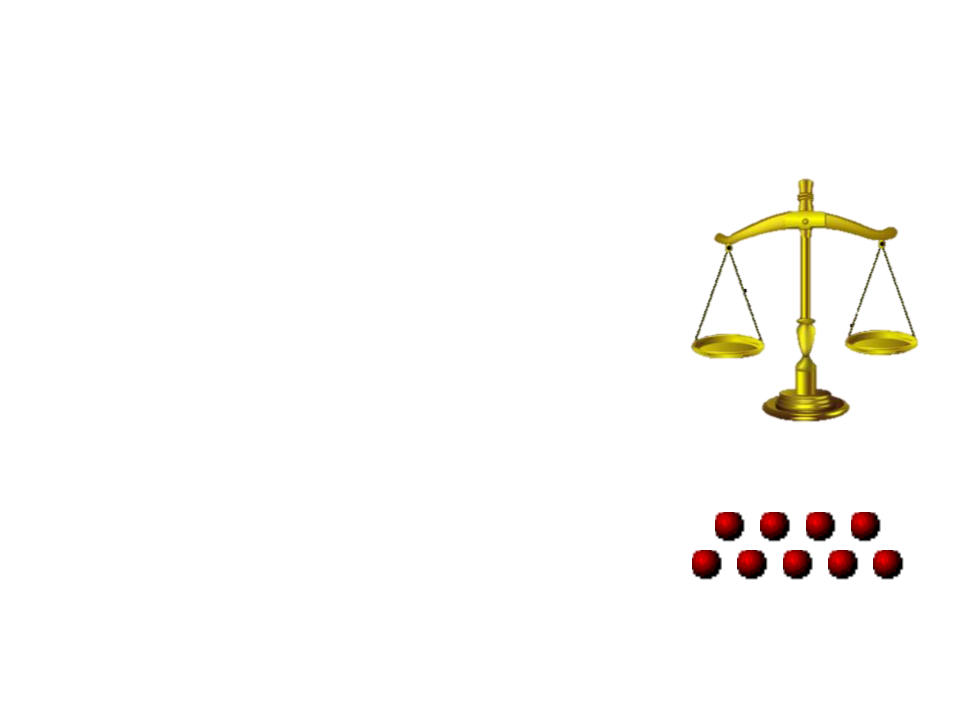
Desafio 2
•
•
Considere o seguinte ambiente:
–
1 balança (como a do desenho ao lado)
–
9 bolas - sendo que uma é mais leve do que as
demais.
Objetivo: Descobrir qual é a bola mais leve
com o menor número possível de pesagens.
Desafio 2 – Solução 1
•
1ª pesagem:
–
1ª possibilidade: pesos iguais - bola
extra é a mais leve!
–
2ª possibilidade: a bola mais leve está
no grupo mais leve - descarta-se a bola
extra e o grupo mais pesado e realiza-se
nova pesagem.
•
•
2ª pesagem:
–
descarta-se o grupo mais pesado e
realiza-se nova pesagem.
3ª pesagem:
–
Determina-se a bola mais leve!
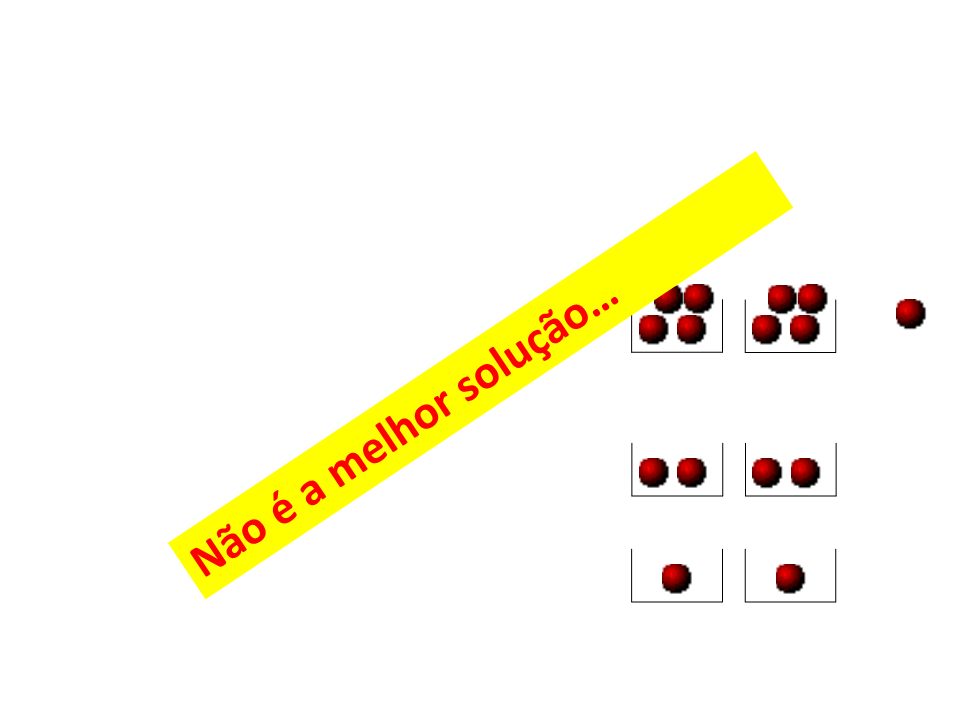
Desafio 2 – Solução 2
•
•
1ª pesagem:
–
1ª possibilidade: pesos iguais - a bola
está no grupo extra - 6 bolas são
descartadas e realiza-se nova
pesagem.
–
2ª possibilidade: pesos diferentes -
bola mais leve está no grupo mais leve
-
6 bolas são descartadas e realiza-se
nova pesagem
2ª pesagem:
–
Determina-se a bola mais leve!

Desafio 2 – Solução
•
Como descrever passo a passo a solução do Desafio 2?
1
2
3
4
5
6
7
8
9
1
1
) Divida as bolas em 3 grupos;
) Escolha dois grupos para pesar e reserve o grupo extra;
) Coloque-os cada um em um lado da balança;
) Se os pesos forem iguais, descarte ambos os grupos;
) Senão, descarte o grupo mais pesado e o grupo extra;
) Divida as bolas em 3 grupos;
) Escolha dois grupos para pesar e reserve o grupo extra;
) Coloque-os cada um em um lado da balança;
) Se os pesos forem iguais descarte ambos os grupos;
0) Senão, descarte o grupo mais pesado e o grupo extra;
1) A bola que restou é a mais leve;

Desafio 2 – Solução
•
Como descrever passo a passo a solução do Desafio 2?
1
2
3
4
5
6
7
) Divida as bolas em 3 grupos;
) Escolha dois grupos para pesar e reserve o grupo extra;
) Coloque-os cada um em um lado da balança;
) Se os pesos forem iguais, descarte ambos os grupos;
) Senão, descarte o grupo mais pesado e o grupo extra;
) Repita os passos 1 a 5 até que reste apenas uma bola;
) A bola que restou é a mais leve;
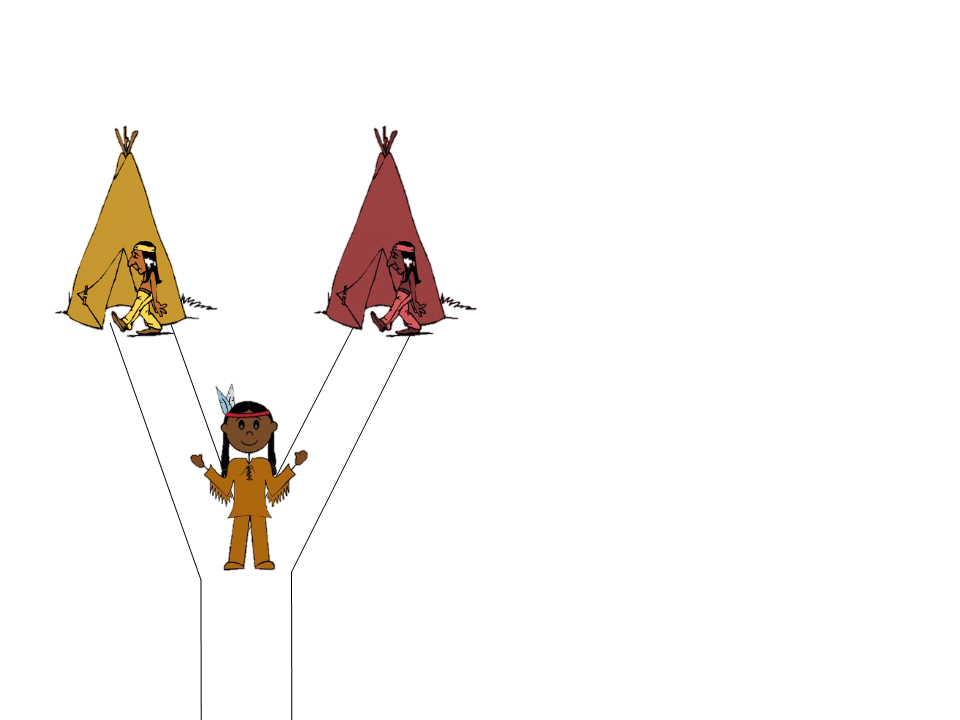
Desafio 3
•
Premissas:
–
–
–
2 aldeias de índios:
• 1 canibal e 1 civilizada
O índio civilizado sempre diz a
verdade.
O índio canibal sempre mente.
•
Objetivo:
–
Ao chegar na encruzilhada fazer
uma única pergunta ao índio
para chegar à aldeia dos índios
civilizados.

Desafio 3 - Solução
Qual o caminho para a
sua aldeia?
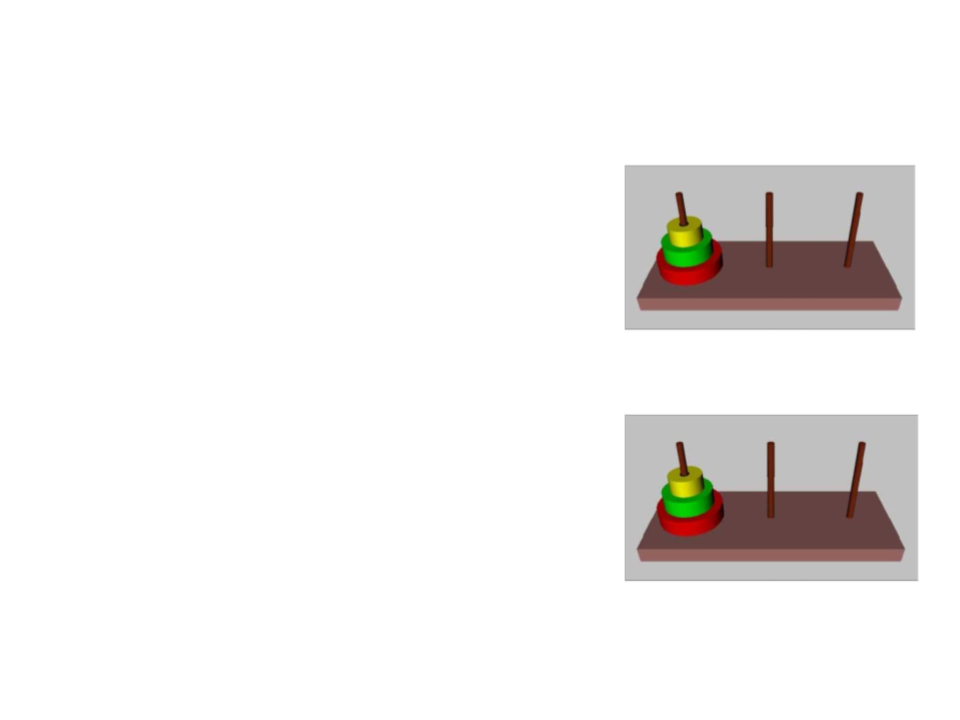
Desafio 4
•
Torre de Hanói
–
–
–
Objetivo: mover os discos da haste
A para a haste C.
Restrições: Um disco NÃO pode
ficar sobre um disco menor que ele.
Qual a sequencia lógica para
resolver este problema?
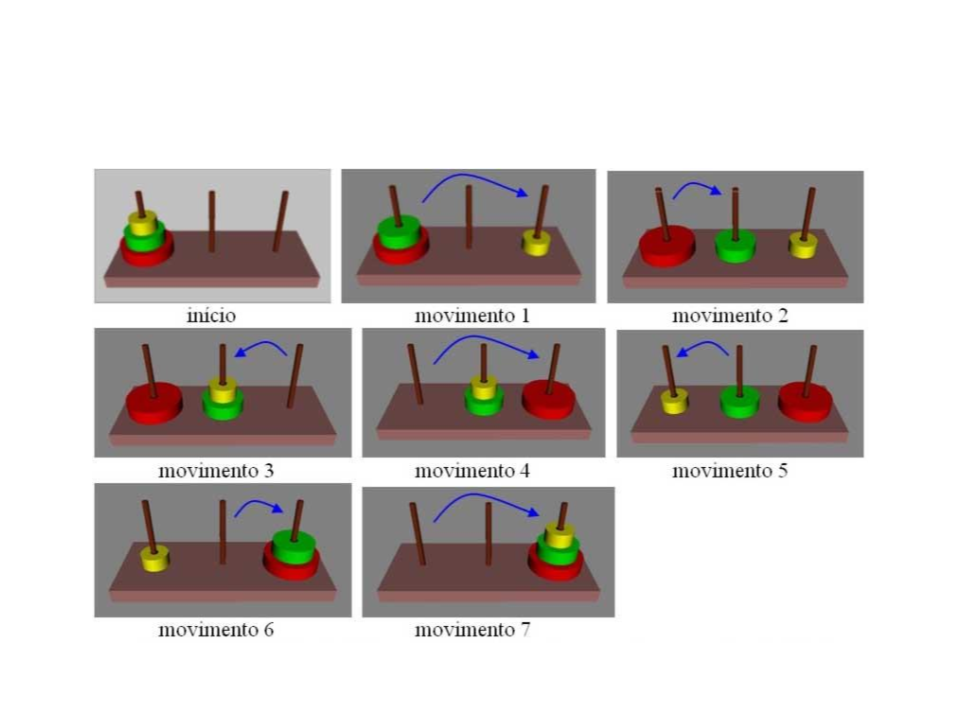
Desafio 4 – Solução

Desafio 5
•
•
O pneu do seu carro furou...
Quais são os passos necessários para trocar o pneu
de um carro?

Desafio 5 - Solução
•
Algoritmo Textual Informal:
–
“Abra o porta-mala e verifique se todos acessórios estão
lá. Em caso negativo, feche o porta-malas e peça carona a
alguém. Em caso positivo, retire o triângulo, posicione-o a
cerca de 30 m do carro, e, depois, retire o estepe e o
macaco. Levante o carro...”
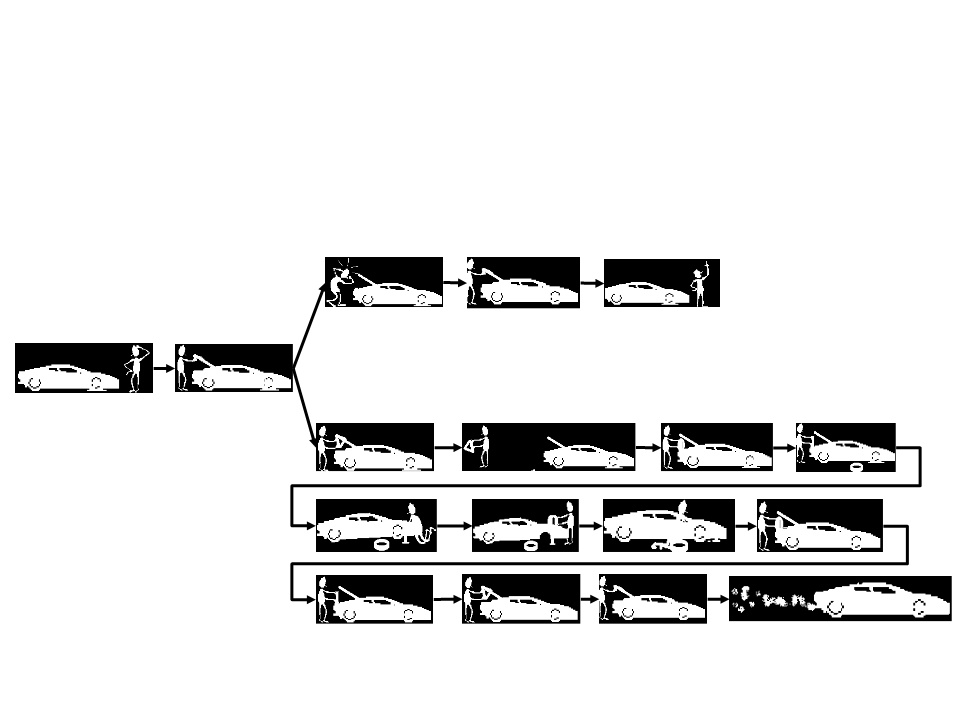
Desafio 5 - Solução
•
Algoritmo Gráfico Informal:

Desafio 5 - Solução
•
Algoritmo Textual Formal:
Abre(porta_malas)
Se acessorio_ok = FALSO Então
fecha(porta_malas)
espera_carona()
Senão
pega_triangulo()
.
.
.

Desafio 6
•
•
Uma lesma encontra-se no fundo de um poço seco de 10
metros de profundidade e quer sair de lá. Durante o dia,
ela consegue subir 2 metros pela parede; mas à noite,
enquanto dorme, escorrega 1 metro.
Depois de quantos dias ela consegue chegar na saída
do poço?
Desafio 6 - Solução
Dia
Subida (m) Descida (m)
Posição atual (m)
1º
2º
3º
4º
5º
6º
7º
8º
9º
2
2
2
2
2
2
2
2
2
1
1
1
1
1
1
1
1
0
1
2
3
4
5
6
7
8
10

Desafio 6 - Solução
Quantidade de dias = 1
Total percorrido = 2
Enquanto Total percorrido < 10 metros
Diminui 1 de Total percorrido (desceu na noite)
Soma 2 em Total percorrido (subiu no dia)
Incrementa 1 na quantidade de dias
Fim Enquanto
Mostrar a quantidade de dias

Exercícios
1
) Três gatos comem três ratos em três minutos.
Cem gatos comem cem ratos em quantos
minutos?
–
3 minutos
2
) O pai do padre é filho do meu pai. O que eu sou
do Padre?
–
Tio
3
) Se um bezerro pesa 75 kg mais meio bezerro,
quanto pesa um bezerro inteiro?
–
150 kg

Exercícios
4
) Qual o próximo número da sequência 7,8,10,13,17,?
–
22
5
) Qual o próximo número da sequência 25, 32, 37, 47,
8,?
5
–
71
6
) Um pai de 80kg e suas 2 filhas (40kg cada), precisam
sair de uma ilha com um barco. Porém a capacidade
do barco é de 80kg. Como farão para sair da ilha?
–
Vão as duas filhas. Uma delas volta. O pai sai. A outra
filha volta. As duas filhas saem juntas.
