REDES NEURAIS / INTELIGÊNCIA ARTIFICIAL
LISTA DE EXERCÍCIOS 6
Aluno:
1
. Defina o problema de busca (espaço de estados, estado inicial, estado final, ações
possíveis, custo) para o seguinte caso: uma pessoa, um lobo, um carneiro e um cesto de
alface estão à beira de um rio. Dispondo de um barco no qual pode carregar apenas um
dos outros três, a pessoa deve transportar tudo para a outra margem. Em nenhum
momento devem ser deixados juntos e sozinhos o lobo e o carneiro ou o carneiro e o
cesto de alface.
2
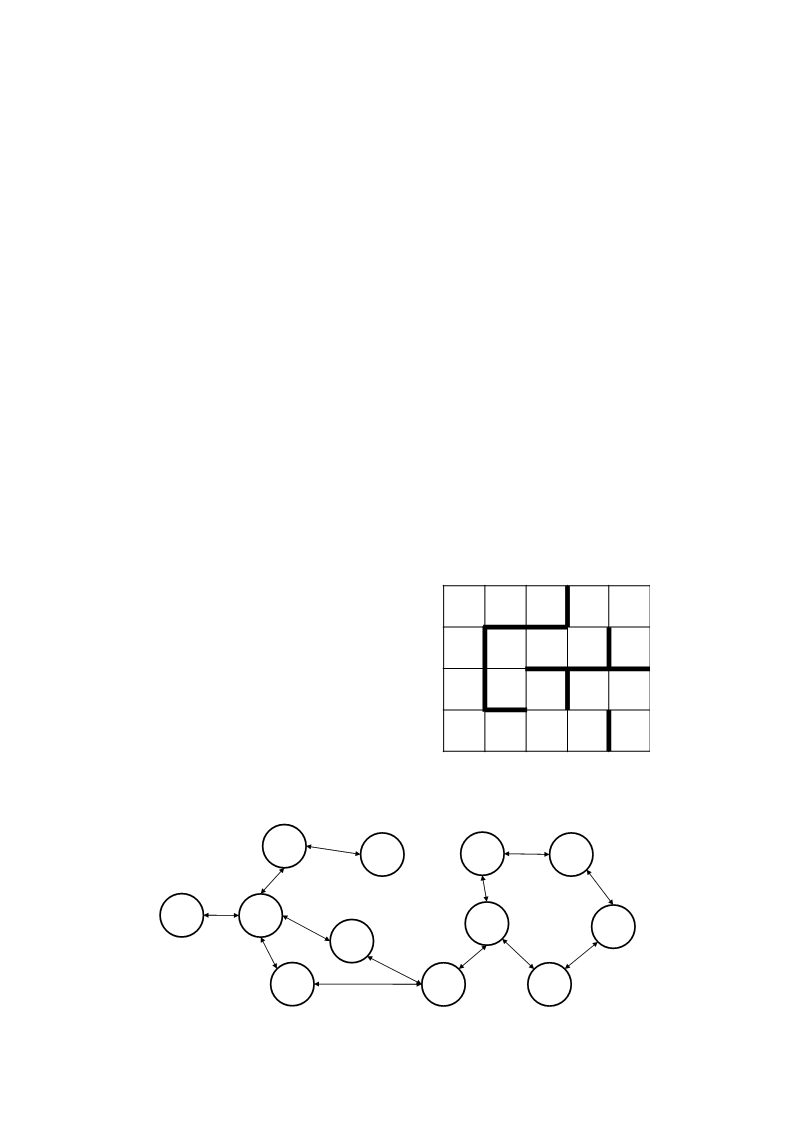
. Em um labirinto, mostrado na figura a seguir, um robô é colocado na célula inicial indicada
por “E” e deve encontrar um caminho até a saída, denotada pela letra “S”. O robô não
pode se mover na diagonal, somente acima, abaixo, direita e esquerda. Ele também não
pode atravessar paredes (as linhas mais grossas da grade) ou as bordas do labirinto, de
modo que ele é forçado a contornar obstáculos. Felizmente, o robô possui um mapa do
ambiente. A solução é o caminho mais curto até a saída e todos os movimentos do robô
possuem os mesmos custos.
(
a) Descreva o problema em termos de
um problema de busca definindo o
espaço de estados, o estado inicial, o
estado final, os operadores de
transição entre os estados (ações) e
o custo.
1
E
2
3
4
5
S
1
2
3
4
(
b) Construa um grafo do espaço de
estados rotulando os arcos com os
operadores de transição adequados.
3
. Considerando o seguinte mapa:
C
D
H
K
1
0
1
2
8
6
1
8
1
0
Start
A
2
5
G
Goal
F
2
0
10
20
1
2
8
B
I
J
1
5
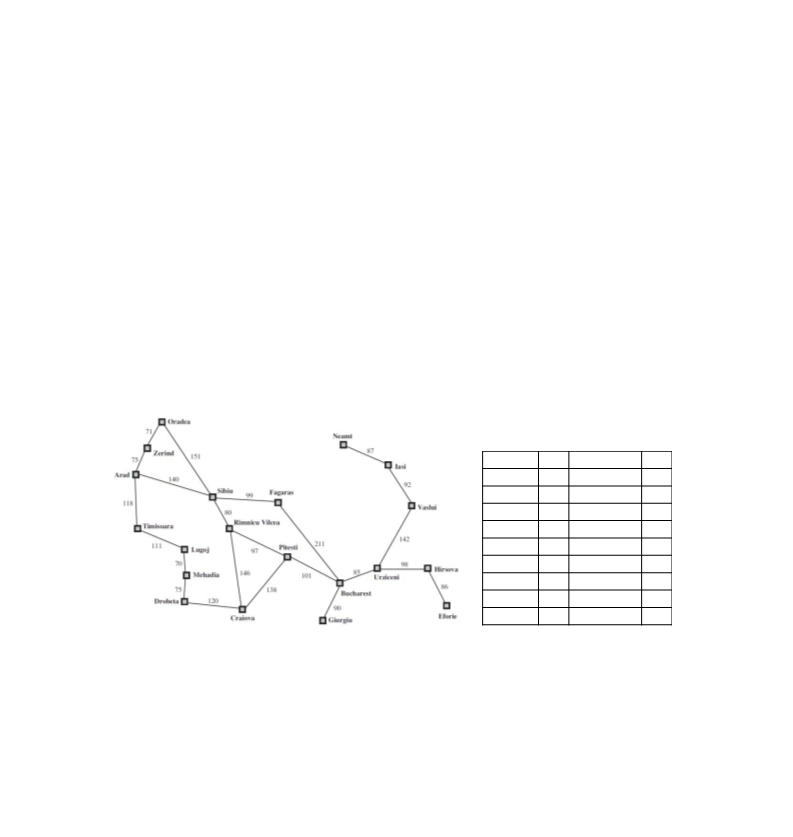
Responda as questões abaixo considerando “Start” como o estado inicial e “Goal” o
estado final buscado.
(
a) Monte as árvores de busca que seriam geradas pelos algoritmos de busca cega vistos
em aula (busca em largura, busca de custo uniforme, busca em profundidade, busca
com aprofundamento iterativo, busca bidirecional).
(b) Qual dos algoritmos apresentou melhor resultado? Considerando o custo do caminho
e o número de nós avaliados até que a solução fosse encontrada.
4
. Realize uma busca utilizando o algoritmo A* para encontrar o melhor caminho para
chegar a Bucharest partindo de Lugoj. Construa a árvore de busca criada pela execução do
algoritmo apresentando os valores de f(n), g(n) e h(n) para cada nó. Utilize a heurística de
distância em linha reta.
Arad
366 Mehadia
0 Neamt
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
160 Oradea
242 Pitesti
161 Rimnicu Vilcea 193
Fagaras
Giurgiu
Iasi
176 Sibiu
253
329
199
374
80
77
Timisoara
226 Vaslui
244 Zerind
151 Urziceni
Lugoj
Hirsova
5
. Você precisa construir um sistema para auxiliar os usuários do metro de Paris a encontrar
a melhor rota entre as diversas estações do metro.
Considere que:
O metro tem somente 4 linhas (Figura 1);
A distância real entre duas estações é dada pela tabela 1 e a distância em linha
reta é dada pela tabela 2;
A velocidade média de um trem é de 40 km/h;
O tempo gasto para trocar de linha dentro da mesma estação é de 5 minutos;
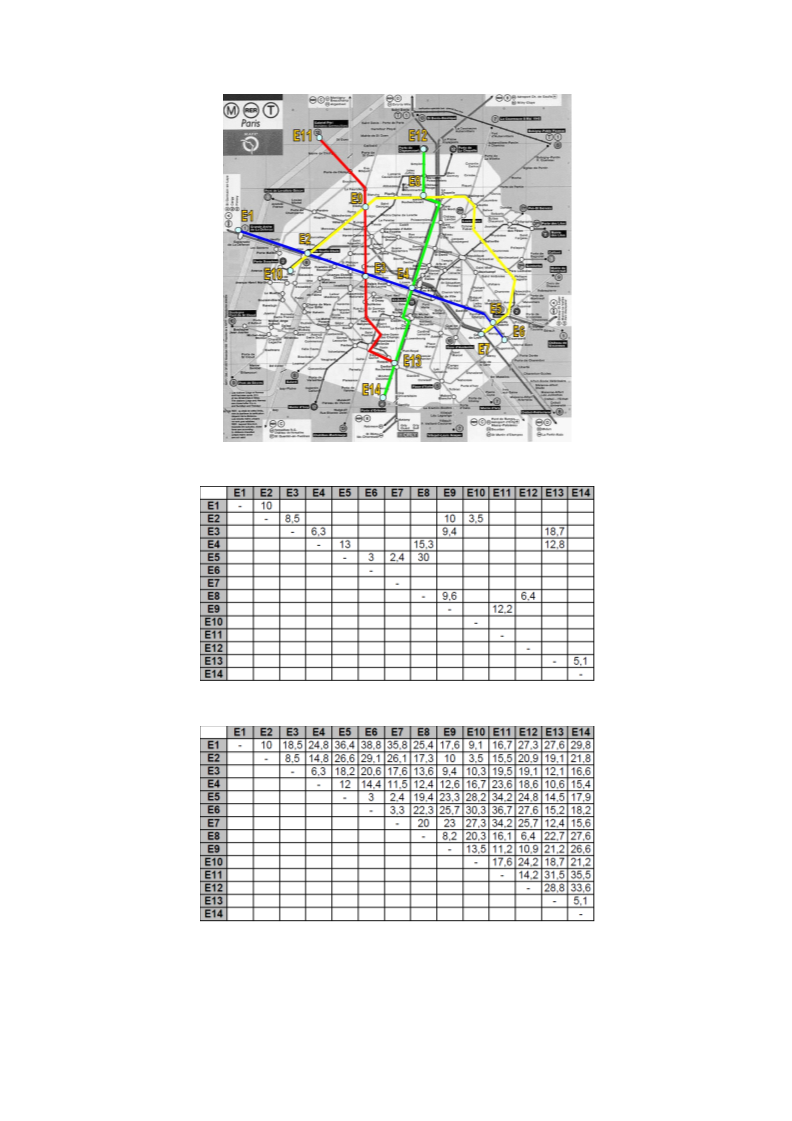
Figura 1: Linhas do metro de Paris.
Tabela 1: Distancias reais entre as estações do metro de Paris.
Tabela 2: Distancias em linha reta entre as estações do metro de Paris.
(a) Descreva o problema em termos de um problema de busca definindo o espaço de
estados, o estado inicial, o estado final, os operadores de transição entre os estados
(ações) e a função de avaliação utilizada pelo algoritmo de busca heurística A*.
(
b) Realize uma busca utilizando o algoritmo A* para encontrar o melhor caminho para
chegar a estação E7 partindo da estação E13. Construa a árvore de busca criada pela
execução do algoritmo apresentando os valores de f(n), g(n) e h(n) para cada nó.
6
. Problema SAT: seja x = (x1, x2,..., xn) um vetor de n variáveis booleanas (i.e. cada variável xi
assume um dos valores em {0,1}). Seja f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)] uma fórmula normal
conjuntiva com m cláusulas, onde cada cláusula cj(x) é uma disjunção de literais, e um
literal é uma das variáveis booleanas ou sua negação.
Por exemplo, considere um vetor com três variáveis x = (x1, x2, x3). Um exemplo de fórmula
normal conjuntiva seria:
f(x) = [(x1)∧ (¬x2) ∧ (x2 ∨ ¬x3) ∧ (x1 ∨ ¬x3)]
Composta pelas seguintes cláusulas:
c1(x) = (x1)
c2(x) = (¬x2)
c3(x) = (x2 ∨ ¬x3)
c4(x) = (x1 ∨ ¬x3)
Uma fórmula é dita satisfatível quando existe uma atribuição de valores para (x1, x2,..., xn)
tal que todas as cláusulas da fórmula sejam satisfeitas, isto é, cj(x) = 1 para j=1,...,m. No
exemplo acima, f(x) é satisfatível e x = (1, 0, 0) é uma possível atribuição de valores para as
variáveis x1, x2 e x3 que tornam verdadeiras todas as quatro cláusulas da fórmula.
O problema SAT consiste em: dada uma fórmula, responder se a fórmula é satisfatível ou
não. Encontrar uma atribuição de valores que satisfaçam uma dada fórmula é uma tarefa
que pode ser formulada como um problema de busca. Assim, para um conjunto qualquer
de variáveis x = (x1, x2,..., xn) e uma dada fórmula f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)], proponha
uma solução para o problema SAT como Algoritmos Genéticos.
Para isso, use o seguinte caso base:
(¬x ∨ ¬z ∨ y) ∧ (¬y ∨ z) ∧ (x ∨ ¬z) ∧ (y) ∧ (¬y ∨ ¬x ∨ ¬w ∨ z)
(
(
(
(
(
(
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para
gerar uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse
processo por 8 gerações ou até que a solução do problema seja encontrada.

7
. Deseja-se construir um sistema para determinar os dias bons para jogar golfe. Para isso,
foi coletado um conjunto de exemplos que incluem informações sobre o Clima,
Temperatura, Humidade, Vento, e também a decisão que indica se aquele caso é um bom
dia para jogar golfe (Saída/Classe). Com base nesse conjunto de exemplos, construa uma
Árvore de Decisão baseada no calculo da entropia dos atributos. Apresente a Árvore de
Decisão criada pelo algoritmo e todos os cálculos da entropia dos atributos.
Clima
Temperatura Humidade Vento Saída/Classe
X1 Ensolarado
X2 Ensolarado
Quente
Quente
Quente
Suave
Frio
Frio
Suave
Frio
Suave
Suave
Suave
Suave
Alta
Alta
Alta
Não
Sim
Não
Não
Sim
Sim
Não
Não
Não
Sim
Sim
Sim
Não
Não
Sim
Sim
Não
Sim
Não
Sim
Sim
Sim
Sim
Não
X3
X4
X5
X6
Nublado
Chuvoso
Chuvoso
Nublado
Alta
Normal
Normal
Alta
Normal
Normal
Normal
Alta
X7 Ensolarado
X8 Ensolarado
X9
Chuvoso
X10 Ensolarado
X11
X12
Nublado
Chuvoso
Alta
8
. Com base nas imagens dos Simpsons utilizadas na Lista de Exercícios 5, selecione um
conjunto de pelo menos 4 características numéricas para serem utilizadas no algoritmo
KNN.
(
a) Utilizando as características escolhidas, crie um conjunto de treinamento (com
pelo menos 10 exemplos) utilizando algumas das imagens que estão no conjunto
de treinamento.
(
b) Selecione 5 imagens do conjunto de teste, gere o vetor de características destas
novas imagens e realize a classificação dos exemplos utilizando o algoritmo KNN.
Em seguida, calcule a precisão da classificação.
9
. Considere o seguinte conjunto de treinamento:
X1 X2 X3 X4 Classe
0
1
1
0
1
0
1
1
1
1
1
1
0
0
1
1
0
0
1
0
a) Defina (desenhe) a estrutura de um Perceptron para realizar a classificação deste
conjunto de dados.
b) Inicialize os pesos aleatoriamente e, em seguida, mostre como os pesos serão
modificados durante o processo de treinamento do Perceptron. Use uma taxa de

aprendizagem de 0.1 e um Threshold Linear de 0.2. Mostre todos os cálculos
realizados.
1
0. Considere o seguinte conjunto de exemplos não rotulados:
ID
1
X1
X2
1.9
7.3
2
3
4
5
6
7
8
9
3.4
2.5
1.5
3.5
2.2
3.4
3,6
5
7.5
6.8
6.5
6.4
5.8
5.2
4
1
2
3
4
5
6
7
8
9
1
2
13
3.2
2.4
2.6
3
11
1
4
1
1
1
1
1
1
1
1
0
1
2
3
4
5
6
7
4.5
6
15
10
16
1.9
1
17
2.7
2.4
2
1.9
0.8
1.6
1
1.8
1
Utilize o algoritmo K-Means para encontrar as 3 classes existentes. Calcule e mostre a
posição dos centróides durante todas as iterações do algoritmo.
