
INF 1771 – Inteligência Artificial
Aula 08 – Lógica de Primeira Ordem
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Agente Baseado em Conhecimento
•
•
O componente central de um agente baseado em conhecimento
é sua base de conhecimento.
A base de conhecimento é formada por um conjunto de
sentenças expressadas através de uma linguagem lógica de
representação de conhecimento.
•
Deve ser possível adicionar novas sentenças à base e consultar o
que se conhece. Ambas as tarefas podem envolver inferência
(derivação de novas sentenças a partir de sentenças antigas).

Limitações da Lógica Proposicional
•
•
Muito simples para representar o conhecimento de
ambientes complexos de uma forma concisa.
Falta de capacidade de expressão para descrever um
ambiente com muitos objetos.
–
Exemplo em linguagem natural:
• “quadrados adjacentes a poços possuem brisa”
–
Em lógica proposicional:
•
B1,1⇔(P1,2 ∨ P2,1) - (Seria necessário declarar todas as salas!)

Linguagem Natural
Objetos: pessoas, casas, números, cores, jogos, séculos...
Relações:
•
•
–
–
–
Unárias: propriedades de um objeto.
•
Exemplo: vermelho, redondo, falso
n-árias: relacionam grupos de objetos.
•
Exemplo: irmão de, maior que, interior a, parte de...
Funções: um objeto está relacionado a exatamente um objeto.
•
Exemplo: pai de, melhor amigo de, terceiro turno de, uma unidade maior que...
•
Linguagem da lógica de primeira ordem é elaborada em torno
de objetos e relações.

Lógica de Primeira Ordem
•
Principal diferença entre lógica proposicional e a lógica
de primeira ordem é o compromisso ontológico, ou seja,
o que cada linguagem pressupões sobre a natureza da
realidade:
–
Lógica Proposicional: pressupõe que existem fatos que são
válidos ou não-válidos no mundo.
–
Lógica de Primeira Ordem: pressupõe que o mundo
consiste em objetos com certas relações entre eles que são
válidas ou não-válidas.
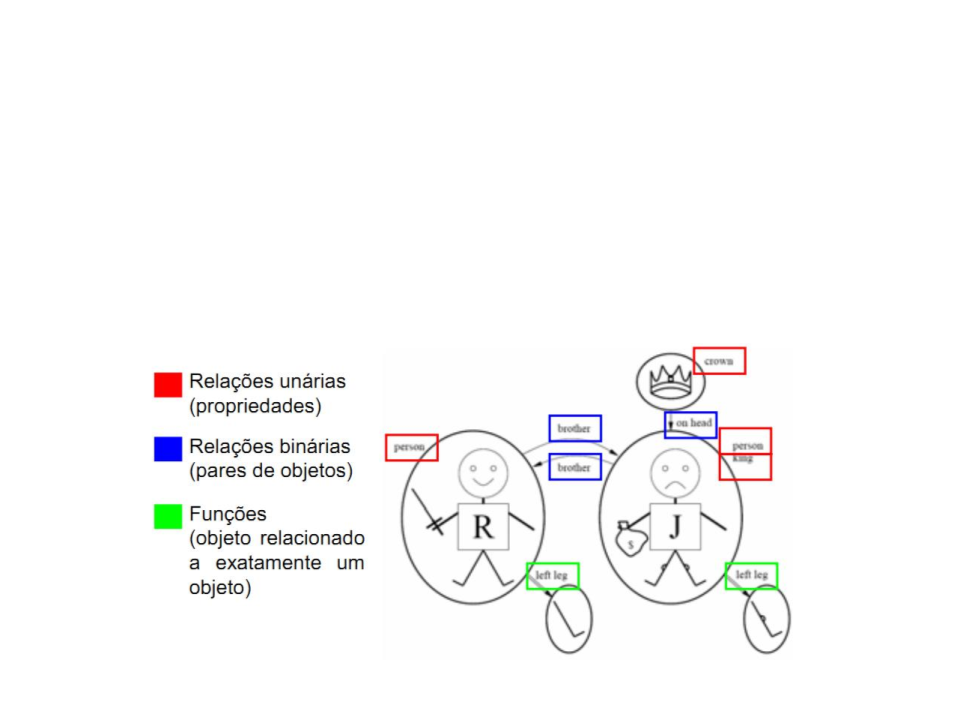
Modelo em Lógica de Primeira Ordem
•
Exemplo: Ricardo Coração de Leão, rei da Inglaterra
de 1189 a 1199 e seu irmão mais jovem, o perverso
rei João, que governou de 1199 a 1215:

Sintaxe da Lógica de Primeira Ordem
•
Símbolos - Começam com letras maiúsculas e podem ser de
três tipos:
–
–
–
Símbolos de constantes: Representam objetos.
Exemplo: Ricardo e João
Símbolos de predicados: Representam relações.
Exemplo: Irmão, NaCabeça, Pessoa
Símbolos de funções: Representam funções.
Exemplo: PernaEsquerda
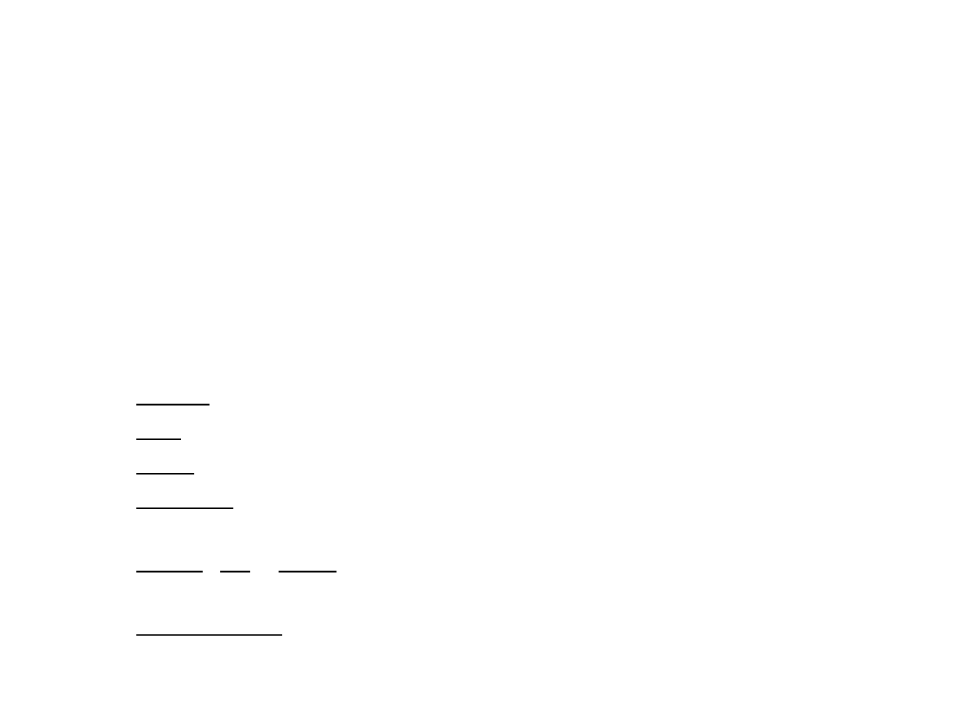
Sintaxe da Lógica de Primeira Ordem
•
•
Interpretação - Especifica quais objetos, relações e funções
são referidos pelos símbolos de constantes, predicados e
funções:
Interpretação pretendida:
–
–
–
–
Ricardo se refere a “Ricardo Coração de Leão”
…João se refere ao “perverso rei João”
…Irmão se refere à “relação de fraternidade”
NaCabeça se refere à relação “na cabeça” que é válida entre a coroa e o rei
João
–
–
Pessoa, Rei e Coroa se referem aos conjuntos de objetos que são pessoas,
reis e coroas
PernaEsquerda se refere à função “perna esquerda”.

Sintaxe da Lógica de Primeira Ordem
•
•
Sentenças atômicas são formadas a partir de um símbolo de
predicado seguido por uma lista de termos entre parênteses.
Exemplos:
–
–
Irmão(Ricardo, João)
Casado(Pai(Ricardo), Mãe(João))
Uma sentença atômica é verdadeira em um modelo, sob uma
dada interpretação, se a relação referida pelo símbolo de
predicado é válida entre os objetos referidos pelos
argumentos.

Sintaxe da Lógica de Primeira Ordem
•
•
Sentenças complexas podem ser formadas pelo uso
de conectivos lógicos, da mesma maneira que na
lógica proposicional.
Exemplos:
–
–
–
–
¬Irmão(PernaEsquerda(Ricardo), João)
Irmão(Ricardo,João) ∧ Irmão(João, Ricardo)
Rei(Ricardo) ∨ Rei(João)
¬Rei(Ricardo) ⇒ Rei(João)

Sintaxe da Lógica de Primeira Ordem
•
•
Quantificadores (∀, ∃) são utilizados para expressar propriedades de
coleções inteiras de objetos.
Quantificador Universal (∀): “Para todo...” ∀x P, onde P é qualquer
expressão lógica, afirma que P é verdadeira para todo objeto x.
Exemplo:
∀x Rei(x) ⇒ Pessoa(x)
•
Quantificador Existencial (∃): “Para algum...” ∃x P afirma que P é
verdadeira para pelo menos um x.
Exemplo:
∃
x Rei(x)

Sintaxe da Lógica de Primeira Ordem
•
•
Quantificadores aninhados são usados em sentenças
complexas compostas.
Exemplos:
–
–
–
–
∀x ∀y Irmão(x,y) ⇒ Parente(x,y)
• “Irmãos são parentes”
∀x,y Parente(x,y) ⇔ Parente(y,x)
•
“Parente é uma relação simétrica”
∀x ∃y Ama(x,y)
•
“Todo mundo ama alguém”
∃y ∀x Ama(x,y)
•
“Existe alguém que é amado por todo mundo”

Sintaxe da Lógica de Primeira Ordem
•
•
Os quantificadores (∀, ∃) estão conectados um ao outro por
meio de negação.
Exemplos:
–
…∀x ¬Gosta(x,Cenouras) ≡¬∃x Gosta(x,Cenouras)
“todo mundo detesta cenouras” ≡ “não existe alguém que goste de
cenouras”
–
∀x Gosta(x,Sorvete) ≡¬∃x ¬Gosta(x,Sorvete)
“
todo mundo gosta de sorvete” ≡ “não existe alguém que não goste de
sorvete”

Sintaxe da Lógica de Primeira Ordem
•
•
Em lógica de primeira ordem pode-se usar o símbolo
de igualdade para fazer declarações afirmando que
dois termos se referem ao mesmo objeto.
Exemplo:
–
Pai(João) = Henrique

Sintaxe da Lógica de Primeira Ordem
Sentença → SentençaAtômica
|
|
|
(Sentença Conectivo Sentença)
Quantificador Variável, ...Sentença
¬Sentença
SentençaAtômica → Predicado(Termo,...) | Termo=Termo
Termo → Função (Termo,...)
|
Constante
|
Variável
Conectivo →⇒ | ∧ | ∨ | ⇔
Quantificador →∀ | ∃
Constante → A | X1 | João | ...
Variável → a | x | s | ...
Predicado → Antes | TemCor | Chovendo | ...
Função → Mãe | PernaEsquerda | ...
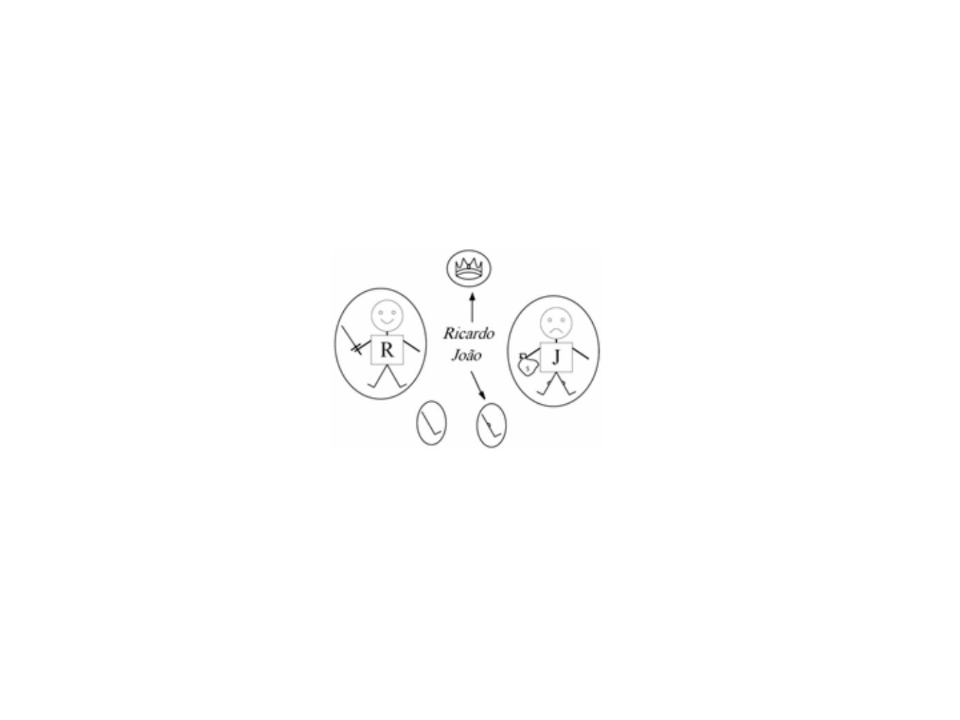
Semântica da Lógica de Primeira Ordem
•
Se existem 5 objetos, existem 25 interpretações para os símbolos
Ricardo e João.
•
•
Número de modelos pode ser ilimitado (pode incluir, por exemplo
os números reais). Logo, o número de modelos possível é ilimitado.
Verificar consequência lógica pela enumeração de todos os
modelos não é uma opção.

Exemplo - Parentesco
•
•
•
•
•
•
•
Objetivo:
Determinar o parentesco de grupos de pessoas.
Fatos:
“Elizabeth é a mãe de Charles”, “Charles é o pai de William”
Regras:
“a avó de uma pessoa é a mãe do pai de uma pessoa”
„Objetos:
Pessoas
Predicados unários:
Masculino e Feminino
„Predicados (relações de parentesco):
Ancestral, Parente, Irmão, ...
„Funções:
Mãe e Pai (cada pessoa tem apenas um de cada)

Exemplo - Parentesco
•
•
•
A mãe de alguém é o ancestral feminino de alguém
–
∀m,c Mãe(c)=m ⇔ Feminino(m) ∧ Ancestral(m,c)
O marido de alguém é o cônjuge masculino de alguém
–
∀w,h Marido(h,w) ⇔ Masculino(h) ∧ Cônjuge(h,w)
Masculino e feminino são categorias disjuntas
–
∀x Masculino(x) ⇔¬Feminino(x)

Exemplo - Parentesco
•
•
•
Ancestral e descendente são relações inversas
–
∀p,c Ancestral(p,c) ⇔ Descendente(c,p)
Avô é um pai do pai de alguém
–
∀g,c Avô(g,c) ⇔∃p Pai(g,p) ∧ Pai(p,c)
Um parente é outro descendente dos ancestrais de alguém
–
∀x,y Parente(x,y) ⇔ x ≠ y ∧ ∃p Ancestral(p,x) ∧ Ancestral(p,y)

Exemplo - Wumpus
•
Estrutura da Base de Conhecimento:
–
–
–
São armazenadas as sentenças representando as percepções do agente e a
hora em que elas ocorreram.
Fedor, Brisa e Resplendor são constantes inseridas em uma lista.
•
Exemplo: Percepção ([Fedor, Brisa, Resplendor, Nenhum, Nenhum], 5)
Ações:
•
Virar(Direita), Virar(Esquerda), Avançar, Atirar, Agarrar, Soltar.
•
Consultas:
–
∃x MelhorAção(x,5)
–
ASK deve retornar uma lista de vinculação como {a/Agarrar}
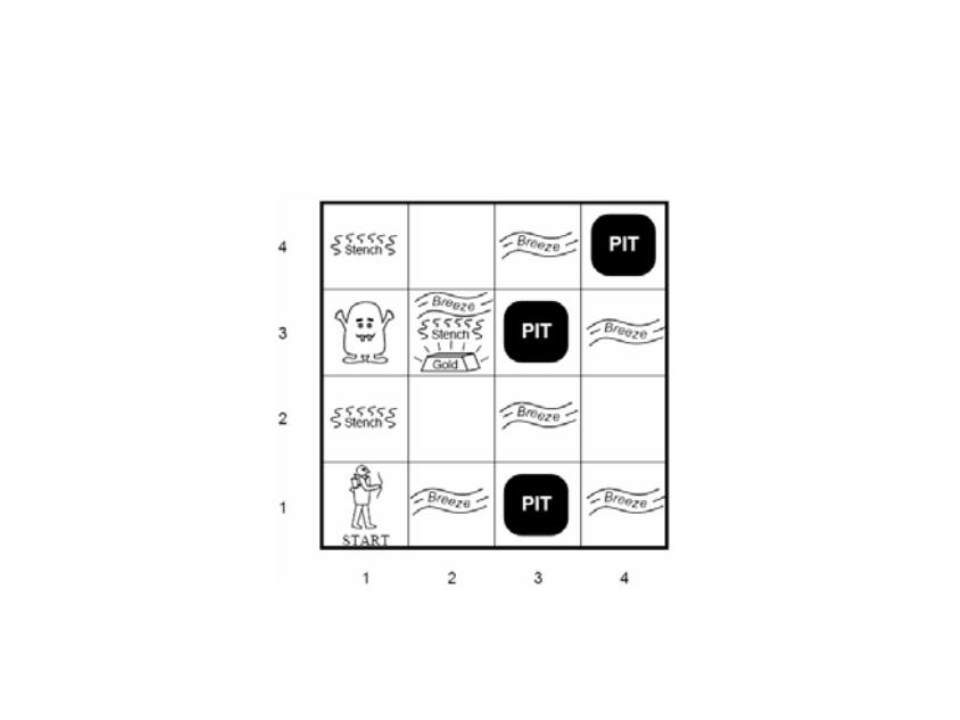
Exemplo - O Mundo de Wumpus

Exemplo - Wumpus
•
•
Os dados brutos da percepção implicam certos fatos sobre o
estado atual.
Exemplos:
–
∀t,s,g,m,c Percepção([s,Brisa,g,m,c],t) ⇒ Brisa(t)
–
∀t,s,b,m,c Percepção([s,b,Resplendor,m,c],t) ⇒ Resplendor(t)
Comportamentos simples podem ser implementados por
sentenças de implicação quantificadas.
Exemplo:
–
∀t Resplendor(t) ⇒ MelhorAção(Agarrar,t)

Exemplo - Wumpus
•
•
Adjacência de dois quadrados:
–
∀x,y,a,b Adjacente([x,y],[a,b]) ⇔ [a,b] ∈ {[x+1,y], [x-1,y], [x,y+1], [x,y-1]}
Se o agente estiver em um quadrado e perceber uma brisa,
então esse quadrado é arejado:
–
∀s,t Em(Agente,s,t) ∧ Brisa(t) ⇒ Arejado(s)

Exemplo - Wumpus
•
Regras de diagnóstico: algumas causas ocultas do ambiente
conduzem a novas percepções.
–
–
∀s Arejado(s) ⇒∃r Adjacente(r,s) ∧ Poço(r)
∀s ¬Arejado(s) ⇒¬∃r Adjacente(r,s) ∧ Poço(r)

Construção da Base de Conhecimento
(
(
(
(
(
(
(
1) Identificar a tarefa;
2) Agregar conhecimento relevante;
3) Definir um vocabulário de predicados, funções e constantes;
4) Codificar o conhecimento geral sobre o domínio;
5) Codificar uma descrição da instância específica do problema;
6) Formular consultas ao procedimento de inferência e obter respostas;
7) Depurar a base de conhecimento;

Prolog
•
O Prolog é uma linguagem de programação baseada em lógica
de primeira ordem.
•
•
Não é padronizada.
Algumas implementações: SICStus Prolog, Borland Turbo
Prolog, SWI-Prolog...
•
Geralmente é interpretado, mas pode ser compilado.

Leitura Complementar
•
Russell, S. and Norvig, P. Artificial Intelligence: a
Modern Approach, 3nd Edition, Prentice-Hall,
2009.
•
•
Capítulo 8: First-Order Logic
Capítulo 9: Inference in First-Order Logic
