INF1771 - INTELIGÊNCIA ARTIFICIAL
LISTA DE EXERCÍCIOS 2
Aluno:
1
. Você precisa construir um sistema para auxiliar os usuários do metro de Paris a encontrar
a melhor rota entre as diversas estações do metro.
Considere que:
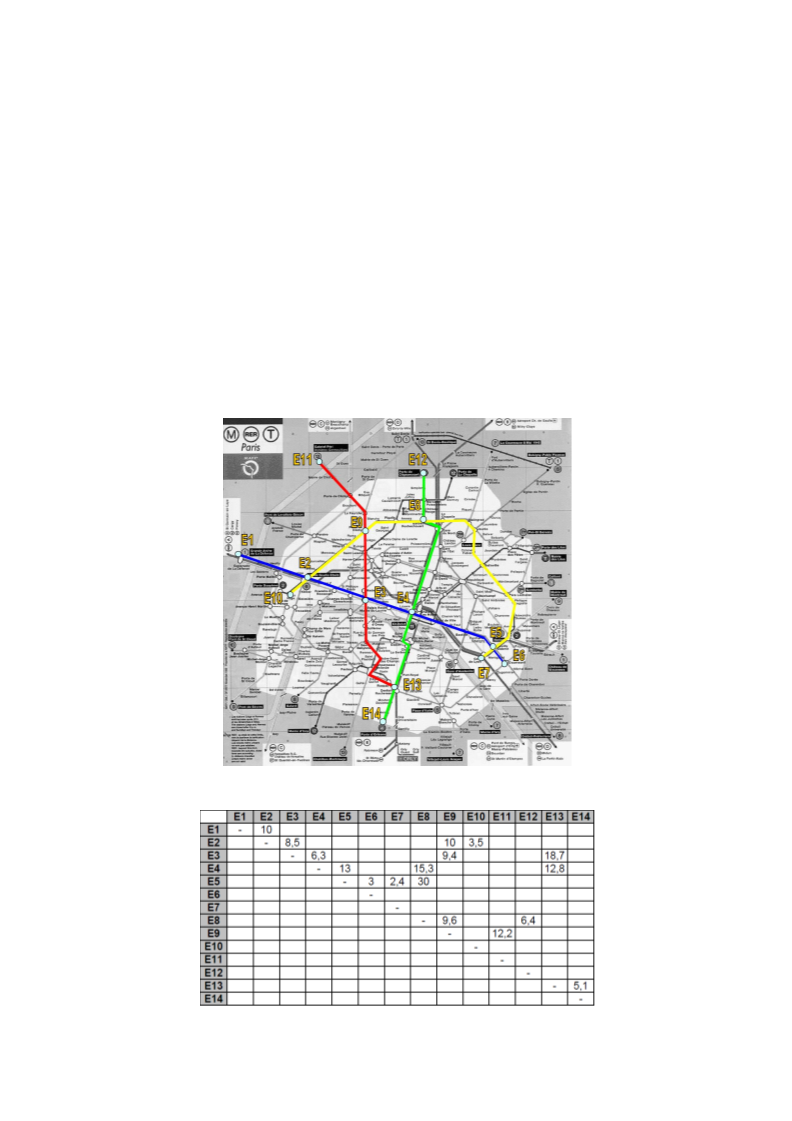
O metro tem somente 4 linhas (Figura 1);
A distância real entre duas estações é dada pela tabela 1 e a distância em linha
reta é dada pela tabela 2;
A velocidade média de um trem é de 40 km/h;
O tempo gasto para trocar de linha dentro da mesma estação é de 5 minutos;
Figura 1: Linhas do metro de Paris.
Tabela 1: Distancias reais entre as estações do metro de Paris.
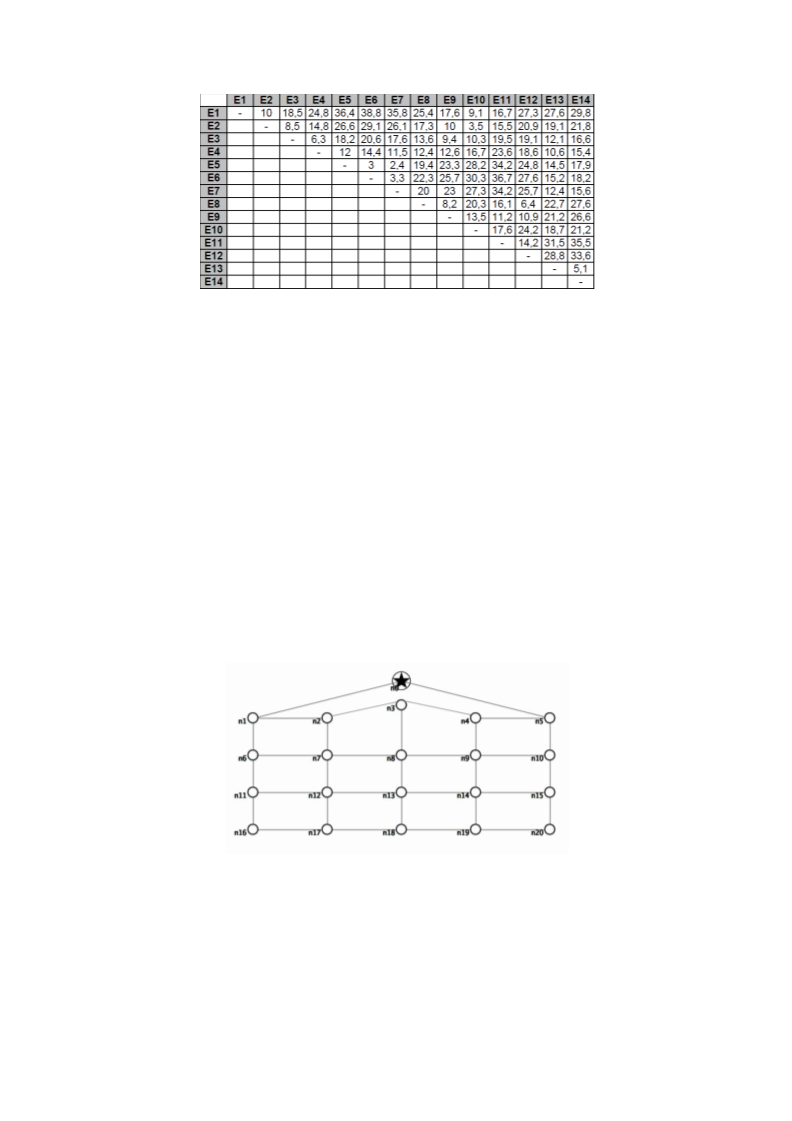
Tabela 2: Distancias em linha reta entre as estações do metro de Paris.
(a) Descreva o problema em termos de um problema de busca definindo o espaço de
estados, o estado inicial, o estado final, os operadores de transição entre os estados
(ações) e a função de avaliação utilizada pelo algoritmo de busca heurística A*.
(
b) Realize uma busca utilizando o algoritmo A* para encontrar o melhor caminho para
chegar a estação E7 partindo da estação E13. Construa a árvore de busca criada pela
execução do algoritmo apresentando os valores de f(n), g(n) e h(n) para cada nó.
2
. Utilize o algoritmo de busca local Hill Climbing na rede mostrada abaixo para chegar ao nó
em formato de estrela (n0) partindo do nó n18. Mostre a sequencia de nós visitados
durante a execução do algoritmo. Utilize a distancia em linha reta aproximada para
calcular a função heurística. Caso o algoritmo fique preso em um mínimo local, utilize o a
variação do Hill Climbing com reinicialização aleatória.
2
3
23
1
2
12
8
5
5
5
1
0
10
10
10
3
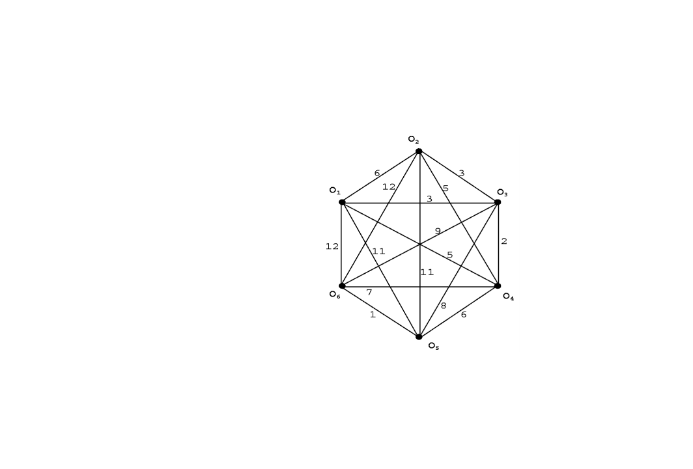
. O grafo abaixo mostra a localização de 6 itens em um mapa e as respectivas distâncias em
quilômetros:
Tem-se um problema onde é necessário coletar os 6 itens com o menor custo possível
usando um algoritmo genético.
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para gerar
uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse processo
por 5 gerações ou até que a solução do problema seja encontrada.
5
. Considere a seguinte equação:
3 2
x + y - w + z + x = 256
8
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para gerar
uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse processo
por 5 gerações ou até que a solução do problema seja encontrada.
6
. Problema SAT
Seja x = (x1, x2,..., xn) um vetor de n variáveis booleanas (i.e. cada variável xi assume um dos
valores em {0,1}). Seja f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)] uma fórmula normal conjuntiva com
m cláusulas, onde cada cláusula cj(x) é uma disjunção de literais, e um literal é uma das
variáveis booleanas ou sua negação.
Por exemplo, considere um vetor com três variáveis x = (x1, x2, x3). Um exemplo de fórmula
normal conjuntiva seria:
f(x) = [(x1)∧ (¬x2) ∧ (x2 ∨ ¬x3) ∧ (x1 ∨ ¬x3)]
Composta pelas seguintes cláusulas:
c1(x) = (x1)
c2(x) = (¬x2)
c3(x) = (x2 ∨ ¬x3)
c4(x) = (x1 ∨ ¬x3)
Uma fórmula é dita satisfatível quando existe uma atribuição de valores para (x1, x2,..., xn)
tal que todas as cláusulas da fórmula sejam satisfeitas, isto é, cj(x) = 1 para j=1,...,m. No
exemplo acima, f(x) é satisfatível e x = (1, 0, 0) é uma possível atribuição de valores para as
variáveis x1, x2 e x3 que tornam verdadeiras todas as quatro cláusulas da fórmula.
O problema SAT consiste em: dada uma fórmula, responder se a fórmula é satisfatível ou
não. Encontrar uma atribuição de valores que satisfaçam uma dada fórmula é uma tarefa
que pode ser formulada como um problema de busca. Assim, para um conjunto qualquer
de variáveis x = (x1, x2,..., xn) e uma dada fórmula f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)], proponha
uma solução para o problema SAT como Algoritmos Genéticos.
Para isso, use o seguinte caso base:
(¬x ∨ ¬z ∨ y) ∧ (¬y ∨ z) ∧ (x ∨ ¬z) ∧ (y) ∧ (¬y ∨ ¬x ∨ ¬w ∨ z)
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para gerar
uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse processo
por 5 gerações ou até que a solução do problema seja encontrada.
