
INF 1771 – Inteligência Artificial
Aula 09 – Introdução ao Prolog
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Introdução
•
O Prolog é uma linguagem de programação baseada
em lógica de primeira ordem.
•
•
Não é padronizada.
Algumas implementações: SICStus Prolog, Borland
Turbo Prolog, SWI-Prolog...
•
Geralmente é interpretado, mas pode ser compilado.

Prolog x Outras Linguagens
•
•
•
Linguagens Procedimentais (C, Pascal, Basic...):
Especifica-se como realizar determinada tarefa.
Linguagens Orientadas a Objetos (C++, Java, C#...):
Especifica-se objetos e seus métodos.
Prolog: Especifica-se o quê se sabe sobre um
problema e o quê deve ser feito. É mais direcionada
ao conhecimento e menos direcionada a algoritmos.

Programação em Prolog
•
Programar em Prolog envolve:
–
–
–
Declarar alguns fatos a respeito de objetos e seus
relacionamentos.
Definir algumas regras sobre os objetos e seus
relacionamentos.
Fazer perguntas sobre os objetos e seus
relacionamentos.

SWI-Prolog
•
•
•
•
Open Source.
Multiplataforma.
Possui interface com as linguagens C e C++.
www.swi-prolog.org
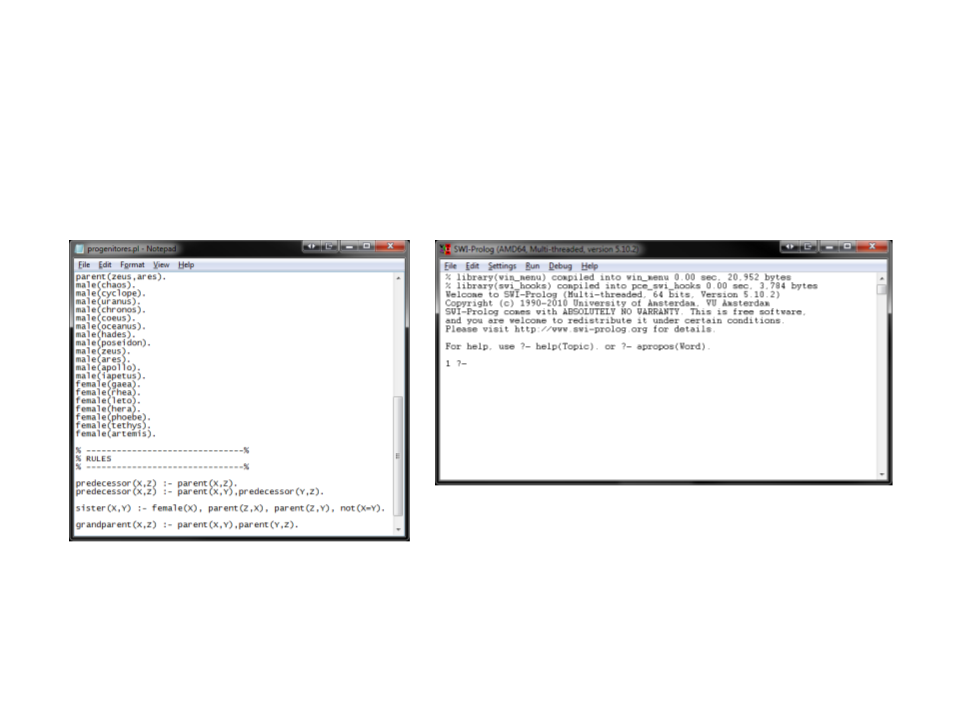
SWI-Prolog - Interface

Sentenças Prolog
•
•
Nomes de constantes e predicados iniciam sempre com letra
minúscula.
O predicado (relação unária, n-ária ou função) é escrito
primeiro e os objetos relacionados são escritos depois entre
parênteses.
•
•
•
Variáveis sempre começam por letra maiúscula.
Toda sentença termina com ponto “.”
Exemplo: gosta(maria, jose).

Operadores Lógicos
Símbolo
Conectivo
Operação Lógica
:
-
IF
Implicação
Conjunção
Disjunção
Negação
,
AND
OR
;
not
NOT

Operadores Relacionais
Operador
X = Y
Significado
Igual a
X \= Y
X < Y
Não igual a
Menor que
Y > X
Maior que
Y =< X
Y >= X
Menor ou igual a
Maior ou igual a

Regras
•
Regras são utilizadas para expressar dependência entre um
fato e outro fato:
–
criança(X) :- gosta(X,sorvete).
–
criança(X) :- not odeia(X,sorvete).
•
Ou grupo de fatos:
– avó(X,Z) :- (mãe(X,Y),mãe(Y,Z)); (mãe(X,Y),pai(Y,Z)).
•
Podem conter listas:
– compra(ana, [roupa, comida, brinquedo])
Definindo Relações por Fatos
•
Exemplo de relações familiares:
–
O fato que Abraão é um progenitor de
Isaque pode ser escrito em Prolog como:
progenitor(abraão, isaque).
–
Neste caso definiu-se progenitor como o
nome de uma relação; abraão e isaque
são seus argumentos.
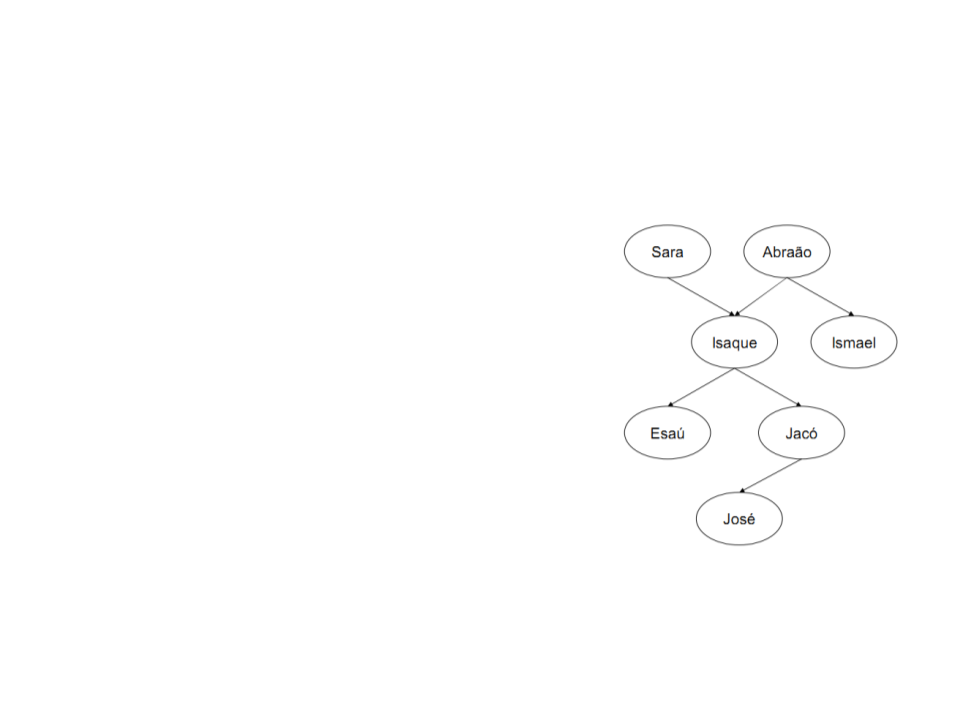
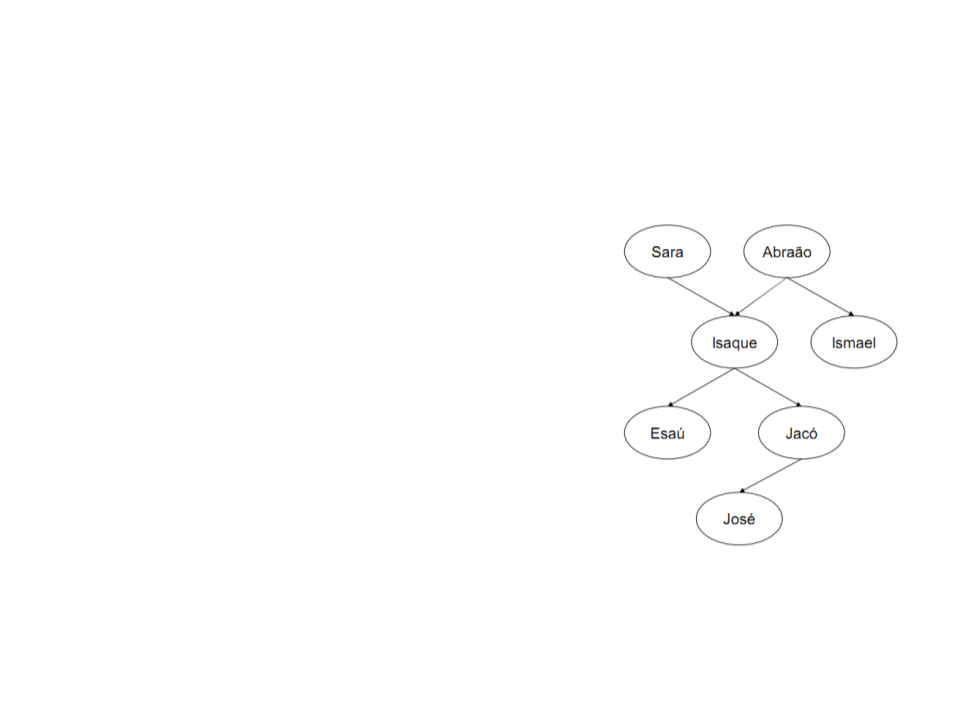
Definindo Relações por Fatos
•
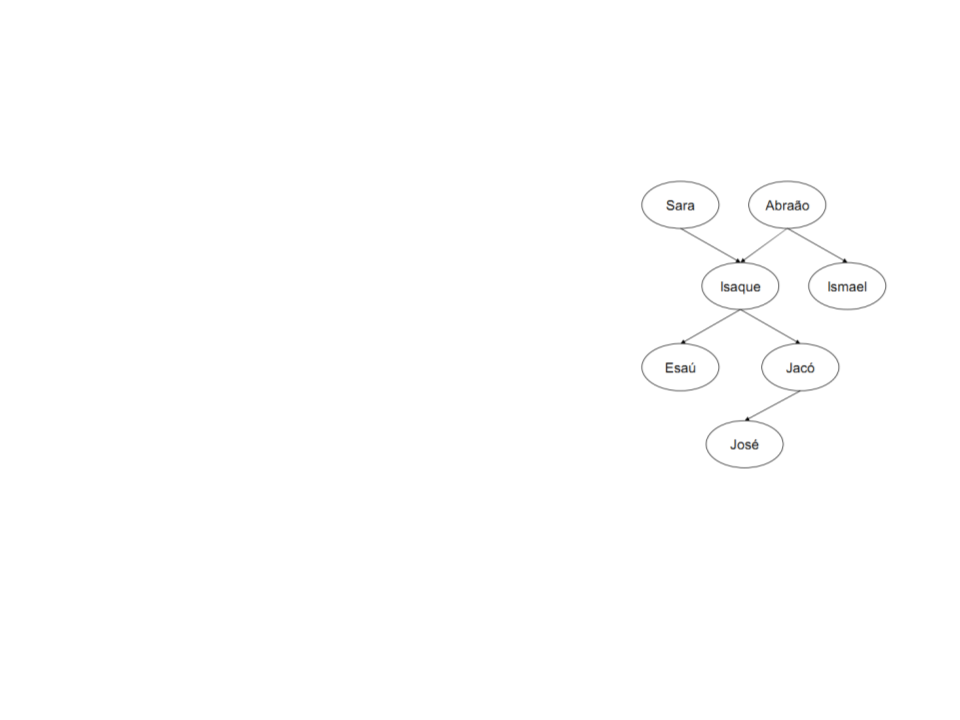
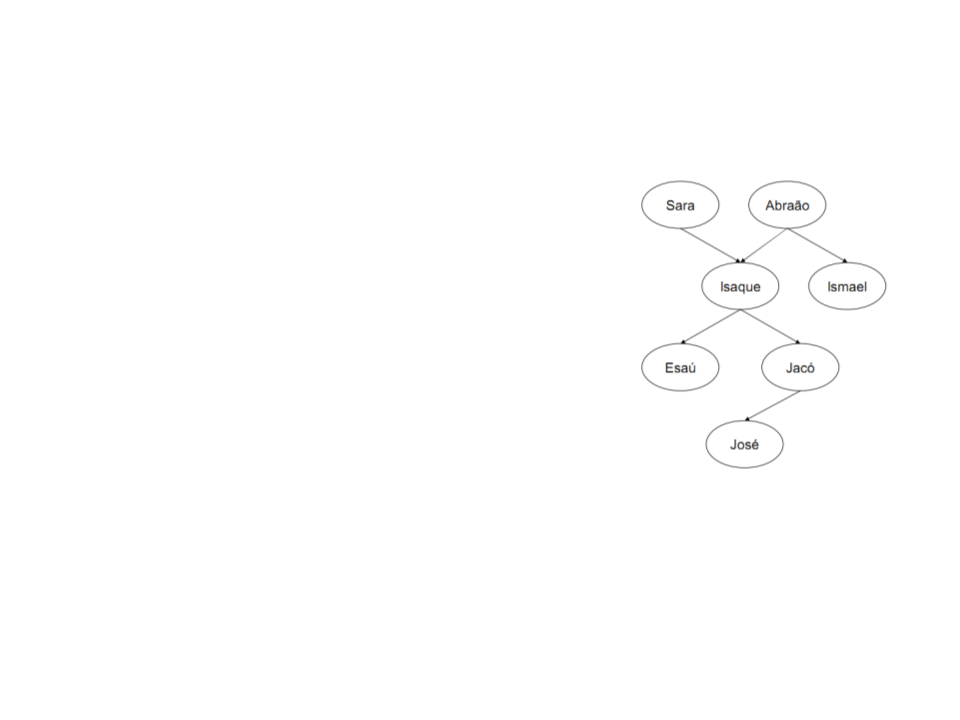
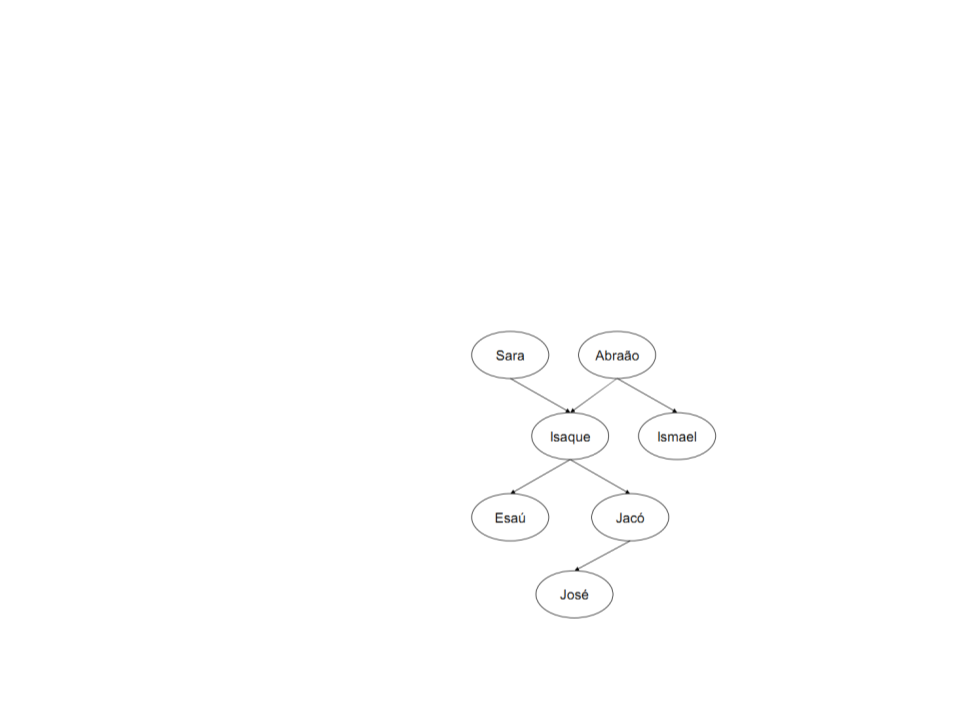
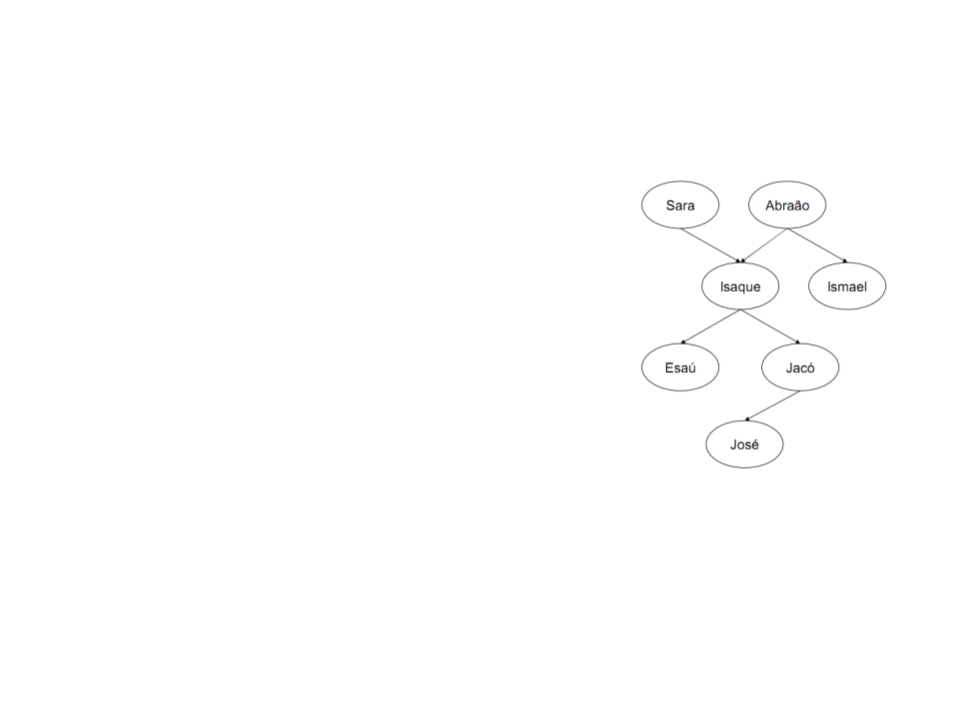
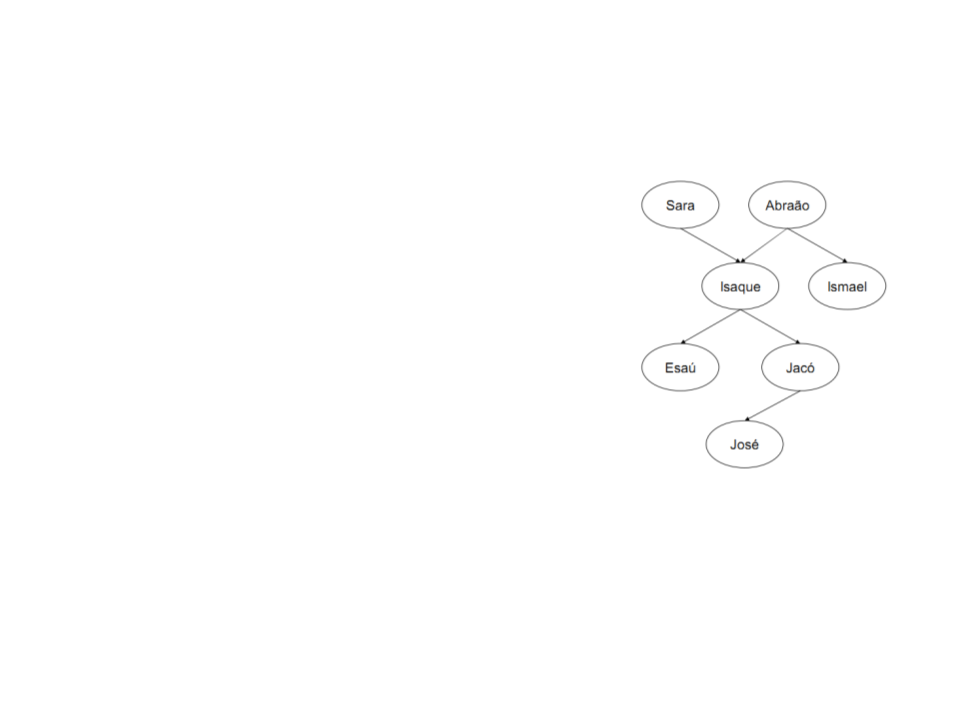
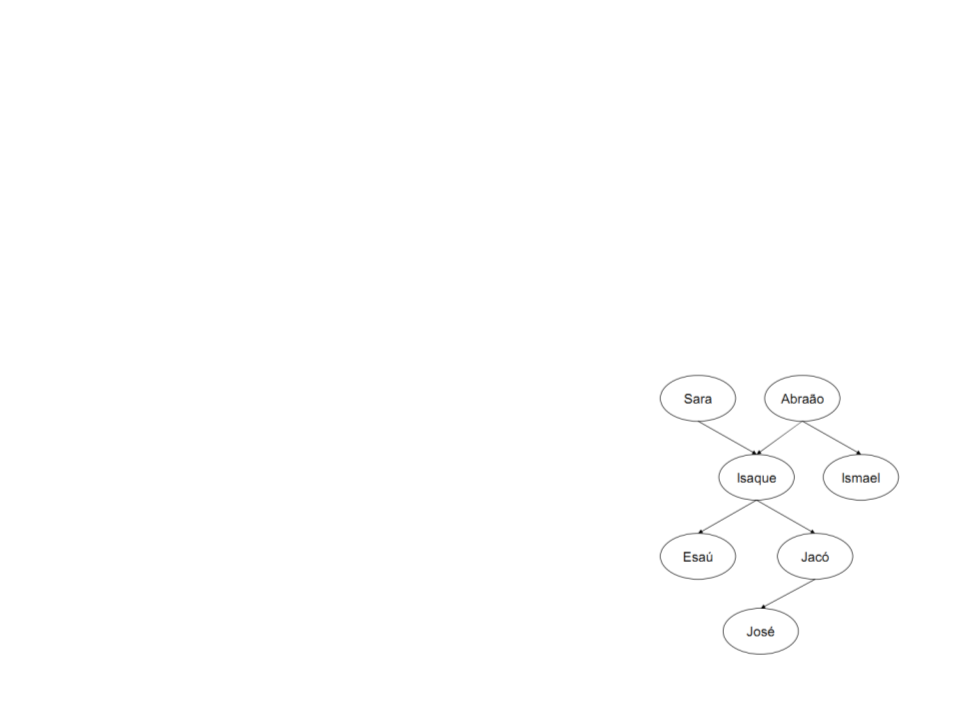
Árvore familiar completa em Prolog:
–
–
–
–
–
–
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
•
Cada cláusula declara um fato sobre a
relação progenitor.
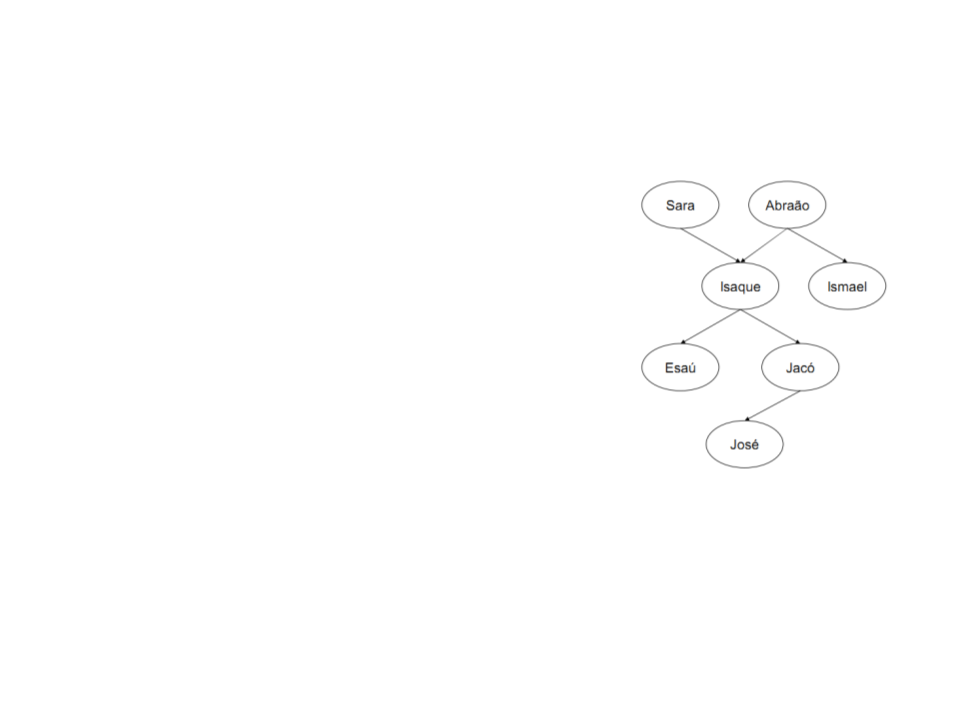
Definindo Relações por Fatos
•
•
Quando o programa é interpretado,
pode-se questionar o Prolog sobre a
relação progenitor, por exemplo:
Isaque é o pai de Jacó?
?- progenitor(isaque,jacó).
Como o Prolog encontra essa
pergunta como um fato inserido em
sua base, ele responde:
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
true
Definindo Relações por Fatos
•
•
•
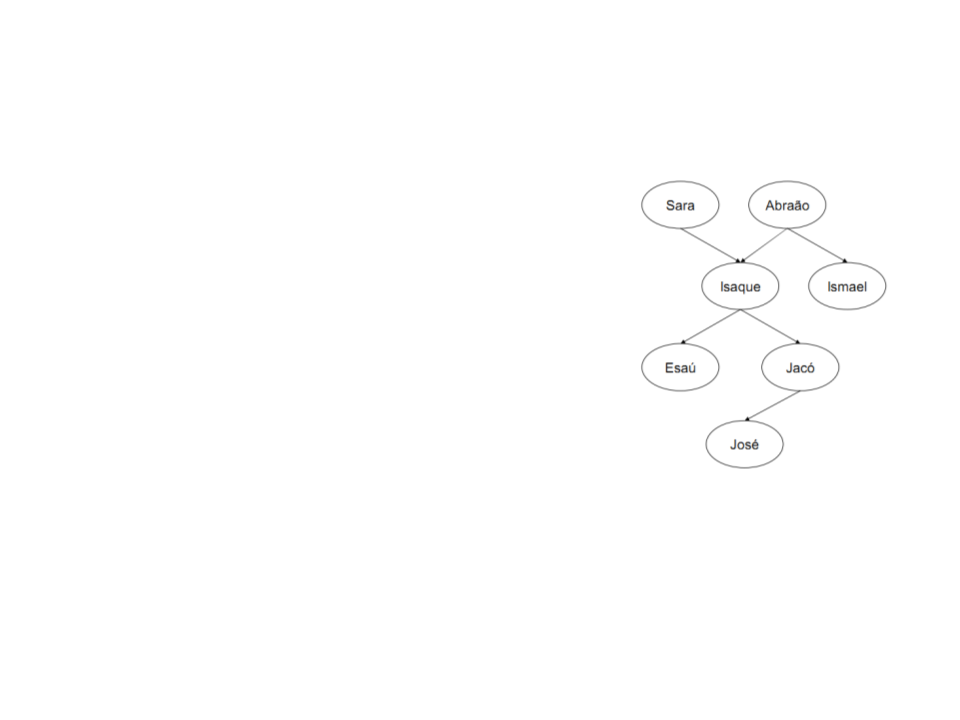
Uma outra pergunta pode ser:
?- progenitor(ismael,jacó).
O Prolog responde:
false
O Prolog também pode responder a pergunta:
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
?
- progenitor(jacó,moisés).
false
Definindo Relações por Fatos
•
•
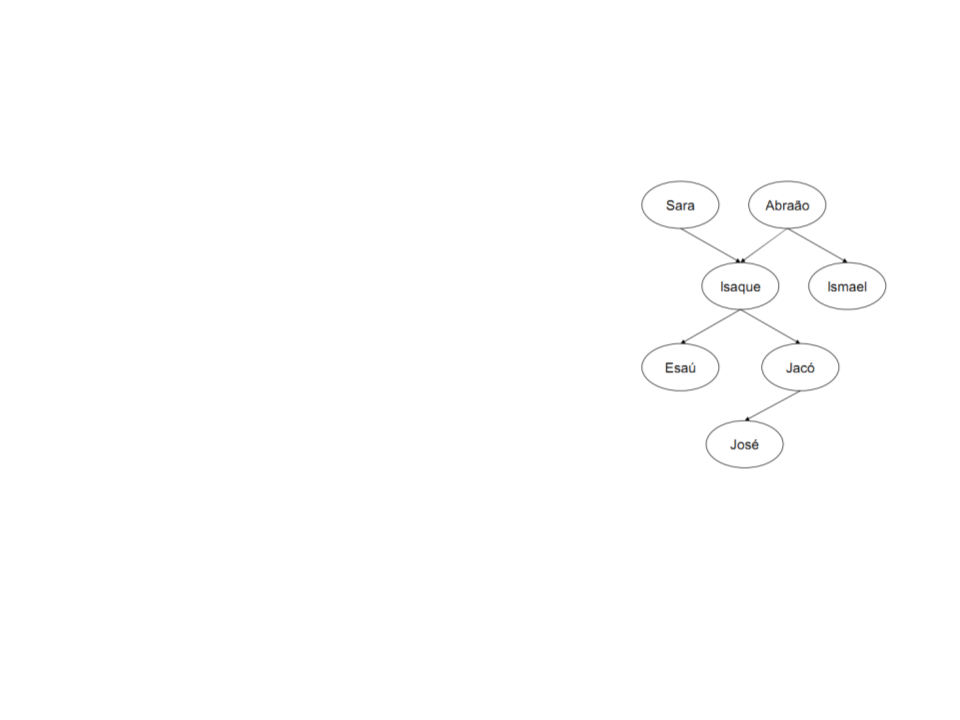
Perguntas mais interessantes também podem
ser efetuadas:
Quem é o progenitor de Ismael?
?- progenitor(X,ismael).
Neste caso, o Prolog não vai responder
apenas true ou false. O Prolog fornecerá o
valor de X tal que a pergunta acima seja
verdadeira‰. Assim a resposta é:
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
X = abraão
Definindo Relações por Fatos
•
•
A pergunta “Quais os filhos de Isaque?” pode
ser escrita como:
?
- progenitor(isaque,X).
Neste caso, há mais de uma resposta
possível. O Prolog primeiro responde com
uma solução:
–
X = esaú
•
•
Pode-se requisitar uma outra solução
digitando ;) e o Prolog a encontra:
(
–
X = jacó
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
Se mais soluções forem requisitadas, o Prolog
ira responder “false”, pois todas as soluções
foram retornadas (false = sem mais soluções).
Definindo Relações por Fatos
•
•
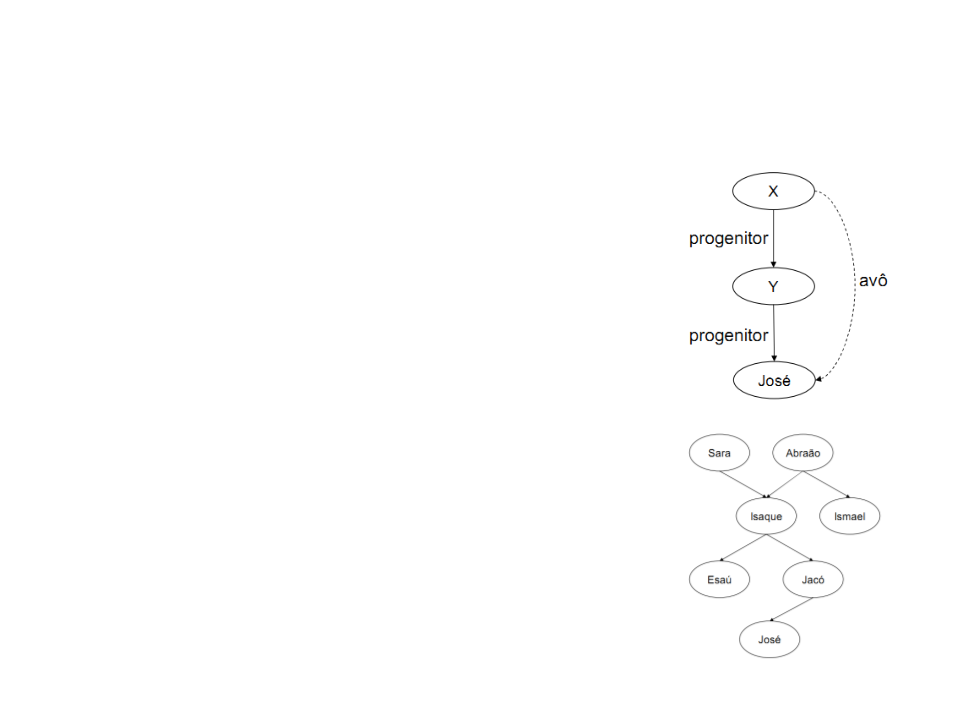
Perguntas mais complexas também podem ser
efetuadas, tais como: Quem é o avô de José?
Como o programa não conhece diretamente a
relação avô, esta pergunta deve ser desmembrada
em dois passos
–
–
(1) Quem é o progenitor de José? Assuma que é um Y
(2) Quem é o progenitor de Y? Assuma que é um X
•
Esta pergunta composta pode ser escrita em
Prolog como:
?- progenitor(Y,josé), progenitor(X,Y).
X = isaque
Y = jacó
Definindo Relações por Fatos
•
De maneira similar, podemos perguntar:
Quem são os netos de Abraão?
?- progenitor(abraão,X), progenitor(X,Y).
X = isaque
Y = esaú
X = isaque
Y = jacó
progenitor(sara,isaque).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
Definindo Relações por Fatos
•
É possível expandir o programa sobre relações familiares de várias formas.
Pode-se, por exemplo, adicionar a informação sobre o sexo das pessoas
envolvidas.
mulher(sara).
homem(abraão).
homem(isaque).
homem(ismael).
homem(esaú).
homem(jacó).
homem(josé).
Definindo Relações por Regras
•
•
Pode-se estender o programa utilizando
regras. Por exemplo, criando a relação filho
como o inverso da relação progenitor.
É possível definir filho de maneira similar à
relação progenitor, ou seja enumerando uma
lista de fatos sobre a relação filho, mas esta
não é a forma correta!
filho(isaque,sara).
progenitor(sara,isaque).
filho(isaque,abraão).
filho(ismael,abraão).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
.
..
Definindo Relações por Regras
•
•
A relação filho pode ser definida de modo
mais elegante:
Para todo X e Y, Y é um filho de X se X é um
progenitor de Y.
Em Prolog:
filho(Y,X) :- progenitor(X,Y).

Definindo Relações por Regras
•
•
A cláusula Prolog filho(Y,X) :- progenitor(X,Y) é
chamada de regra (rule).
Há uma diferença importante entre fatos e regras:
–
Um fato é sempre verdadeiro (verdade incondicional).
–
Regras especificam coisas que são verdadeiras se alguma condição é
satisfeita.

Definindo Relações por Regras
•
•
•
Após definir a regra filho, é possível perguntar ao Prolog se Ismael é filho
de Abraão:
?- filho(ismael, abraão).
Como não existem fatos sobre a relação filho, a única forma do Prolog
responder esta pergunta é aplicando a regra filho:
filho(Y,X) :- progenitor(X,Y).
A regra filho é aplicável a qualquer objeto X e Y; portanto ela pode
também ser aplicada a objetos ismael e abraão.

Definindo Relações por Regras
•
Para aplicar a regra a ismael e abraão, Y tem que ser substituído por
ismael e X por abraão. Ou seja, as variáveis X e Y estão instanciadas a:
X = abraão e Y = ismael
•
•
Depois da instanciação, obtêm-se um caso especial da regra:
filho(ismael,abraão) :- progenitor(abraão,ismael).
Se o Prolog provar que progenitor(abraão,ismael) é verdadeiro, então ele
pode afirmar que filho(ismael,abraão) também é verdade.

Definindo Relações por Regras
•
•
É possível também incluir a especificação da relação mãe,
com base no seguinte fundamento lógico:
Para todo X e Y,
–
–
–
X é a mãe de Y se
X é um progenitor de Y e
X é uma mulher.
•
Traduzindo para Prolog:
mãe(X,Y) :- progenitor(X,Y), mulher(X).
Definindo Relações por Regras
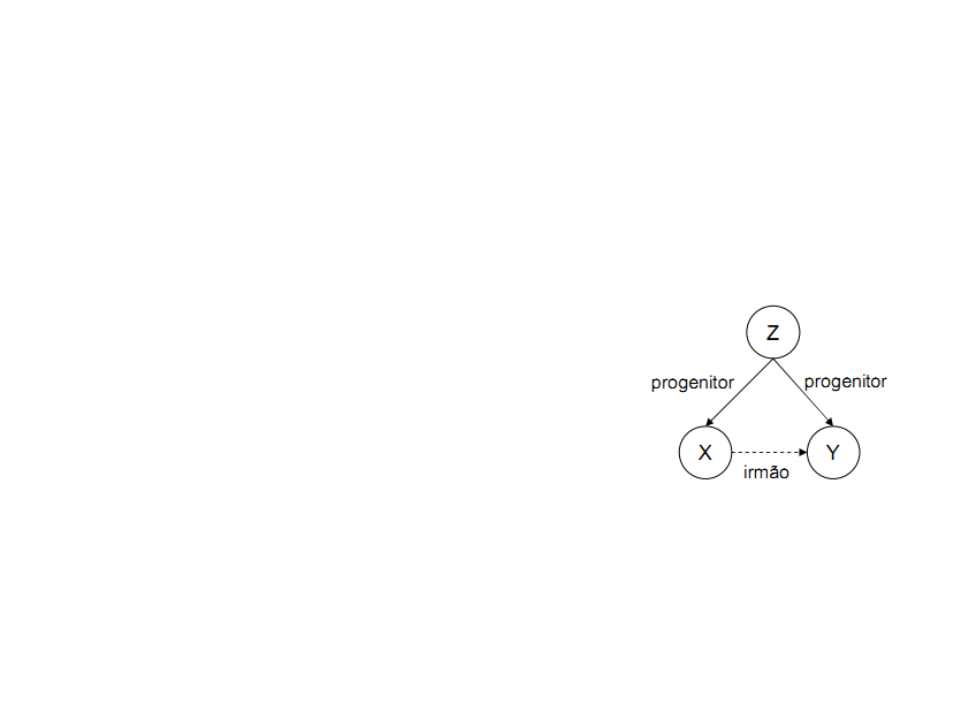
A relação irmão pode ser definida como:
Para todo X e Y,
•
•
–
X é irmão de Y se
–
ambos X e Y têm um progenitor em comum.
•
Em Prolog:
irmão(X,Y) :- progenitor(Z,X), progenitor(Z,Y).

Interpretação Prolog
•
•
A interpretação do programa pode Prolog ser lógica ou procedimental.
A interpretação procedimental corresponde a satisfazer cada subgoal
mediante processos sucessivos de matching.
•
Exemplo:
pai(fred, marcos).
pai(ricardo, pedro).
pai(pedro, paulo).
avo(X,Y) :- pai(X, Z), pai(Z, Y).
---
?- avo(X,paulo).

Programas Prolog
•
•
Programas Prolog podem ser estendidos simplesmente pela
adição de novas cláusulas.
Cláusulas Prolog são de três tipos: fatos, regras e perguntas.
–
–
–
Fatos declaram coisas que são sempre (incondicionalmente)
verdadeiras.
Regras declaram coisas que são verdadeiras dependendo de
determinadas condições.
Através de perguntas, o usuário pode questionar o programa sobre
quais coisas são verdadeiras.
Regras Recursivas
•
•
Para criar uma relação ancestral é necessária a criação de
uma regra recursiva:
ancestral(X,Z) :- progenitor(X,Z).
ancestral(X,Z) :- progenitor(X,Y), ancestral(Y,Z).
Quais os descendentes de Sara?
?- ancestral(sara,X).
X = isaque;
X = esaú;
X = jacó;
X = josé

Programa Exemplo
progenitor(sara,isaque).
filho(Y,X) :- progenitor(X,Y).
progenitor(abraão,isaque).
progenitor(abraão,ismael).
progenitor(isaque,esaú).
progenitor(isaque,jacó).
progenitor(jacó,josé).
mae(X,Y) :- progenitor(X,Y), mulher(X).
avo(X,Z) :- progenitor(X,Y), progenitor(Y,Z).
irmao(X,Y) :- progenitor(Z,X), progenitor(Z,Y).
ancestral(X,Z) :- progenitor(X,Z).
mulher(sara).
homem(abraão).
homem(isaque).
homem(ismael).
homem(esaú).
homem(jacó).
homem(josé).
ancestral(X,Z) :- progenitor(X,Y), ancestral(Y,Z).

Variáveis
•
•
Variáveis são representadas através de cadeias de letras,
números ou _ sempre começando com letra maiúscula:
–
X, Resultado, Objeto3, Lista_Alunos, ListaCompras...
O escopo de uma variável é valido dentro de uma mesma
regra ou dentro de uma pergunta.
–
–
Isto significa que se a variável X ocorre em duas regras/perguntas, então são
duas variáveis distintas.
A ocorrência de X dentro de uma mesma regra/pergunta significa a mesma
variável.

Variáveis
•
•
Uma variável pode estar:
–
Instanciada: Quando a variável já referencia (está unificada a) algum
objeto.
–
Livre ou não-instanciada: Quando a variável não referencia (não está
unificada a) um objeto.
Uma vez instanciada, somente Prolog pode torná-la não-
instanciada através de seu mecanismo de inferência (nunca o
programador).

Variável Anônima
•
•
Variáveis anônimas podem ser utilizadas em sentenças cujo
valor atribuído a variável não é importante. Por exemplo, a
regra tem_filho:
Tem_filho(X) :- progenitor(X,Y).
Para relação “ter filhos” não é necessário saber o nomes dos
filhos. Neste vaso utiliza-se uma variável anônima
representada por “_”.
Tem_filho(X) :- progenitor(X,_).

Variável Anônima
•
•
Cada vez que uma variável anônima aparece em uma
cláusula, ele representa uma nova variável anônima. Por
exemplo:
alguém_tem_filho :- progenitor(_,_).
É equivale à:
alguém_tem_filho :- progenitor(X,Y).

Estruturas
•
Objetos estruturados são objetos de dados com vários
componentes.
•
•
Cada componente da estrutura pode ser outra estrutura.
Por exemplo, uma data pode ser vista como uma estrutura
com três componentes: dia, mês, ano.
–
data(4,maio,2003)
Estruturas
•
•
•
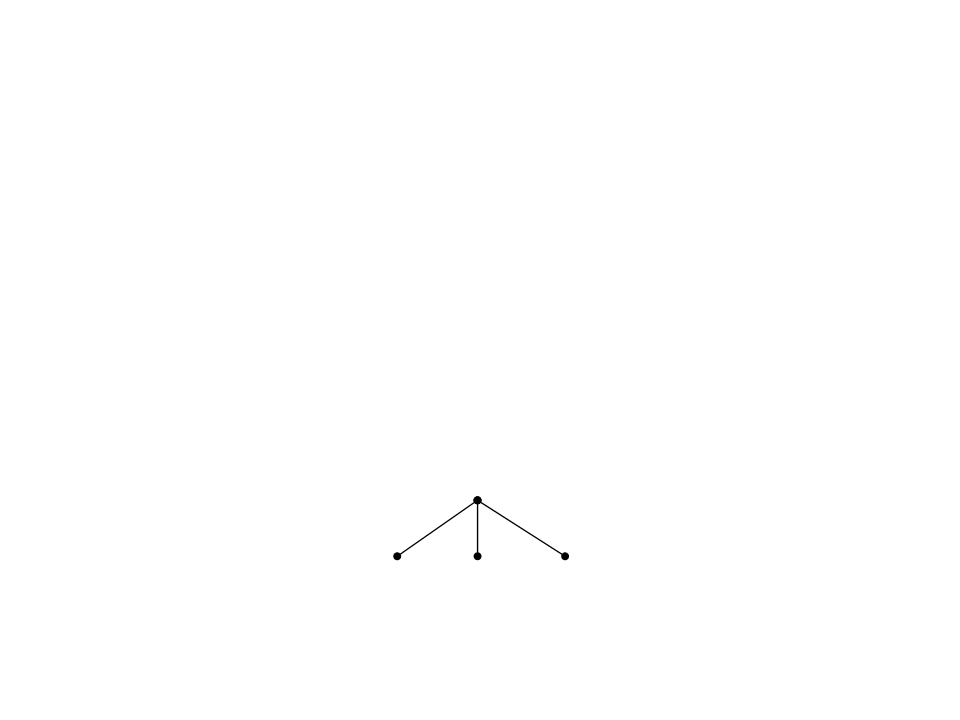
Todos os objetos estruturados são representados como
árvores.
A raiz da árvore é o funtor e os filhos da raiz são os
componentes.
data(4,maio,2003):
data
4
maio
2003
Estruturas
•
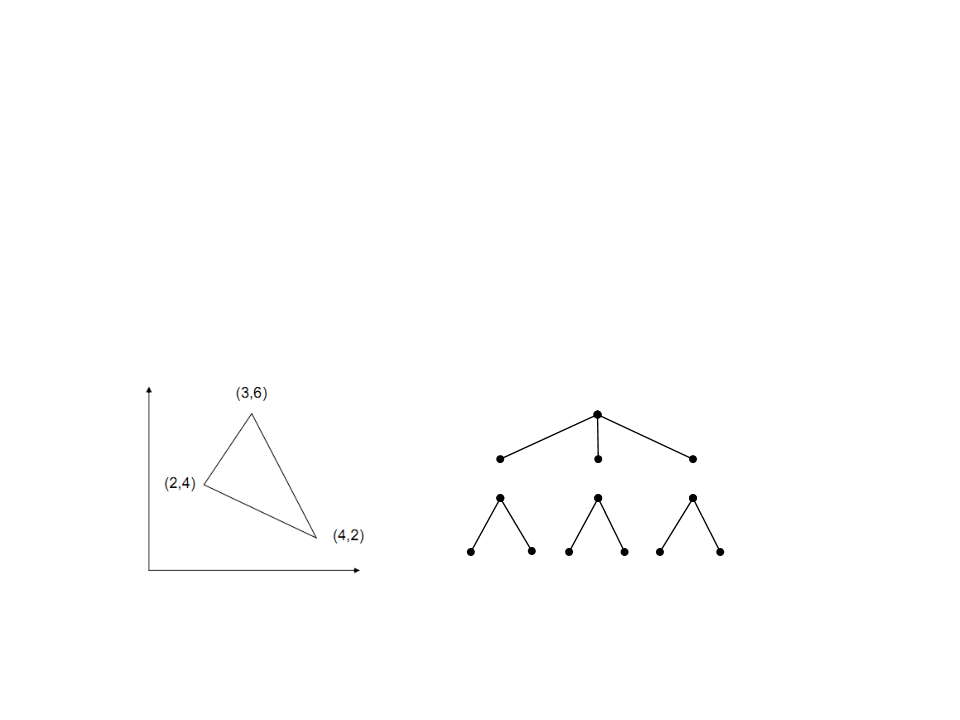
Um triângulo pode ser representado da seguinte forma:
–
triângulo(ponto(2,4), ponto(3,6), ponto(4,2))
triângulo
ponto
2
ponto
ponto
4 3
6 4
2
Operadores
Operadores Aritméticos
Operadores Relacionais
Adição
+
-
X > Y
X é maior do que Y
X é menor do que Y
X é maior ou igual a Y
X é menor ou igual a Y
X é igual a Y
Subtração
X < Y
Multiplicação
Divisão
*
X >= Y
X =< Y
X == Y
X = Y
/
Divisão Inteira
Resto da Divisão
Potência
//
Mod
**
is
X unifica com Y
X \== Y
X é diferente de Y
Atribuição

Operadores
•
•
O operador “=” realiza apenas a unificação de termos:
?- X = 1 + 2.
X = 1 + 2
O operador “is” força a avaliação aritmética:
?- X is 1 + 2.
X = 3

Operadores
•
Se a variável à esquerda do operador “is” já estiver
instanciada, o Prolog apenas compara o valor da variável com
o resultado da expressão à direita de “is”:
?- X = 3, X is 1 + 2.
X = 3
?- X = 5, X is 1 + 2.
false

Unificação de Termos
•
Dois termos se unificam (matching) se:
–
Eles são idênticos ou‰as variáveis em ambos os termos
podem ser instanciadas a objetos de maneira que após a
substituição das variáveis os termos se tornam idênticos.
•
Por exemplo, existe a unificação entre os termos‰
data(D,M,2003) e data(D1,maio,A) instanciando D = D1, M =
maio, A = 2003.

Unificação de Termos
data(D,M,2003) = data(D1,maio,A), data(D,M,2003) = data(15,maio,A1).
D = 15
M = maio
D1 = 15
A = 2003
A1 = 2003
•
Por outro lado, não existe unificação entre os
termos:
data(D,M,2003), data(D1,M1,1948)

Unificação de Termos
•
A unificação é um processo que toma dois termos e
verifica se eles unificam:
–
–
Se os termos não unificam, o processo falha (e as variáveis não se
tornam instanciadas).
Se os termos unificam, o processo tem sucesso e também instancia as
variáveis em ambos os termos para os valores que os tornam
idênticos.

Unificação de Termos
•
As regras que regem se dois termos S e T unificam são:
–
–
–
Se S e T são constantes, então S e T unificam somente se são o mesmo
objeto.
Se S for uma variável e T for qualquer termo, então unificam e S é
instanciado para T.
Se S e T são estruturas, elas unificam somente se‰:
•
S e T têm o mesmo funtor principal.
•
Todos seus componentes correspondentes unificam.

Comparação de Termos
Operadores Relacionais
X = Y
X unifica com Y, é verdadeiro quando dois termos são o
mesmo. Entretanto, se um dos termos é uma variável, o
operador = causa a instanciação da variável.
X \= Y
X == Y
X não unifica com Y
X é literalmente igual a Y (igualdade literal), que é verdadeiro
se os termos X e Y são idênticos, ou seja, eles têm a mesma
estrutura e todos os componentes correspondentes são os
mesmos, incluindo o nome das variáveis.
X \== Y
X não é literalmente igual a Y que é o complemento de X==Y

Comparação de Termos
?
- f(a,b) == f(a,b).
true
?
- f(a,b) == f(a,X).
false
?
- f(a,X) == f(a,Y).
false
- X == X.
true
?
?
- X == Y.
false
?
- X \== Y.
true
?
- g(X,f(a,Y)) == g(X,f(a,Y)).
true

Predicados para Verificação de Tipos de Termos
Predicado
var(X)
Verdadeiro se:
X é uma variável não instanciada
X não é uma variável ou X é uma variável instanciada
X é uma sentença atômica
X é um inteiro
nonvar(X)
atom(X)
integer(X)
float(X)
X é um número real
atomic(X)
compound(X)
X é uma constante
X é uma estrutura

Predicados para Verificação de Tipos de Termos
?
true
?
true
?
false
?
true
- atomic(3.14).
?
- var(Z), Z = 2.
Z = 2
- Z = 2, var(Z).
false
- integer(Z), Z = 2.
false
- Z = 2, integer(Z), nonvar(Z).
Z = 2
- atom(3.14).
false
- atom(==>).
?
- atom(p(1)).
?
- compound(2+X).
?
?

Exemplo: Macaco e as Bananas
•
Um macaco encontra-se próximo à porta de uma sala. No meio da sala há
uma banana pendurada no teto. O macaco tem fome e quer comer a
banana mas ela está a uma altura fora de seu alcance. Perto da janela da
sala encontra-se uma caixa que o macaco pode utilizar para alcançar a
banana. O macaco pode realizar as seguintes ações:
–
–
–
–
Caminhar no chão da sala;
Subir na caixa (se estiver ao lado da caixa);
Empurrar a caixa pelo chão da sala (se estiver ao lado da caixa);
Pegar a banana (se estiver parado sobre a caixa diretamente embaixo da banana).
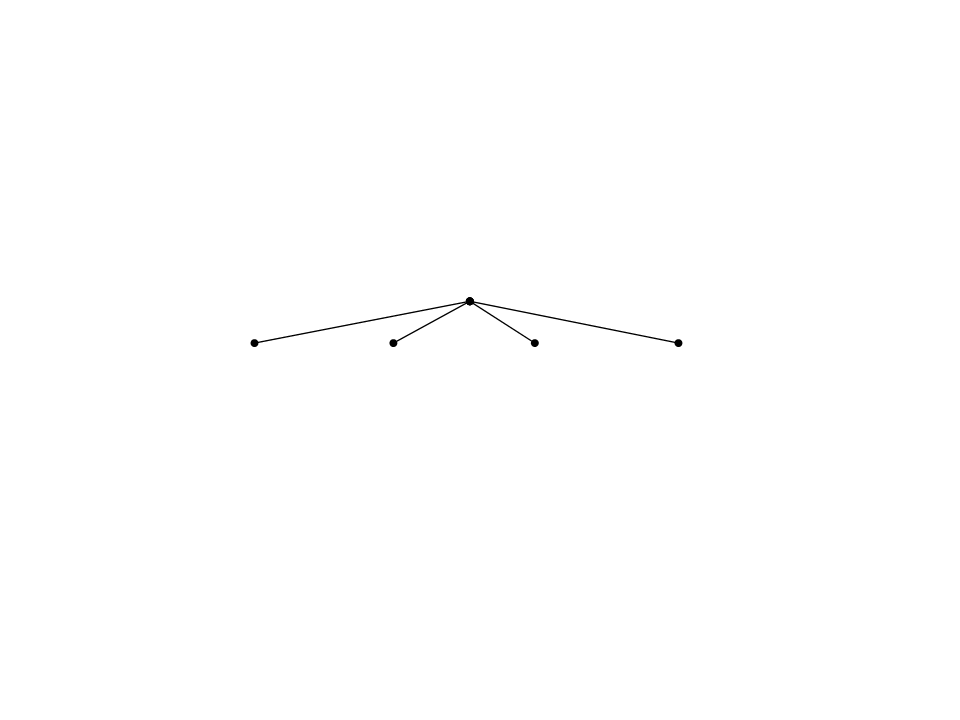
Exemplo: Macaco e as Bananas
•
É conveniente combinar essas 4 informações em uma estrutura de
estado:
estado
na_porta
no_piso
na_janela
não_tem
•
•
O estado inicial é determinado pela posição dos objetos.
O estado final é qualquer estado onde o último componente da
estrutura é “tem”:
estado(_,_,_,tem)

Exemplo: Macaco e as Bananas
•
Possíveis valores para os argumentos da estrutura estado:
–
–
–
–
1º argumento (posição do macaco):
na_porta, no_centro, na_janela
2º argumento (posição vertical do macaco):
no_chão, acima_caixa
3º argumento (posição da caixa):
na_porta, no_centro, na_janela
4º argumento (macaco tem ou não tem banana): tem,
não_tem

Exemplo: Macaco e as Bananas
•
•
Movimentos permitidos que alteram o mundo de um estado
para outro:
–
–
–
–
Pegar a banana;
Subir na caixa;
Empurrar a caixa;
Caminhar no chão da sala;
Nem todos os movimentos são possíveis em cada estado do
mundo. Por exemplo, “pegar a banana” somente é possível se
o macaco estiver em cima da caixa, diretamente em baixo da
banana e o macaco ainda não possuir a banana.

Exemplo: Macaco e as Bananas
•
•
Formalizando o problema em Prolog é possível estabelecer a
seguinte relação:
move(Estado1,Movimento,Estado2)
Onde:
–
–
–
Estado1 é o estado antes do movimento (pré-condição);
Movimento é o movimento executado;
Estado2 é o estado após o movimento;

Exemplo: Macaco e as Bananas
•
•
O movimento “pegar a banana” pode ser definido por:
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro, acima_caixa, no_centro, tem)
)
.
Este fato diz que após o movimento “pegar_banana” o
macaco tem a banana e ele permanece em cima da caixa no
meio da sala.

Exemplo: Macaco e as Bananas
•
Também é necessário expressar o fato que o macaco no chão pode
caminhar de qualquer posição “Pos1” para qualquer posição “Pos2”:
move(
estado(Pos1, no_chão, Caixa, Banana),
caminhar(Pos1,Pos2),
estado(Pos2, no_chão, Caixa, Banana)
).
•
De maneira similar, é possível especificar os movimentos “empurrar” e
“subir”.

Exemplo: Macaco e as Bananas
•
A pergunta principal que o programa deve responder
é:
O macaco consegue, a partir de um estado inicial,
pegar as bananas?

Exemplo: Macaco e as Bananas
•
Para isso é necessário formular duas regras que definam quando o estado
final é alcançável:
–
Para qualquer estado no qual o macaco já tem a banana, o predicado
“consegue” certamente deve ser verdadeiro e nenhum movimento é
necessário:
consegue(estado(_,_,_,tem)).
–
Nos demais casos, um ou mais movimentos são necessários; o macaco pode
obter a banana em qualquer estado “Estado1” se existe algum movimento de
“
banana no “Estado2”:
Estado1” para algum estado “Estado2” tal que o macaco consegue pegar a
consegue(Estado1) :- move(Estado1, Movimento, Estado2),
consegue(Estado2).

Exemplo: Macaco e as Bananas
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro, acima_caixa, no_centro,tem)
).
move(
estado(P, no_chão, P, Banana),
subir,
estado(P, acima_caixa, P, Banana)
).
move(
estado(P1, no_chão, P1, Banana),
empurrar(P1, P2),
estado(P2, no_chão, P2, Banana)
).
move(
estado(P1, no_chão, Caixa, Banana),
caminhar(P1, P2),
estado(P2, no_chão, Caixa, Banana)
).
consegue(estado(_, _, _, tem)).
consegue(Estado1) :- move(Estado1, Movimento, Estado2), consegue(Estado2).
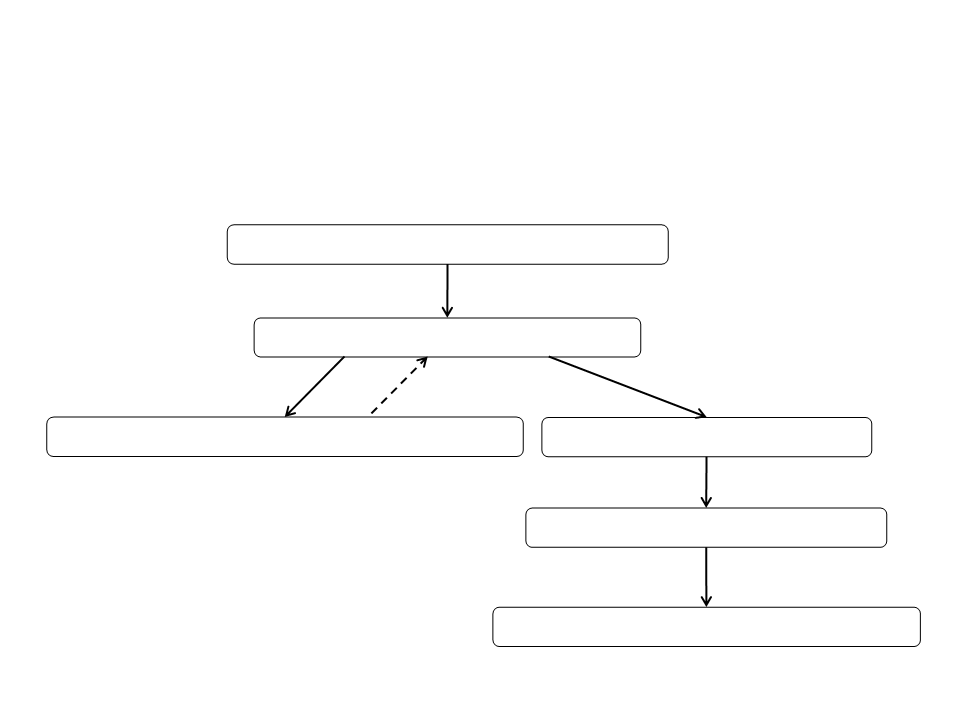
Exemplo: Macaco e as Bananas
•
?- consegue(estado(na_porta, no_chão, na_janela, não_tem)).
estado(na_porta, no_chão, na_janela, não_tem)
caminhar(na_porta,P2)
estado(P2, no_chão, na_janela, não_tem)
empurrar(P2,P2’)
subir
backtrack
estado(na_janela, acima_caixa, na_janela, não_tem)
estado(P2’, no_chão, P2’, não_tem)
subir
estado(P2’, acima_caixa, P2’, não_tem)
Pegar_banana
P2’=no_centro
estado(no_centro,acima_caixa,no_centro,tem)

Listas
•
Lista é uma das estruturas mais simples em Prolog e
pode ser aplicada em diversas situações.
•
•
Uma lista pode ter qualquer comprimento.
Uma lista contendo os elementos “ana”, “tênis” e
“pedro” pode ser escrita em Prolog como:
[
ana, tênis, pedro]

Listas
•
•
O uso de colchetes é apenas uma melhoria da notação, pois
internamente listas são representadas como árvores, assim
como todos objetos estruturados em Prolog.
Internamente o exemplo [ana, tênis, pedro] é representando
da seguinte maneira:
.
ana
tênis
pedro
.
.(ana, .(tênis, .(pedro, []) ) )
.
[
]

Listas
?- Lista1 = [a,b,c], Lista2 = .(a,.(b,.(c,[]))).
Lista1 = [a, b, c]
Lista2 = [a, b, c]
?
- Hobbies1 = .(tênis, .(música,[])), Hobbies2 = [esqui, comida], L =
[ana,Hobbies1,pedro,Hobbies2].
Hobbies1 = [tênis,música]
Hobbies2 = [esqui,comida]
L = [ana, [tênis,música], pedro, [esqui,comida]]

Listas
•
•
Para entender a representação de listas do Prolog, é
necessário considerar dois casos:
–
Lista vazia [].
–
E lista não vazia, onde:
•
O primeiro item é chamado de cabeça (head) da lista.
•
A parte restante da lista é chamada cauda (tail).
No exemplo [ana, tênis, pedro]:
–
ana é a Cabeça da lista.
–
[tênis, pedro] é a Cauda da lista.

Listas
•
•
Em geral, é comum tratar a cauda como um objeto simples.
Por exemplo, L = [a,b,c] pode ser escrito como:
Cauda = [b,c]
L = [a, Cauda]
O Prolog também fornece uma notação alternativa para
separar a cabeça da cauda de uma lista, a barra vertical:
L = [a | Cauda]

Operações em Listas - Busca
•
•
Frequentemente existe a necessidade de se realizar
operações em listas, por exemplo, buscar um
elemento que faz parte de uma lista.
Para verificar se um nome está na lista, é preciso
verificar se ele está na cabeça ou se ele está na cauda
da lista.

Operações em Listas - Busca
•
•
A primeira regra para verificar se um elemento X pertence à
lista é verificar se ele se encontra na cabeça da lista. Isto
pode ser especificado da seguinte maneira:
pertence(X,[X|Z]).
A segunda condição deve verificar se o elemento X pertence
à cauda da lista. Esta regra pode ser especificada da seguinte
maneira:
pertence(X,[W|Z]) :- pertence(X,Z).

Operações em Listas - Busca
•
•
O programa para buscar por um item em uma lista pode ser
escrito da seguinte maneira:
pertence(Elemento,[Elemento|Cauda]).‰
pertence(Elemento,[Cabeca|Cauda]) :- pertence(Elemento,Cauda).
Após a definição do programa, é possível interrogá-lo.
?
- pertence(a,[a,b,c]).
true

Operações em Listas - Busca
?
- pertence(d,[a,b,c]).
false
?
- pertence(X,[a,b,c]).
X = a ;
X = b ;
X = c ;
false
•
•
E se as perguntas forem:
?
?
- pertence(a,X).
- pertence(X,Y).
Existem infinitas respostas.

Operações em Listas – Último Elemento
•
•
O último elemento de uma lista que tenha somente um elemento é o
próprio elemento:
ultimo(Elemento, [Elemento]).
O último elemento de uma lista que tenha mais de um elemento é o
ultimo elemento da cauda:
ultimo(Elemento, [Cabeca|Cauda]) :- ultimo(Elemento, Cauda).
•
Programa completo:
ultimo(Elemento, [Elemento]).
ultimo(Elemento, [Cabeca|Cauda]) :- ultimo(Elemento, Cauda).

Exemplo: Macaco e as Bananas
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro,acima_caixa,no_centro,tem)
).
move(
estado(P,no_chão,P,Banana),
subir,
estado(P,acima_caixa,P,Banana)
).
move(
estado(P1,no_chão,P1,Banana),
empurrar(P1,P2),
estado(P2,no_chão,P2,Banana)
).
move(
estado(P1,no_chão,Caixa,Banana),
caminhar(P1,P2),
estado(P2,no_chão,Caixa,Banana)
).
consegue(estado(_,_,_,tem),[]).
consegue(Estado1,[Movimento|Resto]) :- move(Estado1,Movimento,Estado2), consegue(Estado2,Resto).

Adicionando Novos Fatos a Base de
Conhecimento
O predicado assert é utilizado pelo Prolog para adicionar
novas sentenças na base de conhecimento.
•
•
Exemplos:
–
assert(homem(joao)).
–
assert(filho(Y,X) :- progenitor(X,Y)).

Adicionando Novos Fatos a Base de
Conhecimento
•
•
•
•
O predicado assert permite adicionar fatos e regras a base de
conhecimento.
Normalmente, o SWI-Prolog compila o código de forma que não é possível
modificar fatos durante a execução do programa.
Para indicar ao Prolog que determinada sentença pode ser modificado
durante a execução do programa é possível utilizar o predicado dynamic.
Exemplo:
–
:- dynamic homem/1.

Removendo Fatos da Base de
Conhecimento
•
Também é possível remover fatos e regras da base
de conhecimento utilizando o predicado retract.
•
•
Funciona de forma similar ao assert.
Exemplos:
–
retract(homem(joao)).
–
retract(filho(Y,X) :- progenitor(X,Y)).

Predicados do SWI-Prolog
•
O SWI-Prolog inclui diversas sentenças predefinidas para para
diversos usos, como por exemplo:
–
–
–
–
–
–
–
Manipulação de listas;
Comparação de tipos de dados;
Leitura e escrita de dados em arquivos;
Entrada e saída de dados pelo console;
Manipulação de arquivos;
Execução de comandos no sistema operacional;
Entre outros.
•
http://www.swi-prolog.org/pldoc/refman/

Utilizando o SWI-Prolog em C++
•
Download:
–
http://www.swi-prolog.org/download/stable
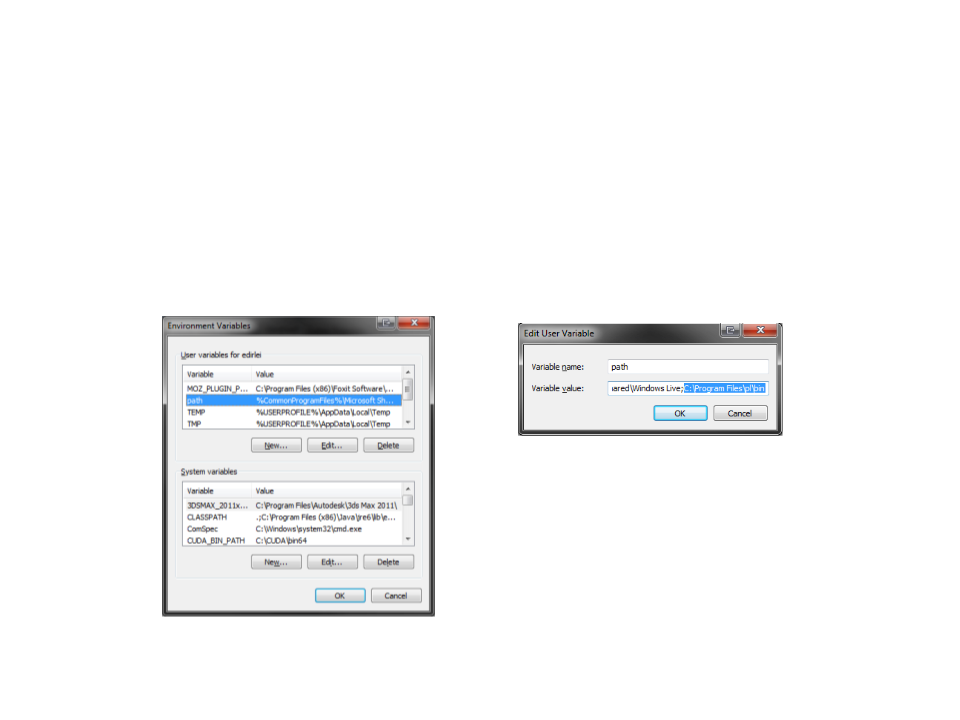
Configuração - Visual Studio
•
•
Control Panel -> System ->Advanced-> Environment Variables
Adicionar o diretório “C:\Program Files (x86)\swipl\bin” a variável “PATH” do
sistema.
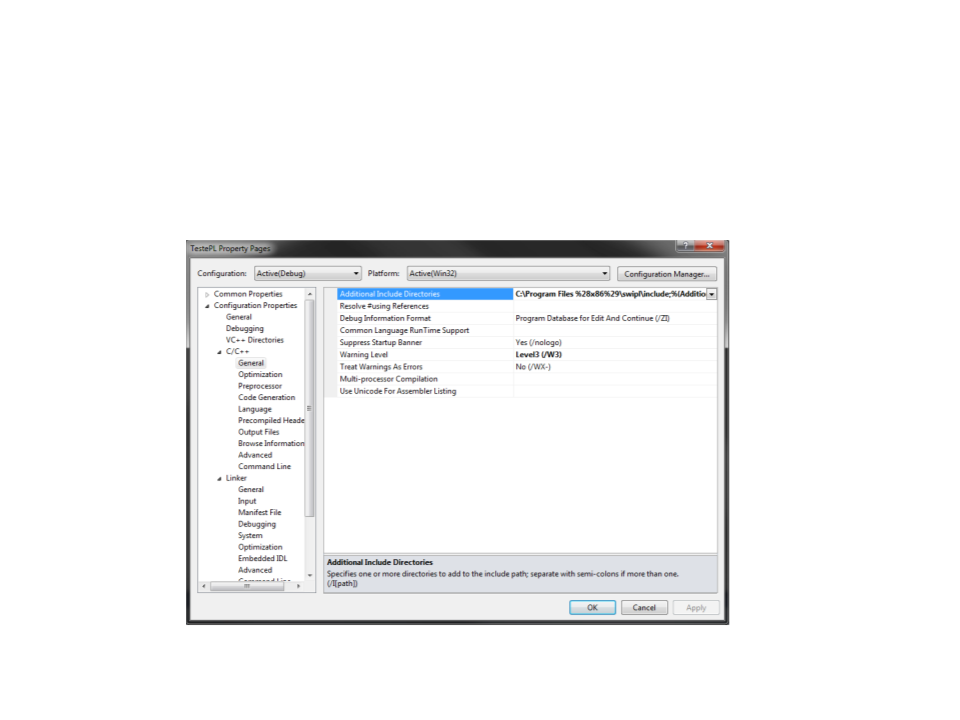
Configuração - Visual Studio
•
Include Directory: “C:\Program Files (x86)\swipl\include”
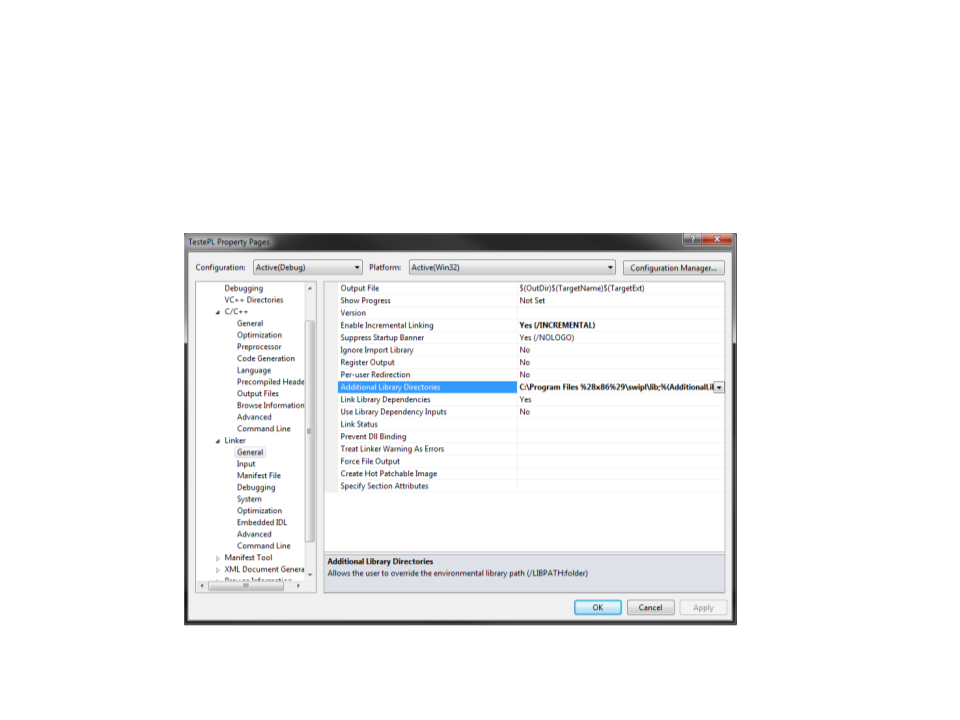
Configuração - Visual Studio
•
Library Directory: “C:\Program Files (x86)\swipl\lib”
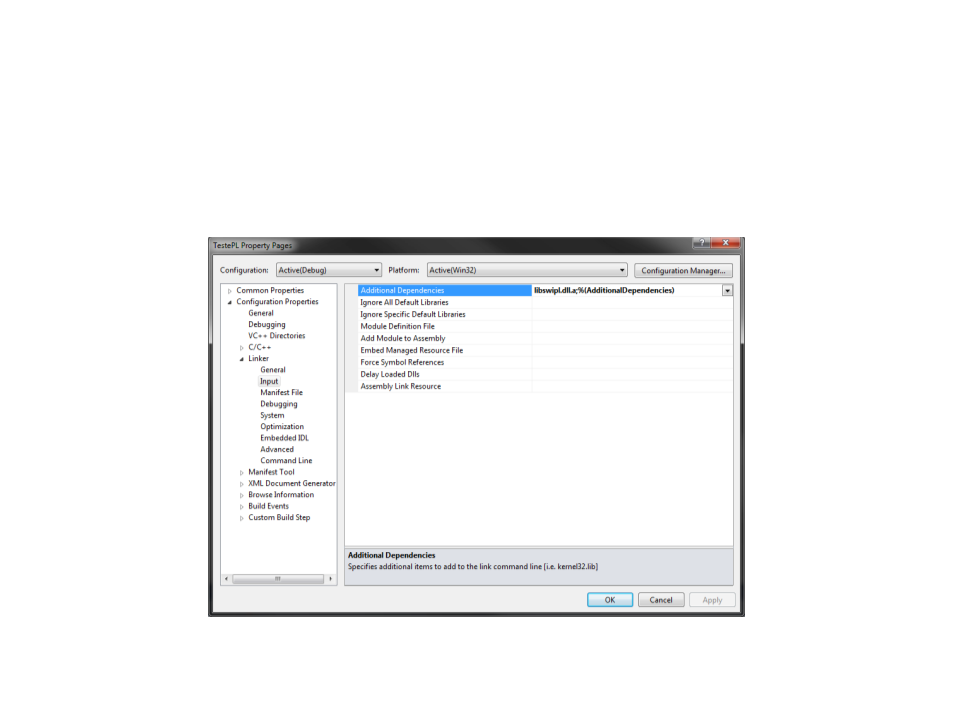
Configuração – Visual Studio
•
Dependência: libswipl.dll.a
Exemplo de Programa
progenitor(sara,isaque).
progenitor(abraao,isaque).
progenitor(abraao,ismael).
progenitor(isaque,esau).
progenitor(isaque,jaco).
progenitor(jaco,jose).
mulher(sara).
homem(abraao).
homem(isaque).
homem(ismael).
homem(esau).
homem(jaco).
homem(jose).
filho(Y,X) :- progenitor(X,Y).
mae(X,Y) :- progenitor(X,Y), mulher(X).
avo(X,Z) :- progenitor(X,Y), progenitor(Y,Z).
irmao(X,Y) :- progenitor(Z,X), progenitor(Z,Y).
ancestral(X,Z) :- progenitor(X,Z).
ancestral(X,Z) :- progenitor(X,Y), ancestral(Y,Z).

Exemplo de Programa
#
#
include <SWI-cpp.h>
include <iostream>
using namespace std;
int main(){
char* argv[] = {"swipl.dll", "-s", "D:\\teste.pl", NULL};
_
putenv("SWI_HOME_DIR=C:\\Program Files (x86)\\swipl");
PlEngine e(3,argv);
PlTermv av(2);
av[1] = PlCompound("jose");
PlQuery q("ancestral", av);
while (q.next_solution())
{
cout << (char*)av[0] << endl;
}
cin.get();
return 1;
}

Manual
•
http://www.swi-prolog.org/pldoc/index.html

Bibliografia Complementar
•
•
Bratko, I., “Prolog Programming for Artificial
Intelligence” (3rd edition), Addison Wesley, 2000.
Clocksin, W.F., Mellish, C.S., “Programming in
Prolog” (5th edition), Springer, 2003.
•
Sterling, L., Shapiro, E., “The Art of Prolog” (2th
edition), MIT Press, 1994.
