INF1771 - INTELIGÊNCIA ARTIFICIAL
LISTA DE EXERCÍCIOS 2
Aluno:
1
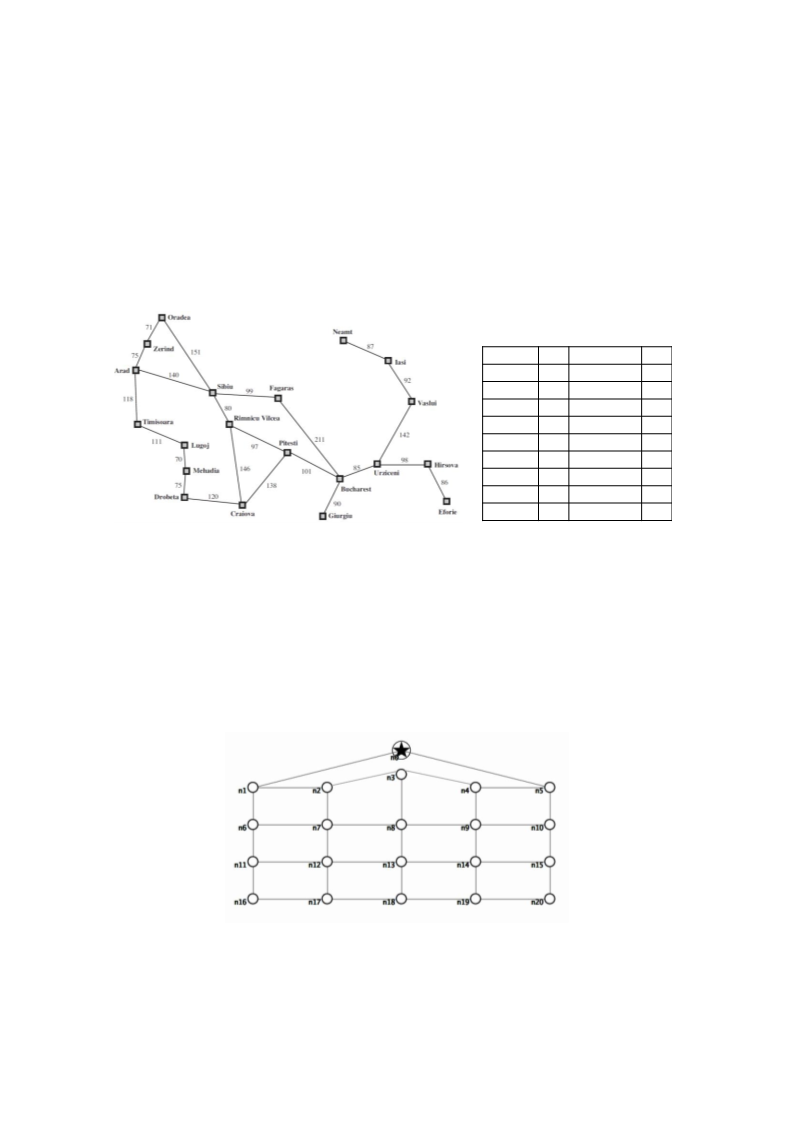
. Realize uma busca utilizando o algoritmo A* para encontrar o melhor caminho para
chegar a Bucharest partindo de Lugoj. Construa a árvore de busca criada pela execução do
algoritmo apresentando os valores de f(n), g(n) e h(n) para cada nó. Utilize a heurística de
distância em linha reta.
Arad
366 Mehadia
0 Neamt
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
160 Oradea
242 Pitesti
161 Rimnicu Vilcea 193
Fagaras
Giurgiu
Iasi
176 Sibiu
253
329
199
374
80
77
Timisoara
226 Vaslui
244 Zerind
151 Urziceni
Lugoj
Hirsova
2
. Utilize o algoritmo de busca local Hill Climbing na rede mostrada abaixo para chegar ao nó
em formato de estrela (n0) partindo do nó n18. Mostre a sequencia de nós visitados
durante a execução do algoritmo. Utilize a distancia em linha reta aproximada para
calcular a função heurística. Caso o algoritmo fique preso em um mínimo local, utilize o a
variação do Hill Climbing com reinicialização aleatória.
2
3
23
1
2
12
8
5
5
5
1
0
10
10
10

3
. O grafo abaixo mostra a ligação entre 5 cidades e as respectivas distâncias em
quilômetros:
Tem-se um problema onde é necessário passar por todas as cidades, apenas uma vez.
O objetivo é encontrar uma rota de menor custo usando um algoritmo genético.
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Gere dois cromossomos e avalie a aptidão deles.
d) Realize o cruzamento entre os cromossomos.
e) Aplique uma mutação em um gene dos cromossomos.
f) Aplique a função de aptidão nos descendentes gerados verificando se a solução
encontrada é melhor ou não.
4
. Considere a seguinte equação:
2 3
x + y + w + z = 185
5
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para gerar
uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse processo
por 8 gerações ou até que a solução do problema seja encontrada.
5
. Problema SAT
Seja x = (x1, x2,..., xn) um vetor de n variáveis booleanas (i.e. cada variável xi assume um dos
valores em {0,1}). Seja f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)] uma fórmula normal conjuntiva com
m cláusulas, onde cada cláusula cj(x) é uma disjunção de literais, e um literal é uma das
variáveis booleanas ou sua negação.
Por exemplo, considere um vetor com três variáveis x = (x1, x2, x3). Um exemplo de fórmula
normal conjuntiva seria:
f(x) = [(x1)∧ (¬x2) ∧ (x2 ∨ ¬x3) ∧ (x1 ∨ ¬x3)]
Composta pelas seguintes cláusulas:
c1(x) = (x1)
c2(x) = (¬x2)
c3(x) = (x2 ∨ ¬x3)
c4(x) = (x1 ∨ ¬x3)
Uma fórmula é dita satisfatível quando existe uma atribuição de valores para (x1, x2,..., xn)
tal que todas as cláusulas da fórmula sejam satisfeitas, isto é, cj(x) = 1 para j=1,...,m. No
exemplo acima, f(x) é satisfatível e x = (1, 0, 0) é uma possível atribuição de valores para as
variáveis x1, x2 e x3 que tornam verdadeiras todas as quatro cláusulas da fórmula.
O problema SAT consiste em: dada uma fórmula, responder se a fórmula é satisfatível ou
não. Encontrar uma atribuição de valores que satisfaçam uma dada fórmula é uma tarefa
que pode ser formulada como um problema de busca. Assim, para um conjunto qualquer
de variáveis x = (x1, x2,..., xn) e uma dada fórmula f(x) = [c1(x) ∧ c2(x) ∧,..., ∧ cm(x)], proponha
uma solução para o problema SAT como Algoritmos Genéticos.
Para isso, use o seguinte caso base:
(¬x ∨ ¬z ∨ y) ∧ (¬y ∨ z) ∧ (x ∨ ¬z) ∧ (y) ∧ (¬y ∨ ¬x ∨ ¬w ∨ z)
a) Proponha uma maneira de codificar os cromossomos.
b) Defina uma função de aptidão para avaliar a qualidade dos cromossomos.
c) Defina como o método de seleção dos pais será utilizado.
d) Defina os operadores genéticos de recombinação e mutação.
e) Gere uma população inicial de 4 cromossomos e avalie a aptidão deles.
f) Aplique os operadores de recombinação e mutação sobre essa população para gerar
uma nova geração, em seguida avalie a aptidão da nova geração. Repita esse processo
por 8 gerações ou até que a solução do problema seja encontrada.
