
INF 1771 – Inteligência Artificial
Aula 04 – Busca Heurística
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Métodos de Busca
•
Busca Cega ou Exaustiva:
–
Não sabe qual o melhor nó da fronteira a ser expandido. Apenas
distingue o estado objetivo dos não objetivos.
•
•
Busca Heurística:
–
Estima qual o melhor nó da fronteira a ser expandido com base em
funções heurísticas.
Busca Local:
–
Operam em um único estado e movem-se para a vizinhança deste
estado.

Busca Heurística
•
Algoritmos de Busca Heurística:
–
Busca Gulosa
–
A*
•
•
A busca heurística leva em conta o objetivo para decidir qual
caminho escolher.
Conhecimento extra sobre o problema é utilizado para guiar o
processo de busca.

Busca Heurística
•
Como encontrar um barco perdido?
–
–
Busca Cega -> Procura no oceano inteiro.
Busca Heurística -> Procura utilizando informações
relativas ao problema.
•
Exemplo: correntes marítimas, vento, etc.

Busca Heurística
•
•
Função Heurística (h)
–
Estima o custo do caminho mais barato do estado atual até
o estado final mais próximo.
–
São específicas para cada problema.
Exemplo:
–
Encontrar a rota mais curta entre duas cidades:
•
h(n) = distância em linha reta direta entre o nó n e o nó final.
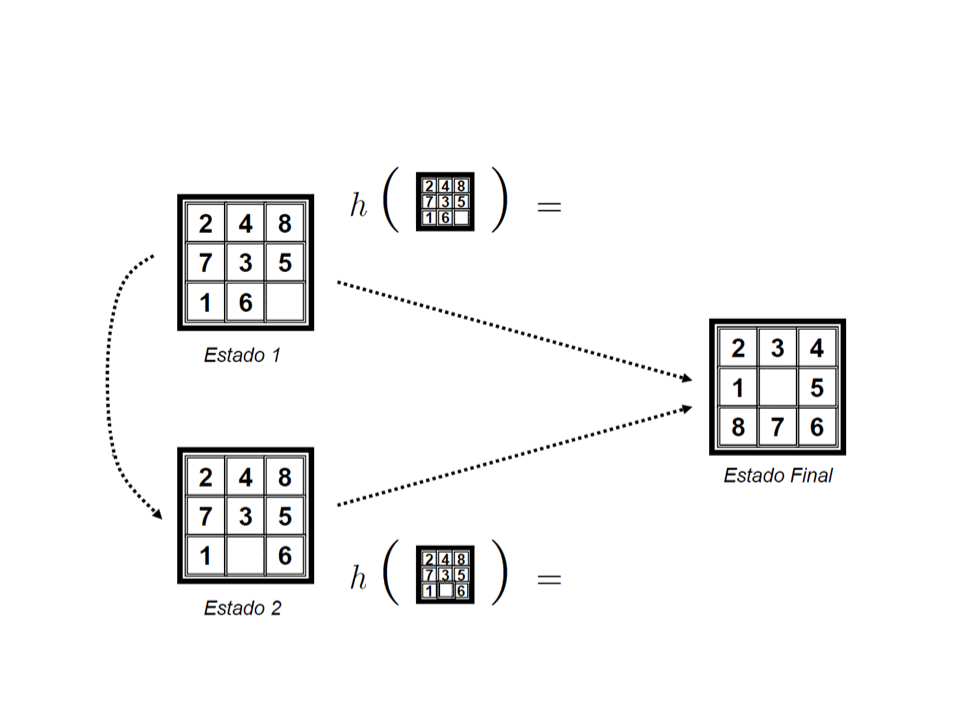
Função Heurística
Estado Atual
Estado Objetivo

Busca Heurística
•
Algoritmos de Busca Heurística:
–
–
Busca Gulosa
A*

Busca Gulosa
•
Estratégia:
–
Expande os nós que se encontram mais próximos do
objetivo (uma linha reta conectando os dois pontos no
caso de distancias), desta maneira é provável que a busca
encontre uma solução rapidamente.
•
A implementação do algoritmo se assemelha ao utilizado na
busca cega, entretanto utiliza-se uma função heurística para
decidir qual o nó deve ser expandido.
Busca Gulosa
Arad
366
Sibiu
253
Timissoara
329
Zerind
374
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Arad
366
Fagaras
176
Oradea
380
Rimnicu Vilcea
Bucharest
193
Craiova
160
242
161
176
77
Drobeta
Eforie
Rimnicu Vilcea 193
Sibiu
263
Bucharest
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
0
Timisoara
Vaslui
226
244
151
Lugoj
Zerind
Função Heurística (h):
Distancia em linha reta
Hirsova
Urziceni

Busca Gulosa
•
•
Custo de busca mínimo:
– No exemplo, não expande nós fora do caminho.
Não é ótima:
–
No exemplo, escolhe o caminho que é mais econômico à
primeira vista, via Fagaras.
–
Porém, existe um caminho mais curto via Rimnicu Vilcea.
•
Não é completa:
–
Pode entrar em loop se não detectar a expansão de
estados repetidos.
–
Pode tentar desenvolver um caminho infinito.
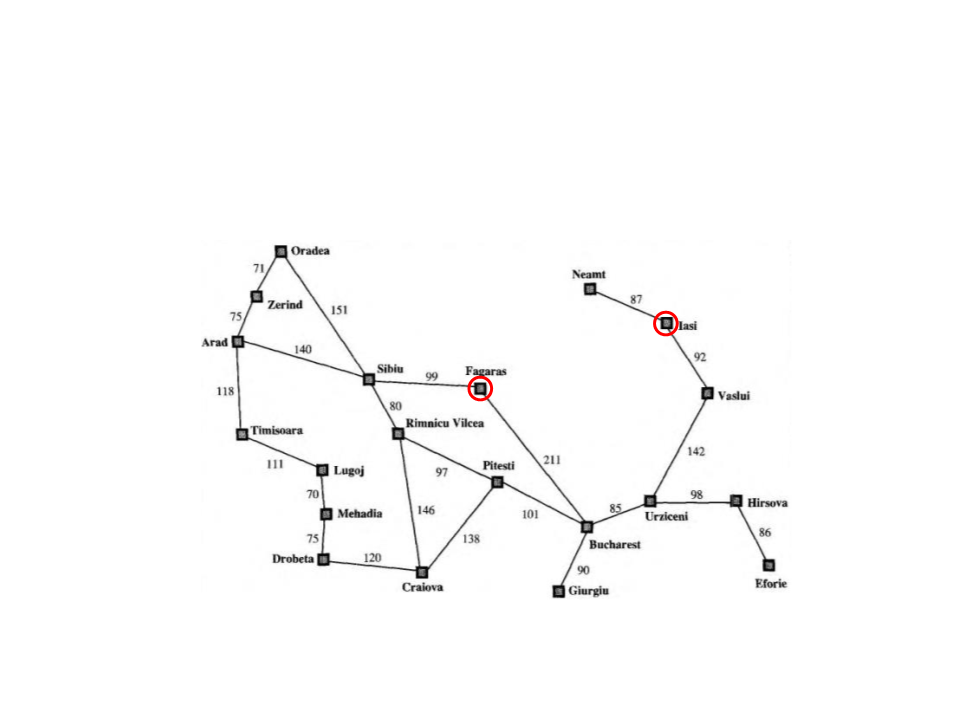
Busca Gulosa
•
Ir de Iasi para Fagaras?

Busca A*
•
Estratégia:
–
Combina o custo do caminho g(n) com o valor da
heurística h(n)
–
–
g(n) = custo do caminho do nó inicial até o nó n
h(n) = valor da heurística do nó n até um nó objetivo
(distancia em linha reta no caso de distancias espaciais)
–
f(n) = g(n) + h(n)
•
É a técnica de busca mais utilizada.
Busca A*
Arad
0+366=366
Sibiu
Timissoara
Zerind
1
40+253=393 118+329=447 75+374=449
Arad
Fagaras
Oradea
Rimnicu Vilcea
220+193=413
2
80+366=646 239+176=415 291+380=671
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
Sibiu
38+253=591
Bucharest
Craiova
Pitesti
Sibiu
160
242
161
176
77
3
450+0=450
366+160=526 317+100=417 300+253=553
Rimnicu Vilcea 193
Bucharest
418+0=418
Craiova
Rimnicu Vilcea
414+193=607
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
455+160=615
Timisoara
Vaslui
226
244
151
Lugoj
Zerind
Hirsova
Urziceni

Busca A*
•
•
A estratégia é completa e ótima.
Custo de tempo:
–
Exponencial com o comprimento da solução, porém boas funções heurísticas
diminuem significativamente esse custo.
d
•
•
Custo memória: O(b )
–
Guarda todos os nós expandidos na memória.
Nenhum outro algoritmo ótimo garante expandir menos nós.

Definindo Heurísticas
•
•
•
Cada problema exige uma função
heurística diferente.
Não se deve superestimar o custo
real da solução.
Como escolher uma boa função
heurística para o jogo 8-Puzzle?
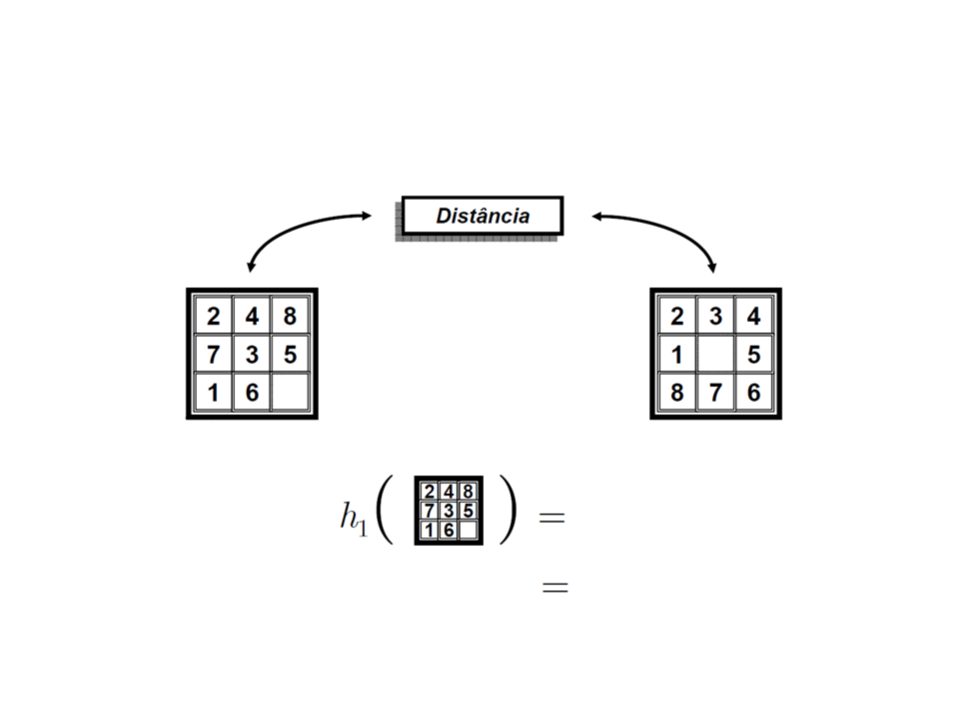
Definindo Heurísticas
Estado Atual
Estado Objetivo
A quantidade de
peças for a do lugar
7
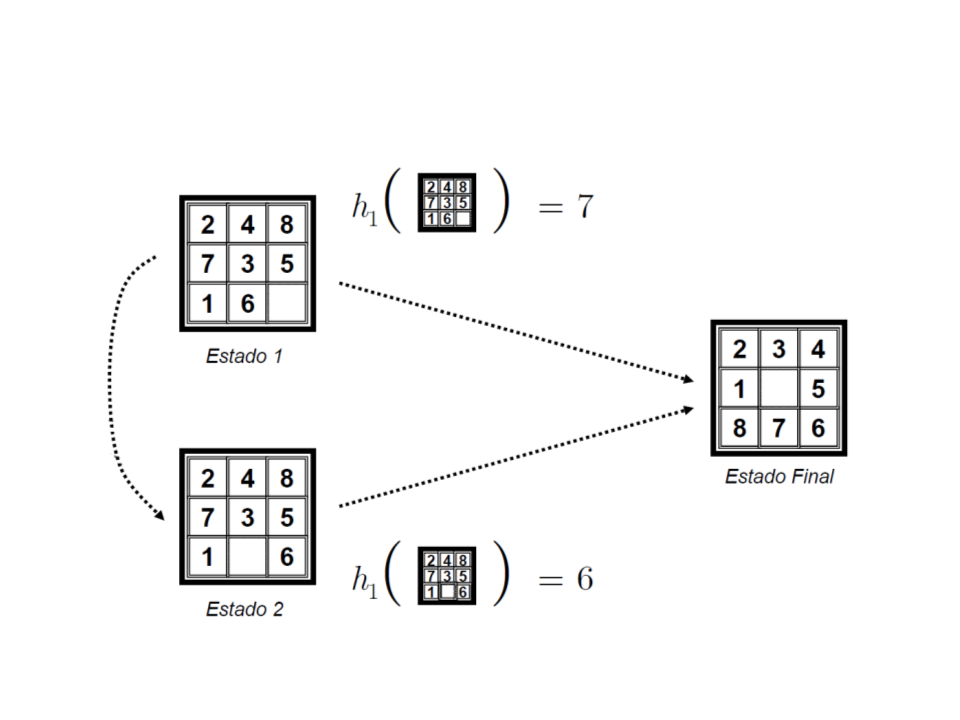
Definindo Heurísticas
Definindo Heurísticas
2
Outra Heurística?
Definindo Heurísticas
Número de movimentos
necessários para colocar
cada peça no seu lugar
2
10
Definindo Heurísticas
1
0
2
9
2

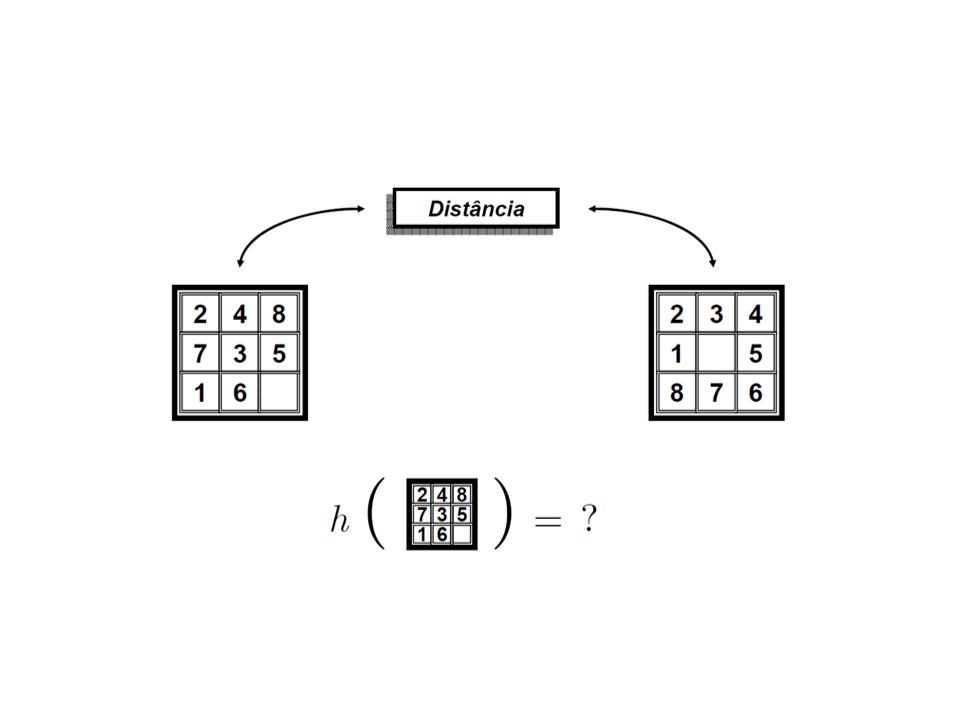
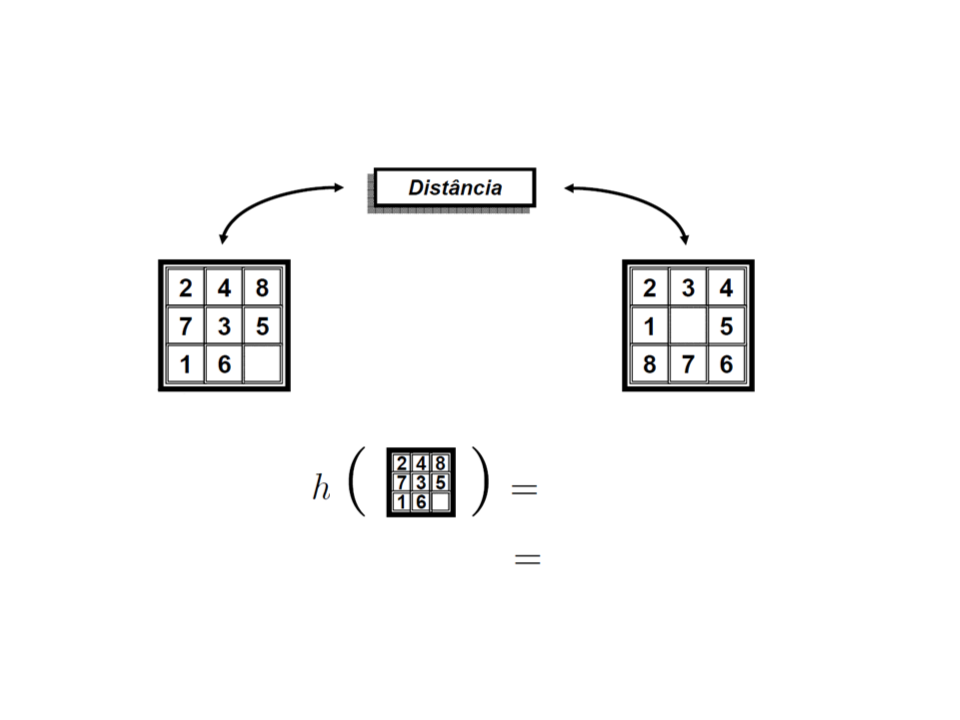
Definindo Heurísticas
•
Como escolher uma boa função
heurística para o jogo 8-Puzzle?
–
–
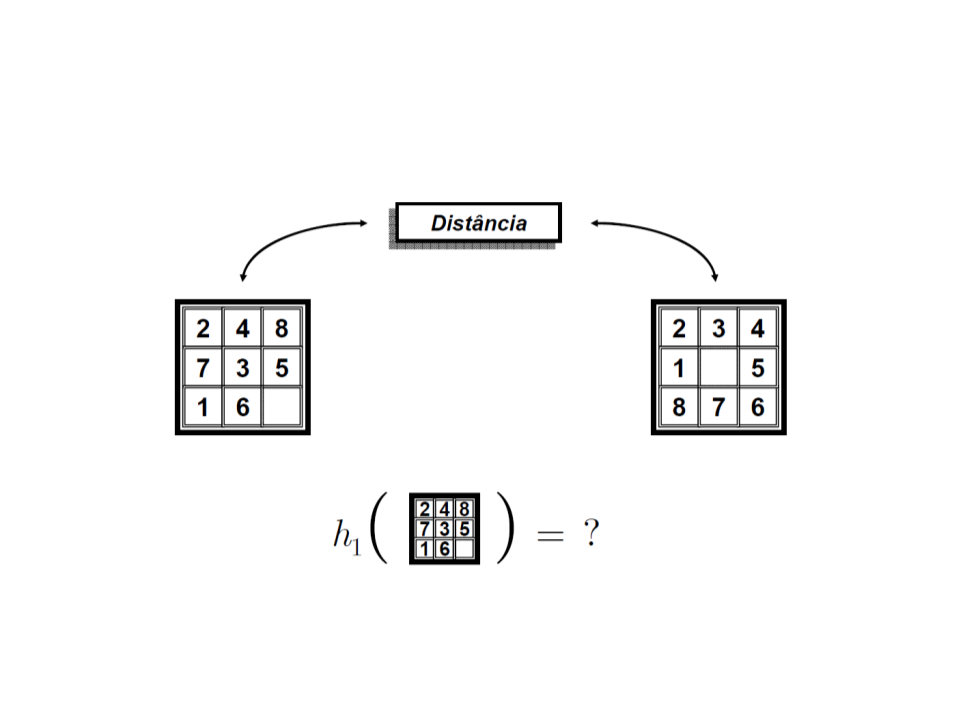
h¹ = número de elementos fora do lugar.
h² = soma das distâncias de cada número à
sua posição final (movimentação horizontal e
vertical).
•
Qual das heurísticas é melhor?

Exemplo - A*
1
2 3 4 5
X
1
2
☺
3
4

Exemplo - A*
•
•
•
Qual é o espaço de estados?
Quais são as ações possíveis?
Qual será o custo das ações?

Exemplo - A*
•
•
Heurística do A*: f(n) = g(n) + h(n)
–
g(n) = custo do caminho
–
h(n) = função heurística
Qual seria a função heurística h(n) mais adequada
para este problema?
–
A distancia em linha reta é uma opção.
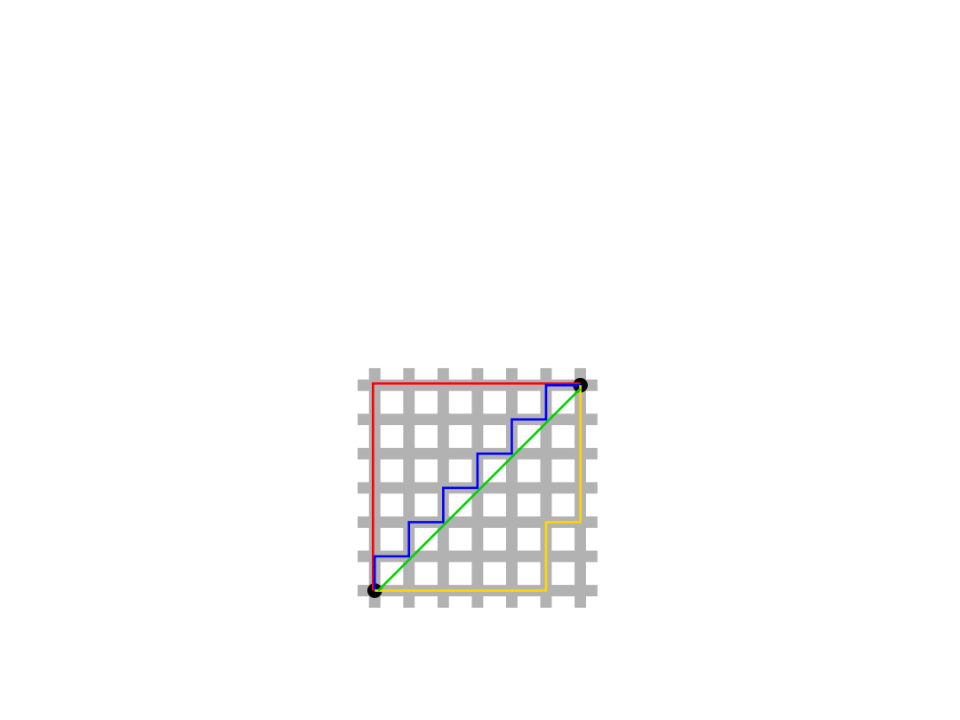
Exemplo - A*
•
Como calcular a heurística h(n)?
–
Distancia de Manhattan

Exemplo - A*
•
O próximo passo é gerar a árvore de busca e
expandir os nós que tiverem o menor valor
resultante da função heurística f(n).
–
f(n) = g(n) + h(n)
Exemplo - A*
[
1,1]
[
2,1]
[
1,2]
[
[
1,2] = f(n) = ?? + ??
2,1] = f(n) = ?? + ??

Exemplo - A*
1
2 3 4 5
X
1
2
☺
3
4
Exemplo - A*
[
1,1]
[
2,1]
[
1,2]
[
1,1]
[2,2]
[
[
1,1] = f(n) = ?? + ??
2,2] = f(n) = ?? + ??

Exemplo - A*
1
2 3 4 5
1
2
☺
X
3
4
Exercícios
•
(1) Qual seria uma boa heurística para o jogo
da velha?

Exercícios
•
(2) Supondo que é necessário utilizar um algoritmo de busca
para resolver um problema no qual são necessárias respostas
instantâneas. Mas, mesmo utilizando o A* com uma boa
função heurística, o tempo gasto com o processo de busca
ainda está muito grande. O que pode ser feito para otimizar
esse processo?
–
–
Caminhos pré-calculados.
Custos pré-calculados.
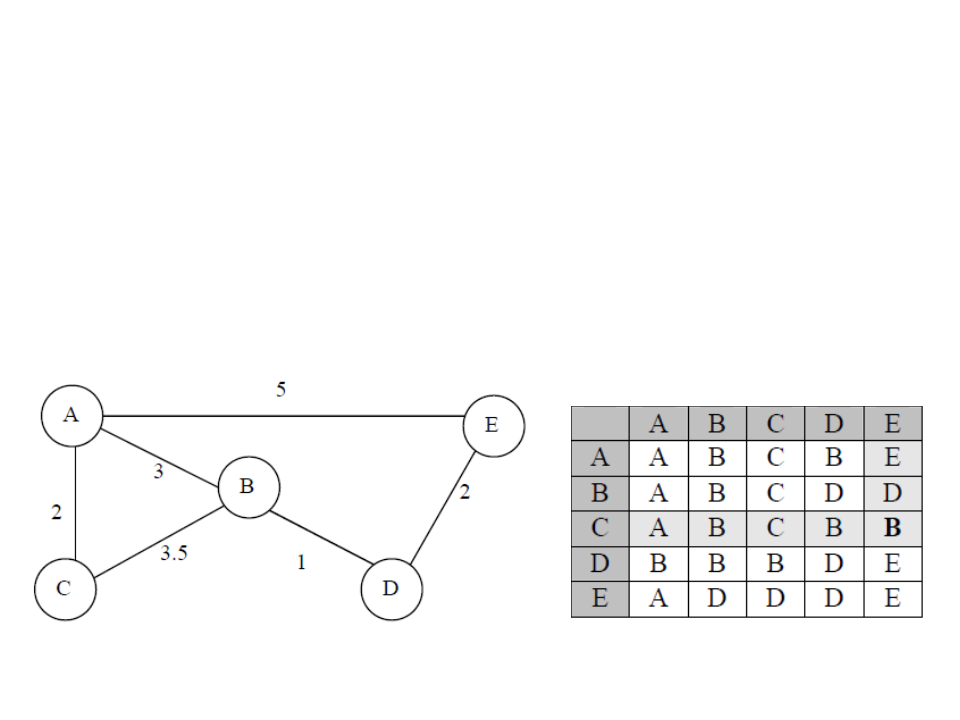
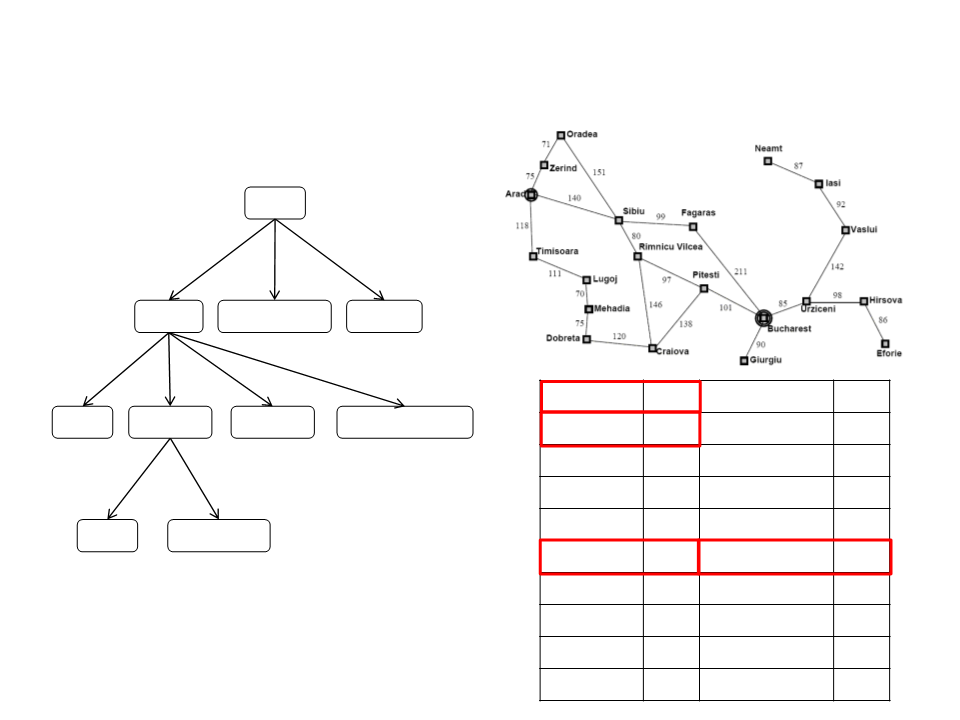
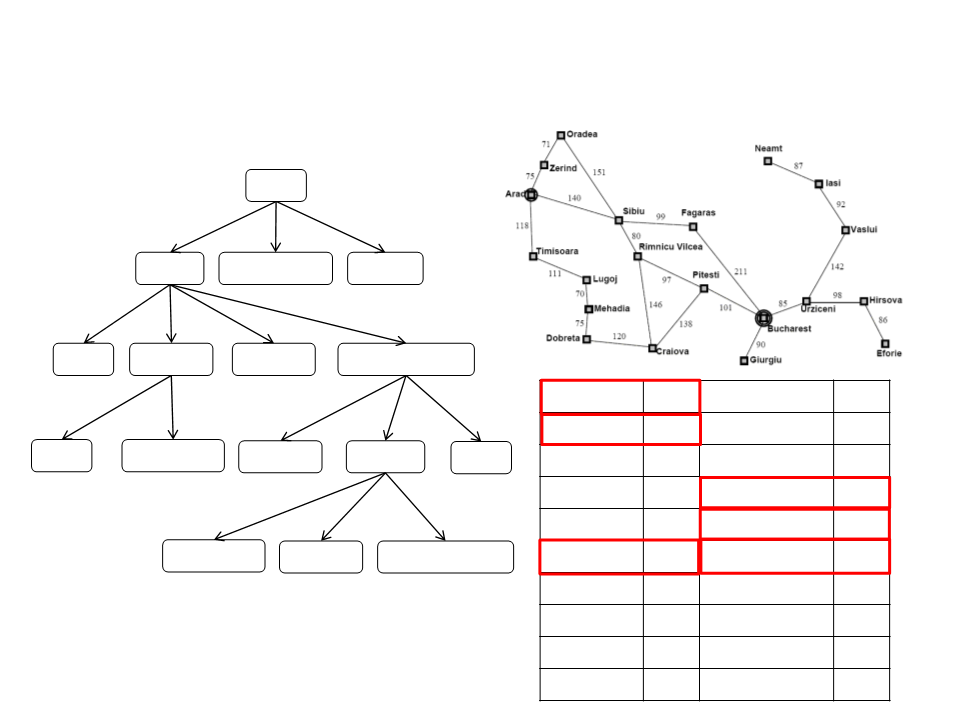
Caminhos Pré-Calculados
•
•
Tabela pré-calculada com os melhores caminhos.
Armazena-se somente o próximo nó que deve ser seguindo do nó
atual ao nó destino.
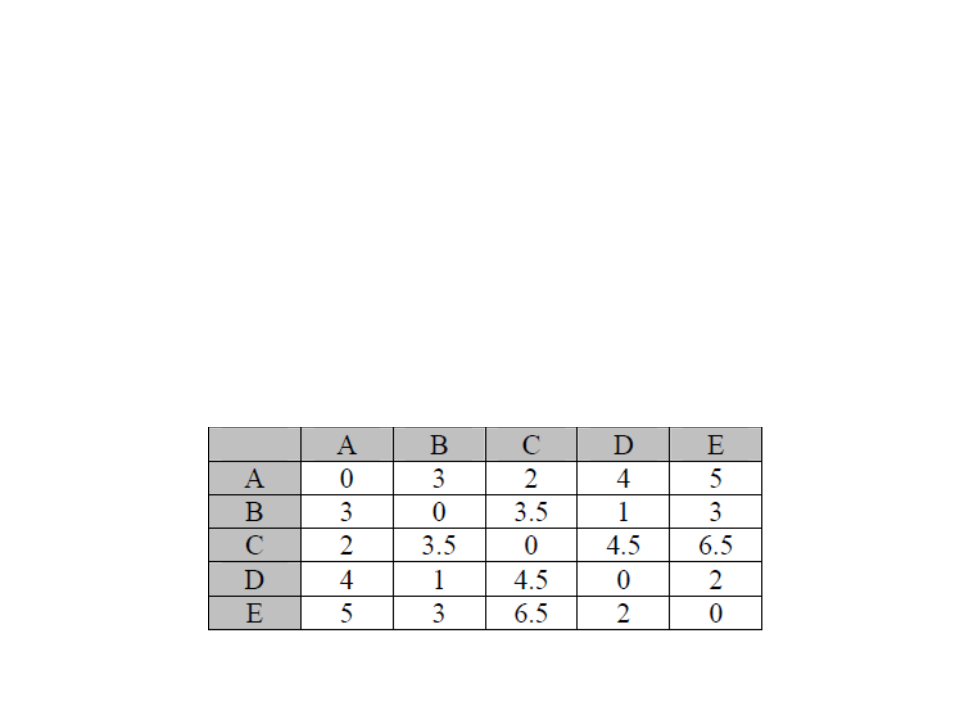
Custos Pré-Calculados
•
•
Saber qual o melhor caminho entre dois nós somente é útil
quando se sabe onde se deseja ir.
Uma tabela pré-calculada com os custos de locomoção entre
quaisquer dois nós também é uma informação muito util.

Leitura Complementar
•
Russell, S. and Novig, P. Artificial Intelligence: a
Modern Approach, 2nd Edition, Prentice-Hall,
2003.
•
Capítulo 4: Informed Search and Exploration
