
INF 1771 – Inteligência Artificial
Aula 03 – Resolução de Problemas por
Meio de Busca
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Introdução
•
Agentes Autônomos:
– Entidades autônomas capazes de observar o ambiente e
agir de forma de forma autônoma com o objetivo de
atingir determinado objetivo.
•
Tipos de Agentes:
–
–
–
–
–
Agentes reativos simples;
Agentes reativos baseado em modelo;
Agentes baseados em objetivos;
Agentes baseados na utilidade;
Agentes baseados em aprendizado;

Problema de Busca
•
•
Objetivo: Conjunto de estados que satisfazem o objetivo.
Tarefa de Busca: Encontrar a sequencia de ações que leva do
estado atual até um estado objetivo.
•
•
•
Quais são os estados?
Quais são as ações?
Nível de abstração?
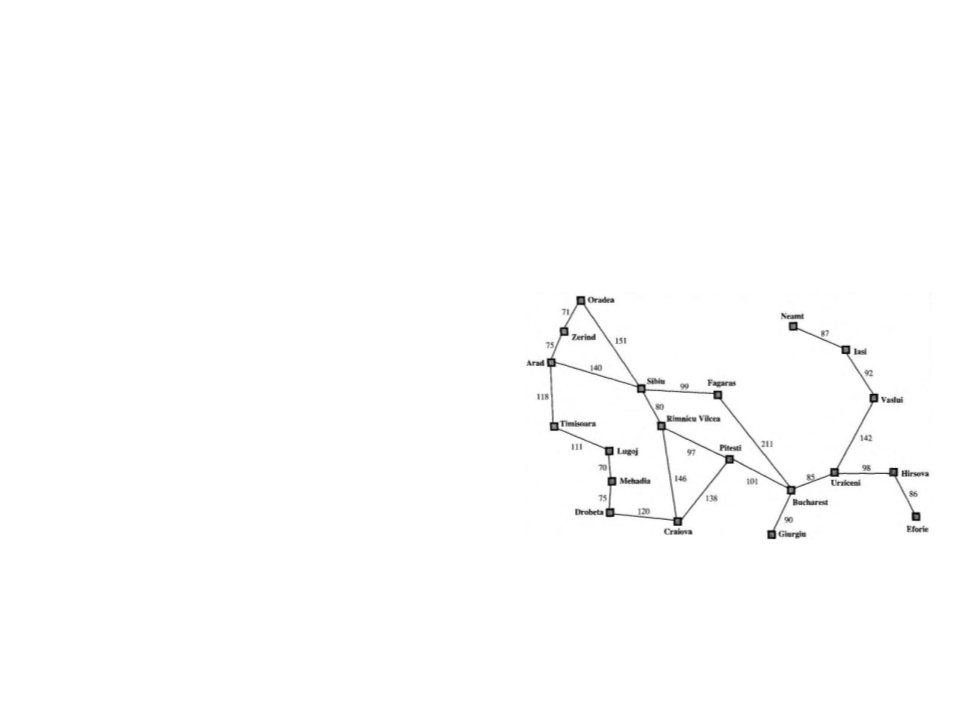
Problema de Busca
Bucharest
Timisoara
Sibiu
Zerind
Arad
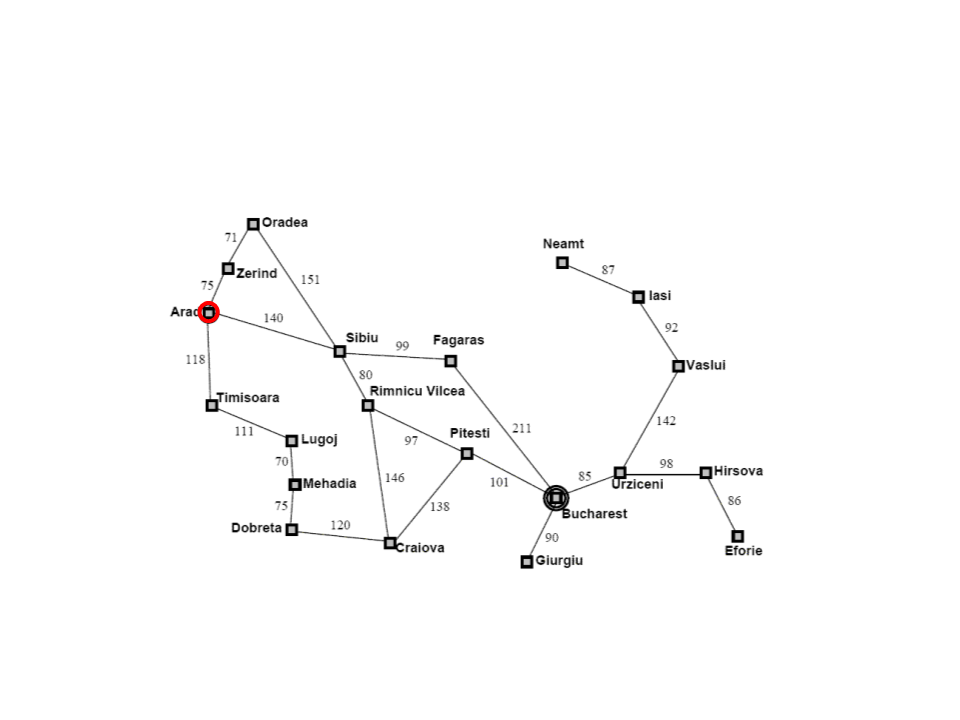
Problema de Busca

Problema de Busca
•
O processo de tentar encontrar uma sequencia de ações
que leva de um estado até um estado objetivo é
chamado de busca.
•
•
Uma vez encontrada a solução, o agente pode executar a
sequencia de ações para chegar no objetivo.
Fases:
–
–
–
Formular objetivo
Buscar objetivo
Executar sequencia de ações

Problema de Busca
function SIMPLE-PROBLEM-SOLVING-AGENT(percept) return an action
static: seq, an action sequence
state, some description of the current world state
goal, a goal
problem, a problem formulation
state ← UPDATE-STATE(state, percept)
if seq is empty then
goal ← FORMULATE-GOAL(state)
problem ← FORMULATE-PROBLEM(state,goal)
seq ← SEARCH(problem)
action ← FIRST(seq)
seq ← REST(seq)
return action

Definição do Problema
•
•
A definição do problema é a primeira e mais
importante etapa do processo de resolução de
problemas de inteligência artificial por meio de
buscas.
Consiste em analisar o espaço de possibilidades de
resolução do problema, encontrar sequências de
ações que levem a um objetivo desejado.

Definição de um Problema
•
•
•
•
Estado Inicial: Estado inicial do agente.
–
Ex: Em(Arad)
Estado Final: Estado buscado pelo agente.
–
Ex: Em(Bucharest)
Ações Possíveis: Conjunto de ações que o agente pode executar.
–
Ex: Ir(Cidade, PróximaCidade)
Espaço de Estados: Conjunto de estados que podem ser atingidos a partir do
estado inicial.
–
Ex: Mapa da Romênia.
•
Custo: Custo numérico de cada caminho.
–
Ex: Distância em KM entre as cidades.

Considerações em Relação ao Ambiente
•
Estático:
–
O Ambiente não pode mudar enquanto o agente está realizando a resolução
do problema.
•
•
Observável:
– O estado inicial do ambiente precisa ser conhecido previamente.
Determinístico:
–
O próximo estado do agente deve ser determinado pelo estado atual + ação. A
execução da ação não pode falhar.
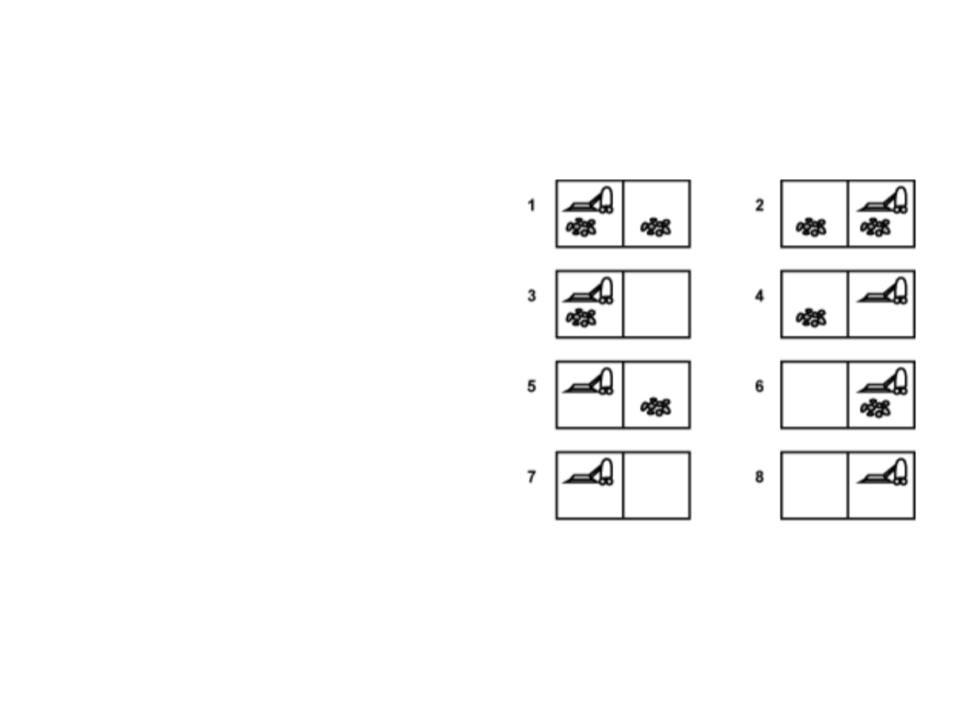
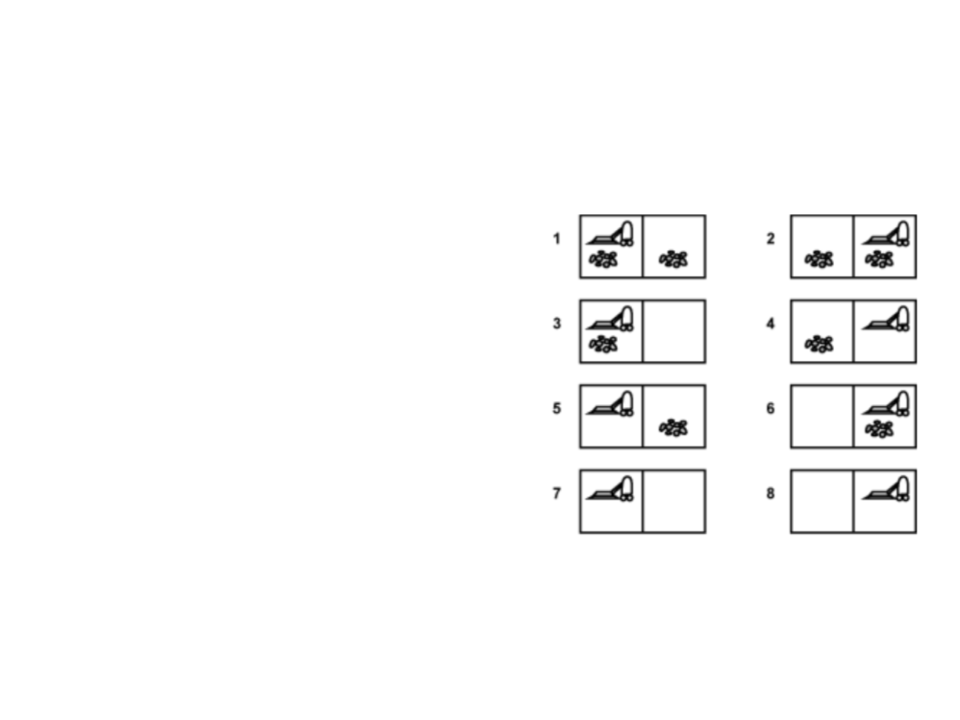
Exemplo: Aspirador de Pó
•
Espaço de Estados: 8 estados possíveis
(
figura ao lado);
•
•
Estado Inicial: Qualquer estado;
Estado Final: Estado 7 ou 8 (ambos
quadrados limpos);
•
•
Ações Possíveis: Mover para direita,
mover para esquerda e limpar;
Custo: Cada passo tem o custo 1, assim o
custo do caminho é definido pelo número
de passos;
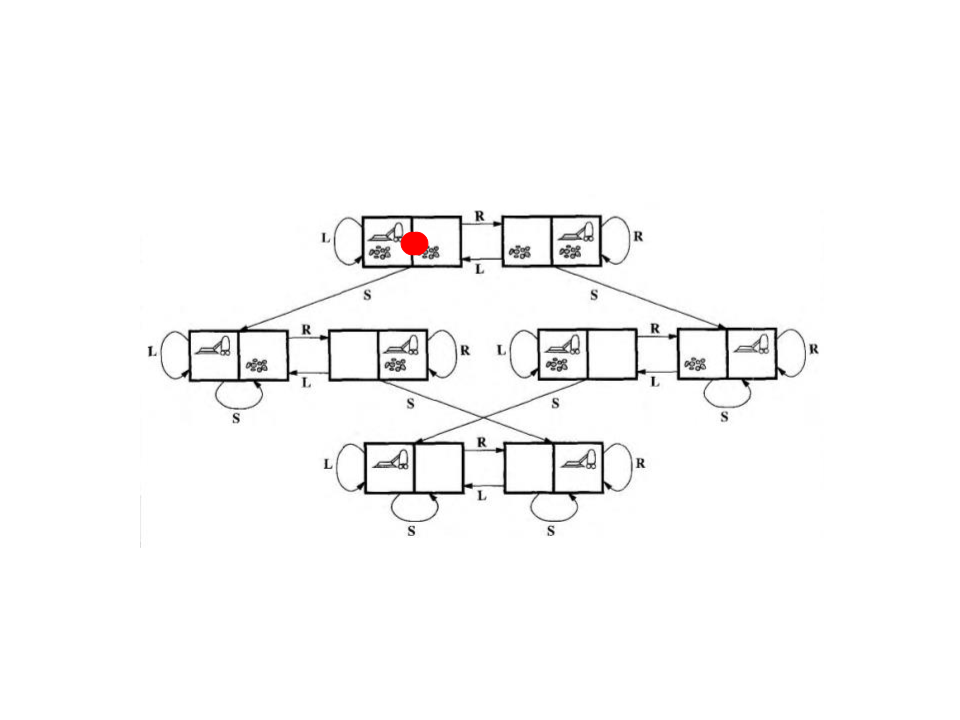
Exemplo: Aspirador de Pó

Exemplo: 8-Puzzle
•
•
•
•
Espaço de Estados: 181.440 possíveis estados;
Estado Inicial: Qualquer estado;
Estado Final: Figura ao lado – Goal State;
Ações Possíveis: Mover o quadrado vazio para
direita, para esquerda, para cima ou para baixo;
•
Custo: Cada passo tem o custo 1, assim o custo do
caminho é definido pelo número de passos;
•
•
15-puzzle (4x4) – 1.3 trilhões estados possíveis.
24-puzzle (5x5) – 10²⁵ estados possíveis.

Exemplo: Xadrez
4
0
•
•
•
Espaço de Estados: Aproximadamente 10
possíveis estados (Claude Shannon, 1950);
Estado Inicial: Posição inicial de um jogo de
xadrez;
Estado Final: Qualquer estado onde o rei
adversário está sendo atacado e o adversário
não possui movimentos válidos;
•
•
Ações Possíveis: Regras de movimentação de
cada peça do xadrez;
Custo: Quantidade de posições examinadas;

Exemplo: 8 Rainhas (Incremental)
•
Espaço de Estados: Qualquer disposição de 0
a 8 rainhas no tabuleiro (1.8 x 10¹⁴ possíveis
estados);
•
•
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8
rainhas estão no tabuleiro e nenhuma esta
sendo atacada;
•
•
Ações Possíveis: Colocar uma rainha em um
espaço vaio do tabuleiro;
Custo: Não importa nesse caso;
*
diferentes rotações e reflexões). E apenas 12 soluções únicas.
O jogo possui apenas 92 possíveis soluções (considerando

Exemplo: 8 Rainhas (Estados Completos)
•
Espaço de Estados: Tabuleiro com n rainhas,
uma por coluna, nas n colunas mais a esquerda
sem que nenhuma rainha ataque outra (2057
possíveis estados);
•
•
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8
rainhas estão no tabuleiro e nenhuma esta
sendo atacada;
•
•
Ações Possíveis: Adicionar uma rainha em
qualquer casa na coluna vazia mais à esquerda
de forma que não possa ser atacada;
Custo: Não importa nesse caso;
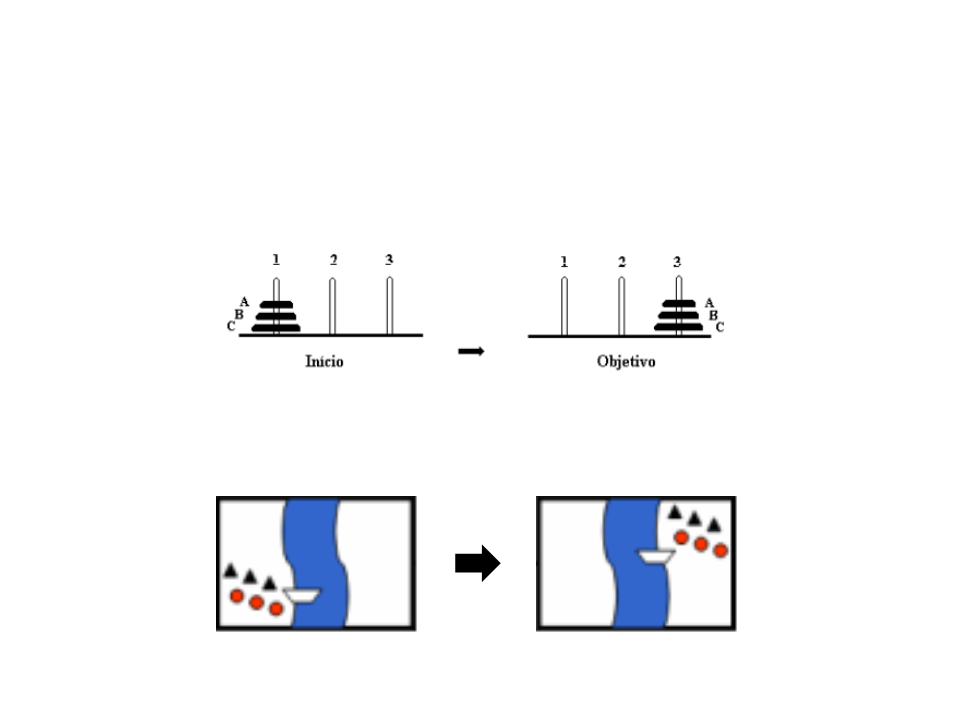
Exercícios
•
•
Torre de Hanói?
Canibais e Missionários?

Exercícios
•
Torre de Hanói:
–
–
–
Espaço de Estados: Todas as possíveis configurações de argolas em
todos os pinos (27 possíveis estados).
Ações Possíveis: Mover a primeira argola de qualquer pino para o pino
da direita ou da esquerda.
Custo: Cada movimento tem 1 de custo.
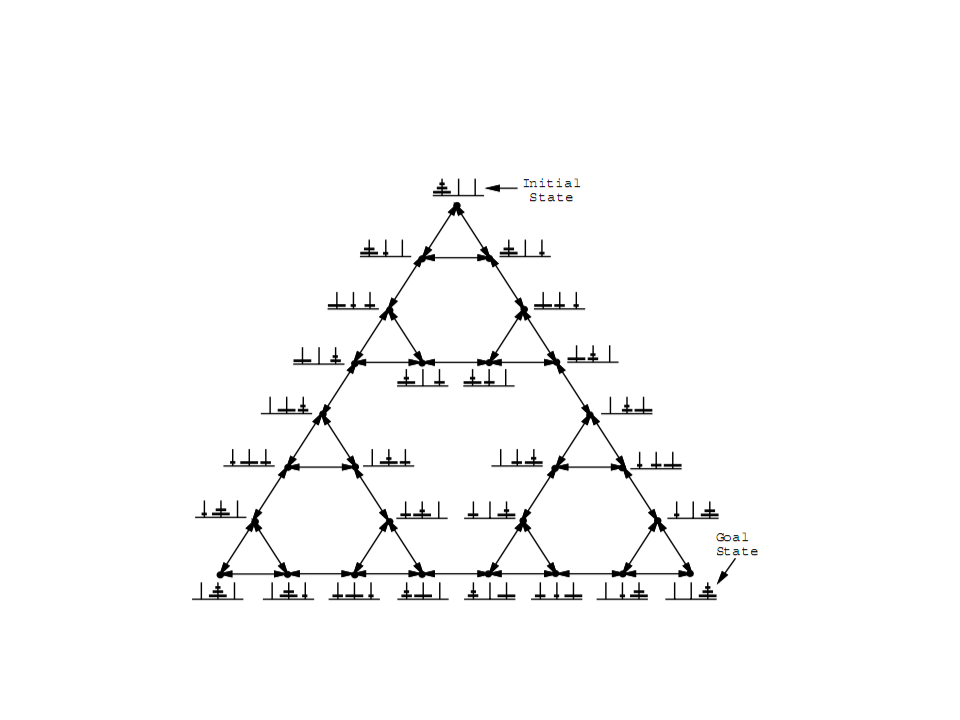
Exercícios

Exercícios
•
Canibais e Missionários:
–
–
Espaço de Estados: Todas as possíveis configurações validas de
canibais e missionários em cada lado do rio (16 possíveis estados).
Ações Possíveis: Mover 1 ou 2 personagens (canibais ou missionários)
para o outro lado do rio. O número de canibais em um determinado
lado do rio não pode ser maior do que o número de missionários.
–
Custo: Cada movimento tem 1 de custo.
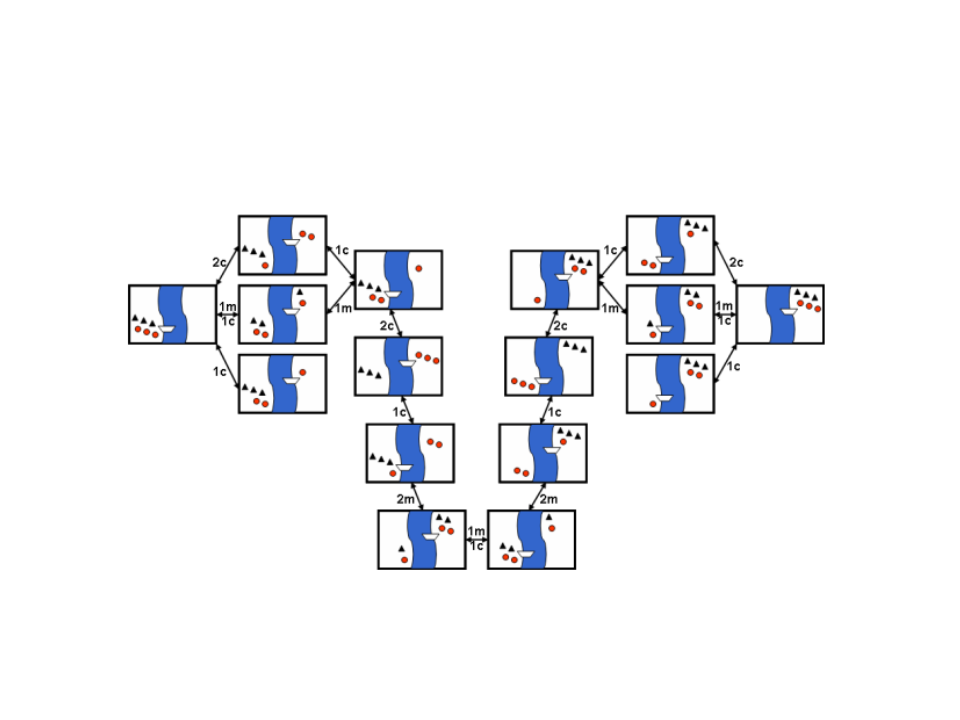
Exercícios

Aplicações em Problemas Reais
•
•
Cálculo de Rotas:
–
–
–
–
–
Planejamento de rotas de aviões;
Sistemas de planejamento de viagens;
Caixeiro viajante;
Rotas em redes de computadores;
Jogos de computadores (rotas dos personagens);
Alocação
–
Salas de aula;
–
Máquinas industriais;

Aplicações em Problemas Reais
•
•
Circuitos Eletrônicos:
–
Posicionamento de componentes;
–
Rotas de circuitos;
Robótica:
–
Navegação e busca de rotas em ambientes reais;
–
Montagem de objetos por robôs;

Como Encontrar a Solução?
•
•
Uma vez o problema bem formulado, o estado final
(objetivo) deve ser “buscado” no espaço de estados.
A busca é representada em uma árvore de busca:
–
Raiz: corresponde ao estado inicial;
–
Expande-se o estado corrente, gerando um novo conjunto de
sucessores;
–
–
Escolhe-se o próximo estado a expandir seguindo uma estratégia de
busca;
Prossegue-se até chegar ao estado final (solução) ou falhar na busca
pela solução;
Buscando Soluções
•
Exemplo: Ir de Arad para Bucharest
Arad
Sibiu
Timissoara
Fagaras
Zerind
Arad
Orades
Rimnico Vilcea
Buscando Soluções
•
•
O espaço de estados é diferente da árvore de buscas.
Exemplo:
–
–
–
20 estados no espaço de estados;
Número de caminhos infinito;
Árvore com infinitos nós;

Código Descritivo – Busca em Árvore
Função BuscaEmArvore(Problema, Estratégia) retorna solução ou falha
Inicio
Inicializa a arvore usando o estado inicial do Problema
loop do
se não existem candidatos para serem expandidos então
retorna falha
Escolhe um nó folha para ser expandido de acordo com
a Estratégia
se Se o nó possuir o estado final então
retorna solução correspondente
se não
expande o nó e adiciona os nós resultantes a
arvore de busca
Fim

Pseudocódigo – Busca em Árvore
Função BuscaEmArvore(Problema, fronteira) retorna solução ou falha
Inicio
fronteira ← InsereNaFila(FazNó(Problema[EstadoInicial]), fronteira)
loop do
se FilaVazia(fronteira) então
retorna falha
nó ← RemovePrimeiro(fronteira)
se nó[Estado] for igual a Problema[EstadoFinal] então
retorna Solução(nó)
fronteira ← InsereNaFila(ExpandeFronteira(nó, Problema), fronteira)
Fim
-
-
A função Solução retorna a sequência de nós necessários para
retornar a raiz da arvore.
Considera-se fronteira uma estrutura do tipo fila.

Medida de Desempenho
•
•
Desempenho do Algoritmo:
–
(1) O algoritmo encontrou alguma solução?
–
(2) É uma boa solução?
•
Custo de caminho (qualidade da solução).
–
(3) É uma solução computacionalmente barata?
• Custo da busca (tempo e memória).
Custo Total
–
Custo do Caminho + Custo de Busca.

Métodos de Busca
•
Busca Cega ou Exaustiva:
–
Não sabe qual o melhor nó da fronteira a ser expandido. Apenas
distingue o estado objetivo dos não objetivos.
•
•
Busca Heurística:
–
Estima qual o melhor nó da fronteira a ser expandido com base em
funções heurísticas.
Busca Local:
–
Operam em um único estado e movem-se para a vizinhança deste
estado.

Busca Cega
•
Algoritmos de Busca Cega:
–
–
–
–
Busca em largura;
Busca de custo uniforme;
Busca em profundidade;
Busca com aprofundamento iterativo;
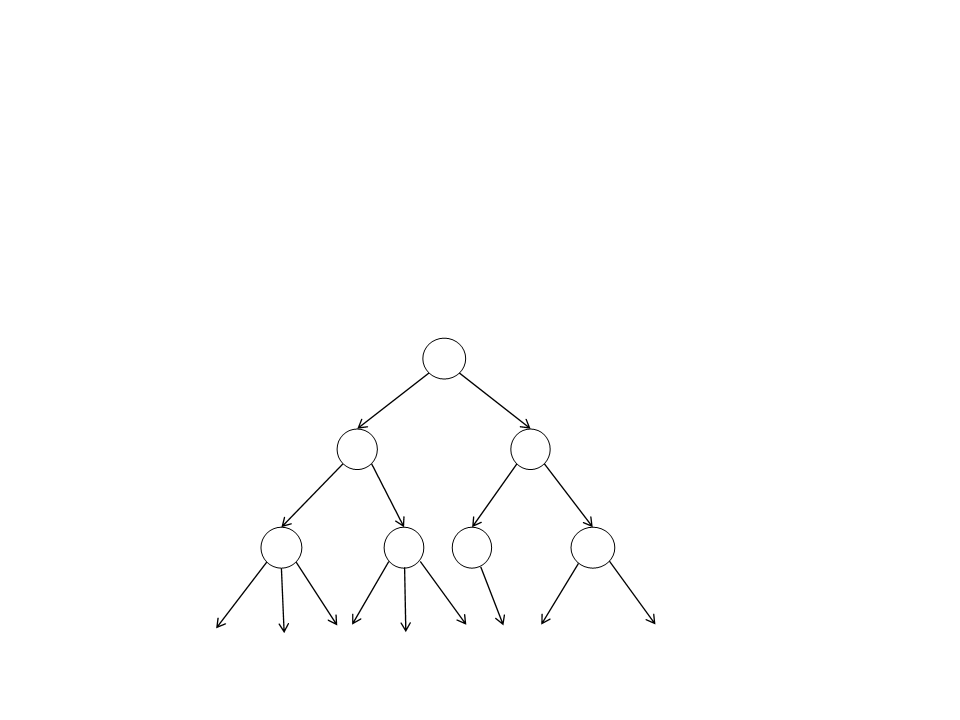
Busca em Largura
•
Estratégia:
–
O nó raiz é expandido, em seguida todos os nós sucessores são
expandidos, então todos próximos nós sucessores são expandidos, e
assim em diante.
A
B
C
D
E
F
G
Busca em Largura
•
•
Pode ser implementado com base no pseudocódigo da função
“
BuscaEmArvore” apresentado anteriormente. Utiliza-se uma
estrutura de fila (first-in-first-out) para armazenar os nós das
fronteira.
d+1
Complexidade: O(b )
Profundidade (d) Nós
Tempo
0.11 ms
11 ms
Memória
107 KB
10.6 MB
1 GB
2
4
6
8
1
1
1
1100
111,100
7
10
1.1 seg
2 min
9
10
103 GB
10 TB
1
1
3
0
2
4
10
3 horas
13 dias
3.5 anos
1
10
1 PB
1
5
10
99 PB
*
1
Considerando o número de folhas b = 10 e cada nó ocupando
KB de memória.
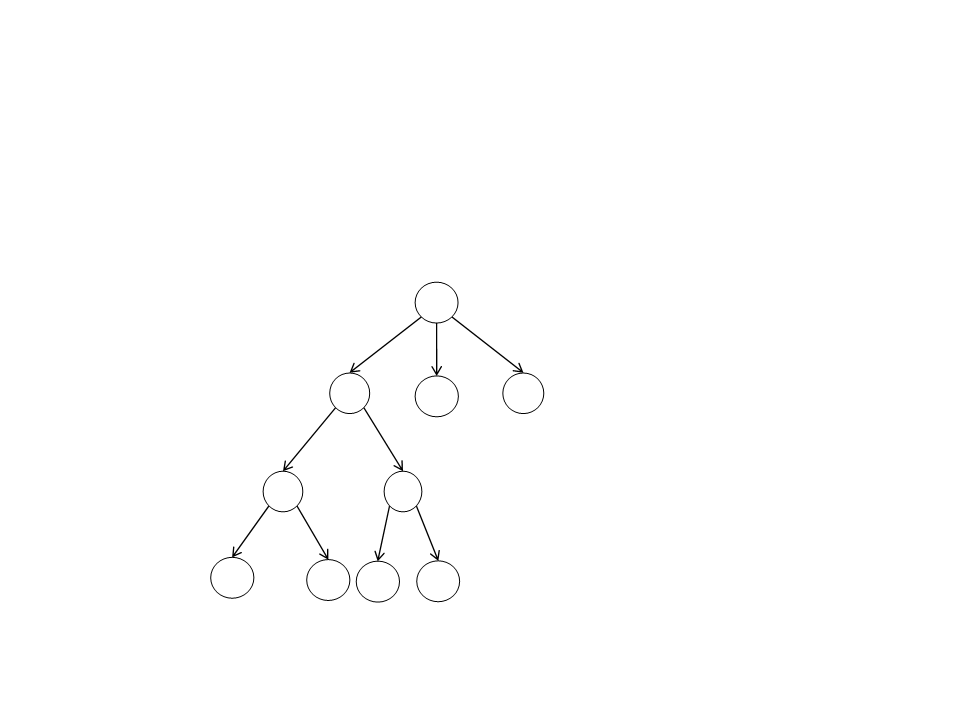
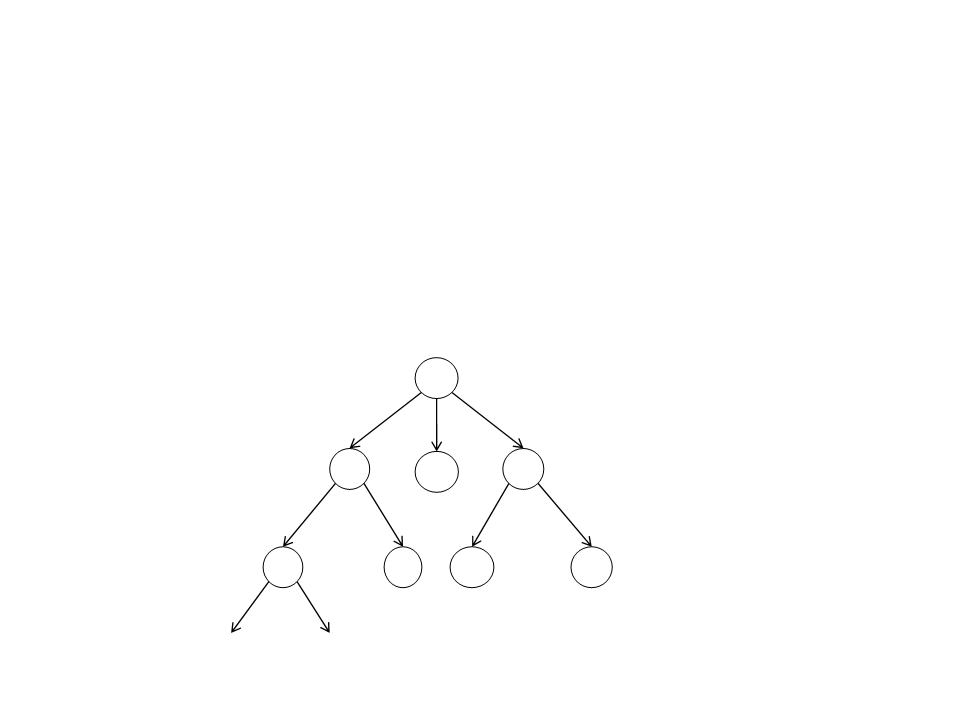
Busca em Profundidade
•
Estratégia:
–
Expande os nós da vizinhança até o nó mais profundo.
A
B
D
C
E
F
M
N
P
Q

Busca em Profundidade
•
Pode ser implementado com base no pseudocódigo da
função “BuscaEmArvore” apresentado anteriormente.
Utiliza-se uma estrutura de pilha (last-in-first-out) para
armazenar os nós das fronteira.
•
•
Pode também ser implementado de forma recursiva.
Consome pouca memória, apenas o caminho de nós
sendo analisados precisa armazenado. Caminhos que
já foram explorados podem ser descartados da
memória.

Busca em Profundidade
•
•
•
Uso de memória pela busca em largura em uma
arvore com 12 de profundidade: 1000 TB.
Uso de memória pela busca em profundidade em
uma arvore com 12 de profundidade: 118 KB.
Problema: O algoritmo pode fazer uma busca muito
longa mesmo quando a resposta do problema esta
localizado a poucos nós da raiz da árvore.
Busca de Custo Uniforme
•
Estratégia:
–
Expande sempre o nó de menor custo de caminho. Se o custo de todos
os passos for o mesmo, o algoritmo acaba sendo o mesmo que a busca
em largura.
A
75
118
170
B
D
C
75
71
111
99
E
F
G
H

Busca de Custo Uniforme
•
A primeira solução encontrada é a solução ótima se custo do
caminho sempre aumentar ao logo do caminho, ou seja, não
existirem operadores com custo negativo.
•
•
Implementação semelhante a busca em largura. Adiciona-se
uma condição de seleção dos nós a serem expandidos.
1
+(C/)
Complexidade: O(b
)
–
Onde:
C = custo da solução ótima;
α = custo mínimo de uma ação;
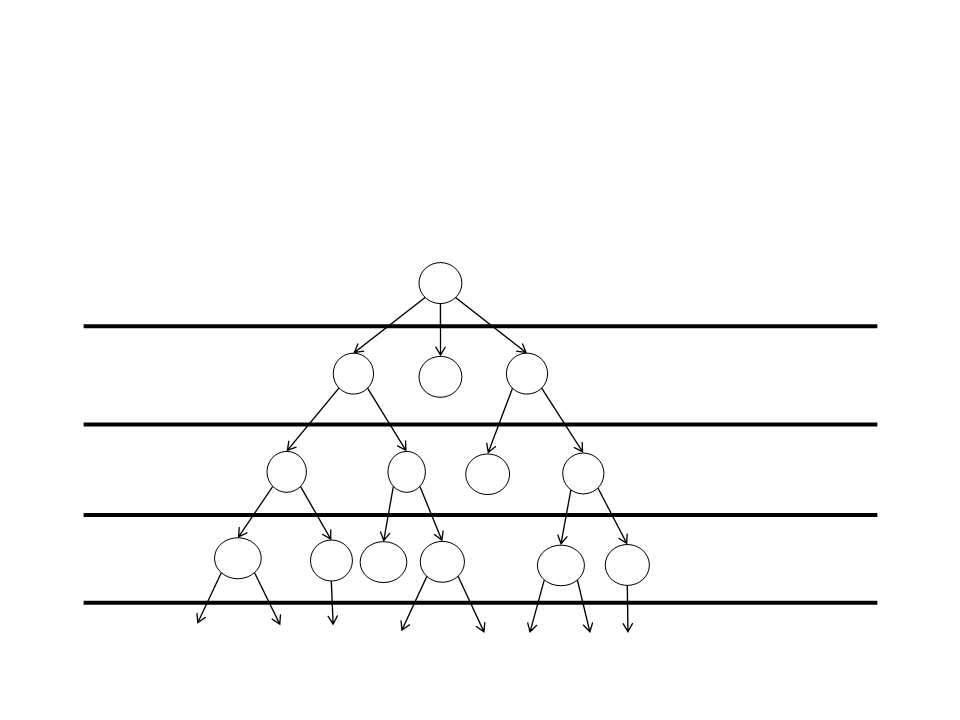
Busca com Aprofundamento Iterativo
•
Estratégia: Consiste em uma busca em profundidade onde o
limite de profundidade é incrementado gradualmente.
A
Limit 0
B
D
C
Limit 1
E
F
H
G
Limit 2
Limit 3
M
N
P
Q
P
Q

Busca com Aprofundamento Iterativo
•
Combina os benefícios da busca em largura com os benefícios
da busca em profundidade.
•
•
Evita o problema de caminhos muito longos ou infinitos.
A repetição da expansão de estados não é tão ruim, pois a
maior parte dos estados está nos níveis mais baixos.
•
‰Cria menos estados que a busca em largura e consome menos
memória.
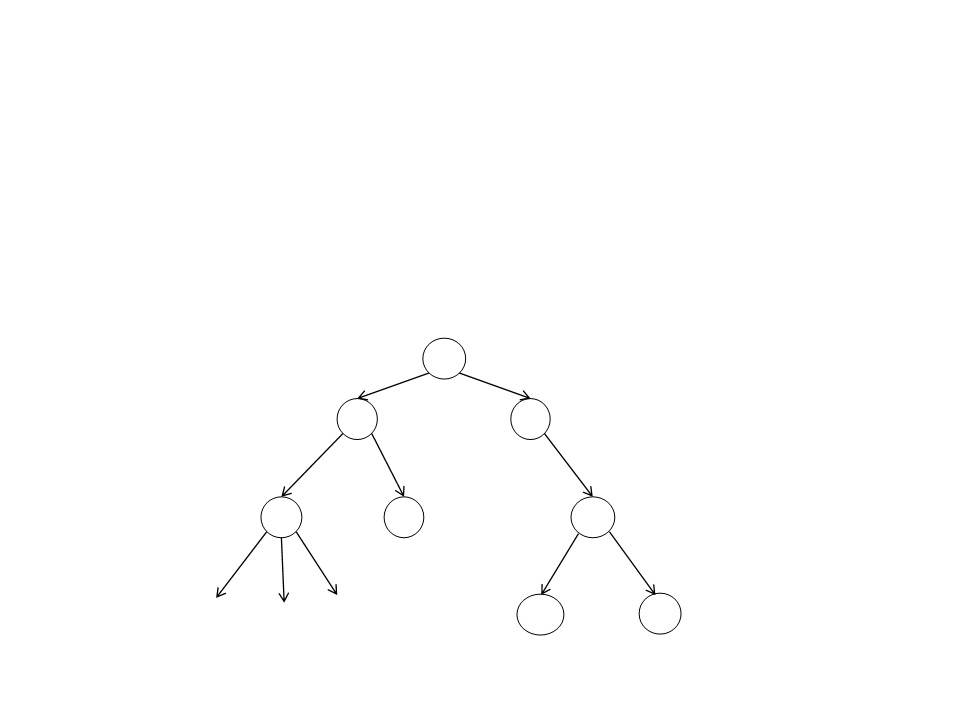
Busca Bidirecional
•
Estratégia:
– A busca se inicia ao mesmo tempo a partir do estado inicial
e do estado final.
A
B
C
D
E
G
M
N

Comparação dos Métodos de Busca Cega
Criterio
Largura Uniforme Profundidade Aprofundamento
Iterativo
Bidirecional
Completo?
Ótimo?
Tempo
Sim ¹
Sim ¹,²
Não
Não
Sim ¹
Sim ³
Sim ¹, ⁴
Sim ³, ⁴
Sim ³
Sim
1+(C/)
d+1
m
d
d /2
O(b ) O(b
)
)
O(b )
O(b )
O(b )
d+1
1+(C/)
d /2
O(bd)
O(b ) O(b
O(bm)
O(b )
Espaço
b = fator de folhas por nó.
d = profundidade da solução mais profunda.
m = profundidade máxima da árvore.
¹
completo se b for finito.
²
³
⁴
completo se o custo de todos os passos for positivo.
ótimo se o custo de todos os passos for idêntico.
se ambas as direções usarem busca em largura.

Como evitar estados repetidos?
•
•
Estados repetidos sempre vão ocorrer em problema
onde os estados são reversíveis.
Como evitar?
–
–
–
Não retornar ao estado “pai”.
Não retorna a um ancestral.
Não gerar qualquer estado que já tenha sido criado antes
(em qualquer ramo).
• Requer que todos os estados gerados permaneçam na memória.

Busca com Informação Parcial
•
•
Anteriormente supomos que o ambiente era estático,
completamente observável e determinístico.
O que fazer se o conhecimento sobre os estados ou ações é
incompleto?

Busca com Informação Parcial
•
•
Agente sem sensores: em alguns casos o agente não
tem nenhum sensor para saber em qual estado ele
está.
–
Podendo estar em um de vários possíveis estados.
–
Cada ação pode levar o agente para um de vários possíveis
estados sucessores.
Exemplo: Aspirador de pó sem sensores.
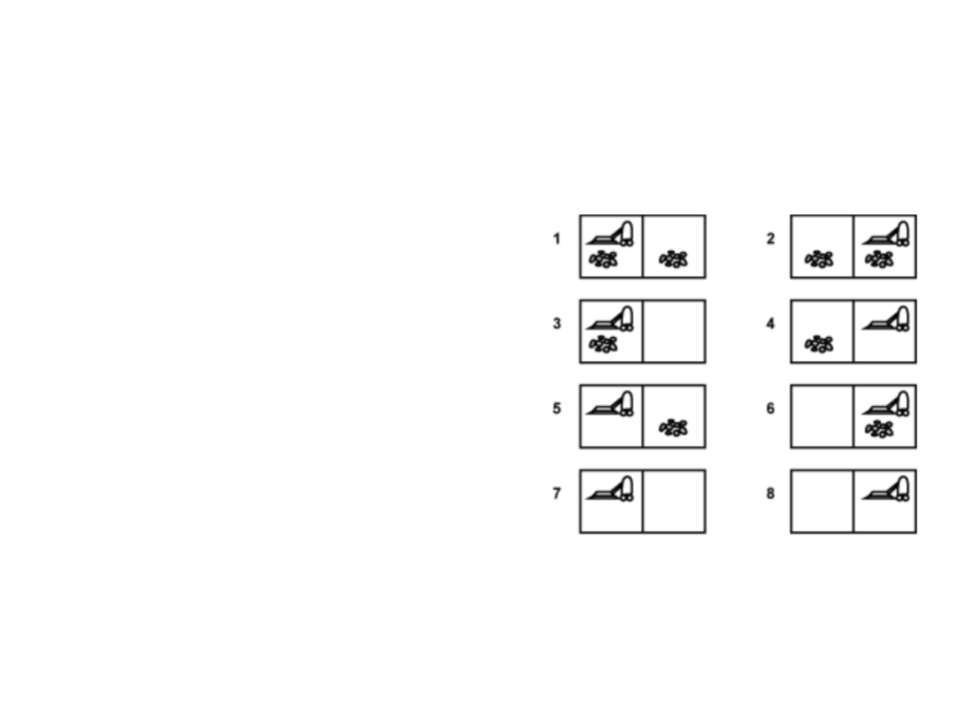
Busca com Informação Parcial
•
•
O estado inicial é um dos possíveis
estados {1, 2, 3, 4, 5, 6, 7, 8}.
Executar a ação MoverDireita sempre vai
levar o agente para um dos estados {2, 4,
6
, 8}.
•
•
A sequencia de ações [MoverDireita,
Limpar] sempre vai levar o agente para
um dos estados {4, 8}.
A sequencia de ações [MoverDireita,
Limpar, MoverEsqueda, Limpar] sempre
vai levar o agente para o estado 7.
Busca com Informação Parcial
•
•
O agente consegue atingir o estado
objetivo sem saber onde ele começou.
O agente deve raciocinar sobre o conjunto
de estados que ele pode estar em vez de
um único estado.
•
•
Estados de crença.
A busca é realizada no espaço de estados
de crença.

Leitura Complementar
•
Russell, S. and Novig, P. Artificial Intelligence: a
Modern Approach, 2nd Edition, Prentice-Hall,
2003.
•
Capítulo 3: Solving Problems by Searching
