
INF 1771 – Inteligência Artificial
Aula 23 – Redes Bayesianas
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Vantagens e Desvantagens da Probabilidade
Possui uma boa fundamentação formal.
Permite encontrar probabilidades “a posteriori”.
Pode chegar a resultados inapropriados para o
presente. O futuro não é sempre similar ao
passado.
Nem sempre é possível realizar um conjunto
suficiente de experimentos.

Vantagens e Desvantagens da Probabilidade
A distribuição de probabilidade conjunta
completa pode responder a qualquer pergunta
sobre o domínio, mas pode tornar-se intratável
quando o número de variáveis aumenta.
A independência e as relações de independência
condicional entre as variáveis podem reduzir
significativamente o número de probabilidades que
devem ser especificadas para definir a distribuição
completa.

Redes Bayesianas
Estrutura de dados para representar as
dependências entre variáveis e fornecer uma
especificação concisa de qualquer distribuição de
probabilidade conjunta total.
Consiste em um grafo dirigido em que cada nó possui
informações quantitativas de probabilidade. É definido
por:
Um conjunto de nós, um para cada variável aleatória.
Um conjunto de links direcionados ou setas ligando os
pares de nós.
Cada nó tem uma distribuição condicional
P(Xi|Parents(Xi)) que quantifica o efeito dos parents
sobre o nó.

Redes Bayesianas - Exemplo
A topologia de uma rede representa relações
de independência condicional:
Clima
Cárie
Dor_De_Dente
Sonda
Clima é independente de outras variáveis.
Dor_De_Dente e Sonda são condicionalmente independentes dado Cárie.
Informalmente, a rede representa o fato de que Cárie é uma causa direta de
Dor_De_Dente e Sonda.

Redes Bayesianas – Exemplo
Você tem um novo alarme contra roubo instalado em
casa. É bastante confiável na detecção de um roubo,
mas dispara também na ocasião para pequenos
terremotos. Você também tem dois vizinhos, João e
Maria, que prometeram ligar para você no trabalho,
quando ouvissem o alarme. João sempre liga quando
ele ouve o alarme, mas às vezes confunde o telefone
com o alarme. Maria, por outro lado, gosta de ouvir
música alta e às vezes não escuta o alarme.

Redes Bayesianas – Exemplo
Variáveis: Roubo, Terremoto, Alarme,
JoãoLiga, MariaLiga.
A topologia da rede reflete conhecimento
“
causal”:
Um roubo pode ativar o alarme.
Um terremoto pode ativar o alarme.
O alarme faz Maria telefonar.
O alarme faz João telefonar.
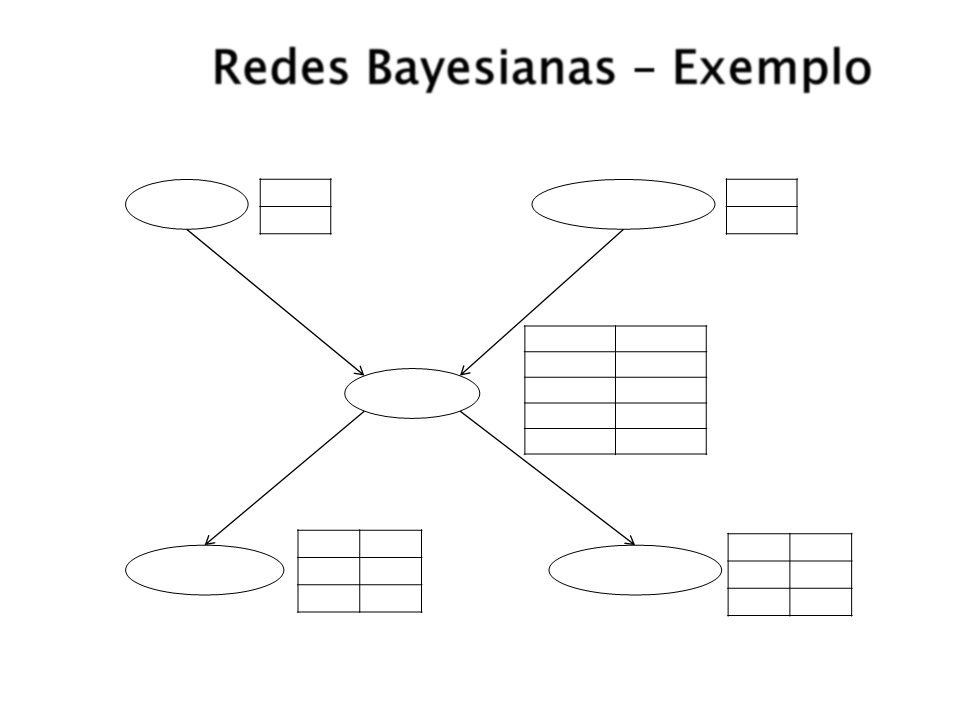
Redes Bayesianas – Exemplo
P(R)
.001
P(T)
Roubo
Terremoto
0
0.002
R
V
V
F
T
V
F
P(A)
0.95
0.94
0.29
0.001
Alarme
V
F
F
A
V
F
P(J)
0.90
0.05
A
V
F
P(M)
0.70
0.01
JoãoLiga
MariaLiga

Exemplo – Topologia da Rede
Roubos e terremotos afetam diretamente a
probabilidade do alarme tocar.
O fato de João e Maria telefonarem só
depende do alarme.
Desse modo, a rede representa as
suposições de que eles não percebem
quaisquer roubos diretamente, não notam os
terremotos e não verificam antes de ligar.

Exemplo – Probabilidades
As probabilidades resumem um conjunto
potencialmente infinito de circunstâncias:
Maria ouve música alta.
João liga quando ouve o telefone tocar;
umidade, falta de energia, etc., podem interferir no
alarme;
João e Maria não estão em casa, etc.
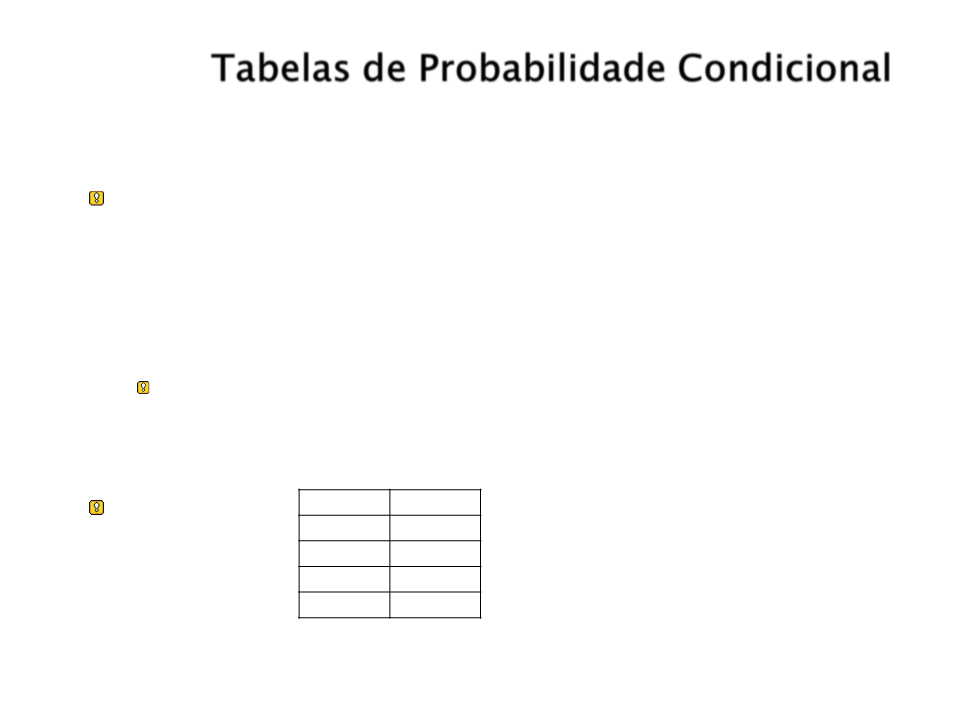
Tabelas de Probabilidade Condicional
Cada linha em uma tabela de probabilidade
condicional contém a probabilidade
condicional de cada valor do nó para um caso
de condicionamento.
Um caso de condicionamento é uma combinação
possível de valores para os nós superiores.
R
V
V
F
T
V
F
P(A)
0.95
0.94
0.29
0.001
Exemplo:
V
F
F

Semântica das Redes Bayesianas
Semântica global (ou numérica): busca
entender as redes como uma representação
da distribuição de probabilidade conjunta.
Indica como construir uma rede.
Semântica local (ou topológica): visualizá-
las como uma codificação de uma coleção de
declarações de independência condicional.
Indica como fazer inferências com uma rede.

Semântica Global
A semântica global (ou numérica) define a
distribuição de probabilidade total como o
produto das distribuições condicionais
locais:
n
i=1
P (X1, … ,Xn) = P (Xi |parents(Xi))
Exemplo: P(j m a r t)
=
=
=
P(j | a) P(m | a) P(a|r t) P(r) P (t)
0.9 x 0.7 x 0.001 x 0.999 x 0.998
0.00063
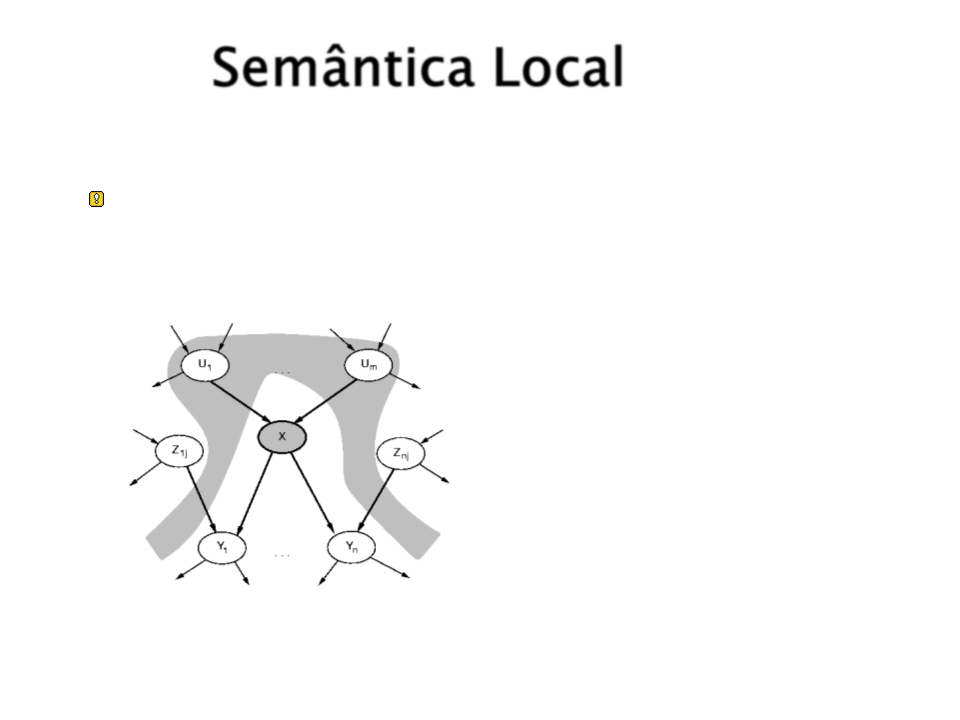
Semântica Local
Semântica local (topológica): cada nó é
condicionalmente independente de seus não-
descendentes dados seus pais.
Um nó X é condicionalmente
independente de seus não
descendentes (Zij) dados seus
pais (Ui).

Semântica Local e Global
A distribuição conjunta pode ser reconstruída
a partir das asserções sobre a independência
condicional e das tabelas de probabilidade
condicional.
Deste modo a semântica numérica e topológica são
equivalentes.

Construindo uma Rede Bayesiana
(
descrevem apropriadamente o domínio.
1) Escolhe-se o conjunto de variáveis Xi que
(
2) Seleciona-se a ordem de distribuição das variáveis
(
Passo importante).
(3) Enquanto ainda existirem variáveis:
(
a) Seleciona-se uma variável X e um nó para ela.
(
nós de forma que a independência condicional seja
satisfeita.
b) Define-se Parent(X) para um conjunto mínimo de
(
c) Define-se a tabela de probabilidade para X.

Ordem para as Variáveis
A ordem correta em que os nós devem ser
adicionados consiste em adicionar primeiro
as “causas de raiz”, depois as variáveis que
elas influenciam e assim por diante, até
chegarmos às folhas, que não tem nenhuma
influência causal direta sobre as outras
variáveis.
Principio Minimalista: Quanto menor a
rede, melhor ela é.
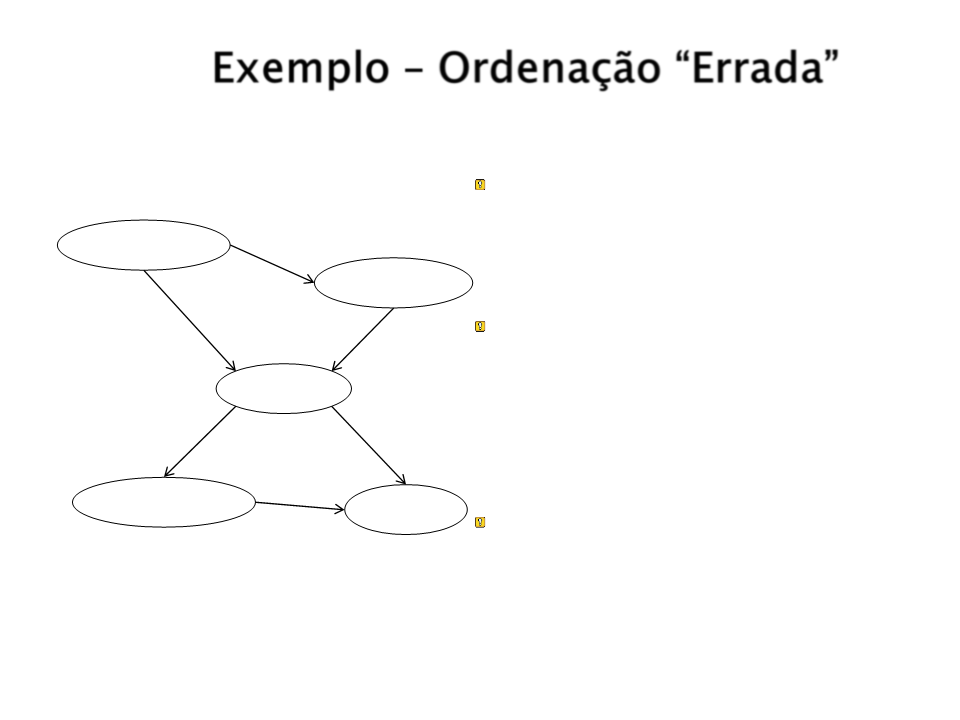
Exemplo – Ordenação “Errada”
A rede resultante terá dois
vínculos a mais que a rede
original e exigirá outras
probabilidades para serem
MariaLiga
JoãoLiga
especificadas.
Alguns dos vínculos apresentam
relacionamentos tênues que
exigem julgamentos de
Alarme
probabilidade difíceis e
antinaturais (probabilidade de
Terremoto, dados Roubo e
Alarme)
Em geral, é melhor pensar de
causas para efeitos (modelo
causal) e não do contrário
Terremoto
Roubo
(modelo de diagnóstico)

Inferência em Redes Bayesianas
Inferência Diagnostica (de efeitos para
causas):
Dado que João liga, qual a probabilidade de roubo?
Ex: P(R|J)
Inferência Casual (de causas para efeitos):
Dado roubo, qual é a probabilidade de:
João ligar? ex: P(J|R).
Maria ligar? ex: P(M|R).

Inferência em Redes Bayesianas
Inferência Intercasual (entre causas de
um evento em comum):
Dado terremoto e alarme, qual a probabilidade de
roubo? Ex: P(R|A T)
Inferência Mista (algumas causas e alguns
efeitos conhecidos):
Dado que João liga e não existe terremoto, qual é a
probabilidade de alarme? Ex: P(A|J ¬T)
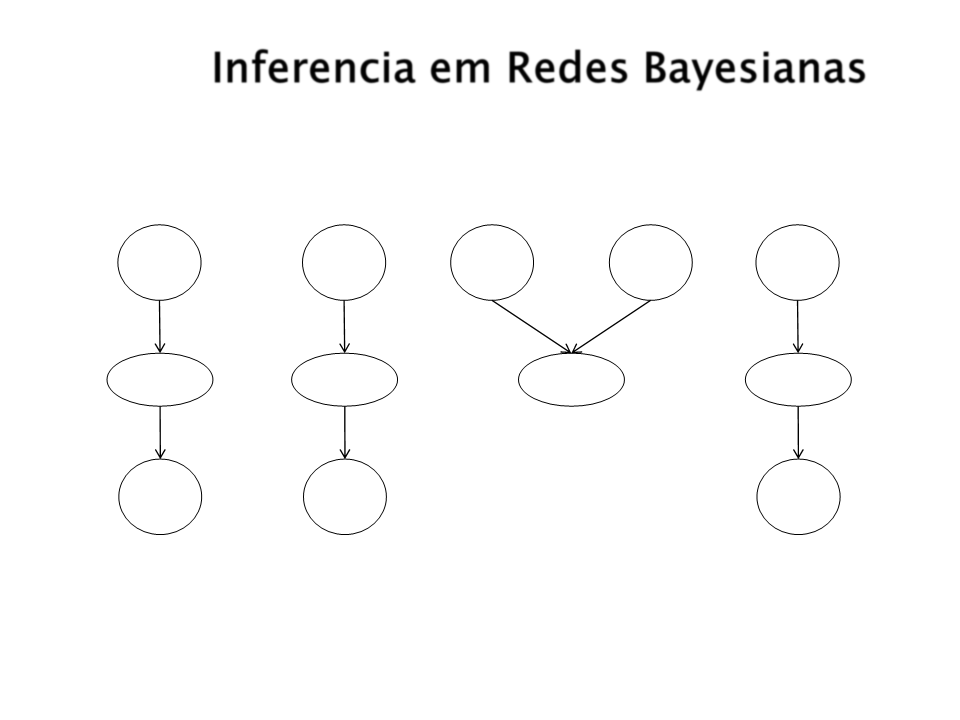
Inferencia em Redes Bayesianas
?
E
E
?
E
?
E
?
E
Inferência
Diagnostica
Inferência
Casual
Inferência
Intercasual
Inferência
Mista
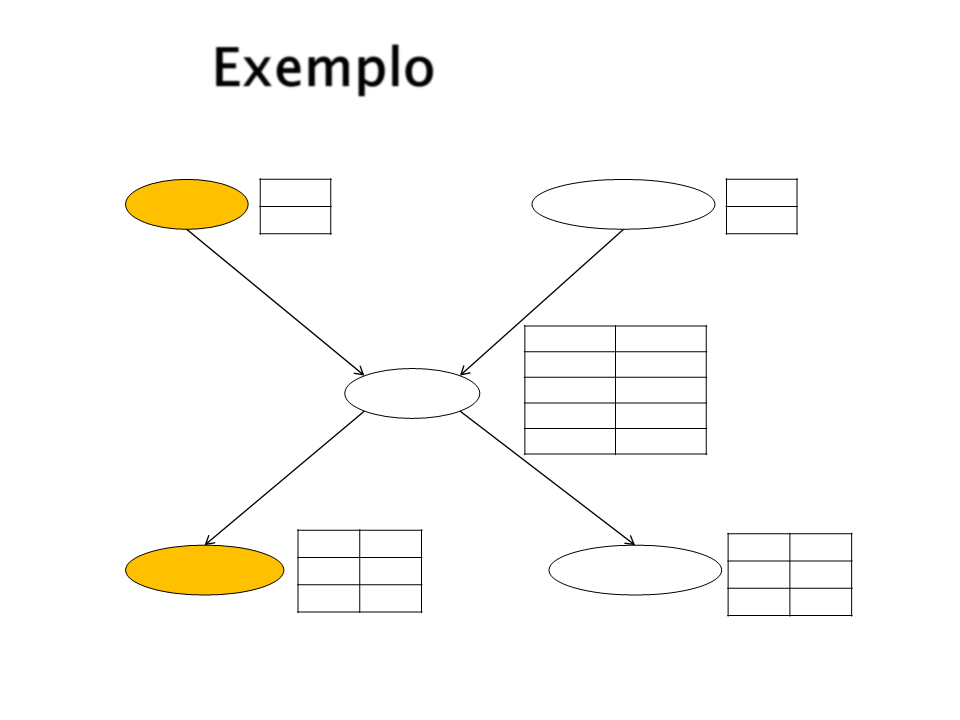
Exemplo
P(R)
P(T)
E
Roubo
Terremoto
0
.001
0.002
R
V
V
F
E
V
F
P(A)
0.95
0.94
0.29
0.001
P(JoãoLiga|Roubo)
Alarme
V
F
F
A
V
F
P(J)
0.90
0.05
A
V
F
P(M)
0.70
0.01
?
JoãoLiga
MariaLiga

Exemplos de Softwares
Microsoft Bayesian Network Editor:
http://research.microsoft.com/en-
us/um/redmond/groups/adapt/msbnx/
Netica:
http://www.norsys.com/download.html
