
INF 1771 – Inteligência Artificial
Aula 22 – Incerteza
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Agentes Vistos Anteriormente
Agentes baseados em busca:
Busca cega
Busca heurística
Busca local
Agentes baseados em lógica:
Lógica proposicional
Lógica de primeira ordem
Agentes baseados em planejamento:
Planejamento de ordem parcial
Planejamento em ambientes não-determinísticos
Incerteza
Agentes raramente tem acesso à toda
verdade sobre o ambiente.
Mundo de Wumpus:
Apenas informações locais.
Maior parte do ambiente não é imediatamente
observável.
Incerteza de fatos:
O mundo real é muito mais complexo do que o mundo
de wumpus. Informações não garantem resultados.

Incerteza
Exemplo: Levar alguém ao aeroporto para pegar um vôo.
Seja a ação At = sair para o aeroporto t minutos antes do
vôo.
At levará o passageiro ao aeroporto a tempo?
Dificuldades de saber o resultado da ação:
Estados parcialmente observáveis.
Estados das estradas, trânsito, etc.
Sensores ruidosos.
Relatórios de trânsito
Incerteza quanto ao efeito das ações.
Acidentes, pneu furado, etc.
Grande complexidade em prever e modelar o trânsito.

Incerteza
Um procedimento puramente lógico não é muito útil
nesse caso:
Arriscaria deduzir algo potencialmente falso:
“
A45 me levará a tempo ao aeroporto”
Levaria a conclusões fracas para tomada de decisões:
“
ocorrer na ponte, se não chover, se nenhum pneu furar,
A45 me levará a tempo ao aeroporto, se nenhum acidente
etc.”
Levaria a conclusões que não práticas:
“
A1440 me levará a tempo ao aeroporto”

Incerteza
O plano escolhido deve maximizar a
performance do agente.
Chegar no aeroporto a tempo.
Não perder tempo esperando no aeroporto.
O agente não tem como garantir nenhum
sucesso em seus objetivos.
Mas ele pode prever um certo grau de crença
que ele terá sucesso em seus objetivos.

Incerteza
A coisa certa a se fazer depende da
importância dos objetivos e da probabilidade
de que eles serão alcançados.
É necessário lidar com a incerteza e a
imprecisão dos ambientes.

Incerteza
Considerando a seguinte regra em lógica de primeira
ordem:
∀p Sintoma(p, Dor_de_Dente) ⇒ Doença(p, Cáries)
A regra esta errada. Nem todas as pessoas que tem dor de
dente tem cáries, algumas podem ter outras doenças.
∀
p Sintoma(p, Dor_de_Dente) ⇒ Doença(p, Cáries) ∨ Doença(p, Gengivite) ∨
Doença(p, Abscesso)...
∨
Para tornar essa regra verdadeira seria necessário adicionar
a ela uma lista infinita de possibilidades.

Incerteza
Tentar utilizar lógica de primeira ordem para lidar com um
domínio de diagnóstico médico falha por três razões:
Preguiça: É muito trabalho listar o conjunto completo de sentenças
necessárias para garantir uma regra sem exceção.
Ignorância teórica: A medicina não tem nenhuma teoria completa para
todos os domínios.
Prático ignorância: Mesmo conhecendo todas as regras, poderiam
existir dúvidas sobre um determinado paciente.
Este tipo de problema afeta também outros domínios:
Negócios, Direito, Design, Reparação automóveis,
Jardinagem...

Fontes de Incerteza
Informações precisas podem ser muito complexas
para serem modeladas.
É necessário lidar com informações incompletas.
Implicações podem ser modeladas de forma mais
fraca:
Dor_de_Dente(0.7) ⇒ Doença(Cáries)
Quantificação do número de vezes
em que a regra se aplica.
Fontes de Incerteza
Conflito de informações:
Especialistas distintos podem fornecer informações conflitantes
e incertas.
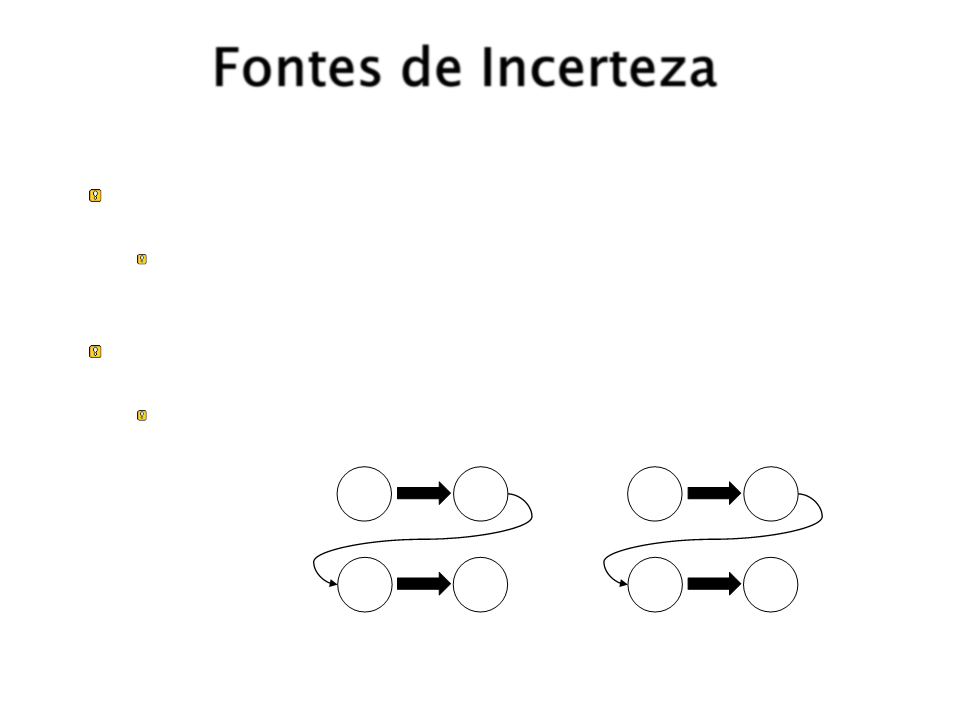
Propagação de incertezas:
Fatos com um certo grau de incerteza implicam em outros fatos
com um grau de incerteza ainda maior.
1
0.7
a
b
b
c
a
b
b
c
Exemplo:
a ⇒ b
b ⇒ c
1
0.6

Lidando com a Incerteza
A principal ferramenta para se lidar com a incerteza é
a teoria da probabilidade. Busca-se atribuir um
grau de crença numérica (entre 0 e 1) a cada
sentença.
Modela-se o grau de crença de um agente dadas as
evidências disponíveis:
“
“
“
A25 chegará a tempo ao aeroporto com probabilidade 0.04”
A45 chegará a tempo ao aeroporto com probabilidade 0.85”
A60 chegará a tempo ao aeroporto com probabilidade 0.95”

Probabilidade
A probabilidade subjetiva ou bayesiana estabelece
o estado de crença do agente em uma sentença dadas
as evidências.
P(A25|nenhum acidente) = 0.06
A probabilidade de um sentença muda quando novas
evidências chegam.
P(A25|nenhum acidente) = 0.06
P(A25|nenhum acidente, 5 a.m.) = 0.15

Decisões sob Incerteza
Supondo o seguinte conjunto de crenças:
P(A25|...) = 0.04
P(A90|...) = 0.70
P(A120|...) = 0.95
P(A1440|...) = 0.9999
Que ação o agente deve tomar?
Depende da preferência entre perder o vôo versus o
tempo esperando no aeroporto.
Teoria da utilidade = representação de preferências
Teoria da decisão = teoria da probabilidade + teoria da utilidade

Introdução à Probabilidade
Elemento básico da probabilidade é uma variável
aleatória.
Semelhante a lógica proposicional e de primeira
ordem, onde os mundos possíveis são definidos pela
atribuição de valores às variáveis.
Cada variável aleatória tem um domínio que determina
seus valores possíveis.
Tipos de domínio:
Booleano, exemplo: Cárie possui valores em
<verdadeiro,falso>
Discreto, exemplo: Clima possui valores em <ensolarado,
chuvoso, nublado, neve>
Contínuo, exemplo: Temperatura

Introdução à Probabilidade
Proposições elementares:
São construídas através da atribuição de valores a
variáveis.
Exemplo: Cárie = falso, Clima = chuvoso
Proposições complexas:
São formadas a partir de proposições elementares
e conectivos lógicos padrão.
Exemplo: Clima = chuvoso ∧ Cárie = falso

Introdução à Probabilidade
Um evento atômico consiste da especificação
completa do estado do mundo sobre o qual o
agente está incerto.
Uma atribuição de valores a TODAS as variáveis das
quais o mundo é formado.
Exemplo:
Cárie = verdadeiro ∧ DorDeDente = verdadeiro
Cárie = verdadeiro ∧ DorDeDente = falso
Cárie = falso ∧ DorDeDente = verdadeiro
Cárie = falso ∧ DorDeDente = falso
Probabilidade a priori
O grau de crença em uma proposição na ausência de
outras informações pode ser definida da seguinte
maneira:
P(Cárie = verdadeiro) = 0.1
P(Clima = ensolarado) = 0.72
Distribuição de probabilidades:
P(Clima) = (0.7, 0.2, 0.08, 0.02)
Distribuição de probabilidade da variavel randomica
Clima = (ensolarado, chuvoso, nublado, neve)

Distribuição de Probabilidade Conjunta
Probabilidades de todas as combinações de
valores de um conjunto de variáveis aleatórias.
P(Clima, Cárie) = tabela 4 x 2 de valores de probabilidade.
Clima
ensolarado
0.144
chuvoso
0.02
nublado
0.016
neve
0.02
0.08
Cárie = verdadeiro
Cárie = falso
0.576
0.08
0.064
Uma distribuição conjunta total especifica a
probabilidade de qualquer evento atômico.
Qualquer probabilidade nesse domínio pode ser calculada a
partir da distribuição conjunta total.

Probabilidade Condicional ou “a posteriori”
O grau de crença em uma proposição dada a
presença de novas evidências pode ser
definido utilizando a notação P(a|b):
P(Cárie = verdadeiro | Dor_De_Dente = verdadeiro) = 0.6
P(Cárie = verdadeiro | Dor_De_Dente = verdadeiro,
Escova_Dentes_Regularmente = false) = 0.7
P(a|b) = “A probabilidade de a dado todo o
conhecimento b”.

Probabilidade Condicional
A probabilidade condicional pode ser definida em
termos de probabilidades a priori:
P(a | b) = P(a b)
P(b)
se P(b) > 0
A mesma equação também pode ser escrita da
seguinte maneira utilizando a regra do produto:
P(a b) = P(a |b)P(b)
Ou:
P(a b) = P(b| a)P(a)

Axiomas da Probabilidade
Para quaisquer proposições A, B:
P(A) ≥ 0 e P(A) ≤ 1
P(Verdade) = 1
P(Falso) = 0
P(A ∨ B) = P(A) + P(B) - P(A ∧ B)

Probabilidade
A probabilidade de uma proposição é igual à
soma das probabilidades dos eventos
atômicos em que ela é válida:
P(a) = P(ei )
eie(a)
Essa equação permite calcular a
probabilidade de qualquer proposição dada
uma distribuição conjunta total que
especifique todos os eventos atômicos.

Inferência Probabilística
Inferência probabilística consiste na computação
da distribuição de probabilidade posterior para um
conjunto de variáveis de consulta C dada alguma
evidência observada.
A inferência é realizada com o uso de distribuições
conjuntas totais. Ou seja, uma base de
conhecimento a partir da qual são derivadas respostas
para todas as consultas.
Inferência Probabilística
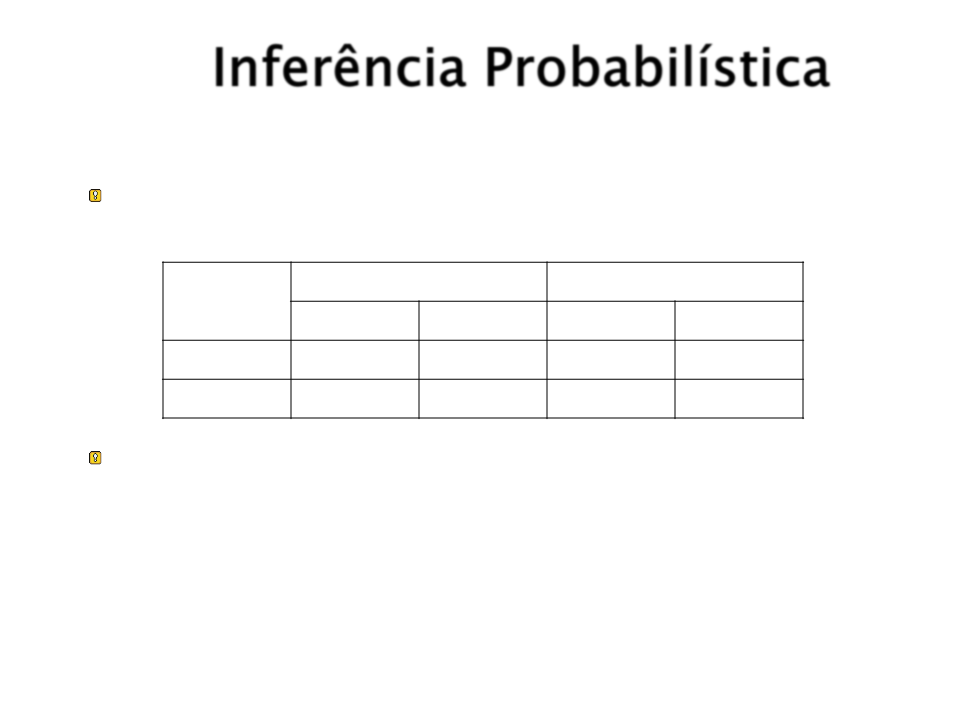
Suponha um domínio com a seguinte distribuição
conjunta total:
Dor_De_Dente
¬Dor_De_Dente
Sonda ¬Sonda Sonda ¬Sonda
Cárie
0.108
0.012
0.064
0.072
0.144
0.008
0.576
¬Cárie 0.016
Para qualquer proposição a, P(a) é a soma dos
eventos atômicos w onde a ocorre: P(a) =
P(ei )
eie(a)
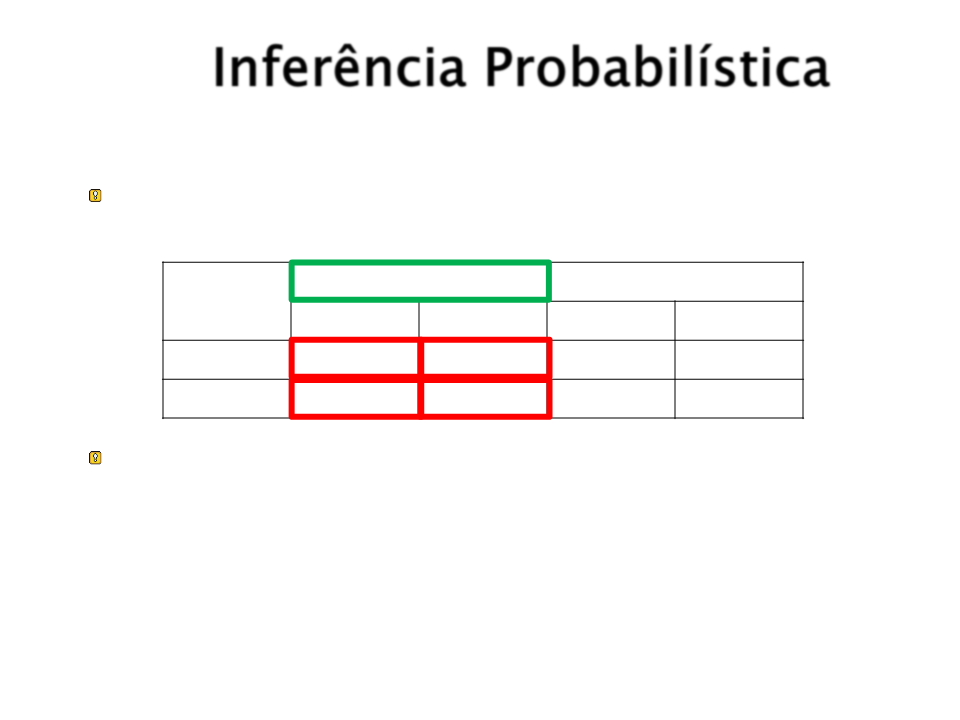
Inferência Probabilística
Suponha um domínio com a seguinte distribuição
conjunta total:
Dor_De_Dente
¬Dor_De_Dente
Sonda ¬Sonda Sonda ¬Sonda
Cárie
¬Cárie
0.108
0.016
0.012
0.064
0.072
0.144
0.008
0.576
Para qualquer proposição a, P(a) é a soma dos
eventos atômicos w onde a ocorre: P(a) =
P(ei )
eie(a)
P(Dor_De_Dente) = 0.108 + 0.012 + 0.016 + 0.064 = 0.2
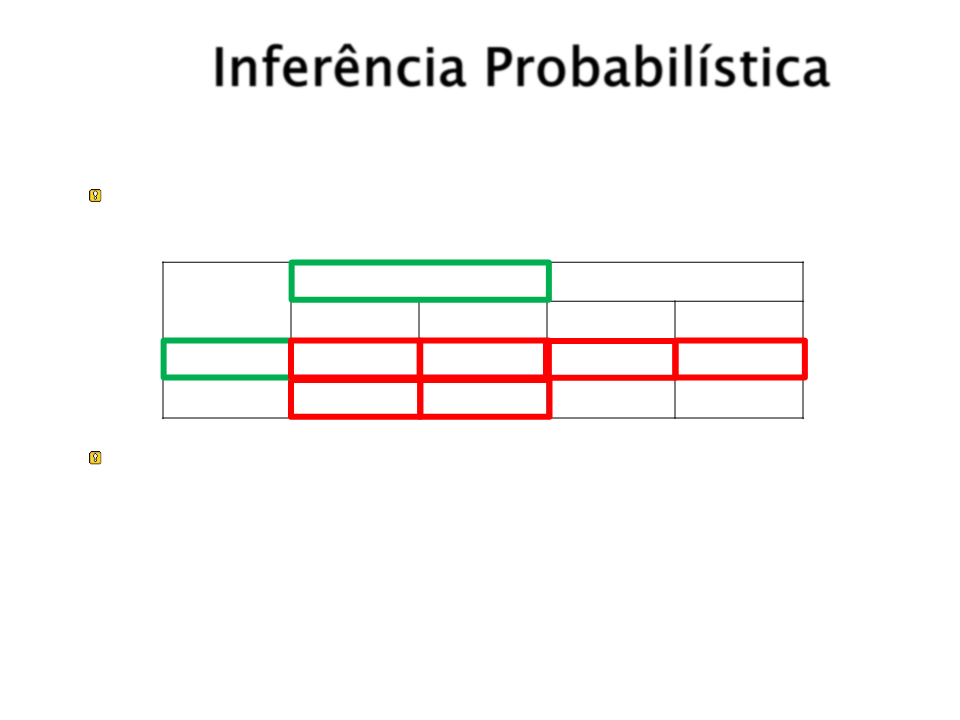
Inferência Probabilística
Suponha um domínio com a seguinte distribuição
conjunta total:
Dor_De_Dente
¬Dor_De_Dente
Sonda ¬Sonda Sonda ¬Sonda
Cárie
0.108
0.012
0.064
0.072
0.144
0.008
0.576
¬Cárie 0.016
Para qualquer proposição a, P(a) é a soma dos
eventos atômicos w onde a ocorre: P(a) =
P(ei )
eie(a)
P(Dor_De_Dente Cárie) = 0.108 + 0.012 + 0.016 + 0.064
+ 0.072 + 0.008 = 0.28
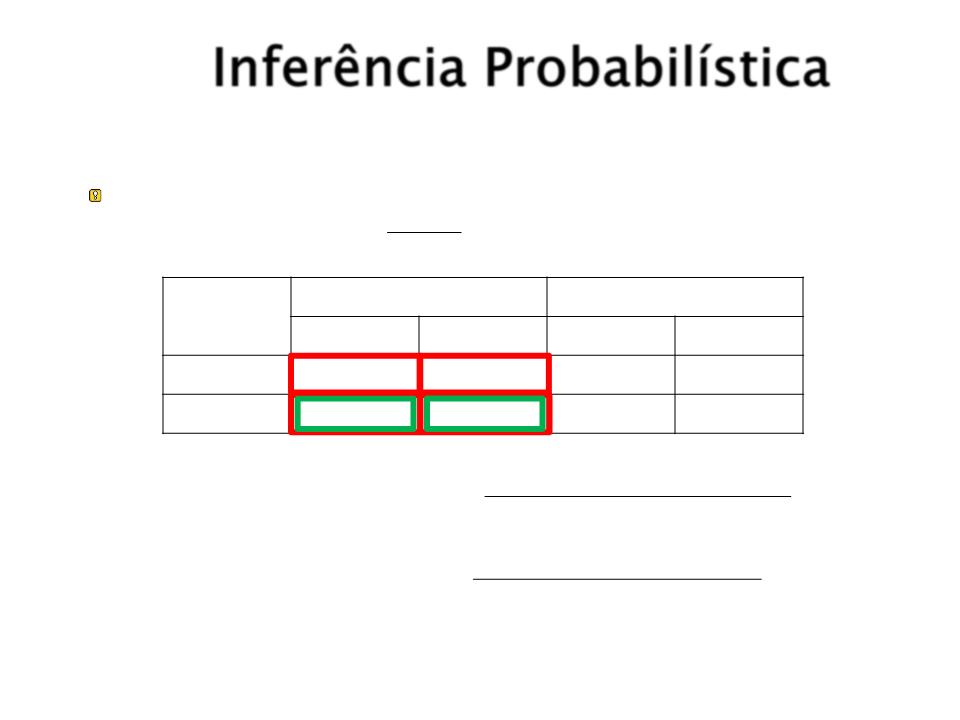
Inferência Probabilística
É possível também cPa(alcub)lar probabilidades
condicionais:P(a | b) =
P(b)
Dor_De_Dente
¬Dor_De_Dente
Sonda ¬Sonda Sonda ¬Sonda
Cárie
0.108
0.012
0.064
0.072
0.144
0.008
0.576
¬Cárie 0.016
P(Cárie Dor _ De _ Dente)
P(Dor _ De _ Dente)
P(Cárie| Dor _ De _ Dente) =
0
.016+ 0.064
P(Cárie| Dor _ De _ Dente) = 0.108+ 0.012+ 0.016+ 0.064 = 0.4
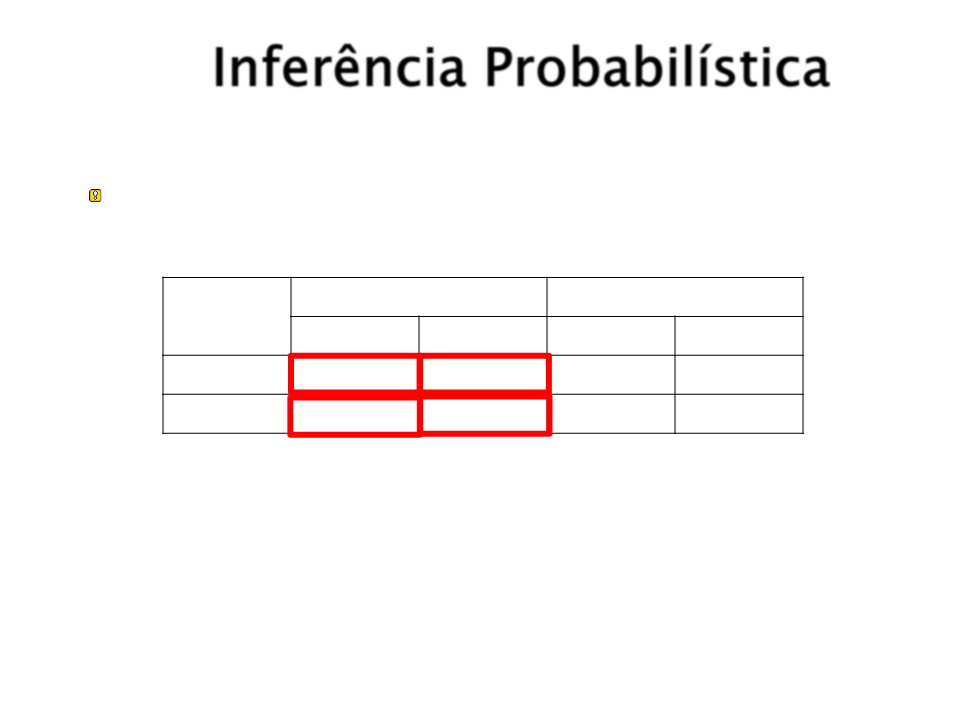
Inferência Probabilística
O denominador pode ser visto como uma constante de
normalização α.
Dor_De_Dente
¬Dor_De_Dente
Sonda ¬Sonda Sonda ¬Sonda
Cárie
0.108
0.012
0.064
0.072
0.144
0.008
0.576
¬Cárie 0.016
P(Cárie| Dor _ De _ Dente) =P(Cárie, Dor _ De _ Dente)
=
=
=
=
[P(Cárie, Dor _ De _ Dente,Sonda) + P(Cárie, Dor _ De _ Dente,Sonda)]
[ 0.108,0.016 + 0.012,0.064 ]
[ 0.12,0.08 ]
0.6,0.4

Problemas com a inferência por enumeração
Complexidade de tempo (pior caso): O(dn)
onde d é a cardinalidade do maior domínio e n é o
número de variáveis.
Complexidade de espaço: O(dn) para
armazenar a distribuição conjunta.
Como encontrar as probabilidades para
n
O(d ) elementos?
Independência
X e Y são independentes se e somente se:
P(X|Y) = P(X) ou P(Y|X) = P(Y) ou P(X,Y) = P(X)P(Y)
Exemplo: P(Dor_De_Dente, Sonda, Cárie, Clima)
Tabela com 32 elementos.
P(Dor_De_Dente,Cárie,Sonda,Clima) = P(Dor_De_Dente,Cárie,Sonda)P(Clima)
Dor_De_Dente
Cárie Sonda
Decomposição
Dor_De_Dente
Sonda
Cárie
Tabela com
12 elementos
Clima
Clima

Teorema de Bayes
Seja:
P(A | B) a probabilidade de que a hipótese A seja verdadeira
dada a evidência B.
P(B | A) a probabilidade que a evidência B será observada se a
hipótese A for verdadeira.
P(A) a probabilidade “a priori” que a hipótese A é verdadeira na
ausência de qualquer evidência específica.
k o número de hipóteses possíveis.
O Teorema de Bayes é formulado como:
P(B | A)*P(A)
P(A| B) = P(B | A)P(A)
P(B)
P(A| B) =
k
P(B | An )*(P(An )
n=0

Regra de Bayes – Exemplo
Para aplicar a regra de Bayes é necessário
três termos:
Uma probabilidade condicional.
Duas probabilidades incondicionais.
Exemplo de diagnostico médico:
“
um médico sabe que a meningite causa torcicolo
em 50% dos casos. Porém, o médico também
conhece algumas probabilidades incondicionais
que dizem que, um caso de meningite atinge
1
/50000 pessoas e, a probabilidade de alguém ter
torcicolo é de 1/20”.

Regra de Bayes – Exemplo
Considerando:
T = probabilidade incondicional de um paciente ter
torcicolo:
P(T) = 1/20
M = probabilidade incondicional de um paciente ter
meningite.
P(M) = 1/50000
P(T|M) = 0.5 (probabilidade de ter torcicolo tendo
meningite)

Regra de Bayes – Exemplo
Aplicando a regra de Bayes:
P(M |T) = P(T | M )P(M )
P(T)
P(M |T) = 0.51/50000
1
/ 20
P(M |T) = 0.0002
É esperado que apenas 1 em 5000 pacientes
com torcicolo tenha meningite.

Regra de Bayes – Exemplo
Apesar de torcicolo ser um fortemente
indicativo de meningite (com probabilidade
0
paciente permanece pequena.
.5), a probabilidade de meningite no
