
INF 1771 – Inteligência Artificial
Aula 07 – Lógica de Primeira Ordem
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Problemas da Lógica Proposicional
Muito simples para representar o
conhecimento de ambientes complexos de
uma forma concisa.
Falta de capacidade de expressão para
descrever um ambiente com muitos objetos.
Exemplo em linguagem natural:
“quadrados adjacentes a poços possuem brisa”
Em lógica proposicional:
B1,1⇔(P1,2 ∨ P2,1) - (Seria necessário declarar todas as salas!)

Linguagem Natural
Objetos: pessoas, casas, números, cores, jogos,
séculos...
Relações:
Unárias: propriedades de um objeto.
Exemplo: vermelho, redondo, falso
n-árias: relacionam grupos de objetos.
Exemplo: irmão de, maior que, interior a, parte de...
Funções: um objeto está relacionado a exatamente um objeto.
Exemplo: pai de, melhor amigo de, terceiro turno de, uma unidade
maior que...
Linguagem da lógica de primeira ordem é
elaborada em torno de objetos e relações.

Lógica de Primeira Ordem
Principal diferença entre lógica proposicional e a
lógica de primeira ordem é o compromisso
ontológico, ou seja, o que cada linguagem
pressupões sobre a natureza da realidade:
Lógica Proposicional: pressupõe que existem fatos que
são válidos ou não-válidos no mundo.
Lógica de Primeira Ordem: pressupõe que o mundo
consiste em objetos com certas relações entre eles que
são válidas ou não-válidas.
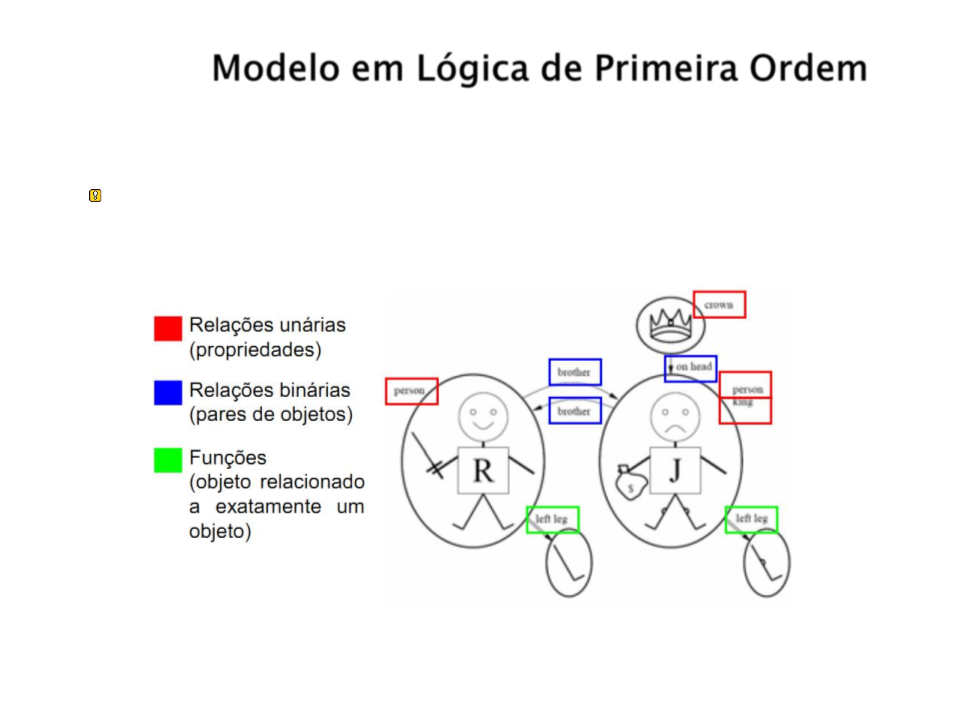
Modelo em Lógica de Primeira Ordem
Exemplo: Ricardo Coração de Leão, rei da Inglaterra
de 1189 a 1199 e seu irmão mais jovem, o perverso
rei João, que governou de 1199 a 1215:

Sintaxe da Lógica de Primeira Ordem
Símbolos - Começam com letras maiúsculas
e podem ser de três tipos:
Símbolos de constantes: Representam objetos.
Exemplo: Ricardo e João
Símbolos de predicados: Representam relações.
Exemplo: Irmão, NaCabeça, Pessoa
Símbolos de funções: Representam funções.
Exemplo: PernaEsquerda
Sintaxe da Lógica de Primeira Ordem
Interpretação - Especifica quais objetos, relações e
funções são referidos pelos símbolos de constantes,
predicados e funções:
Interpretação pretendida:
Ricardo se refere a “Ricardo Coração de Leão”
…
João se refere ao “perverso rei João”
…Irmão se refere à “relação de fraternidade”
NaCabeça se refere à relação “na cabeça” que é válida entre a
coroa e o rei João
Pessoa, Rei e Coroa se referem aos conjuntos de objetos que
são pessoas, reis e coroas
PernaEsquerda se refere à função “perna esquerda”.

Sintaxe da Lógica de Primeira Ordem
Sentenças atômicas são formadas a partir de um
símbolo de predicado seguido por uma lista de termos
entre parênteses. Exemplos:
Irmão(Ricardo, João)
Casados(Pai(Ricardo), Mãe(João))
Uma sentença atômica é verdadeira em um modelo,
sob uma dada interpretação, se a relação referida pelo
símbolo de predicado é válida entre os objetos
referidos pelos argumentos.

Sintaxe da Lógica de Primeira Ordem
Sentenças complexas podem ser formadas
pelo uso de conectivos lógicos, da mesma
maneira que na lógica proposicional.
Exemplos:
¬Irmão(PernaEsquerda(Ricardo), João)
Irmão(Ricardo,João) ∧ Irmão(João, Ricardo)
Rei(Ricardo) ∨ Rei(João)
¬Rei(Ricardo) ⇒ Rei(João)

Sintaxe da Lógica de Primeira Ordem
Quantificadores (∀, ∃) são utilizados para expressar
propriedades de coleções inteiras de objetos.
Quantificador Universal (∀): “Para todo...” ∀x P, onde P é
qualquer expressão lógica, afirma que P é verdadeira para
todo objeto x.
Exemplo:
∀x Rei(x) ⇒ Pessoa(x)
Quantificador Existencial (∃): “Para algum...” ∃x P afirma
que P é verdadeira para pelo menos um x.
Exemplo:
∃x Rei(x)

Sintaxe da Lógica de Primeira Ordem
Quantificadores aninhados são usados em
sentenças complexas compostas.
Exemplos:
∀
∀
∀
x ∀y Irmão(x,y) ⇒ Parente(x,y)
“Irmãos são parentes”
x,y Parente(x,y) ⇔ Parente(y,x)
“
Parente é uma relação simétrica”
x ∃y Ama(x,y)
“
Todo mundo ama alguém”
∃y ∀x Ama(x,y)
“Existe alguém que é amado por todo mundo”

Sintaxe da Lógica de Primeira Ordem
Os quantificadores (∀, ∃) estão conectados um ao
outro por meio de negação.
Exemplos:
…
“
∀x ¬Gosta(x,Cenouras) ≡¬∃x Gosta(x,Cenouras)
todo mundo detesta cenouras” ≡ “não existe alguém
que goste de cenouras”
∀
x Gosta(x,Sorvete) ≡¬∃x ¬Gosta(x,Sorvete)
todo mundo gosta de sorvete” ≡ “não existe alguém
que não goste de sorvete”
“

Sintaxe da Lógica de Primeira Ordem
Em lógica de primeira ordem pode-se usar o
símbolo de igualdade para fazer declarações
afirmando que dois termos se referem ao
mesmo objeto.
Exemplo:
Pai(João) = Henrique

Sintaxe da Lógica de Primeira Ordem
Sentença → SentençaAtômica
(Sentença Conectivo Sentença)
|
|
|
Quantificador Variável, ...Sentença
¬Sentença
SentençaAtômica → Predicado(Termo,...) | Termo=Termo
Termo → Função (Termo,...)
|
|
Constante
Variável
Conectivo →⇒ | ∧ | ∨ | ⇔
Quantificador →∀ | ∃
Constante → A | X1 | João | ...
Variável → a | x | s | ...
Predicado → Antes | TemCor | Chovendo | ...
Função → Mãe | PernaEsquerda | ...

Semântica da Lógica de Primeira Ordem
Se existem 5 objetos, existem 25 interpretações para os
símbolos Ricardo e João.
Número de modelos pode ser ilimitado (pode incluir, por
exemplo os números reais). Logo, o número de modelos
possível é ilimitado.
Verificar consequência lógica pela enumeração de
todos os modelos não é uma opção.

Exemplo - Parentesco
Objetivo:
Determinar o parentesco de grupos de pessoas.
Fatos:
“
Elizabeth é a mãe de Charles”, “Charles é o pai de William”
Regras:
“
a avó de uma pessoa é a mãe do pai de uma pessoa”
„Objetos:
Pessoas
Predicados unários:
Masculino e Feminino
„Predicados (relações de parentesco):
Ancestral, Parente, Irmão, ...
„
Mãe e Pai (cada pessoa tem apenas um de cada)
Funções:

Exemplo - Parentesco
A mãe de alguém é o ancestral feminino de alguém
∀m,c Mãe(c)=m ⇔ Feminino(m) ∧ Ancestral(m,c)
O marido de alguém é o cônjuge masculino de alguém
∀w,h Marido(h,w) ⇔ Masculino(h) ∧ Cônjuge(h,w)
Masculino e feminino são categorias disjuntas
∀x Masculino(x) ⇔¬Feminino(x)

Exemplo - Parentesco
Ancestral e descendente são relações inversas
∀p,c Ancestral(p,c) ⇔ Descendente(c,p)
Avô é um pai do pai de alguém
∀g,c Avô(g,c) ⇔∃p Pai(g,p) ∧ Pai(p,c)
Um parente é outro descendente dos ancestrais de
alguém
∀x,y Parente(x,y) ⇔ x ≠ y ∧ ∃p Ancestral(p,x) ∧ Ancestral(p,y)
Exemplo - Wumpus
Estrutura da Base de Conhecimento:
São armazenadas as sentenças representando as percepções do
agente e a hora em que elas ocorreram.
Fedor, Brisa e Resplendor são constantes inseridas em uma
lista.
Exemplo: Percepção ([Fedor, Brisa, Resplendor, Nenhum, Nenhum], 5)
Ações:
Virar(Direita), Virar(Esquerda), Avançar, Atirar, Agarrar, Soltar.
Consultas:
∃x MelhorAção(x,5)
ASK deve retornar uma lista de vinculação como {a/Agarrar}

Exemplo - Wumpus
Os dados brutos da percepção implicam certos fatos
sobre o estado atual.
Exemplos:
∀t,s,g,m,c Percepção([s,Brisa,g,m,c],t) ⇒ Brisa(t)
∀t,s,b,m,c Percepção([s,b,Resplendor,m,c],t) ⇒ Resplendor(t)
Comportamentos simples podem ser implementados
por sentenças de implicação quantificadas.
Exemplo:
∀t Resplendor(t) ⇒ MelhorAção(Agarrar,t)

Exemplo - Wumpus
Adjacência de dois quadrados:
∀x,y,a,b Adjacente([x,y],[a,b]) ⇔ [a,b] ∈ {[x+1,y], [x-1,y],
[x,y+1], [x,y-1]}
Se o agente estiver em um quadrado e perceber uma
brisa, então esse quadrado é arejado:
∀s,t Em(Agente,s,t) ∧ Brisa(t) ⇒ Arejado(s)

Exemplo - Wumpus
Regras de diagnóstico: algumas causas ocultas do
ambiente conduzem a novas percepções.
∀s Arejado(s) ⇒∃r Adjacente(r,s) ∧ Poço(r)
∀s ¬Arejado(s) ⇒¬∃r Adjacente(r,s) ∧ Poço(r)
Regras causais: refletem a suposta orientação da
causalidade no mundo
∀r Poço(r) ⇒ [∀r Adjacente(r,s) ⇒ Arejado(s)]
∀s [∀r Adjacente(r,s) ⇒¬Poço(r)] ⇒¬Arejado(s)

Construção da Base de Conhecimento
(
(
(
(
(
(
1) Identificar a tarefa;
2) Agregar conhecimento relevante;
3) Definir um vocabulário de predicados, funções e constantes;
4) Codificar o conhecimento geral sobre o domínio;
5) Codificar uma descrição da instância específica do problema;
6) Formular consultas ao procedimento de inferência e obter
respostas;
(7) Depurar a base de conhecimento;

Prolog
O Prolog é uma linguagem de programação
baseada em lógica de primeira ordem.
Não é padronizada.
Algumas implementações: SICStus Prolog,
Borland Turbo Prolog, SWI-Prolog...
Geralmente é interpretado, mas pode ser
compilado.
