
INF 1771 – Inteligência Artificial
Aula 06 – Lógica Proposicional
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Lógica Proposicional
Lógica simples.
A sentenças são formadas por conectivos como: “e”,
“ou”, “então”.
É necessário definir:
Sintaxe (sentenças válidas).
…Semântica (modo pelo qual a verdade das sentenças é
determinada).
Consequência lógica (relação entre uma sentença e
outra que decorre dela).
Algoritmo para inferência lógica.

Sintaxe em Lógica Proposicional
A sintaxe da lógica proposicional define as
sentenças permitidas. É formada por:
Símbolos: nomes em letras maiúsculas (P, Q, R, ...) que
podem assumir verdadeiro e falso;
…Sentenças atômicas: constituídas por elementos
sintáticos indivisíveis (símbolo proposicional);
Sentenças complexas: são construídas a partir de
sentenças mais simples com a utilização de conectivos
lógicos: ¬ (não), ∧ (e), ∨ (ou), ⇒ (implica), ⇔ (dupla
implicação)
Sentença cujo principal conectivo é ∧: conjunção
Sentença cujo principal conectivo é ∨: disjunção

Gramática da Lógica Proposicional
Sentença → SentençaAtômica | SentençaComplexa
…
SentençaAtômica → Verdadeiro | Falso | Símbolo
Símbolo → P | Q | R | ...
SentençaComplexa → ¬Sentença
…
|
|
|
|
(Sentença ∧ Sentença)
(Sentença ∨ Sentença)
(Sentença ⇒ Sentença)
(Sentença ⇔ Sentença)

Exempos de Sentenças Validas
P
Verdadeiro
P ∧ Q
(P ∨ Q) ⇒ S
(P ∧ Q) ∨ R ⇒ S
¬(P ∨ Q)
¬(P ∨ Q) ⇒ R ∧ S

Implicação Lógica (⇒)
P ⇒ Q
Se P é verdade então Q também é
verdade.
Se esta chovendo então as ruas estão
molhadas.

Equivalencia Lógica (⇔)
P ⇔ Q
Se P é verdade então Q também é verdade. Se Q é
verdade então P também é verdade.
Se dois lados de um triangulo são iguais então os
dois ângulos da base do tribulo são iguais.
A equivalência por ser substituída por duas
sentenças de implicação: (P ⇒ Q) ∧ (Q ⇒ P)
Semântica da Lógica Proposicional
F
P
A criança sabe escrever
V
Pré-Escola
2° Serie

Semântica em Lógica Proposicional
Descreve como calcular o valor verdade de qualquer
sentença com base em um mesmo modelo. É necessário
definir como calcular a verdade de sentenças atômicas e
como calcular a verdade de sentenças formadas com cada
um dos cinco conectivos (¬, ∧, ∨, ⇒, ⇔).
Sentenças atômicas:
Verdadeiro é verdadeiro e falso é falso em todo modelo.
O valor-verdade de todos os outros símbolos proposicionais
deve ser especificado diretamente no modelo.
Sentenças complexas:
As regras em cada conectivo são resumidas em uma tabela-
verdade.
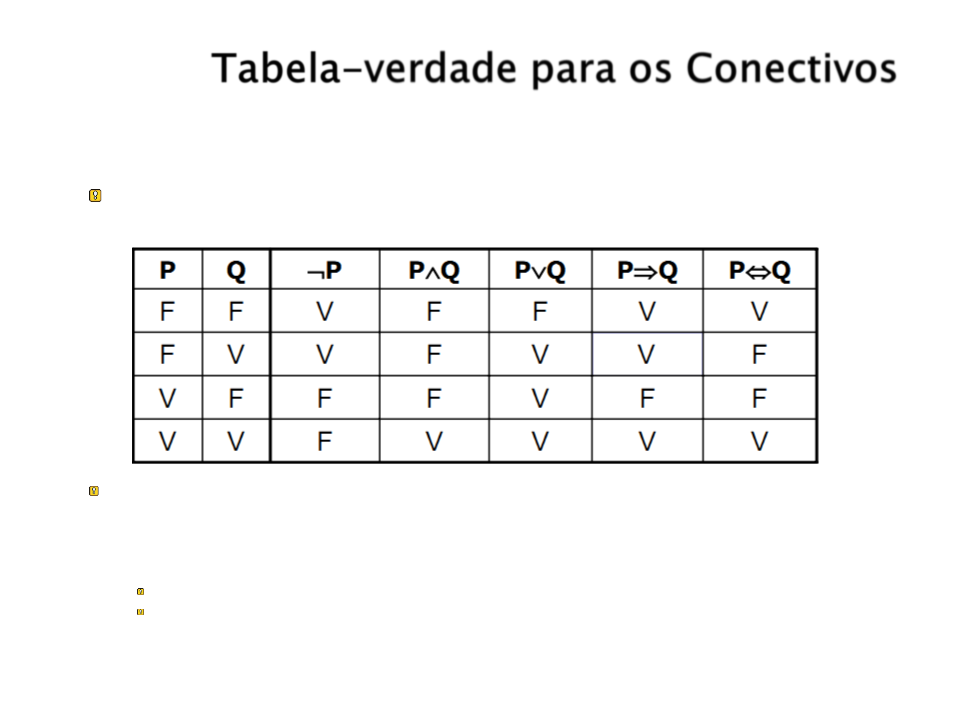
Tabela-verdade para os Conectivos
Para os cinco conectivos lógicos apresentados,
teremos:
*
(
*) Lógica proposicional não exige relação de causa e efeito entre P
e Q. Deve-se entender esta relação como “se P é verdadeira, então
Q é verdadeira. Caso contrário, não estou fazendo nenhuma
afirmação”. Exemplo:
“5 é ímpar implica que Tóquio é capital do Japão” (V)
5 é par implica que João é inteligente” (V)
“
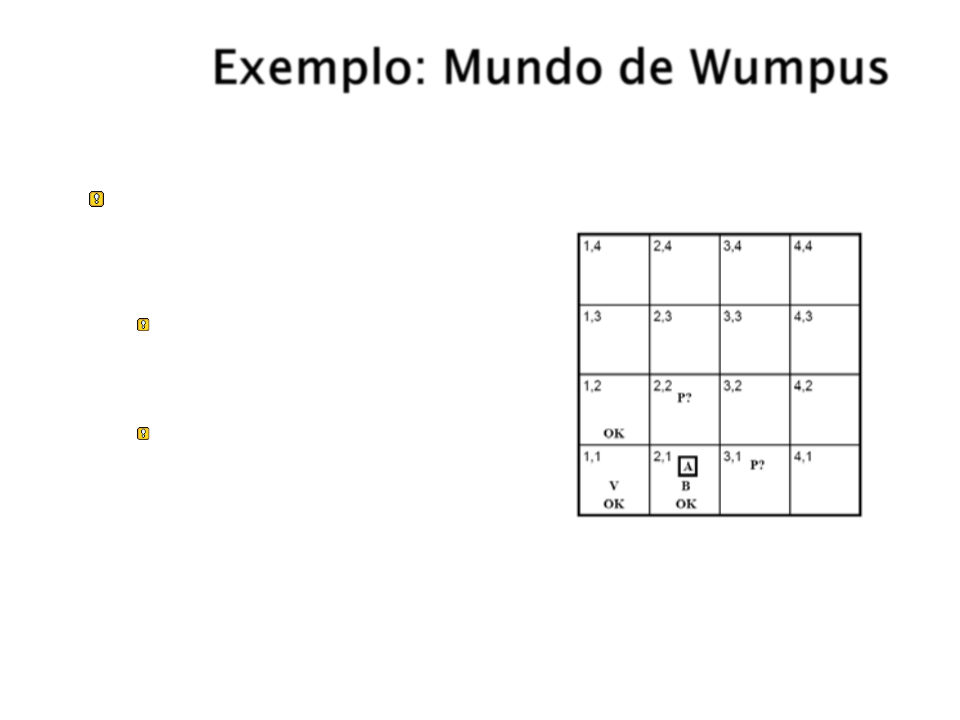
Exemplo: Mundo de Wumpus
Vocabulário de símbolos
proposicionais:
Seja Pi,j verdadeiro se
existe poço em [i,j]
Seja Bi,j verdadeiro se
existe brisa em [i,j]
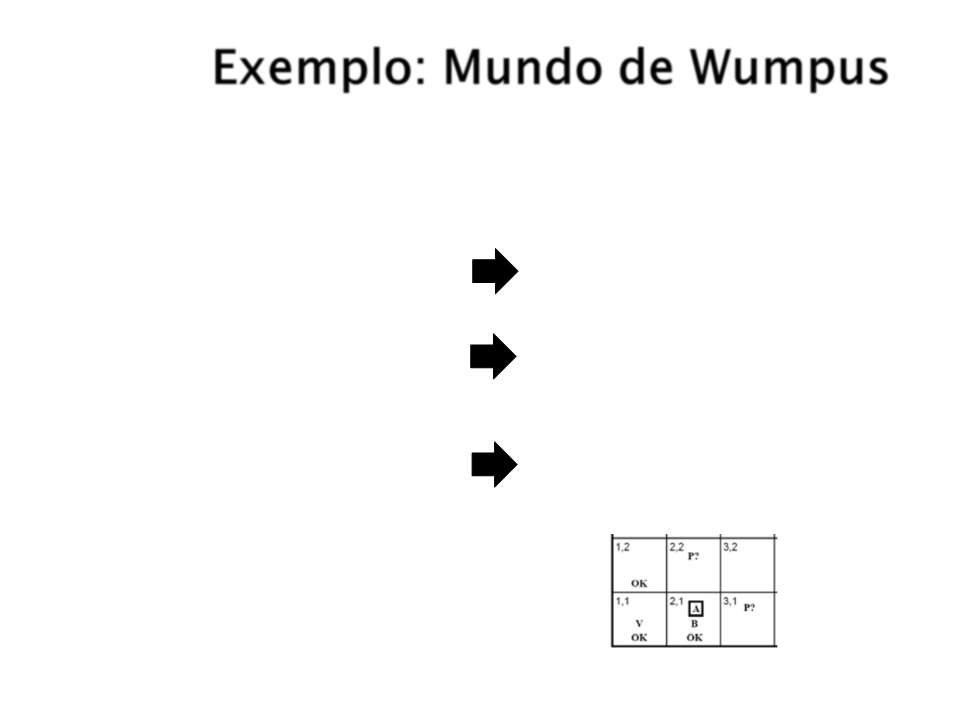
Exemplo: Mundo de Wumpus
Base de Conhecimento:
R1: ¬P1,1
Não há poço em [1,1].
Um quadrado tem uma brisa se e somente
se existe um poço em um quadrado vizinho
(todos os quadrados devem ser declarados).
R2: B1,1 ⇔ (P1,2 ∨ P2,1)
R3: B2,1 ⇔ (P1,1 ∨ P2,2 ∨ P3,1)
R4: ¬B1,1
R5: B2,1
Percepções adquiridas pelo agente do
mundo em que ele se encontra.

Inferência - Mundo de Wumpus
Inferência: derivação de novas sentenças a partir de
sentenças antigas.
Objetivo: decidir se BC╞ α para alguma sentença α.
Exemplos: P1,2? P2,2?
Algoritmo: enumerar todos os modelos e verificar se
α é verdadeira em todo modelo no qual BC é
verdadeira.
Símbolos proposicionais relevantes:
B1,1, B2,1, P1,1, P1,2, P2,1, P2,2, P3,1
7
símbolos → 27=128 modelos possíveis
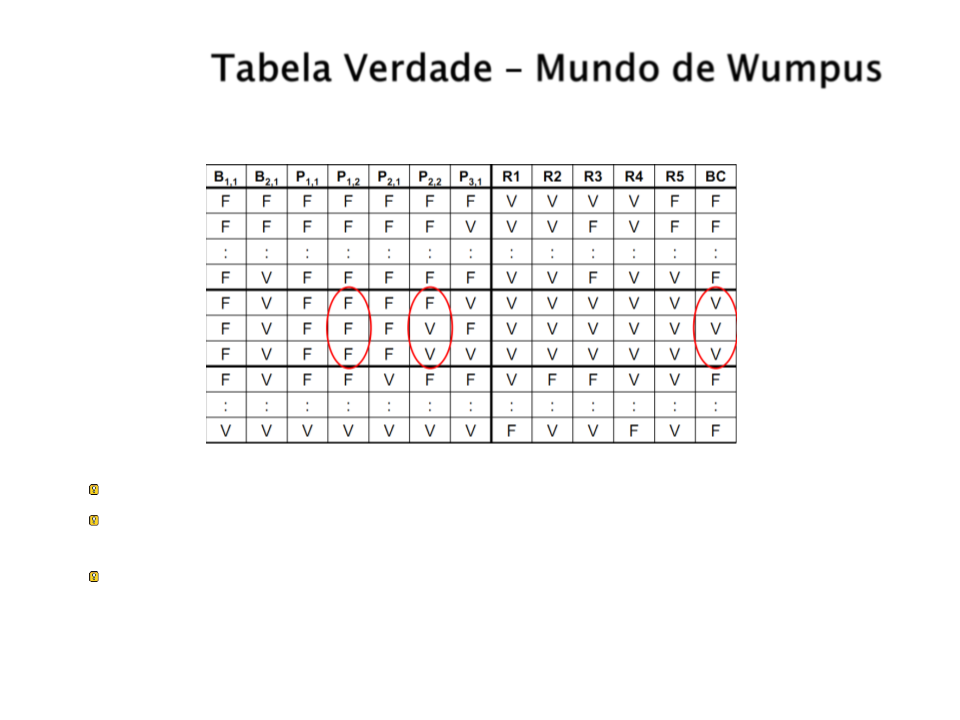
Tabela Verdade – Mundo de Wumpus
Em três desses modelos toda a base de conhecimento é verdadeira.
Nesses três modelos, ¬P1,2 é verdadeira. Dessa maneira conclui-se
que não existe poço em [1,2].
P2,2 é verdadeira em dois dos três modelos e falsa em um. Assim,
não podemos dizer ainda se existe um poço em [2,2].

Equivalência
Duas sentenças α e β são logicamente
equivalentes (α ⇔ β) se são verdadeiras no
mesmo conjunto de modelos.
(α∧β) ≡ (β∧α) comutatividade de ∧
(α∨β) ≡ (β∨α) comutatividade de ∨
(α∧β)∧γ ≡ α∧(β∧γ) associatividade de ∧
(α∨β)∨γ ≡ α∨(β∨γ) associatividade de ∨
¬¬α ≡ α eliminação de dupla negação
(
(
(
α⇒β) ≡ (¬β⇒¬α) contraposição
α⇒β) ≡ (¬α∨ β) eliminação de implicação
α⇔β) ≡ ((α⇒β) ∧ (β⇒α)) eliminação de bicondicional
¬
¬
(α∧β) ≡ (¬α∨¬β) de Morgan
(α∨β) ≡ (¬α∧¬β) de Morgan
(
(
α∧(β∨γ)) ≡ ((α∧β)∨(α∧γ)) distributividade de ∧ sobre ∨
α∨(β∧γ)) ≡ ((α∨β)∧(α∨γ)) distributividade de ∨ sobre ∧

Padrões de Raciocínio em Logica Proposicional
Modus Ponens: A partir de uma
implicação e a premissa da implicação,
pode-se inferir a conclusão.
Eliminação de E: De uma conjunção,
pode-se inferir qualquer um dos
conjuntores.
Resolução Unitária: De uma
disjunção, se um dos disjuntores é falso,
então pode-se inferir que o outro é
verdadeiro.
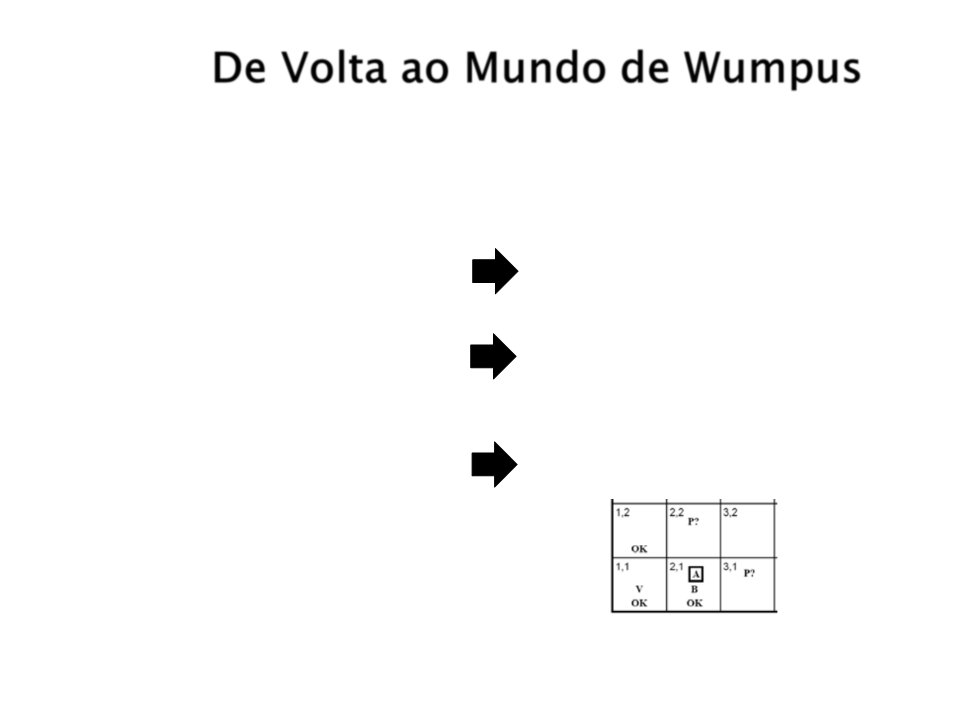
De Volta ao Mundo de Wumpus
Base de Conhecimento:
R1: ¬P1,1
Não há poço em [1,1].
Um quadrado tem uma brisa se e somente
se existe um poço em um quadrado vizinho
(todos os quadrados devem ser declarados).
R2: B1,1 ⇔ (P1,2 ∨ P2,1)
R3: B2,1 ⇔ (P1,1 ∨ P2,2 ∨ P3,1)
R4: ¬B1,1
R5: B2,1
Percepções adquiridas pelo agente do
mundo ele se encontra.
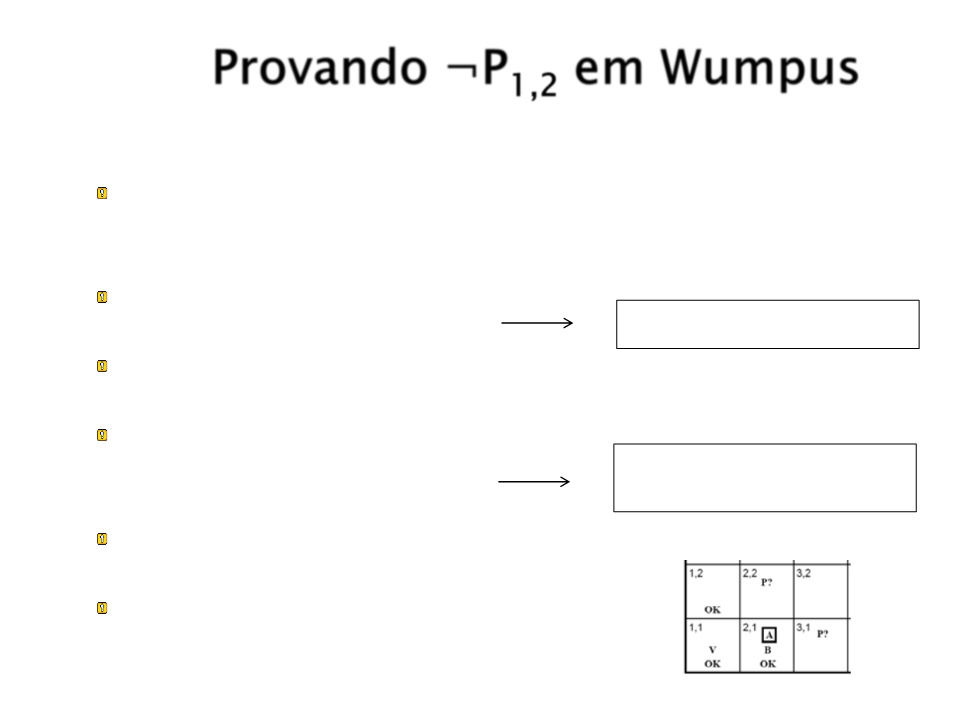
Provando ¬P1,2 em Wumpus
Eliminação bicondicional em R2:
R2: B1,1 ⇔ (P1,2 ∨ P2,1)
R6: (B1,1 ⇒ (P1,2 ∨ P2,1)) ∧ ((P1,2 ∨ P2,1) ⇒ B1,1)
Eliminação de “e” em R6:
R7: (P1,2 ∨ P2,1) ⇒ B1,1
De uma conjunção, pode-se inferir
qualquer um dos conjuntores.
Contraposição em R7:
R8: ¬B1,1 ⇒¬(P1,2 ∨ P2,1)
Modus Ponens (R4 + R8)
A partir de uma implicação e a
premissa da implicação, pode-se
R4: ¬B1,1
inferir a conclusão.
R9: ¬(P1,2 ∨ P2,1)
Regra de Morgan em R9:
R10: ¬P1,2 ∧¬P2,1
Eliminação de “e” em R10: ¬P1,2

Prova Lógica
A aplicação de uma sequencia de regras de
inferências para derivar uma conclusão é
chamado de prova lógica.
A aplicação de inferências logicas é uma
alternativa a enumeração de modelos
vista anteriormente.
Como saber quais regras de inferência
devem ser utilizadas?

Limitações da Lógica Proposicional
A lógica proposicional é simples de
mais para representar alguns
problemas do mundo real.
Em problemas complexos pode ser
necessário a utilização de um número
muito grande de sentenças para a
criação de um agente realmente
inteligente.
