
INF 1771 – Inteligência Artificial
Aula 24 – Aprendizado Por Reforço
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Formas de Aprendizado
Aprendizado Supervisionado
Árvores de Decisão.
K-Nearest Neighbor (KNN).
Support Vector Machines (SVM).
Redes Neurais.
Aprendizado Não-Supervisionado
Aprendizado Por Reforço
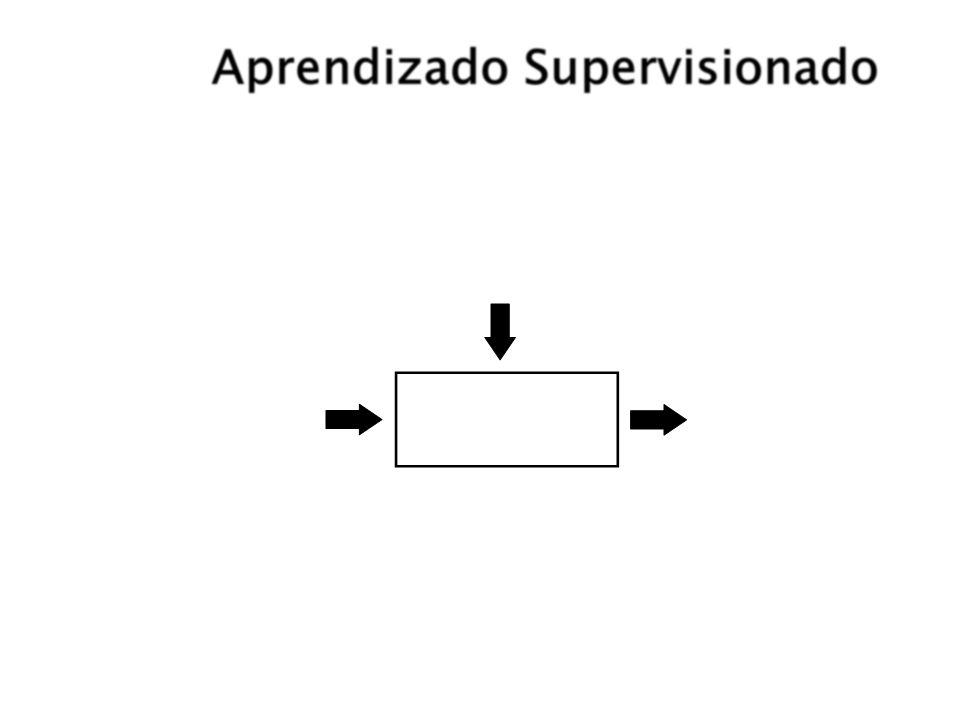
Aprendizado Supervisionado
Informação de Treinanento = Entradas + Saídas
Sistema de Aprendizado
Supervisionado
Entrada
Saída
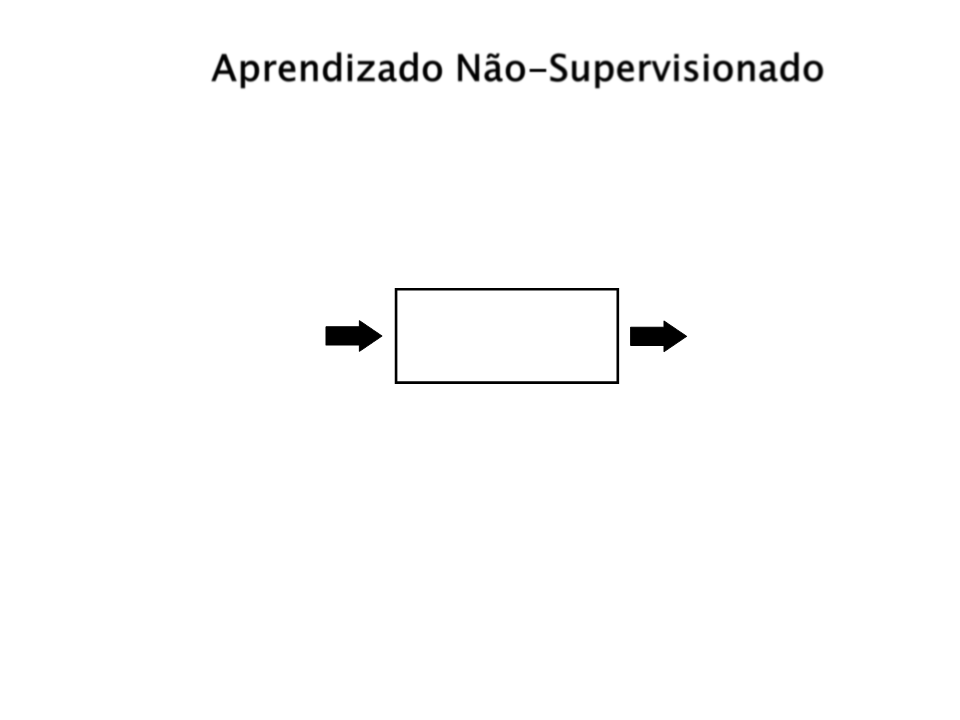
Aprendizado Não-Supervisionado
Sistema de Aprendizado
Não-Supervisionado
Entrada
Saída
Objetivo: Agrupar objetos semelhantes
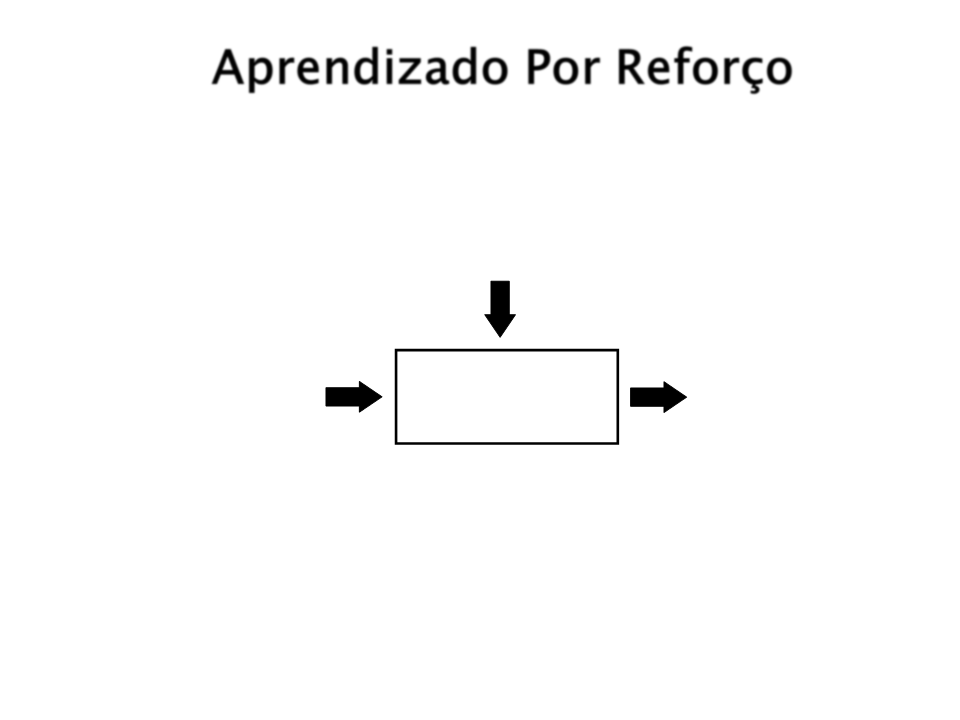
Aprendizado Por Reforço
Informação de Treinanento = Avaliação(Recompenças, Punições)
Sistema de Aprendizado
Por Reforço
Entrada
Saída
Objetivo: Conseguir o máximo de reforço possível

Introdução
Como um agente aprende a escolher ações
apenas interagindo com o ambiente?
Muitas vezes é impraticável o uso de aprendizado
supervisionado.
Como obter exemplos do comportamento correto e
representativo para qualquer situação?
E se o agente for atuar em um ambiente desconhecido?
Exemplos:
Criança adquirindo coordenação motora.
Robô interagindo com um ambiente para atingir objetivos.
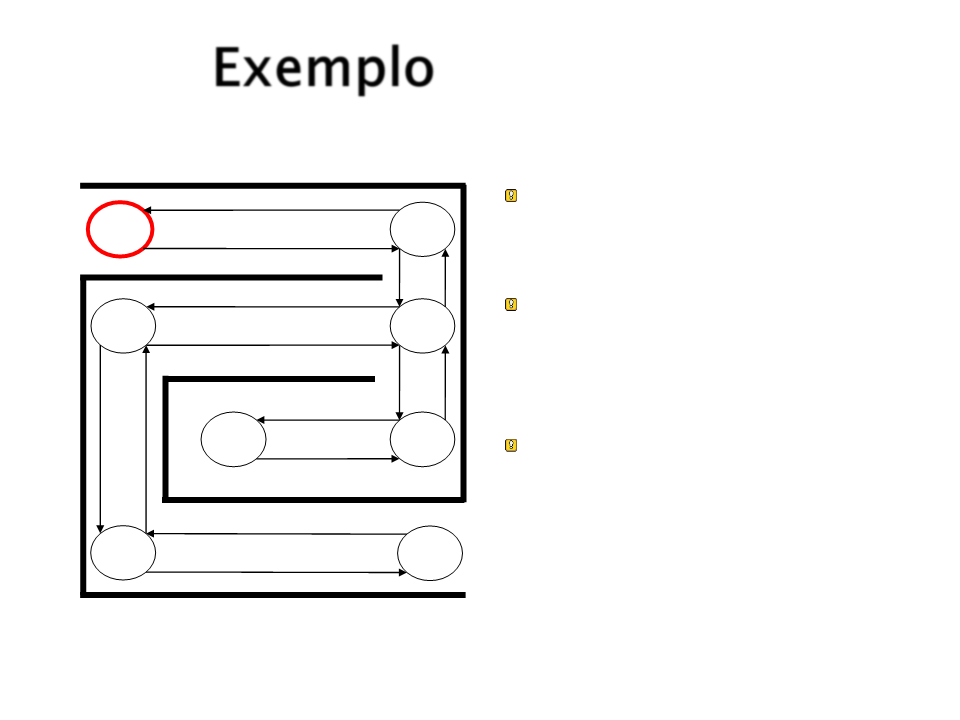
Exemplo
As setas indicam a “força”
entre dois estados.
S1
S4
S2
S3
Inicialmente todas as
setas possuem o mesmo
valor de força.
S8
S7
Iniciando em S1 como
chegar em S6?
S5
S6
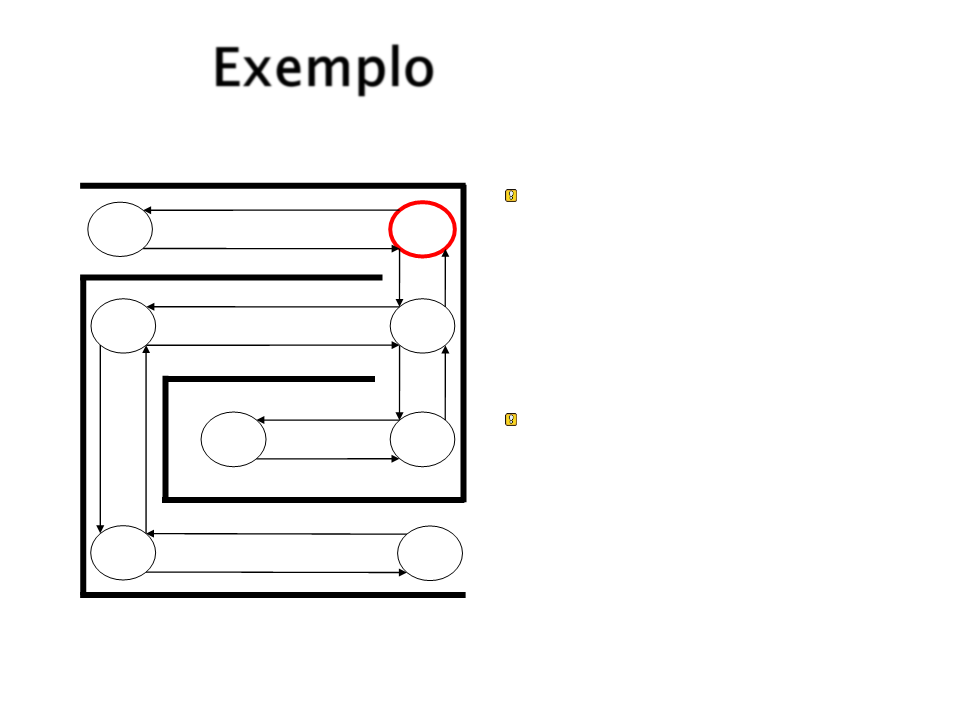
Exemplo
Próximo estado é
escolhido aleatoriamente
de um dos próximos
estados possíveis
S1
S4
S2
S3
(
ponderado pela força da
associação).
A primeira ação só pode
levar para S2.
S8
S7
S5
S6
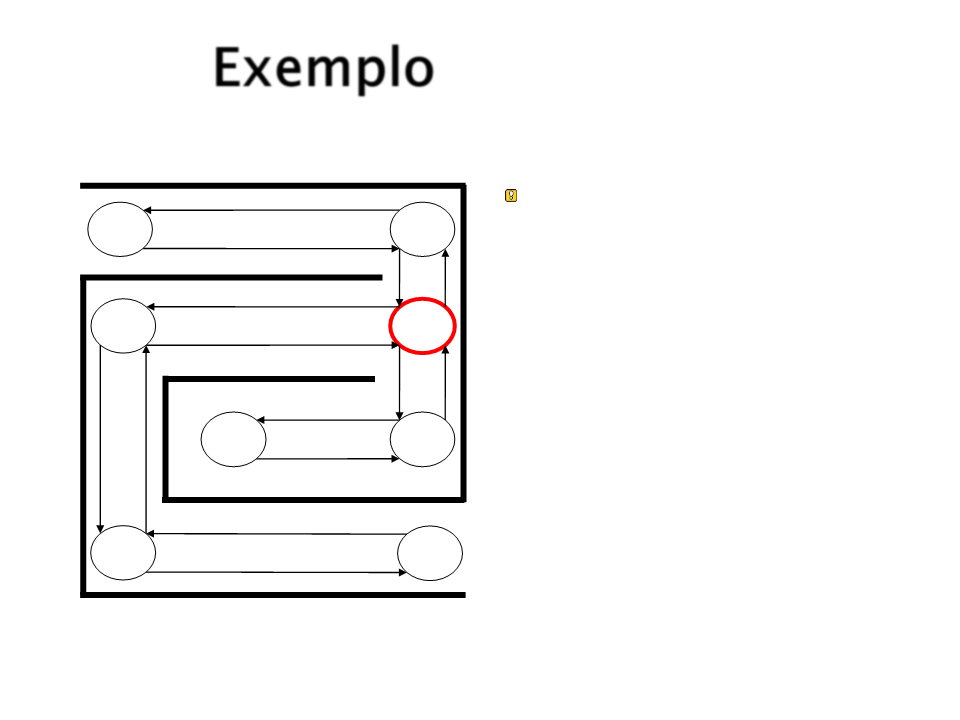
Exemplo
Supondo que a próxima
escolha leve a S3.
S1
S4
S2
S3
S8
S7
S5
S6
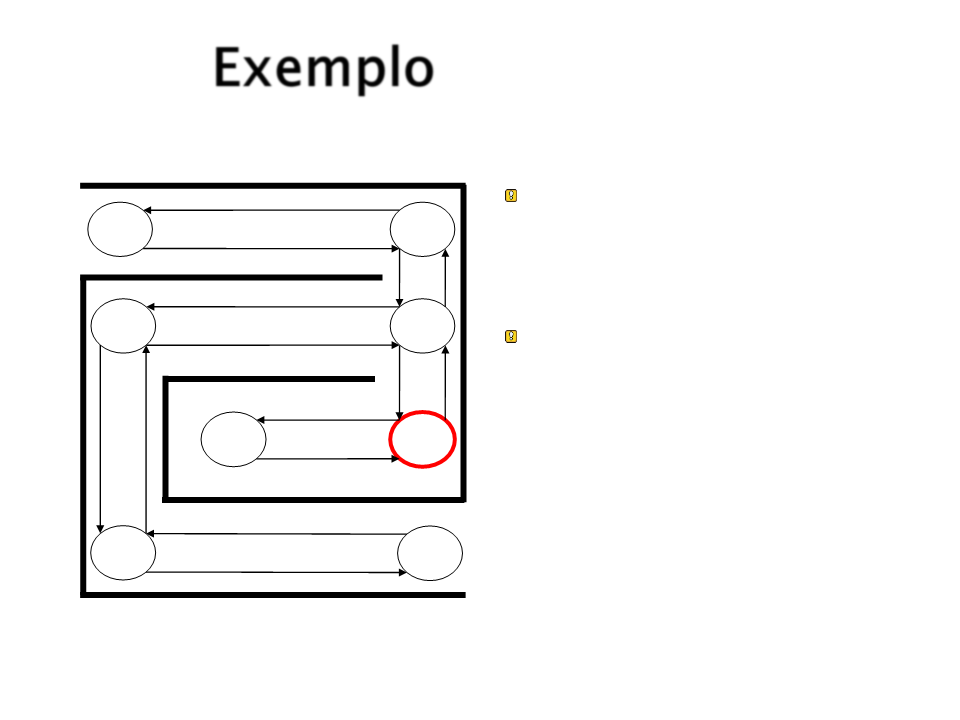
Exemplo
Em S3, as possíveis
escolhas são S2, S4, ou
S7.
S1
S4
S2
S3
Vamos supor que S7 é
escolhido aleatoriamente.
S8
S7
S5
S6
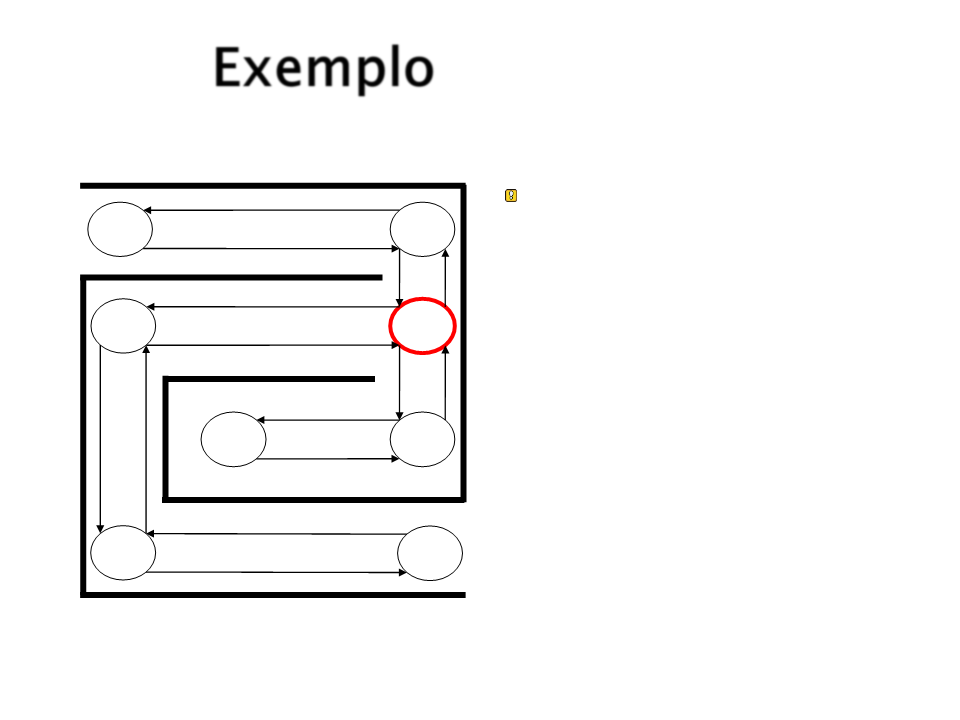
Exemplo
Por sorteio, S3 é o
próximo escolhido.
S1
S4
S2
S3
S8
S7
S5
S6
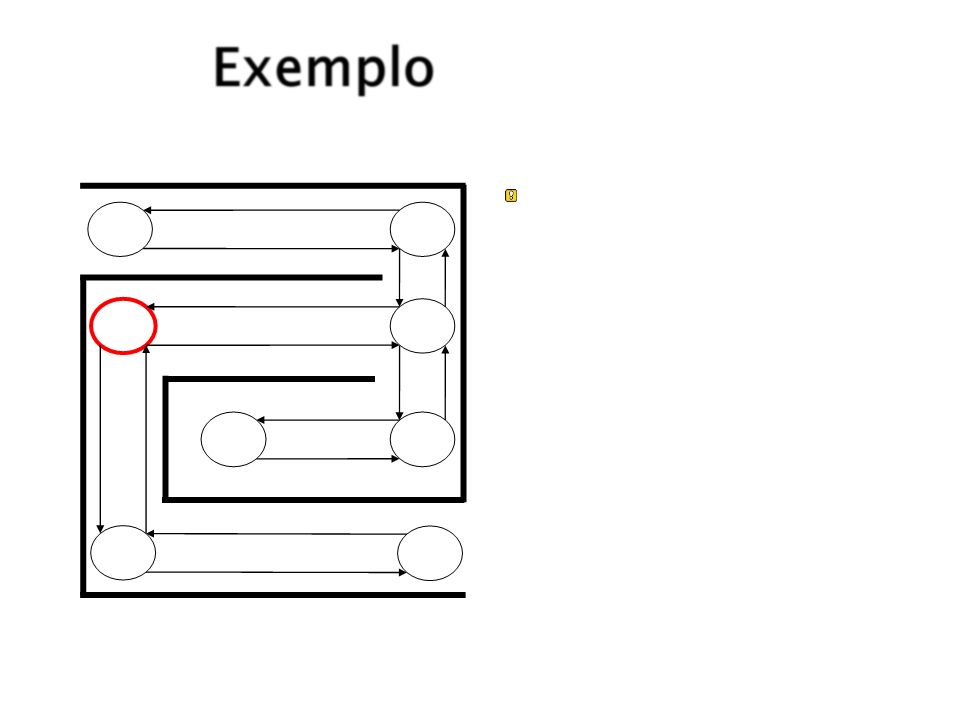
Exemplo
O próximo é S4.
S1
S4
S2
S3
S8
S7
S5
S6
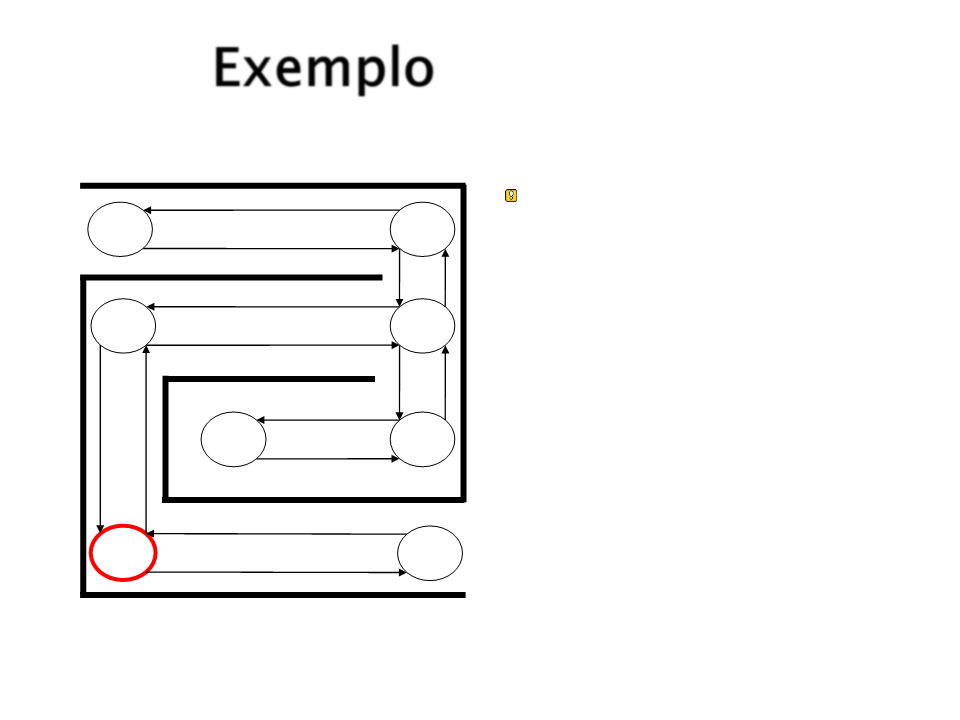
Exemplo
E então S5 é escolhido
aleatoriamente.
S1
S4
S2
S3
S8
S7
S5
S6
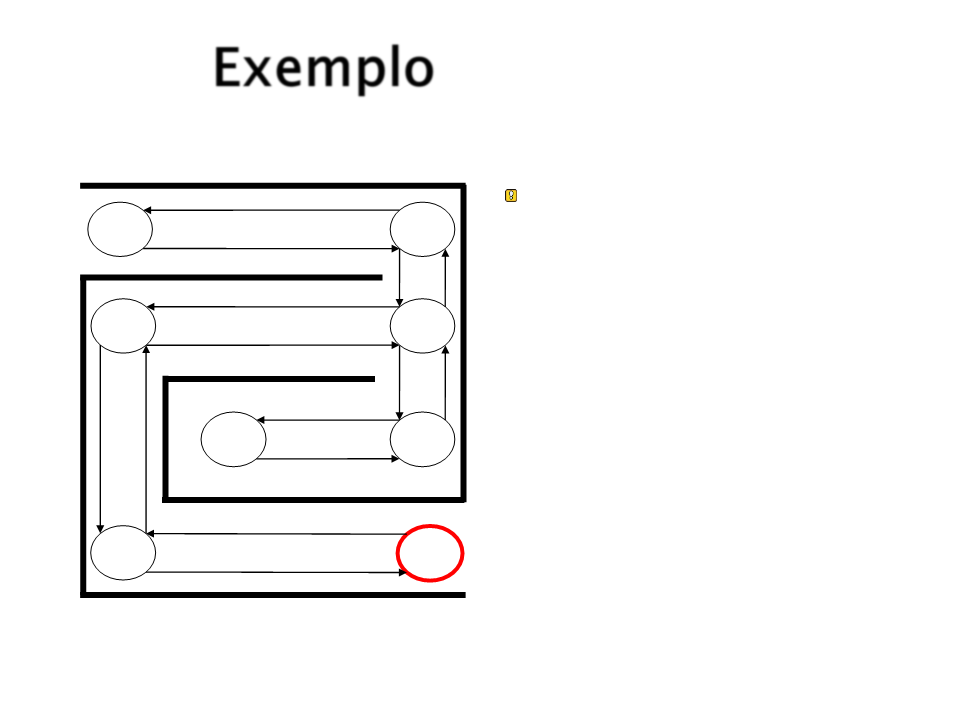
Exemplo
E finalmente atingimos o
objetivo S6.
S1
S4
S2
S3
S8
S7
S5
S6
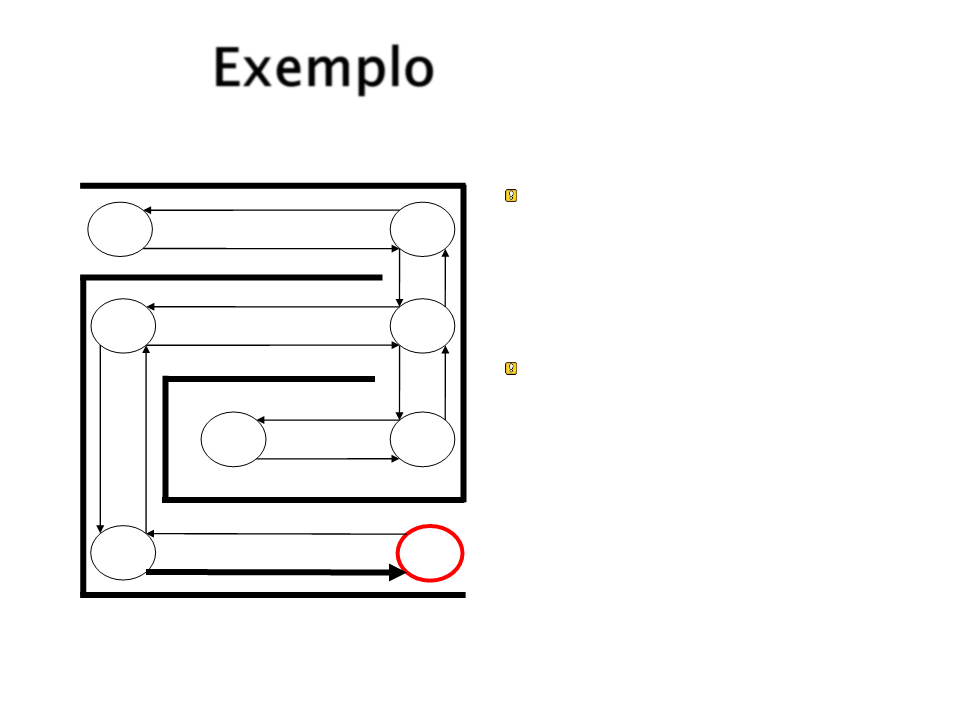
Exemplo
Quando o estado objetivo
é atingida, reforça-se a
conexão entre ele e o
estado que levou a ele.
S1
S4
S2
S3
Na próxima vez que S5
for alcançado, parte da
força de associação será
passada para S4.
S8
S7
S5
S6
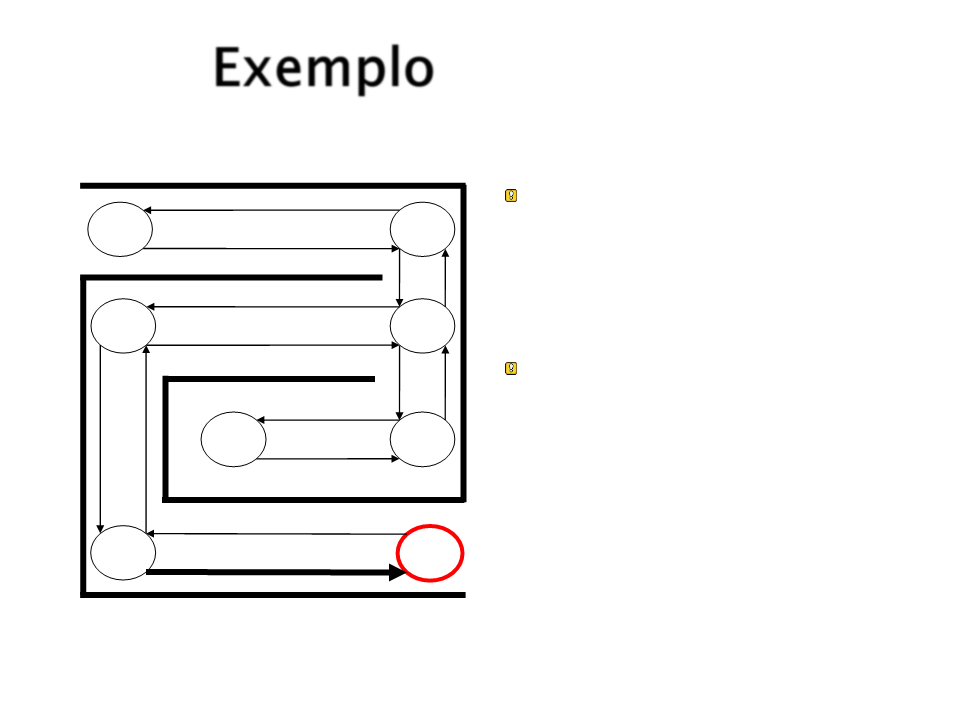
Exemplo
Quando o estado objetivo
é atingida, reforça-se a
conexão entre ele e o
estado que levou a ele.
S1
S4
S2
S3
Na próxima vez que S5
for alcançado, parte da
força de associação será
passada para S4.
S8
S7
S5
S6
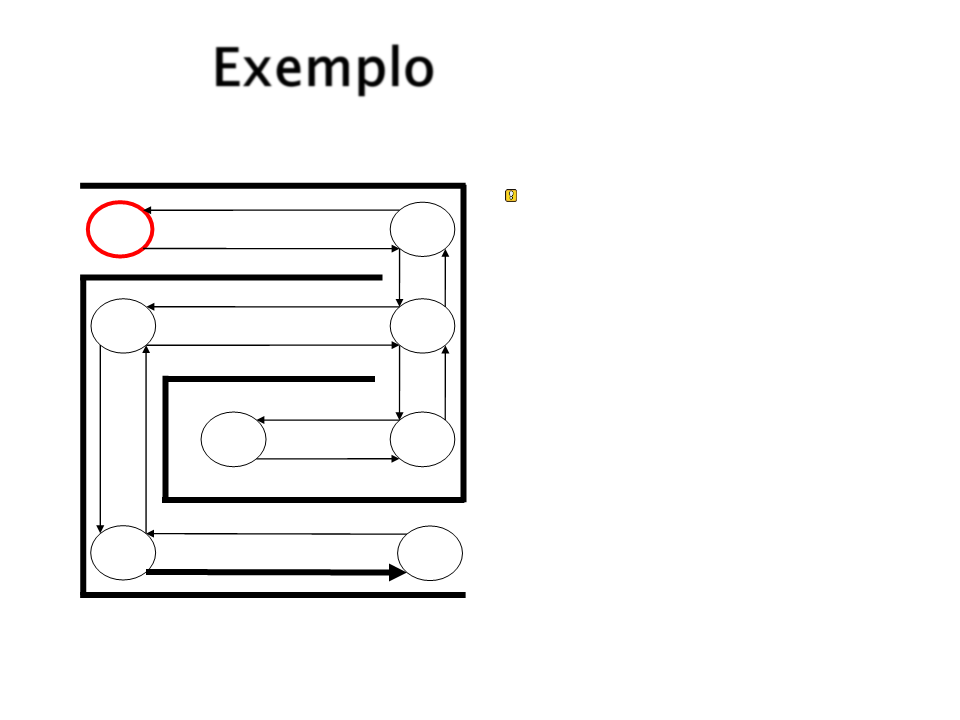
Exemplo
Iniciando novamente o
percurso.
S1
S4
S2
S3
S8
S7
S5
S6
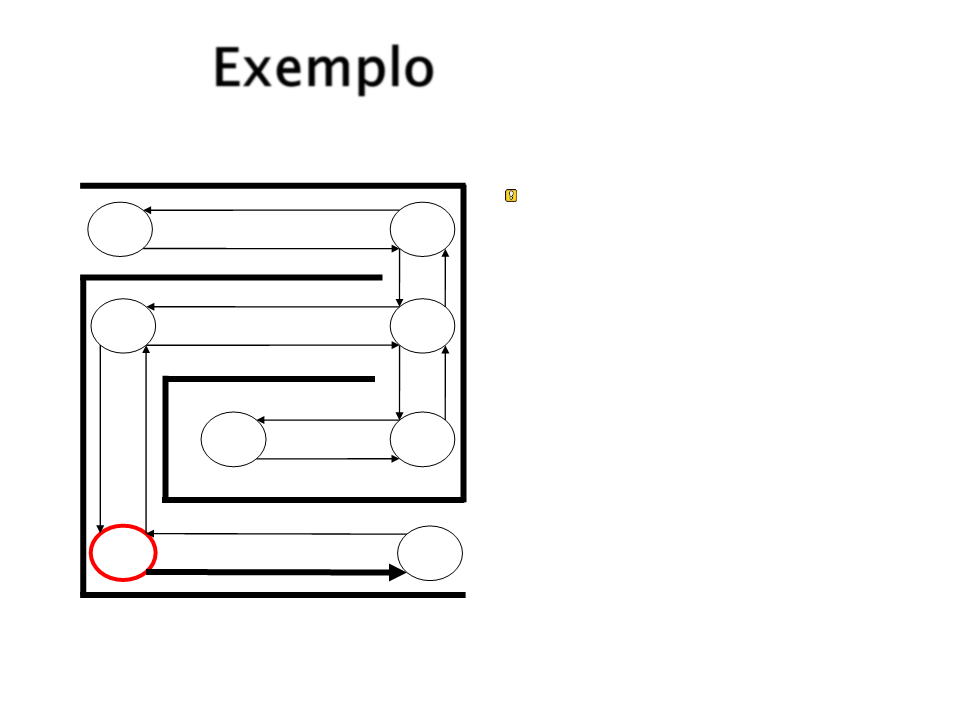
Exemplo
Supondo que após alguns
movimentos o agente
chega novamente em S5.
S1
S4
S2
S3
S8
S7
S5
S6
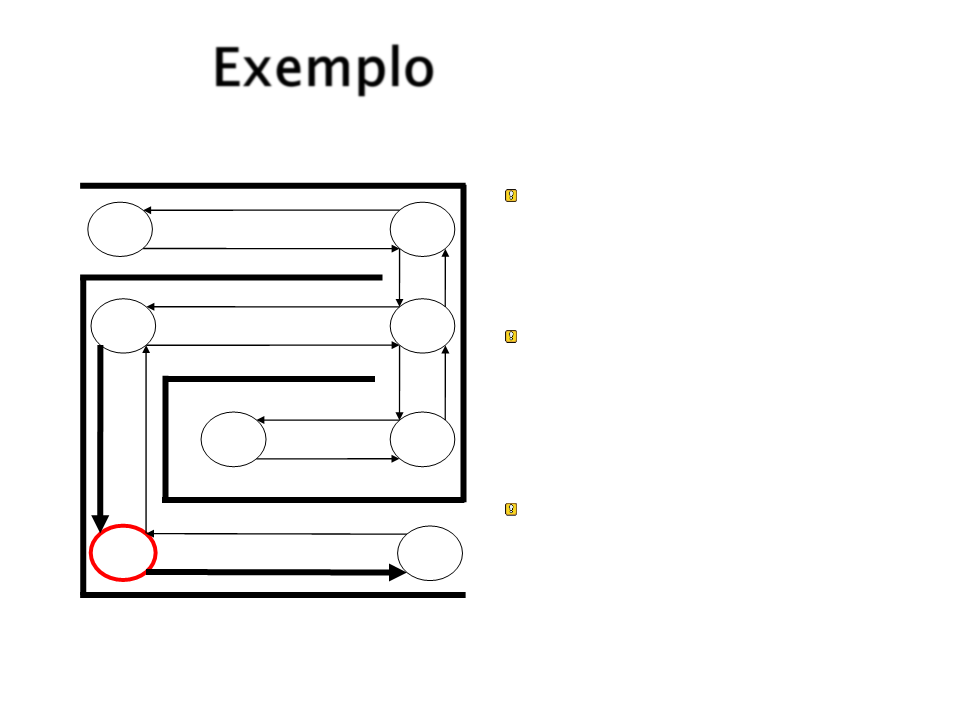
Exemplo
S5 tem grande chance de
atingir a meta pela rota
com mais força.
S1
S4
S2
S3
Em aprendizado por
reforço, essa “força” é
passada de volta para o
estado anterior.
S8
S7
Esse processo leva a criar
um caminho entre o início
e a meta.
S5
S6
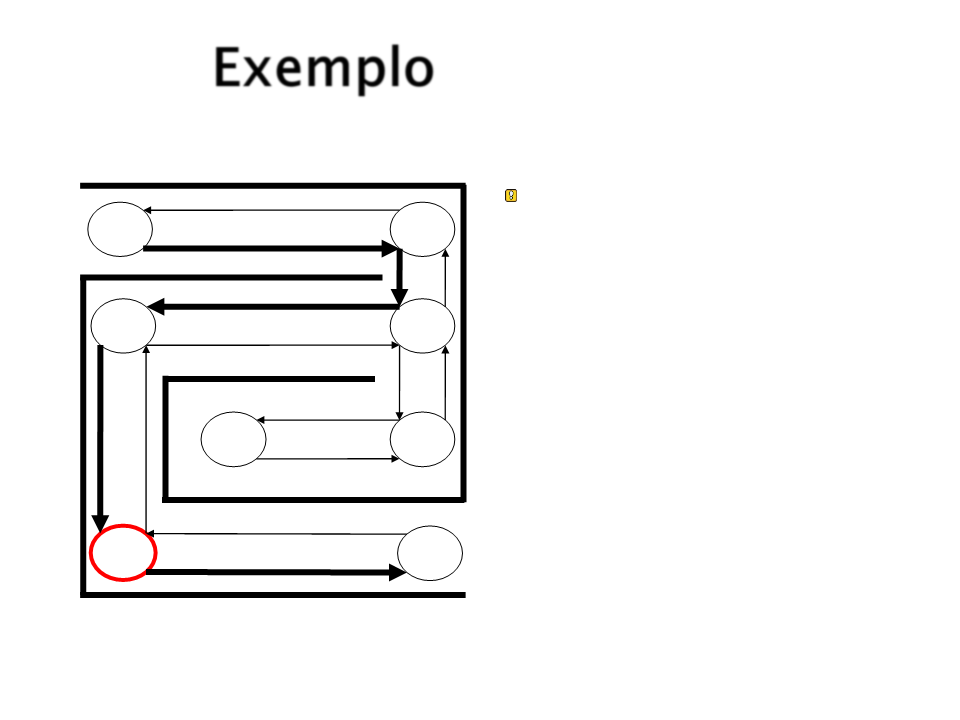
Exemplo
Após reiniciar o percurso
varias vezes, o agente
aprenderia o melhor
S1
S4
S2
S3
caminho a ser seguido.
S8
S7
S5
S6

Aprendizado Por Reforço
Um agente em um ambiente.
A cada instante do tempo t:
o agente está em um estado s.
executa uma ação a.
vai para um estado s’.
recebe uma recompensa r.
Problema da aprendizagem por reforço:
Como escolher uma política de ações que maximize o
total de recompensas recebidas pelo agente.
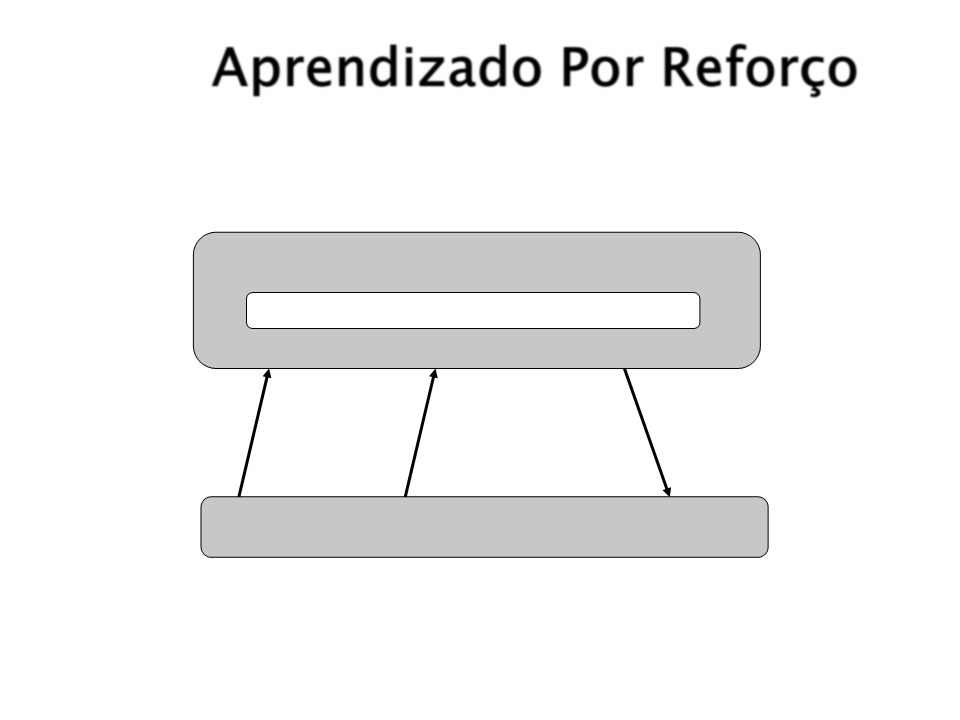
Aprendizado Por Reforço
Agente autômato otimizador adaptativo
Estado Interno (modelo do mundo)
Percepções
Reforço (+/-)
Ação
Ambiente

Aprendizado Por Reforço
Processo de decisão de Markov (MDP)
Conjunto de estados S.
Conjunto de ações A.
Uma função de recompensa r(s, a).
Uma função de transição de estados α(s, a).
Política de ações π(s):
π : S → A

Estados e Ações
Estado: conjunto de características que descrevem o
ambiente.
Formado pelas percepções do agente + modelo do
mundo.
Deve prover informação para o agente de quais ações
podem ser executadas.
A representação deste estado deve ser suficiente para
que o agente tome suas decisões.
A decisão de que ação tomar não pode depender
da sequência de estados anteriores.
Um tabuleiro de dama satisfaz esta propriedade, mas de xadrez não.

A Função de Recompensa
Feedback do ambiente sobre o
comportamento do agente.
Indicada por R(S, A) → R
r(s,a) indica a recompensa recebida
quando o agente está no estado s e
executa a ação a.
Pode ser determinística ou estocástica

Função de Transição de Estados
α(S, A) → S
α(s, a) indica em qual estado o agente está, dado que:
Estava no estado s.
executou a ação a.
Ambientes não-determinísticos:
α(s, a, s’)
Indica a probabilidade de ir para um estado s’ dado que
estava em s e executou a ação a.

Exemplos de Problemas
Problema
Estados
Ações
Recompensas
Agente jogador
de damas.
Configurações do Mover uma
+ Capturas
– Perdas
tabuleiro.
determinada
peça.
Agente em jogo Posição,energia
Mover-se em
uma direção,
+ Tirar energia
do oponente.
- Perder energia.
de luta.
dos lutadores,
tempo, estar ou lançar magia,
estar sendo
bater, etc...
atacado, etc...
Agente
patrulhador.
Posição no mapa Ir para algum Ociosidade
lugar vizinho do (tempo sem
Mapa visitas) do lugar
visitado
(atual e
passadas),
ociosidade da
vizinhança, etc...
Atualmente.

Política de Ações π(s)
Função que modela o comportamento do agente
Mapeia estados em ações.
Pode ser vista como um conjunto de regras do tipo sn →
am
Exemplo:
Se estado s = (inimigo próximo, estou perdendo) então
ação a = (usar magia);
Se estado s =(outro estado) então
ação a = (outra ação);

Função Valor dos Estados Vπ(s) (S → R)
Como saber se um determinado estado é
bom ou ruim?
A função valor Vπ(s) expressa esta noção, em
termos das recompensas e da política de ações.
Representa a recompensa a receber em um
estado s, mais as recompensas futuras se ele
seguir uma política de ações π.
Exemplo: tornar-se diretor é bom pelo que o cargo
permite e permitirá nas próximas promoções.
Vπ(s0) = r0 + r1 + r2 + r3 + ...
Problema: se o tempo for infinito, a função valor do
estado tende a infinito.

Função Valor das Ações Qπ(s, a) : (S, A) → R
A função valor das ações Qπ(s, a) indica a
soma das recompensas a obter, dado que:
o agente está no estado s.
executou uma ação a.
a partir daí, seguiu uma política de ações π.
Qπ(s, a) = r(s, a) + Vπ(s’), onde:
S’ = α(s,a) = indica em qual estado o agente está,
dado que ele estava no estado s e executou a ação
a.
O valor da ação é a recompensa da ação mais
o valor do estado para onde o agente vai
devido à ação.

Aprendizado Por Reforço
O aprendizado por reforço consiste em
aprender uma política de ações π*
ótima, que maximiza a função Vπ(V*) ou a
função Qπ(Q*)
π* = argmaxπ[Vπ(s)]
Em outras palavras, de que maneira o
agente deve agir para maximizar as suas
recompensas futuras.

Aprendendo uma Política Ótima
Se o ambiente é determinístico α(s, a) = s’ (função
de transição de estados) é conhecida e r(s, a) (função
de recompensa) é conhecida, é possível computar
uma política ótima:
V*(s) =maxa[r(s,a) + V*(α(s,a))]
π*(s) = argmaxa[r(s,a) + V*(α(s,a))]
Tempo polinomial.
Problema: se não temos conhecimento prévio das
recompensas e transição de estados.
Se o ambiente é não-determinístico, mas a função
de probabilidade de transição de estados for
conhecida, também é possível computar π*
Problema: É difícil estimar probabilidades.
Q Learning
Algoritmo Q Learning
Para todo estado s e ação a, inicialize a
tabela Q[s][a] = 0;
Usufruir valores
conhecidos ou
explorar valores
não computados?
Para sempre, faça:
Observe o estado atual s;
Escolha uma ação a e execute;
Observe o próximo estado s’ e recompensa r.
Atualize a tabela Q:
Q[s][a] = r + maxa’(Q[s’][a’])

Dilema de Explorar ou Usufruir
Usufruir
Escolher a ação que atualmente está com maior
valor Q(s,a)
Explorar
Escolher uma ação randômica, para que seu valor
Q(s,a) seja atualizado
Dilema
Dado que eu aprendi que Q(s, a) vale 100, vale a
pena tentar executar a ação a’ se Q(s, a’) por
enquanto vale 20?
Depende do ambiente, da quantidade de ações já
tomadas e da quantidade de ações restantes.

Aplicações
[
Tesauro, 1995] Modelagem do jogo
de gamão como um problema de
aprendizagem por reforço:
Vitória: +100
Derrota: –100
Após 1 milhão de partidas contra ele
mesmo, joga tão bem quanto o melhor
jogador humano.
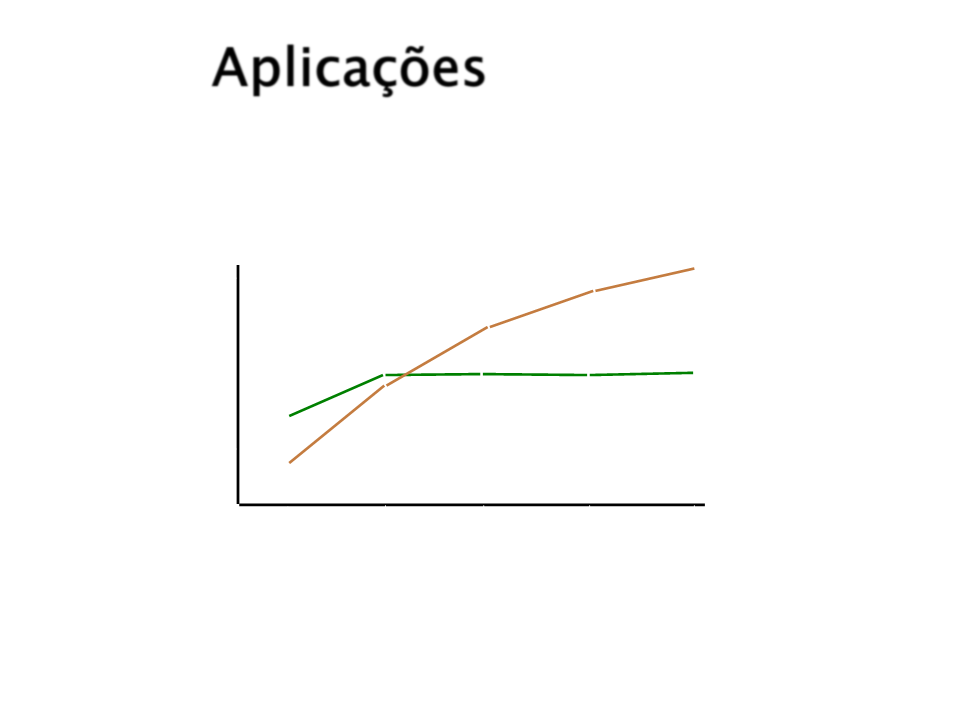
Aplicações
TD-Gammon
7
0%
self-play
Tesauro, 1992
performance
against
Neurogammon
gammontool
trained with 15,000
expert-labeled examples
5
0%
0
10
20
40
80
Aplicações
[Crites and Barto, 1996] Controle de Elevadores
1
0 andares, 4 cabines
Estados: estados dos botões;
posição, direção, e estado
de movimentação dos
elevadores; passageiros nos
elevadores e esperando.
Ações: parar em, passar,
próximo andar.
Recompensas: simplesmente
-
1 por tempo em que cada
pessoa ficava esperando.
