
INF 1771 – Inteligência Artificial
Aula 09 – Prolog
Edirlei Soares de Lima
<elima@inf.puc-rio.br>

Variáveis
Variáveis são representadas através de cadeias de
letras, números ou _ sempre começando com letra
maiúscula:
X, Resultado, Objeto3, Lista_Alunos, ListaCompras...
O escopo de uma variável é valido dentro de uma
mesma regra ou dentro de uma pergunta.
Isto significa que se a variável X ocorre em duas
regras/perguntas, então são duas variáveis distintas.
A ocorrência de X dentro de uma mesma regra/pergunta
significa a mesma variável.

Variáveis
Uma variável pode estar:
Instanciada: Quando a variável já referencia (está
unificada a) algum objeto.
Livre ou não-instanciada: Quando a variável não
referencia (não está unificada a) um objeto.
Uma vez instanciada, somente Prolog pode torná-la
não-instanciada através de seu mecanismo de
inferência (nunca o programador).

Variável Anônima
Variáveis anônimas podem ser utilizadas em
sentenças cujo valor atribuído a variável não é
importante. Por exemplo, a regra tem_filho:
Tem_filho(X) :- progenitor(X,Y).
Para relação “ter filhos” não é necessário saber o
nomes dos filhos. Neste vaso utiliza-se uma variável
anônima representada por “_”.
Tem_filho(X) :- progenitor(X,_).

Variável Anônima
Cada vez que uma variável anônima aparece em uma
cláusula, ele representa uma nova variável anônima.
Por exemplo:
alguém_tem_filho :- progenitor(_,_).
É equivale à:
alguém_tem_filho :- progenitor(X,Y).

Estruturas
Objetos estruturados são objetos de dados com
vários componentes.
Cada componente da estrutura pode ser outra
estrutura.
Por exemplo, uma data pode ser vista como uma
estrutura com três componentes: dia, mês, ano.
data(4,maio,2003)
Estruturas
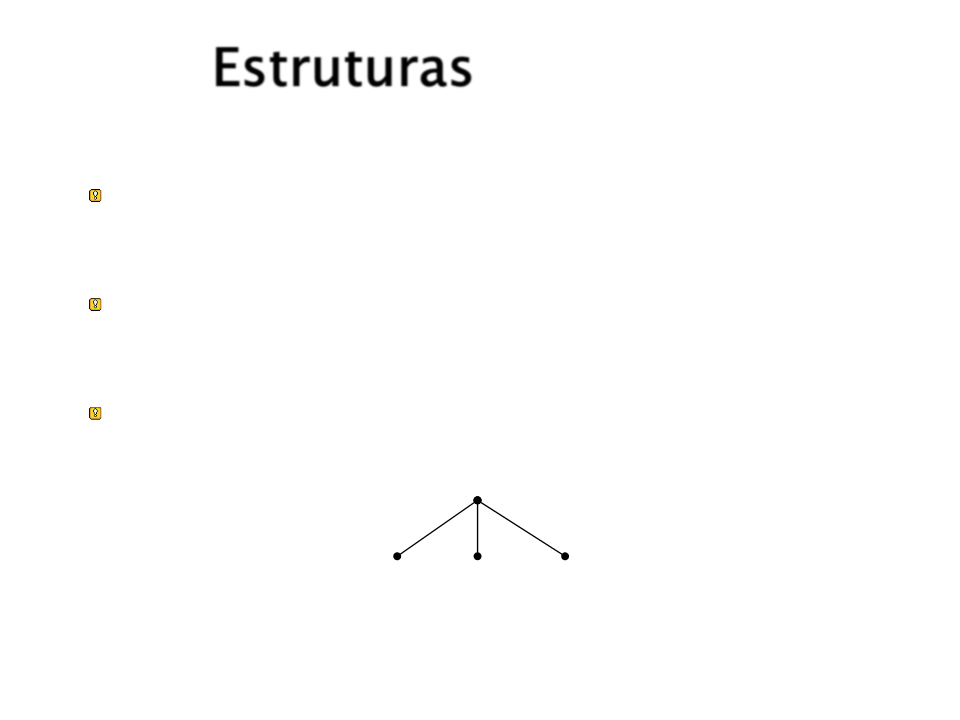
Todos os objetos estruturados são representados
como árvores.
A raiz da árvore é o funtor e os filhos da raiz são os
componentes.
data(4,maio,2003):
data
4
maio 2003
Estruturas
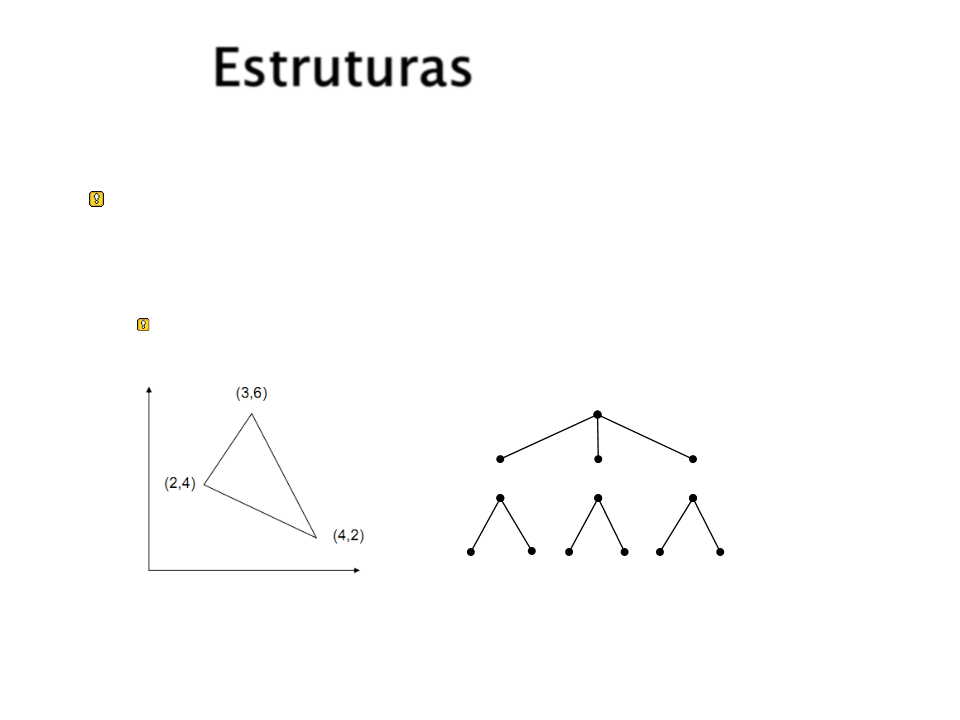
Um triângulo pode ser representado da
seguinte forma:
triângulo(ponto(2,4),ponto(3,6),ponto(4,2))
triângulo
ponto ponto ponto
2
4 3 6 4 2
Operadores
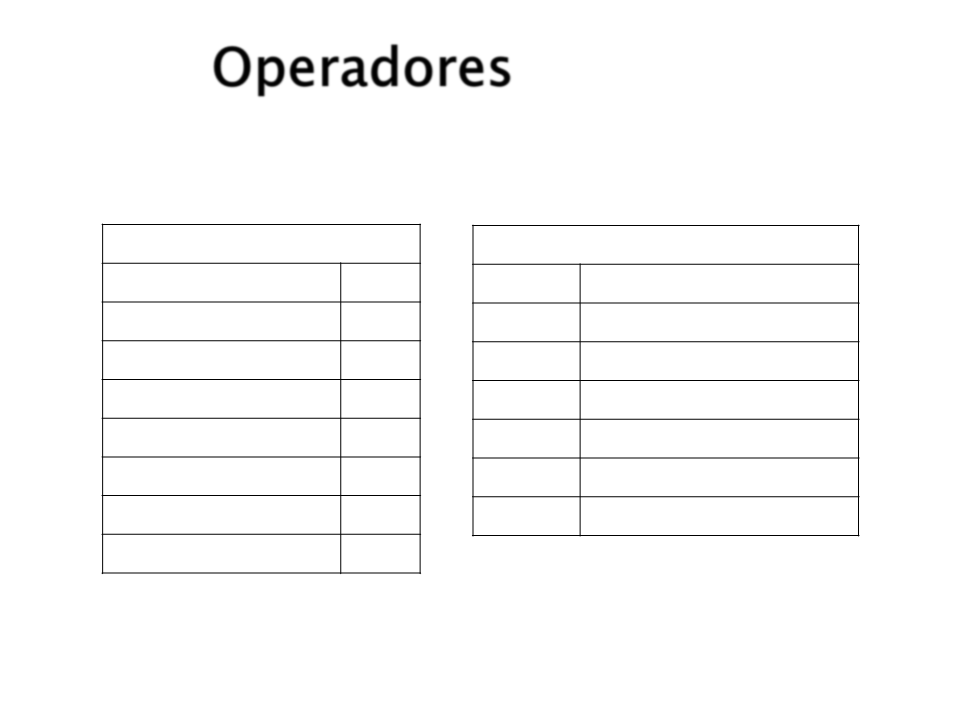
Operadores Aritméticos
Operadores Relacionais
Adição
+
-
X > Y
X < Y
X é maior do que Y
X é menor do que Y
Subtração
Multiplicação
Divisão
*
X >= Y X é maior ou igual a Y
X =< Y X é menor ou igual a Y
X =:= Y X é igual a Y
/
Divisão Inteira
Resto da Divisão
Potência
//
Mod
**
is
X = Y
X unifica com Y
X =\= Y X é diferente de Y
Atribuição

Operadores
O operador “=” realiza apenas a unificação de
termos:
?- X = 1 + 2.
X = 1 + 2
O operador “is” força a avaliação aritmética:
?- X is 1 + 2.
X = 3

Operadores
Se a variável à esquerda do operador “is” já estiver
instanciada, o Prolog apenas compara o valor da
variável com o resultado da expressão à direita de
“
is”:
?- X = 3, X is 1 + 2.
X = 3
?- X = 5, X is 1 + 2.
false

Unificação de Termos
Dois termos se unificam (matching) se:
Eles são idênticos ouƒas variáveis em ambos os
termos podem ser instanciadas a objetos de
maneira que após a substituição das variáveis os
termos se tornam idênticos.
Por exemplo, existe a unificação entre os termosƒ
data(D,M,2003) e data(D1,maio,A) instanciando
D = D1, M = maio, A = 2003.

Unificação de Termos
data(D,M,2003) = data(D1,maio,A), data(D,M,2003) = data(15,maio,A1).
D = 15
M = maio
D1 = 15
A = 2003
A1 = 2003
Por outro lado, não existe unificação entre os
termos:
data(D,M,2003), data(D1,M1,1948)

Unificação de Termos
A unificação é um processo que toma dois
termos e verifica se eles unificam:
Se os termos não unificam, o processo falha (e as
variáveis não se tornam instanciadas).
Se os termos unificam, o processo tem sucesso e
também instancia as variáveis em ambos os termos para
os valores que os tornam idênticos.

Unificação de Termos
As regras que regem se dois termos S e T
unificam são:
Se S e T são constantes, então S e T unificam
somente se são o mesmo objeto.
Se S for uma variável e T for qualquer termo,
então unificam e S é instanciado para T.
Se S e T são estruturas, elas unificam somente
seƒ:
S e T têm o mesmo funtor principal.
Todos seus componentes correspondentes unificam.

Comparação de Termos
Operadores Relacionais
X = Y
X unifica com Y, é verdadeiro quando dois termos são o
mesmo. Entretanto, se um dos termos é uma variável, o
operador = causa a instanciação da variável.
X \= Y
X não unifica com Y
X == Y
X é literalmente igual a Y (igualdade literal), que é
verdadeiro se os termos X e Y são idênticos, ou seja,
eles têm a mesma estrutura e todos os componentes
correspondentes são os mesmos, incluindo o nome das
variáveis.
X \== Y
X não é literalmente igual a Y que é o complemento de
X==Y

Comparação de Termos
?
- f(a,b) == f(a,b).
true
?
- f(a,b) == f(a,X).
false
?
- f(a,X) == f(a,Y).
false
?
- X == X.
true
?
- X == Y.
false
?
- X \== Y.
true
?
- g(X,f(a,Y)) == g(X,f(a,Y)).
true

Predicados para Verificação de Tipos de Termos
Predicado
Verdadeiro se:
var(X)
X é uma variável não instanciada
X não é uma variável ou X é uma variável instanciada
X é um átomo
nonvar(X)
atom(X)
integer(X)
float(X)
X é um inteiro
X é um número real
atomic(X)
compound(X)
X é uma constante (átomo ou número)
X é uma estrutura

Predicados para Verificação de Tipos de Termos
?
- var(Z), Z = 2.
Z = 2
- Z = 2, var(Z).
false
?
?
- integer(Z), Z = 2.
false
?
- Z = 2, integer(Z), nonvar(Z).
Z = 2
?
- atom(3.14).
false
?
- atomic(3.14).
true
?
- atom(==>).
true
?
- atom(p(1)).
false
?
- compound(2+X).
true

Exemplo: Macaco e as Bananas
Um macaco encontra-se próximo à porta de uma sala. No
meio da sala há uma banana pendurada no teto. O macaco
tem fome e quer comer a banana mas ela está a uma altura
fora de seu alcance. Perto da janela da sala encontra-se
uma caixa que o macaco pode utilizar para alcançar a
banana. O macaco pode realizar as seguintes ações:
Caminhar no chão da sala;
Subir na caixa (se estiver ao lado da caixa);
Empurrar a caixa pelo chão da sala (se estiver ao lado da caixa);
Pegar a banana (se estiver parado sobre a caixa diretamente embaixo da
banana).
Exemplo: Macaco e as Bananas
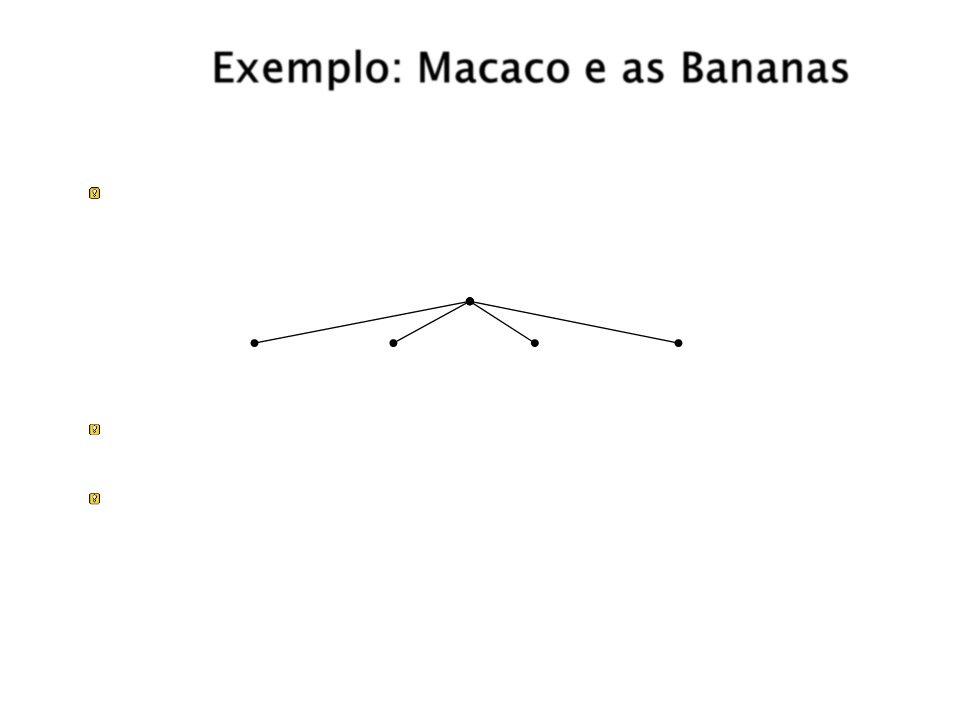
É conveniente combinar essas 4 informações em uma
estrutura de estado:
estado
na_porta no_piso na_janela não_tem
O estado inicial é determinado pela posição dos objetos.
O estado final é qualquer estado onde o último componente
da estrutura é “tem”:
estado(_,_,_,tem)

Exemplo: Macaco e as Bananas
Possíveis valores para os argumentos da
estrutura estado:
1
º argumento (posição do macaco):
na_porta, no_centro, na_janela
º argumento (posição vertical do macaco):
no_chão, acima_caixa
º argumento (posição da caixa):
na_porta, no_centro, na_janela
º argumento (macaco tem ou não tem banana):
tem, não_tem
2
3
4

Exemplo: Macaco e as Bananas
Movimentos permitidos que alteram o mundo de
um estado para outro:
Pegar a banana;
Subir na caixa;
Empurrar a caixa;
Caminhar no chão da sala;
Nem todos os movimentos são possíveis em cada
estado do mundo.Por exemplo, “pegar a banana”
somente é possível se o macaco estiver em cima da
caixa, diretamente em baixo da banana e o macaco
ainda não possuir a banana.

Exemplo: Macaco e as Bananas
Formalizando o problema em Prolog é possível
estabelecer a seguinte relação:
move(Estado1,Movimento,Estado2)
Onde:
Estado1 é o estado antes do movimento (pré-condição);
Movimento é o movimento executado;
Estado2 é o estado após o movimento;

Exemplo: Macaco e as Bananas
O movimento “pegar a banana” pode ser definido por:
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro, acima_caixa, no_centro, tem)
).
Este fato diz que após o movimento “pegar_banana” o
macaco tem a banana e ele permanece em cima da
caixa no meio da sala.

Exemplo: Macaco e as Bananas
Também é necessário expressar o fato que o macaco no
chão pode caminhar de qualquer posição “Pos1” para
qualquer posição “Pos2”:
move(
estado(Pos1, no_chão, Caixa, Banana),
caminhar(Pos1,Pos2),
estado(Pos2, no_chão, Caixa, Banana)
).
De maneira similar, é possível especificar os movimentos
“empurrar” e “subir”.

Exemplo: Macaco e as Bananas
A pergunta principal que o programa deve
responder é:
O macaco consegue, a partir de um estado
inicial, pegar as bananas?

Exemplo: Macaco e as Bananas
Para isso é necessário formular duas regras que definam
quando o estado final é alcançável:
Para qualquer estado no qual o macaco já tem a banana,
o predicado “consegue” certamente deve ser verdadeiro e
nenhum movimento é necessário:
ƒconsegue(estado(_,_,_,tem)).
Nos demais casos, um ou mais movimentos são necessários;
o macaco pode obter a banana em qualquer estado “Estado1”
se existe algum movimento de “Estado1” para algum estado
“
“
Estado2” tal que o macaco consegue pegar a banana no
Estado2”:
consegue(Estado1) :- move(Estado1, Movimento, Estado2),
consegue(Estado2).

Exemplo: Macaco e as Bananas
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro, acima_caixa, no_centro,tem)
).
move(
estado(P, no_chão, P, Banana),
subir,
estado(P, acima_caixa, P, Banana)
).
move(
estado(P1, no_chão, P1, Banana),
empurrar(P1, P2),
estado(P2, no_chão, P2, Banana)
).
move(
estado(P1, no_chão, Caixa, Banana),
caminhar(P1, P2),
estado(P2, no_chão, Caixa, Banana)
).
consegue(estado(_, _, _, tem)).
consegue(Estado1) :- move(Estado1, Movimento, Estado2), consegue(Estado2).
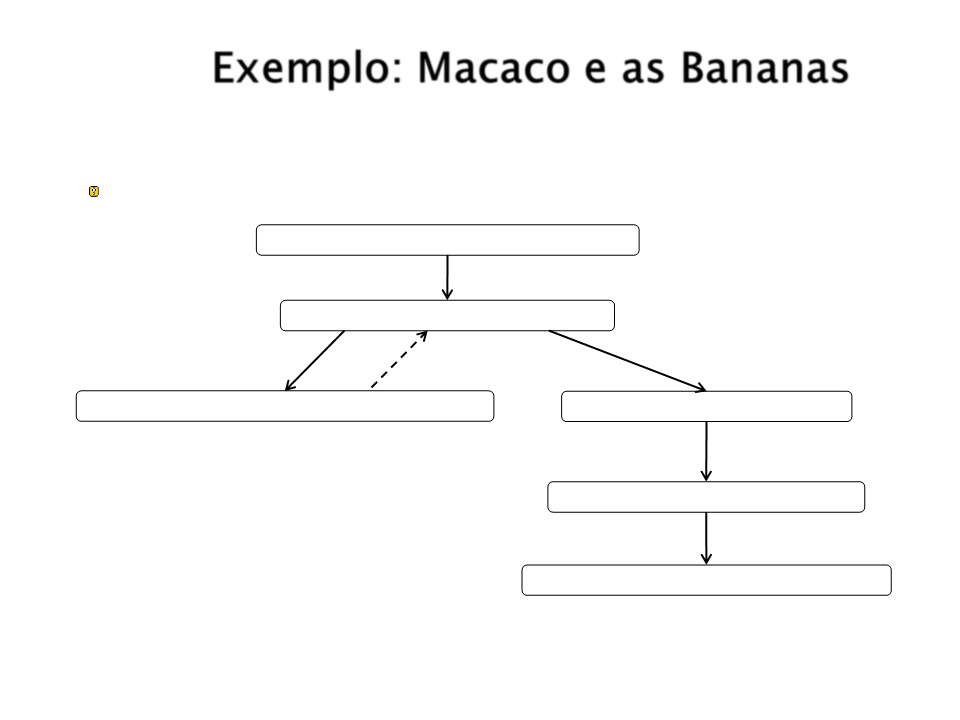
Exemplo: Macaco e as Bananas
?
- consegue(estado(na_porta, no_chão, na_janela, não_tem)).
estado(na_porta, no_chão, na_janela, não_tem)
caminhar(na_porta,P2)
estado(P2, no_chão, na_janela, não_tem)
empurrar(P2,P2’)
subir
backtrack
estado(na_janela, acima_caixa, na_janela, não_tem)
estado(P2’, no_chão, P2’, não_tem)
subir
estado(P2’, acima_caixa, P2’, não_tem)
Pegar_banana
P2’=no_centro
estado(no_centro,acima_caixa,no_centro,tem)

Listas
Lista é uma das estruturas mais simples em
Prolog e pode ser aplicada em diversas
situações.
Uma lista pode ter qualquer comprimento.
Uma lista contendo os elementos “ana”, “tênis”
e “pedro” pode ser escrita em Prolog como:
[
ana, tênis, pedro]

Listas
O uso de colchetes é apenas uma melhoria da
notação, pois internamente listas são representadas
como árvores, assim como todos objetos estruturados
em Prolog.
Internamente o exemplo [ana, tênis, pedro] é
representando da seguinte maneira:
.
ana
.
.(ana, .(tênis, .(pedro, []) ) )
.
tênis
pedro
[]

Listas
?- Lista1 = [a,b,c], Lista2 = .(a,.(b,.(c,[]))).
Lista1 = [a, b, c]
Lista2 = [a, b, c]
?- Hobbies1 = .(tênis, .(música,[])), Hobbies2 = [esqui,
comida], L = [ana,Hobbies1,pedro,Hobbies2].
Hobbies1 = [tênis,música]
Hobbies2 = [esqui,comida]
L = [ana, [tênis,música], pedro, [esqui,comida]]

Listas
Para entender a representação de listas do
Prolog, é necessário considerar dois casos:
Lista vazia [].
E lista não vazia, onde:
O primeiro item é chamado de cabeça (head) da lista.
A parte restante da lista é chamada cauda (tail).
No exemplo [ana, tênis, pedro]:
ana é a Cabeça da lista.
[
tênis, pedro] é a Cauda da lista.

Listas
Em geral, é comum tratar a cauda como um objeto simples.
Por exemplo, L = [a,b,c] pode ser escrito como:
Cauda = [b,c]
L = [a, Cauda]
O Prolog também fornece uma notação alternativa para
separar a cabeça da cauda de uma lista, a barra vertical:
L = [a | Cauda]

Operações em Listas - Busca
Frequentemente existe a necessidade de se
realizar operações em listas, por exemplo,
buscar um elemento que faz parte de uma
lista.
Para verificar se um nome está na lista, é
preciso verificar se ele está na cabeça ou se
ele está na cauda da listaƒ.

Operações em Listas - Busca
A primeira regra para verificar se um elemento X pertence à
lista é verificar se ele se encontra na cabeça da lista.
Isto pode ser especificado da seguinte maneira:
pertence(X,[X|Z]).
A segunda condição deve verificar se o elemento X
pertence à cauda da lista. Esta regra pode ser
especificada da seguinte maneira:
pertence(X,[W|Z]) :- pertence(X,Z).

Operações em Listas - Busca
O programa para buscar por um item em uma lista
pode ser escrito da seguinte maneira:
pertence(Elemento,[Elemento|Cauda]).ƒ
pertence(Elemento,[Cabeca|Cauda]) :- pertence(Elemento,Cauda).
Após a definição do programa, é possível interrogá-lo.
?
- pertence(a,[a,b,c]).
true

Operações em Listas - Busca
?- pertence(d,[a,b,c]).
false
?- pertence(X,[a,b,c]).
X = a ;
X = b ;
X = c ;
false
E se as perguntas forem:
?
?
- pertence(a,X).
- pertence(X,Y).
Existem infinitas respostas.

Operações em Listas – Último Elemento
O último elemento de uma lista que tenha somente um
elemento é o próprio elemento:
ultimo(Elemento, [Elemento]).
O último elemento de uma lista que tenha mais de um
elemento é o ultimo elemento da cauda:
ultimo(Elemento, [Cabeca|Cauda]) :- ultimo(Elemento, Cauda).
Programa completo:
ultimo(Elemento, [Elemento]).
ultimo(Elemento, [Cabeca|Cauda]) :- ultimo(Elemento, Cauda).

Exemplo: Macaco e as Bananas
move(
estado(no_centro, acima_caixa, no_centro, não_tem),
pegar_banana,
estado(no_centro,acima_caixa,no_centro,tem)
).
move(
estado(P,no_chão,P,Banana),
subir,
estado(P,acima_caixa,P,Banana)
)
.
move(
estado(P1,no_chão,P1,Banana),
empurrar(P1,P2),
estado(P2,no_chão,P2,Banana)
)
.
move(
estado(P1,no_chão,Caixa,Banana),
caminhar(P1,P2),
estado(P2,no_chão,Caixa,Banana)
)
.
consegue(estado(_,_,_,tem),[]).
consegue(Estado1,[Movimento|Resto]) :- move(Estado1,Movimento,Estado2), consegue(Estado2,Resto).

Adicionando Novos Fatos a Base de Conhecimento
O predicado assert é utilizado pelo Prolog
para adicionar novas sentenças na base de
conhecimento.
Exemplos:
assert(homem(joao)).
assert(filho(Y,X) :- progenitor(X,Y)).

Adicionando Novos Fatos a Base de Conhecimento
O predicado assert permite adicionar fatos e regras a base
de conhecimento.
Normalmente, o SWI-Prolog compila o código de forma que
não é possível modificar fatos durante a execução do
programa.
Para indicar ao Prolog que determinada sentença pode ser
modificado durante a execução do programa é possível
utilizar o predicado dynamic.
Exemplo:
:- dynamic homem/1.

Removendo Fatos da Base de Conhecimento
Também é possível remover fatos e regras
da base de conhecimento utilizando o
predicado retractall.
Funciona de forma similar ao assert.
Exemplos:
retract(homem(joao)).
retract(filho(Y,X) :- progenitor(X,Y)).
Predicados do SWI-Prolog
O SWI-Prolog inclui diversos predefinidas
para para diversos usos, como por exemplo:
Manipulação de listas;
Comparação de tipos de dados;
Leitura e escrita de dados em arquivos;
Entrada e saída de dados pelo console;
Manipulação de arquivos;
Execução de comandos no sistema operacional;
Entre outros.
http://www.swi-prolog.org/pldoc/refman/
