
INF 1771 – Inteligência Artificial
Aula 03 – Resolução de Problemas por
Meio de Busca
Edirlei Soares de Lima
<elima@inf.puc-rio.br>
Introdução
Agentes Autônomos:
Entidades autônomas capazes de observar o
ambiente e agir de forma a atingir determinado
objetivo.
Tipos de Agentes:
Agentes reativos simples;
Agentes reativos baseado em modelo;
Agentes baseados em objetivos;
Agentes baseados na utilidade;
Agentes baseados em aprendizado;
Problema de Busca
Bucharest
Timisoara
Arad
Sibiu
Zerind
Problema de Busca

Definição do Problema
A definição do problema é a primeira e
mais importante etapa do processo de
resolução de problemas de inteligência
artificial por meio de buscas.
Consiste em analisar o espaço de
possibilidades de resolução do problema,
encontrar sequências de ações que levem a
um objetivo desejado.

Definição de um Problema
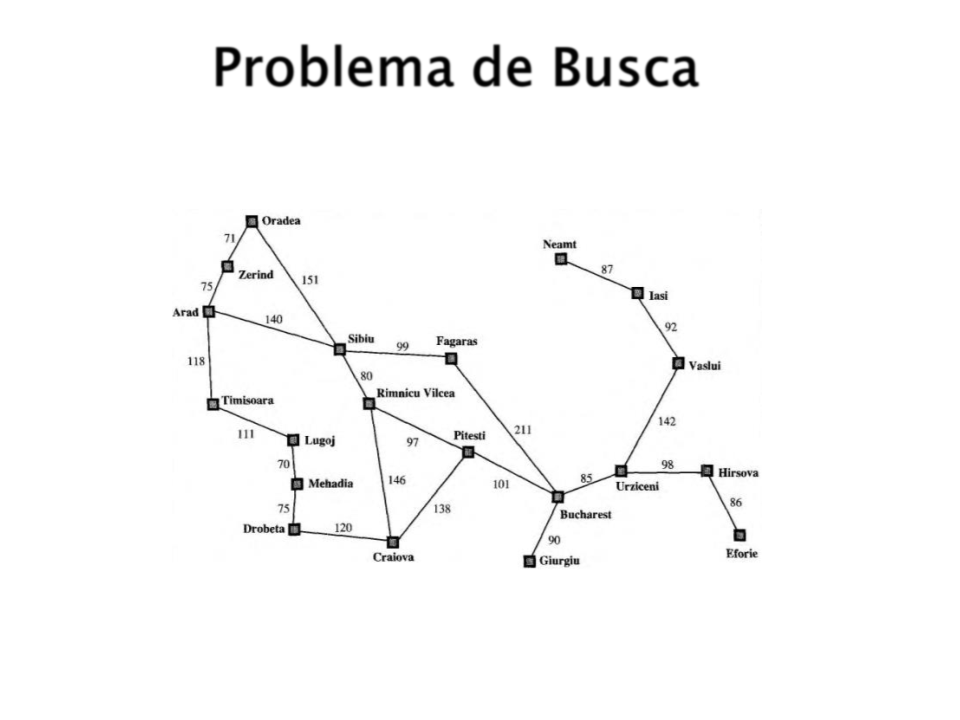
Estado Inicial: Estado inicial do agente.
Ex: Em(Arad)
Estado Final: Estado buscado pelo agente.
Ex: Em(Bucharest)
Ações Possíveis: Conjunto de ações que o agente pode executar.
Ex: Ir(Cidade, PróximaCidade)
Espaço de Estados: Conjunto de estados que podem ser atingidos
a partir do estado inicial.
Ex: Mapa da Romênia.
Custo: Custo numérico de cada caminho.
Ex: Distância em KM entre as cidades.

Considerações em Relação ao Ambiente
Estático:
O Ambiente não pode mudar enquanto o agente está realizando a
resolução do problema.
Observável:
O estado inicial do ambiente precisa ser conhecido previamente.
Determinístico:
O próximo estado do agente deve ser determinado pelo estado atual +
ação. A execução da ação não pode falhar.
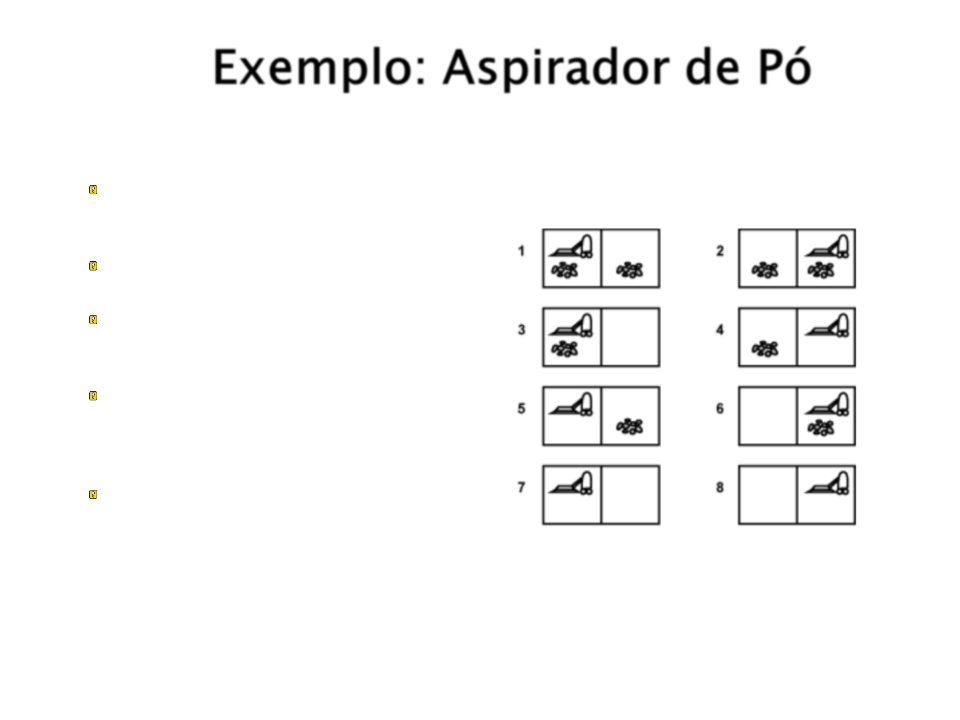
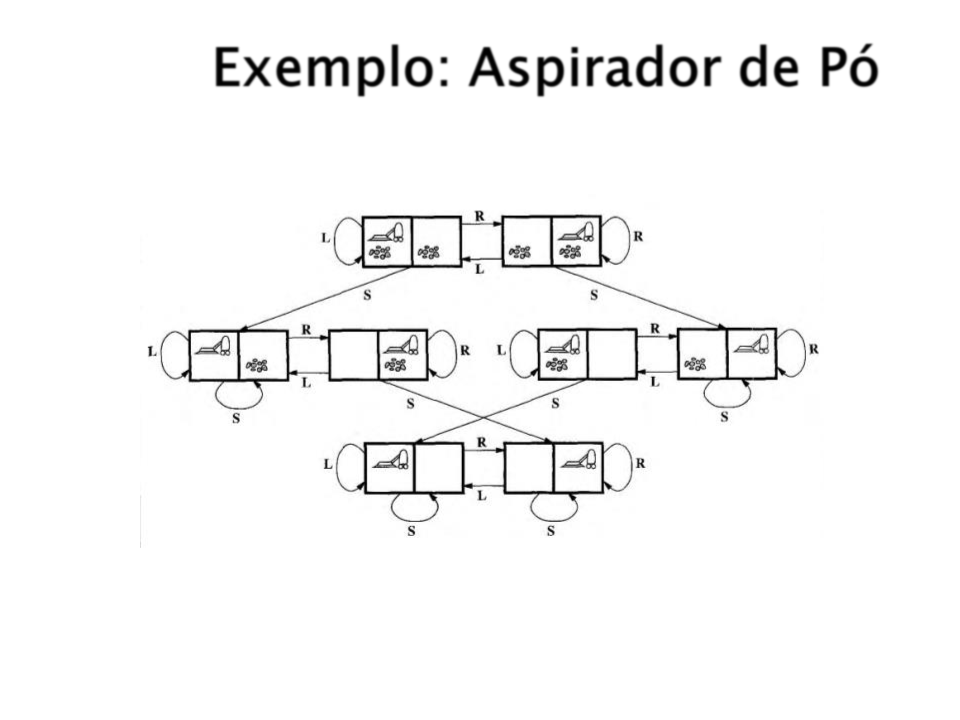
Exemplo: Aspirador de Pó
Espaço de Estados: 8 estados
possíveis (figura ao lado);
Estado Inicial: Qualquer estado;
Estado Final: Estado 7 ou 8 (ambos
quadrados limpos);
Ações Possíveis: Mover para
direita, mover para esquerda e
limpar;
Custo: Cada passo tem o custo 1,
assim o custo do caminho é definido
pelo numero de passos;
Exemplo: Aspirador de Pó
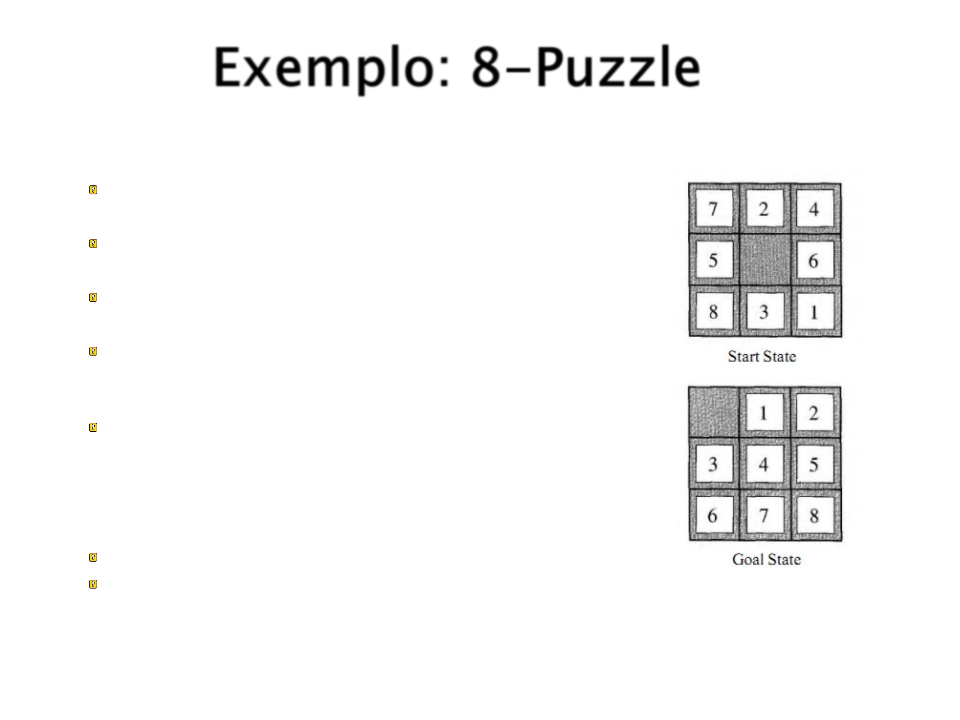
Exemplo: 8-Puzzle
Espaço de Estados: 181.440 possíveis estados;
Estado Inicial: Qualquer estado;
Estado Final: Figura ao lado – Goal State;
Ações Possíveis: Mover o quadrado vazio para
direita, para esquerda, para cima ou para baixo;
Custo: Cada passo tem o custo 1, assim o custo do
caminho é definido pelo numero de passos;
1
2
5-puzzle (4x4) – 1.3 trilhões estados possíveis.
4-puzzle (5x5) – 10²⁵ estados possíveis.

Exemplo: Xadrez
4
0
Espaço de Estados: Aproximadamente 10
possíveis estados (Claude Shannon, 1950);
Estado Inicial: Posição inicial de um jogo de
xadrez;
Estado Final: Qualquer estado onde o rei adversário
está sendo atacado e o adversário não possui
movimentos válidos;
Ações Possíveis: Regras de movimentação de cada
peça do xadrez;
Custo: Quantidade de posições examinadas;

Exemplo: 8 Rainhas (Incremental)
Espaço de Estados: Qualquer disposição de 0 a 8
rainhas no tabuleiro (1.8 x 10¹⁴ possíveis estados);
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8 rainhas
estão no tabuleiro e nenhuma esta sendo atacada;
Ações Possíveis: Colocar uma rainha em um
espaço vaio do tabuleiro;
Custo: Não importa nesse caso;
*
O jogo possui apenas 92 possíveis soluções (considerando
diferentes rotações e reflexões). E apenas 12 soluções únicas.

Exemplo: 8 Rainhas (Estados Completos)
Espaço de Estados: Tabuleiro com n rainhas, uma
por coluna, nas n colunas mais a esquerda sem que
nenhuma rainha ataque outra (2057 possíveis
estados);
Estado Inicial: Nenhuma rainha no tabuleiro;
Estado Final: Qualquer estado onde as 8 rainhas
estão no tabuleiro e nenhuma esta sendo atacada;
Ações Possíveis: Adicionar uma rainha em
qualquer casa na coluna vazia mais à esquerda de
forma que não possa ser atacada;
Custo: Não importa nesse caso;
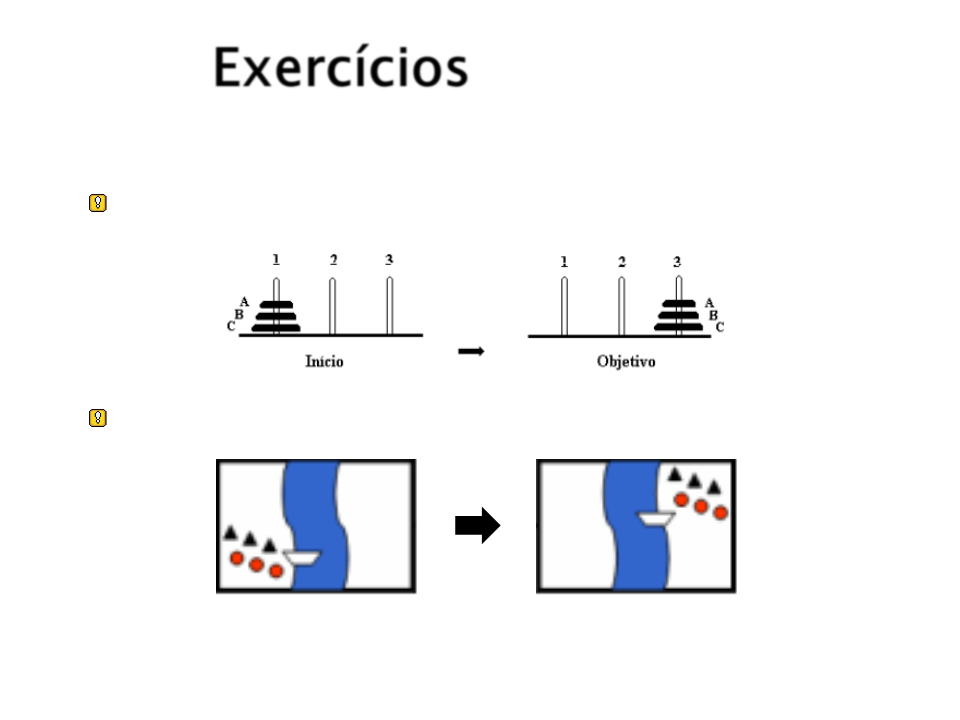
Exercícios
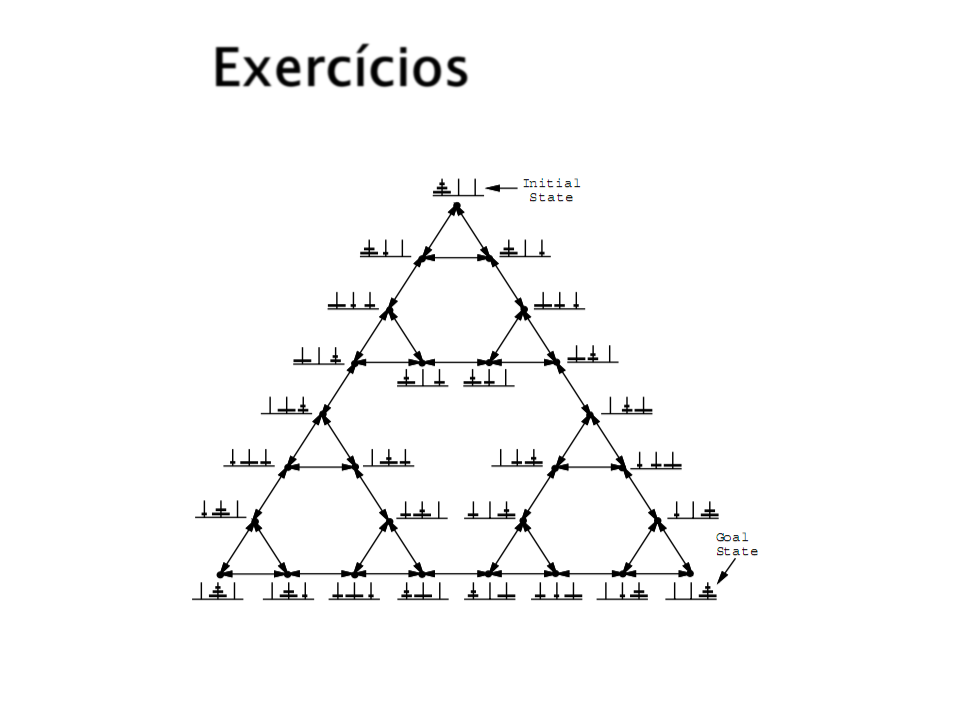
Torre de Hanói?
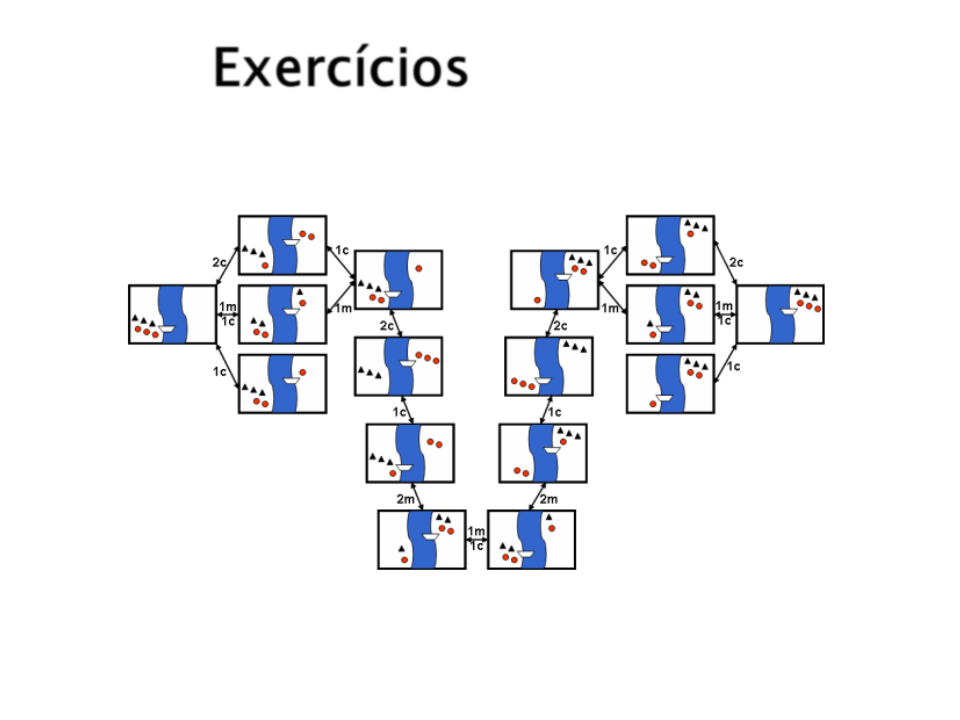
Canibais e Missionários?
Exercícios
Torre de Hanói:
Espaço de Estados: Todas as possíveis configurações de
argolas em todos os pinos (27 possíveis estados).
Ações Possíveis: Mover a primeira argola de qualquer pino
para o pino da direita ou da esquerda.
Custo: Cada movimento tem 1 de custo.
Canibais e Missionários:
Espaço de Estados: Todas as possíveis configurações validas
de canibais e missionários em cada lado do rio (16 possíveis
estados).
Ações Possíveis: Mover 1 ou 2 personagens (canibais ou
missionários) para o outro lado do rio. O número de canibais em
um determinado lado do rio não pode ser maior do que o
número de missionários.
Custo: Cada movimento tem 1 de custo.
Exercícios
Exercícios

Aplicações em Problemas Reais
Cálculo de Rotas:
Planejamento de rotas de aviões;
Sistemas de planejamento de viagens;
Caixeiro viajante;
Rotas em redes de computadores;
Jogos de computadores (rotas dos personagens);
Alocação
Salas de aula;
Máquinas industriais;

Aplicações em Problemas Reais
Circuitos Eletrônicos:
Posicionamento de componentes;
Rotas de circuitos;
Robótica:
Navegação e busca de rotas em ambientes reais;
Montagem de objetos por robôs;

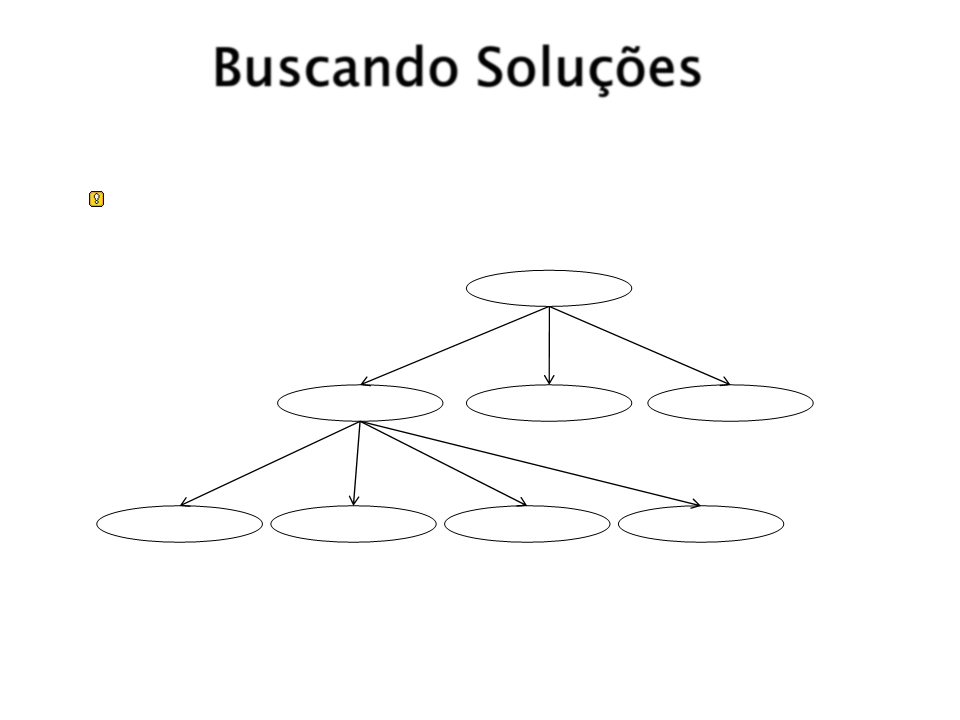
Como Encontrar a Solução?
Uma vez o problema bem formulado, o estado final
(
objetivo) deve ser “buscado” no espaço de estados.
A busca é representada em uma árvore de busca:
Raiz: corresponde ao estado inicial;
Expande-se o estado corrente, gerando um novo conjunto de
sucessores;
Escolhe-se o próximo estado a expandir seguindo uma
estratégia de busca;
Prossegue-se até chegar ao estado final (solução) ou falhar na
busca pela solução;
Buscando Soluções
Exemplo: Ir de Arad para Bucharest
Arad
Sibiu
Timissoara
Fagaras
Zerind
Arad
Orades
Rimnico Vilcea
Buscando Soluções
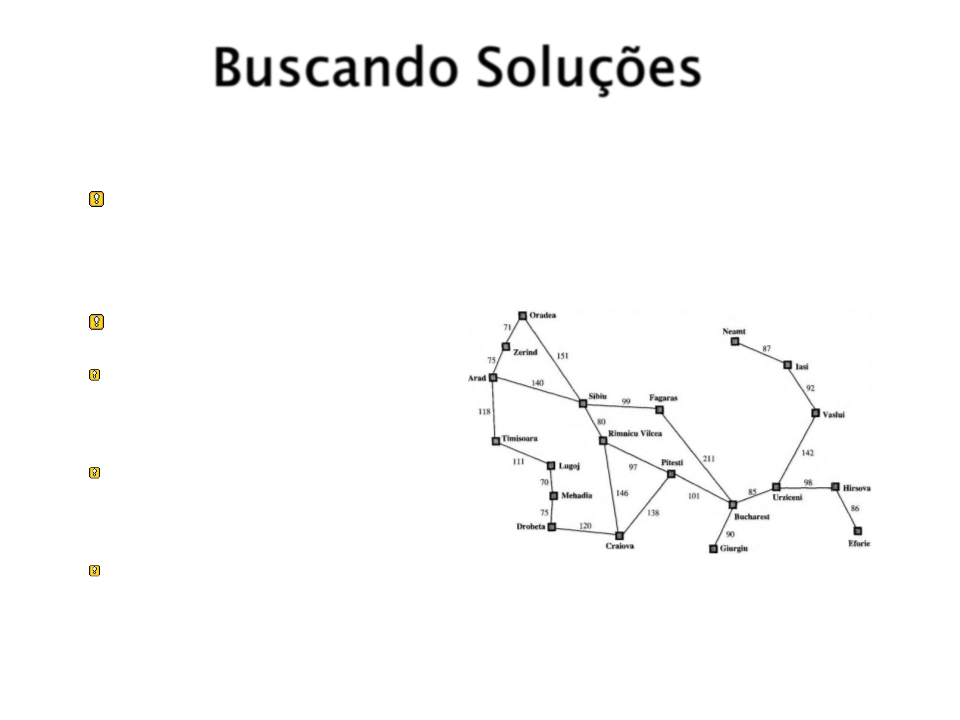
O espaço de estados é diferente da árvore
de buscas.
Exemplo:
2
0 estados no espaço de
espaços;
Número de caminhos
infinito;
Árvore com infinitos nós;

Código Descritivo – Busca em Árvore
Função BuscaEmArvore(Problema, Estratégia) retorna solução ou falha
Inicio
Inicializa a arvore usando o estado inicial do Problema
loop do
se não existem candidatos para serem expandidos então
retorna falha
Escolhe um nó folha para ser expandido de acordo com
a Estratégia
se Se o nó possuir o estado final então
retorna solução correspondente
se não
expande o nó e adiciona os nós resultantes a
arvore de busca
Fim

Pseudocódigo – Busca em Árvore
Função BuscaEmArvore(Problema, fronteira) retorna solução ou falha
Inicio
fronteira ← InsereNaFila(FazNó(Problema[EstadoInicial]), fronteira)
loop do
se FilaVazia(fronteira) então
retorna falha
nó ← RemovePrimeiro(fronteira)
se nó[Estado] for igual a Problema[EstadoFinal] então
retorna Solução(nó)
fronteira ← InsereNaFila(ExpandeFronteira(nó, Problema), fronteira)
Fim
-
-
A função Solução retorna a sequência de nós necessários para retornar a
raiz da arvore.
Considera-se fronteira uma estrutura do tipo fila.

Medida de Desempenho
Desempenho do Algoritmo:
(1) O algoritmo encontrou alguma solução?
(
2) É uma boa solução?
Custo de caminho (qualidade da solução).
(
3) É uma solução computacionalmente barata?
Custo da busca (tempo e memória).
Custo Total
Custo do Caminho + Custo de Busca.

Métodos de Busca
Busca Cega ou Exaustiva:
Não sabe qual o melhor nó da fronteira a ser
expandido. Apenas distingue o estado objetivo dos
não objetivos.
Busca Heurística:
Estima qual o melhor nó da fronteira a ser
expandido com base em funções heurísticas.
Busca Local:
Operam em um único estado e movem-se para a
vizinhança deste estado.

Busca Cega
Algoritmos de Busca Cega:
Busca em largura;
Busca de custo uniforme;
Busca em profundidade;
Busca com aprofundamento iterativo;
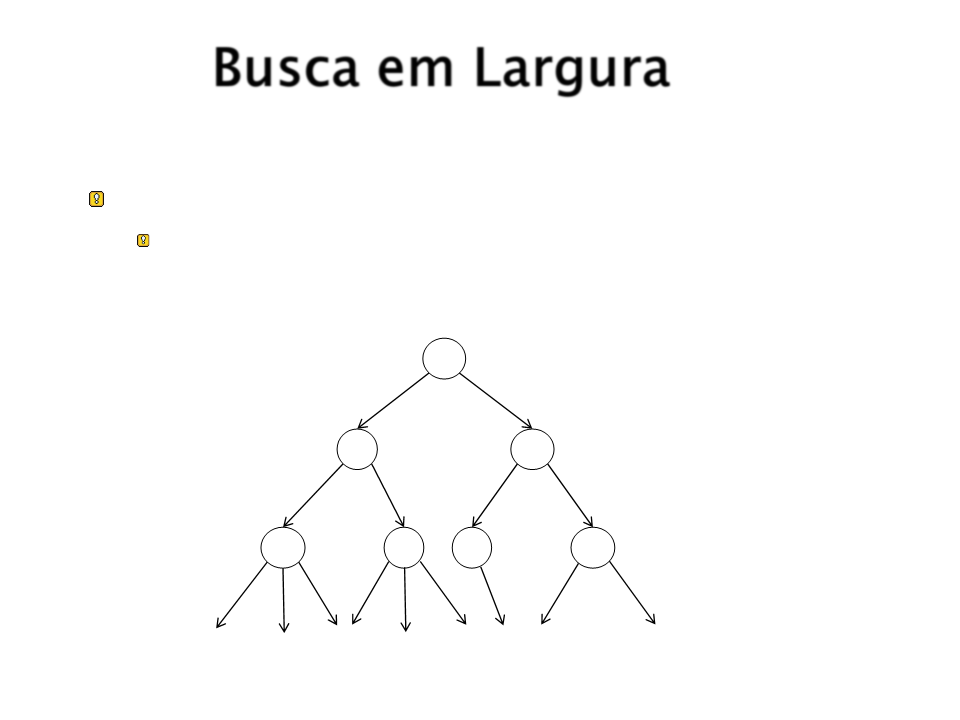
Busca em Largura
Estratégia:
O nó raiz é expandido, em seguida todos os nós
sucessores são expandidos, então todos próximos
nós sucessores são expandidos, e assim em diante.
A
B
C
D
E
F
G

Busca em Largura
Pode ser implementado com base no pseudocódigo da
função “BuscaEmArvore” apresentado anteriormente.
Utiliza-se uma estrutura de fila (first-in-first-out) para
armazenar os nós das fronteira.
d +1
Complexidade: O(b )
Profundidade (d)
Nós
Tempo
0.11 ms
11 ms
Memória
107 KB
10.6 MB
1 GB
2
4
6
8
1100
111,100
107
1.1 seg
2 min
109
103 GB
10 TB
1
1
1
0
2
4
1011
1013
1015
3 horas
13 dias
3.5 anos
1 PB
99 PB
*
Considerando o numero de folhas b = 10 e cada nó ocupando 1KB de memória
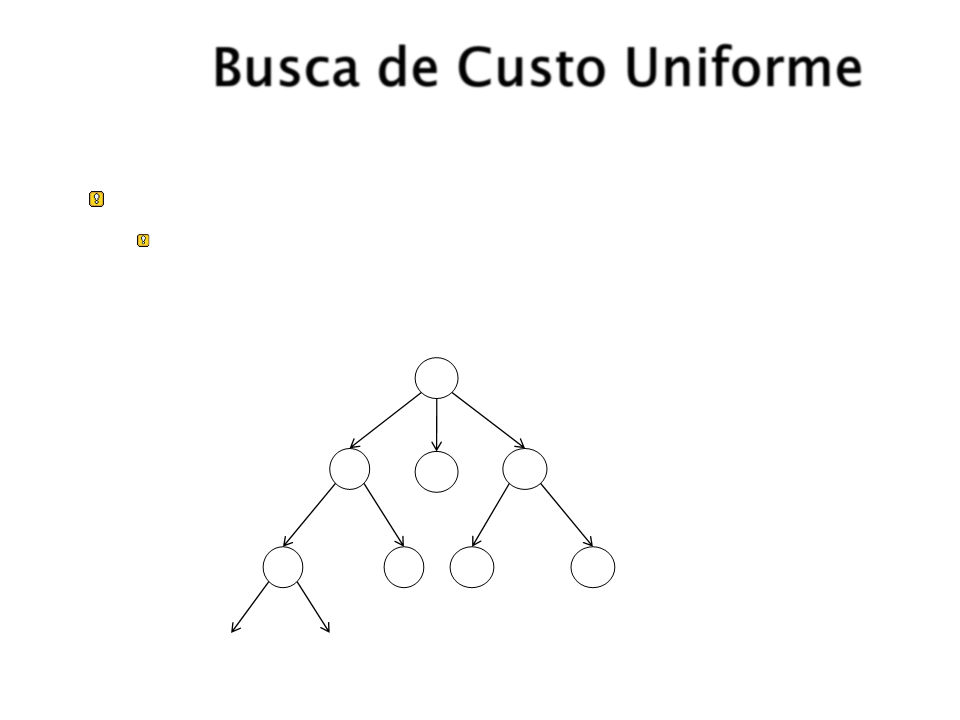
Busca de Custo Uniforme
Estratégia:
Expande sempre o nó de menor custo de caminho.
Se o custo de todos os passos for o mesmo, o
algoritmo acaba sendo o mesmo que a busca em
largura.
A
7
5
118
1
70
B
D
C
7
5
7
1
111
H
9
9
E
F
G

Busca de Custo Uniforme
A primeira solução encontrada é a solução ótima se
custo do caminho sempre aumentar ao logo do
caminho, ou seja, não existirem operadores com custo
negativo.
Implementação semelhante a busca em largura.
Adiciona-se uma condição de seleção dos nós a
serem expandidos.
1+(C / )
Complexidade: O(b
)
Onde:
C = custo da solução ótima;
α = custo mínimo de uma ação;
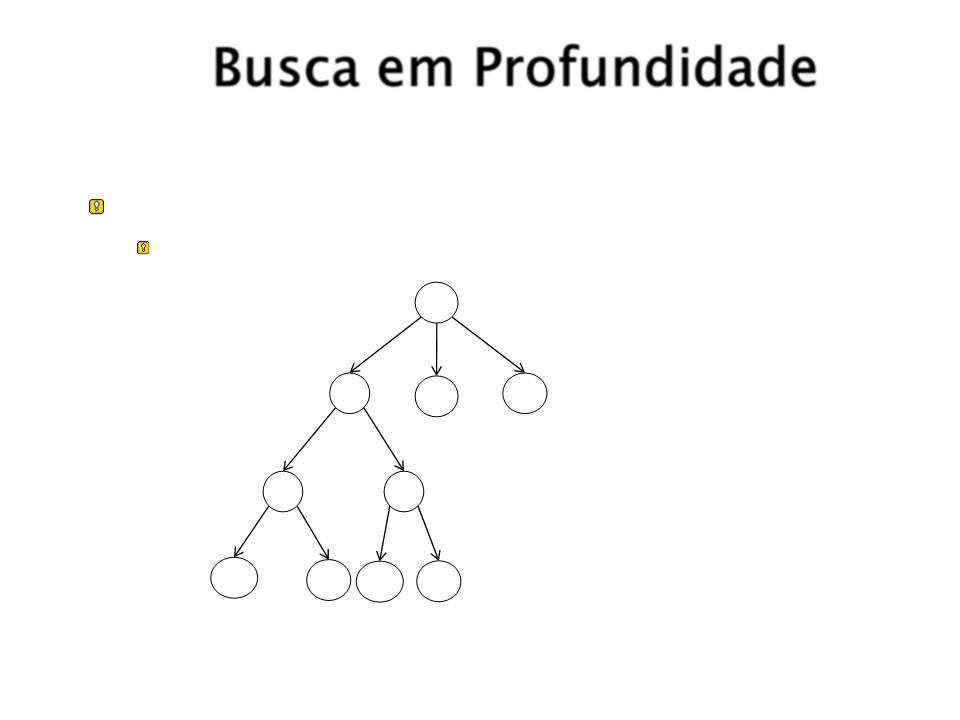
Busca em Profundidade
Estratégia:
Expande os nós da vizinhança até o nó mais
profundo.
A
B
D
C
E
F
M
N
P
Q

Busca em Profundidade
Pode ser implementado com base no pseudocódigo da
função “BuscaEmArvore” apresentado anteriormente.
Utiliza-se uma estrutura de pilha (last-in-first-out)
para armazenar os nós das fronteira.
Pode também ser implementado de forma recursiva.
Consome pouca memória, apenas o caminho de nós
sendo analisados precisa armazenado. Caminhos que
já foram explorados podem ser descartados da
memória.

Busca em Profundidade
Uso de memória pela busca em largura em uma
arvore com 12 de profundidade: 1000 TB.
Uso de memória pela busca em profundidade em
uma arvore com 12 de profundidade: 118 KB.
Problema: O algoritmo pode fazer uma busca muito
longa mesmo quando a resposta do problema esta
localizado a poucos nós da raiz da árvore.
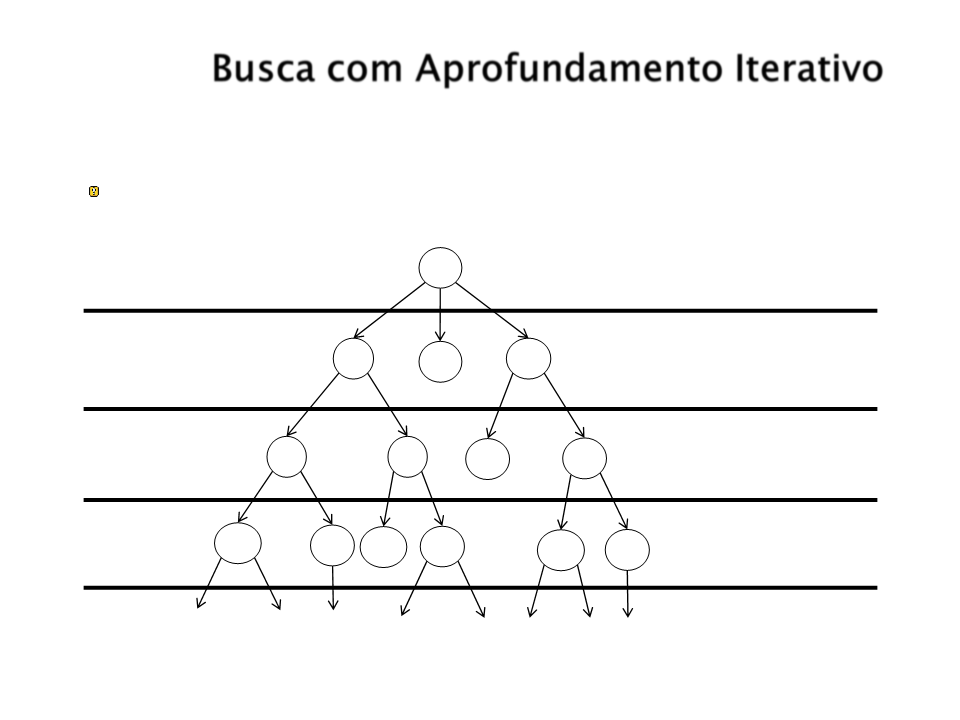
Busca com Aprofundamento Iterativo
Estratégia: Consiste em uma busca em profundidade onde o limite
de profundidade é incrementado gradualmente.
A
Limit 0
Limit 1
B
D
C
E
F
H
G
Limit 2
Limit 3
M
N
P
Q
P
Q

Busca com Aprofundamento Iterativo
Combina os benefícios da busca em largura com os
benefícios da busca em profundidade.
Evita o problema de caminhos muito longos ou
infinitos.
A repetição da expansão de estados não é tão ruim,
pois a maior parte dos estados está nos níveis mais
baixos.
‰Cria menos estados que a busca em largura e
consome menos memória.
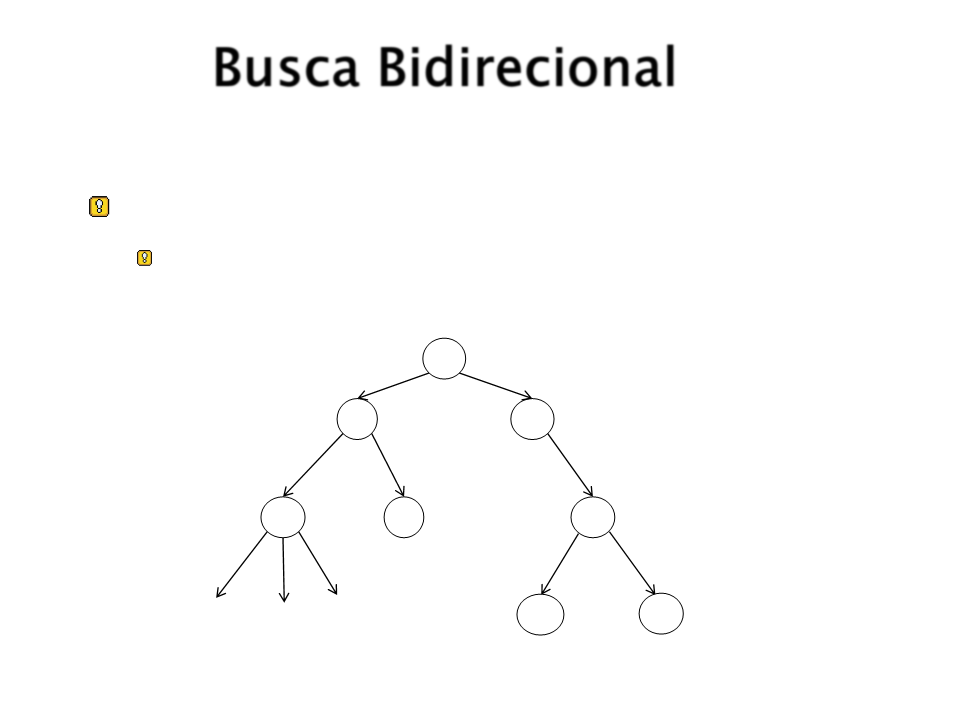
Busca Bidirecional
Estratégia:
A busca se inicia ao mesmo tempo a partir
do estado inicial e do estado final.
A
B
C
D
E
G
M
N

Comparação dos Metodos de Busca Cega
Criterio
Largura Uniforme Profundidade Aprofundamento
Iterativo
Bidirecional
Completo?
Ótimo?
Tempo
Sim ¹
Sim ¹,²
Não
Não
Sim ¹
Sim ³
Sim ¹, ⁴
Sim ³, ⁴
Sim ³
Sim
d +1
1+(C / )
m
d
d / 2
O(b ) O(b
)
)
O(b )
O(b )
O(b )
d +1
1+(C / )
d / 2
Espaço
O(b ) O(b
O(bd)
O(b )
O(bm)
b = fator de folhas por nó.
d = profundidade da solução mais profunda.
m = profundidade máxima da árvore.
¹
²
³
⁴
completo se b for finito.
completo se o custo de todos os passos for positivo.
ótimo se o custo de todos os passos for idêntico.
se ambas as direções usarem busca em largura.

Como evitar estados repetidos?
Estados repetidos sempre vão ocorrer em
problema onde os estados são reversíveis.
Como evitar?
Não retornar ao estado “pai”.
Não retorna a um ancestral.
Não gerar qualquer estado que já tenha sido criado
antes (em qualquer ramo).
Requer que todos os estados gerados permaneçam na
memória.

Busca Heurística
Algoritmos de Busca Heurística:
Busca Gulosa
A*
A busca heurística leva em conta o objetivo
para decidir qual caminho escolher.
Conhecimento extra sobre o problema é
utilizado para guiar o processo de busca.

Busca Heurística
Como encontrar um barco perdido?
Busca Cega -> Procura no oceano inteiro.
Buca Heurística -> Procura utilizando
informações relativas ao problema. Ex: correntes
marítimas, vento, etc.

Busca Heurística
Função Heurística (h)
Estima o custo do caminho mais barato do
estado atual até o estado final mais
próximo.
São específicas para cada problema.
Exemplo:
Encontrar a rota mais curta entre duas
cidades:
h(n) = distância em linha reta direta entre o nó
n e o nó final.

Busca Gulosa
Estratégia:
Expande os nós que se encontram mais próximos
do objetivo (uma linha reta conectando os dois
pontos no caso de distancias), desta maneira é
provável que a busca encontre uma solução
rapidamente.
A implementação do algoritmo se assemelha ao
utilizado na busca cega, entre tanto utiliza-se uma
função heurística para decidir qual o nó deve ser
expandido.
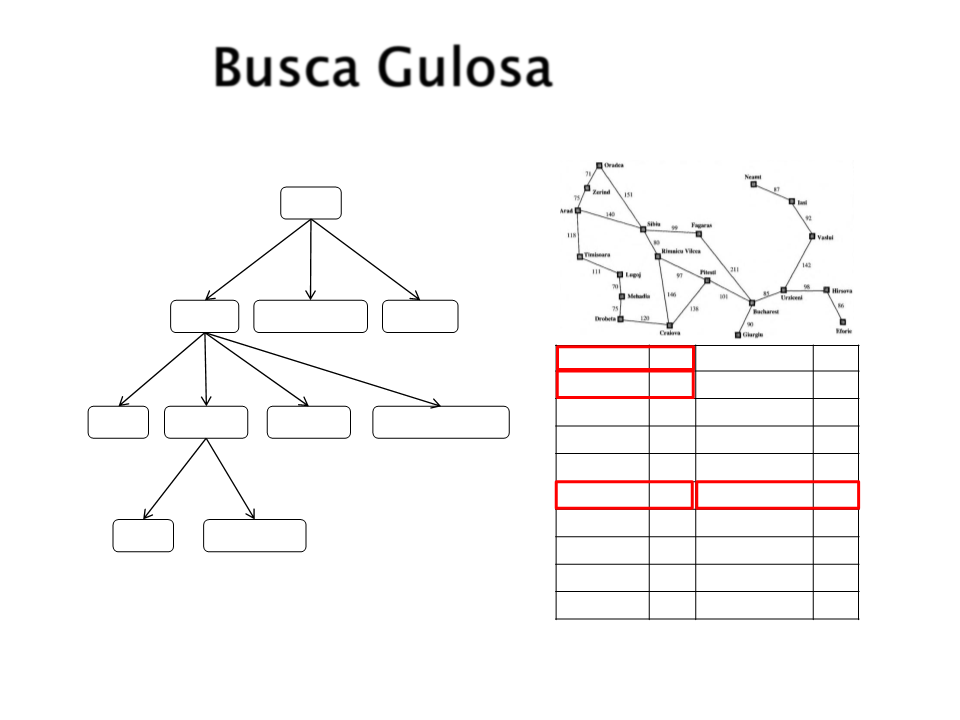
Busca Gulosa
Arad
366
Sibiu
53
Timissoara
329
Zerind
374
2
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
160
242
161
Arad
66
Fagaras
176
Oradea
380
Rimnicu Vilcea
193
3
Rimnicu Vilcea 193
Fagaras
Giurgiu
Iasi
176
77
Sibiu
253
329
199
374
80
Timisoara
Vaslui
Sibiu
63
Bucharest
0
226
244
151
2
Lugoj
Zerind
Urziceni
Hirsova
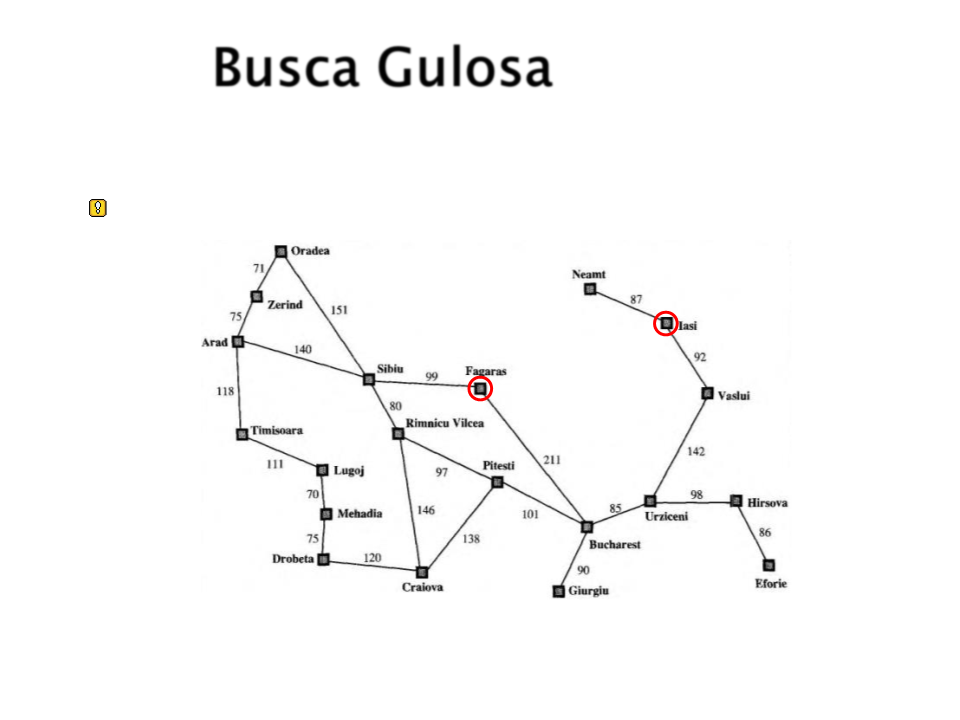
Busca Gulosa
Ir de Iasi para Fagaras?

A*
Estratégia:
Combina o custo do caminho g(n) com o valor da
heurística h(n)
g(n) = custo do caminho do nó inicial até o nó n
h(n) = valor da heurística do nó n até um nó
objetivo (distancia em linha reta no caso de
distancias espaciais)
f(n) = g(n) + h(n)
É a técnica de busca mais utilizada.
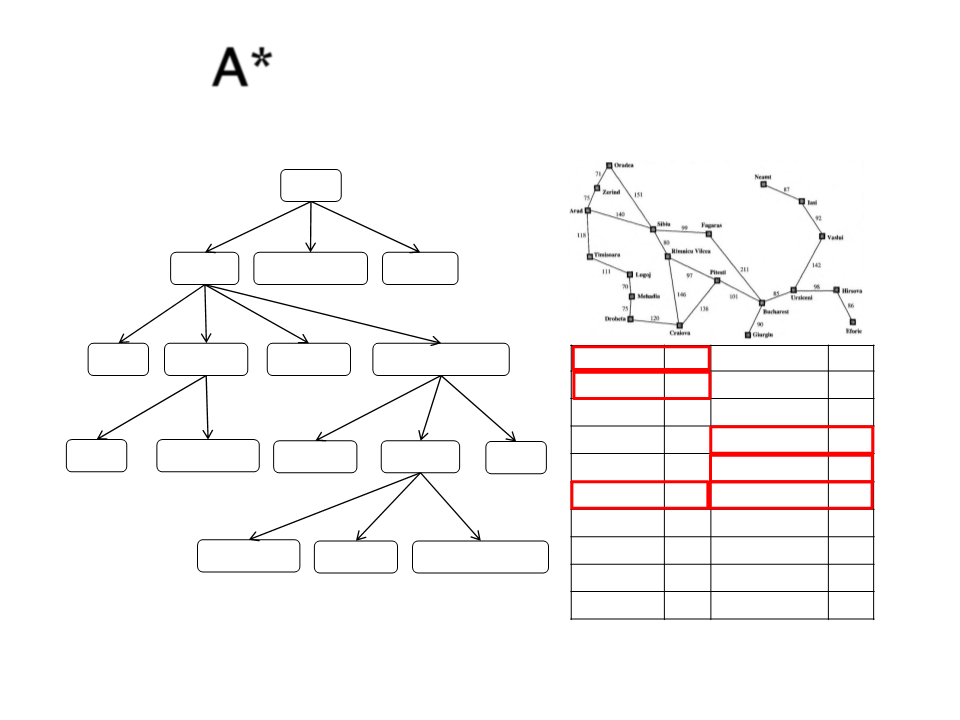
A*
Arad
0+366=366
Sibiu
Timissoara
Zerind
1
40+253=393 118+329=447 75+374=449
Arad
80+366=646 239+176=415 291+380=671
Fagaras
Oradea
Rimnicu Vilcea
220+193=413
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
2
Bucharest
Craiova
Drobeta
Eforie
160
242
161
Sibiu
38+253=591
Bucharest
450+0=450
Craiova
366+160=526 317+100=417 300+253=553
Pitesti
Sibiu
Rimnicu Vilcea 193
3
Fagaras
Giurgiu
Iasi
176
77
Sibiu
253
329
199
374
80
Timisoara
Vaslui
226
244
151
Bucharest
418+0=418
Craiova
455+160=615
Rimnicu Vilcea
414+193=607
Lugoj
Zerind
Urziceni
Hirsova

A*
A estratégia é completa e ótima.
Custo de tempo:
Exponencial com o comprimento da solução, porém boas
funções heurísticas diminuem significativamente esse custo.
d
O(b )
Custo memória:
Guarda todos os nós expandidos na memória.
Nenhum outro algoritmo ótimo garante expandir
menos nós.
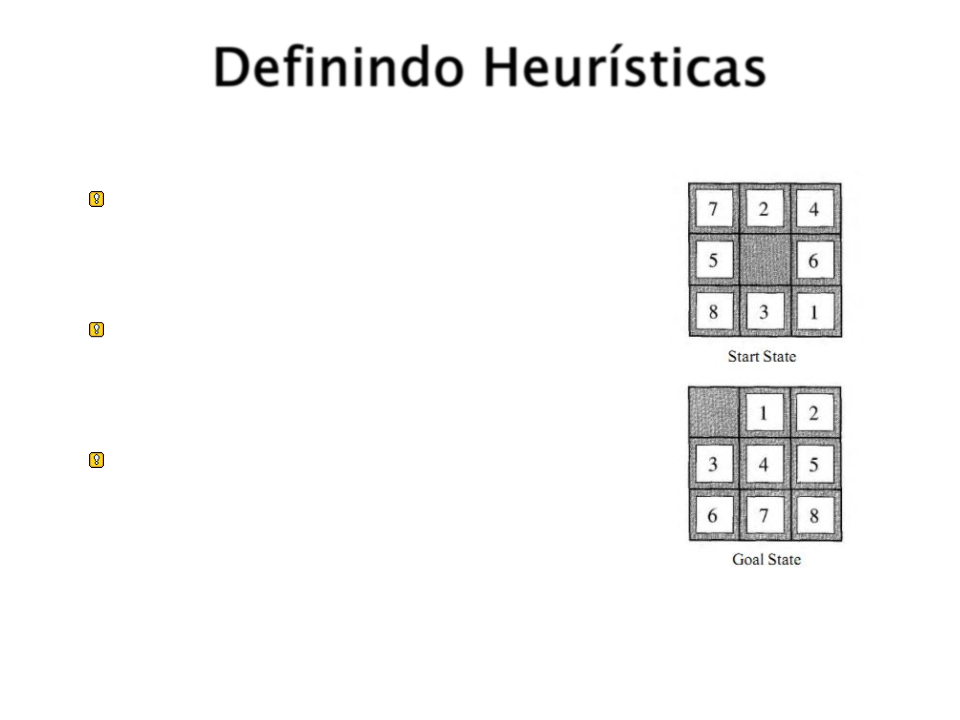
Definindo Heurísticas
Cada problema exige uma
função heurística diferente.
Não se deve superestimar o
custo real da solução.
Como escolher uma boa função
heurística para o jogo 8-Puzzle?
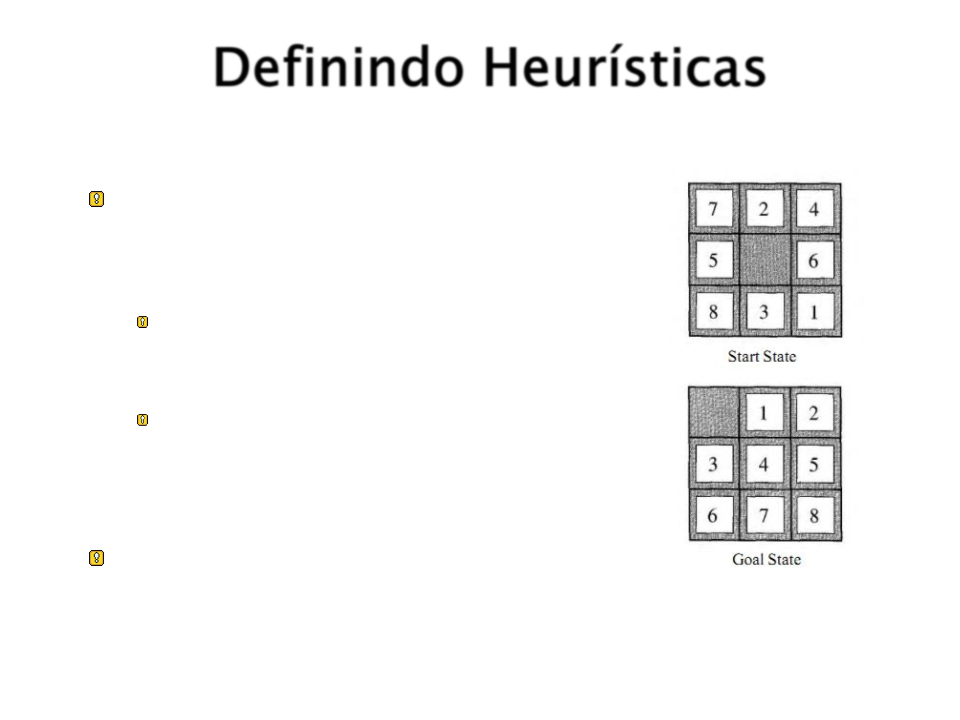
Definindo Heurísticas
Como escolher uma boa função
heurística para o jogo 8-Puzzle?
h¹ = número de elementos fora do
lugar.
h² = soma das distâncias de cada
número à sua posição final
(movimentação horizontal e vertical).
Qual das heurísticas é melhor?

Exemplo - A*
1
2 3 4 5
1
2
3
4
☺
X

Exemplo - A*
Qual é o espaço de estados?
Quais são as ações possíveis?
Qual será o custo das ações?

Exemplo - A*
Heurística do A*: f(n) = g(n) + h(n)
g(n) = custo do caminho
h(n) = função heurística
Qual seria a função heurística h(n)
mais adequada para este problema?
A distancia em linha reta é uma opção.
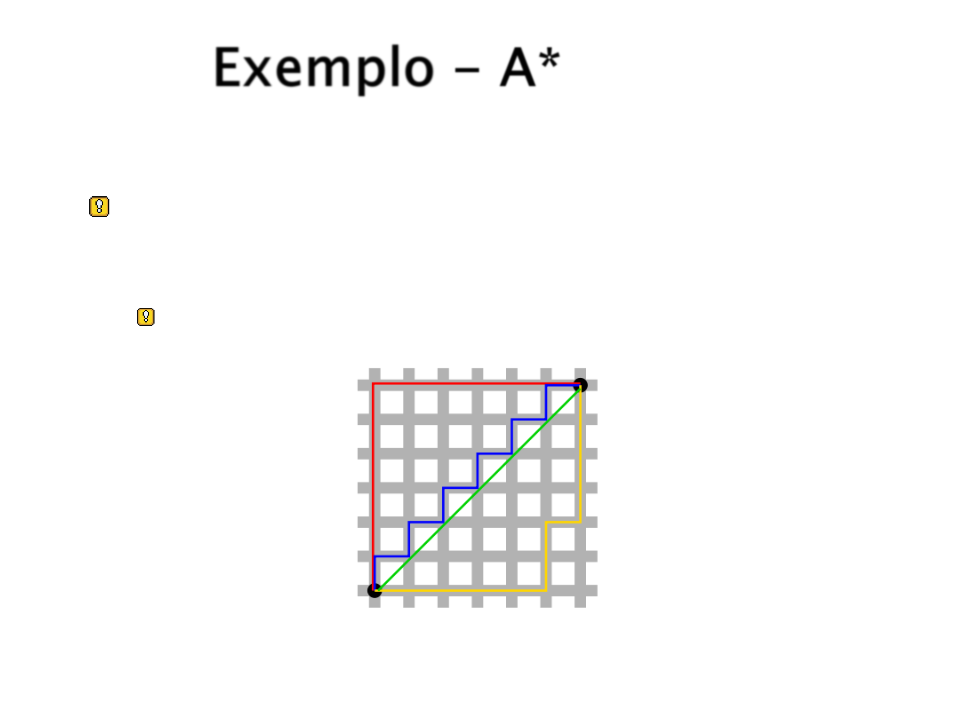
Exemplo - A*
Como calcular a heurística h(n)?
Distancia de Manhattan

Exemplo - A*
O próximo passo é gerar a árvore de
busca e expandir os nós que tiverem o
menor valor resultante da função
heurística f(n).
f(n) = g(n) + h(n)
Exemplo - A*
[
1,1]
[
2,1]
[
1,2]
[
[
1,2] = f(n) = ?? + ??
2,1] = f(n) = ?? + ??

Exemplo - A*
1
2 3 4 5
1
2
3
4
☺
X
Exemplo - A*
[
1,1]
[
2,1]
[
1,2]
[
1,1]
[2,2]
[
[
1,1] = f(n) = ?? + ??
2,2] = f(n) = ?? + ??

Exemplo - A*
1
2 3 4 5
1
2
3
4
☺
X

Busca Local
Em muitos problemas o caminho
para a solução é irrelevante.
Jogo das n-rainhas: o que importa é a
configuração final e não a ordem em que as
rainhas foram acrescentadas.
Outros exemplos:
Projeto de Circuitos eletronicos;
Layout de instalações industriais;
Escalonamento de salas de aula;
Otimização de redes;

Busca Local
Algoritmos de busca local operam sobre um
unico estado corrente, ao invés de vários
caminhos.
Em geral se movem apenas para os vizinhos
desse estado.
O caminho seguido pelo algoritmo não é
guardado.

Busca Local
Vantagens:
Ocupam pouquíssima memória (normalmente
constante).
Podem encontrar soluções razoáveis em grandes
ou infinitos espaços de estados.
São uteis para resolver problemas de
otimização.
Buscam por estados que atendam a uma função
objetivo.
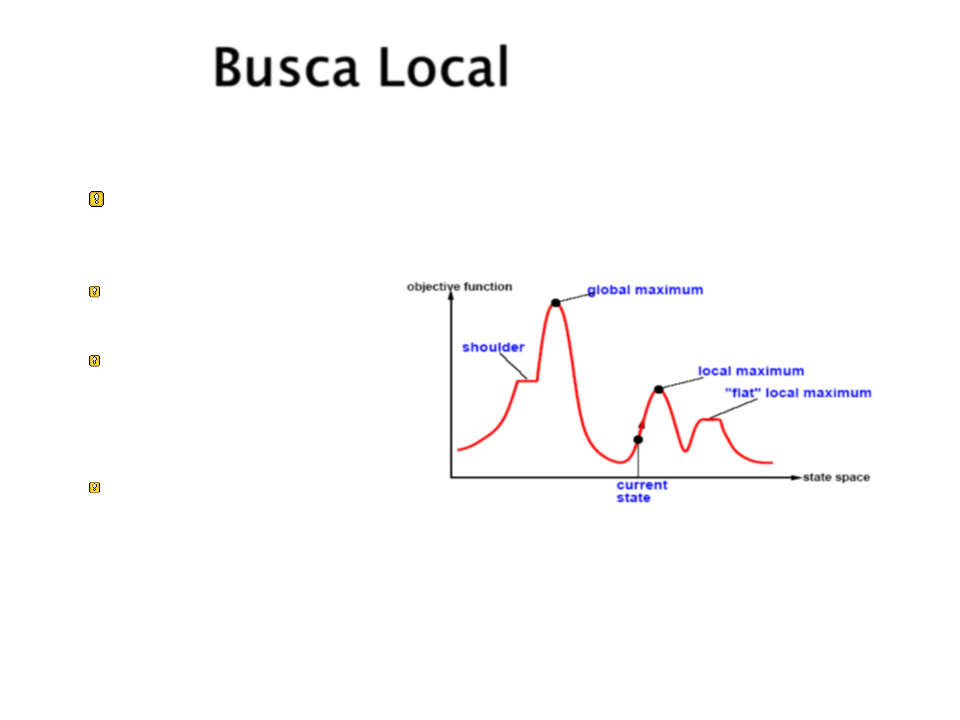
Busca Local
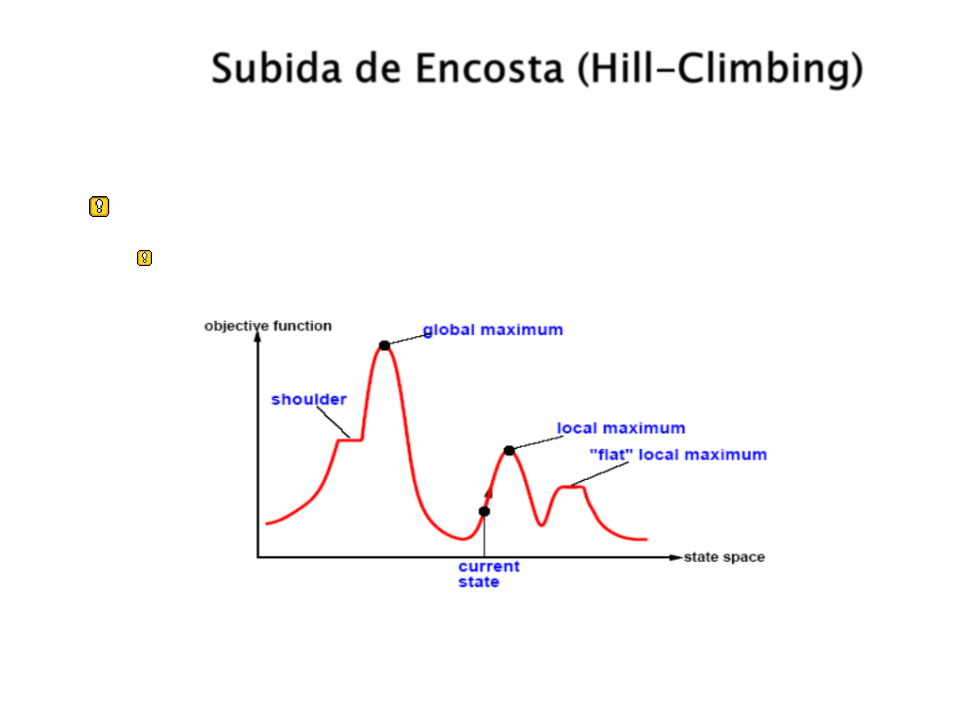
Panorama do Espaço de Estados:
Location = Estado;
Elevation = Valor de
custo da função
heurística;
Busca-se o maximo
ou minimo global;

Subida de Encosta (Hill-Climbing)
Estratégia:
Se move de forma contínua no sentido do valor
crescente da heurística;
Termina ao alcançar um pico em que nenhum vizinho
possui um valor mais alto;
Não mantém nenhuma árvore de busca, somente o
estado e o valor da função objetivo;
Não examina antecipadamente valores de estados além
de seus vizinhos imediatos;
“
meio a um denso nevoeiro e sofrendo de amnésia”.
É como tentar encontrar o topo do monte Everest em

Subida de Encosta (Hill-Climbing)
Processo:
Inicialize (aleatoriamente) o ponto x no espaço de estados do
problema.
A cada iteração, um novo ponto x’ é selecionado aplicando-se
uma pequena perturbação no ponto atual, ou seja,
selecionando-se um ponto x’ que esteja na vizinhança de x.
Se este novo ponto apresenta um melhor valor para a função de
avaliação, então o novo ponto torna-se o ponto atual.
O método é terminado quando nenhuma melhora significativa é
alcançada, um número fixo de iterações foi efetuado, ou um
objetivo foi atingido.

Pseudocódigo – Hill-Climbing
Função Hill-Climbing(Problema) retorna um estado que é o maximo local
Inicio
EstadoAtual ← FazNó(Problema[EstadoInicial])
loop do
Vizinho ← SucessorDeMaiorValor(EstadoAtual)
se Vizinho[Valor] for menor ou igual EstadoAtual[Valor] então
retorna EstadoAtual
EstadoAtual ← Vizinho
Fim
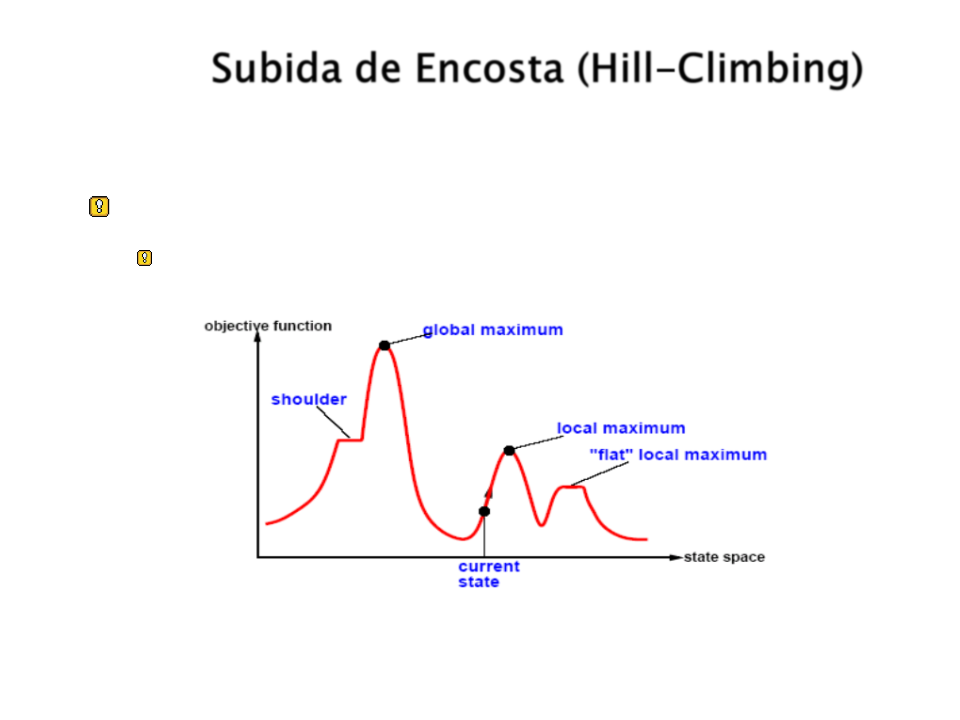
Subida de Encosta (Hill-Climbing)
Problemas:
Máximos Locais:
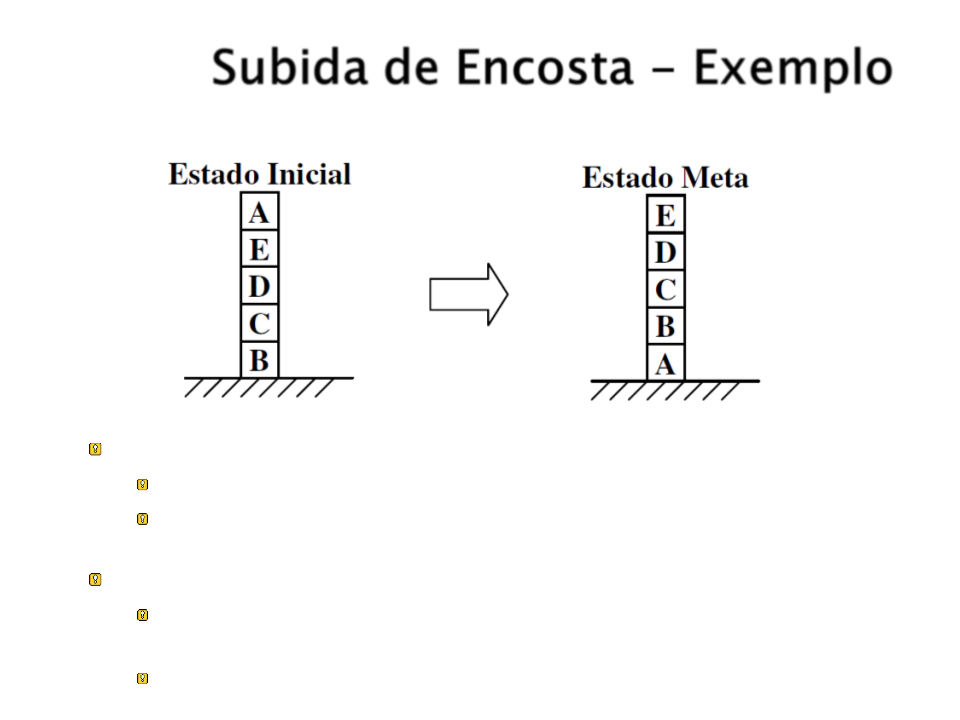
Subida de Encosta - Exemplo
Ações Possíveis:
Pegar um bloco e colocar ele sobre a mesa.
Pegar um bloco e colocar ele sobre outro bloco.
Heurística:
+
1 para cada bloco em cima do bloco onde ele deve
estar.
1 para cada bloco em cima do bloco errado.
-
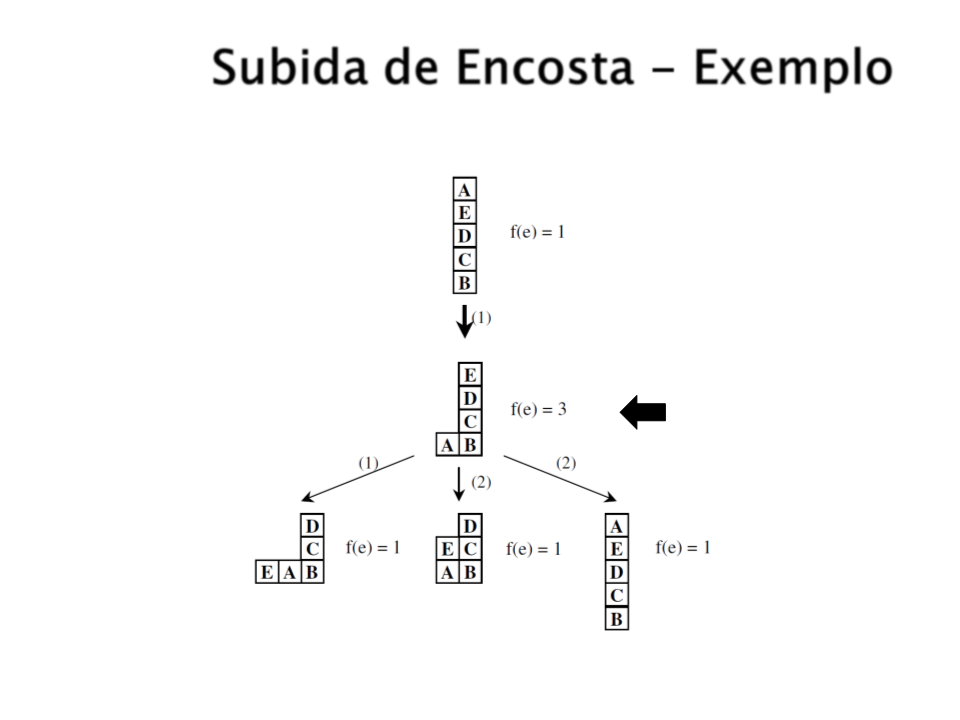
Subida de Encosta - Exemplo
Máximo Local
Subida de Encosta (Hill-Climbing)
Problemas:
Planícies:

Subida de Encosta (Hill-Climbing)
Problemas:
Encostas e Picos:

Subida de Encosta (Hill-Climbing)
Não é ótimo e não é completo.
Variações:
Random-Restart Hill-Climbing;
