
Artificial Intelligence
Lecture 09 – Machine Learning
Edirlei Soares de Lima
<edirlei.slima@gmail.com>
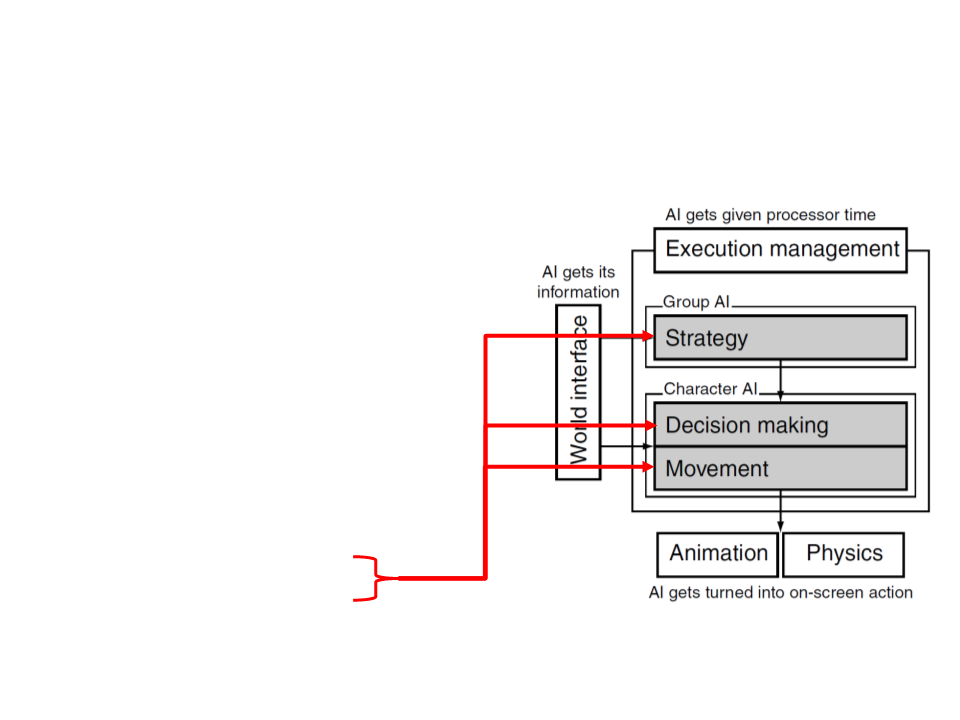
Game AI – Model
•
•
•
•
•
•
•
•
Pathfinding
Steering behaviours
Finite state machines
Automated planning
Behaviour trees
Randomness
Sensor systems
Machine learning
Learning in Games
•
•
Learning is a hot topic in games.
In principle, learning AI has the potential to adapt to each
player, learning their tricks and techniques and providing
consistent challenges.
–
Produce more believable characters.
–
Reduce the effort needed to create game-specific AI.
•
In practice, it hasn’t yet fulfilled its promises.
–
Applying learning to a game requires careful planning and an
understanding of its pitfalls.

Online vs. Offline Learning
•
•
Online Learning: learning is performed during the game, while
the player is playing.
–
Allows characters to adapt dynamically to the player’s style.
–
Predictability and testing problems: if the game is constantly changing,
it can be difficult to replicate bugs and problems.
Offline Learning: learning occurs during the development of
the game.
–
Performed by processing data about real games and trying to calculate
strategies or parameters.
–
Unpredictable learning algorithms can be tried out and their results to
be tested exhaustively.

Behavior Learning
•
•
Intra-Behavior Learning: change only a small area of a
character’s behavior.
–
Examples: learn to target correctly projectiles, learn the best patrol
routes, learn the best cover points, etc.
–
Easy to control and test.
Inter-Behavior Learning: learn new behavior.
–
Examples: learn that the best way to kill an enemy is to lay an ambush,
learn to tie a rope across a backstreet to stop an escaping motorbike.
–
This kind of AI is almost pure fantasy.
Warning About Learning in Games
•
In reality, learning is not as widely used in games as you might
think.
–
Main problems: complexity, reproducibility, and quality control.
•
•
Be careful with hyped-up papers about learning and games.
–
Always constrain the kinds of things that can be learned in your game.
Learning algorithms are attractive because you can do less
implementation work.
–
But on the other hand, you need to do a different work: collect and
present data to the algorithm and make sure the results are valid.
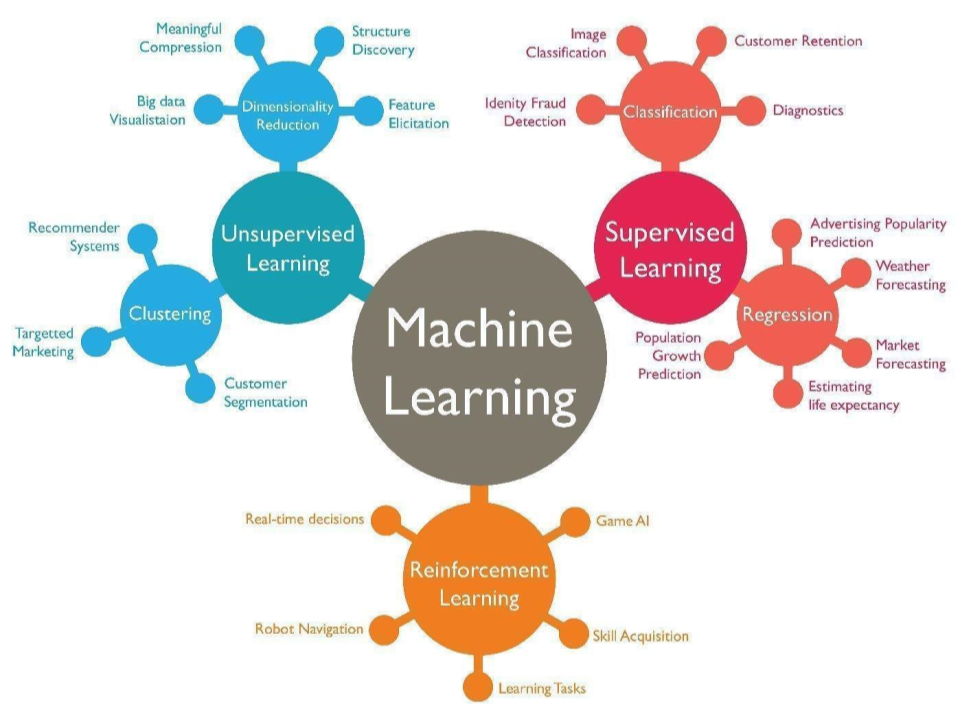
What is Machine Learning?

Machine Learning Tasks
•
•
•
Supervised Learning: learning a function that maps an input
to an output based on example input-output pairs.
Unsupervised Learning: learning a function to describe hidden
structure from "unlabeled" data.
Reinforcement Learning: simulates how agents take actions in
an environment so as to maximize “rewards”.
Learning Phases
•
Train:
–
–
–
Training examples are presented to the system;
The system learns from the examples;
The system gradually adjusts its parameters to produce the desired
output.
•
•
Test:
–
Unseen examples are presented to the system;
–
The system tries to recognize the unseen examples using the
knowledge obtained during the training phase.
Use:
–
After being tested and validated, the system is used for its intended
purpose.
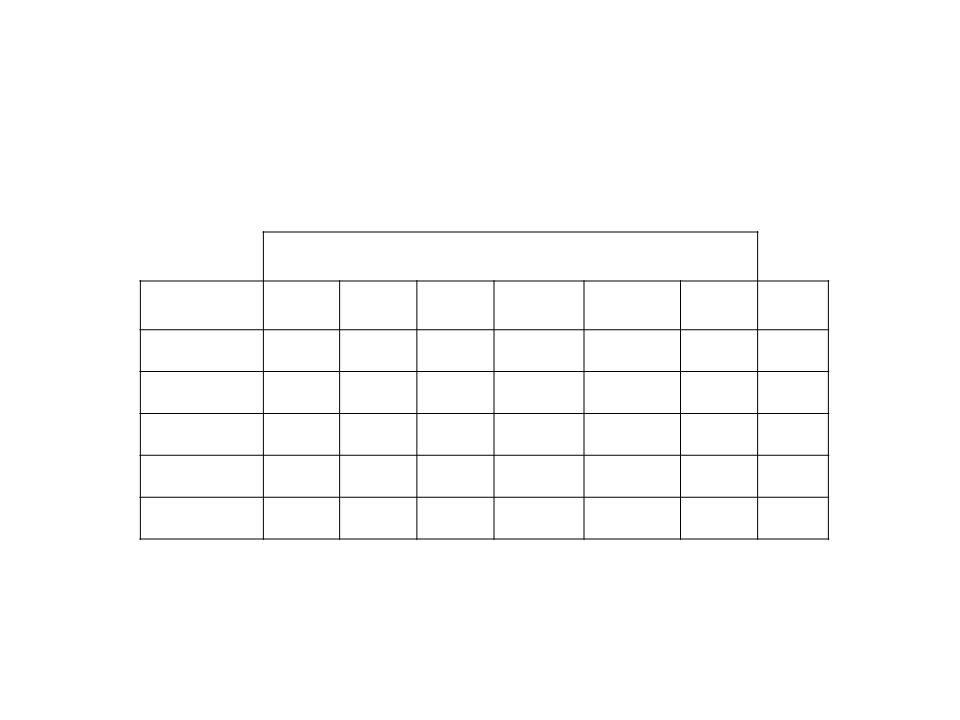
Training Examples
Supervised Learning)
(
Attributes/Features
Example
Attrib1 Attrib2 Attrib3
Attrib4
-0.020360
0.0065762
-0.002901
0.001992
-0.014341
Attrib5
0.429731
0.431444
0.423145
0.422416
0.420937
Attrib6
-0.2935
Class
X1
X2
X3
X4
X5
0.24829
0.24816
0.24884
0.24802
0.24775
0.49713
0.49729
0.49924
0.50013
0.49343
0.00692
0.00672
0.01047
0.01172
0.01729
1
1
3
2
2
-0.29384
-0.28956
-0.29092
-0.29244
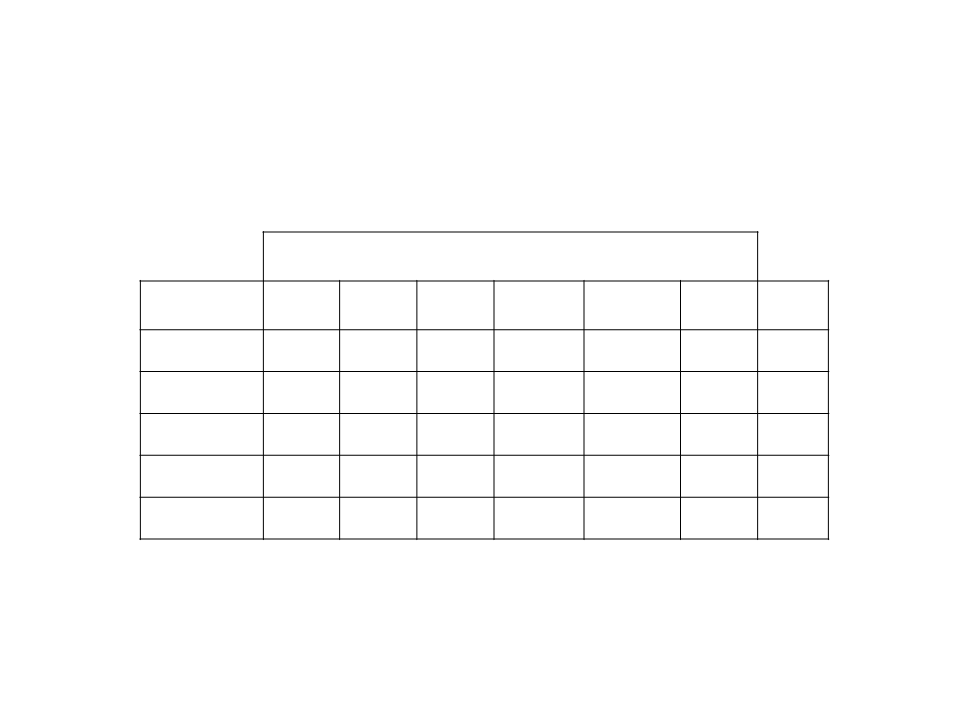
Classification of Unseen Examples
Attributes/Features
Example
Attrib1 Attrib2 Attrib3
Attrib4
-0.010360
0.0045762
-0.003901
0.002992
-0.015341
Attrib5
0.419731
0.421444
0.433145
0.412416
0.430937
Attrib6
-0.2845
Class
X1
X2
X3
X4
X5
0.22829
0.21816
0.23884
0.23002
0.24575
0.48713
0.48729
0.49824
0.49013
0.49243
0.00592
0.00572
0.01447
0.02172
0.01029
?
?
?
?
?
-0.28484
-0.24956
-0.28092
-0.28244

Training Examples
•
•
Suppose we are writing a racing game and we want an AI
character to learn a player’s style of going around corners.
We want to learn when is the best moment to slow down
(break).
–
Output (classes): break, not break;
–
Important game information (attributes): speed and distance to a
corner.
•
To get training data, we can record some gameplay sessions.
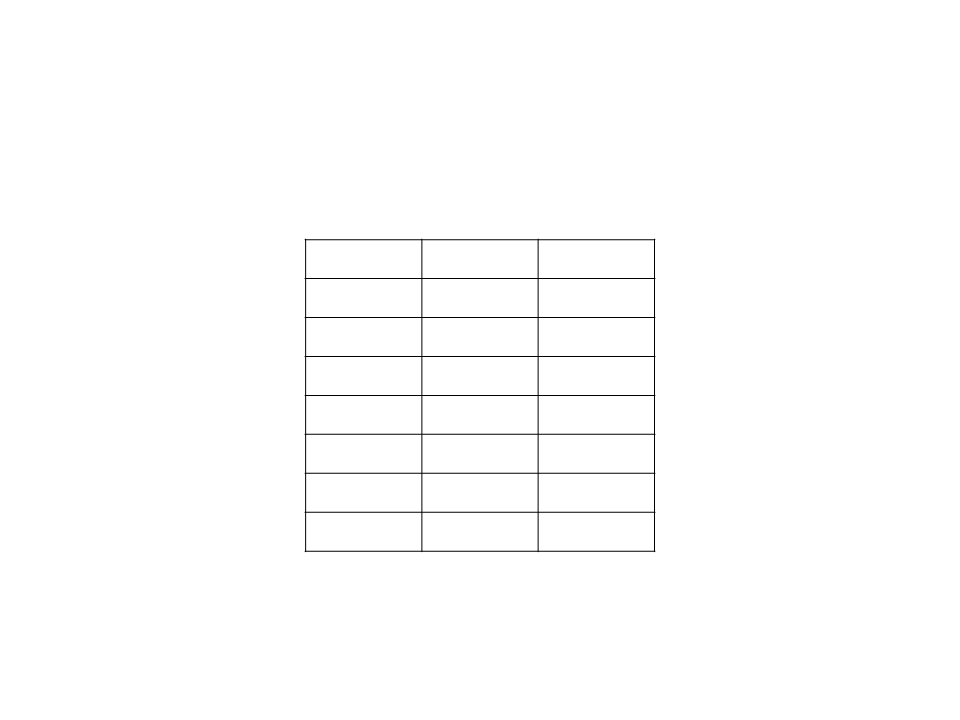
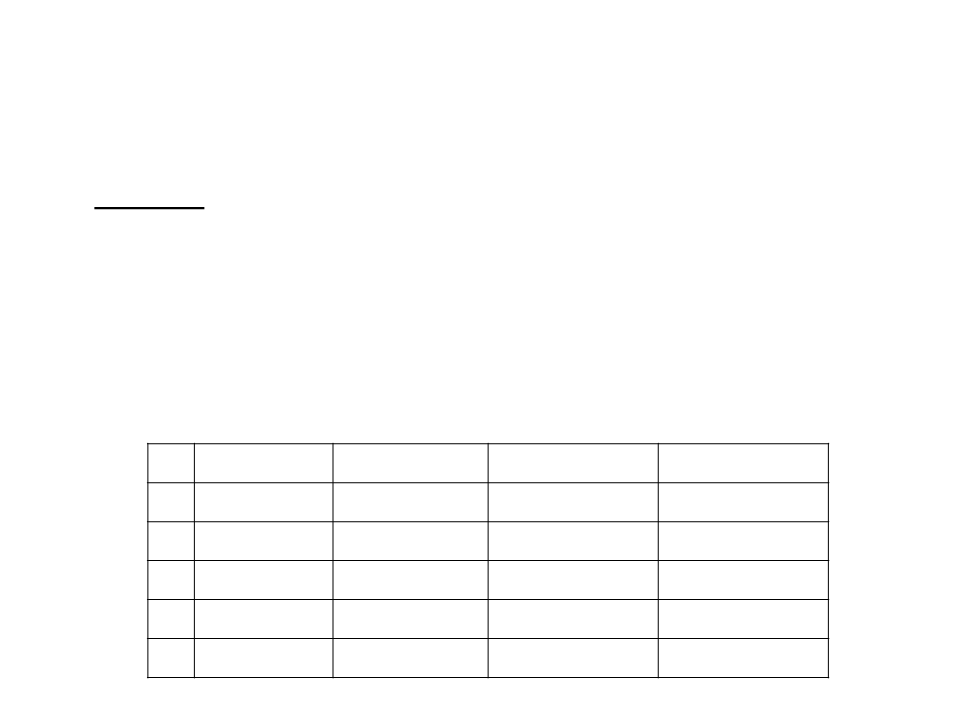
Training Examples
•
Gameplay data:
Distance Speed
Break?
Yes
2
3
7
8
2
8
3
.4
11.3
70.2
72.7
89.4
15.2
8.6
.2
Yes
5.7
0.6
.8
No
Yes
No
2.1
Yes
.8
69.4
Yes

Training Examples
•
Sometimes it is important to make the data as obvious as
possible. We can categorize distances as “near” or “far” and
speed as “slow” or “fast”.
–
When making decisions, most human players don’t consider precise
velocity or distance. They usually categorize the information.
Distance Speed
Break?
Yes
Near
Near
Far
Slow
Fast
Fast
Fast
Slow
Slow
Fast
Yes
No
Far
Yes
Near
Far
No
Yes
Near
Yes
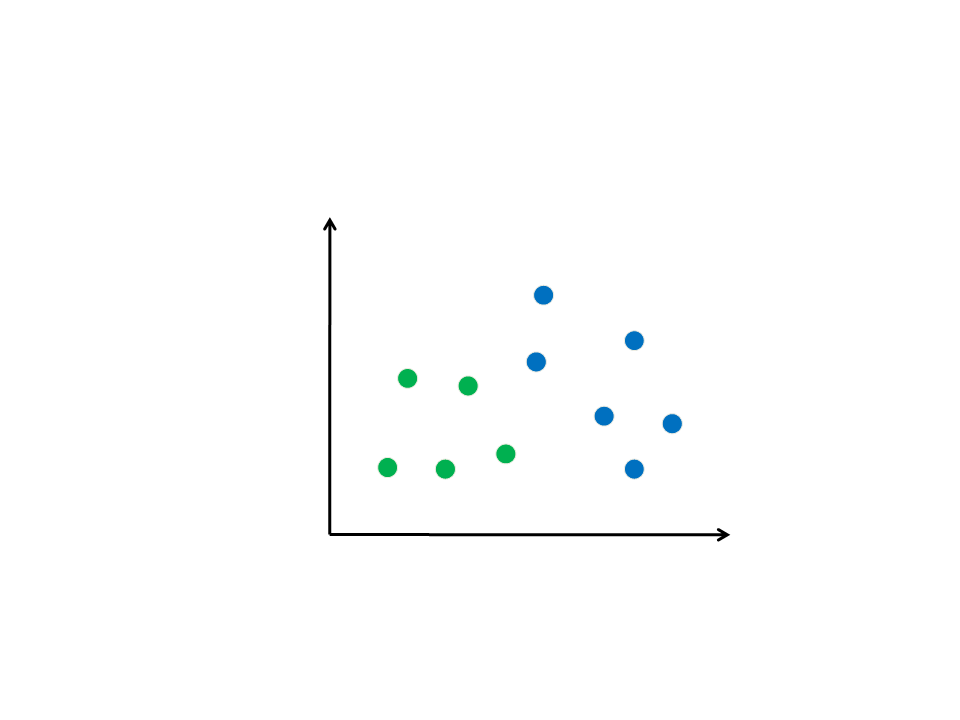
Classification Problem
(Feature Space)
2,20
2,00
1,80
1,60
1,40
1,20
1,10
Height
20
40
60
70
90
110 130 150
Weight
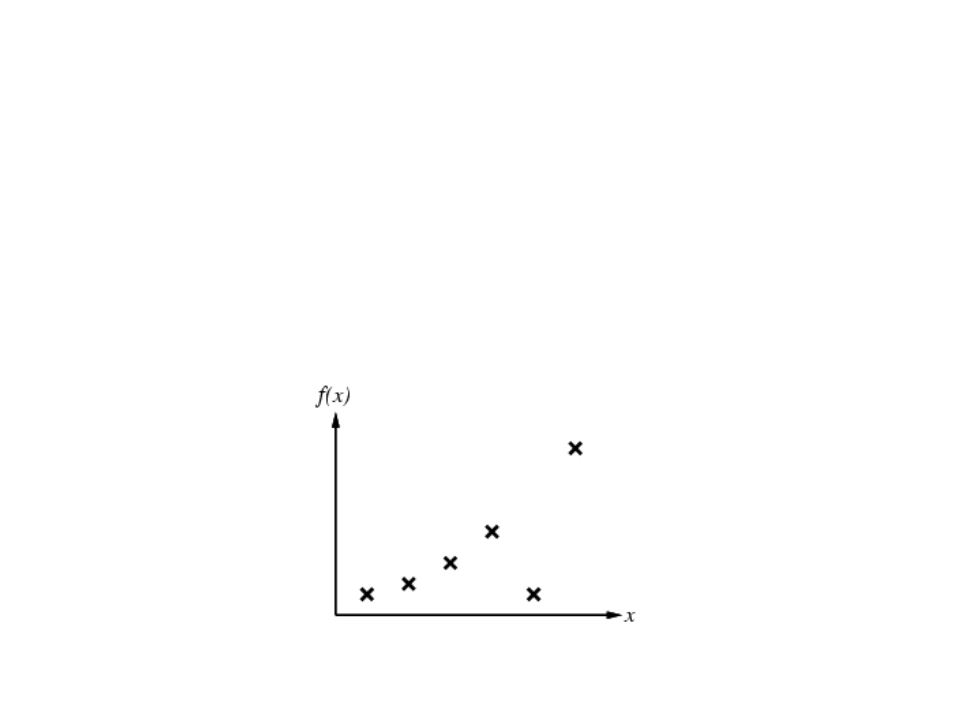
Supervised Learning
•
•
Given a finite amount of training data, we need to find a function h that
approximates the real function f(x) (that generated the data and is unknown).
There is a infinite number o functions h.
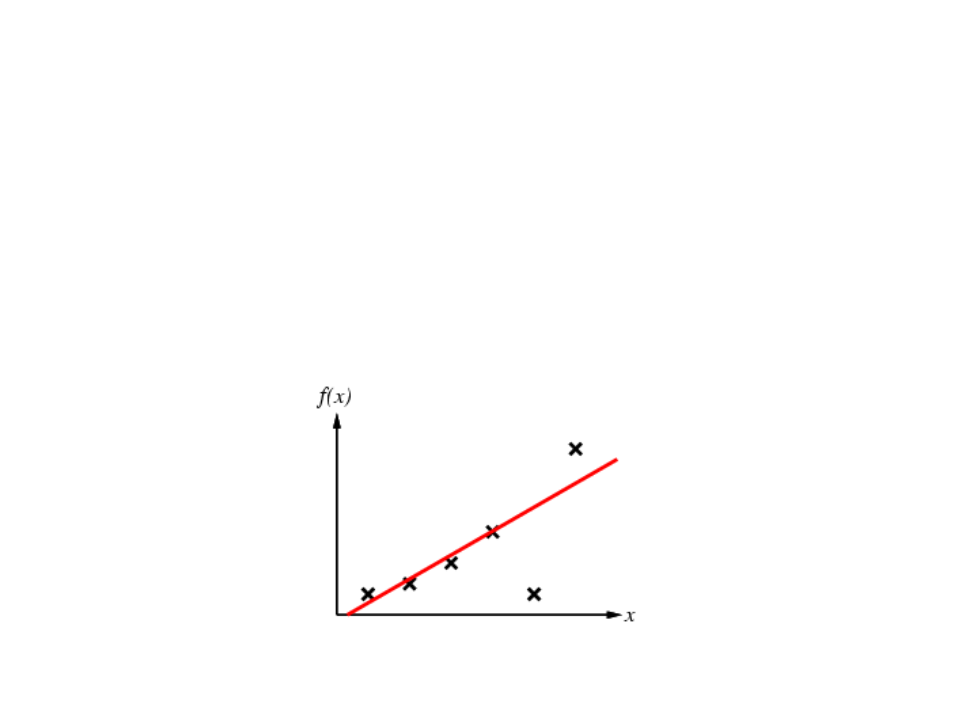
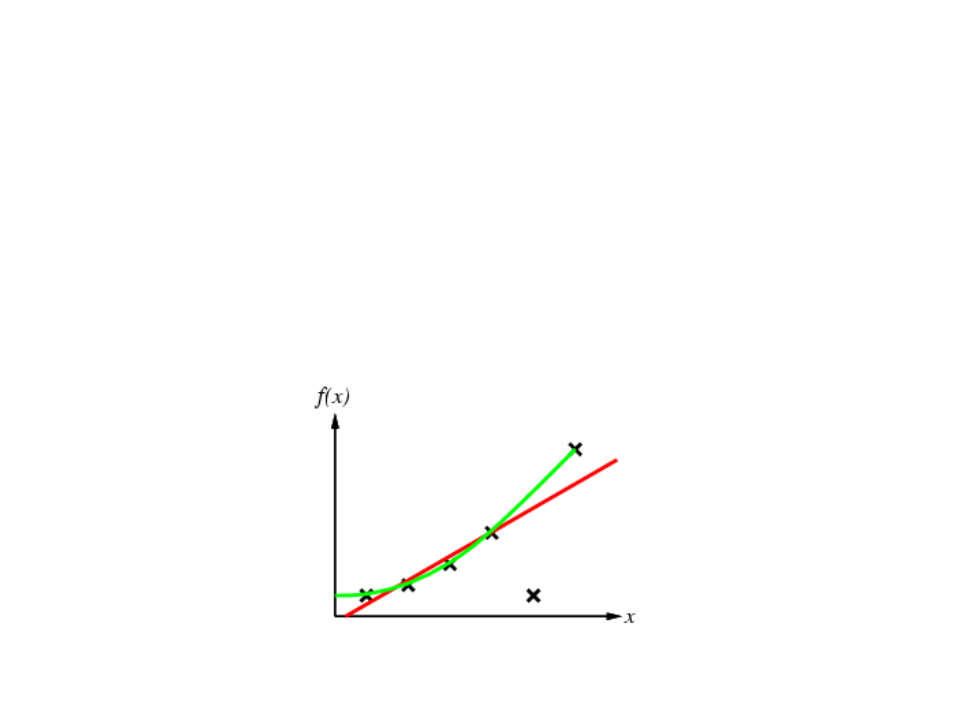
Supervised Learning
•
•
Given a finite amount of training data, we need to find a function h that
approximates the real function f(x) (that generated the data and is unknown).
There is a infinite number o functions h.
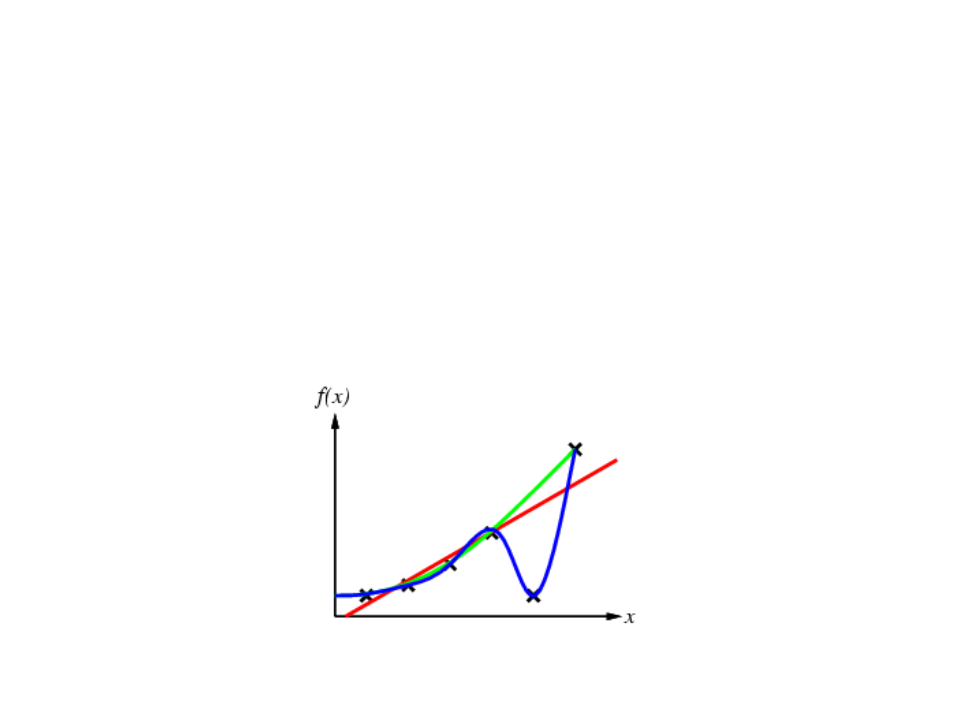
Supervised Learning
•
•
Given a finite amount of training data, we need to find a function h that
approximates the real function f(x) (that generated the data and is unknown).
There is a infinite number o functions h.
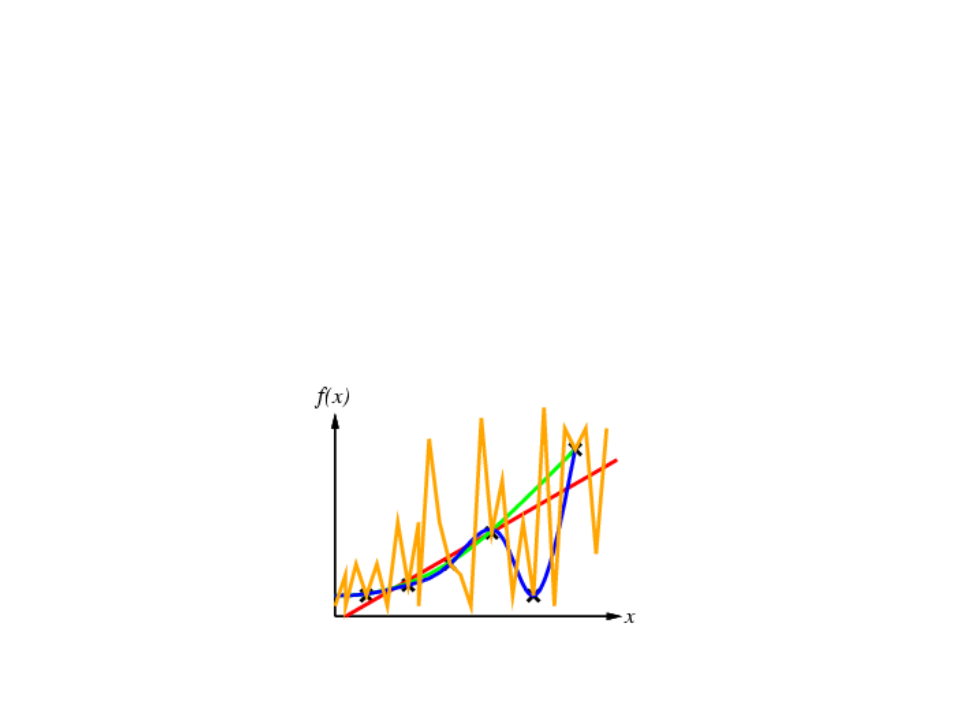
Supervised Learning
•
•
Given a finite amount of training data, we need to find a function h that
approximates the real function f(x) (that generated the data and is unknown).
There is a infinite number o functions h.
Supervised Learning
•
•
Given a finite amount of training data, we need to find a function h that
approximates the real function f(x) (that generated the data and is unknown).
There is a infinite number o functions h.

Learning Algorithms
•
There are many machine learning algorithms:
–
–
–
–
–
–
–
–
–
–
–
Decision Trees
Artificial Neural Networks
Support Vector Machines
K-Nearest Neighbors
Naive Bayes
K-Means
Linear Regression
Logistic Regression
Random Forest
Q-Learning
…
Decision Tree
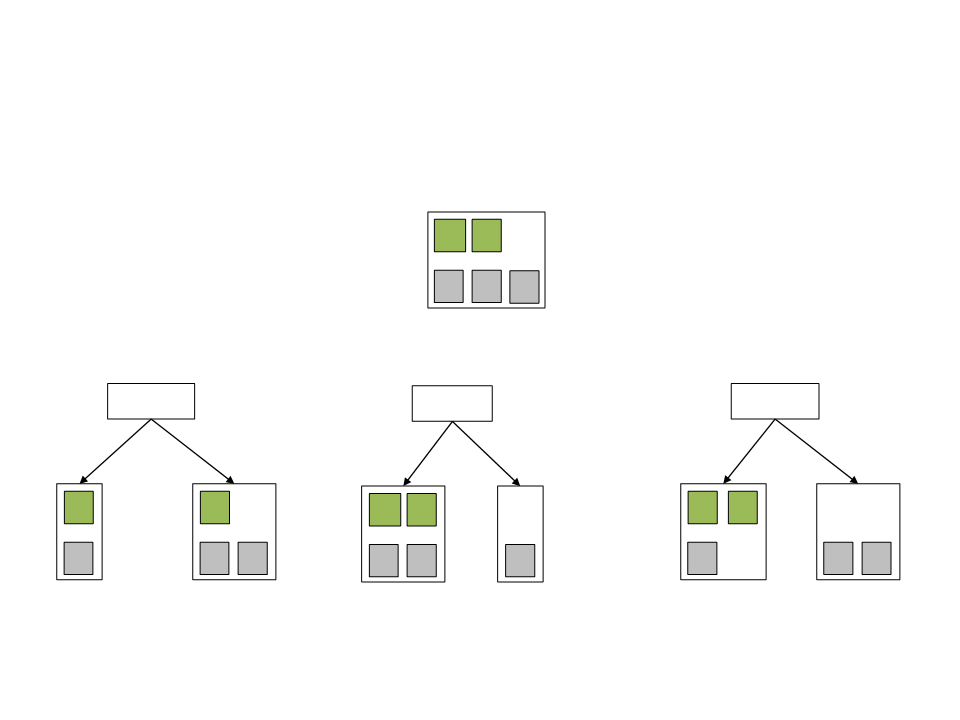
•
A decision tree is a tree structure with a series of decisions
that generate an action to take based on a set of observations.
–
At each branch some aspect of the game world is considered and a
different branch is chosen. Eventually, the series of branches lead to an
action (leaf node).
Decision Tree
•
•
Decision trees can be efficiently learned: constructed
dynamically from sets of observations and actions.
–
The constructed trees can then be used to make decisions during
gameplay.
There are a range of different decision tree learning
algorithms. Those used in game AI are typically based on
the ID3 algorithm.
–
ID3 is a simple to implement, relatively efficient decision tree
learning algorithm.
ID3 Algorithm
1. The algorithm starts with a single leaf node in a decision tree and assigns
a set of examples to the leaf node.
2. It then splits its current node (initially the single start node) so that it
divides the examples into groups.
a) The division process looks at each attribute in turn (i.e., each possible way to
make a decision) and calculates the information gain for each possible
division. The division with the highest information gain is chosen as the
decision for this node.
b) When the division is made, each of the two new nodes is given the subset of
examples that applies to them, and the algorithm repeats for each of them.
3
. This algorithm is recursive: starting from a single node it replaces them
with decisions until the whole decision tree has been created.
Decision Tree – Example
•
•
Example: learn when is the best moment to attack and
defend.
–
Two possible actions: attack and defend.
–
Three attributes: health, cover, and ammo.
Dataset:
ID Health
Cover
Ammo
Action
Attack
Attack
Defend
Defend
Defend
1
2
3
4
5
Healthy
Hurt
In Cover
In Cover
In Cover
In Cover
Exposed
With Ammo
With Ammo
Empty
Healthy
Hurt
Empty
Hurt
With Ammo
Decision Tree – Example
Training Set
1
3
2
4
Attack Examples:
Defend Examples:
5
Health?
Ammo?
Cover?
Healthy
Hurt
With Ammo
Empty
In Cover
Exposed
1
3
2
4
1
5
2
1
3
2
5
3
4
4
5

Entropy and Information Gain
•
•
In order to decide which attribute should be considered at
each step, ID3 uses the entropy and information gain of the
actions in the set.
Entropy is a measure of the information in a set of examples.
–
If all the examples have the same action, the entropy will be 0.
–
If the actions are distributed evenly, then the entropy will be 1.
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢇ = −ꢅ+ ꢈꢄꢉ2 ꢅ+ −ꢅꢊ ꢈꢄꢉ2 ꢅꢊ
•
Information gain is simply the reduction in overall entropy.
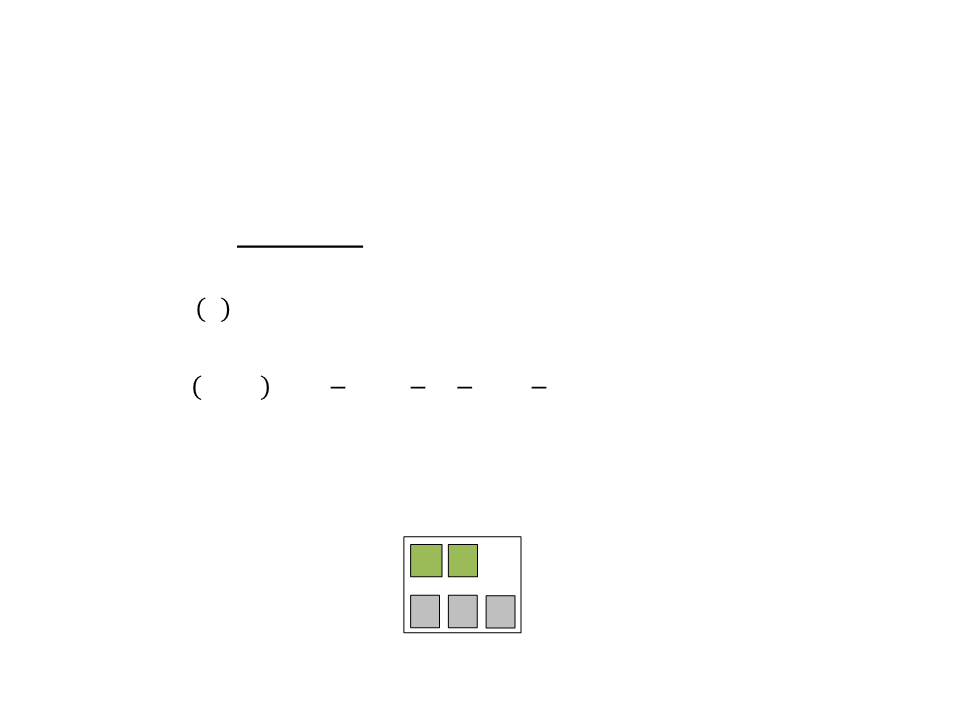
Decision Tree – Example
•
For the two possible outcomes (attack and defend) the
entropy of whole set is given by:
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢇ = −ꢅꢋ ꢈꢄꢉ2 ꢅꢋ −ꢅꢌ ꢈꢄꢉ2 ꢅꢌ
ꢍ
ꢍ 3
3
ꢀ
ꢁꢂꢃꢄꢅꢆ [ꢍ, 3] = − 5 ꢈꢄꢉ2 − ꢈꢄꢉ2 5 = 0.9709
5 5
Training Set
1
3
2
4
Entropy =
= 0.9709
5
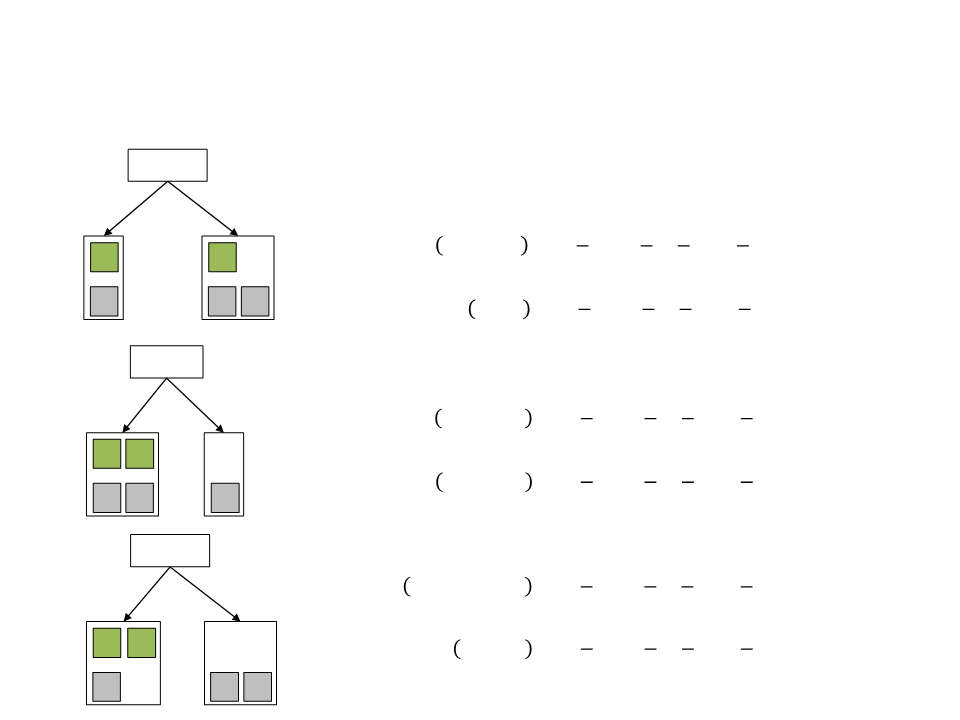
Decision Tree – Example
Health?
Healthy
Hurt
1
1 1
1
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢎꢏꢐꢈꢂℎꢆ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 1.0000
1
3
2
4
ꢍ
1
ꢍ ꢍ
1 ꢍ
ꢍ
ꢍ
5
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢎꢑꢃꢂ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 0.918ꢍ
3
3 3
3
Cover?
In Cover
Exposed
ꢍ
ꢍ ꢍ
ꢍ
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢒꢁ ꢓꢄꢔꢏꢃ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 1.0000
4
0
4 4
0 1
4
1
1
3
2
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢀꢕꢅꢄꢖꢏꢗ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 0.0000
4
5
1
1 1
1
Ammo?
ꢍ
ꢍ 1
1
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢘꢙꢂℎ ꢚꢛꢛꢄ = − 3 ꢈꢄꢉ2 3 − 3 ꢈꢄꢉ2 3 = 0.918ꢍ
With Ammo
Empty
0
0 ꢍ
ꢁꢂꢃꢄꢅꢆ ꢀꢛꢅꢂꢆ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 0.0000
ꢍ ꢍ
ꢍ
1
5
2
ꢀ
ꢍ
ꢍ
3
4

Decision Tree – Example
•
The information gain for each division is the reduction in
entropy from the current example set (0.971) to the entropies
of the children sets.
ꢜꢐꢙꢁ ꢅ = ꢀꢁꢂꢃꢄꢅꢆ ꢇ − ꢅ+ ∗ ꢀꢁꢂꢃꢄꢅꢆ ꢅ+ − ꢅꢊ ∗ ꢀꢁꢂꢃꢄꢅꢆ ꢅꢊ
ꢍ
3
ꢜꢐꢙꢁ ℎꢏꢐꢈꢂℎ = 0.971 − 5 ∗ 1.0000 − 5 ∗ 0.918ꢍ = 0.0ꢍ00
4
1
ꢜꢐꢙꢁ ꢝꢄꢔꢏꢃ = 0.971 − ∗ 1.0000 − ∗ 0.0000 = 0.1710
5
5
3
ꢍ
ꢜꢐꢙꢁ ꢐꢛꢛꢄ = 0.971 − ∗ 0.918ꢍ − ∗ 0.0000 = 0.4ꢍ00
5
5
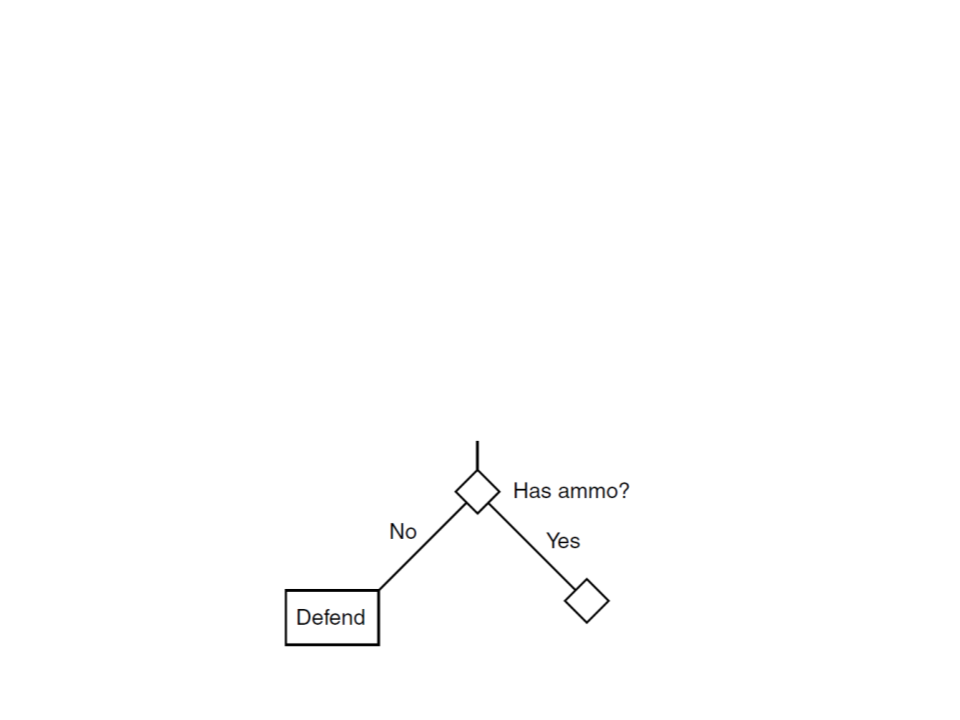
Decision Tree – Example
•
•
Ammo is the best indicator of what action we need to take
(this makes sense, since we cannot possibly attack without
ammo).
By the principle of learning, we use ammo as our first branch
in the decision tree:
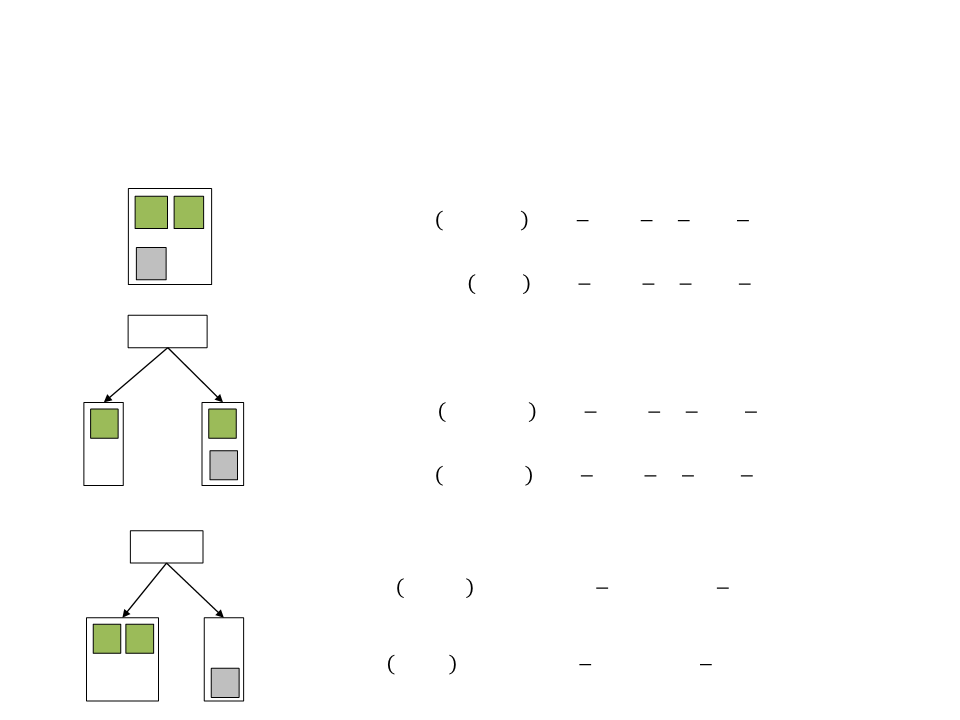
Decision Tree – Example
Remaining Set
1
1 0
0
1
5
2
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢎꢏꢐꢈꢂℎꢆ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 0.0000
1
1
1 1
1 1
1
1
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢎꢑꢃꢂ = − ꢈꢄꢉ2 − ꢈꢄꢉ2 = 1.0000
ꢍ
ꢍ ꢍ
ꢍ
Health?
Healthy
1
Hurt
ꢍ
ꢍ 0
0
ꢀ
ꢁꢂꢃꢄꢅꢆ ꢒꢁ ꢓꢄꢔꢏꢃ = − ꢍ ꢈꢄꢉ2 ꢍ − ꢍ ꢈꢄꢉ2 ꢍ = 0.0000
2
5
0
ꢁꢂꢃꢄꢅꢆ ꢀꢕꢅꢄꢖꢏꢗ = − 1 ꢈꢄꢉ2 1 − 1 ꢈꢄꢉ2 1 = 0.0000
0 1
1
ꢀ
Cover?
ꢍ 1
ꢜꢐꢙꢁ ℎꢏꢐꢈꢂℎ = 0.918ꢍ − ∗ 0.0000 − ∗ 1.0000 = 0.5848
3 3
In Cover
1
Exposed
2
ꢍ
1
ꢜꢐꢙꢁ ꢝꢄꢔꢏꢃ = 0.9181 − ∗ 0.0000 − ∗ 0.0000 = 0.918ꢍ
3
3
5
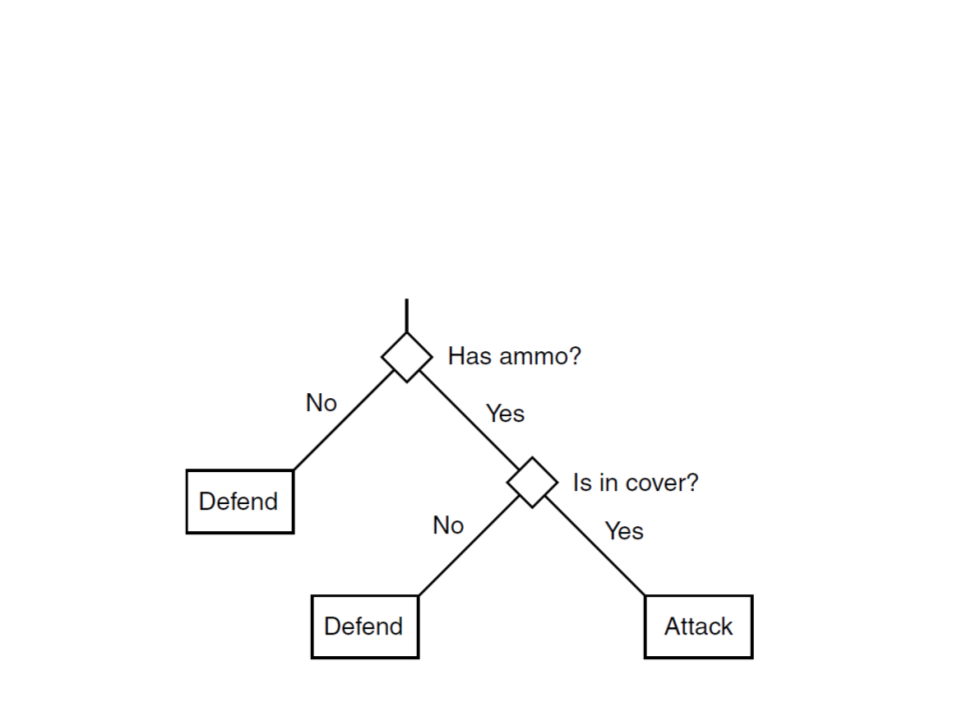
Decision Tree – Example
•
By adding the cover attribute to the decision tree, all training
examples can be correctly classified.

Decision Tree - Generalizations
•
•
The same process works with more than two actions. In this
case the entropy calculation generalizes to:
ꢀ
ꢁꢂꢃꢄꢅꢆ = − ꢅꢞ ꢈꢄꢉ2 ꢅꢞ
ꢞꢟꢠ…ꢡ
–
where n is the number of actions, and pi is the proportion of each
action in the example set.
When there are more than two categories for a attribute, the
formula for information gain generalizes to:
ꢖꢞ
ꢜꢐꢙꢁ = ꢀꢢ −
∗ ꢀꢁꢂꢃꢄꢅꢆ(ꢇꢞ)
ꢇ
ꢞꢟꢠ…ꢡ

Decision Tree in Unity
•
•
•
Decision Tree in C#:
https://github.com/Zolomon/decision-tree
–
Adapted code to Unity:
– http://www.inf.puc-rio.br/~elima/game-ai/decision-tree.zip
ARFF Dataset Format:
@
@
@
.
.
@
@
@
(
.
.
relation (DatasetName)
attribute (AtribName1) (AtribType1)
attribute (AtribName2) (AtribType2)
attribute (AtribNameN) (AtribTypeN)
attribute (Class) {(Class1, Class2, … ClassN)}
data
Atrib1), (Atrib2), … , (AtribN),(Class)

Decision Tree in Unity
•
ARFF Example:
@
RELATION AttackOrDefend
@
@
@
@
ATTRIBUTE health
ATTRIBUTE cover {incover,exposed}
ATTRIBUTE ammo
ATTRIBUTE action
{healthy,hurt}
{withammo,empty}
{attack,defend}
@
DATA
healthy,incover,withammo,attack
hurt,incover,withammo,attack
healthy,incover,empty,defend
hurt,incover,empty,defend
hurt,exposed,withammo,defend

Decision Tree in Unity
•
Unity DecisionTree Class:
using System.Collections.Generic;
using UnityEngine;
using System.IO;
using decisiontree;
public class DecisionTree : MonoBehaviour {
private DecisionBuilder builder;
private Node tree;
void Start(){
ArffReader reader = new ArffReader();
Arff arff = reader.Parse(new StreamReader("Assets\\test.arff"));
builder = new DecisionBuilder(arff);
tree = builder.BuildTree(arff.Data, arff.Attributes, false);
...

Decision Tree in Unity
//test example to test the decision tree
Dictionary<string, string> example = new Dictionary<string,
string>();
example.Add("health", "healthy");
example.Add("cover", "incover");
example.Add("ammo", "empty");
string action = ClassifyExample(tree, example);
if (action == "attack"){
Debug.Log("Attack!!!");
}
else if (action == "defend"){
Debug.Log("Defend!!!");
}
}
.
..

Decision Tree in Unity
private string ClassifyExample(Node node, Dictionary<string,
string> example){
Node currentNode = node;
while (currentNode != null){
foreach (KeyValuePair<string, Node> child in
currentNode.children){
if (example[currentNode.attribute.Name] == child.Key){
currentNode = child.Value;
break;
}
}
if (currentNode.IsLeaf()){
return currentNode.Display(1);
}
}
return "";
}
}
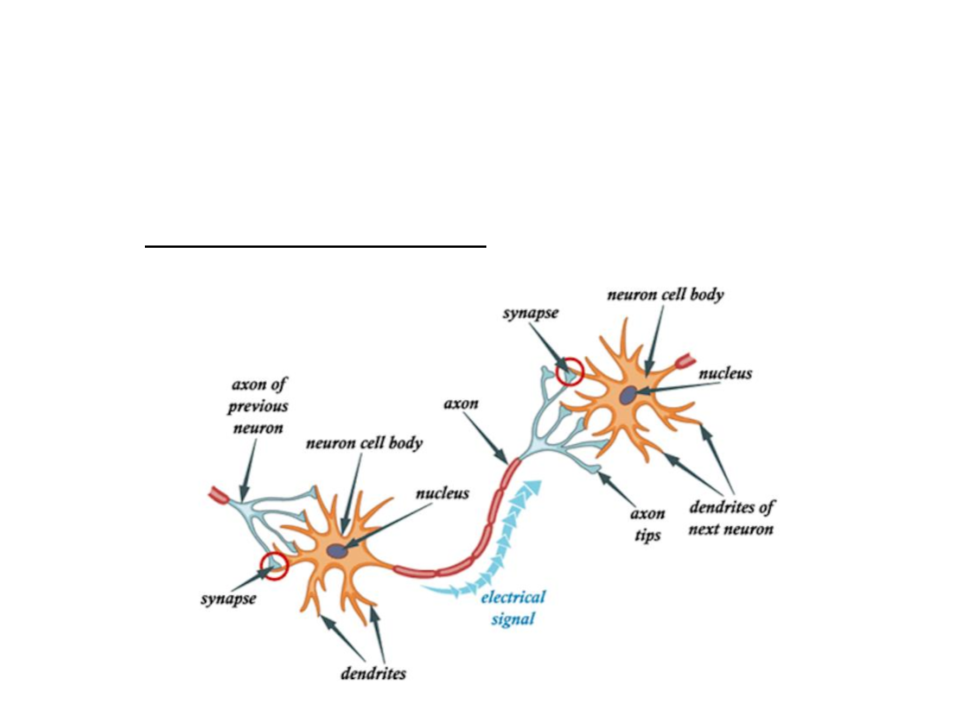
Artificial Neural Networks
•
Artificial neural networks are computing systems inspired by
the biological neural networks that constitute animal brains.
Artificial Neural Networks
•
Neural networks consist of a large number of relatively simple
nodes, each running the same algorithm.
–
These nodes are the artificial neurons, originally intended to simulate
the operation of a single brain cell.
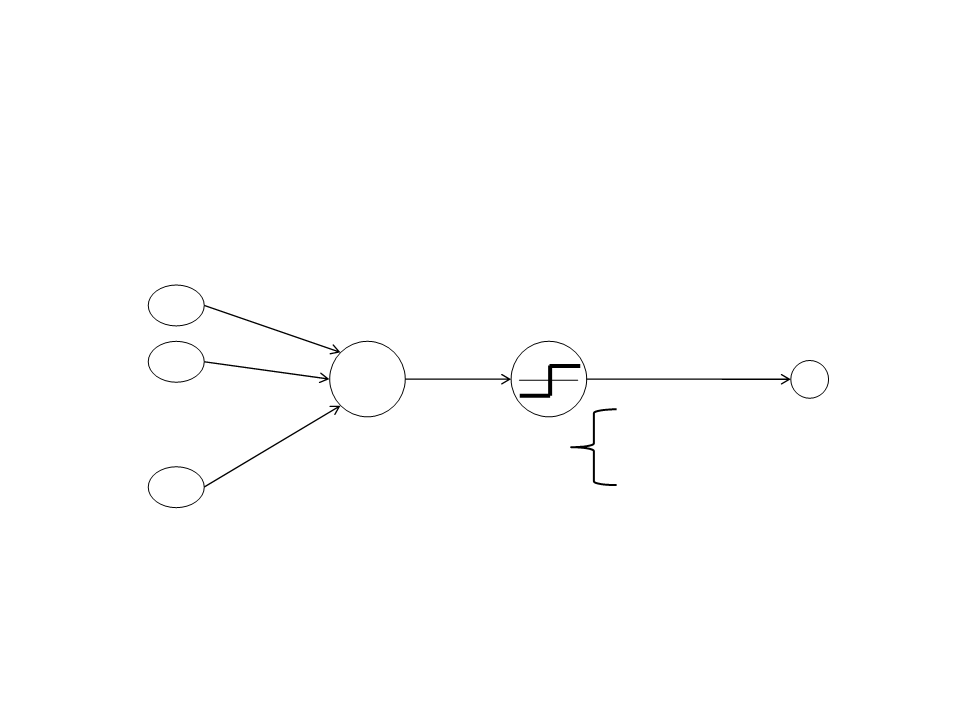
Artificial Neuron
•
Threshold Unit:
W1
X1
X2
W2
.
.
.
n
n
1
if
wi xi 0
wi xi
i=0
i=0
Wn
−
1 otherwise
Xn
Artificial Neuron – Learning
•
•
In order to learn a function, the perceptron must adjust its
weights based on the difference between the desired output
and its current output.
Learning Rule:
Desired output: t
wi = wi + wi
x1
x1
x2
x2
...
...
xn
xn
o
t
wi =(t − o)xi
–
Where:
•
t = Desired output.
o = Current output.
= Learning rate.
•
•
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
0
0
1
1
B Output
A
B
0
.3
0
1
0
1
0
0
0
1
T=0.2
-
0.1
wi = wi + wi
wi =(t − o)xi
A B
Sum
Output
Error
0
0
1
1
0
1
0
1
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
0
0
1
1
B Output
A
B
0
.3
0
1
0
1
0
0
0
1
T=0.2
-
0.1
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.3)+(0*-0.1) = 0
(0*0.3)+(1*-0.1) = -0.1
(1*0.3)+(0*-0.1) = 0.3
(1*0.3)+(1*-0.1) = 0.2
0
0
1
1
0
0
-1
0
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
B Output
A
B
0
.2
0
0
1
1
0
1
0
1
0
0
0
1
T=0.2
-
0.1
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.2)+(0*-0.1) = 0
(0*0.2)+(1*-0.1) = -0.1
(1*0.2)+(0*-0.1) = 0.2
(1*0.2)+(1*-0.1) = 0.1
0
0
1
0
0
0
-1
1
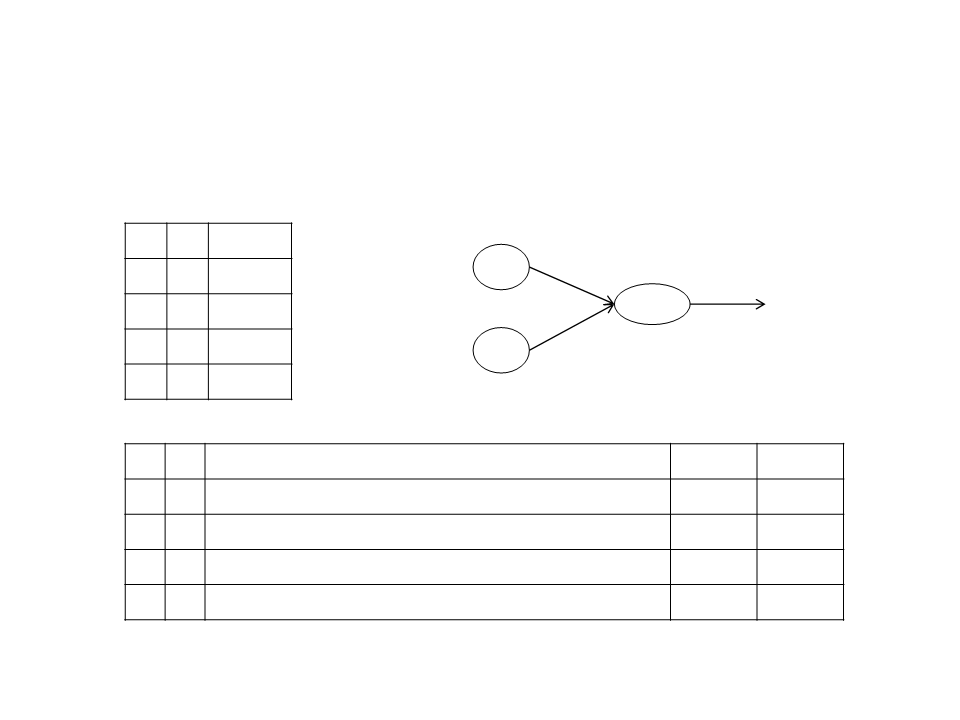
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
0
0
1
1
B Output
A
B
0
.1
0
1
0
1
0
0
0
1
T=0.2
-
0.1
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.1)+(0*-0.1) = 0
(0*0.1)+(1*-0.1) = -0.1
(1*0.1)+(0*-0.1) = 0.1
(1*0.1)+(1*-0.1) = 0
0
0
0
0
0
0
0
1
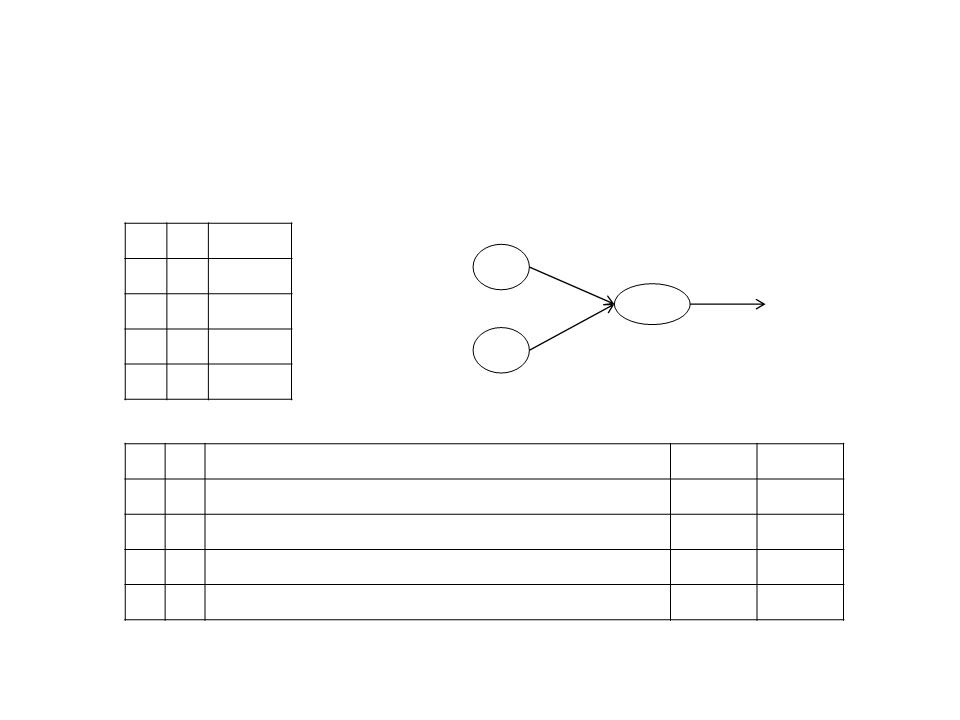
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A B Output
A
B
0
.2
0
0
1
1
0
1
0
1
0
0
0
1
T=0.2
0.0
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.2)+(0*-0.0) = 0
(0*0.2)+(1*-0.0) = 0
(1*0.2)+(0*-0.0) = 0.2
(1*0.2)+(1*-0.0) = 0.2
0
0
1
1
0
0
-1
0
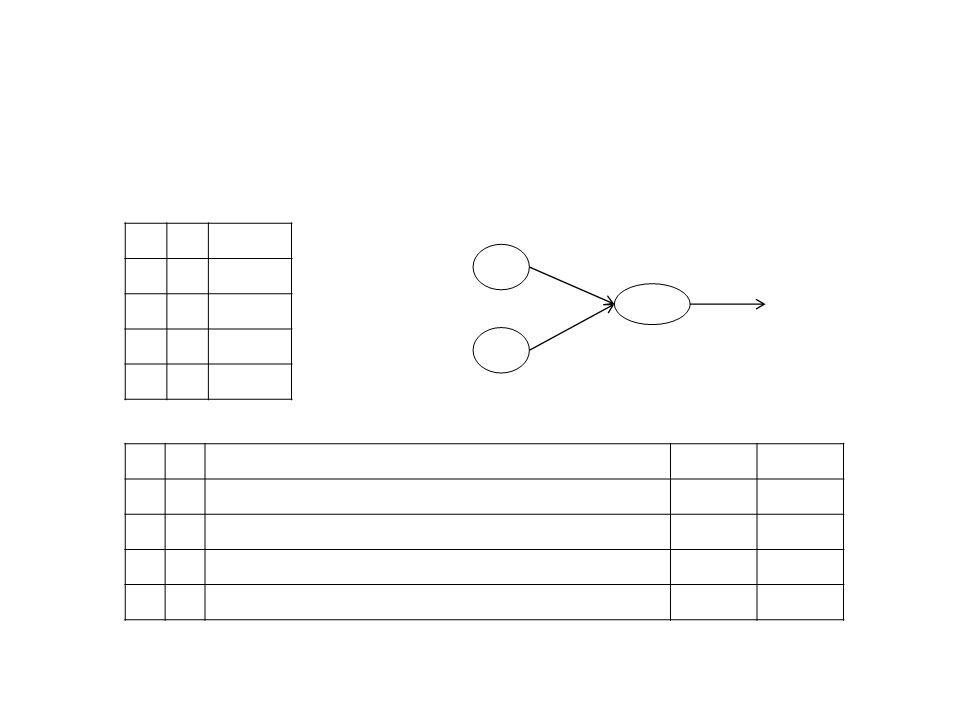
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
B Output
A
B
0
.1
0
0
1
1
0
1
0
1
0
0
0
1
T=0.2
0.0
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.1)+(0*0.0) = 0
(0*0.1)+(1*0.0) = 0
(1*0.1)+(0*0.0) = 0.1
(1*0.1)+(1*0.0) = 0.1
0
0
0
0
0
0
0
1
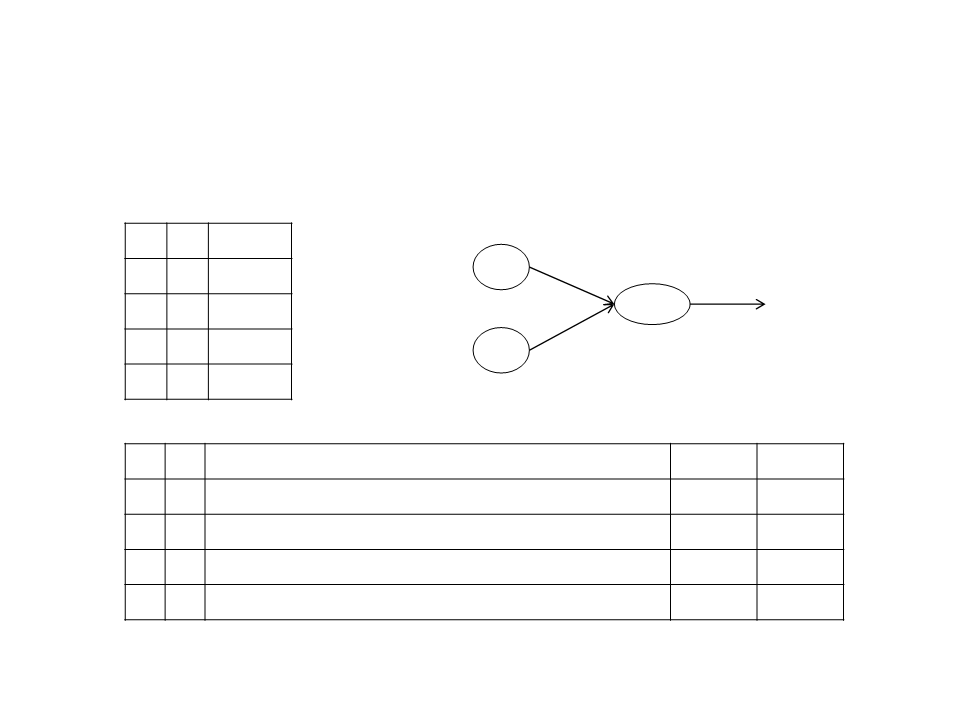
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
0
0
1
1
B Output
A
B
0
.2
0
1
0
1
0
0
0
1
T=0.2
0.1
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.2)+(0*0.1) = 0
(0*0.2)+(1*0.1) = 0.1
(1*0.2)+(0*0.1) = 0.2
(1*0.2)+(1*0.1) = 0.3
0
0
1
1
0
0
-1
0
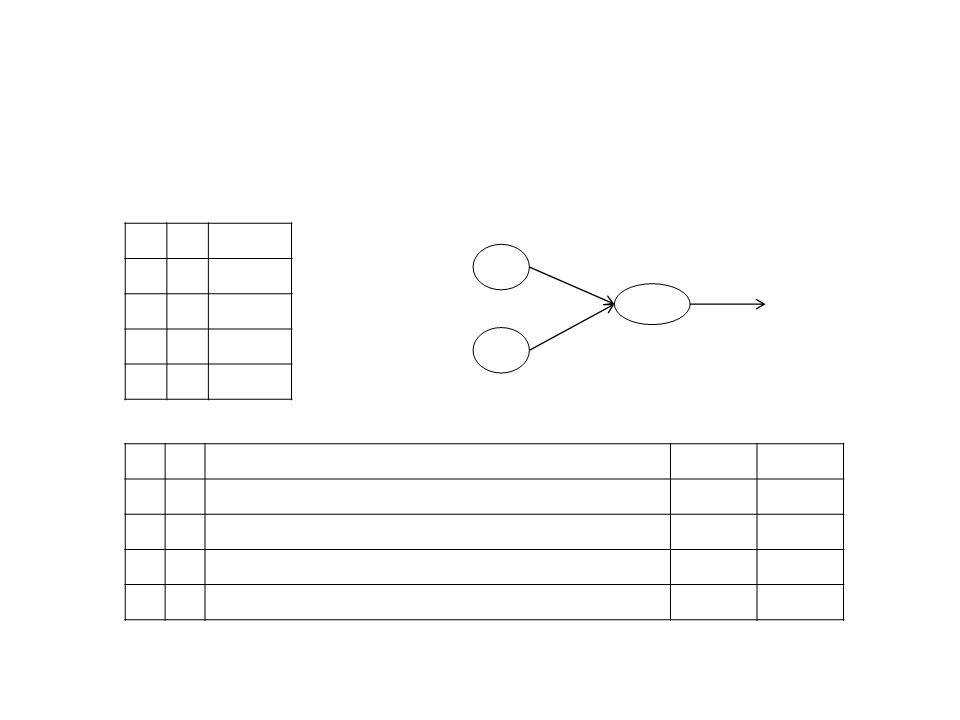
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
0
0
1
1
B Output
A
B
0
.1
0
1
0
1
0
0
0
1
T=0.2
0.2
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.1)+(0*0.2) = 0
(0*0.1)+(1*0.2) = 0.2
(1*0.1)+(0*0.2) = 0.1
(1*0.1)+(1*0.2) = 0.3
0
1
0
1
0
-1
0
0
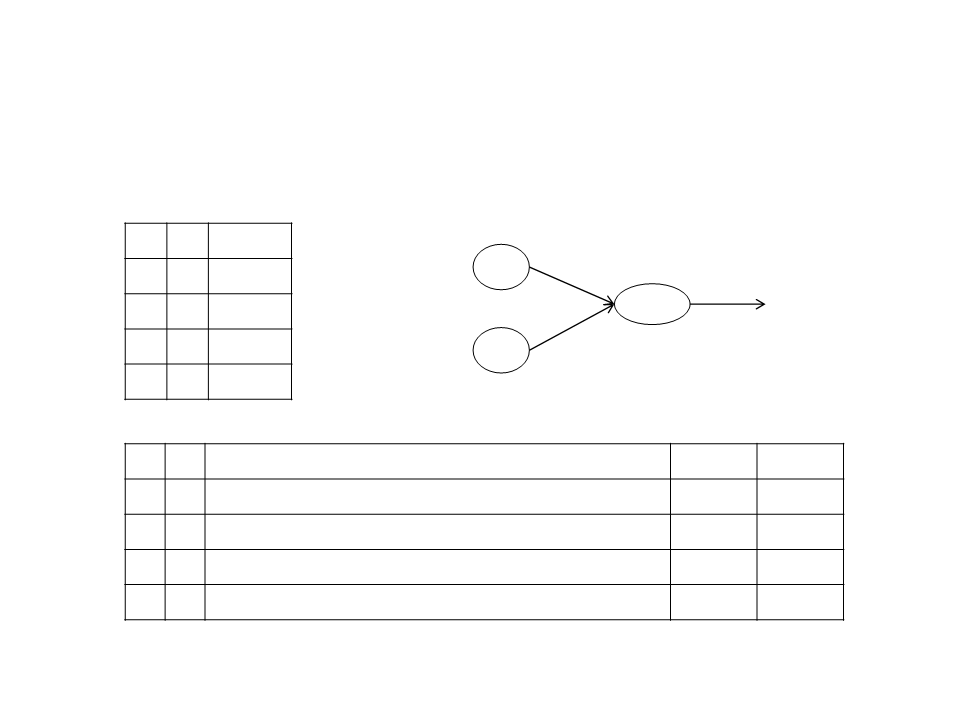
Training a Neuron – Example
And Operator
Threshold = 0.2
Learning Rate = 0.1
A
B Output
A
B
0
.1
0
0
1
1
0
1
0
1
0
0
0
1
T=0.2
0.1
wi = wi + wi
wi =(t − o)xi
A
0
0
1
1
B
0
1
0
1
Sum
Output
Error
(0*0.1)+(0*0.1) = 0
(0*0.1)+(1*0.1) = 0.1
(1*0.1)+(0*0.1) = 0.1
(1*0.1)+(1*0.1) = 0.2
0
0
0
1
0
0
0
0
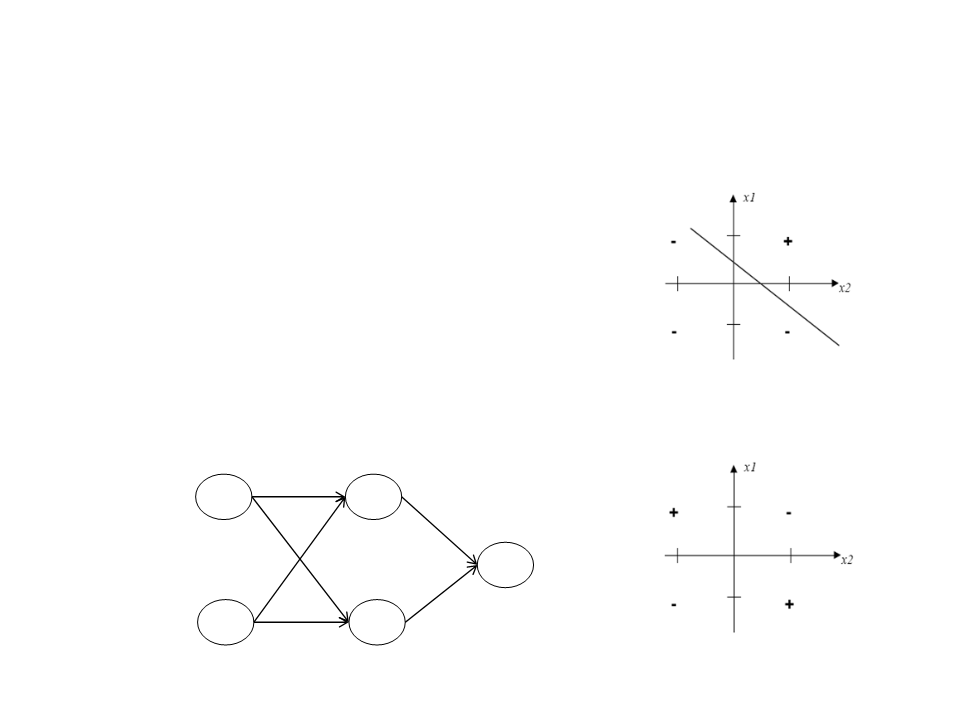
Limitations
•
•
A single Perceptron can only solve linear
functions.
However, we can combine several
neurons to generate more complex
functions.
-
0.5
h1
1
X1
1
1
o
1
1
-
0.5
-
1
X2
h2
Multi-Layer Neural Network
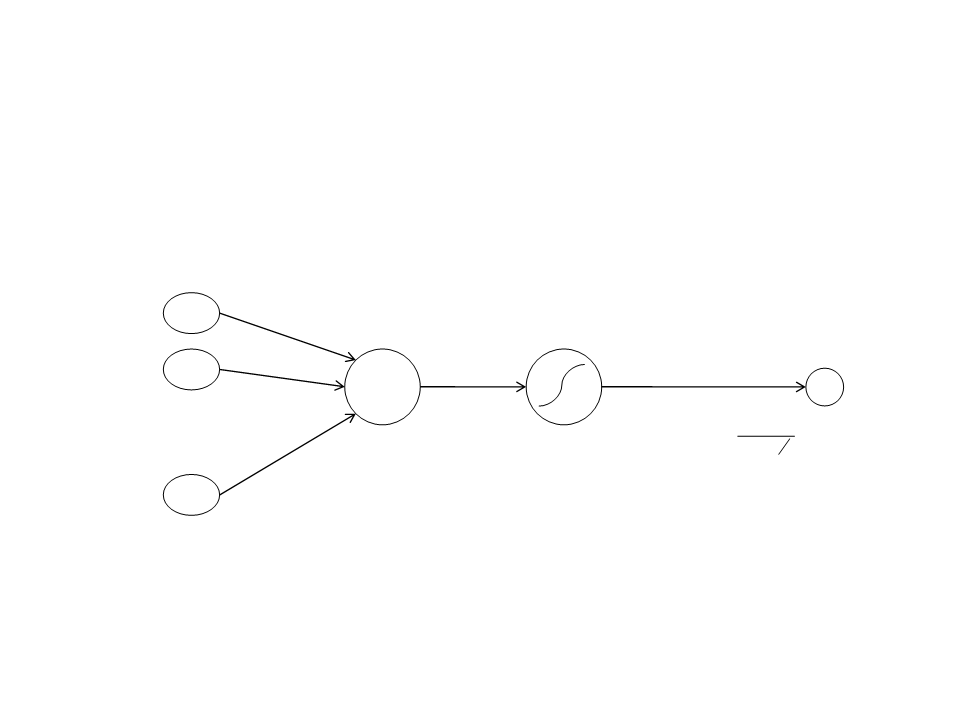
Artificial Neuron
•
Sigmoid Unit:
W1
X1
W2
X2
.
.
.
n
1
net = wi xi
o = (net) =
−h p
Wn
i=0
1+ e
Xn
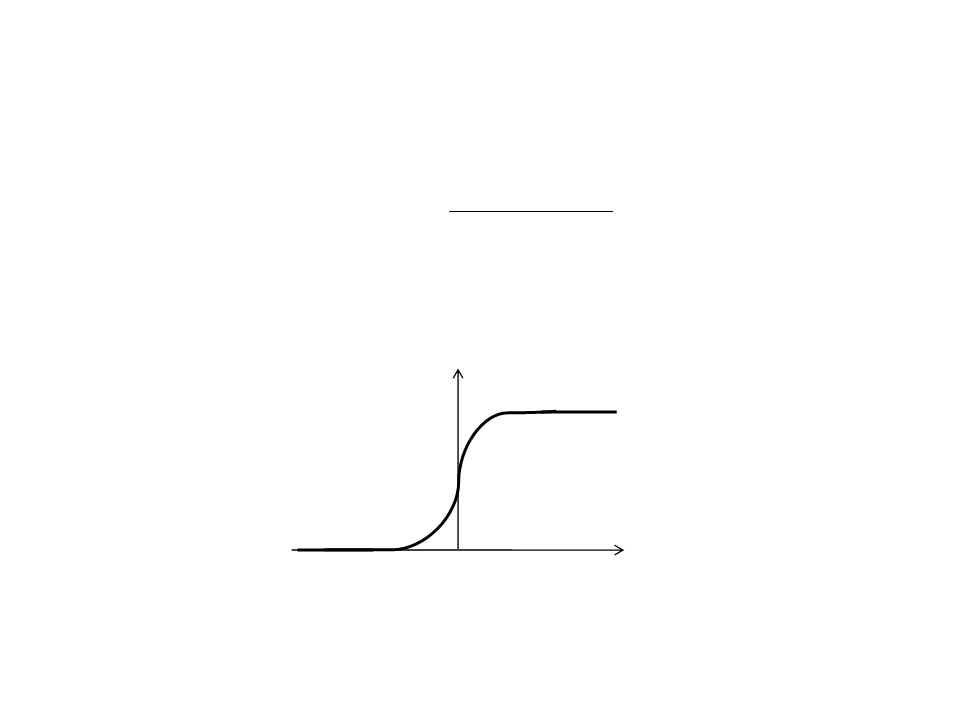
Sigmoid Function
1
−(neti (t)− )/
fi (neti (t)) = 1
+ e
1
= 0.1
0
1
-1
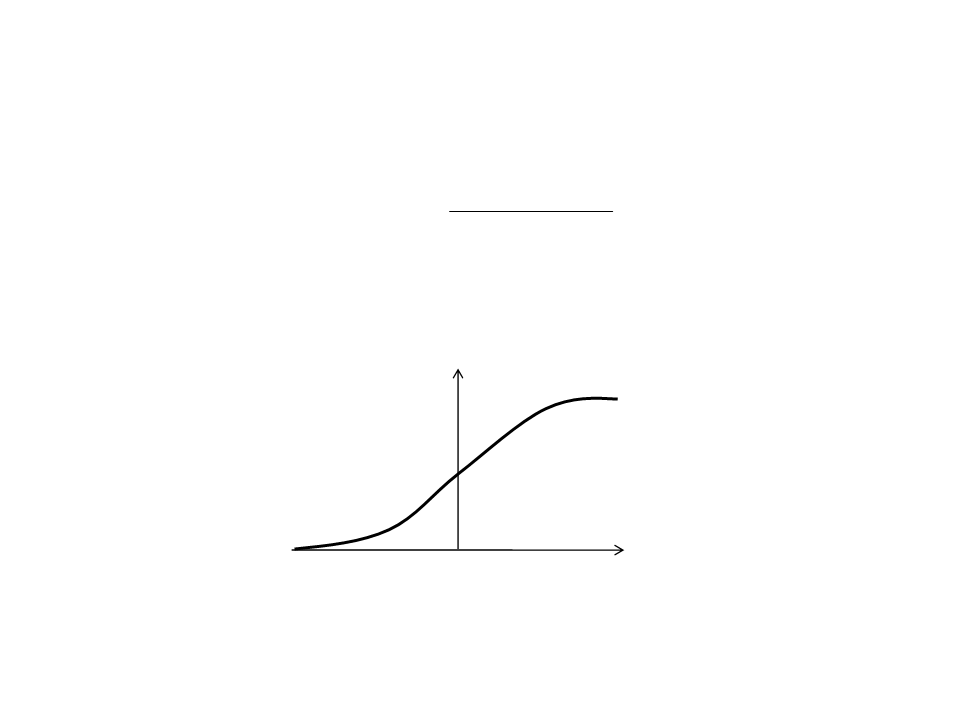
Sigmoid Function
1
−(neti (t)− )/
fi (neti (t)) = 1
+ e
1
=1
0
1
-1
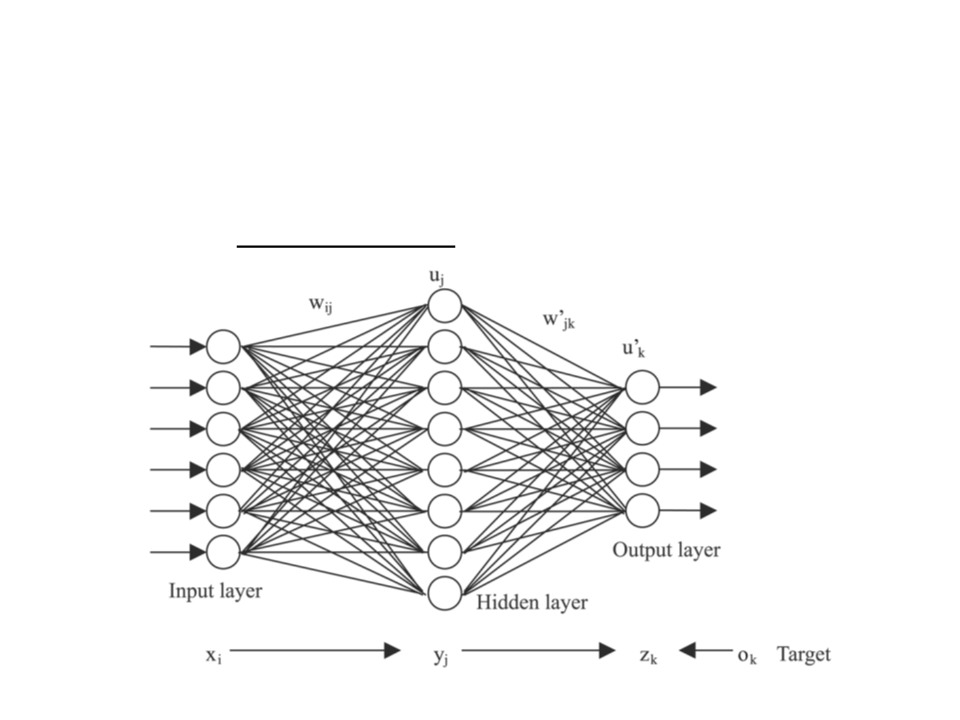
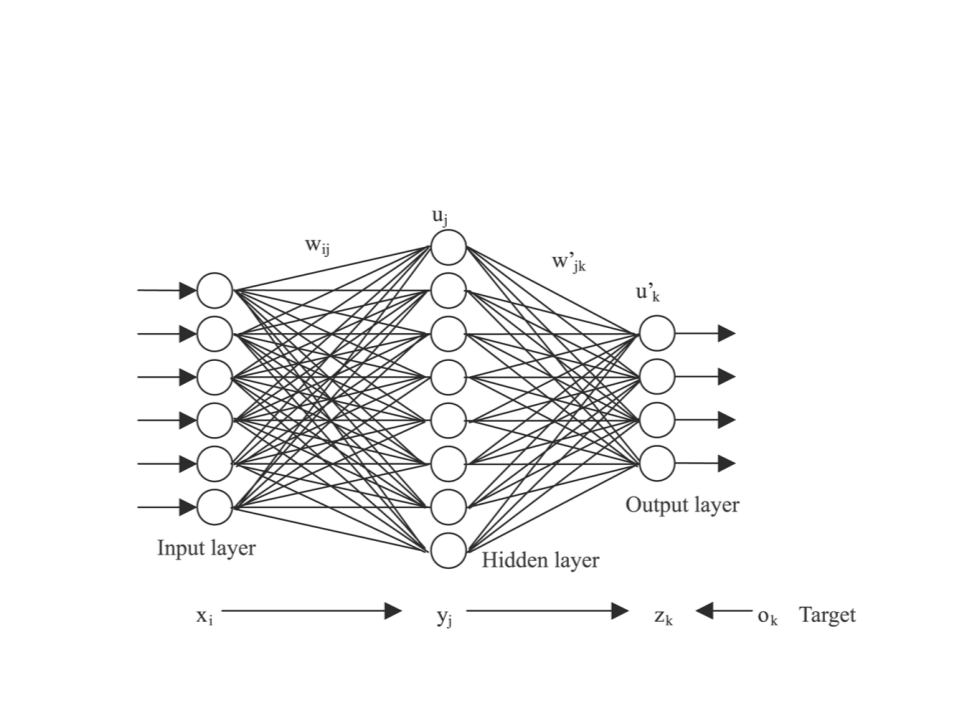
Training a Multi-Layer Neural Network
•
The most common algorithm used to train a multi-layer neural
network is backpropagation.
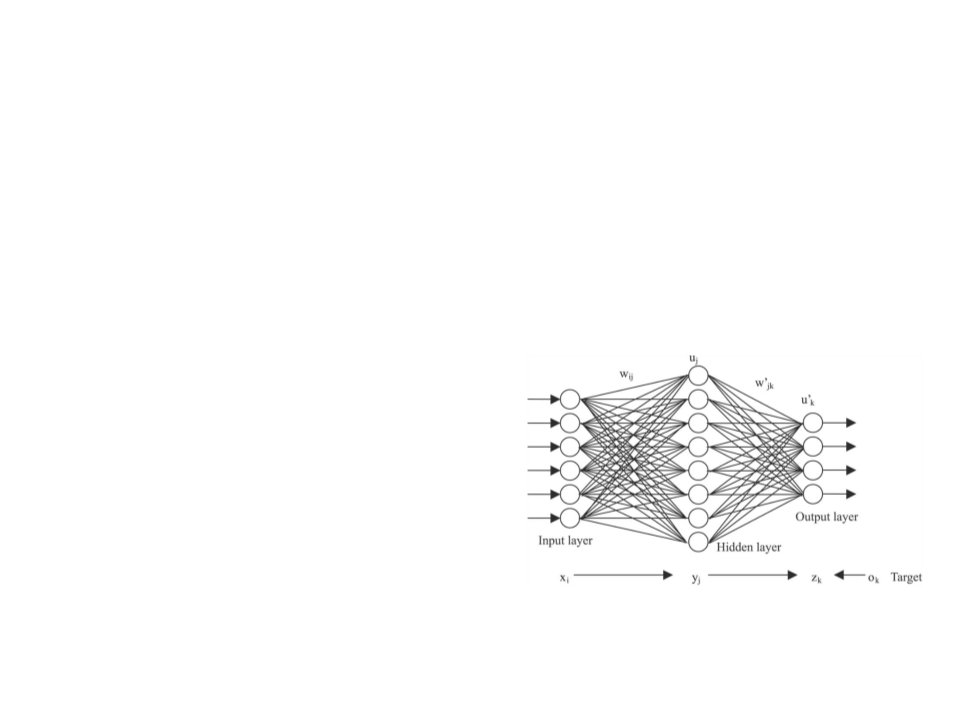
Backpropagation Algorithm
Initialize each weight wi with a small random value.
While stop condition not achieved do
{
For each training example do
{
Send example data forward through the network to generate the output value(s) (ok)
For each output unit k do
{
k ok (1−ok )(tk −ok )
}
For each hidden unit h do
{
h oh (1− oh ) wh,kk
k outputs
}
For each weight wj do
{
wi, j wi, j + wi, j
where wi, j = j xi, j
}
}
}
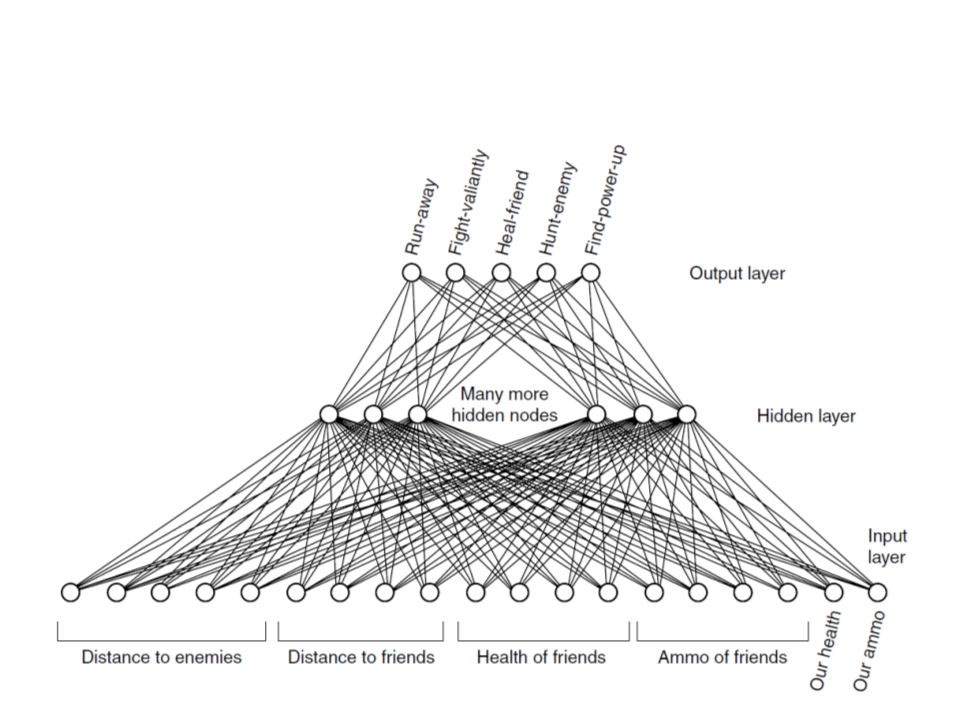
Neural Network – Example

Neural Network – Example
•
Example Dataset:
– enemy1_distance, enemy2_distance, enemy3_distance,
enemy4_distance, enemy5_distance, friend1_distance,
friend2_distance, friend3_distance, friend4_distance,
friend1_health, friend2_health, friend3_health,
friend4_health, friend1_ammo, friend2_ammo, friend3_ammo,
friend4_ammo, npc_health, npc_ammo, output_1, output_2,
output_3, output_4, output_5.
38.66639 24.33377 42.02419 30.08049 6.865509 6.836913 14.03836 22.79428 2.829218 77 44 94 84 84 22 38 69 82 37 0 1 0 0 0
16.61636 8.189857 38.72226 44.58482 27.93692 30.83033 13.37324 15.70575 17.51968 7 73 16 85 7 78 84 26 72 89 0 1 0 0 0
21.39196 7.802973 4.604796 33.43155 21.54505 44.25414 23.44657 32.52487 19.25208 43 86 98 75 39 9 23 11 27 71 0 1 0 0 0
25.10197 25.31712 40.84161 26.15318 34.83861 3.897014 44.4931 42.89812 19.62424 11 98 84 6 87 99 94 63 96 88 0 0 0 1 0
31.29582 43.86897 41.10728 39.88687 11.66713 2.803209 20.70098 2.086438 13.35874 9 63 69 15 46 43 76 71 78 96 0 0 0 1
35.0895 34.01117 41.12255 36.36316 43.55266 33.24846 6.954234 9.050363 35.59743 53 34 82 21 3 97 72 94 3 7 0 0 0 0 1
24.66118 38.50056 20.31548 33.68458 31.04514 20.71192 35.30664 19.74172 44.19277 35 1 6 3 26 54 10 24 89 30 0 0 1 0 0
31.33946 38.89338 39.39215 43.40701 35.70232 34.58619 20.71613 6.100486 18.00656 -1 4 63 76 82 46 85 63 16 8 0 0 0 0 1
15.06403 23.0914 39.81666 11.20308 5.064096 36.92915 33.80843 3.121126 44.42622 37 90 76 -1 90 95 87 60 29 2 1 0 0 0 0
9.559992 11.26607 24.1834 20.52185 10.86952 26.05703 13.62671 35.59985 39.43266 7 58 37 41 72 -1 27 30 85 77 0 1 0 0 0
.
.
.

Neural Networks in Unity
•
Weka (great tool to evaluate machine learning algorithms):
–
https://www.cs.waikato.ac.nz/ml/weka/
–
Dataset in ARFF format:
•
http://www.inf.puc-rio.br/~elima/game-ai/game_example_dataset.arff
•
•
Artificial Neural Network in C#:
–
https://visualstudiomagazine.com/articles/2015/04/01/back-
Adapted code to Unity:
–
http://www.inf.puc-rio.br/~elima/game-ai/NeuralNetwork.cs

Neural Networks in Unity
•
NeuralNet Class:
using System.IO;
using UnityEngine;
public class NeuralNet : MonoBehaviour {
public int numInput = 19;
public int numHidden = 25;
public int numOutput = 5;
public int numExamples = 100;
public int maxEpochs = 1000;
public double learnRate = 0.01;
public double momentum = 0.005;
public int splitSeed = 1;
private NeuralNetwork neuralnetwork;
private double[][] fulldataset;
...

Neural Networks in Unity
public double[][] LoadDataset(string filename)
{
double[][] allData = new double[numExamples][];
for (int i = 0; i < numExamples; ++i)
allData[i] = new double[numInput + numOutput];
using (TextReader reader = File.OpenText(filename))
{
for (int i = 0; i < numExamples; ++i)
{
string text = reader.ReadLine();
string[] data = text.Split(' ');
for (int x = 0; x < data.Length; x++)
{
allData[i][x] = double.Parse(data[x]);
}
}
}
return allData;
}

Neural Networks in Unity
public NeuralNetwork TrainNeuralNetwork(double[][] dataset)
{
NeuralNetwork nn = new NeuralNetwork(numInput, numHidden,
numOutput);
double[] weights = nn.Train(dataset, maxEpochs, learnRate,
momentum);
return nn;
}
public int ClassifyExample(NeuralNetwork nn, string exampleData)
{
double[] example = new double[numInput];
string[] data = exampleData.Split(' ');
for (int x = 0; x < data.Length; x++)
{
example[x] = double.Parse(data[x]);
}
return nn.Predict(example);
}

Neural Networks in Unity
void Start(){
fulldataset = LoadDataset("Assets\\game_dataset.txt");
neuralnetwork = TrainNeuralNetwork(fulldataset);
int actionId = ClassifyExample(neuralnetwork, "25.10197 25.31712
40.84161 26.15318 34.83861 3.897014 44.4931
42.89812 19.62424 11 98 84 6 87 99 94 63 96 88");
if (actionId == 0)
Debug.Log("Run Away!!!");
else if (actionId == 1)
Debug.Log("Fight!!!");
else if (actionId == 2)
Debug.Log("Heal Friend!!!");
else if (actionId == 3)
Debug.Log("Hunt Enemy!!!");
else if (actionId == 4)
Debug.Log("Find Power-Up!!!");
}

Neural Networks in Unity
public void EvaluateAccuracy(double[][] dataset)
{
double[][] trainData;
double[][] testData;
SplitTrainTest(dataset, 0.80, splitSeed, out trainData,
out testData);
NeuralNetwork nn = new NeuralNetwork(numInput, numHidden,
numOutput);
nn.Train(trainData, maxEpochs, learnRate, momentum);
double trainAcc = nn.Accuracy(trainData);
Debug.Log("Accuracy on training data: " + trainAcc * 100 + "%");
double testAcc = nn.Accuracy(testData);
Debug.Log("Accuracy on test data: " + testAcc * 100 + "%");
}
private void SplitTrainTest(double[][] allData, double trainPct,
int seed, out double[][] trainData,
out double[][] testData){
System.Random rnd = new System.Random(seed);
...

Neural Networks in Unity
int totRows = allData.Length;
int numTrainRows = (int)(totRows * trainPct);
int numTestRows = totRows - numTrainRows;
trainData = new double[numTrainRows][];
testData = new double[numTestRows][];
double[][] copy = new double[allData.Length][];
for (int i = 0; i < copy.Length; ++i)
copy[i] = allData[i];
for (int i = 0; i < copy.Length; ++i){
int r = rnd.Next(i, copy.Length);
double[] tmp = copy[r];
copy[r] = copy[i];
copy[i] = tmp;
}
for (int i = 0; i < numTrainRows; ++i)
trainData[i] = copy[i];
for (int i = 0; i < numTestRows; ++i)
testData[i] = copy[i + numTrainRows];
}
}

Machine Learning in Games
•
•
Racing games:
FPS and Action games:

Machine Learning in Games
•
Camera Control:
A
B C
D
E
Machine Learning in Games
•
•
Player Modeling
–
–
–
Player Archetypes
Personality and Behavior
Difficult Adjustment
Game Analytics

Further Reading
•
Millington, I., Funge, J. (2009). Artificial Intelligence
for Games (2nd ed.). CRC Press. ISBN: 978-
0123747310.
–
Chapter 7: Learning.
•
Russell, S. and Norvig, P. (2009). Artificial Intelligence:
A Modern Approach (3rd ed.). Prentice-Hall, ISBN:
ISBN: 0-13-604259-7.
–
Chapter 18: Learning from Observations
