
Artificial Intelligence
Lecture 05 – Randomness and Probability
Edirlei Soares de Lima
<edirlei.slima@gmail.com>
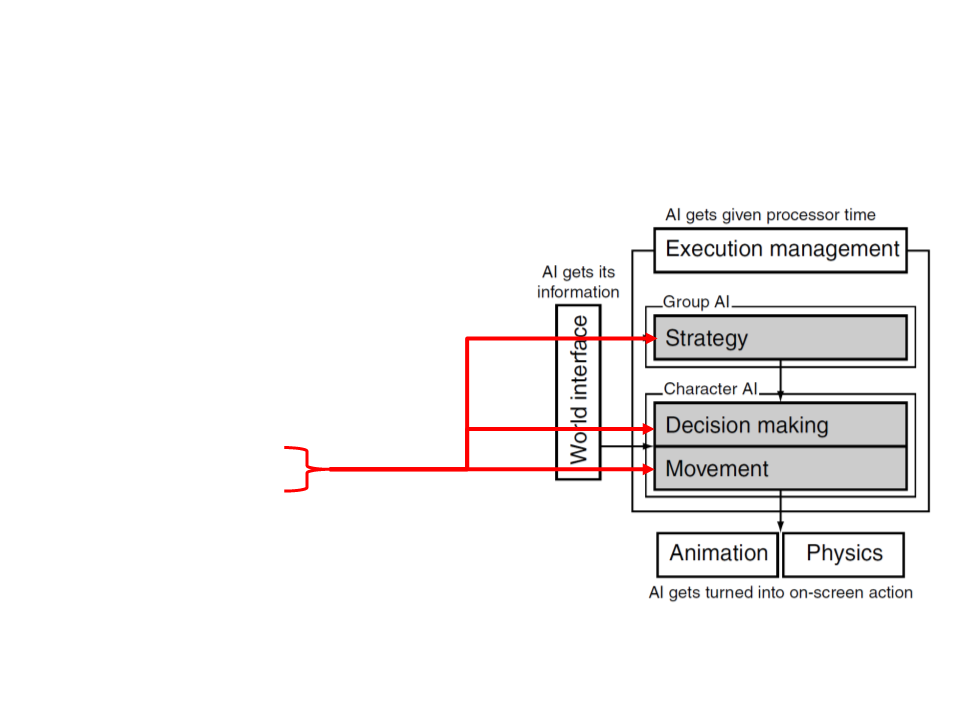
Game AI – Model
•
•
•
•
•
•
•
•
Pathfinding
Steering behaviours
Finite state machines
Automated planning
Behaviour trees
Randomness
Sensor systems
Machine learning
Randomness in Games
•
Game programmers have a special relationship with random
numbers. They can be used for several tasks:
–
–
–
–
–
–
–
–
–
–
Damage calculation;
Critical hits probability;
Item drop probability;
Reward probability;
Enemy stats;
Spawning enemies and items;
Shooting spread zones;
Decision making;
Procedural content generation;
…

Randomness and Probability
•
Although most programming languages include functions to
generate pseudo-random numbers, there are some situations
where some control over the random numbers is extremely
important.
–
–
Gaussian Randomness: normal distribution of random numbers.
Filtered Randomness: manipulation of random numbers so they
appear more random to players over short time frames.
–
Perlin Noise: consecutive random numbers that are related to each
other.

Gaussian Randomness
•
Normal distributions (also known as Gaussian distributions)
are all around us, hiding in the statistics of everyday life.
Height of Trees
Height of People

Gaussian Randomness
•
Normal distributions (also known as Gaussian distributions)
are all around us, hiding in the statistics of everyday life.
Speed of Runners in a Marathon
Speed of Cars on a Highway

Gaussian Randomness
•
•
There is randomness in previous examples, but they are not
uniformly random.
Example:
–
The chance of a man growing to be 170 cm tall is not the same as the
chance of him growing to a final height of 150 cm tall or 210 cm tall.
–
We see a normal distribution with the height of men centered around
1
70 cm.
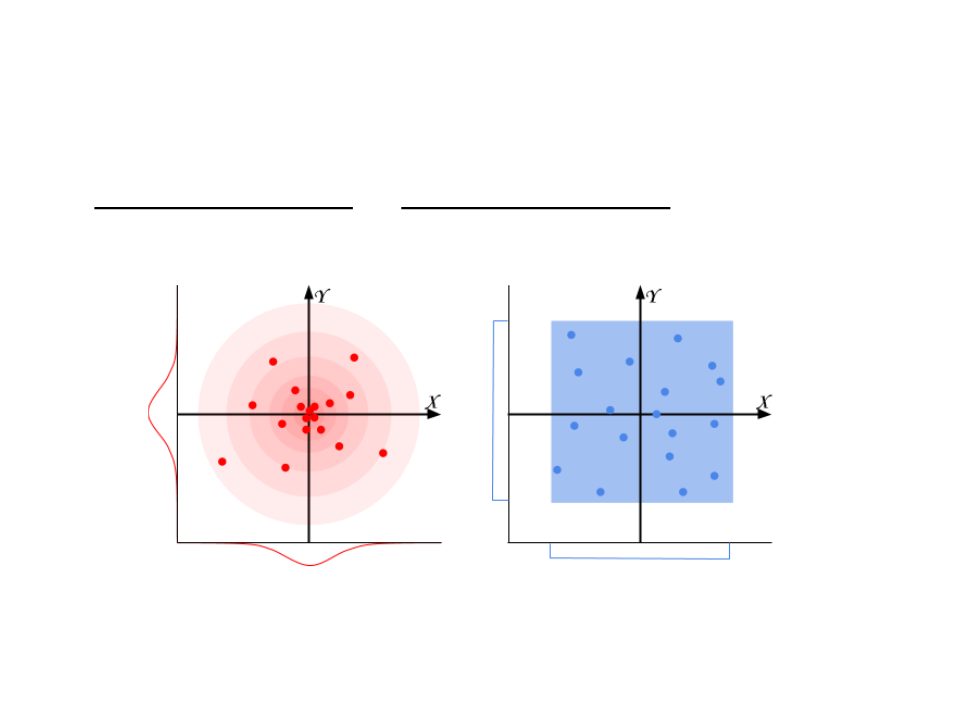
Gaussian Randomness
•
Normal Distribution vs. Uniform Distribution:
Normal Distribution
Uniform Distribution
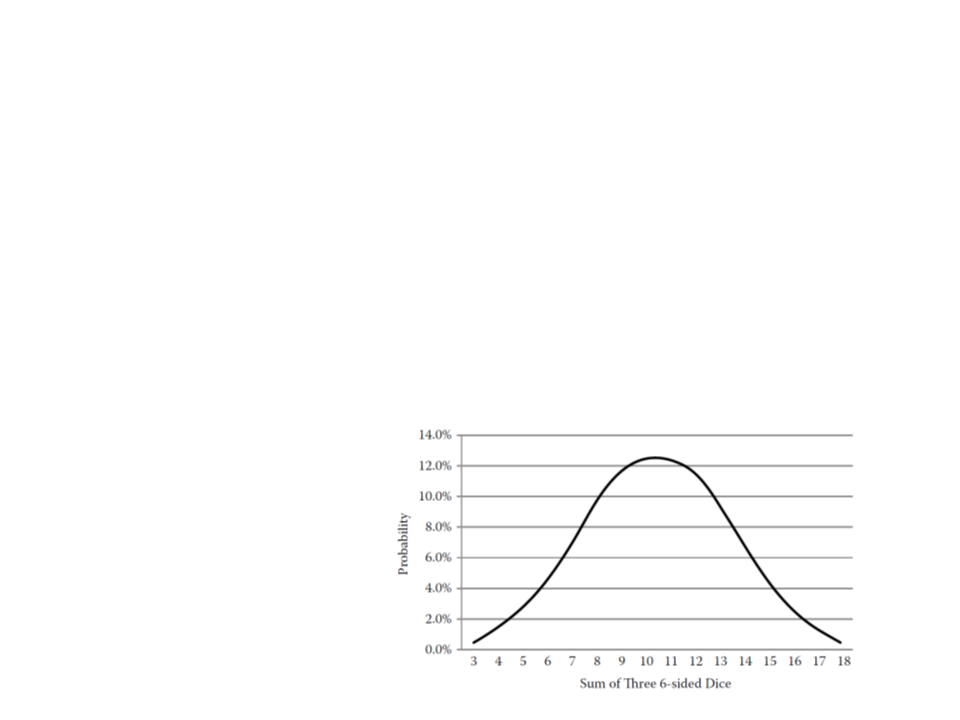
Gaussian Randomness
•
•
The large majority of distributions in life are closer to a
normal distribution than a uniform distribution.
Central Limit Theorem: when several independent random
variables are added together, the resulting sum will follow a
normal distribution.
–
Example: roll and sum
three 6-sided dices.

Gaussian Randomness
•
•
Why do most distributions in life follow a normal distribution?
–
Almost everything in the universe has more than one contributing
factor, and those factors have random aspects associated with them.
Example: what determines how tall a tree will grow?
–
Genes, precipitation, soil quality, air quality, amount of sunlight,
temperature, exposure to insects, ...
–
For an entire forest, each tree experiences varying aspects of each
quality, depending on where the tree is located.

Gaussian Randomness
•
How Gaussian randomness can be generated?
–
Box-Muller Transform (Marsaglia polar method):
public static float NextGaussian()
{
float v1, v2, s;
do{
v1 = 2.0f * Random.Range(0f, 1f) - 1.0f;
v2 = 2.0f * Random.Range(0f, 1f) - 1.0f;
s = v1 * v1 + v2 * v2;
}while (s >= 1.0f || s == 0f);
s = Mathf.Sqrt((-2.0f * Mathf.Log(s)) / s);
return v1 * s;
}

Gaussian Randomness
•
•
We can change the normal distribution according to a specific
mean and standard deviation:
public static float NextGaussian(float mean, float std_dev)
{
return mean + NextGaussian() * std_dev;
}
We can also guarantee that values never fall outside the
limits:
public static float NextGaussian(float mean, float std_dev,
float min, float max){
float v;
do{
v = NextGaussian(mean, standard_deviation);
}while (v < min || v > max);
return v;
}

Gaussian Randomness
•
Testing the gaussian random numbers:
void Start () {
Texture2D texture = new Texture2D(128, 128);
GetComponent<Renderer>().material.mainTexture = texture;
for (int x = 0; x < 300; x++) {
texture.SetPixel((int)NextGaussian(64, 10, 0, 128),
(int)NextGaussian(64, 10, 0, 128),
Color.black);
}
texture.Apply();
}

Applications of Gaussian Randomness
Uniform
Distribution Distribution
Gaussian
•
•
Gun aiming variation.
Any aspect of an NPC that may
vary within a population:
o Average or max acceleration.
5
0 Bullets
1
2
4
00 Bullets
00 Bullets
00 Bullets
o Size, width, height, or mass.
o Fire or reload rate for firing.
o Refresh rate or cool-down rate for
healing or special abilities.
o Chance of striking a critical hit.
o Level of intelligence.

Exercise 1
1
) Create a random population of 100 characters whose
height follow a normal distribution in Unity. You can use
any object to represent the characters, such as cubes or
cylinders.

Randomness Test
•
•
Exercise 1: grab a piece of paper and start writing down 0’s
and 1’s in a random sequence with a 50% chance of each—do
it until you have a list of 100 numbers.
Exercise 2: take out a coin and start flipping it, recording the
sequence of heads and tails as 0s and 1s. Flip it 100 times and
write the results in the paper.

Randomness Test
•
Exercise 3: compare the two lists you made to a list created by
a pseudo-random number generator function, with the same
5
0% chance of either a 0 or a 1. Example:
0
1
1101100001100001010000001001011110011100111000110
0101011011111101001011110011111101011111101000011
What are the differences between the hand-generated list,
the coin flip list, and the computer generated one?

Randomness Test
•
It’s very likely that the coin flip and computer generated lists
contain many more long runs of 0’s or 1’s compared to the
hand-generated list.
–
Most people don’t realize that real randomness almost always
contains these long runs.
–
Most people simply don’t believe a fair coin or real randomness will
produce those long runs of heads or tails.
Randomness in Games
•
Many games include situations where a uniformly distributed
random number determines something that affects the player,
either positively or negatively.
•
•
Players have expectations and they believe in “fair probability”.
Randomness is too random for many uses in games:
–
If the player don’t believes in the game randomness, he/she will thing
that the game is either broken or cheating—all of which are terrible
qualities to attribute to a game or an AI.

Randomness in Games
•
•
We have now entered the realm of psychology, and we have
temporarily left mathematics.
–
If the player thinks the game is cheating, then the game effectively is
cheating despite what is really happening.
–
Perception is far more important than reality when it comes to the
player’s enjoyment of the game.
Solution?
–
Make the numbers slightly less random!
–
When generating a random sequence of numbers, if the next number
will hurt the appearance of randomness, pretend that you never saw it
and generate a new number.

Identifying Anomalies
•
What makes a sequence of random numbers look less
random?
1
. The sequence has a pattern that stands out (e.g. 11001100 or
11000).
. The sequence has a long run of the same number (e.g.
1011111110).
1
2
0
•
The goal is to write some rules to identify these anomalies,
and then throw out the last number that triggers a rule.

Filtering Binary Randomness
•
Rules:
1
. If the newest value will produce a run of 4 or more equal values,
then there is a 75% chance to flip the newest value.
•
This doesn’t make runs of 4 or more impossible, but progressively much less likely
(the probability of a run of 4 occurring goes from 1/8 to 1/128).
2. If the newest value causes a repeating pattern of four values, then
flip the last value.
•
Example: 11001100 becomes 11001101
3. If the newest value causes a repeating pattern of two values with
three repetitions each, then flip the last value.
•
Example: 111000 becomes 111001

Filtering Binary Randomness
•
•
Original sequence:
0
1
1101100001100001010000001001011110011100111000110
0101011011111101001011110011111101011111101000011
Filtered sequence (highlighted numbers are flipped):
0
1
1101100011000101010001001001011100111001110010110
0101011011101101001011100111011101011101101000110

Filtering Binary Randomness
public class BinaryRandom {
private List<int> generatedNumbers;
private int maxHistory;
public BinaryRandom(int historySize){
maxHistory = historySize;
generatedNumbers = new List<int>();
}
public int NextBinary(){
int value = Random.Range(0, 2);
if (generatedNumbers.Count > maxHistory)
generatedNumbers.RemoveAt(0);
if (FilterValue(value))
value = FlipValue(value);
generatedNumbers.Add(value);
return value;
}
...

Filtering Binary Randomness
...
private int FlipValue(int value){
if (value == 1)
return 0;
else
return 1;
}
private bool FilterValue(int value){
if (FourRunsBinaryRule(value))
return true;
if (FourRepetitionsPatternBinaryRule(value))
return true;
if (TwoRepetitionsPatternBinaryRule(value))
return true;
return false;
}
...

Filtering Binary Randomness
...
private bool FourRunsBinaryRule(float value){
if (generatedNumbers.Count < 3)
return false;
for (int i = generatedNumbers.Count - 1;
i >= generatedNumbers.Count - 3; i--)
{
if (generatedNumbers[i] != value)
return false;
}
if (Random.Range(0, 4) == 0)
return false;
return true;
}
Rule 1: if the newest value will produce a
run of 4 or more equal values, then there
is a 75% chance to flip the newest value.
...

Filtering Binary Randomness
...
private bool FourRepetitionsPatternBinaryRule(float value){
if (generatedNumbers.Count < 7)
return false;
if (generatedNumbers[generatedNumbers.Count - 1] != value)
return false;
int count = 0;
for (int i = generatedNumbers.Count - 2;
i >= generatedNumbers.Count - 7; i-=2)
{
if (generatedNumbers[i] == generatedNumbers[i - 1])
count++;
}
if (count < 3)
return false;
return true;
Rule 2: if the newest value causes a
repeating pattern of four values, then
flip the last value.
}
.
..

Filtering Binary Randomness
...
private bool TwoRepetitionsPatternBinaryRule(float value){
if (generatedNumbers.Count < 5)
return false;
if ((generatedNumbers[generatedNumbers.Count - 1] != value) ||
(generatedNumbers[generatedNumbers.Count - 2] != value))
return false;
for (int i = generatedNumbers.Count - 3;
i >= generatedNumbers.Count - 5; i--)
{
if (generatedNumbers[i] == value)
return false;
}
return true;
}
}
Rule 3: if the newest value causes a repeating
pattern of two values with three repetitions
each, then flip the last value.

Filtering Integer Ranges
•
Rules:
1
2
3
4
. Repeating numbers.
• Example: [7, 7] or [3, 3].
. Repeating numbers separated by one digit.
•
Example: [8, 3, 8] or [6, 2, 6].
. A counting sequence of 4 that ascends or descends.
•
Example: [3, 4, 5, 6].
. Too many values (4) at the top or bottom of a range within the last
10 values.
•
Example: [6, 8, 7, 9, 8, 6, 9].
5. Patterns of two numbers that appear in the last 10 values.
• Example: [5, 7, 3, 1, 5, 7].
6
. Too many (4) of a particular number in the last 10 values.
•
Example: [9, 4, 5, 9, 7, 8, 9, 0, 2, 9].

Filtering Integer Ranges
•
•
Original sequence:
2
5
2312552222577750677564061448482102435500989388459
9607889964957780753281574605482138446235103745368
Filtered sequence (highlighted numbers are thrown out):
2
5
2312552222577750677564061448482102435500989388459
9607889964957780753281574605482138446235103745368

Exercise 2
2
) Based on the binary filter, create a class to filter integer
ranges according to the following rules:
1. Avoid repeating numbers (e.g.: [7, 7] or [3, 3]).
2
. Avoid repeating numbers separated by one digit (e.g.: [8, 3, 8] or
[
6, 2, 6].
. Avoid ascends or descends counting sequences of 4 numbers
e.g.: [3, 4, 5, 6]).
. Avoid 4 repetitions of a particular number in the last 10 values
e.g.: [9, 4, 5, 9, 7, 8, 9, 0, 2, 9]).
3
4
(
(

Filtering Floating-Point Ranges
•
Rules:
1. Reroll if two consecutive numbers differ by less than 0.02.
• Example: [0.875, 0.856].
2
. Reroll if three consecutive numbers differ by less than 0.1.
•
Example: [0.345, 0.421, 0.387].
3. Reroll if there is an increasing or decreasing run of 5 values.
• Example: [.342, 0.572, 0.619, 0.783, 0.868].
4. Reroll if there are too many values (4) at the top or bottom of a
range within the last 10 values.
•
Example: [0.325, 0.198, 0.056, 0.432, 0.119, 0.043].
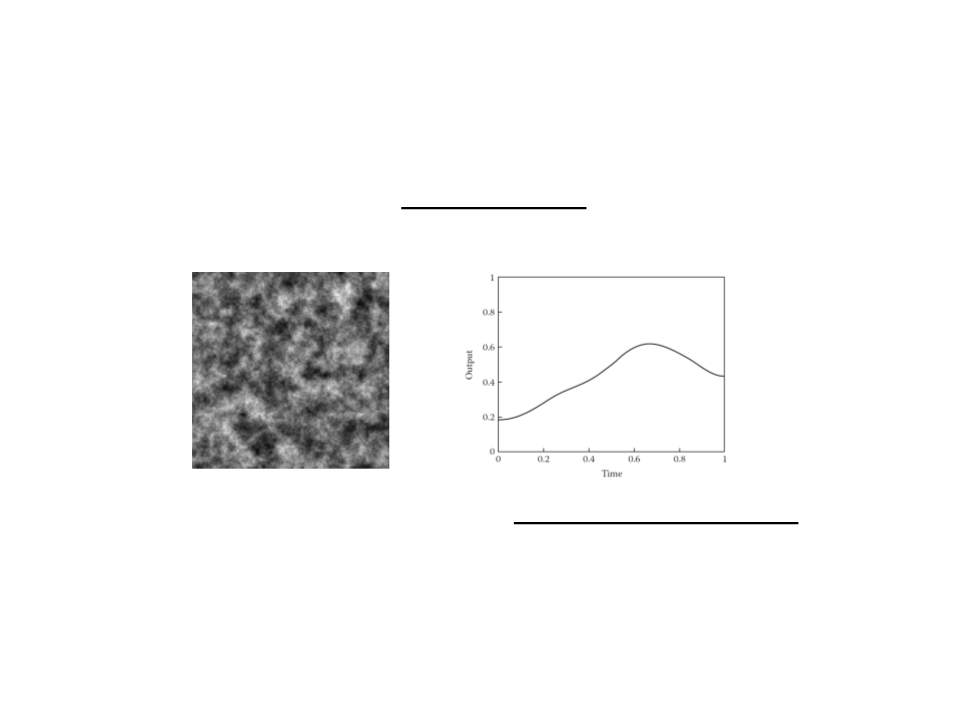
Perlin Noise for Game AI
•
•
Perlin noise is a type of gradient noise typically used in
computer graphics to generate organic textures.
Perlin noise generates a form of coherent randomness, where
consecutive random numbers are related to each other.
–
This “smooth” nature of randomness don’t generates wild jumps from
one random number to another, which can be a very desirable trait.

Perlin Noise for Game AI
•
Possible applications of Perlin noise for game AI:
–
–
–
–
–
Movement (direction, speed, acceleration);
Layered onto animation (adding noise to facial movement or gaze);
Attention (guard alertness, response time);
Play style (defensive, offensive);
Mood (calm, angry, happy, sad, depressed, manic, bored, engaged);

Perlin Noise in Unity
•
Unity has a function to compute 2D Perlin noise:
float Mathf.PerlinNoise(float x, float y);
•
•
It returns the Perlin noise value between 0.0 and 1.0.
Although the noise plane is two-dimensional, we can ignore
one coordinate and sample the noise from just one-dimension.

Perlin Noise in Unity
•
Example: movement direction:
public class WanderAgent : MonoBehaviour
{
public float speed = 2;
public float rotationFactor = 1.2f;
public float seed = 0.5f;
void Update ()
{
transform.forward = new Vector3(Mathf.PerlinNoise(Time.time *
seed, 0.0f) * rotationFactor,
transform.forward.y, transform.forward.z);
transform.position += transform.forward * Time.deltaTime * speed;
}
}

Further Reading
•
Rabin, S., Goldblatt, J., and Silva, F. (2013). Game AI Pro: Collected
Wisdom of Game AI Professionals. Steven Rabin (ed.), A K Peters/CRC
Press, ISBN: 978-1466565968.
–
Chapter 3: Advanced Randomness Techniques for Game AI
