
Artificial Intelligence
Lecture 07 – Randomness and Genetic
Algorithms
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
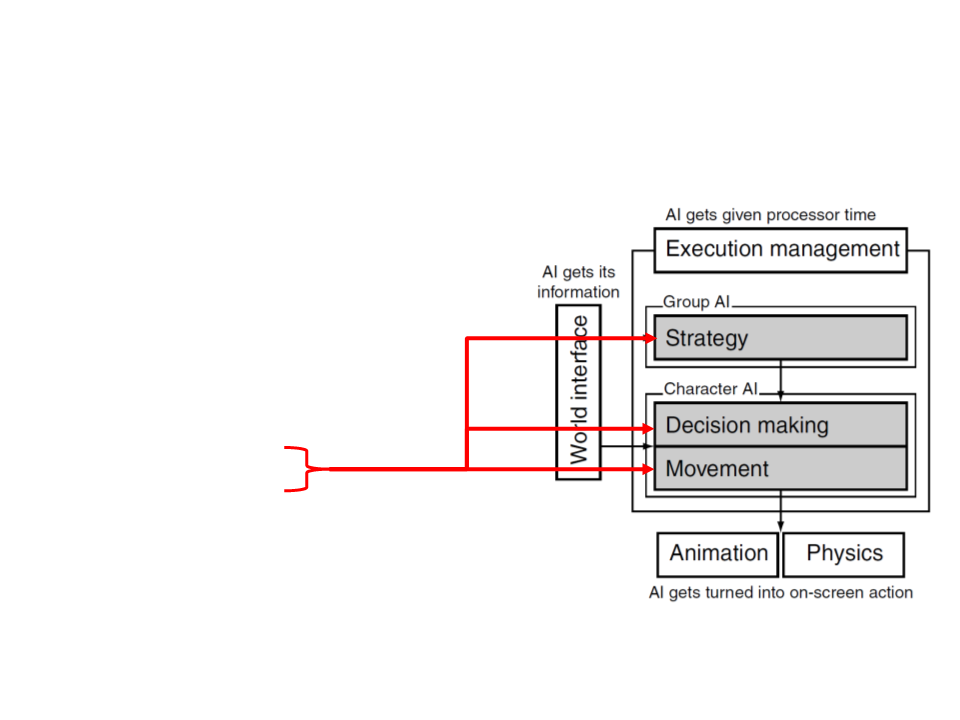
Game AI – Model
•
•
•
•
•
•
•
•
Pathfinding
Steering behaviours
Finite state machines
Automated planning
Behaviour trees
Randomness
Sensor systems
Machine learning
Randomness in Games
•
Game programmers have a special relationship with random
numbers. They can be used for several tasks:
–
–
–
–
–
–
–
–
–
–
Damage calculation;
Critical hits probability;
Item drop probability;
Reward probability;
Enemy stats;
Spawning enemies and items;
Shooting spread zones;
Decision making;
Procedural content generation;
…

Randomness and Probability
•
Although most programming languages include functions to
generate pseudo-random numbers, there are some situations
where some control over the random numbers is extremely
important.
–
–
Gaussian Randomness: normal distribution of random numbers.
Filtered Randomness: manipulation of random numbers so they
appear more random to players over short time frames.
–
Perlin Noise: consecutive random numbers that are related to each
other.

Gaussian Randomness
•
Normal distributions (also known as Gaussian distributions)
are all around us, hiding in the statistics of everyday life.
Height of Trees
Height of People

Gaussian Randomness
•
Normal distributions (also known as Gaussian distributions)
are all around us, hiding in the statistics of everyday life.
Speed of Runners in a Marathon
Speed of Cars on a Highway

Gaussian Randomness
•
•
There is randomness in previous examples, but they are not
uniformly random.
Example:
–
The chance of a man growing to be 170 cm tall is not the same as the
chance of him growing to a final height of 150 cm tall or 210 cm tall.
–
We see a normal distribution with the height of men centered around
1
70 cm.

Gaussian Randomness
•
Normal Distribution vs. Uniform Distribution:
Normal Distribution
Uniform Distribution
Gaussian Randomness
•
•
The large majority of distributions in life are closer to a
normal distribution than a uniform distribution.
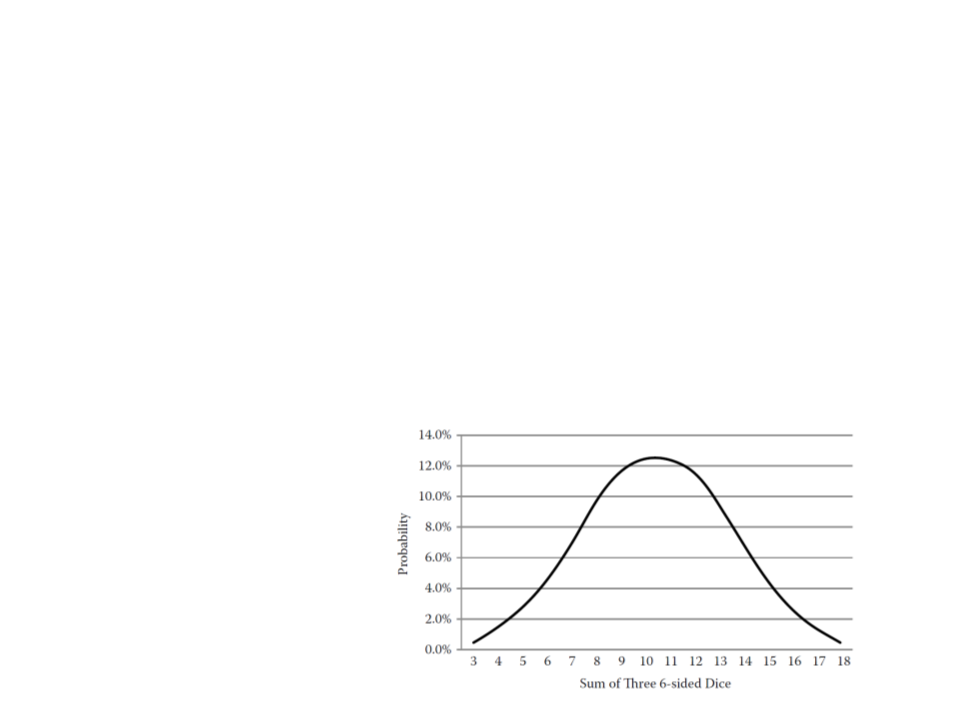
Central Limit Theorem: when several independent random
variables are added together, the resulting sum will follow a
normal distribution.
–
Example: roll and sum
three 6-sided dices.

Gaussian Randomness
•
•
Why do most distributions in life follow a normal distribution?
–
Almost everything in the universe has more than one contributing
factor, and those factors have random aspects associated with them.
Example: what determines how tall a tree will grow?
–
Genes, precipitation, soil quality, air quality, amount of sunlight,
temperature, exposure to insects, ...
–
For an entire forest, each tree experiences varying aspects of each
quality, depending on where the tree is located.

Gaussian Randomness
•
How Gaussian randomness can be generated?
–
Box-Muller Transform (Marsaglia polar method):
public static float NextGaussian()
{
float v1, v2, s;
do{
v1 = 2.0f * Random.Range(0f, 1f) - 1.0f;
v2 = 2.0f * Random.Range(0f, 1f) - 1.0f;
s = v1 * v1 + v2 * v2;
}while (s >= 1.0f || s == 0f);
s = Mathf.Sqrt((-2.0f * Mathf.Log(s)) / s);
return v1 * s;
}

Gaussian Randomness
•
•
We can change the normal distribution according to a specific
mean and standard deviation:
public static float NextGaussian(float mean, float std_dev)
{
return mean + NextGaussian() * std_dev;
}
We can also guarantee that values never fall outside the
limits:
public static float NextGaussian(float mean, float std_dev,
float min, float max){
float v;
do{
v = NextGaussian(mean, standard_deviation);
}while (v < min || v > max);
return v;
}

Gaussian Randomness
•
Testing the gaussian random numbers:
void Start () {
Texture2D texture = new Texture2D(128, 128);
GetComponent<Renderer>().material.mainTexture = texture;
for (int x = 0; x < 300; x++) {
texture.SetPixel((int)NextGaussian(64, 10, 0, 128),
(int)NextGaussian(64, 10, 0, 128),
Color.black);
}
texture.Apply();
}

Applications of Gaussian Randomness
Uniform
Distribution Distribution
Gaussian
•
•
Gun aiming variation.
Any aspect of an NPC that may
vary within a population:
o Average or max acceleration.
50 Bullets
100 Bullets
200 Bullets
400 Bullets
o Size, width, height, or mass.
o Fire or reload rate for firing.
o Refresh rate or cool-down rate for
healing or special abilities.
o Chance of striking a critical hit.
o Level of intelligence.

Exercise 1
1
) Create a random population of 100 characters whose
height follow a normal distribution in Unity. You can use
any object to represent the characters, such as cubes or
cylinders.

Randomness Test
•
•
Exercise 1: grab a piece of paper and start writing down 0’s
and 1’s in a random sequence with a 50% chance of each—do
it until you have a list of 100 numbers.
Exercise 2: take out a coin and start flipping it, recording the
sequence of heads and tails as 0s and 1s. Flip it 100 times and
write the results in the paper.

Randomness Test
•
Exercise 3: compare the two lists you made to a list created by
a pseudo-random number generator function, with the same
5
0% chance of either a 0 or a 1. Example:
0
1
1101100001100001010000001001011110011100111000110
0101011011111101001011110011111101011111101000011
What are the differences between the hand-generated list,
the coin flip list, and the computer generated one?

Randomness Test
•
It’s very likely that the coin flip and computer generated lists
contain many more long runs of 0’s or 1’s compared to the
hand-generated list.
–
Most people don’t realize that real randomness almost always
contains these long runs.
–
Most people simply don’t believe a fair coin or real randomness will
produce those long runs of heads or tails.

Randomness in Games
•
Many games include situations where a uniformly distributed
random number determines something that affects the player,
either positively or negatively.
•
•
Players have expectations and they believe in “fair probability”.
Randomness is too random for many uses in games:
–
If the player don’t believes in the game randomness, he/she will thing
that the game is either broken or cheating—all of which are terrible
qualities to attribute to a game or an AI.

Randomness in Games
•
•
We have now entered the realm of psychology, and we have
temporarily left mathematics.
–
If the player thinks the game is cheating, then the game effectively is
cheating despite what is really happening.
–
Perception is far more important than reality when it comes to the
player’s enjoyment of the game.
Solution?
–
Make the numbers slightly less random!
–
When generating a random sequence of numbers, if the next number
will hurt the appearance of randomness, pretend that you never saw it
and generate a new number.

Identifying Anomalies
•
What makes a sequence of random numbers look less
random?
1
2
. The sequence has a pattern that stands out (e.g. 11001100 or
11000).
. The sequence has a long run of the same number (e.g.
1011111110).
1
0
•
The goal is to write some rules to identify these anomalies,
and then throw out the last number that triggers a rule.

Filtering Binary Randomness
•
Rules:
1
. If the newest value will produce a run of 4 or more equal values,
then there is a 75% chance to flip the newest value.
•
This doesn’t make runs of 4 or more impossible, but progressively much less likely
(the probability of a run of 4 occurring goes from 1/8 to 1/128).
2
3
. If the newest value causes a repeating pattern of four values, then
flip the last value.
•
Example: 11001100 becomes 11001101
. If the newest value causes a repeating pattern of two values with
three repetitions each, then flip the last value.
•
Example: 111000 becomes 111001

Filtering Binary Randomness
•
•
Original sequence:
0
1
1101100001100001010000001001011110011100111000110
0101011011111101001011110011111101011111101000011
Filtered sequence (highlighted numbers are flipped):
0
1
1101100011000101010001001001011100111001110010110
0101011011101101001011100111011101011101101000110

Filtering Binary Randomness
public class BinaryRandom {
private List<int> generatedNumbers;
private int maxHistory;
public BinaryRandom(int historySize){
maxHistory = historySize;
generatedNumbers = new List<int>();
}
public int NextBinary(){
int value = Random.Range(0, 2);
if (generatedNumbers.Count > maxHistory)
generatedNumbers.RemoveAt(0);
if (FilterValue(value))
value = FlipValue(value);
generatedNumbers.Add(value);
return value;
}
.
..

Filtering Binary Randomness
.
..
private int FlipValue(int value){
if (value == 1)
return 0;
else
return 1;
}
private bool FilterValue(int value){
if (FourRunsBinaryRule(value))
return true;
if (FourRepetitionsPatternBinaryRule(value))
return true;
if (TwoRepetitionsPatternBinaryRule(value))
return true;
return false;
}
.
..

Filtering Binary Randomness
.
..
private bool FourRunsBinaryRule(float value){
if (generatedNumbers.Count < 3)
return false;
for (int i = generatedNumbers.Count - 1;
i >= generatedNumbers.Count - 3; i--)
{
if (generatedNumbers[i] != value)
return false;
}
if (Random.Range(0, 4) == 0)
return false;
return true;
}
Rule 1: if the newest value will produce a
run of 4 or more equal values, then there
is a 75% chance to flip the newest value.
.
..

Filtering Binary Randomness
.
..
private bool FourRepetitionsPatternBinaryRule(float value){
if (generatedNumbers.Count < 7)
return false;
if (generatedNumbers[generatedNumbers.Count - 1] != value)
return false;
int count = 0;
for (int i = generatedNumbers.Count - 2;
i >= generatedNumbers.Count - 7; i-=2)
{
if (generatedNumbers[i] == generatedNumbers[i - 1])
count++;
}
if (count < 3)
return false;
return true;
Rule 2: if the newest value causes a
repeating pattern of four values, then
flip the last value.
}
.
..

Filtering Binary Randomness
.
..
private bool TwoRepetitionsPatternBinaryRule(float value){
if (generatedNumbers.Count < 5)
return false;
if ((generatedNumbers[generatedNumbers.Count - 1] != value) ||
(generatedNumbers[generatedNumbers.Count - 2] != value))
return false;
for (int i = generatedNumbers.Count - 3;
i >= generatedNumbers.Count - 5; i--)
{
if (generatedNumbers[i] == value)
return false;
}
return true;
}
}
Rule 3: if the newest value causes a repeating
pattern of two values with three repetitions
each, then flip the last value.

Filtering Integer Ranges
•
Rules:
1
2
3
4
. Repeating numbers.
• Example: [7, 7] or [3, 3].
. Repeating numbers separated by one digit.
•
Example: [8, 3, 8] or [6, 2, 6].
. A counting sequence of 4 that ascends or descends.
•
Example: [3, 4, 5, 6].
. Too many values (4) at the top or bottom of a range within the last
10 values.
•
Example: [6, 8, 7, 9, 8, 6, 9].
5
6
. Patterns of two numbers that appear in the last 10 values.
• Example: [5, 7, 3, 1, 5, 7].
. Too many (4) of a particular number in the last 10 values.
•
Example: [9, 4, 5, 9, 7, 8, 9, 0, 2, 9].

Filtering Integer Ranges
•
•
Original sequence:
2
5
2312552222577750677564061448482102435500989388459
9607889964957780753281574605482138446235103745368
Filtered sequence (highlighted numbers are thrown out):
2
5
2312552222577750677564061448482102435500989388459
9607889964957780753281574605482138446235103745368

Exercise 2
2
) Based on the binary filter, create a class to filter integer
ranges according to the following rules:
1
2
. Avoid repeating numbers (e.g.: [7, 7] or [3, 3]).
. Avoid repeating numbers separated by one digit (e.g.: [8, 3, 8] or
[
6, 2, 6].
. Avoid ascends or descends counting sequences of 4 numbers
e.g.: [3, 4, 5, 6]).
. Avoid 4 repetitions of a particular number in the last 10 values
e.g.: [9, 4, 5, 9, 7, 8, 9, 0, 2, 9]).
3
4
(
(

Filtering Floating-Point Ranges
•
Rules:
1
. Reroll if two consecutive numbers differ by less than 0.02.
• Example: [0.875, 0.856].
2
. Reroll if three consecutive numbers differ by less than 0.1.
•
Example: [0.345, 0.421, 0.387].
3
4
. Reroll if there is an increasing or decreasing run of 5 values.
• Example: [0.342, 0.572, 0.619, 0.783, 0.868].
. Reroll if there are too many values (4) at the top or bottom of a
range within the last 10 values.
•
Example: [0.325, 0.198, 0.056, 0.432, 0.119, 0.043].
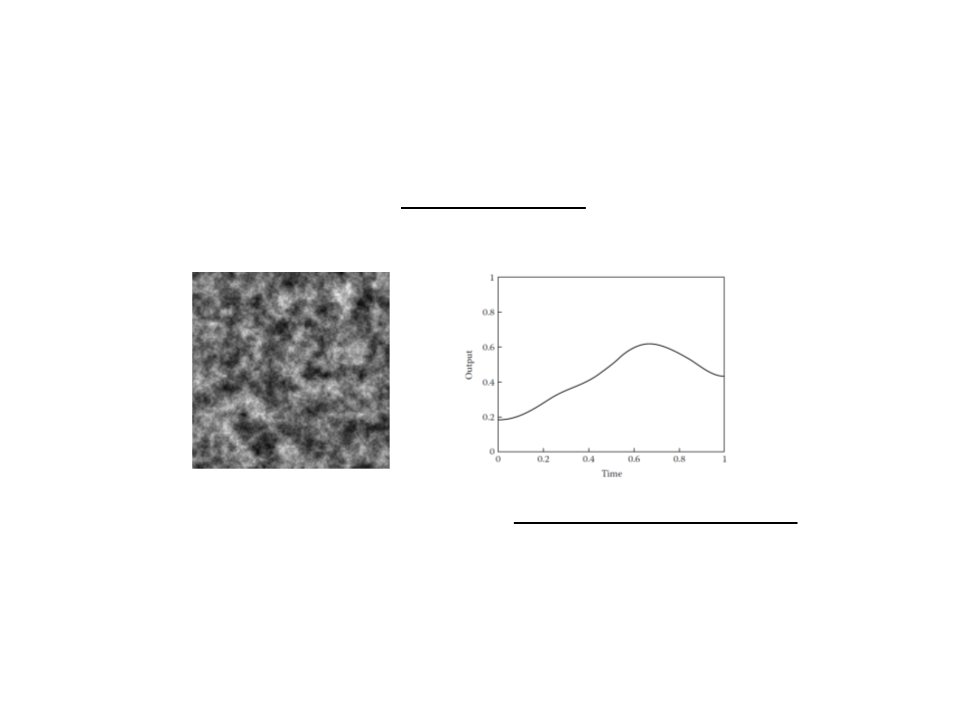
Perlin Noise for Game AI
•
•
Perlin noise is a type of gradient noise typically used in
computer graphics to generate organic textures.
Perlin noise generates a form of coherent randomness, where
consecutive random numbers are related to each other.
–
This “smooth” nature of randomness does not generate wild jumps from
one random number to another, which can be a very desirable trait.

Perlin Noise for Game AI
•
Possible applications of Perlin noise for game AI:
–
–
–
–
–
Movement (direction, speed, acceleration);
Layered onto animation (adding noise to facial movement or gaze);
Attention (guard alertness, response time);
Play style (defensive, offensive);
Mood (calm, angry, happy, sad, depressed, manic, bored, engaged);

Perlin Noise in Unity
•
Unity has a function to compute 2D Perlin noise:
float Mathf.PerlinNoise(float x, float y);
•
•
It returns the Perlin noise value between 0.0 and 1.0.
Although the noise plane is two-dimensional, we can ignore
one coordinate and sample the noise from just one-dimension.

Perlin Noise in Unity
•
Example: movement direction:
public class WanderAgent : MonoBehaviour
{
public float speed = 2;
public float rotationFactor = 1.2f;
public float seed = 0.5f;
void Update ()
{
transform.forward = new Vector3(Mathf.PerlinNoise(Time.time *
seed, 0.0f) * rotationFactor,
transform.forward.y, transform.forward.z);
transform.position += transform.forward * Time.deltaTime * speed;
}
}

Genetic Algorithms
•
Genetic algorithms are inspired by the process of natural
selection proposed by Charles Darwin in 1859 in his famous
work entitled "On the Origin of Species“.
–
–
–
–
In the real world, species constantly evolve in an attempt to better
adapt to their environments.
The best individuals (more adapted) are those who continue to
survive.
Through reproduction, the best individuals are able to pass on their
traits to the next generations.
In addition, sometimes random mutations also can take place during
the reproduction process (good or bad mutations).
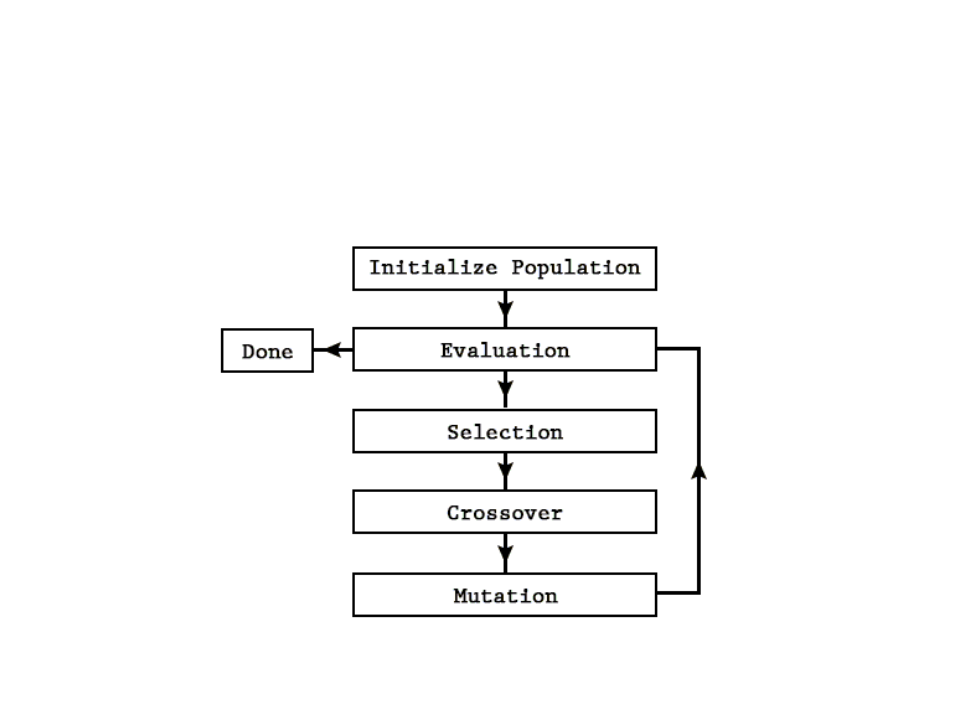
Genetic Algorithms
•
Process Overview:
Genetic Algorithms
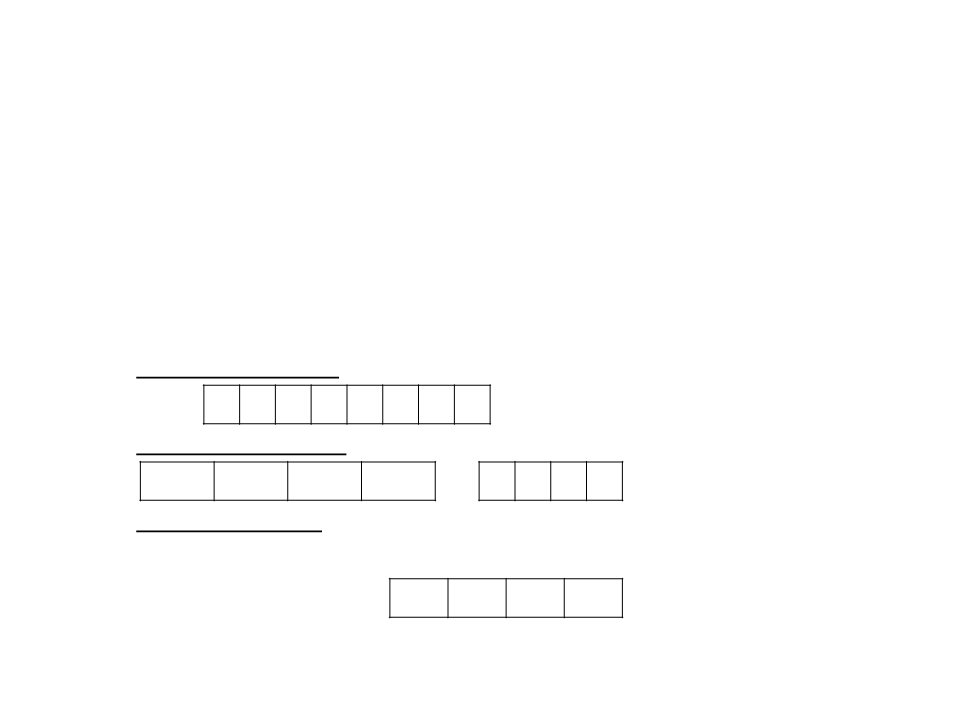
•
•
Encoding individuals: each individual must represent a
possible solution to the problem.
Examples:
–
–
–
Integer to bit array:
1
82 = 1 0 1 1 0 1 1 0
List to Integer array:
WP5 WP2 WP4 WP7 = 5 2 4 7
Behavior to array:
Shooting rate: 0.6
Speed: 100
Patrol rote: P2
…
= 0.6 100 P2
...
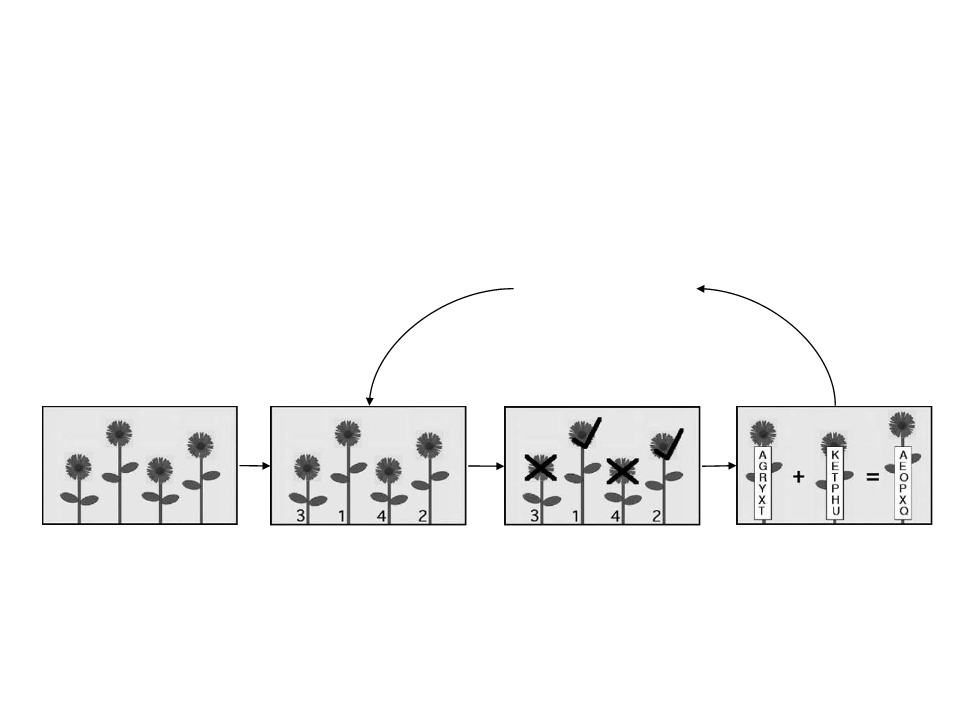
Genetic Algorithms
•
Example: flower generation
New population
Initial population
Evaluation
Selection
Crossover

Genetic Algorithms - Evaluation
•
•
The evaluation function determines the fitness of an
individual.
–
This is the most important part to the genetic algorithm, if this
function is not good, the algorithm will produce bad results.
Examples:
–
Path: WP5 WP2 WP4 WP7
• Fitness = distance(WP5, WP2) + distance(WP2, WP4) + distance(WP4, WP7)
–
Behavior:
0
.6 100 P2
...
•
Fitness = how good the NPC was in a simulated game session (number of lives,
number of kills, score, etc.)
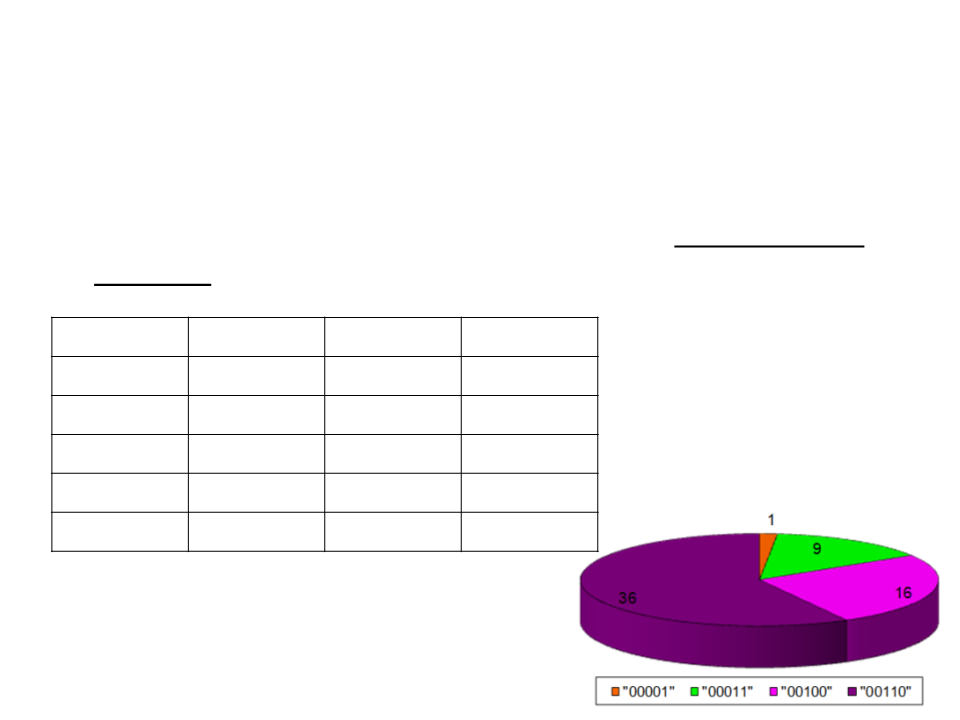
Genetic Algorithms - Selection
•
Selection is the process of selection the individuals for the
crossover process. A common method is the roulette wheel
selection.
Individual Evaluation Chance (%) Chance (°)
0
0
0
0
0001
0011
0100
0110
1
1.61
14.51
25.81
58.07
100.00
5.8
9
52.2
16
36
62
92.9
209.1
360.0
Total

Genetic Algorithms - Crossover
•
•
Crossover is the process of combining the DNA of two selected
individuals to produce a child for the new population.
–
There are several crossover methods: single-point crossover, two-point
crossover, n-point crossover, uniform crossover, etc.
Single-point crossover:
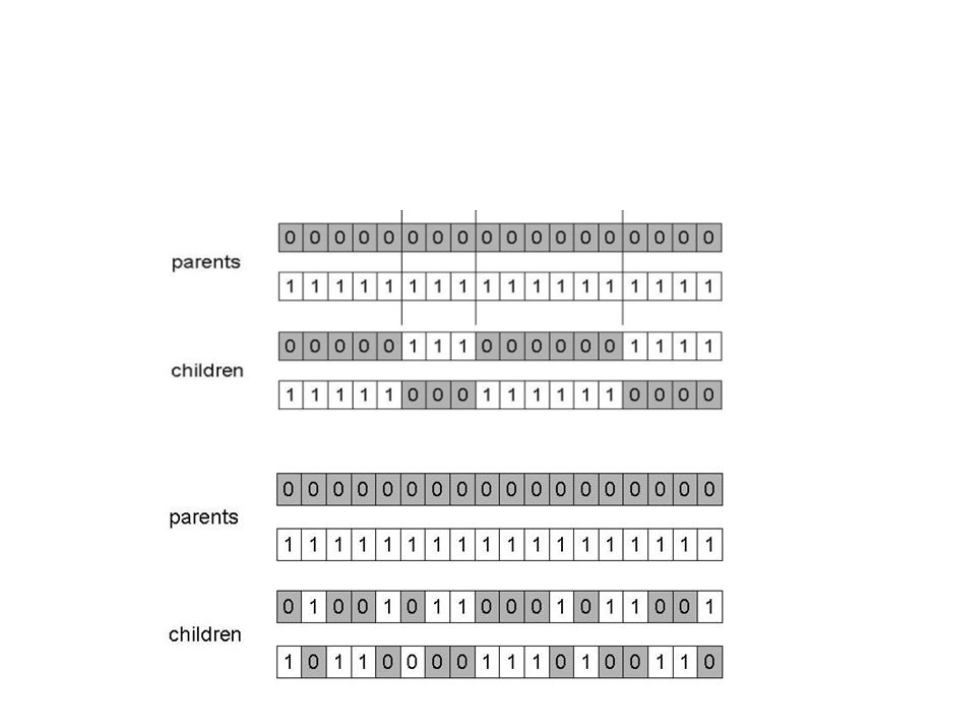
Genetic Algorithms - Crossover
•
•
N-point crossover:
Uniform crossover:
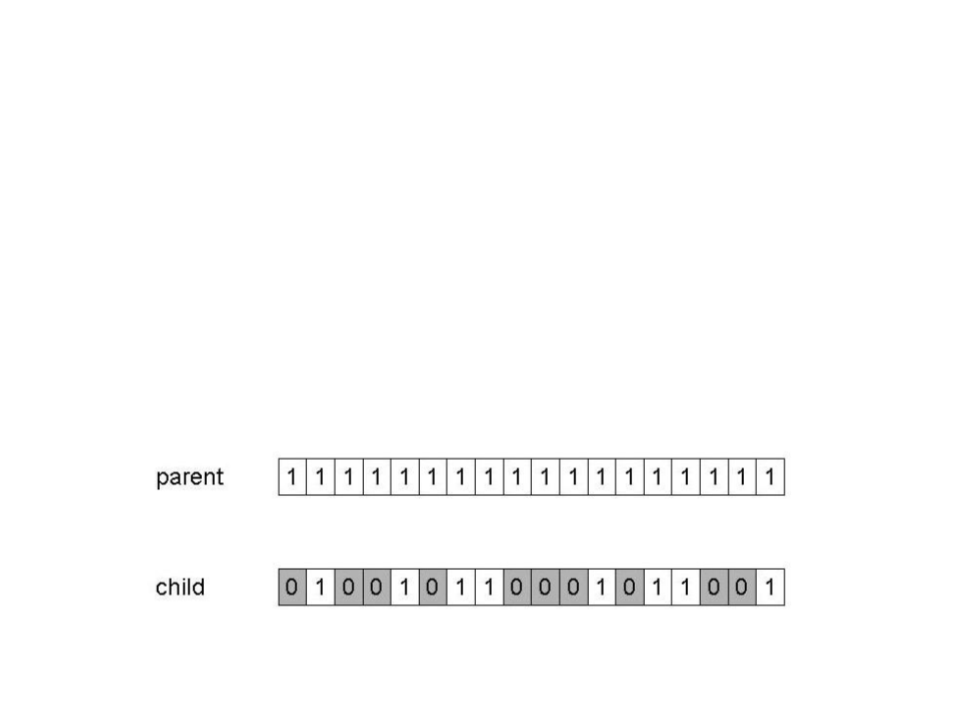
Genetic Algorithms - Mutation
•
•
Mutation allows the algorithm to introduce diversity into the
population, expanding the opportunity to search unexplored
areas in the search space for better solutions.
–
Usually the probability for mutations is small (between 2% or 5%);
Uniform mutation:

Genetic Algorithms – Example
•
Problem: 8-Queens

Genetic Algorithms – Example
Problem: 8-Queens
•
•
How the individuals can be encoded?

Genetic Algorithms – Example
Problem: 8-Queens
•
•
How the individuals can be encoded?
–
8 digits: each one representing the column
position of one queen.
–
Example: (1, 7, 4, 6, 8, 2, 5, 3)

Genetic Algorithms – Example
Problem: 8-Queens
•
•
How the individuals can be encoded?
–
8 digits: each one representing the column
position of one queen.
–
Example: (1, 7, 4, 6, 8, 2, 5, 3)
•
How the individuals can be evaluated?

Genetic Algorithms – Example
Problem: 8-Queens
•
•
How the individuals can be encoded?
–
8 digits: each one representing the column
position of one queen.
–
Example: (1, 7, 4, 6, 8, 2, 5, 3)
•
How the individuals can be evaluated?
–
Number of non-attacking pairs of queens.

Genetic Algorithms – Example
(3, 2, 7, 5, 2, 4, 1, 1) = 23
(2, 4, 7, 4, 8, 5, 5, 2) = 24

Genetic Algorithms – Example
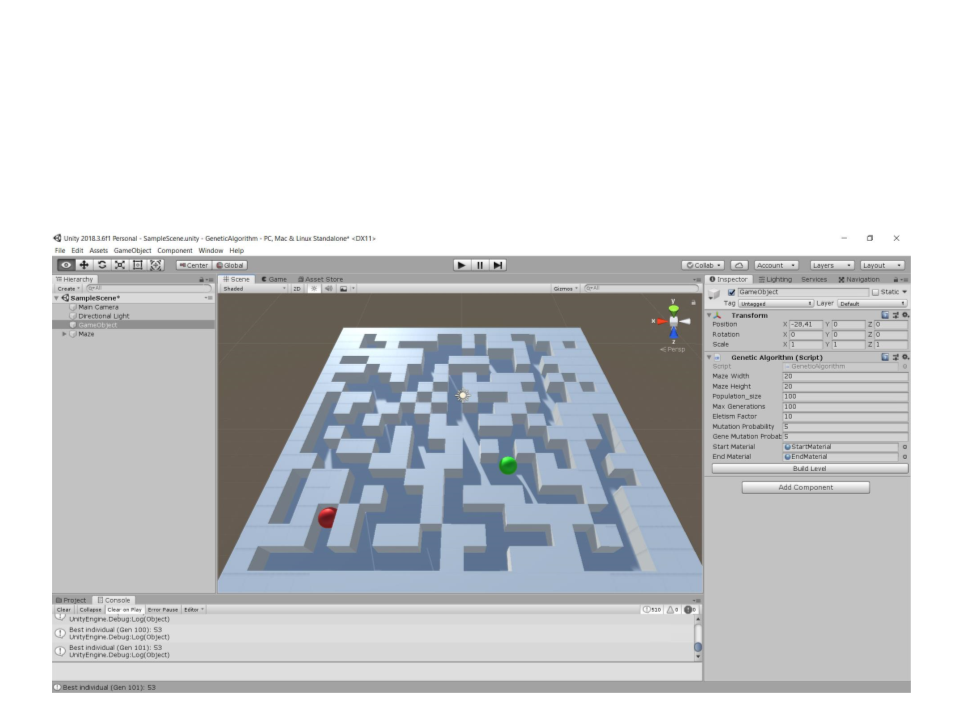
Genetic Algorithms – Unity
•
Maze generation using genetic algorithms:
Genetic Algorithms – Unity
[CustomEditor(typeof(GeneticAlgorithm))]
public class GeneticAlgorithmEditor : Editor
{
public override void OnInspectorGUI()
{
DrawDefaultInspector();
GeneticAlgorithm geneticAlgorithm = (GeneticAlgorithm)target;
if (GUILayout.Button("Build Level"))
{
geneticAlgorithm.BuildLevel();
}
}
}

Genetic Algorithms – Unity
public class Individual
{
public int[,] maze;
public Vector2Int start;
public Vector2Int end;
public float evaluation;
public Individual(int[,] nmaze, Vector2Int nstart,
Vector2Int nend, float nevaluation)
{
maze = nmaze;
start = nstart;
end = nend;
evaluation = nevaluation;
}
}

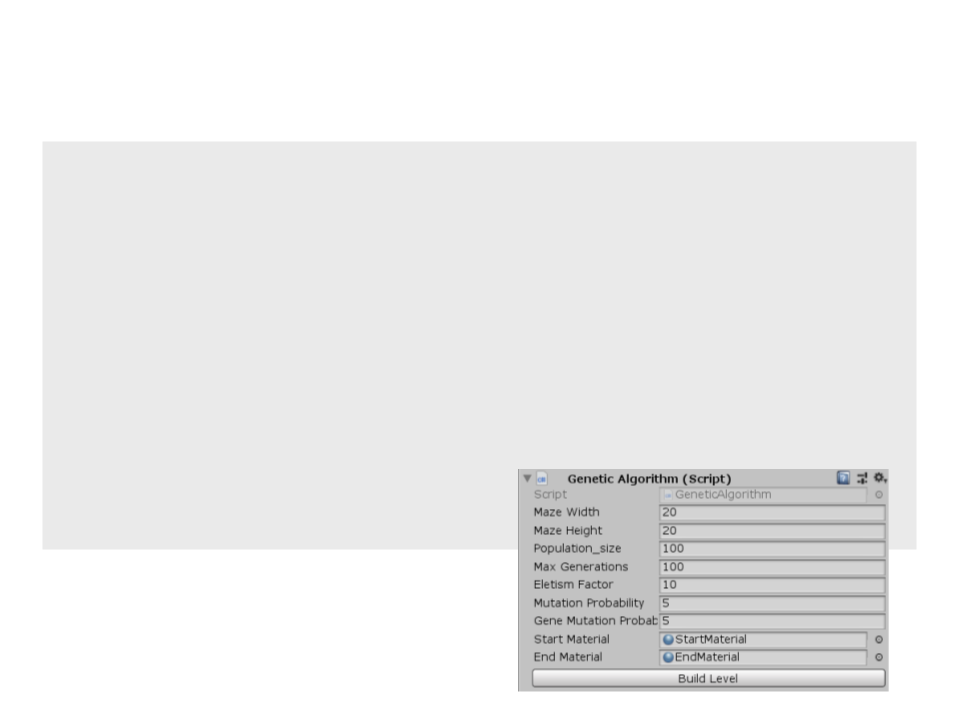
Genetic Algorithms – Unity
public class GeneticAlgorithm : MonoBehaviour
{
public int mazeWidth = 20;
public int mazeHeight = 20;
public int population_size = 100;
public int maxGenerations = 100;
public int eletismFactor = 10;
public int mutationProbability = 5;
public int geneMutationProbability = 5;
public Material startMaterial;
public Material endMaterial;
private Pathfinding pathfinding;
private GameObject lastMaze;
.
..

Genetic Algorithms – Unity
private int[,] GenerateIndividual() { ... }
private List<Individual> GenerateInitialPopulation() { ... }
private void EvaluatePopulation(List<Individual> population) { ... }
private(int parent1, int parent2) Selection(List<Individual>
population) { ... }
private Individual Mutation(Individual individual) { ... }
private (Individual child1, Individual child2) Crossover(
Individual parent1, Individual parent2) { ... }
private Individual RunGeneticAlgorithm() { ... }
private void GenerateLevelGeometry(Individual maze) { ... }
public void BuildLevel() { ... }

Exercise 3
3
) Change the maze generation algorithm to support 3 different
terrain types: grass, sand, and water.
–
–
–
The genetic algorithm must be adapted in order to assign the terrain
type to all areas that are not walls;
The evaluation function must take into account the terrain type when
evaluating an individual;
The costs associated with the terrain types are:
•
Grass: 2
Sand: 3
Water: 4
•
•

Further Reading
•
Rabin, S., Goldblatt, J., and Silva, F. (2013). Game AI Pro: Collected
Wisdom of Game AI Professionals. Steven Rabin (ed.), A K Peters/CRC
Press, ISBN: 978-1466565968.
–
Chapter 3: Advanced Randomness Techniques for Game AI
