
Artificial Intelligence
Lecture 02 - Pathfinding
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
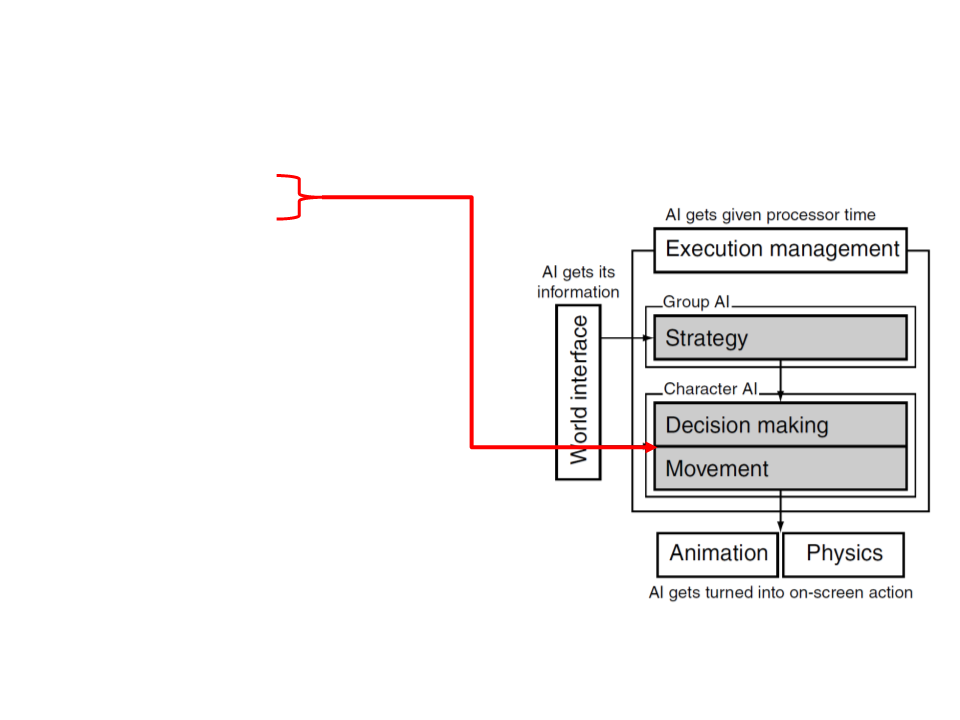
Game AI – Model
•
•
•
•
•
•
•
•
Pathfinding
Steering behaviours
Finite state machines
Automated planning
Behaviour trees
Randomness
Sensor systems
Machine learning

Pathfinding
•
Game characters usually need to move around their level.
•
While simple movements can be manually defined by game
developers (patrol routes or wander regions), more complex
movements must be computed during the game.

Pathfinding
•
Finding a path seems obvious and natural in real life. But how
a computer-controlled character can do that?
–
The computer needs to find the “best” path and do it in real-time.
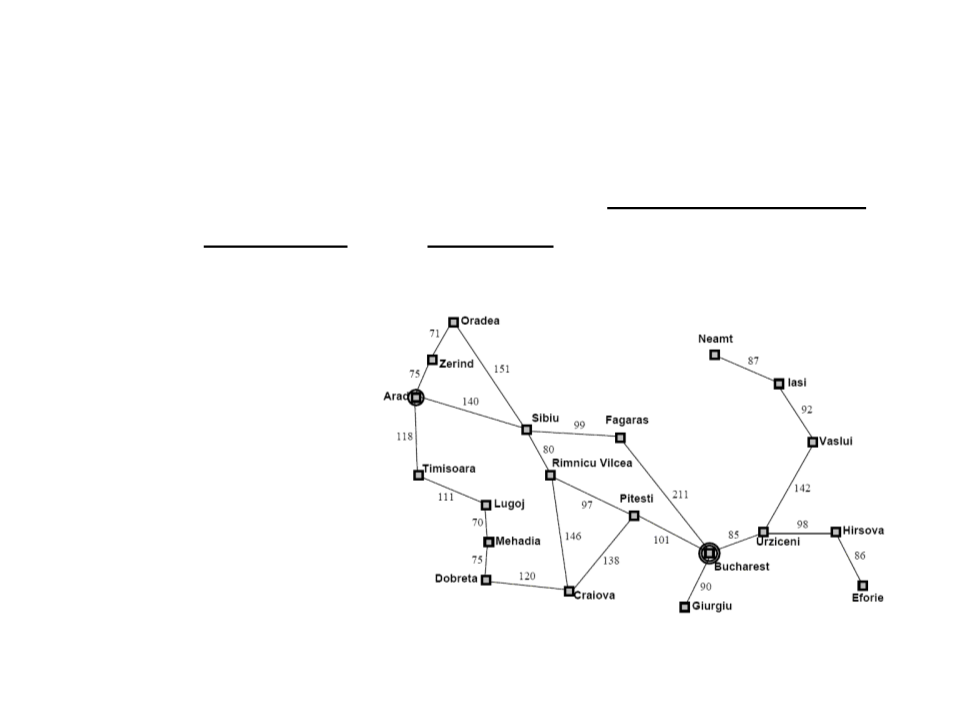
Search Problem
•
•
Pathfinding is a search problem: find a sequence of actions
from an initial state to an goal state.
Problem definition:
–
–
–
–
–
Initial state
Goal state
State space
Set of actions
Cost functions

Search Problem
•
•
•
The process of looking for a sequence of actions that reaches
the goal is called search.
Once a solution is found, the actions it recommends can be
carried out.
Phases:
–
–
–
Goal formulation
Search
Execution
Examples of Search Problems
•
Route-finding:
–
–
–
–
State space: map;
Initial state: current city;
Goal state: destination city;
Set of actions: go from one city to another (only possible if there is a
path between the cities);
–
Action cost: distance between the cities;
Examples of Search Problems
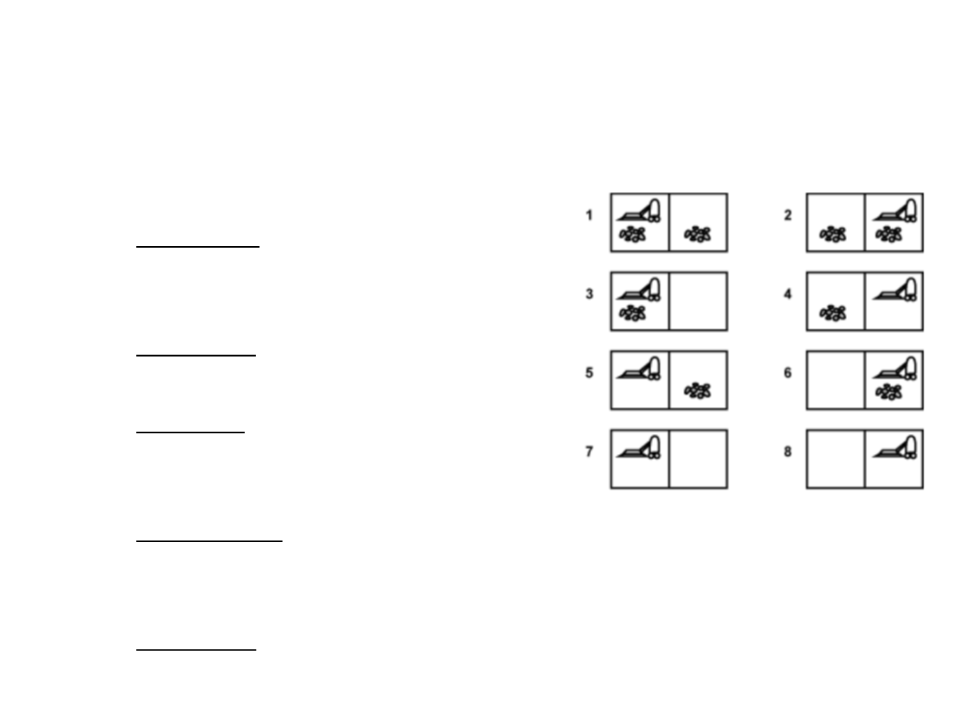
•
Vacuum world:
–
State space: agent location and the dirt
locations (8 possible states);
–
–
Initial state: any state;
Goal state: all locations clean (state 7
or 8);
–
–
Set of actions: move left, move right,
and suck;
Action cost: 1 per action;
Examples of Search Problems
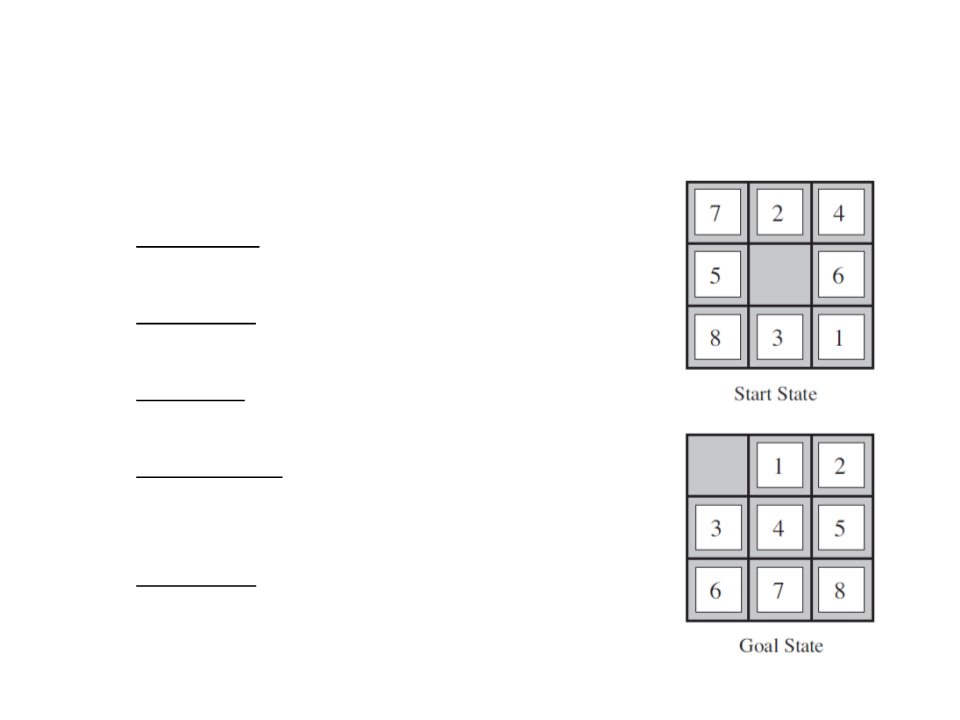
•
8-Puzzle Game:
–
–
–
–
State space: 181.440 possible states;
Initial state: any state;
Goal state: Goal State in the figure;
Set of actions: move the blank space left,
right, up, or down;
–
Action cost: 1 per action;
1
2
5-puzzle (4x4) – 1.3 trillion possible states.
4-puzzle (5x5) – 10²⁵ possible states.

Examples of Search Problems
•
Chess Game:
–
State space: approximately 1040 possible
states;
–
–
–
–
Initial state: start position of a chess game;
Goal state: any checkmate state;
Set of actions: pieces movement rules;
Action cost: examined states;
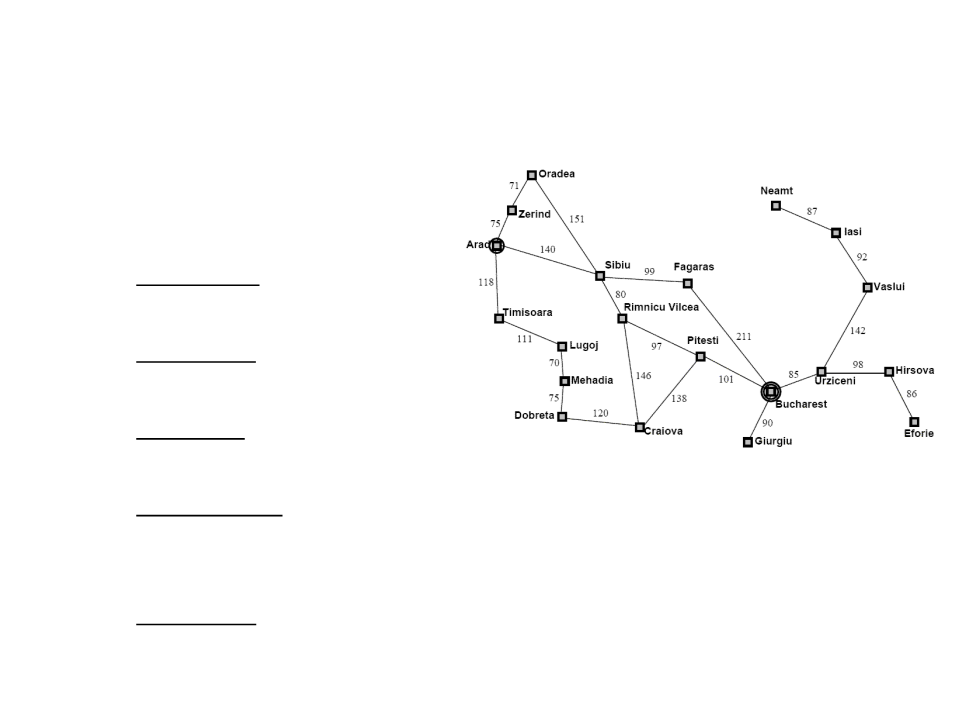
General Pathfinding Problems
•
State space: waypoint graphs or
tiled-based maps;
A
•
•
•
•
Initial state: current location (A);
Goal state: destination location (B);
Set of actions: movements;
B
Action cost: distance or terrain
difficulty;
Navigation Graph
•
Pathfinding algorithms can’t work directly on the level
geometry. They rely on a simplified version of the level,
usually represented in the form of a graph.

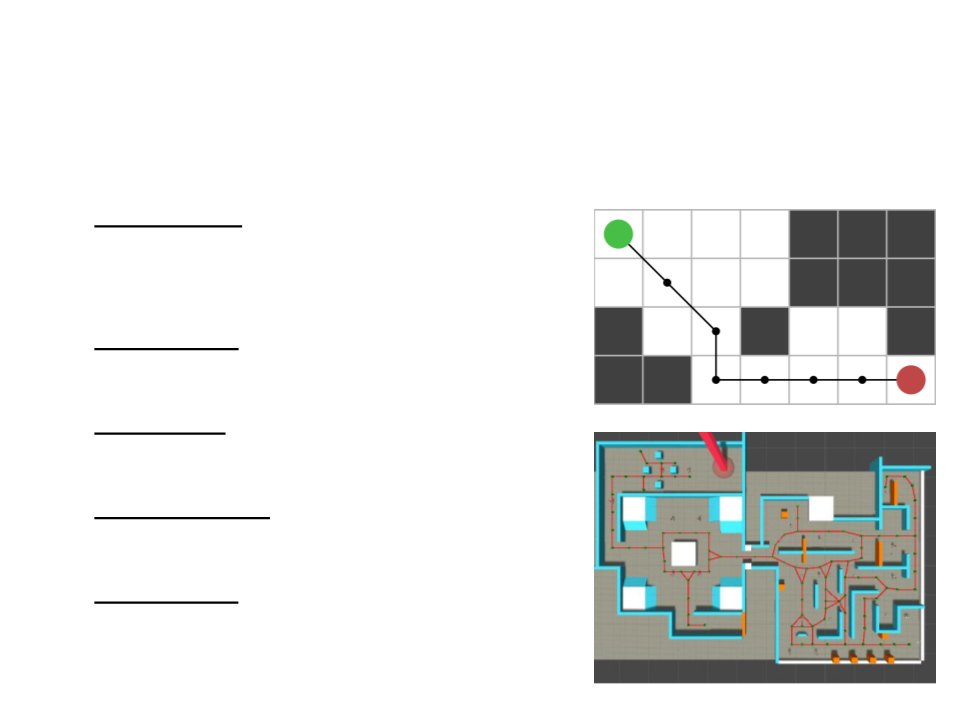
Exercise 1
1
) Create a maze in Unity. This maze will be used to test the
pathfinding algorithms. Example:
General Graph Structure
Edge
•
G = (V, E)
–
–
–
G: graph;
V: set of vertices;
E: set of edges;
Vertex
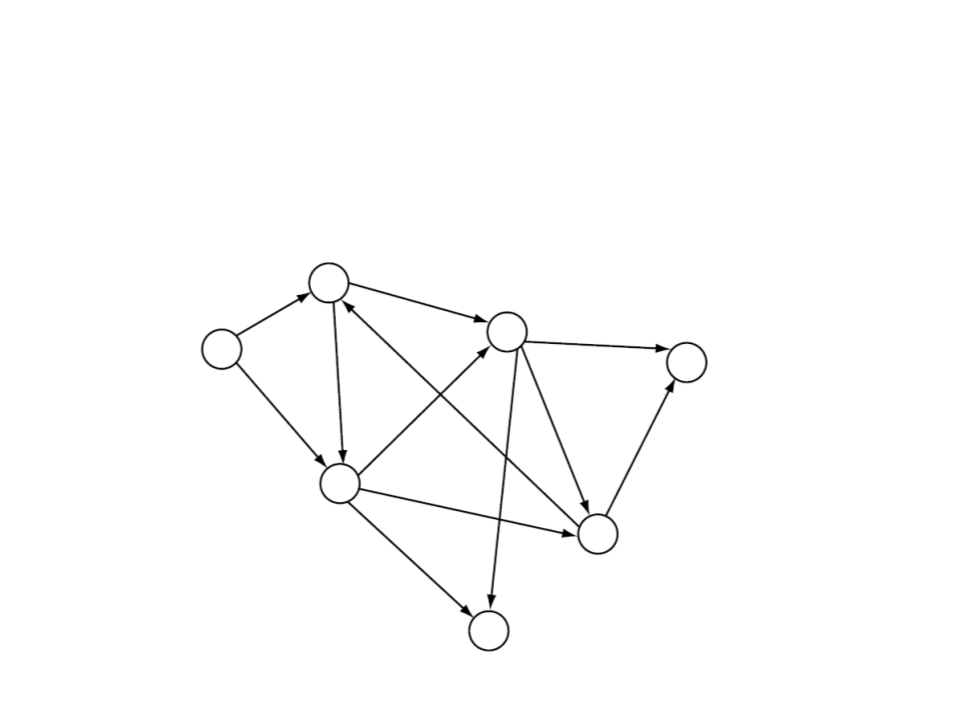
General Graph Structure
•
Directed graph: a graph in which edges have orientations.
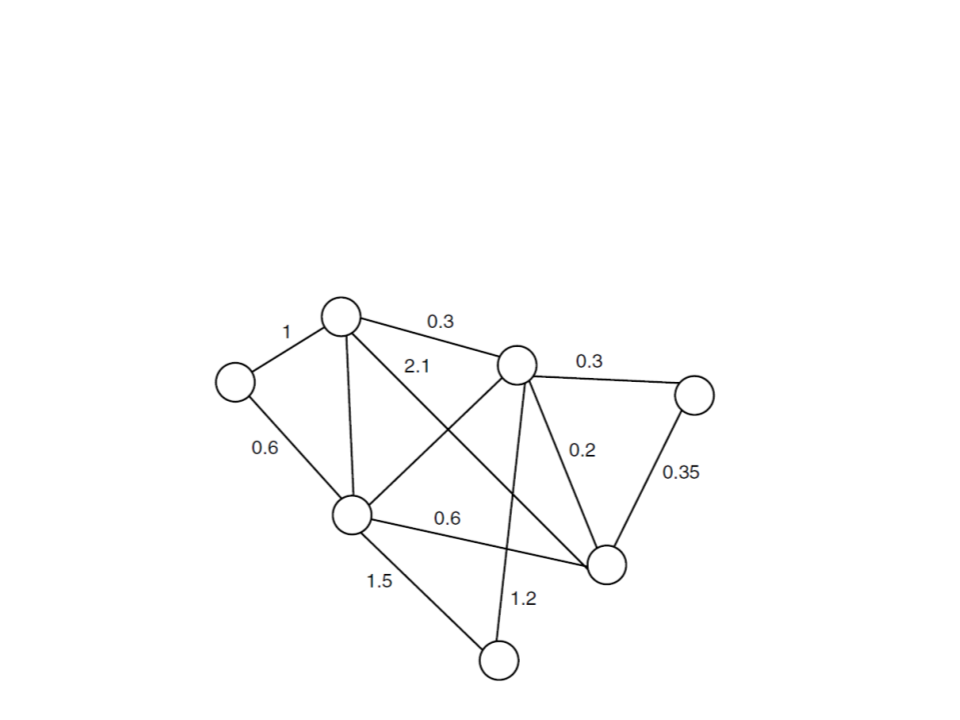
General Graph Structure
•
Weighted graph: directed on undirected graph in which a
number (the weight) is assigned to each edge.
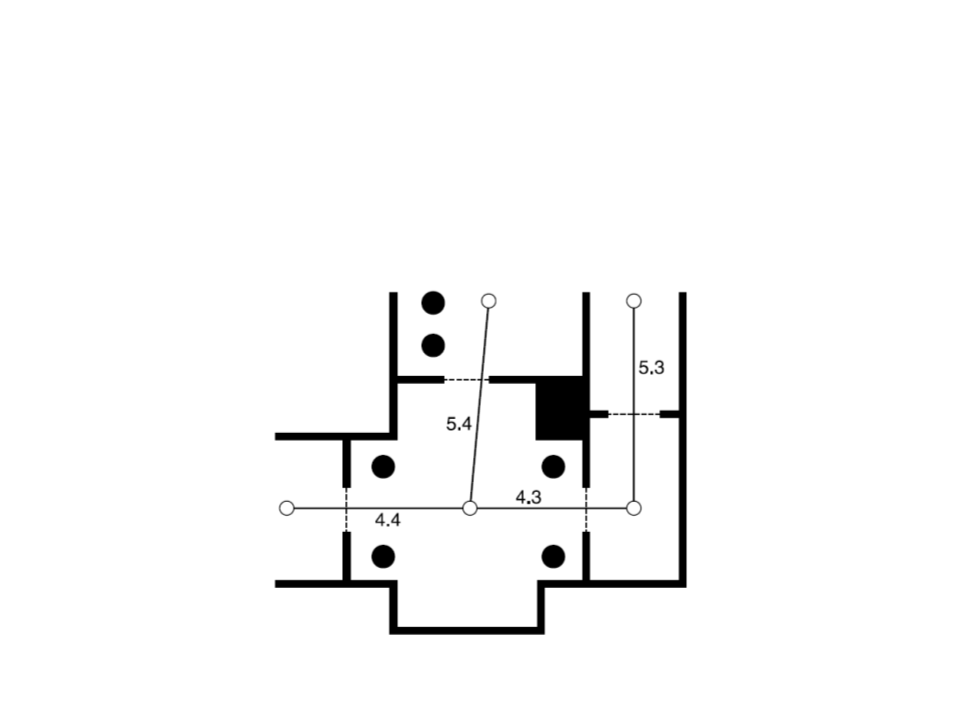
Navigation Graph
•
A simplified version of the game level can be represented in
the form of a graph.
Navigation Graph
•
Tiled-based maps can also be seen as graphs:
A
A
B
B
memory data:
0
0
1
1
0 0 0 1 1 1
0 0 0 1 1 1
0 0 1 0 0 1
1 0 0 0 0 0
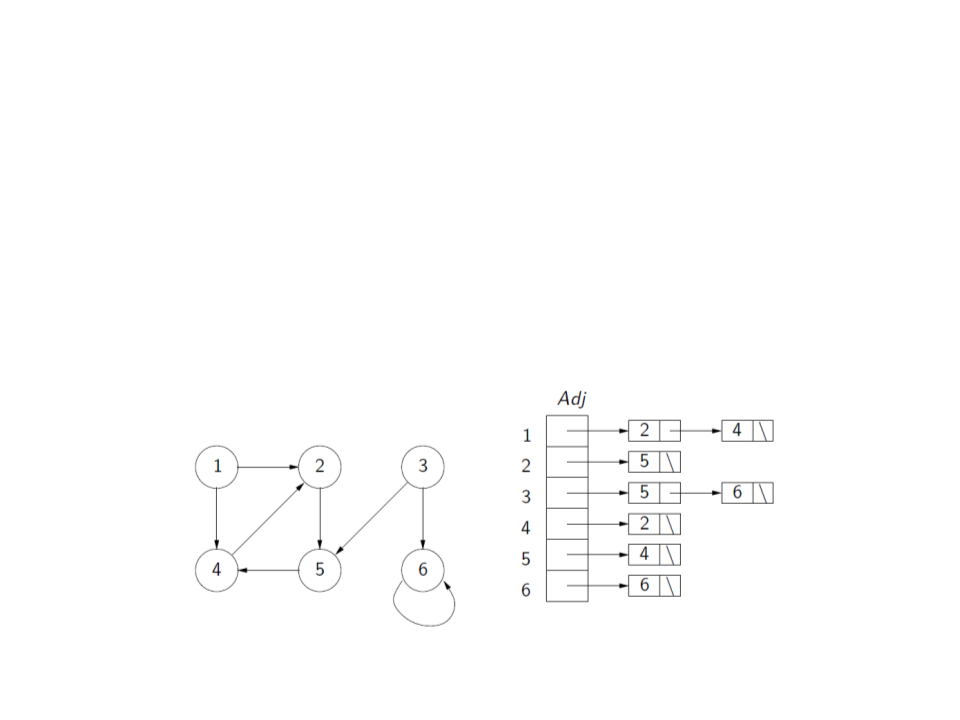
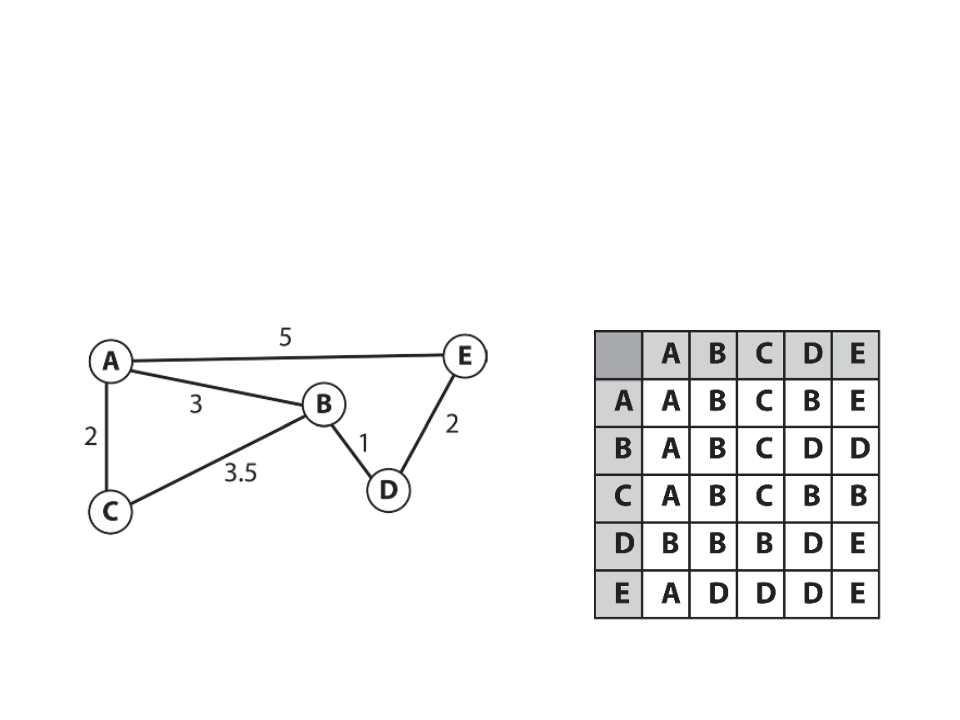
Graph – Representation
•
Adjacency list:
–
Uses a vector or list Adj with |V| adjacency lists, one for each
vertex v ∈ V.
–
For each u ∈ V, Adj[u] contain references for all vertices v such
that (u, v) ∈ A. That is, Adj[u] contains all adjacency vertices of u.
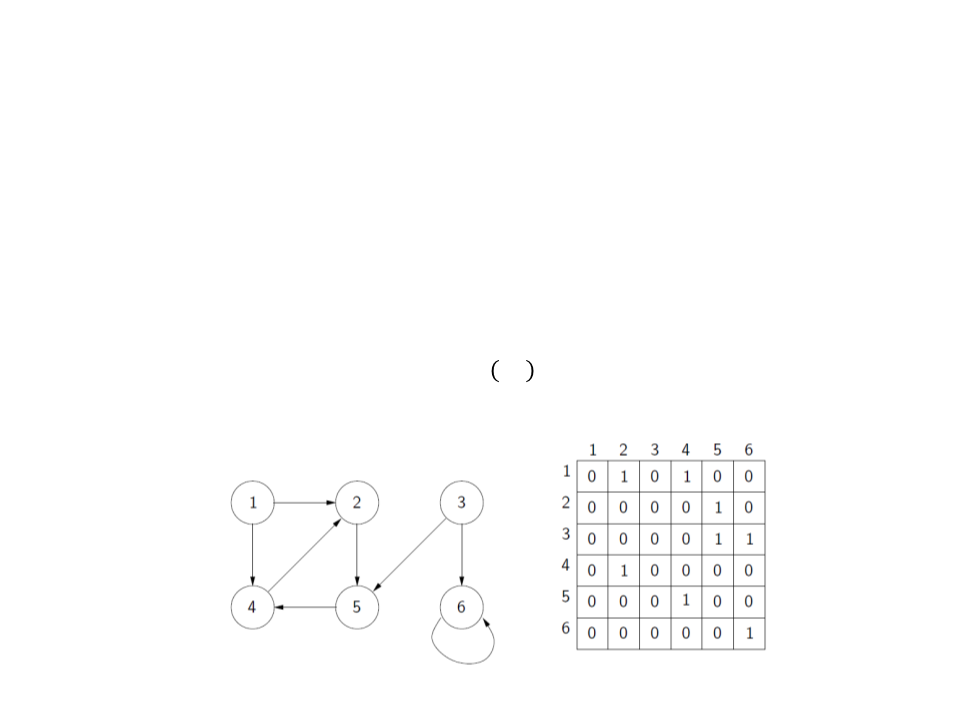
Graph – Representation
•
Adjacency matrix:
–
Given a graph G = (V, E), we assume that vertices are labeled with
numbers 1, 2, . . . , |V|.
–
The adjacency matrix is a matrix Aij of dimensions |V| × |V|,
where:
1
0
ꢃꢄ ꢃ, ꢅ ∈ ꢀ
ꢆꢇℎꢈꢉꢊꢃꢋꢈ
ꢀꢁꢂ
= ቊ

Graph Representation in Unity
•
•
We can easily create an adjacency list by implementing a class
to represent the edges of the graph (called waypoints in the
navigation graph). Each waypoint is connect with a set of
other waypoints (edges):
public class Waypoint : MonoBehaviour {
public Waypoint[] edges;
}
We also need another class to store a reference to all the
vertices of the graph (waypoints):
public class Pathfinding : MonoBehaviour {
public Waypoint[] waypoints;
}
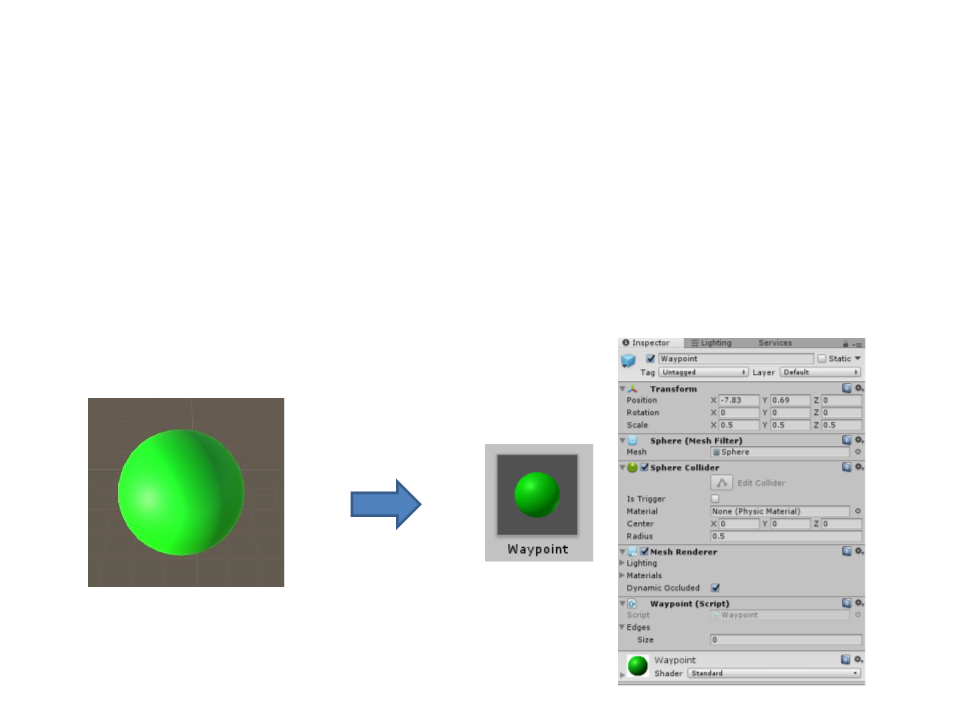
Graph Representation in Unity
•
A waypoint also have a position in the world. But instead of
adding this information to the waypoint class, a better
solution is to associate the class with a game object (such a
sphere) and then create a prefab.
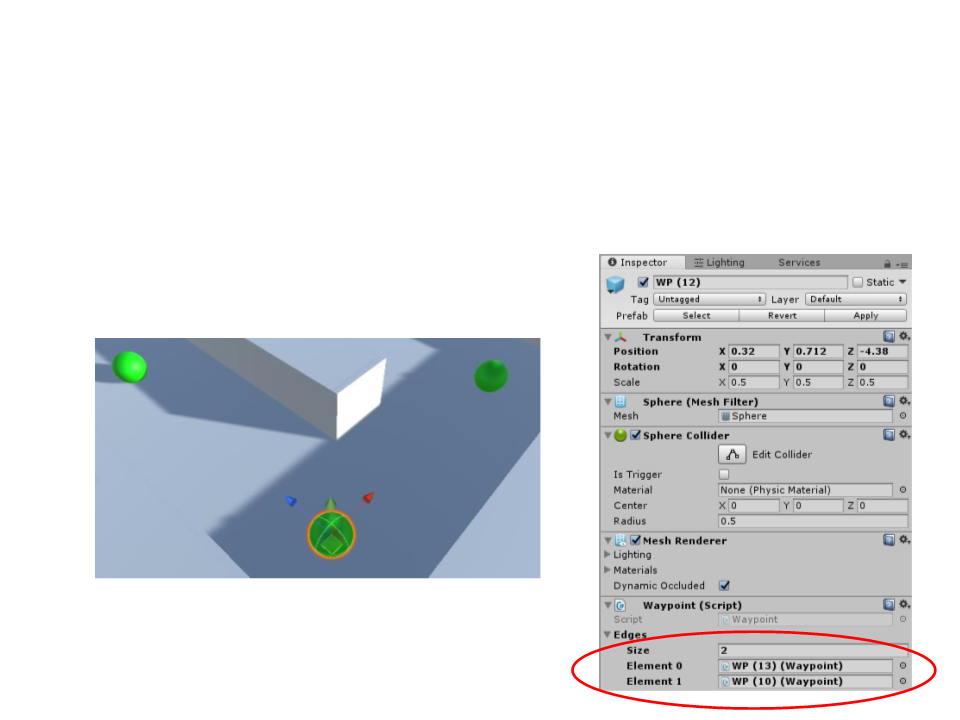
Graph Representation in Unity
•
Now we can place waypoints in the game level and then
connect them.
WP (10)
WP (13)
WP (12)

Graph Representation in Unity
•
To better visualize the connections, we can use gizmos to
draw lines between connected waypoints.
public class Waypoint : MonoBehaviour {
public Waypoint[] edges;
void OnDrawGizmos()
{
Gizmos.color = Color.green;
foreach (Waypoint e in edges)
{
Gizmos.DrawLine(transform.position,
e.gameObject.transform.position);
}
}
}
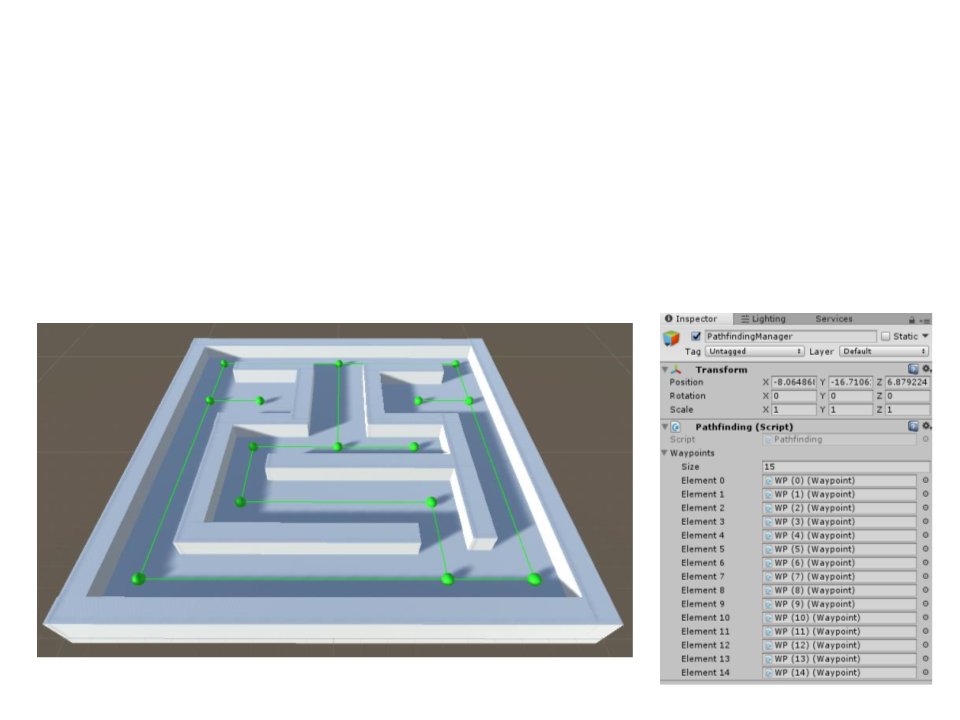
Exercise 2
2
) Place waypoints in the visibility points of the maze created in
the previous exercise. Then, connect all the waypoints to
create the navigation graph.

Pathfinding
•
•
Now that we have the navigation graph, how can we find the
best path to go from one waypoint to another?
There are many graph search algorithms:
–
–
–
–
–
Breadth-first search (BFS)
Depth-first search (DFS)
Dijkstra algorithm
A* algorithm
…
•
Which algorithm is the best?
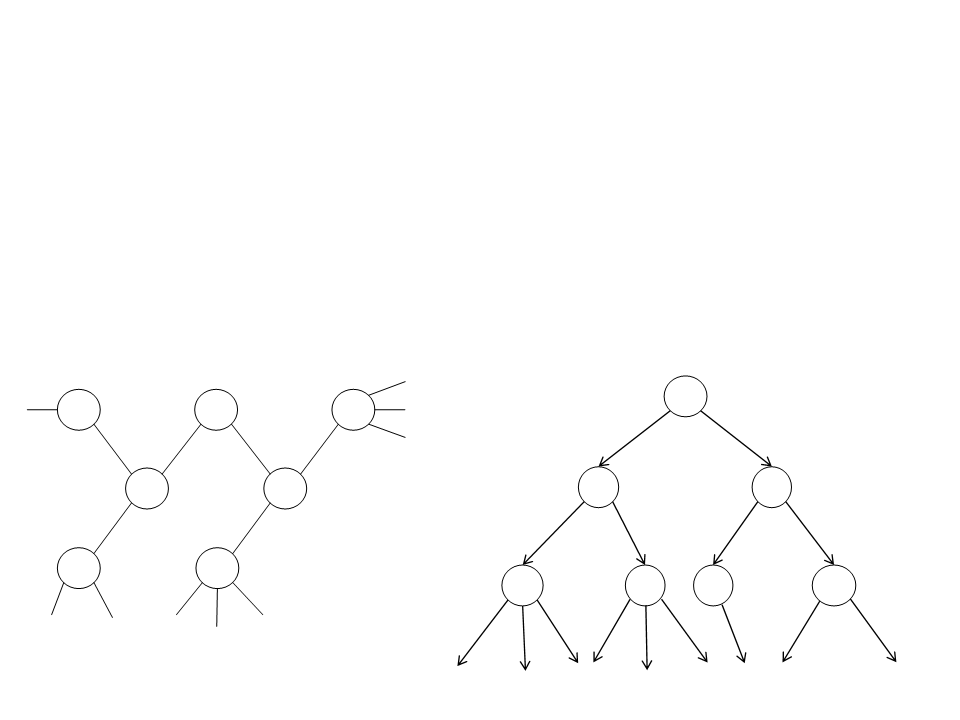
Breadth-first Search (BFS)
•
Strategy:
–
It starts at the root vertex (any arbitrary vertex of the graph) and
explores the neighbor nodes first, before moving to the next level of
neighbors.
Search Tree:
Graph:
A
F
A
E
C
B
B
C
G
D
D
E
F
G
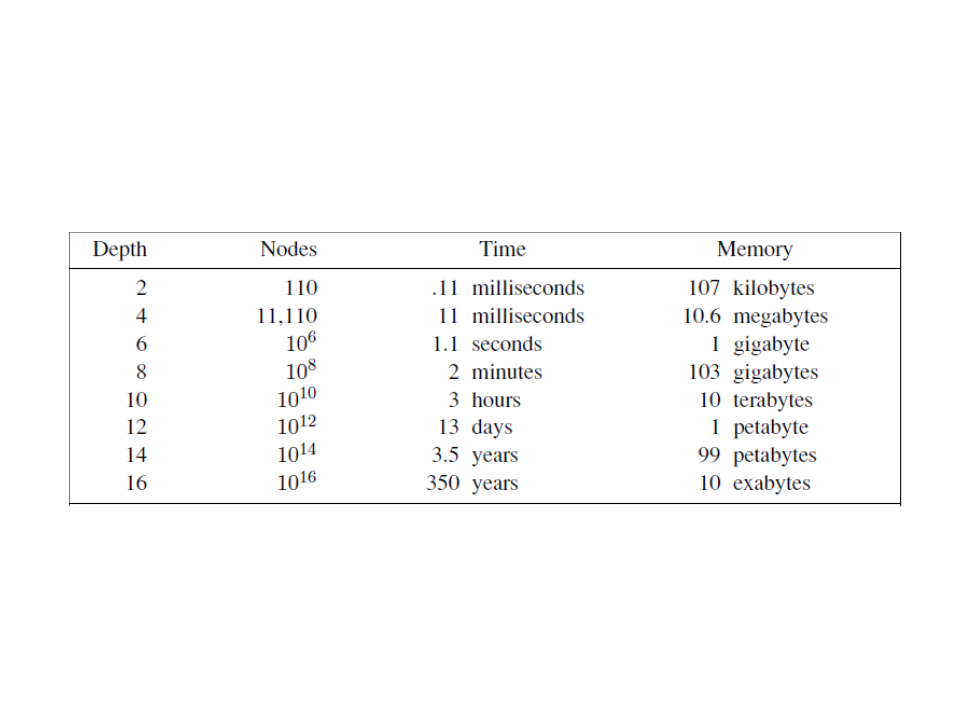
Breadth-first Search (BFS)
d+1
Complexity: O(b )
•
*
processor capable of processing 1 million nodes per second.
Considering a ramification factor b = 10, each node using 1KB of memory, and a
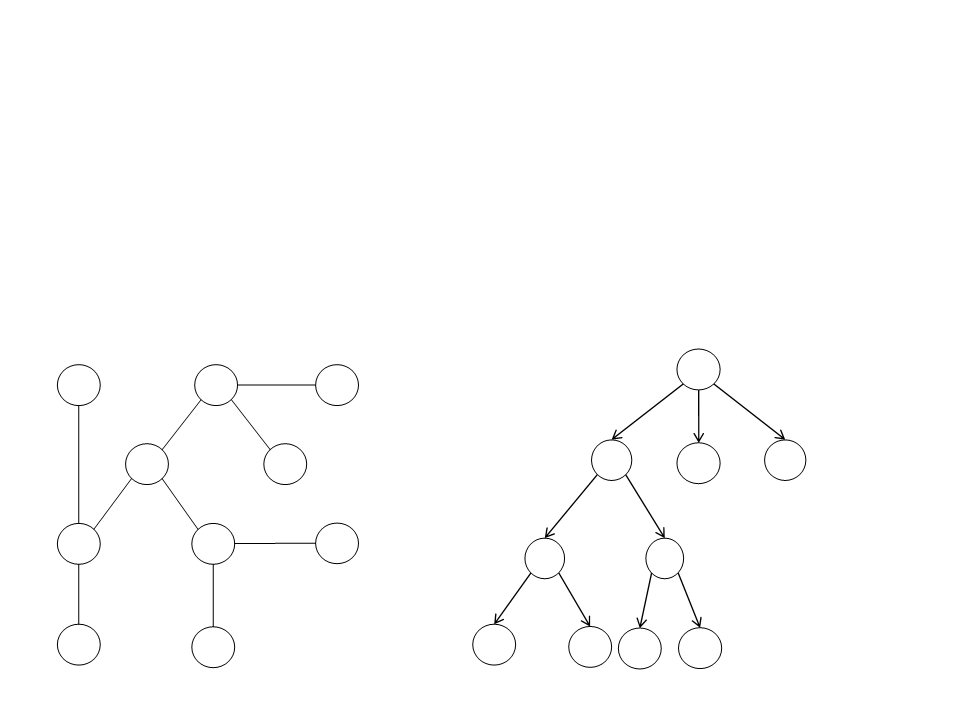
Depth-first Search (DFS)
•
Strategy:
–
It starts at the root vertex (any arbitrary vertex of the graph) and
explores as far as possible along each branch before backtracking.
Search Tree:
Graph:
A
M
A
D
P
B
D
B
C
C
E
F
E
F
N
M
Q
N
P
Q

Depth-first Search (DFS)
•
Consumes less memory than the BFS: once a node has been
expanded, it can be removed from memory as soon as all its
descendants have been fully explored.
•
•
In the previous example, at depth d = 16, DFS would require
only 156 KB of memory (instead of 10 exabytes).
Problem: the algorithm may perform long searches when the
solution is simple (when the goal is close to the root vertex).
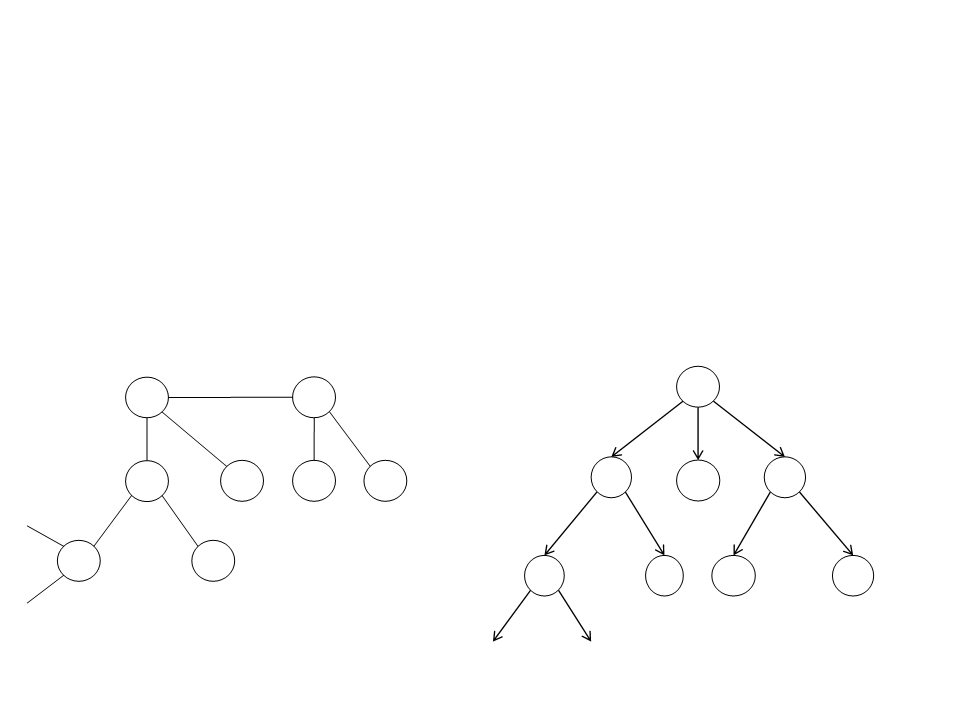
Dijkstra Algorithm
•
Strategy:
–
It starts at the root vertex (any arbitrary vertex of the graph) and
explores the neighbor nodes with the lowest path cost.
Search Tree:
Graph:
A
118
A
D
75
118
170
111
170
7
5
99
B
D
B
C
G
H
C
75
71
75
71
99
111
E
F
E
F
G
H

Dijkstra Algorithm
•
•
•
The first solution found is always the optimal solution (only if
there are no negative costs).
When all step costs are the same, Dijkstra search is similar to
breadth-first search.
Dijkstra is better than BFS and DFS algorithms, but it still
searches the entire graph indiscriminately for the shortest
possible route (it doesn't take into consideration the
objective).

A* Algorithm
•
•
Strategy:
–
–
–
Combines the path cost g(n) with an heuristic value h(n);
g(n) = path cost from the start node to node n;
h(n) = estimated cost of the cheapest path from n to the goal (e.g.
straight-line distance);
–
The evaluation of a node is given by: f(n) = g(n) + h(n);
Pathfinding in games is synonymous with the A* algorithm.
Almost every pathfinding system uses some variation of the
A* algorithm.
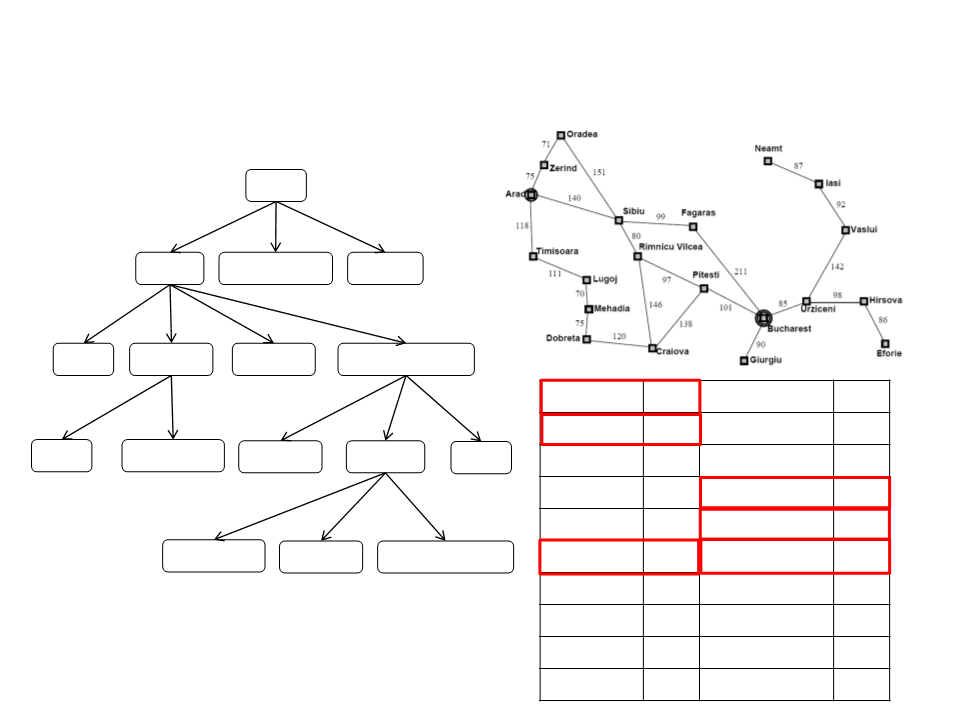
A* Algorithm
Arad
0+366=366
Sibiu
Timissoara
Zerind
1
40+253=393 118+329=447 75+374=449
Arad
Fagaras
Oradea
Rimnicu Vilcea
220+193=413
2
80+366=646 239+176=415 291+380=671
Arad
366
0
Mehadia
Neamt
Oradea
Pitesti
241
234
380
100
Bucharest
Craiova
Drobeta
Eforie
Sibiu
38+253=591
Bucharest
Craiova
Pitesti
Sibiu
160
242
161
176
77
3
450+0=450
366+160=526 317+100=417 300+253=553
Rimnicu Vilcea 193
Bucharest
418+0=418
Craiova
Rimnicu Vilcea
414+193=607
Fagaras
Giurgiu
Iasi
Sibiu
253
329
199
374
80
455+160=615
Timisoara
Vaslui
226
244
151
Lugoj
Zerind
Hirsova
Urziceni

A* Algorithm
•
•
The A* algorithm is complete and optimal.
Complexity: is exponential in the depth of the solution (the
d
shortest path) – O(b ) , but the heuristic function has a major
effect on the practical performance of the algorithm. A good
d
heuristic prunes away many of the b nodes.
•
No other algorithm guarantees to expand less nodes than the
A* algorithm.

A* Algorithm – Pseudocode
function A*(start, goal)
closedSet := {};
openSet := {start}; //priority queue structure
cameFrom := an empty map;
gScore := map with default value of Infinity;
gScore[start] := 0;
fScore := map with default value of Infinity;
fScore[start] := heuristic_cost_estimate(start, goal);
...

A* Algorithm – Pseudocode
...
while openSet is not empty do
current := the node in openSet having the lowest fScore[] value;
if current = goal then
return reconstruct_path(cameFrom, current);
openSet.Remove(current);
closedSet.Add(current);
for each neighbor of current do
if neighbor in closedSet then
continue;
if neighbor not in openSet then
openSet.Add(neighbor);
tentative_gScore := gScore[current] + dist_between(current,
neighbor);
if tentative_gScore >= gScore[neighbor] then
continue;
cameFrom[neighbor] := current;
gScore[neighbor] := tentative_gScore;
fScore[neighbor] := gScore[neighbor] +
heuristic_cost_estimate(neighbor, goal);
return failure;

A* Algorithm – Unity
public List<Waypoint> FindPath(Waypoint start, Waypoint goal) {
List<Waypoint> closedSet = new List<Waypoint>();
SimplePriorityQueue<Waypoint> openSet = new
SimplePriorityQueue<Waypoint>();
openSet.Enqueue(start, Heuristic(start, goal));
Dictionary<Waypoint, Waypoint> cameFrom = new Dictionary<Waypoint,
Waypoint>();
Dictionary<Waypoint, float> gScore = new Dictionary<Waypoint,
float>();
foreach (Waypoint wp in waypoints)
{
gScore.Add(wp, Mathf.Infinity);
}
gScore[start] = 0;
...

...
while (openSet.Count > 0){
Waypoint current = openSet.Dequeue();
if (current == goal)
return ReconstructPath(cameFrom, current, start);
closedSet.Add(current);
foreach (Waypoint neighbor in current.edges){
if (closedSet.Contains(neighbor))
continue;
if (!openSet.Contains(neighbor))
openSet.Enqueue(neighbor, gScore[neighbor] +
Heuristic(neighbor, goal));
float tentative_gScore = gScore[current] + Heuristic(current,
neighbor);
if (tentative_gScore >= gScore[neighbor])
continue;
cameFrom[neighbor] = current;
gScore[neighbor] = tentative_gScore;
openSet.UpdatePriority(neighbor, gScore[neighbor] +
Heuristic(neighbor, goal));
}
}
return new List<Waypoint>();
}

A* Algorithm – Unity
float Heuristic(Waypoint p1, Waypoint p2){
return Vector3.Distance(p1.gameObject.transform.position,
p2.gameObject.transform.position);
}
List<Waypoint> ReconstructPath(Dictionary<Waypoint,Waypoint> cameFrom,
Waypoint current, Waypoint start){
List<Waypoint> total_path = new List<Waypoint>();
total_path.Add(current);
while (current != start){
foreach (Waypoint wp in cameFrom.Keys){
if (wp == current){
current = cameFrom[wp];
total_path.Add(current);
}
}
}
total_path.Reverse();
return total_path;
}

Exercise 3
3
) Implement the A* algorithm in the Pathfinding class created
in the previous exercises.
a) Execute the FindPath function and
show the resulting path in the
console;
b) Add parameters to define the start
and goal waypoints;
c) Test the algorithm with different
start and goal waypoints;
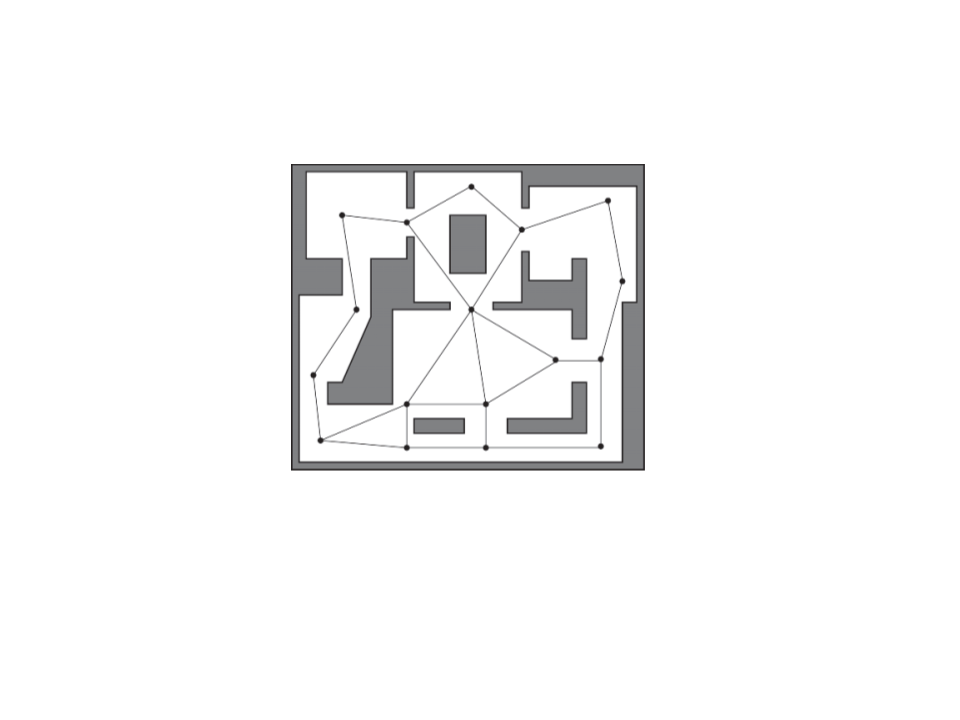
Navigation
X
(
a)
(
b)
O
1
2
3
4
5
6
. Find closest visible node (a) to current location (X);
. Find closest visible node (b) to target location (O);
. Search for the best path from (a) to (b);
. Move to (a);
. Follow path to (b);
. Move to target location (O);

Exercise 4
4
) Add an object (e.g. a capsule) to represent an NPC and then
use the pathfinding algorithm to move the NPC from any
place to any goal destination.
a) Create a function to find the
closest waypoint to use as start
and goal waypoints;
b) Move the NPC slowly though the
computed path;

World Representations
•
•
Pathfinding algorithms don’t work directly on the level
geometry. They rely on a simplified world representation.
Most common techniques for world representation:
–
–
–
–
–
Tile Graphs;
Points of Visibility;
Finely Grained Graphs;
Expanded Geometry;
Navigation Meshes;
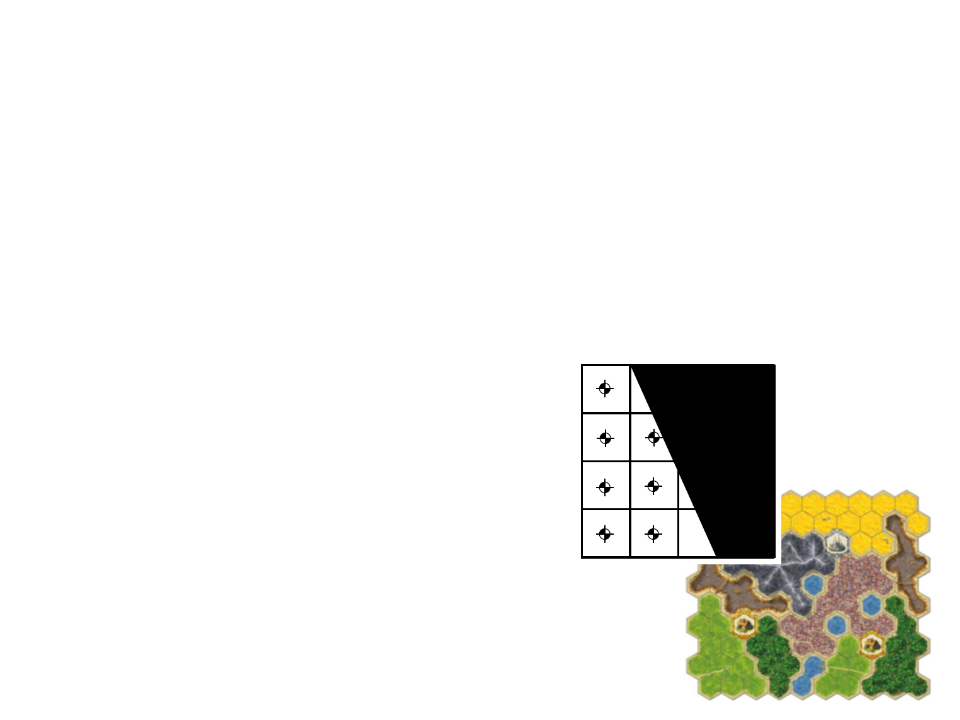
Tiled-Based Graphs
•
Tile-based levels split the whole world into regular, usually
square, regions (although hexagonal regions are occasionally
seen in some games).
–
The whole level can be tiled-based or the tile grid overlays the 3D level;
•
•
Advantages: tile-based graphs are
generated automatically. Easy to estimate
edge’s weights.
Problems: the search spaces can quickly
become extremely large (a 100x100 map
has 10,000 nodes and 78,000 edges!). If no
path smoothing techniques are applied,
character’s movements will be unnatural.
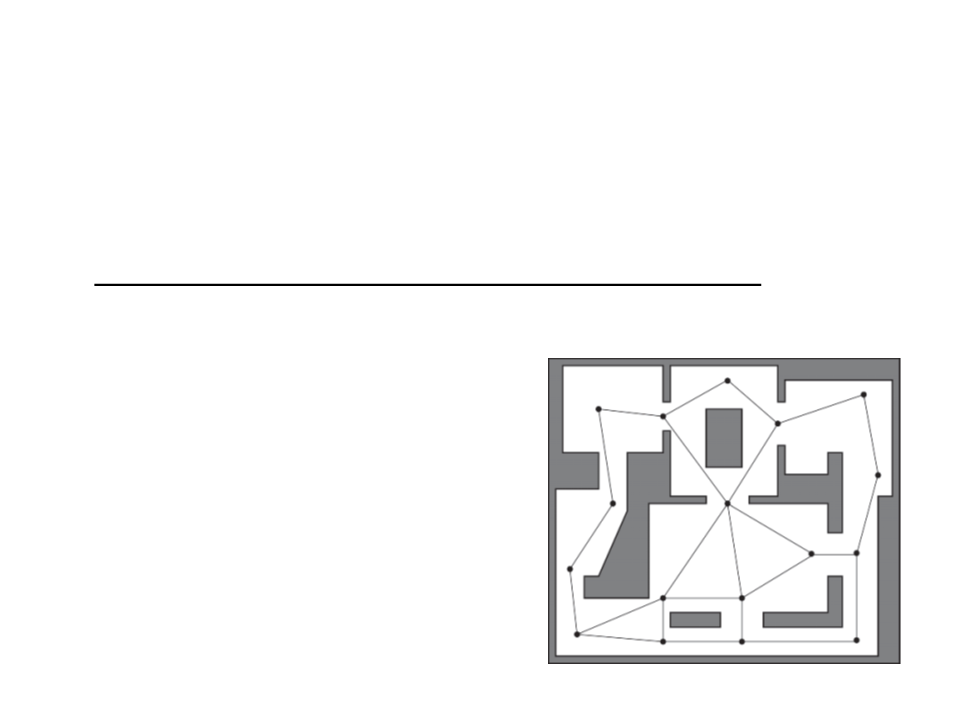
Points of Visibility (POV)
•
A points of visibility navigation graph is created by placing
waypoints at important points in the environment such that
each waypoint has line of sight to at least one other.
–
Usually the waypoints are placed by hand (level designer task);
•
•
Advantages: easy to implement. Easy to
include extra information about
waypoints (e.g. good sniping, cover, or
ambush positions).
Problems: large maps require a lot of
work to place all waypoints manually.
Problematic if the game includes map
generation features. Blind spots problem.
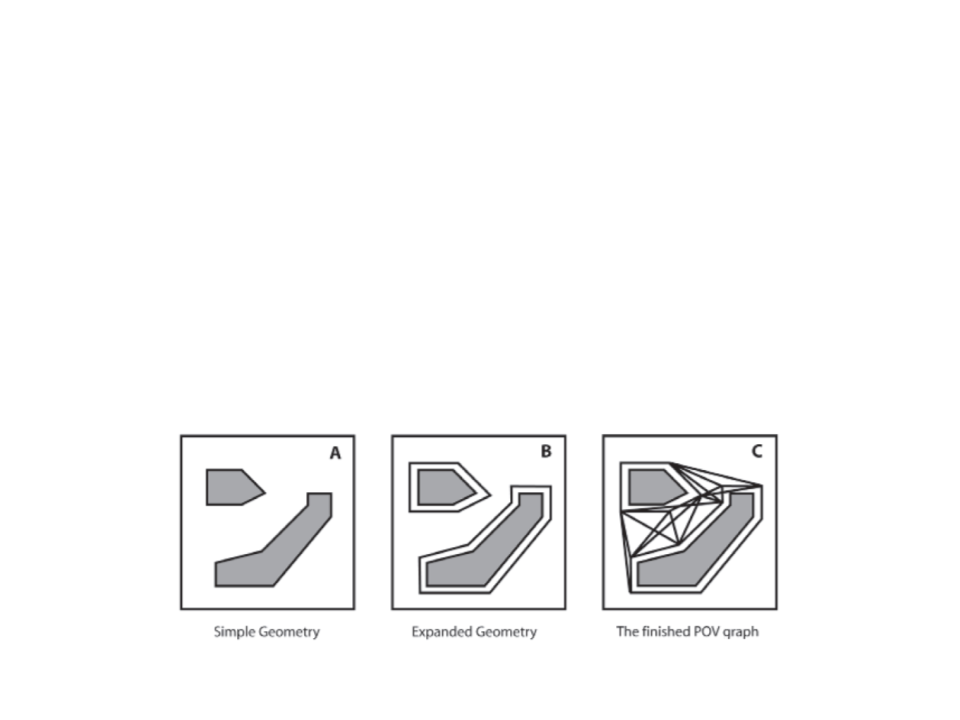
Expanded Geometry
•
A POV graph can be automatically generated using the
expanded geometry technique.
a) Expand geometry (by a amount proportional to the bounding radius
of moving agents);
b) Connect all vertices;
c) Remove non-line of sight edges;

Finely Grained Graphs
•
Poor paths and inaccessible positions can be improved by
increasing the granularity of the navigation graph.
•
Advantages: Removes blind spots and
improves path smoothness. Can be
generated automatically using “flood fill”
algorithm.
•
Problems: can have similar performance
issues as tiled graphs.
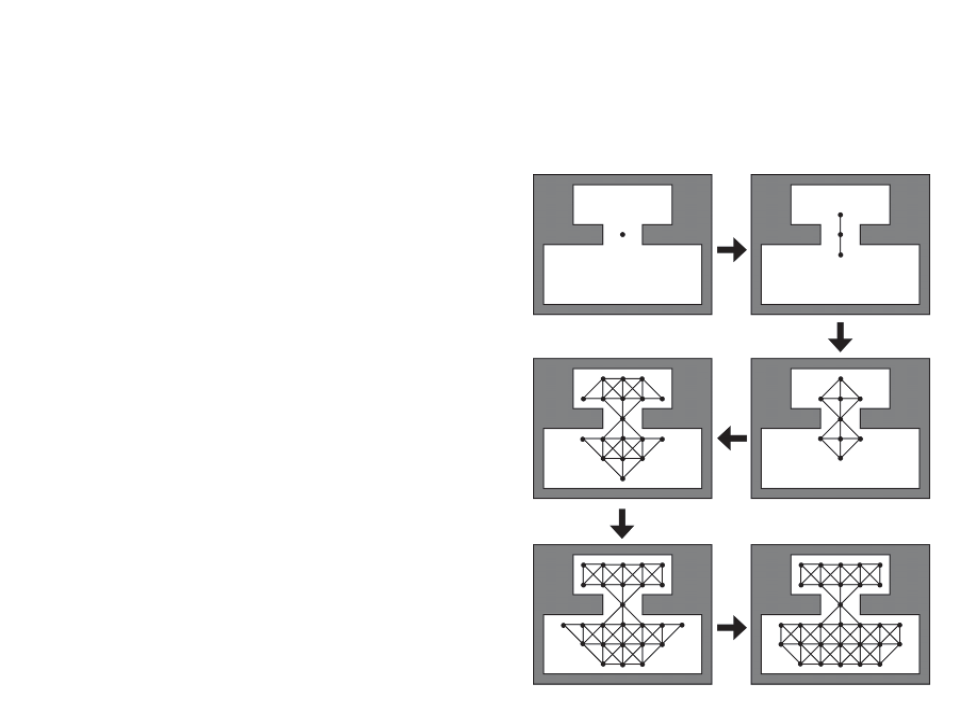
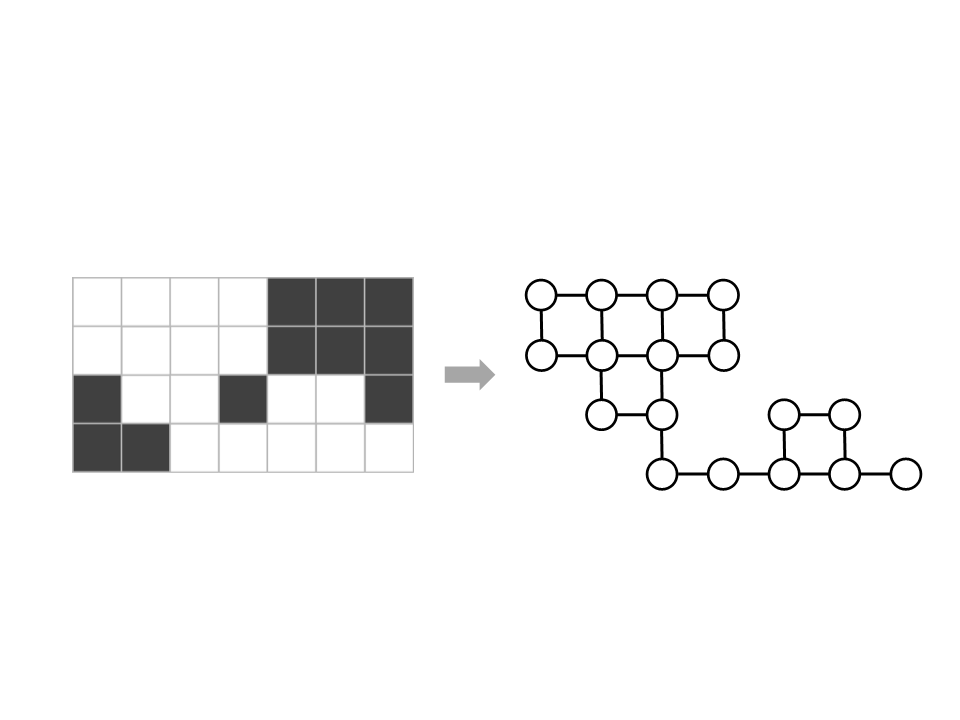
Finely Grained Graphs – Flood Fill
1. Place a seed node somewhere in
the map;
2
. Expand the nodes and edges
outward from the seed in each
available direction (e.g. 8
directions), and then the nodes on
the fringe of the graph;
–
Check for collisions with the level
geometry;
3
. Continue until all the navigable
area is filled.

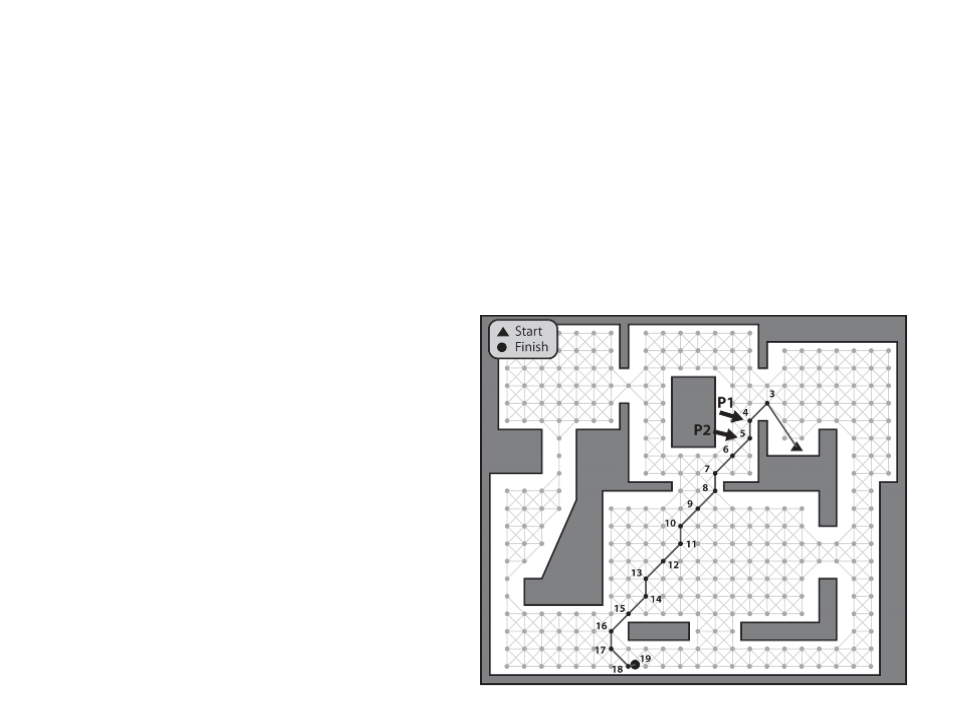
Path to an Item Type
•
What to do when we need a path to an item type (such as a
rocket launcher) that can be found in several locations?
–
In this situation, Dijkstra’s algorithm is a better choice.
Path Smoothing
•
•
When the navigation graph is in the shape of a grid or when
the path have unnecessary edges, the movements of the
agent may look unnatural.
Solution: Path Smoothing
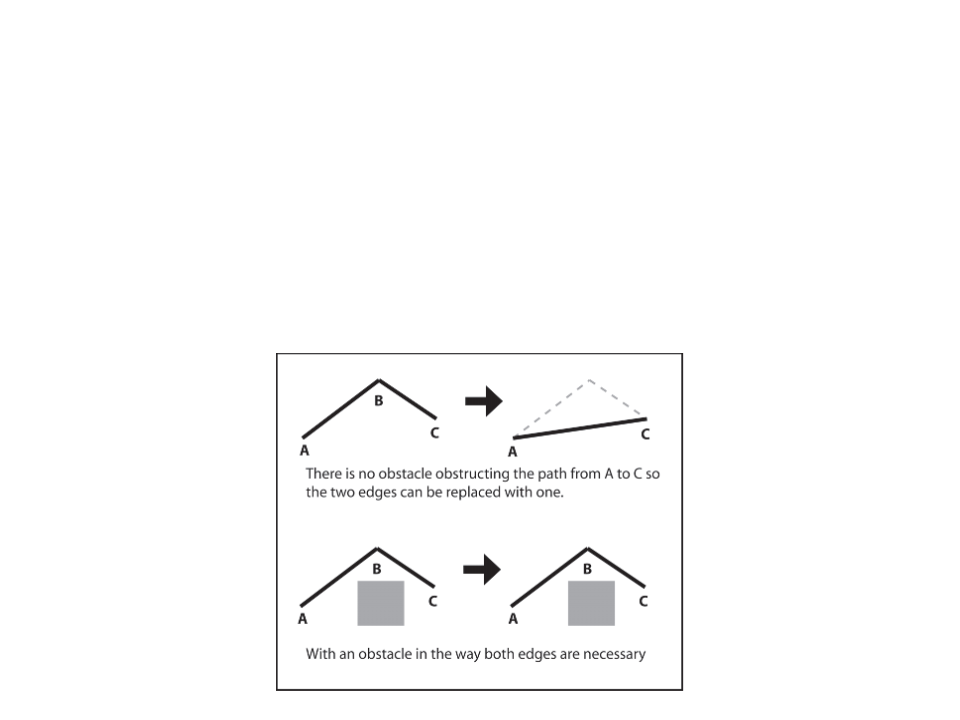
Simple Path Smoothing Algorithm
•
Check for the “passability” between adjacent edges. If one of
the edges is superfluous, the two edges are replaced with one.
–
“passability” can be checked thought a ray-cast. If we can cast a ray
between A and C then waypoint B is not needed.
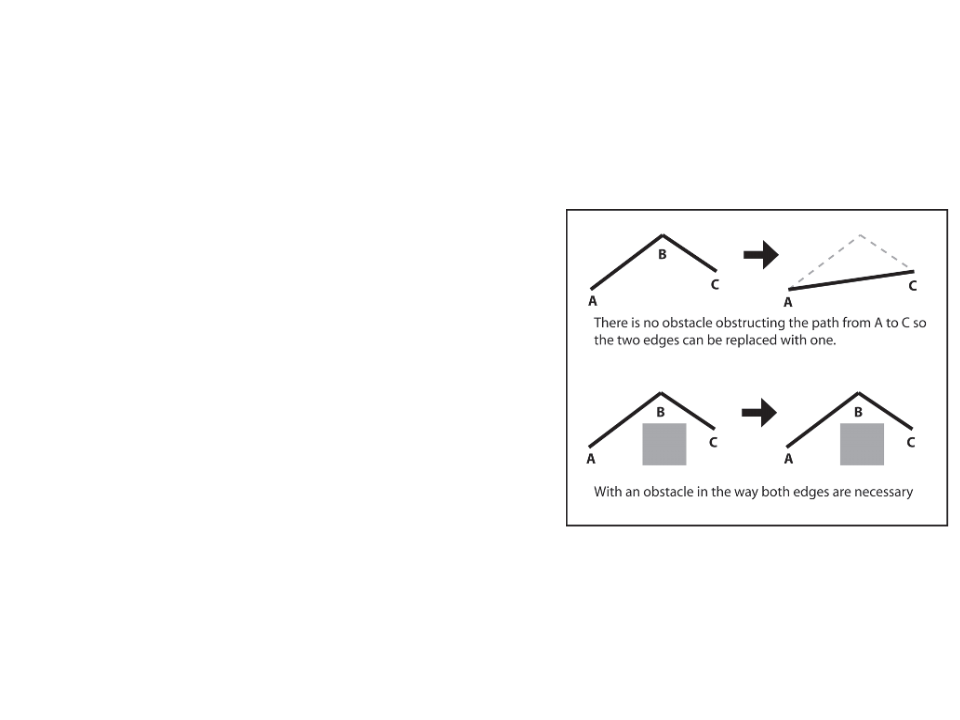
Simple Path Smoothing Algorithm
1
2
3
. Grab source E1 (edge);
. Grab destination E2 (edge);
. If the agent can move between the
source of E1 and destination of E2:
E2
E1
E1
–
a) Assign the destination of E1 to the
destination of E2;
–
–
b) Remove E2;
c) Advance E2;
E2
E1
E1
4
. If the agent cannot move between the
source of E1 and destination of E2:
–
–
a) Assign E2 to E1;
b) Advance E2;
5
. Repeat until the destination of E1 or destination of E2 is the endpoint of
the path;
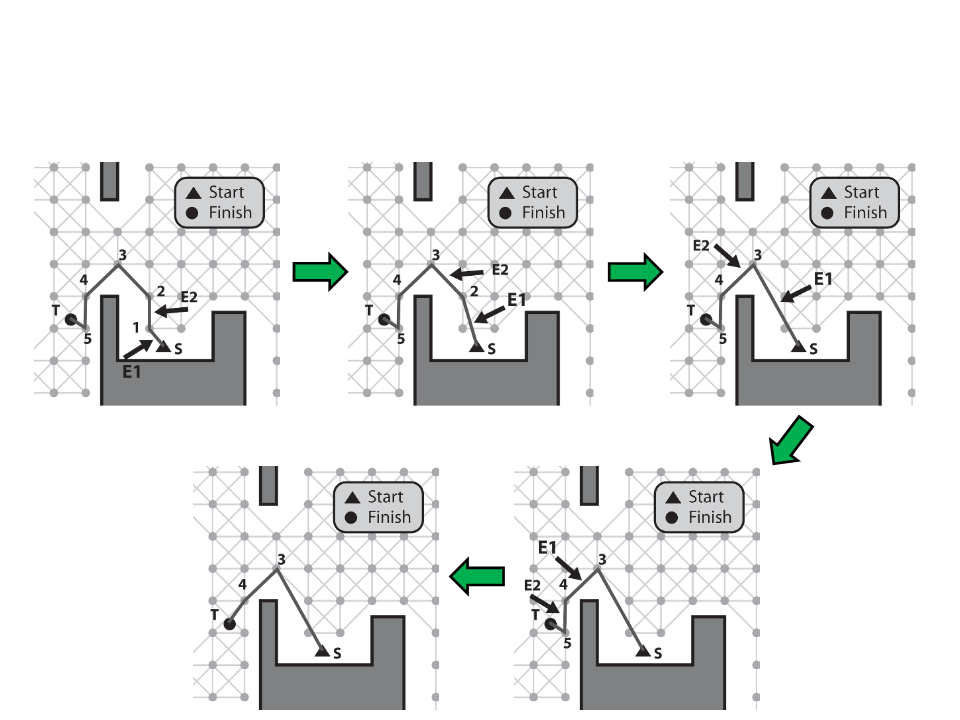
Simple Path Smoothing Algorithm
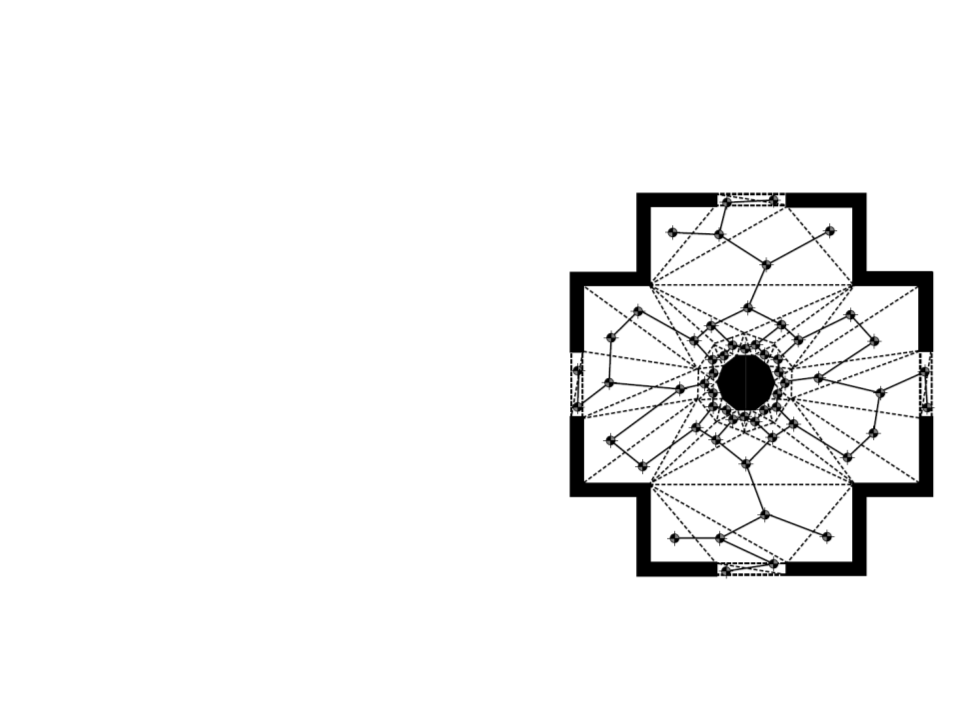
Navigation Mesh
•
•
Tile-based graphs and points of
visibility are useful solutions to
simple problems, but the majority
of modern games use navigation
meshes.
It takes advantage of the fact that
the level designer already needs to
specify the way the level is
connected using polygons/triangles.
–
Can use level geometry or a new
geometry created specially for
navigation.
Navigation Mesh
•
Instead of network of points, a navigation mesh comprises a
network of convex polygons.
–
It has more information than waypoints (i.e., the agent can walk
anywhere in the polygon);
–
While waypoints require a lot of points, the navigation mesh needs
only few polygons to cover same area.

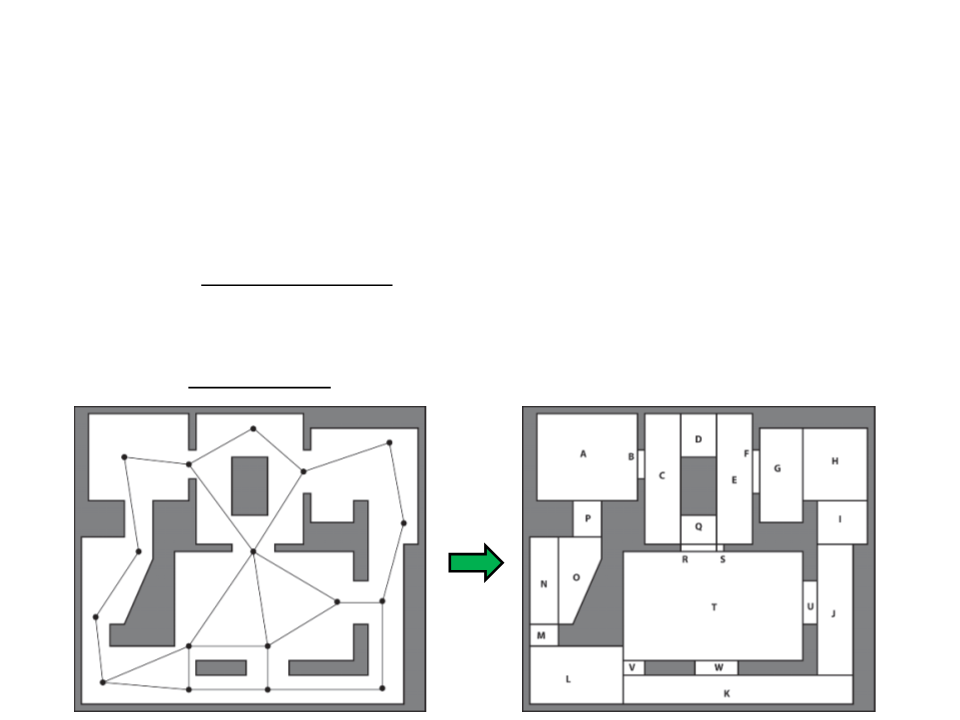
Navigation Mesh
•
Example 1:
Waypoints
Graph
Navigation
Mesh
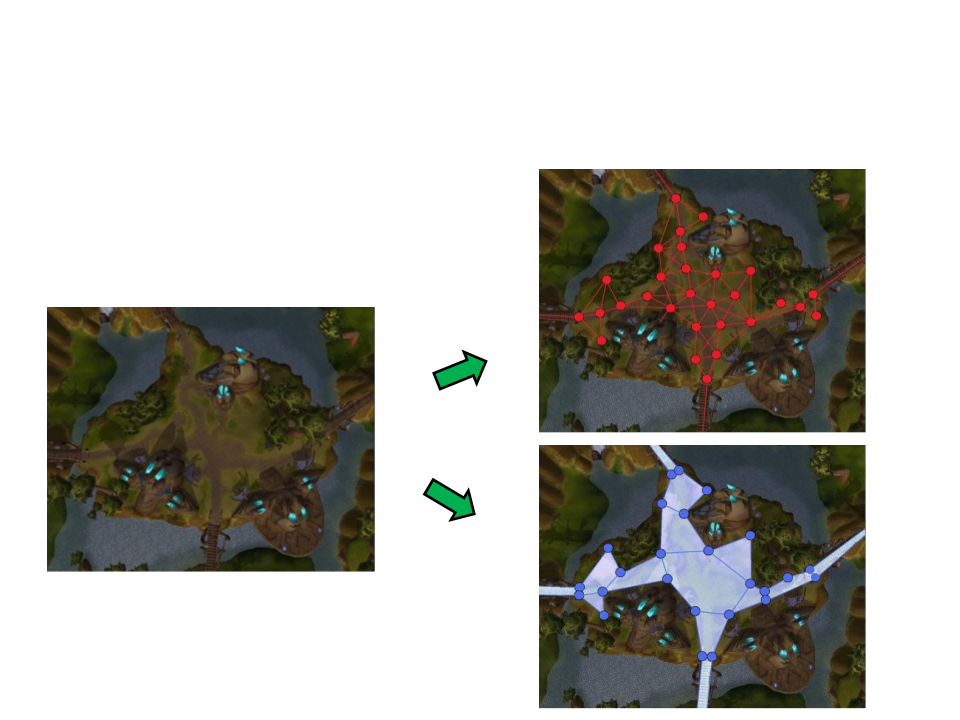
Navigation Mesh
•
Example 2:
Waypoints
Graph
Navigation
Mesh
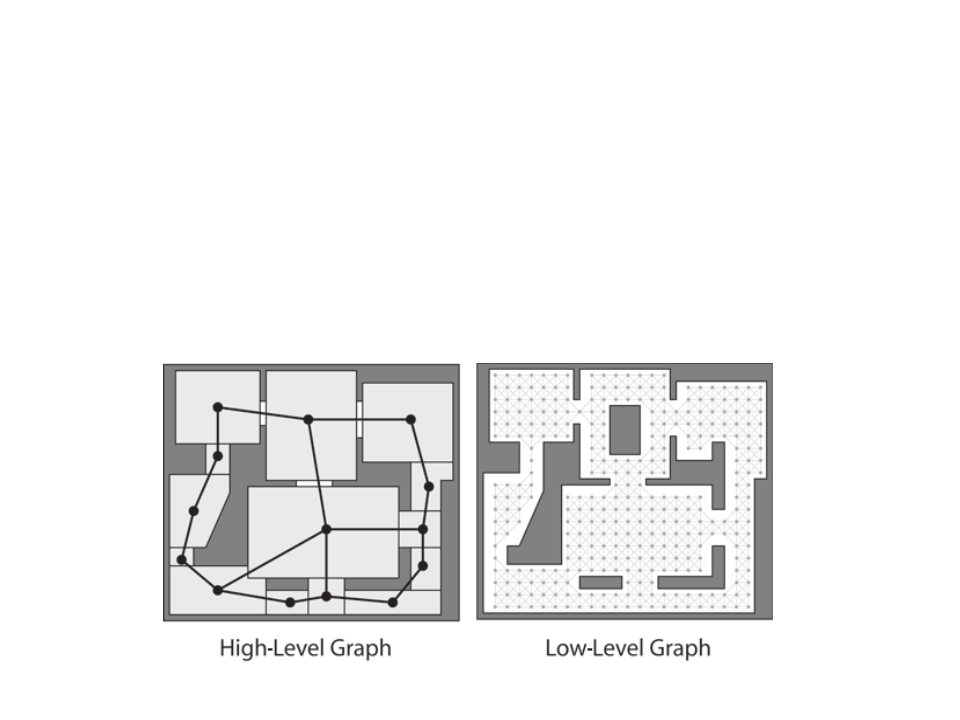
Optimization – Hierarchical Pathfinding
•
Hierarchical pathfinding works in a similar way to how humans
move around their environment.
–
Typically two hierarchical levels, but can be more.
–
First find a path in high-level, then refine in low‐level.
Optimization – Pre-Calculated Paths
•
If the game environment is static and memory usage is not a
problem, a good option to reduce CPU load are pre-calculated
path tables.
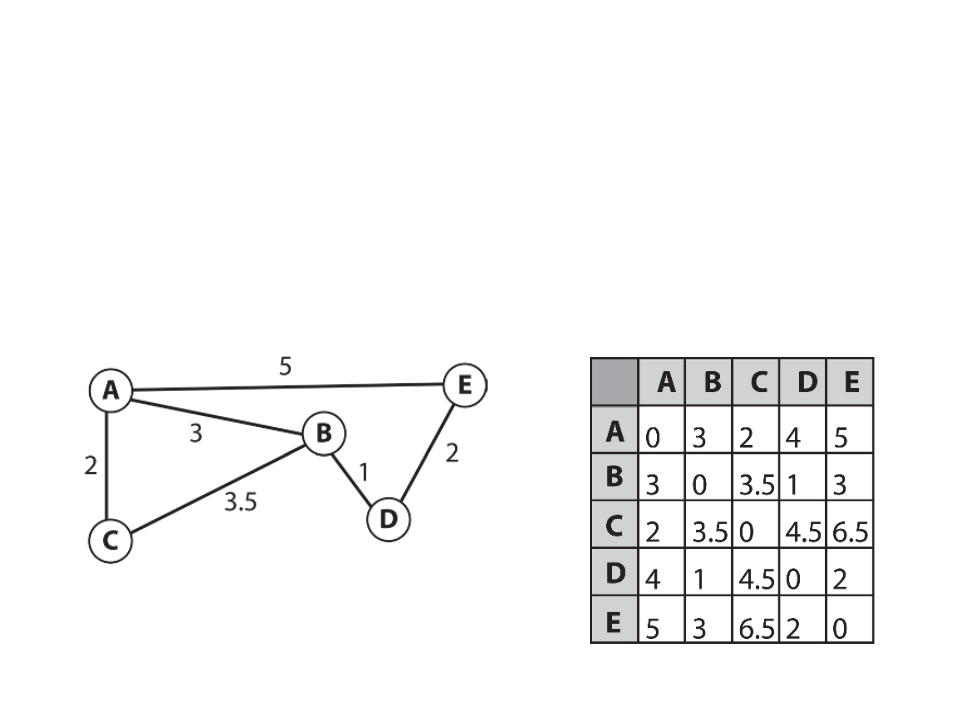
Optimization – Pre-Calculated Costs
•
Sometimes it’s necessary for a agent to calculate the cost of
traveling from one place to another. For example, to decide
which is easiest item to get. This can be done with pre-
calculated cost tables.
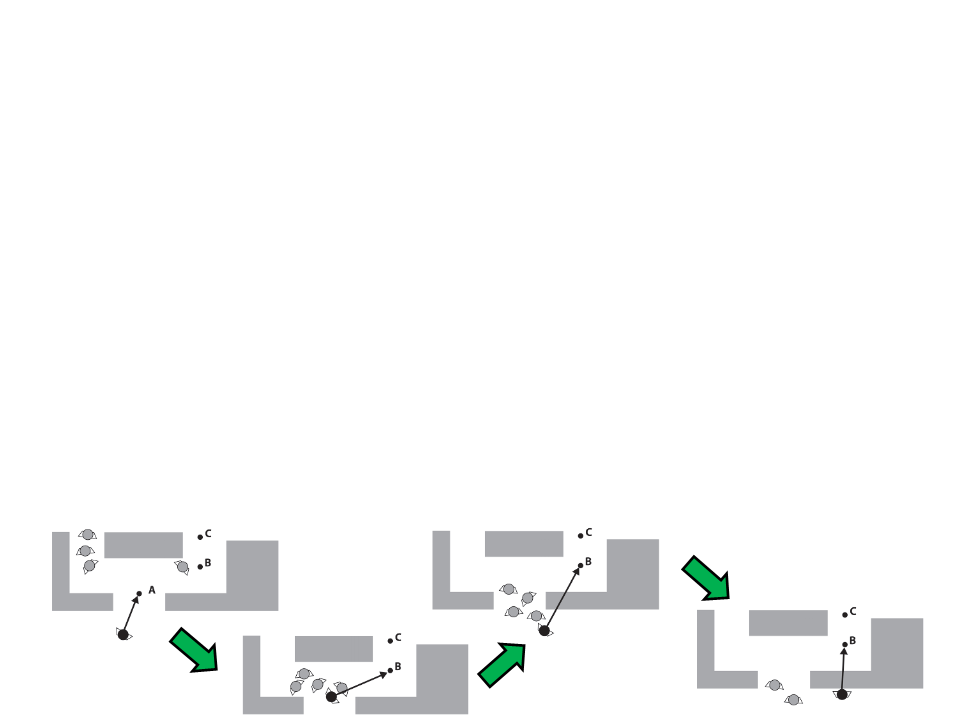
Optimization – Other Techniques
•
Time-Sliced Pathfinding: allocate a fixed amount of CPU
resources per update step for all the search requests and
distribute these resources evenly between the searches.
–
Considerable amount of coding work required!
•
•
Store Path Results: save pathfinding results in memory an
reuse then when necessary.
Recompute paths to avoid sticky situations:

Unity Navigation System
•
Unity’s Navigation System allows characters to intelligently
move around the game world. The system uses navigation
meshes automatically created from the scene geometry.
•
•
•
NavMesh – data structure that describes
the walkable surfaces of the game world.
NavMesh Agent – component to create
moving characters.
Off-Mesh Link – component that allows
navigation shortcuts (e.g. jumps over
holes, floors, or fences).
ꢀ
ꢁꢂꢃꢄꢅꢊꢋꢄꢉꢀꢌꢍꢃ
ꢀꢁꢂꢃꢄꢅꢆꢇꢃꢈꢉ
ꢊꢎꢎꢂꢃꢄꢅꢏꢐꢈꢑ
•
NavMesh Obstacle – component to define
moving obstacles that the agents should
avoid while navigating the world.
ꢀ
ꢁꢂꢃꢄꢅ
Unity Navigation System
•
•
The process of creating a NavMesh from the level geometry
uses the meshes of all Game Objects that are marked as
Navigation Static, and processes them to create a navigation
mesh that approximates the walkable surfaces of the level.
Navigation window:
–
Window -> Navigation
Unity Navigation System
•
Creating a basic NavMesh:
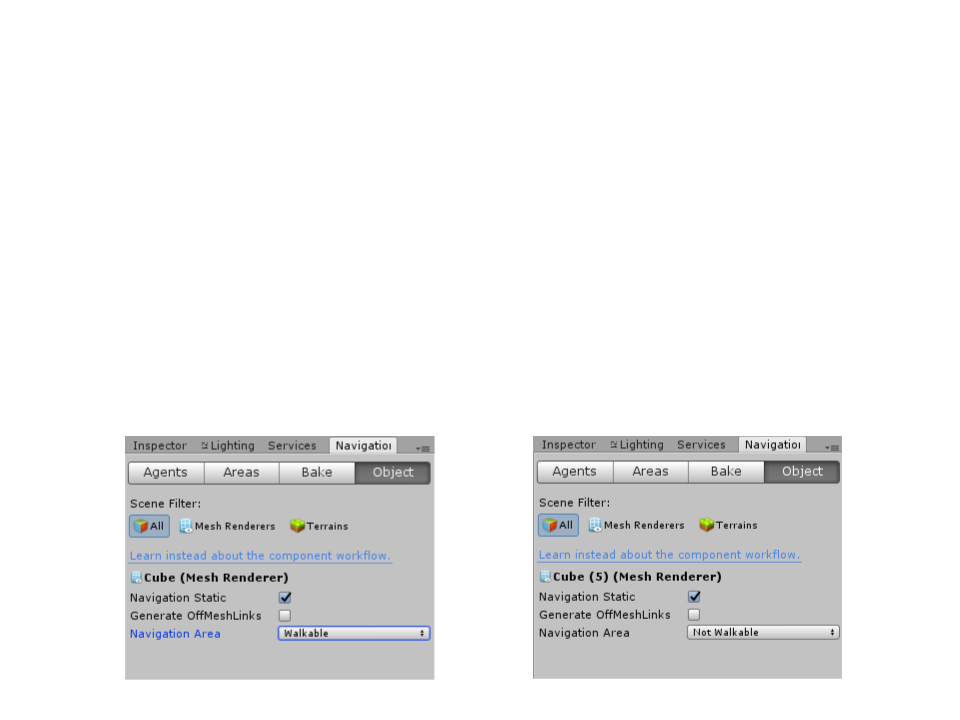
–
(Step 1): Select the objects that represent walkable surfaces and mark
them as “Static Geometry” and “Walkable” in the Object tab of the
Navigation Window.
–
(Step 2): Select the objects that represent not walkable surfaces and
mark them as “Static Geometry” and “Not Walkable” in the Object tab
of the Navigation Window.
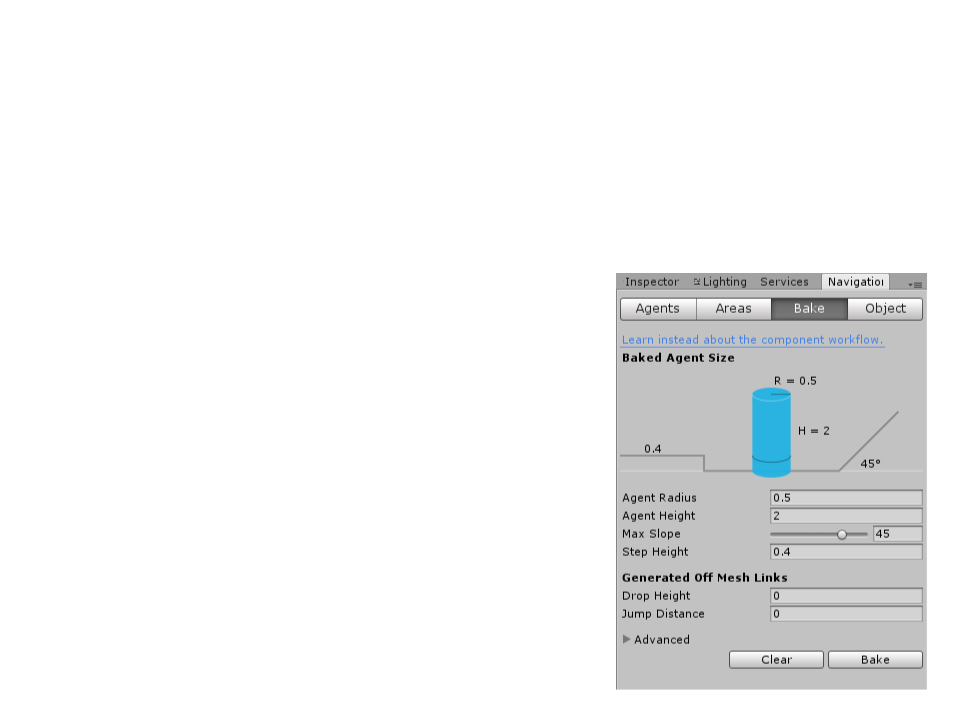
Unity Navigation System
•
Creating a basic NavMesh:
–
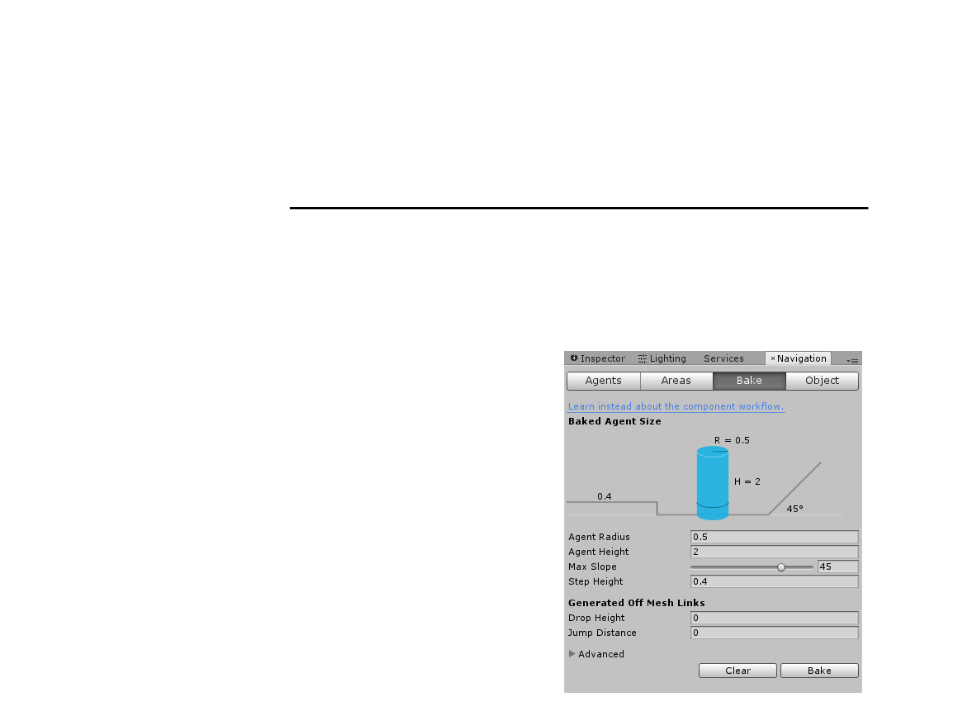
(Step 3): Adjust the bake settings to match the agent properties.
•
•
•
•
Agent Radius: defines how close the agent
center can get to a wall or a ledge.
Agent Height: defines how low the spaces
are that the agent can reach.
Max Slope: defines how steep the ramps
are that the agent walk up.
Step Height: defines how high obstructions
are that the agent can step on.
–
(Step 4): Click bake to build the NavMesh.

Unity Navigation System
•
The resulting NavMesh will be shown in the scene as a blue
overlay on the underlying level geometry:
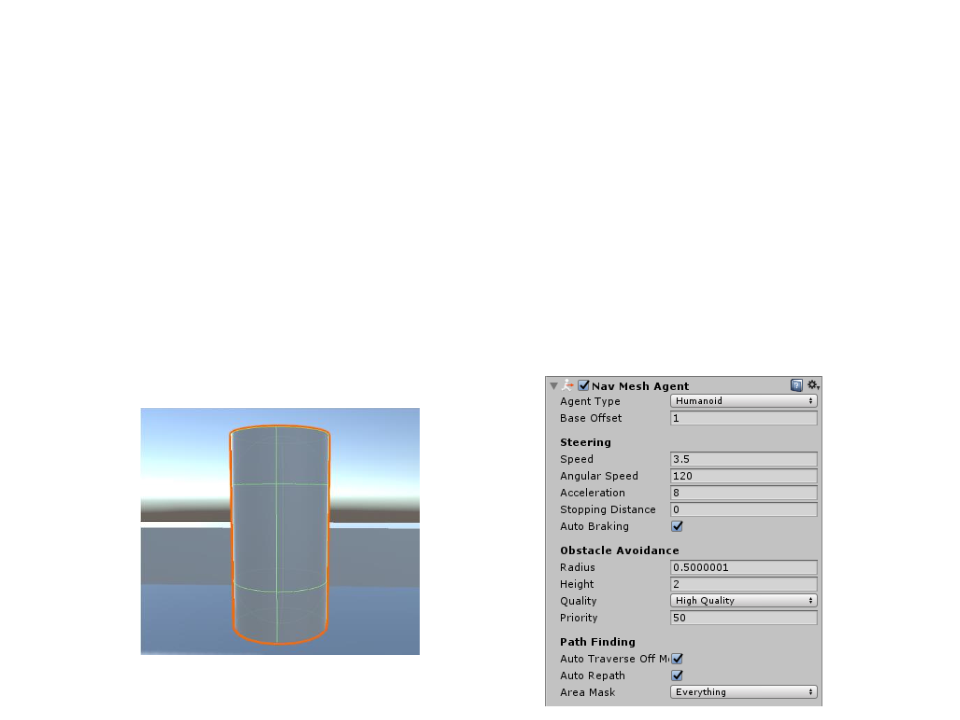
Unity Navigation System
•
Creating a NavMesh Agent:
–
(Step 1): Create an object to represent the agent (e.g. a cylinder).
–
(Step 2): Add a NavMesh Agent component to the object (Component
-> Navigation -> NavMesh Agent).
–
(Step 3): If necessary, adjust the agent radius to match the object.

Unity Navigation System
•
•
The NavMesh Agent component handles both the
pathfinding and the movement of the character.
The simplest way to move the agent towards a destination is
done by setting the desired destination point by script.
public class AgentControl : MonoBehaviour {
public Transform goal;
void Start(){
NavMeshAgent agent = GetComponent<NavMeshAgent>();
agent.destination = goal.position;
}
}
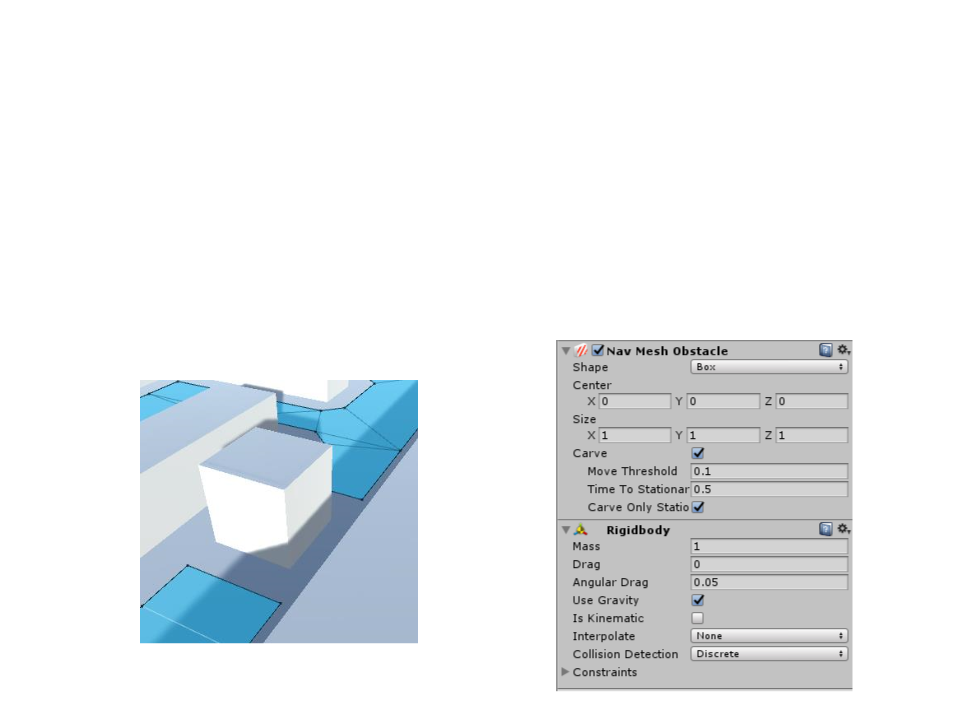
Unity Navigation System
•
NavMesh Obstacle components can be used to describe
obstacles the agents should avoid while navigating.
–
When an object obstructs the agent path, the Navigation System will
automatically find another path (if there is one).
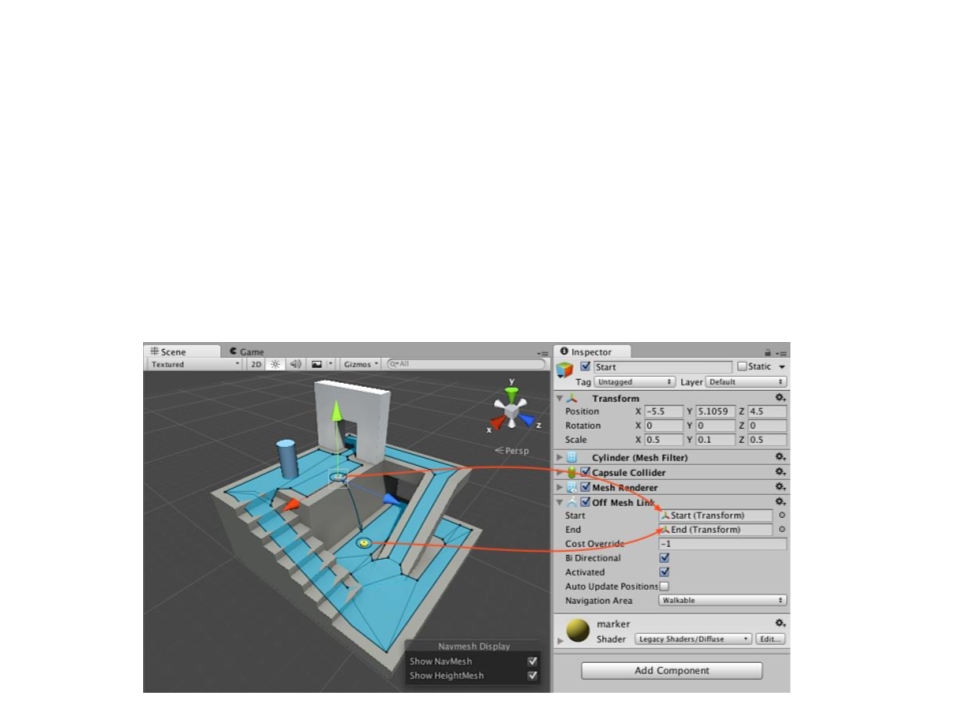
Unity Navigation System
•
Off-Mesh Links are used to create paths crossing outside the
walkable navigation mesh surface.
–
If the path via the off-mesh link is shorter than via walking along the
NavMesh, the off-mesh link will be used.
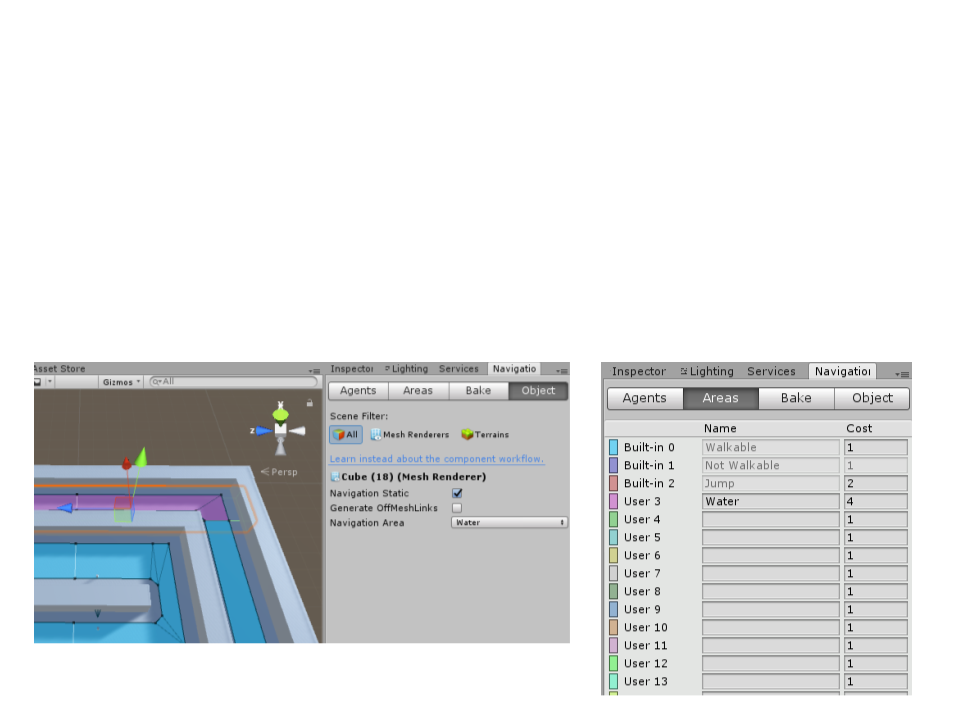
Unity Navigation System
•
The Navigation Areas define how difficult it is to walk across a
specific area, the lower cost areas will be preferred during
path finding.
–
The cost per area type can be set globally in the Areas tab.

Exercise 5
5
) Modify the scene created in Exercise 4 to use the Unity
Navigation System.
a) Create the navigation mesh;
b) Create an agent;
c) Create a set of destination points;
d) Make the agent move through the
destination points;
e) Add different costs to some of the
corridors of the maze.

Further Reading
•
•
Buckland, M. (2004). Programming Game AI by Example. Jones & Bartlett
Learning. ISBN: 978-1-55622-078-4.
–
Chapter 8: Practical Path Planning
Millington, I., Funge, J. (2009). Artificial Intelligence for Games (2nd ed.).
CRC Press. ISBN: 978-0123747310.
–
Chapter 4: Pathfinding
