
Data Structures
Lecture 03: Recursion
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>

Recursive Functions
•
•
In programming, a recursive function is a function that calls
itself.
The recursive call can be:
–
Direct: function A calls itself
–
Indirect: function A calls a function B which in turn calls A
void myFunction(int n)
{
.
..
myFunction(n-1);
..
Recursion
.
}
Recursive Functions
•
Recursive function for the factorial calculation:
Base Case
ꢀ
ꢁꢂꢃꢄꢅꢆꢁꢇ ꢈ = ቊꢈ1, ꢆ×ꢀ ꢀꢈꢁ=ꢂꢃꢄ0ꢅꢆꢁꢇ ꢈ − 1 , ꢆꢀ ꢈ > 0
Recursive Step
Recursive call
int factorial(int n)
{
if (n == 0)
Base Case
return 1;
else
return n * factorial(n-1);
Recursive Step
}

Recursive Functions
•
Behavior of a recursive function:
–
When a function is called recursively, a local environment is created
for each call;
–
Local variables of recursive calls are independent of each other, as if
we were calling different functions.
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start
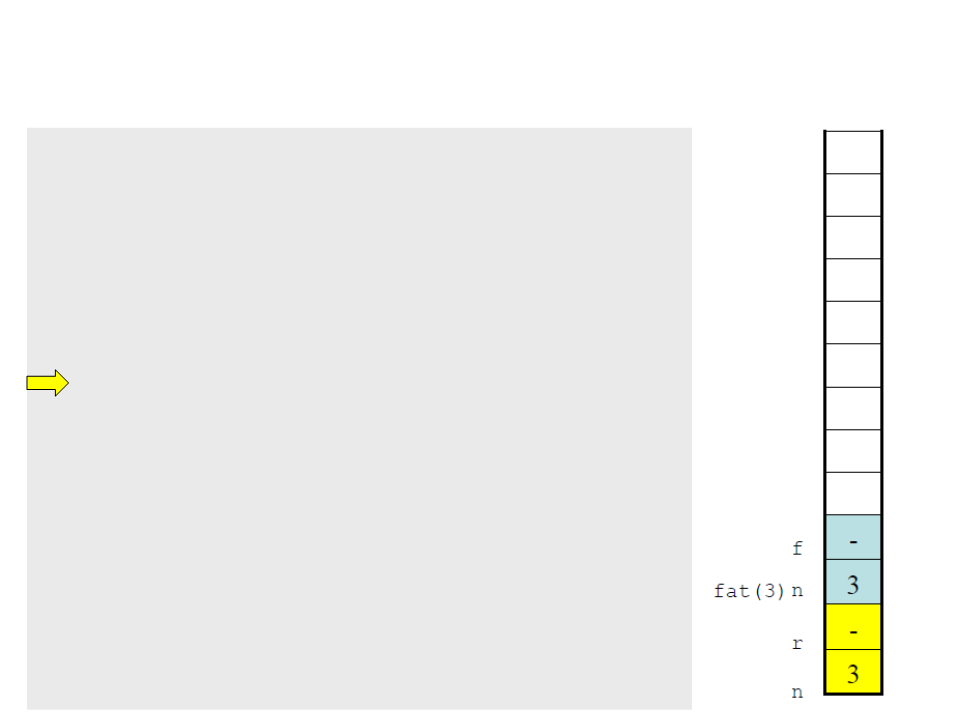
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start
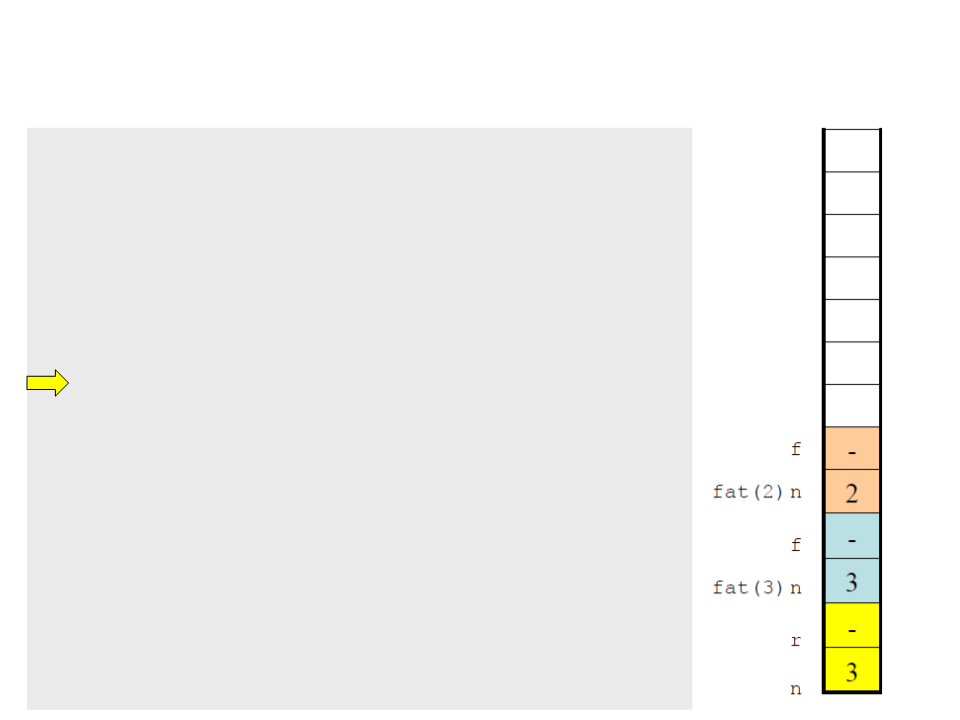
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start

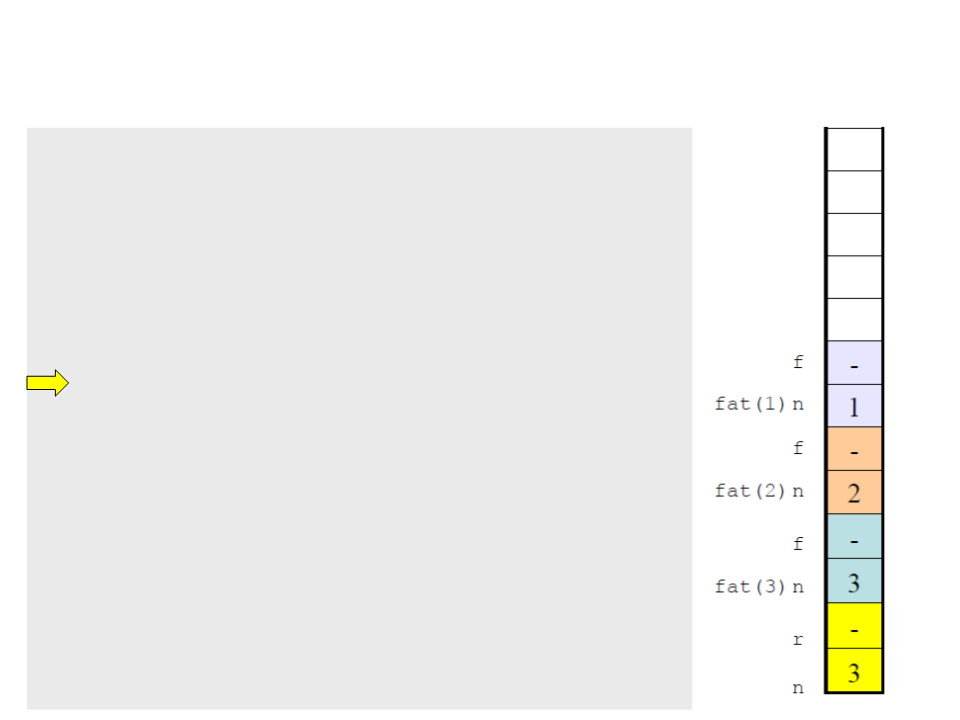
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start

Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start
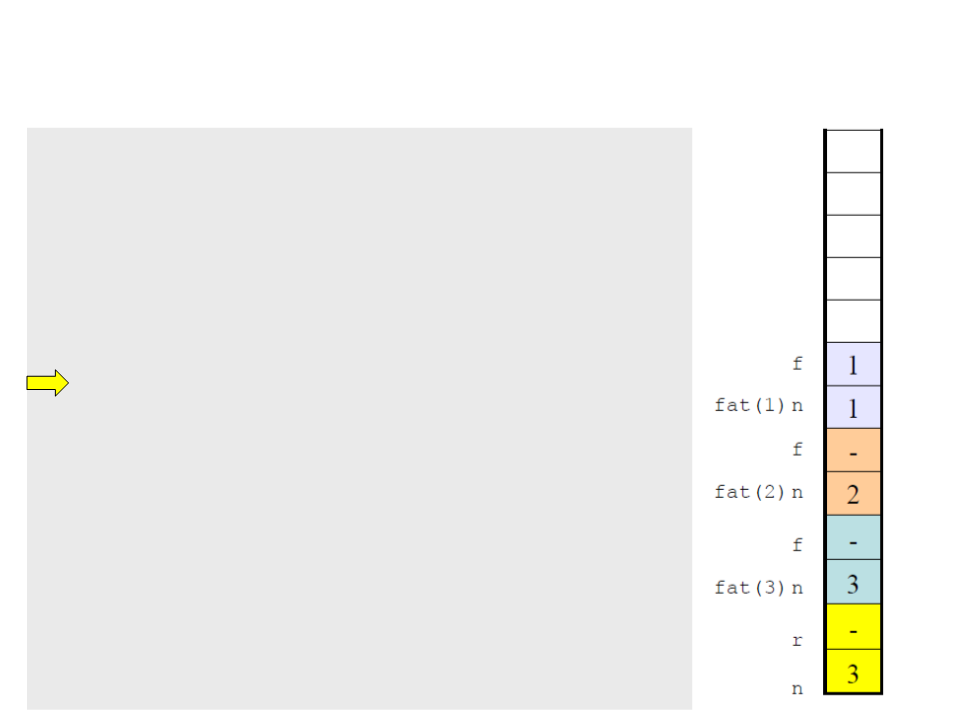
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start
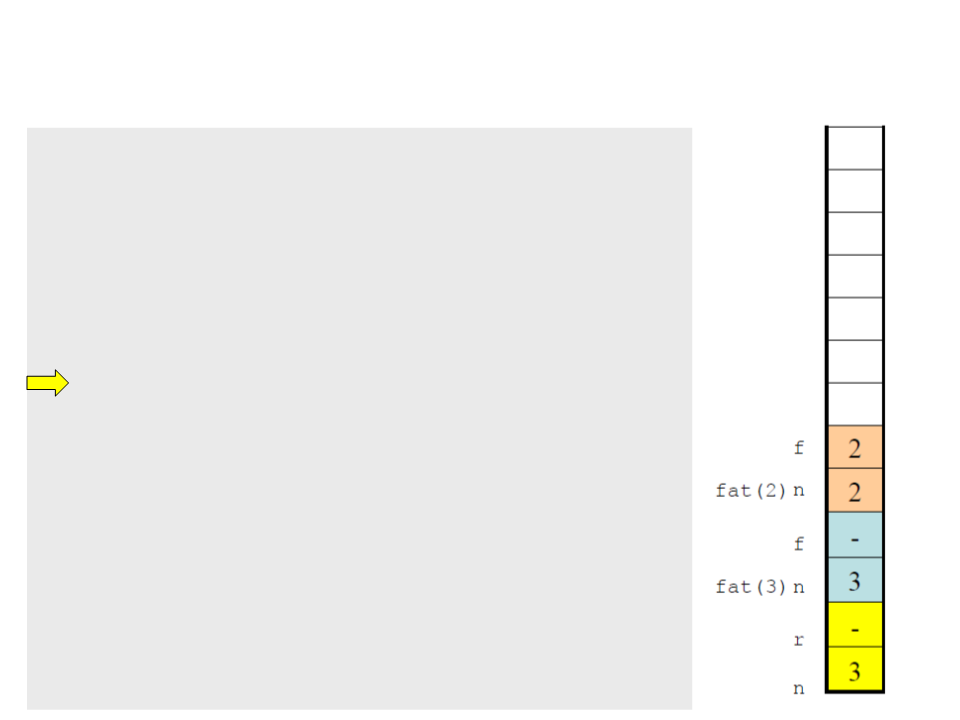
Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start

Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start

Recursive Functions
include <stdio.h>
#
int factorial(int n)
{
int f;
if (n == 0)
f = 1;
else
f = n * factorial(n-1);
return f;
}
void Start()
{
int n = 3, r;
r = factorial(n);
Debug.Log("Factorial of " + n + " = " + r);
}
Start
Assignment – Recursion
1
) Implement the recursive function for the exponentiation
operation:
ꢉꢊ = ൝1, ꢆꢀ ꢈ = 0
ꢉ × ꢉ(ꢊꢋꢌ), ꢆꢀ ꢈ > 0
Base Case
Recursive Step

Further Reading
•
•
Penton, R. (2002). Data Structures for Game Programmers.
Muska & Lipman/Premier-Trade. ISBN: 978-1931841948
–
Chapter 10: Recursion
Sherrod, A. (2007). Data Structures and Algorithms for
Game Developers. Charles River Media. ISBN: 978-
1
584504955
–
Chapter 3: Recursion
