
Data Structures
General Course Information
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>

Data Structures
•
Professor: Edirlei Soares de Lima
–
Education:
•
•
•
B.Sc. in Computer Science – UnC
M.Sc. in Computer Science – UFSM
Ph.D. in Computer Science – PUC-Rio
–
–
Teaching Experience: PUC-Rio, UNIRIO, UERJ, IADE-UE
Game Experience:
•
•
•
Game Engines: RPG Builder, 3D Game Builder;
Research Projects: most are related with Logtell (http://www.icad.puc-rio.br/~logtell/);
Games: Krimson (Best Game Award at SBGames 2010 – Indie Game Development
Festival), and several other prototype games.
–
More Information: https://edirlei.com/

What is a Data Structure?
•
A data structure defines how data is arranged in memory and
can be operated on by using various algorithms.
–
One of the most basic data structures used in general computer
programming is the array.
•
•
All data structures need algorithms to perform tasks and
manipulate data in memory.
Data structures are the foundation of many techniques used
in game programming and are essential to create specific
game mechanics in an efficient and effective way.

Example: Search in an Array
•
Problem:
Input: array a with n numbers and a number d to be
searched.
Output: i if the searched number is at v[i] or -1 if the
searched number is not in the array a;

Example: Search in an Array
•
The first algorithm: iterate over the array a, element by
element, checking if d is equal to one of the elements of a:
int SearchArray(int[] a, int d)
{
int i;
for (i = 0; i < a.Length; i++){
if (a[i] == d){
return i;
}
}
return -1;
}

Example: Search in an Array
•
Worst Case?
–
–
–
d is not in the array
In this case, n tests are necessary
T(n) = n → O(n) - Linear!
•
•
Best Case?
–
d is the first element
T(n) = O(1)
–
Algorithm complexity: when
analyzing an algorithm, we need
to consider the “Worst Case”,
the “Best Case” and the
Average Case?
–
n/2 tests
“Average Case”
–
T(n) = n/2 → O(n) - Linear!

Example: Search in an Array
•
What if the array is sorted?
–
We can improve the algorithm:
int SearchSortedArray(int[] a, int d)
{
int i;
for (i = 0; i < a.Length; i++)
{
if (a[i] == d)
return i;
else if (a[i] > d)
return -1;
}
return -1;
}

Example: Search in an Array
What is the complixity of the new algorithm?
Best Case:
•
•
–
T(n) = O(1)
An algorithm can have the same
complexity of another algorithm,
but it may be more or less efficient
than the other. Efficiency and
•
Worst Case:
–
complexity are different concepts.
T(n) = n → O(n) - Linear!

Example: Search in an Array
•
•
Can we improve the search algorithm?
–
Yes!
Binary search algorithm:
–
–
–
Compare d with the element that is in the middle of a;
if d is less than the middle element, search in the first half of the array;
if d is greater than the middle element, search in the second half of
the array;
–
–
if d is equal to the middle element, retorn its index;
Continue the procedure subdividing the select part of the array until
finding the searched element or reaching the end of the array.

Example: Search in an Array
int BinarySearchArray(int[] a, int d){
int begin = 0;
int end = a.Length - 1;
int middle;
while (begin <= end){
middle = (begin + end) / 2;
if (a[middle] > d)
end = middle - 1;
else if (a[middle] < d)
begin = middle + 1;
else
return middle;
}
return -1;
}
Example: Search in an Array
•
Worst Case: d is not in the array
–
–
–
2 tests are performed at every iteration;
At every iteration, the size of the search area is divided in half;
T(n) = O(log n)
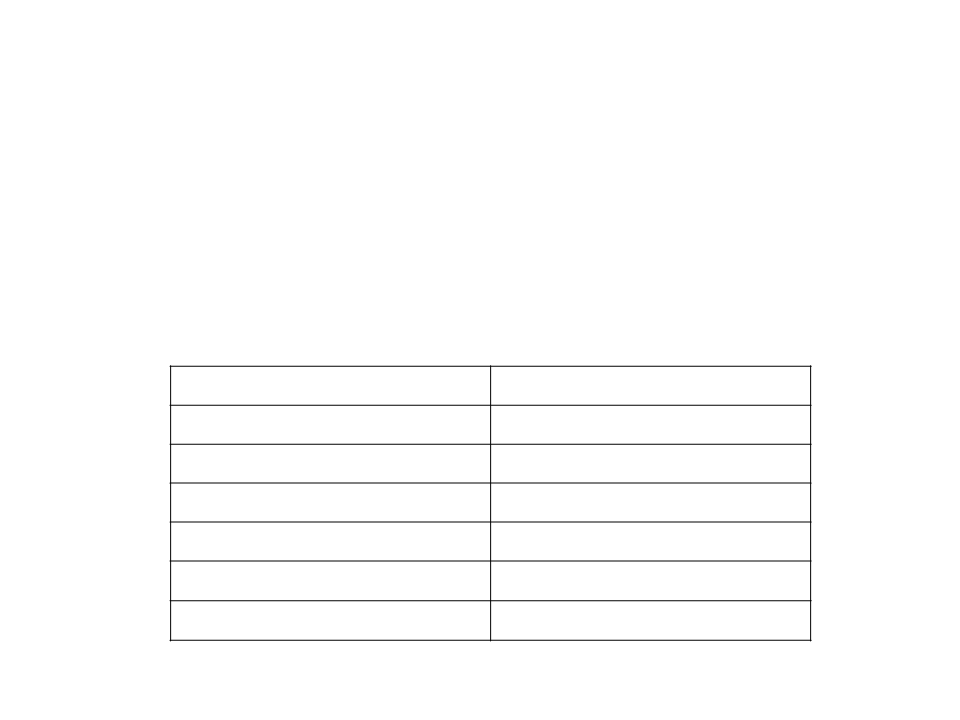
Iteration
Size of the problem
1
2
n
n/2
n/4
n/8
…
3
4
…
log n
1
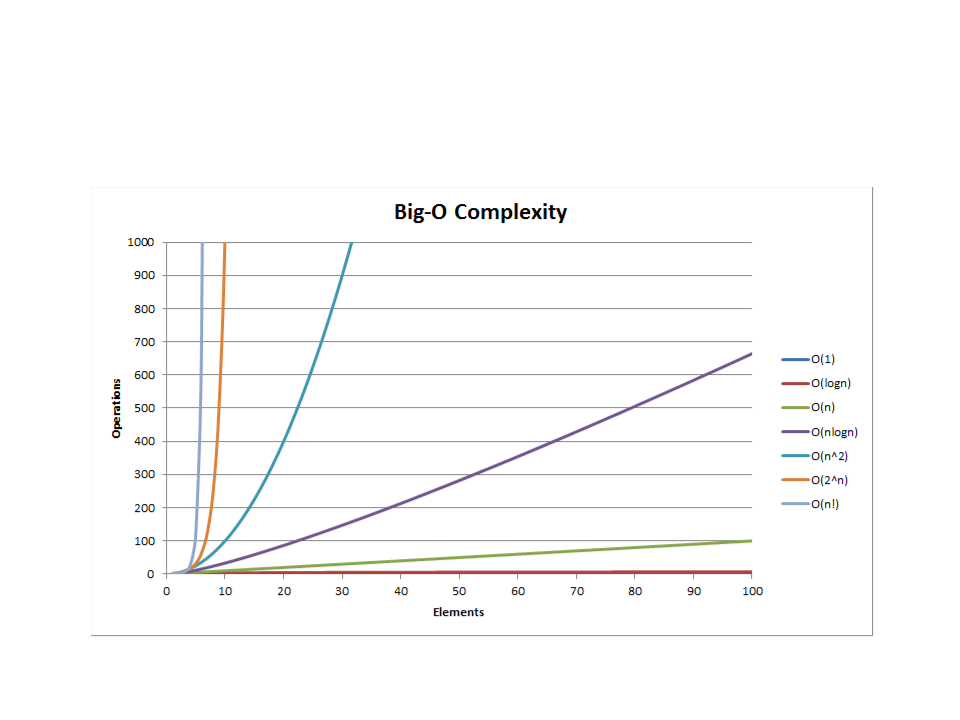
Algorithm Analysis – Complexity Types
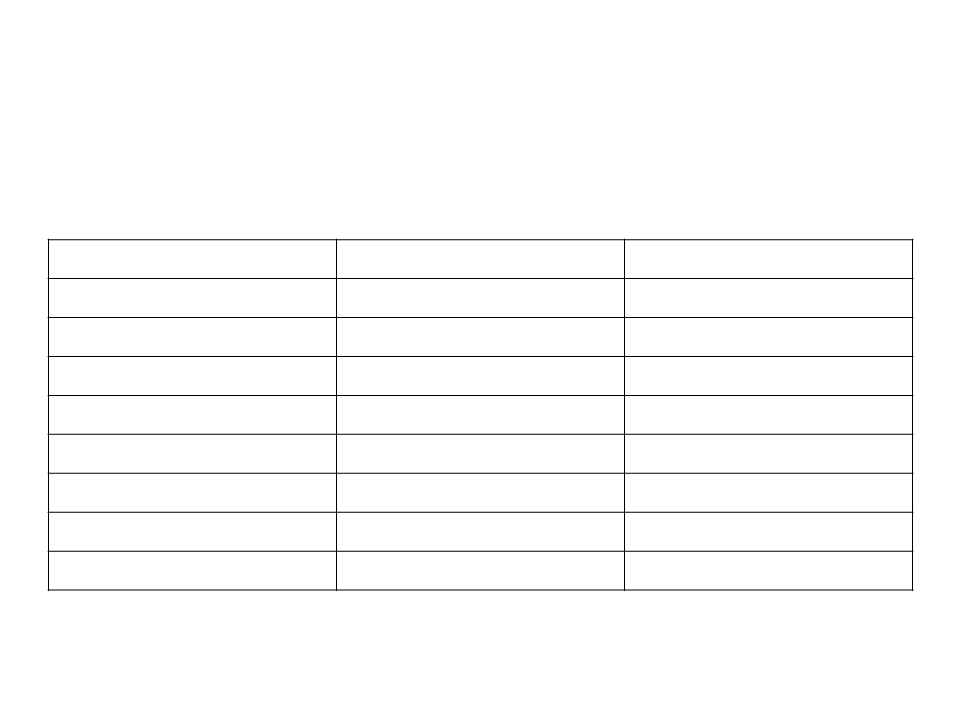
Difference between O(n) and O(log n)
Input Size
O(n)
10 sec
1 min
O(log n)
3 sec
10
0
6
6 sec
6
00
600
6 400
592 000
46 080 000
4 608 000 000
10 min
1 hour
1 day
9 sec
3
12 sec
16 sec
21 sec
30 sec
36 sec
8
2
1 month
1 year
9
9
100 years

Data Structures
•
•
Games Development:
–
Explore the main concepts and applications of algorithms and data
structures used for game programming.
Learning Outcomes:
1
2
3
4
. Determine the complexity of algorithms;
. Implement common data structures used for game development;
. Implement and compare the performance of different algorithms;
. Apply algorithms and data structures in game programming.
Data Structures
•
Module Content:
1. Introduction to Data Structures and Algorithms
2. Data Structures:
a. Arrays
b. Linked Lists
c. Stacks
d. Queues
e. Hash Tables
f. Trees
g. Graphs

Method
•
Active and experiential learning:
–
–
–
Theoretical concepts;
Practical examples;
Implementation exercises;
•
•
Game framework: Unity 2021.x.x
Semester’s PBL team project:
–
Apply the studied algorithms and data structures in the implementation
of the semester’s project.
•
The game must use at least 3 different types of data structures.
•
All choices of data structures must be justified in a final report.

Evaluation
•
Continuous Assessment:
–
[70%] Intermediate assessment:
•
[40%] Individual exercises on the studied concepts;
•
[30%] Second intermediate delivery of the team project (game prototype)
with group discussion.
•
[30%] Practical exam on the concepts learned.
–
[30%] End of term assessment:
•
[100%] Final delivery of the team project (within the semester’s PBL team
project) with individual discussion + final report.
•
Final Assessment:
–
[100%] Practical exam on the concepts learned.

Evaluation
•
Project Deliveries:
–
1st delivery: game specification
•
No evaluation for Data Structures.
–
2nd delivery: working prototype
•
Basic algorithms and data structures + implementation progress + group
discussion.
–
3rd delivery: final version
•
Algorithms and data structures + overall game complexity and game
experience + individual discussion.
•
Requirements:
The game must use at least 3 different types of data structures (Arrays, Linked
Lists, Stacks, Queues, Hash Tables, Trees, or Graphs).
–
–
All choices of data structures must be justified in a final report.

Bibliography
•
•
•
•
Sherrod, A. (2007). Data Structures and Algorithms
for Game Developers. Charles River Media. ISBN:
978-1584504955
Penton, R. (2002). Data Structures for Game
Programmers. Muska & Lipman/Premier-Trade. ISBN:
978-1931841948
Cormen, T., Leiserson, C., Rivest, R., Stein, C. (2009).
Introduction to Algorithms, 3rd Edition, MIT Press.
ISBN: 978-0262033848
Hocking, J. (2018). Unity in Action: Multiplatform
Game Development in C# (2nd ed.). Shelter Island,
NY: Manning Publications. ISBN: 978-1617294969

Game Frameworks
•
•
Canvas: Data Structures
Course webpage:
–
http://edirlei.com/datastructures
•
Contact:
–
–
edirlei.slima@gmail.com
