
Data Structures
Lecture 07: Graphs
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
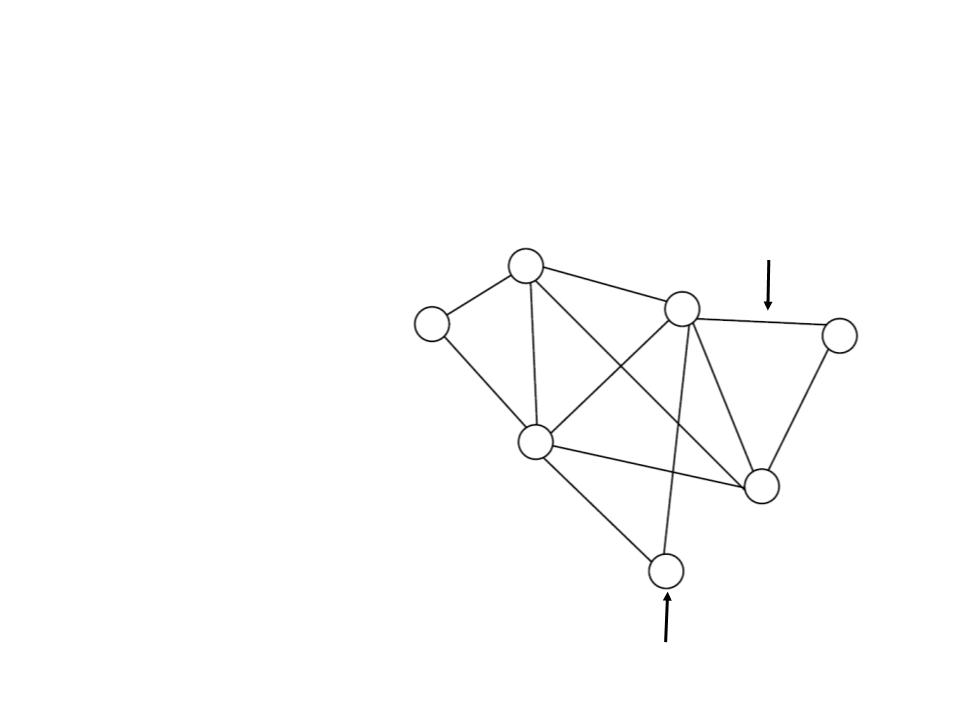
Graphs
Edge
•
G = (V, E)
–
–
–
G: graph;
V: set of vertices;
E: set of edges;
Vertex
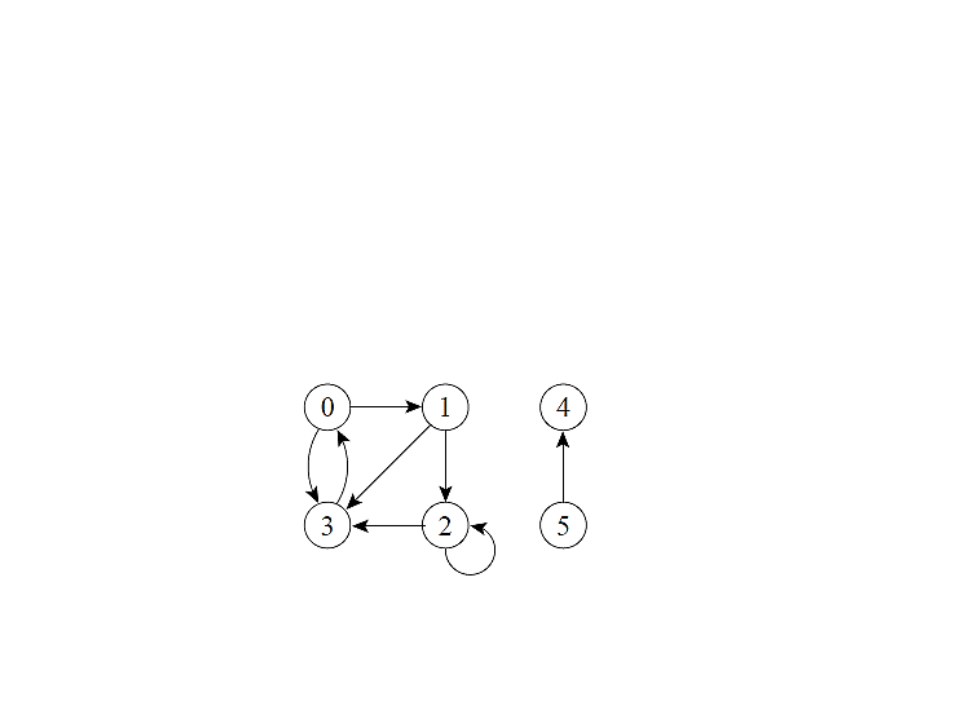
Graphs
•
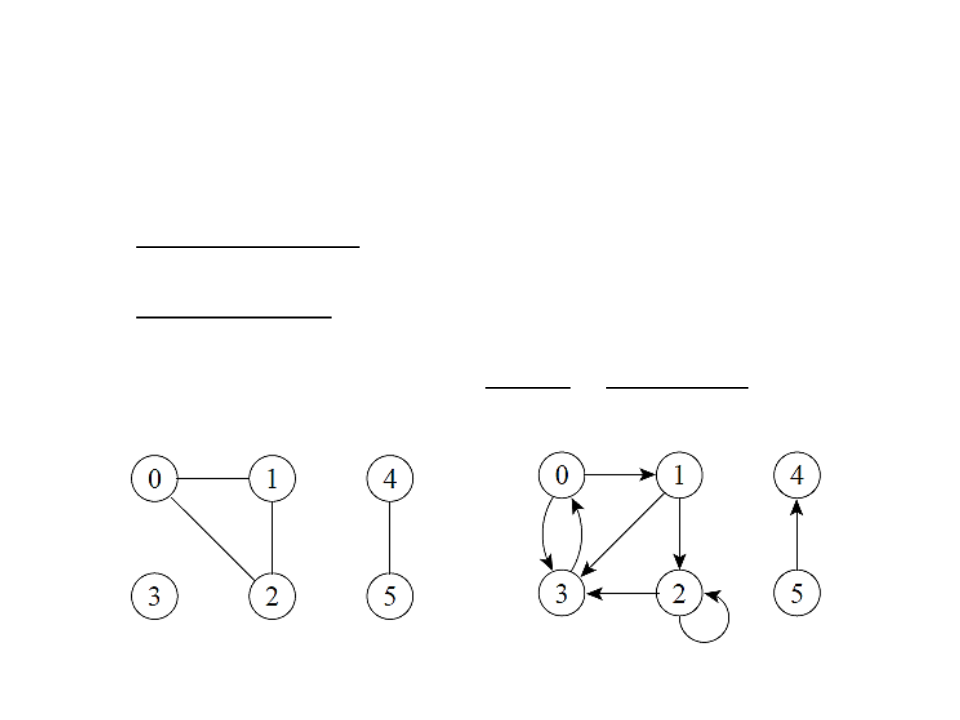
Directed graph: a graph in which edges have orientations.
–
An edge (u, v) leaves vertex u and enters vertex v.
•
Vertex v is adjacent to vertex u.
–
Edges from a vertex to itself are allowed (self-loops).
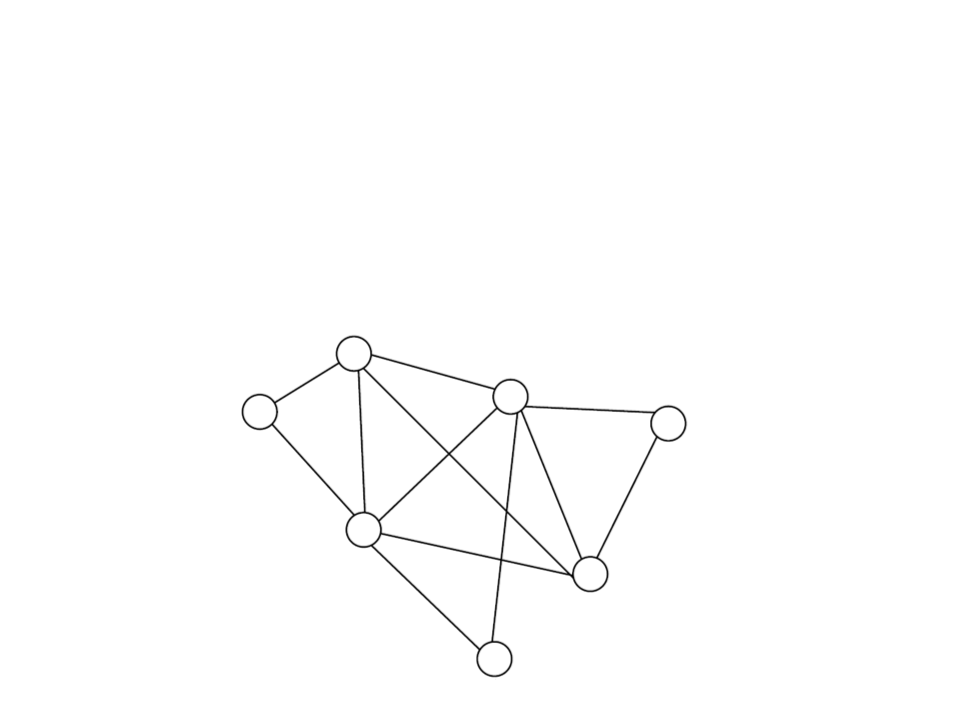
Graphs
•
Undirected graph: a graph in which edges have orientations.
–
Edges (u, v) and (v, u) are considered as a single edge. The adjacency
relationship is symmetric.
–
Self-loops are not allowed.
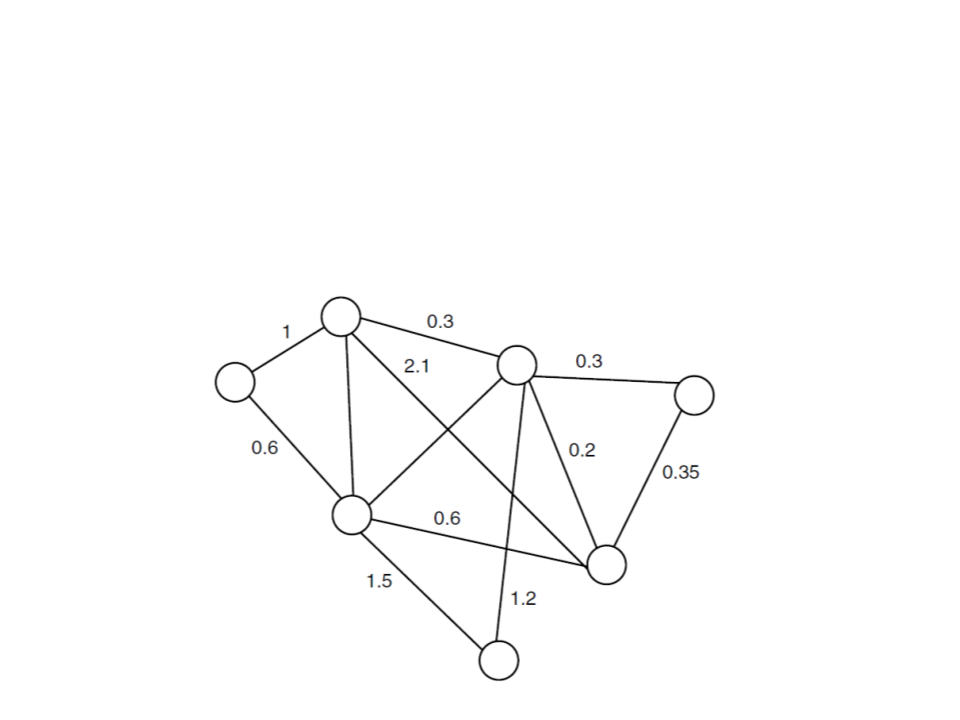
Graphs
•
Weighted graph: directed on undirected graph in which a
number (the weight) is assigned to each edge.
Graphs
•
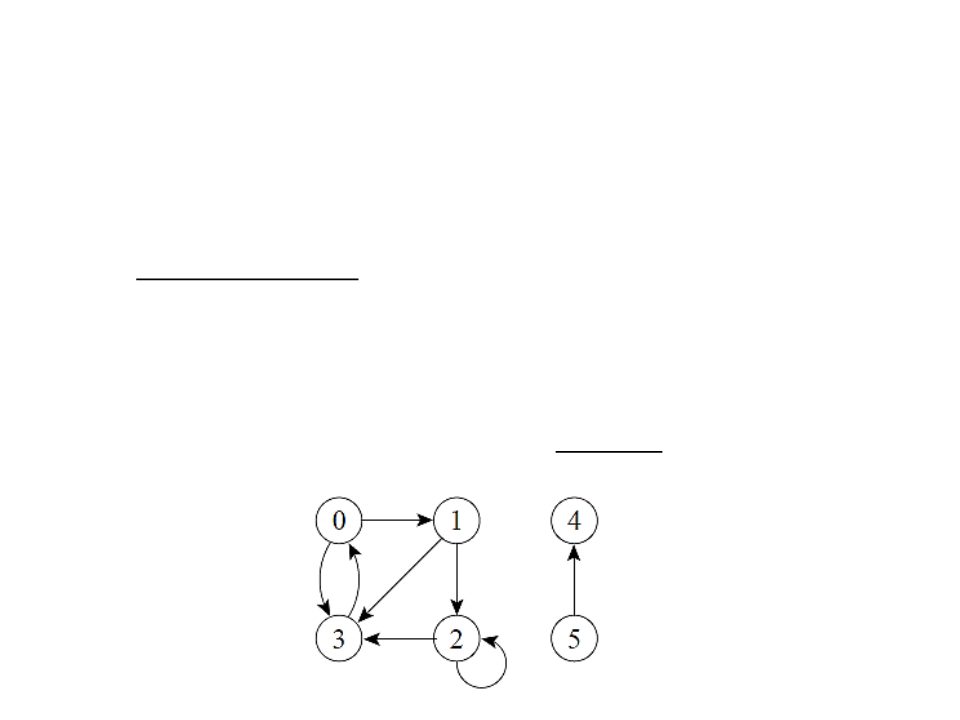
Degree of a vertex:
–
–
–
In undirected graphs: is the number of edges that are incident to the
vertex.
In directed graphs: is the number of edges that leave the vertex (out-
degree) plus the number of edges that enter the vertex (in-dregree).
A vertex of degree zero is called isolated or unconnected.
Graphs
•
Path between vertices:
–
–
–
A path of length k from a vertex x to a vertex y in a graph G = (V, A) is a
sequence of vertices (v0, v1, v2, ... , vk) such that x = v0 and y = vk, and vi ∈
V for i = 1, 2, ... , k.
The length of a path is the number of edges on it, that is, the path
contains the vertices v0, v1, v2, ... , vk and the edges (v0, v1), (v1, v2), ... ,
(
vk-1, vk).
If there is a path c from x to y then y is reachable from x via c.
Graphs
•
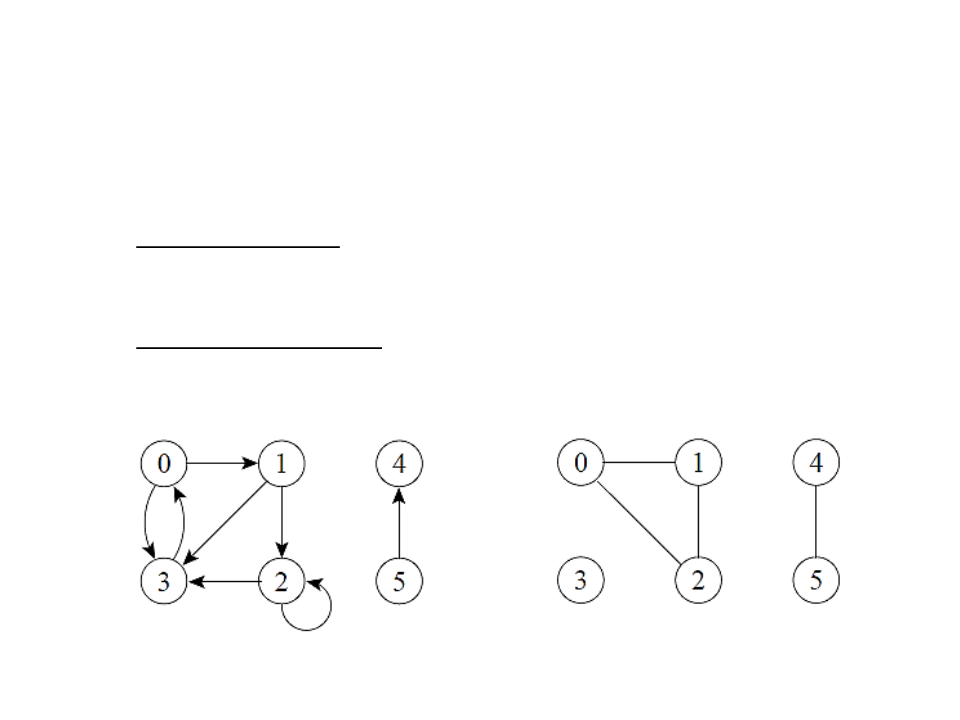
Cycles:
–
In a directed graph: a path (v0, v1, ... , vk) forms a cycle if v0 = vk and the
path contains at least one edge.
•
The self-loop is a size 1 loop.
–
In an undirected graph: a path (v0, v1, ... , vk) forms a cycle if v0 = vk and
the path contains at least three edges.
Graphs
•
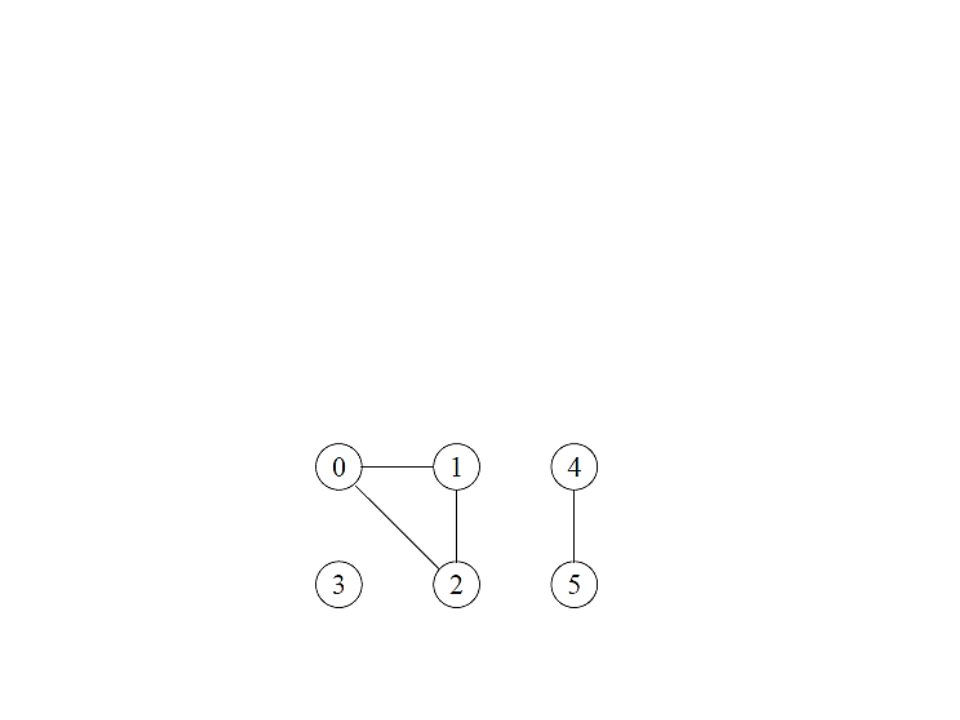
Connected components:
–
An undirected graph is connected if each pair of vertices is connected by
a path.
–
–
Connected components are the connected parts of a graph.
An undirected graph is connected if it has exactly one connected
component.
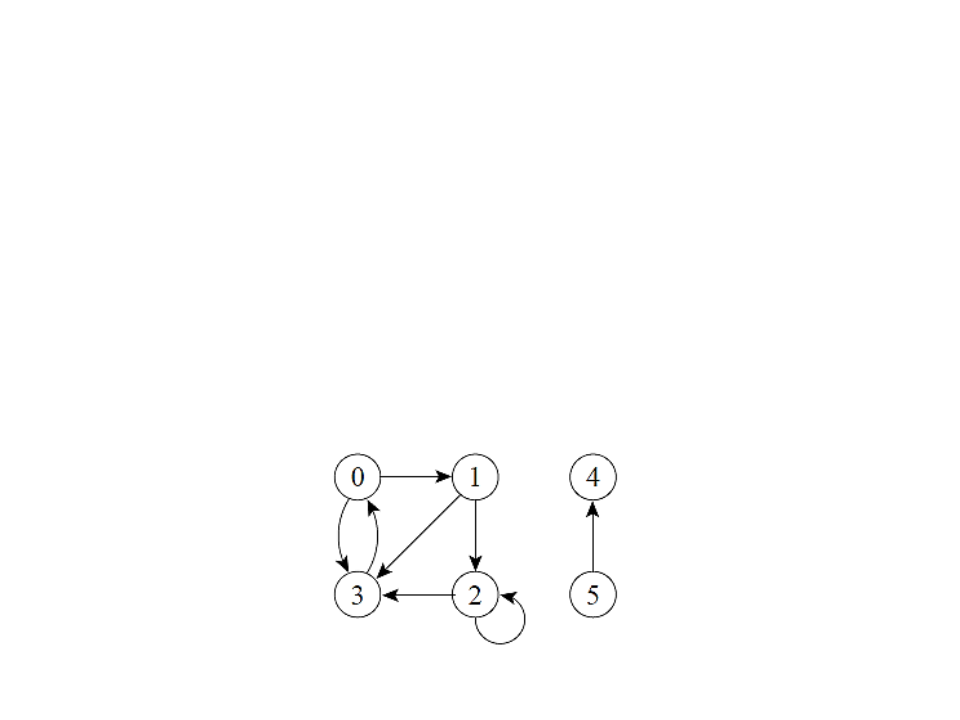
Graphs
•
Strongly connected components:
–
–
–
A directed graph G = (V, A) is strongly connected if any two vertices are
reachable from each other.
The strongly connected components of a directed graph are sets of
vertices under the relationship “are mutually reachable”.
A strongly connected directed graph has only one strongly connected
component.
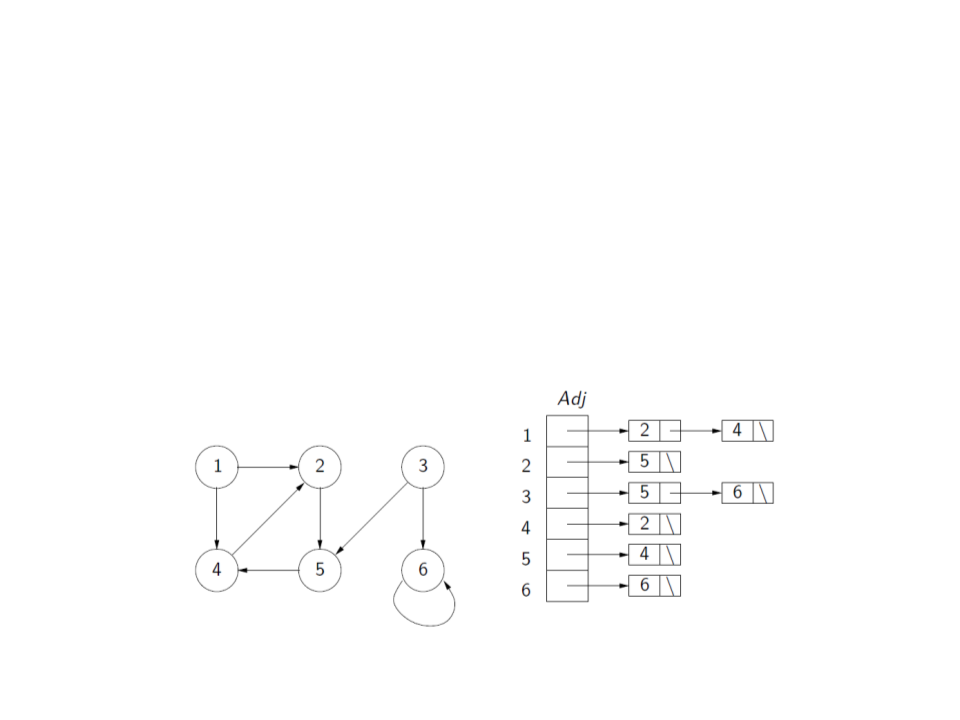
Graph – Representation
•
Adjacency list:
–
Uses an array or linked list Adj with |V| adjacency lists, one for
each vertex v ∈ V.
–
For each u ∈ V, Adj[u] contains references to all vertices v such
that (u, v) ∈ A. That is, Adj[u] contains all adjacency vertices of u.
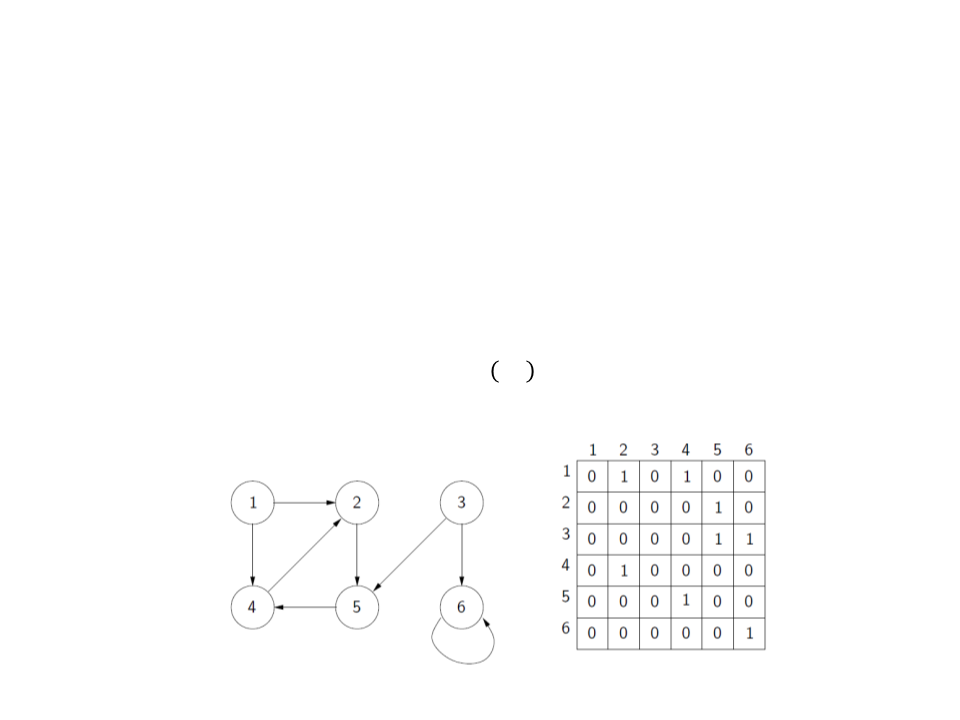
Graph – Representation
•
Adjacency matrix:
–
Given a graph G = (V, E), we assume that vertices are labeled with
numbers 1, 2, . . . , |V|.
–
The adjacency matrix is a matrix Aij of dimensions |V| × |V|,
where:
1
0
ꢃꢄ ꢃ, ꢅ ∈ ꢀ
ꢆꢇꢈꢉꢊꢋꢃꢌꢉ
ꢀꢁꢂ
= ቊ

Graph Vertex – Generic Class
public class GraphVertex<T>
{
private LinkedList<GraphVertex<T>> edges;
private T data;
public GraphVertex(T t){
edges = new LinkedList<GraphVertex<T>>();
data = t;
}
public void AddEdge(GraphVertex<T> v){
edges.InsertAtEnd(v);
}
public LinkedList<GraphVertex<T>> Edges{
get { return edges; }
set { edges = value; }
}
public T Data{
get { return data; }
set { data = value; }
}
}
Graph – Generic Class
public enum GraphType { Directed, Undirected };
public class Graph<T>
{
private LinkedList<GraphVertex<T>> vertices;
public GraphType graphType;
public Graph(GraphType t){
vertices = new LinkedList<GraphVertex<T>>();
graphType = t;
}
...

Graph
•
Basic operations:
–
–
–
CreateVertex: creates a vertex and adds it to the list of vertices of the
graph.
AddEdge: adds an edge (u, v) to the graph (connecting vertex u to
vertex v).
Traversal/Search: traverses or search for the path to a certain element
in the graph. Several traversal strategies can be used:
•
•
•
•
•
Breadth-first search (BFS);
Depth-First Search (DFS);
Dijkstra algorithm;
A* algorithm;
…

Graph – CreateVertex
•
Creates a vertex and adds it to the list of vertices of the
graph.
public GraphVertex<T> CreateVertex(T t)
{
GraphVertex<T> vertex = new GraphVertex<T>(t);
vertices.InsertAtEnd(vertex);
return vertex;
}

Graph – AddEdge
•
Adds an edge (u, v) to the graph (connecting vertex u to
vertex v).
–
If the graph is undirected, also connects vertex v to vertex u.
public void AddEdge(GraphVertex<T> v, GraphVertex<T> u)
{
if (graphType == GraphType.Directed)
{
v.AddEdge(u);
}
if (graphType == GraphType.Undirected)
{
v.AddEdge(u);
u.AddEdge(v);
}
}

Graph – Creating a Directed Graph
•
Example:
Graph<string> directedGraph = new Graph<string>(GraphType.Directed);
GraphVertex<string> u = directedGraph.CreateVertex("u");
GraphVertex<string> v = directedGraph.CreateVertex("v");
GraphVertex<string> w = directedGraph.CreateVertex("w");
GraphVertex<string> x = directedGraph.CreateVertex("x");
GraphVertex<string> y = directedGraph.CreateVertex("y");
GraphVertex<string> z = directedGraph.CreateVertex("z");
directedGraph.AddEdge(u, v);
directedGraph.AddEdge(u, x);
directedGraph.AddEdge(x, v);
directedGraph.AddEdge(v, y);
directedGraph.AddEdge(y, x);
directedGraph.AddEdge(w, y);
directedGraph.AddEdge(w, z);
directedGraph.AddEdge(z, z);

Graph – Creating a Undirected Graph
•
Example:
Graph<int> undirectedGraph = new Graph<int>(GraphType.Undirected);
GraphVertex<int> v1 = undirectedGraph.CreateVertex(1);
GraphVertex<int> v2 = undirectedGraph.CreateVertex(2);
GraphVertex<int> v3 = undirectedGraph.CreateVertex(3);
GraphVertex<int> v4 = undirectedGraph.CreateVertex(4);
GraphVertex<int> v5 = undirectedGraph.CreateVertex(5);
GraphVertex<int> v6 = undirectedGraph.CreateVertex(6);
undirectedGraph.AddEdge(v1, v2);
undirectedGraph.AddEdge(v1, v4);
undirectedGraph.AddEdge(v2, v3);
undirectedGraph.AddEdge(v4, v5);
undirectedGraph.AddEdge(v4, v6);
undirectedGraph.AddEdge(v5, v6);

Breadth-First Search (BFS)
•
•
BFS is one of the simplest algorithms for exploring a graph.
–
Given a graph G = (V, E) and a vertex s, called the source, the algorithm
systematically explores the edges of G in order to visit all vertices that
are reachable from s.
The algorithm expands the boundary between discovered and
undiscovered vertices evenly across the width of the
boundary.
–
The algorithm discovers all vertices at a distance k from the origin
vertex before discovering any vertices at a distance k + 1.
•
The graph can be directed or undirected.
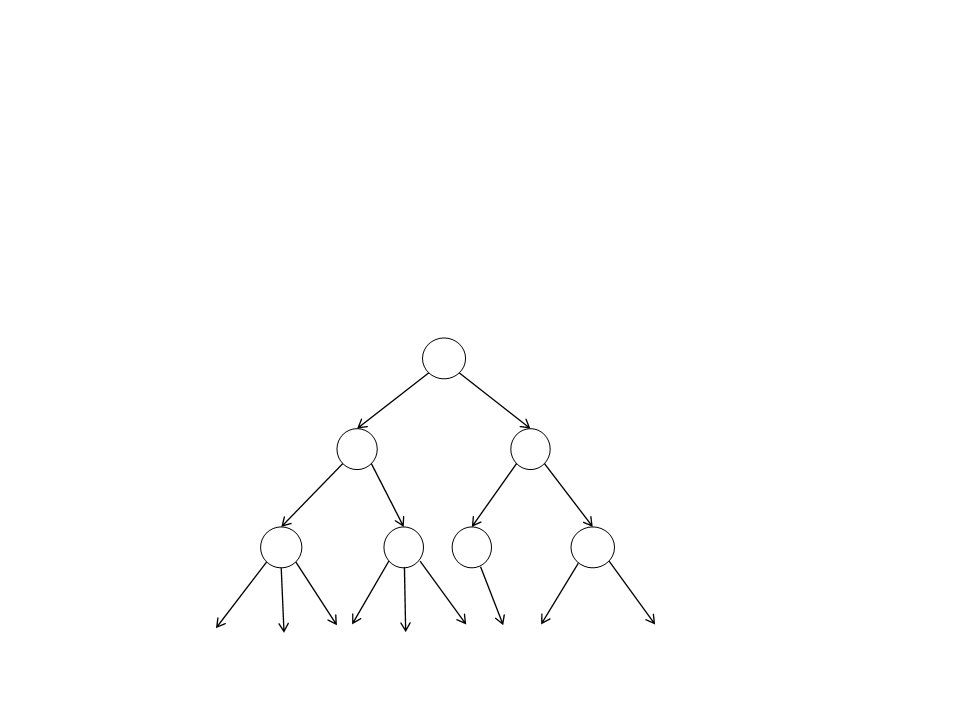
Breadth-First Search (BFS)
•
Strategy:
–
The algorithm discovers all vertices at a distance k from the origin
vertex before discovering any vertices at a distance k + 1.
A
B
C
D
E
F
G

Breadth-First Search (BFS)
•
Algorithm:
–
To control the search, the BFS algorithm paints each vertex
white, gray or black.
–
All vertices start white and can later become gray and then
black.
•
•
•
White: not visited;
Gray: visited;
Black: completely explored (all adjacent nodes were visited).

Breadth-First Search (BFS)
BFS(G, s)
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
Q ← {s} //Queue Structure
while Q ≠ ∅
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
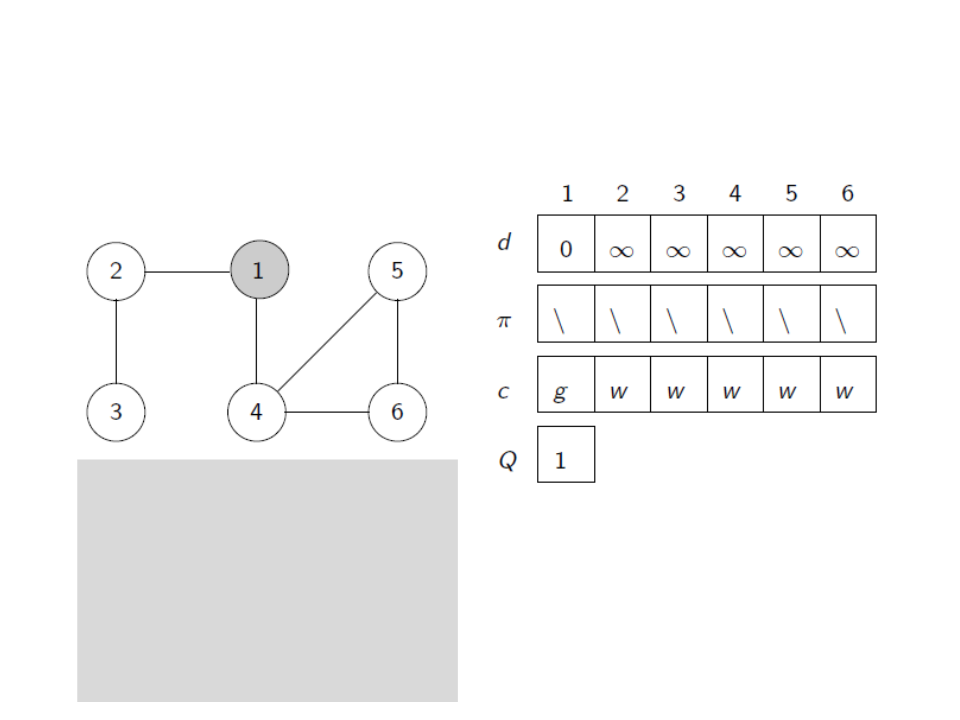
Breadth-First Search (BFS)
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
Q ← {s} //Queue
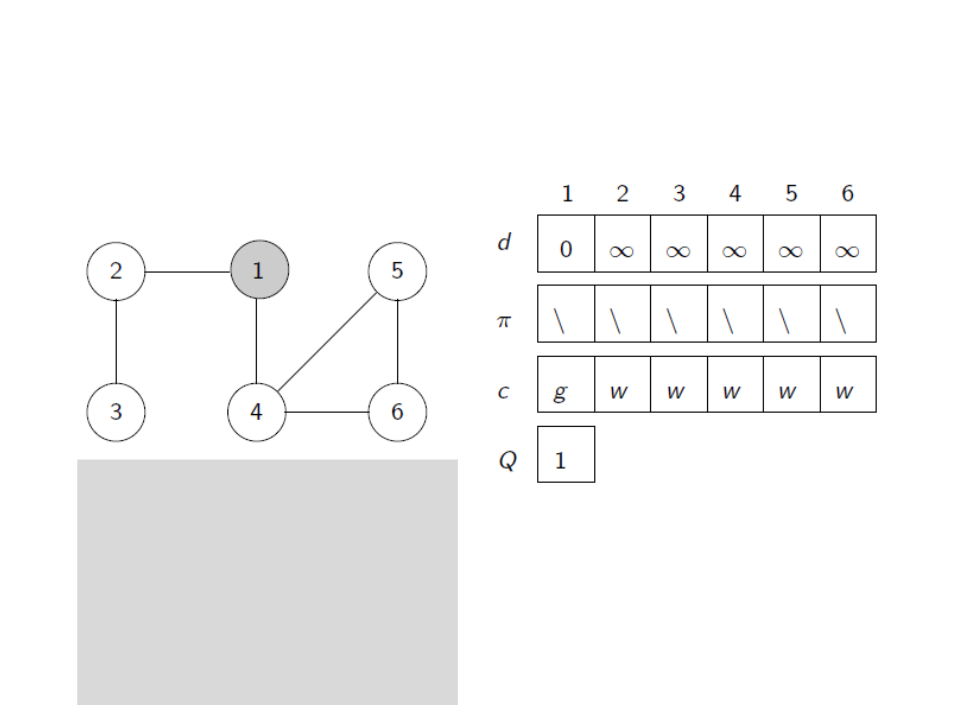
Breadth-First Search (BFS)
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
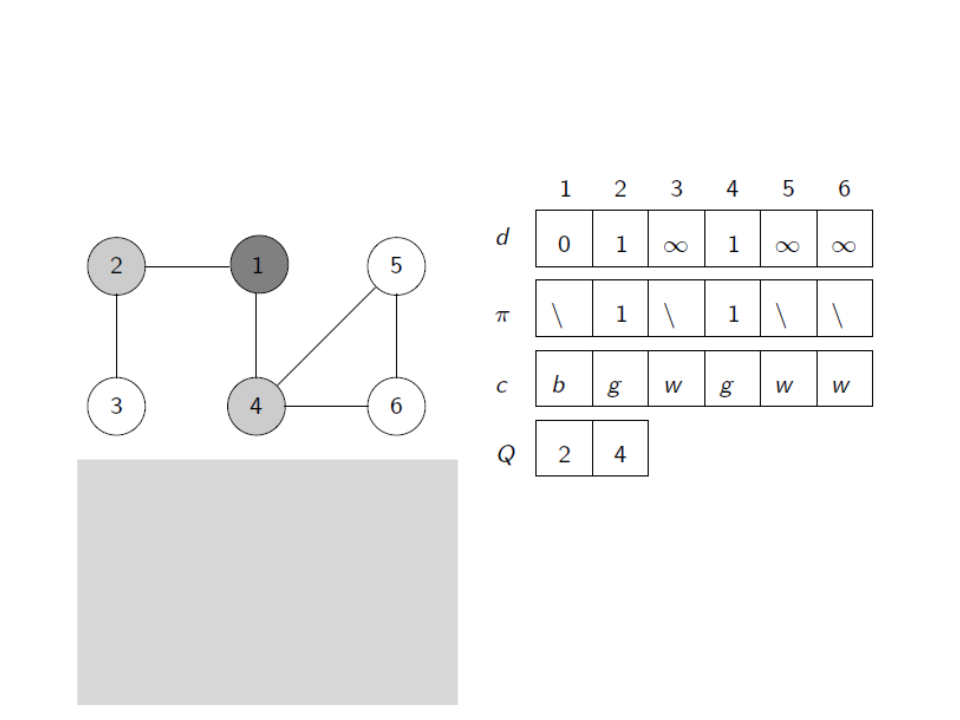
Breadth-First Search (BFS)
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
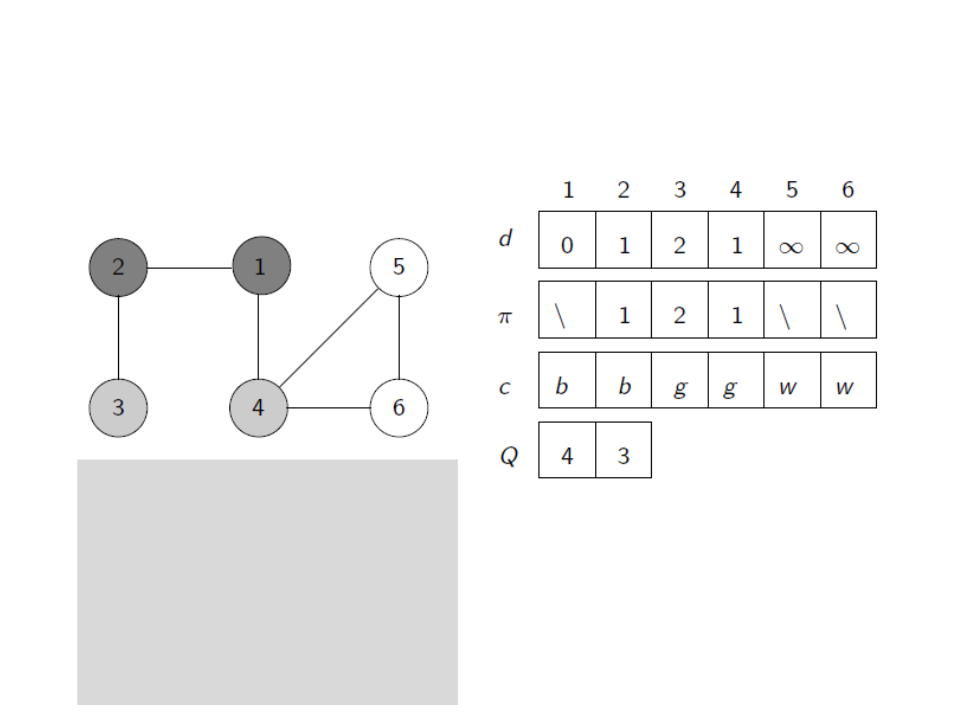
Breadth-First Search (BFS)
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black
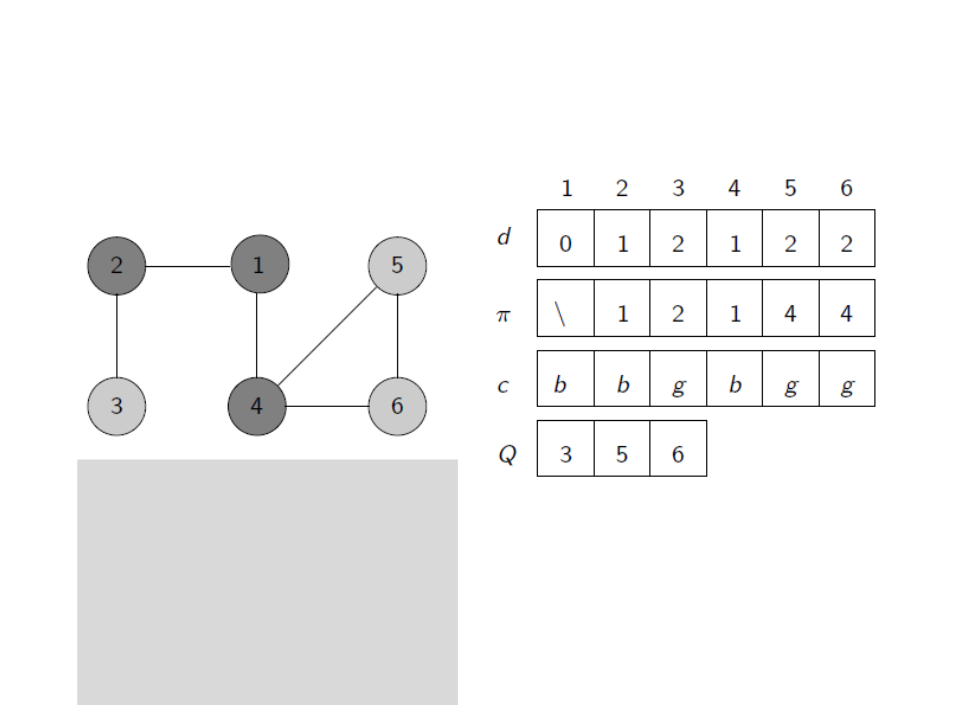
Breadth-First Search (BFS)
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
enqueue(Q,v)
dequeue(Q)
c[u] ← black

Breadth-First Search (BFS) – Analysis
BFS(G, s)
for each u ∈ V[G]
c[u] ← white
d[u] ← ∞
ꢍ[u] ← NULL
c[s] ← gray
d[s] ← 0
Q ← {s} //Queue Structure
while Q ≠ ∅
•
•
Each vertex of V is placed on queue Q at
most once: O(V);
The adjacency list of any vertex of u is
traversed only when the vertex is
removed from the queue;
•
The sum of all adjacent lists is O(E), so
the total time spent on the adjacent lists
is O(E);
u ← head[Q]
for each v ∈ E[u]
if c[v] = white
c[v] ← gray
d[v] ← d[u] + 1
ꢍ[v] ← u
•
•
Queuing and dequeuing cost O(1);
BFS complexity: O(V + E)
enqueue(Q,v)
dequeue(Q)
c[u] ← black

Breadth-First Search (BFS) – C#
public Dictionary<GraphVertex<T>, GraphVertex<T>> BFS(GraphVertex<T> s)
{
Dictionary<GraphVertex<T>, int> d = new Dictionary<GraphVertex<T>, int>();
Dictionary<GraphVertex<T>, int> c = new Dictionary<GraphVertex<T>, int>();
Dictionary<GraphVertex<T>, GraphVertex<T>> pi = new
Dictionary<GraphVertex<T>, GraphVertex<T>>();
Queue<GraphVertex<T>> Q = new Queue<GraphVertex<T>>();
foreach (GraphVertex<T> u in vertices)
{
c[u] = 0; //white
d[u] = int.MaxValue;
pi[u] = null;
}
c[s] = 1; //gray
d[s] = 0;
Q.Enqueue(s);
while (!Q.IsEmpty())
{
QueueNode<GraphVertex<T>> u = Q.Dequeue();
...

Breadth-First Search (BFS) – C#
...
foreach (GraphVertex<T> v in u.Data.Edges)
{
if (c[v] == 0) //white
{
c[v] = 1;
d[v] = d[u.Data] + 1;
pi[v] = u.Data;
Q.Enqueue(v);
}
}
c[u.Data] = 2; //black
}
return pi;
}
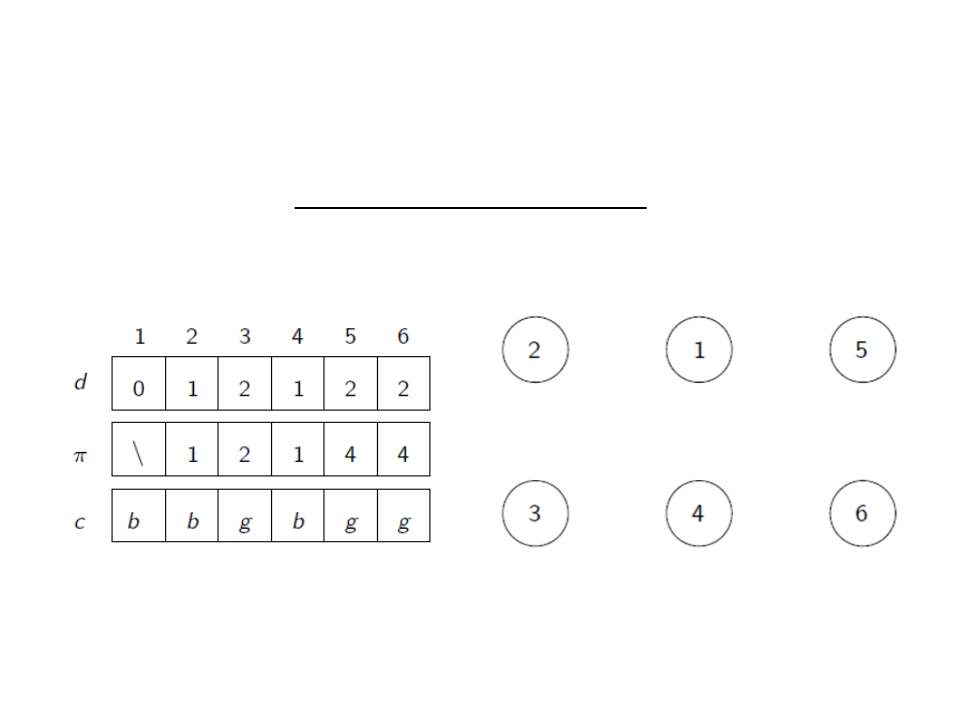
Breadth-First Search (BFS)
•
It is possible to reconstruct the search tree with the information
of π i:
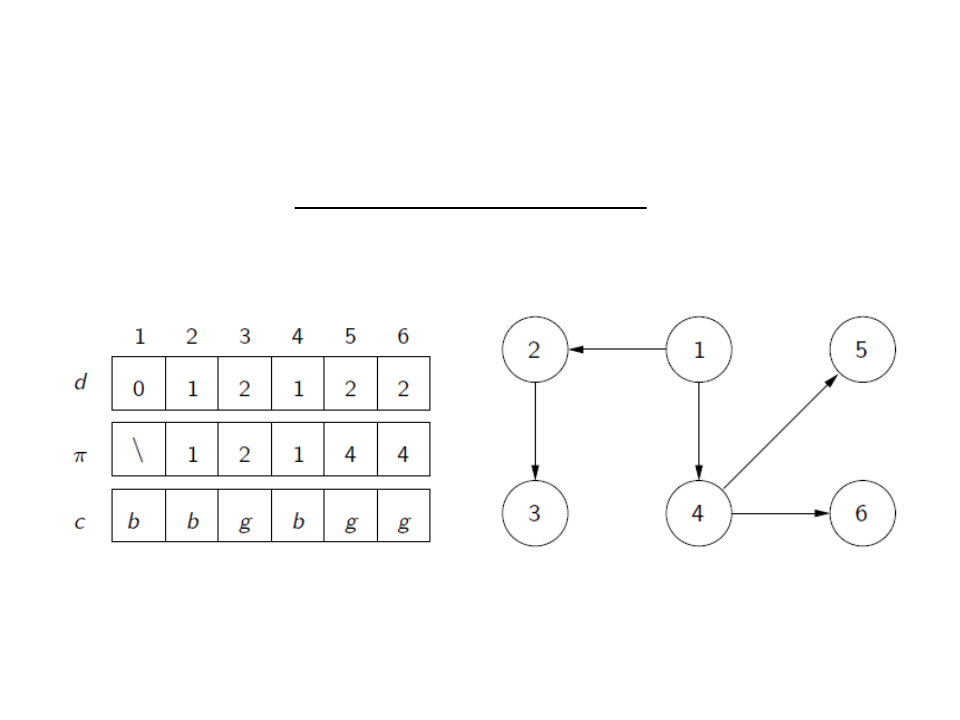
Breadth-First Search (BFS)
•
It is possible to reconstruct the search tree with the information
of π i:

Assignment 1 – Graphs
1
) Create a function to use the information stored in π to print
the path from the start vertex to another vertex of the graph.
–
–
The path must be displayed in the correct order.
Hint: when reading the information from π, the path will be inverted,
but you can use a stack structure to store the vertices from π and
easily retrieve them in the correct order.

Depth-First Search (DFS)
•
•
The DFS strategy is to seek the deepest vertex in the graph
whenever possible:
–
Edges are explored from the most recently discovered vertex v that
still has unexplored edges.
When all edges of v have been explored, the search moves
backwards to explore the edges of the vertex from which v
was discovered (backtracking).
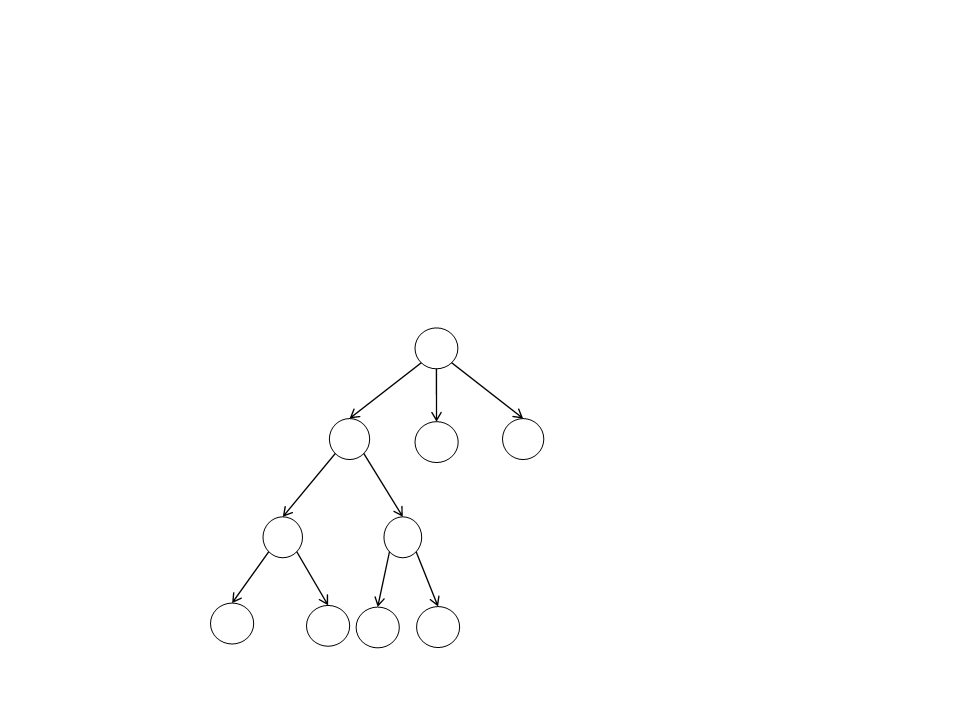
Depth-First Search (DFS)
•
Strategy:
–
Edges are explored from the most recently discovered vertex v that
still has unexplored edges.
A
B
D
C
E
F
M
N
P
Q

Depth-First Search (DFS)
•
Algorithm:
–
To control the search, the DFS algorithm paints each vertex
white, gray or black.
–
All vertices start white and can later become gray and then
black.
•
•
•
White: not visited;
Gray: visited;
Black: completely explored (all adjacent nodes were visited).

Depth-First Search (DFS)
•
Algorithm:
–
The DFS algorithm marks each vertex with a timestamp.
Each vertex has two timestamps:
–
•
•
d[v]: indicates the time when v was visited (painted with grey);
f[v]: indicates the time when v was completely explored (all
adjacent nodes were visited) (painted black).

Depth-First Search (DFS)
DFS(G)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
Visit(u)
Visit(u)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
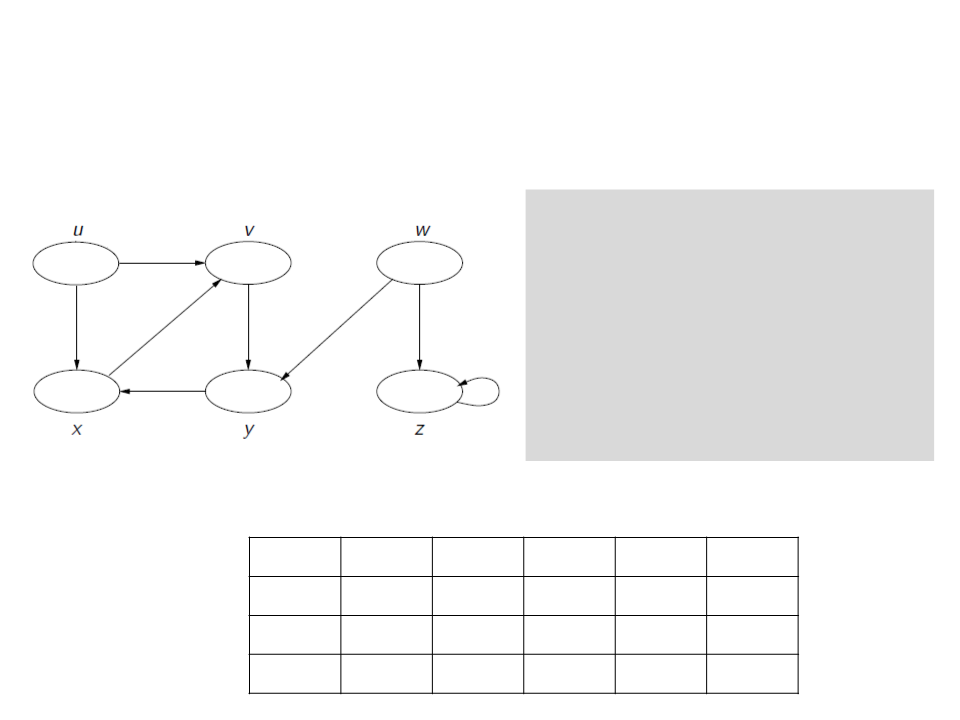
Depth-First Search (DFS)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
Visit(u)
u
w
/
v
w
/
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
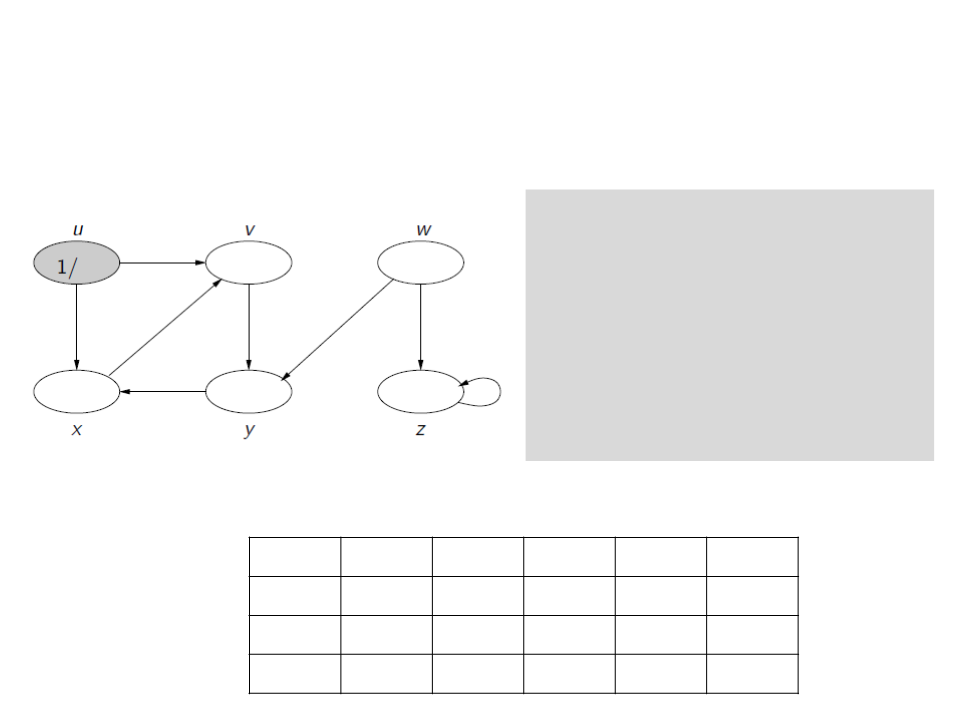
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
w
/
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1
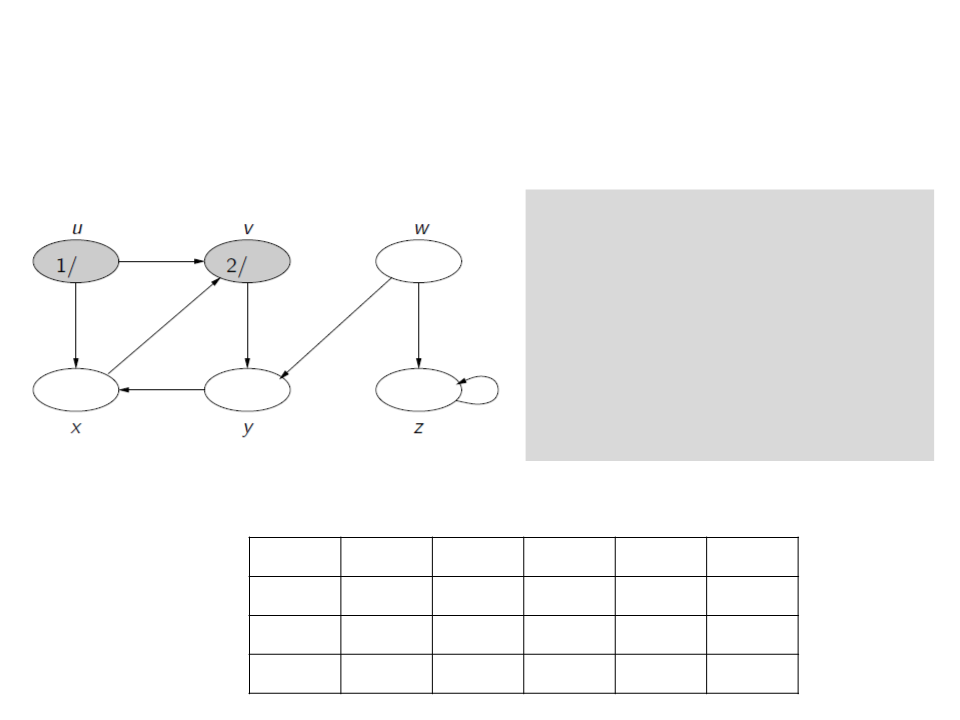
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
w
/
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1
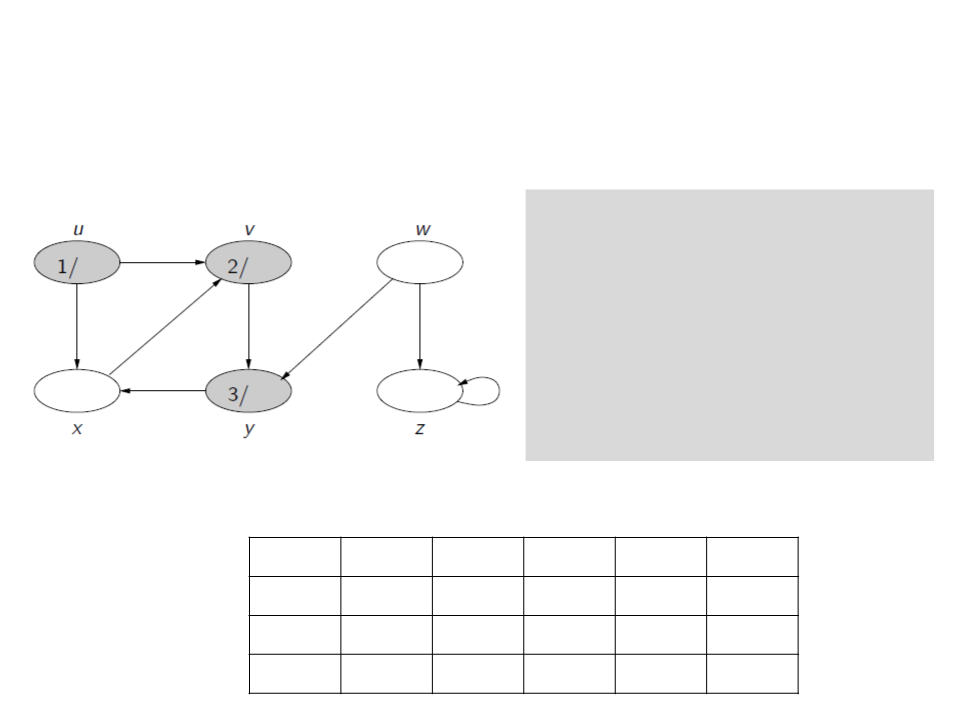
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
w
/
w
w
/
z
w
/
c
ꢍ
d
f
1

Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
g
y
4
w
w
/
z
w
/
c
ꢍ
d
f
1
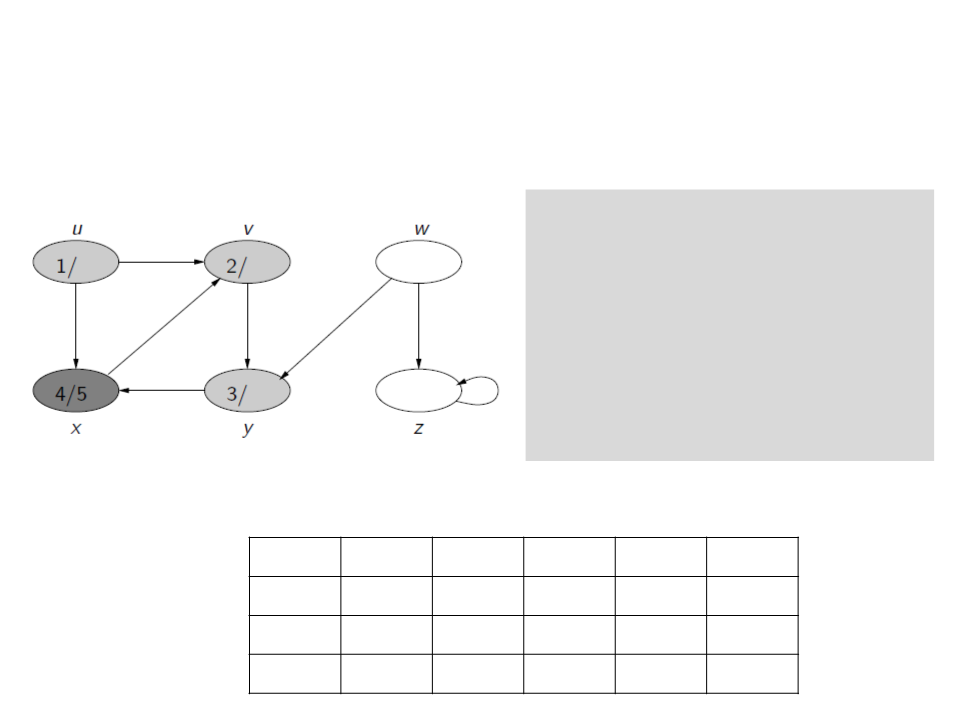
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
g
v
3
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
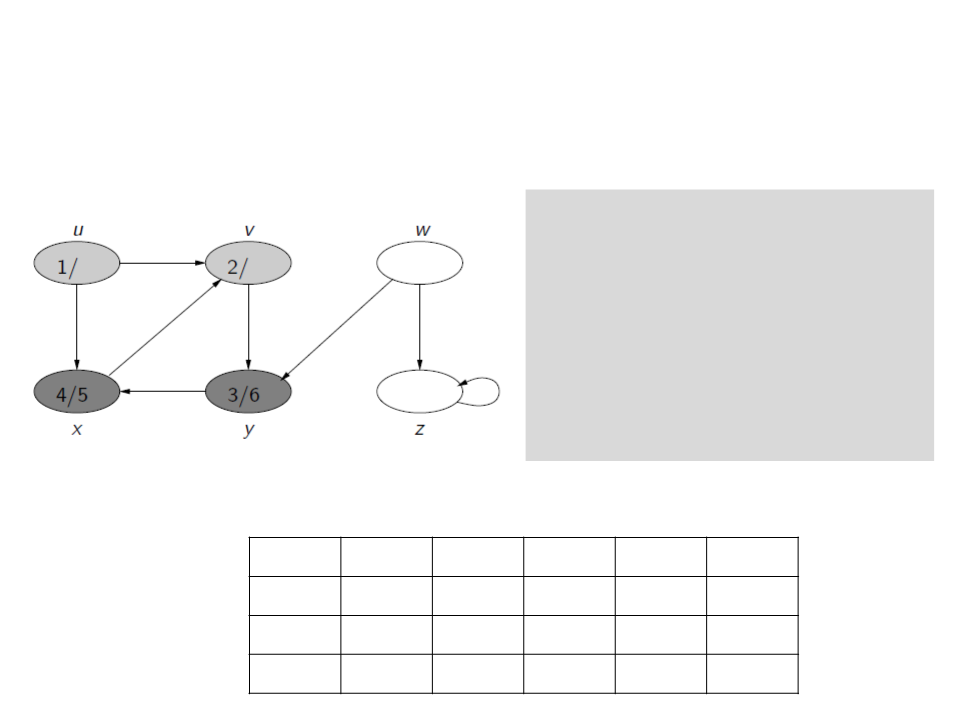
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
g
u
2
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
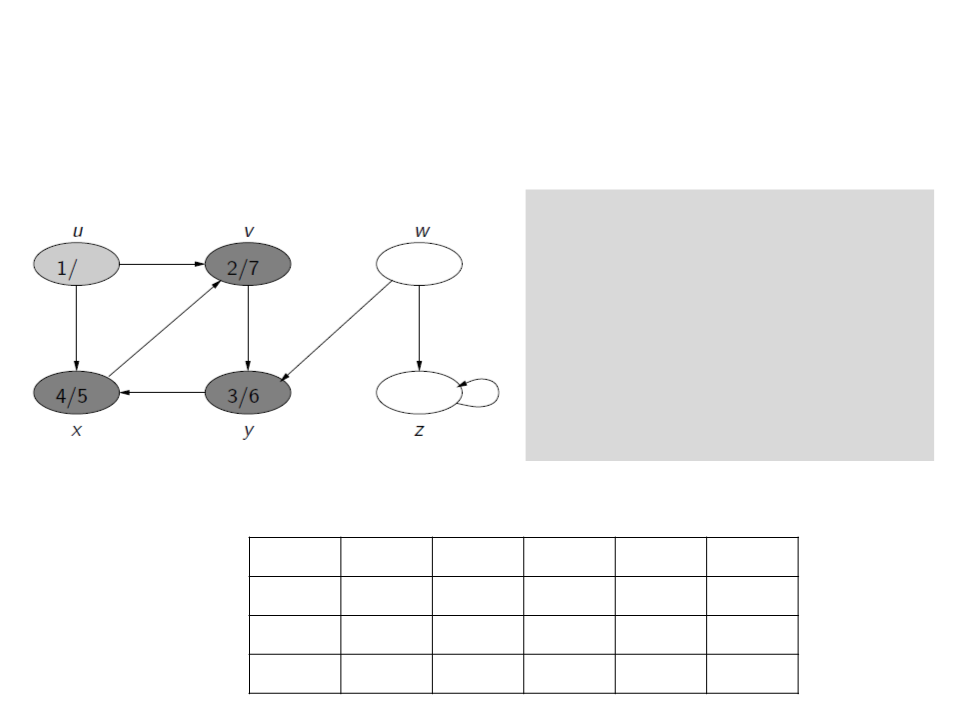
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
g
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
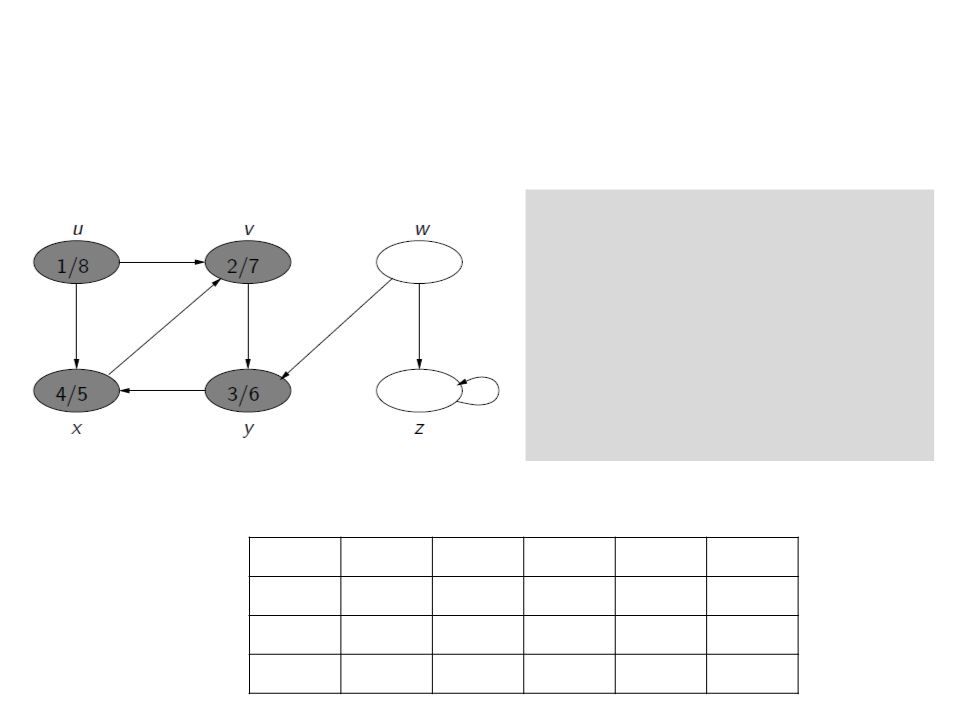
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
8
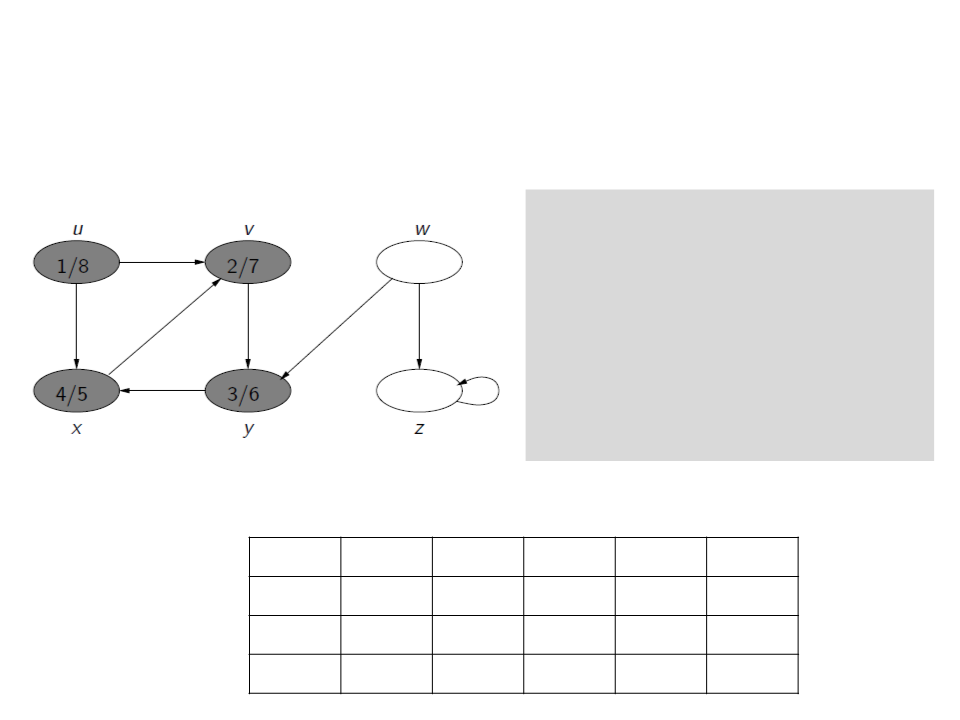
Depth-First Search (DFS)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
time ← 0
for each u ∈ V[G]
if c[u] = white
Visit(u)
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
w
/
z
w
/
c
ꢍ
d
f
1
8
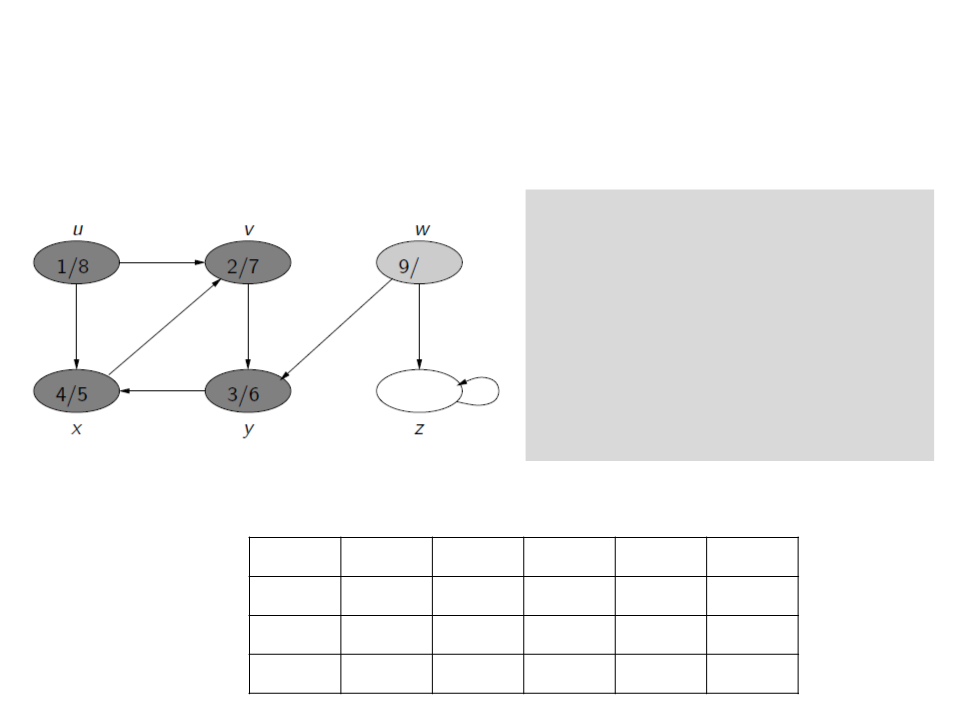
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
g
/
z
w
/
c
ꢍ
d
f
1
8
9

Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
g
/
z
g
c
ꢍ
d
f
w
10
1
8
9
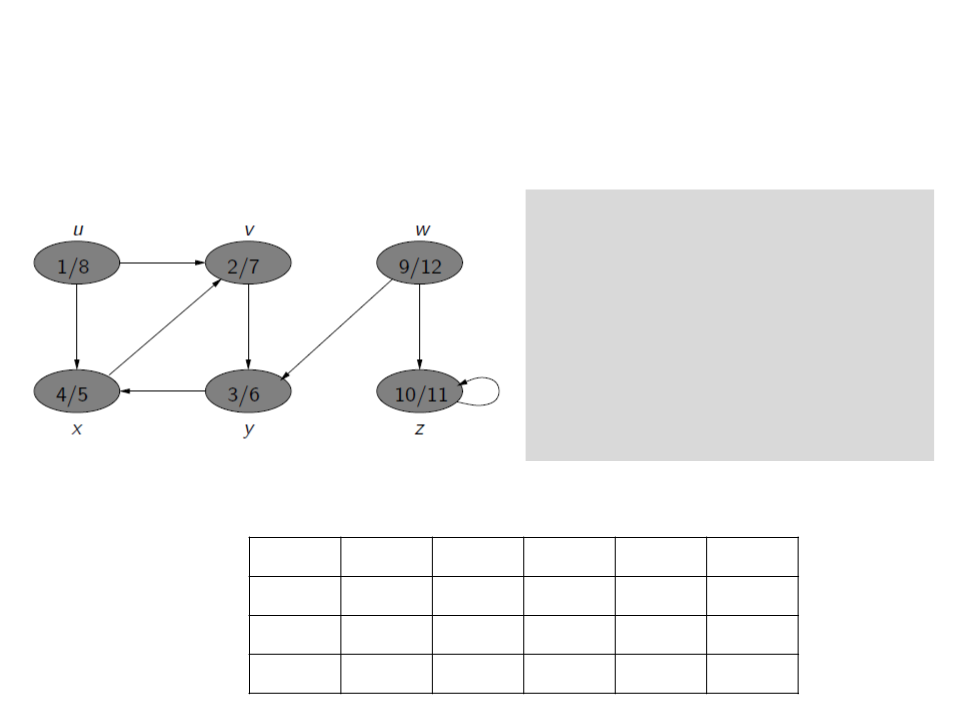
Depth-First Search (DFS)
c[u] ← gray
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1
u
b
/
v
b
u
2
7
y
b
v
3
6
x
b
y
4
5
w
b
z
b
c
ꢍ
d
f
/
w
10
11
1
8
9
12

Depth-First Search (DFS) – Analysis
DFS(G)
for each u ∈ V[G]
c[u] ← white
ꢍ[u] ← NULL
•
The Visit function is called exactly once
for each vertex u ∈ V (visit is called only
for white vertices and the first action is
to paint the vertex gray). Therefore:
O(V);
time ← 0
for each u ∈ V[G]
if c[u] = white
Visit(u)
•
•
The main loop of Visit function is O(E);
Visit(u)
c[u] ← gray
DFS complexity: O(V + E)
d[u] ← time ← time + 1
for each v ∈ E[u]
if c[v] = white
ꢍ[v] ← u
Visit(v)
c[u] ← black
f[u] ← time ← time + 1

Depth-First Search (DFS) – C#
public Dictionary<GraphVertex<T>, GraphVertex<T>> DFS(GraphVertex<T> s)
{
Dictionary<GraphVertex<T>, int> d = new Dictionary<GraphVertex<T>, int>();
Dictionary<GraphVertex<T>, int> c = new Dictionary<GraphVertex<T>, int>();
Dictionary<GraphVertex<T>, int> f = new Dictionary<GraphVertex<T>, int>();
Dictionary<GraphVertex<T>, GraphVertex<T>> pi = new
Dictionary<GraphVertex<T>, GraphVertex<T>>();
int time = 1;
foreach (GraphVertex<T> u in vertices)
{
c[u] = 0; //white
d[u] = int.MaxValue;
f[u] = int.MaxValue;
pi[u] = null;
}
foreach (GraphVertex<T> u in vertices)
{
if (c[u] == 0){ //white
DFSVisit(u, ref time, d, c, f, pi);
}
}
return pi;
}

Depth-First Search (DFS) – C#
private void DFSVisit(GraphVertex<T> u, ref int time,
Dictionary<GraphVertex<T>, int> d,
Dictionary<GraphVertex<T>, int> c,
Dictionary<GraphVertex<T>, int> f,
Dictionary<GraphVertex<T>, GraphVertex<T>> pi)
{
c[u] = 1; //gray
d[u] = time++;
foreach (GraphVertex<T> v in u.Edges)
{
if (c[v] == 0) //white
{
pi[v] = u;
DFSVisit(v, ref time, d, c, f, pi);
}
}
c[u] = 2; //black
f[u] = time++;
}

Applications in Game Programming
•
Pathfinding: while simple movements can be manually
defined (patrol routes or wander regions), more complex
movements must be computed during the game. Pathfinding
algorithms rely on graph structures to represent the level
structure.
•
•
Finite State Machines: are used control the behavior of
characters and are modeled as graph structures. Actions are
associated with state (vertices) and transitions (edges) have
set of associated conditions.
Problem-solving: puzzle games can generally be solved by
searching in the state space for a set of actions that lead from
the current state to a goal state.
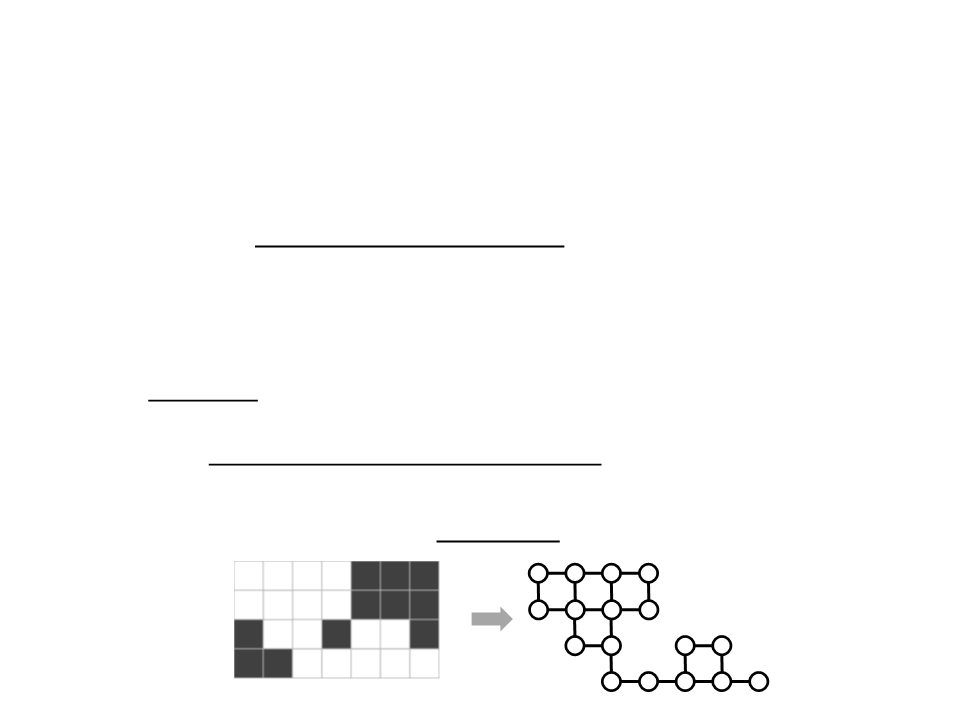
Assignment 2 – Graphs
1
) In the class of Game Frameworks, you have learned how to
implement pathfinding in a tilemap using an existing A*
function. Based on the structure of that example, adapt the
BFS and DFS functions to use them to perform the pathfinding
in a tilemap.
–
Important: the current versions of the BFS and DFS functions are
exploring the entire graph structure. But for pathfinding, the process
must stop when the target vertex is found.
–
The tilemap matrix can be interpreted as a graph structure:

Further Reading
•
•
Penton, R. (2002). Data Structures for Game Programmers.
Muska & Lipman/Premier-Trade. ISBN: 978-1931841948
–
Chapter 17: Graphs
Sherrod, A. (2007). Data Structures and Algorithms for
Game Developers. Charles River Media. ISBN: 978-
1
584504955
–
Chapter 11: Graphs
