
Data Structures
Lecture 06: Trees
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
Trees
•
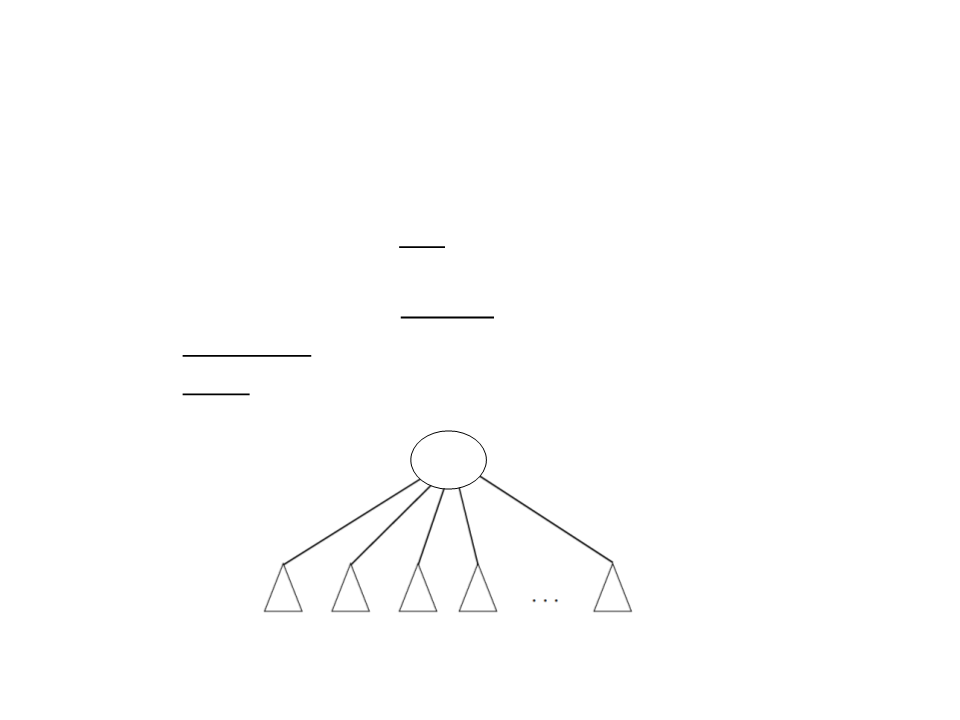
A tree data structure allows data to be organized hierarchically.
–
Examples: file directories, arithmetic expressions, route planning...
Trees
•
A tree comprises a set of nodes, such that:
–
There is a node r, called root, with zero or more subtrees, whose roots
are linked to r;
–
–
–
The root nodes of these subtrees are the children of r;
The inner nodes of the tree are the nodes with children;
The leaves (or outer nodes) of the tree are the nodes without children;
root
subtrees
Trees
•
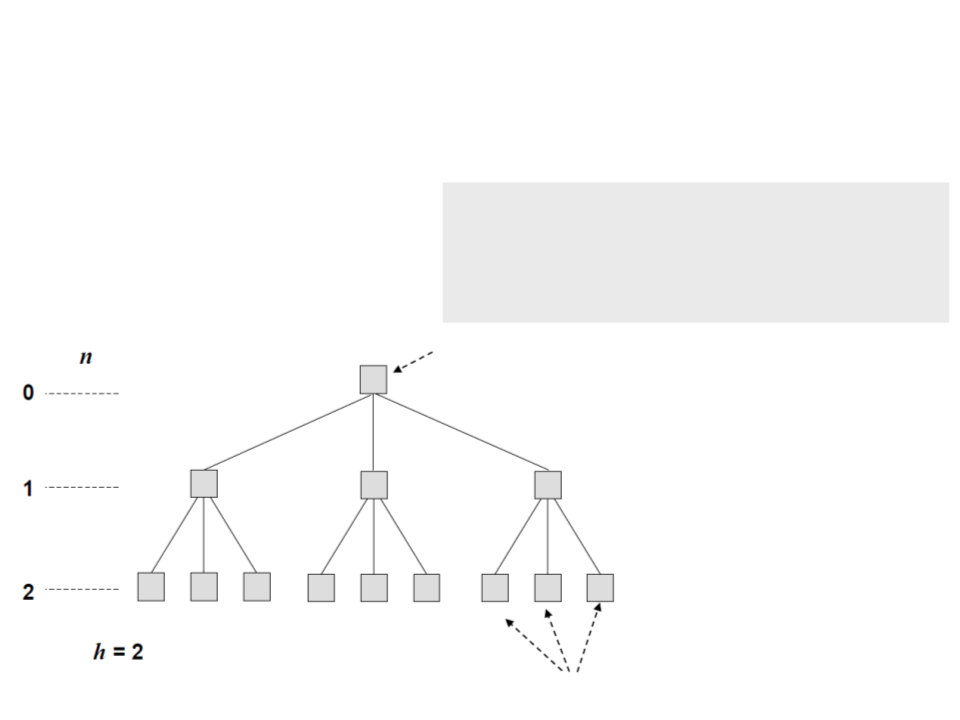
Tree structure
public class TreeNode<T> : IComparable
{
private T data;
private LinkedList<TreeNode<T>> children;
...
root
level
height
leaves
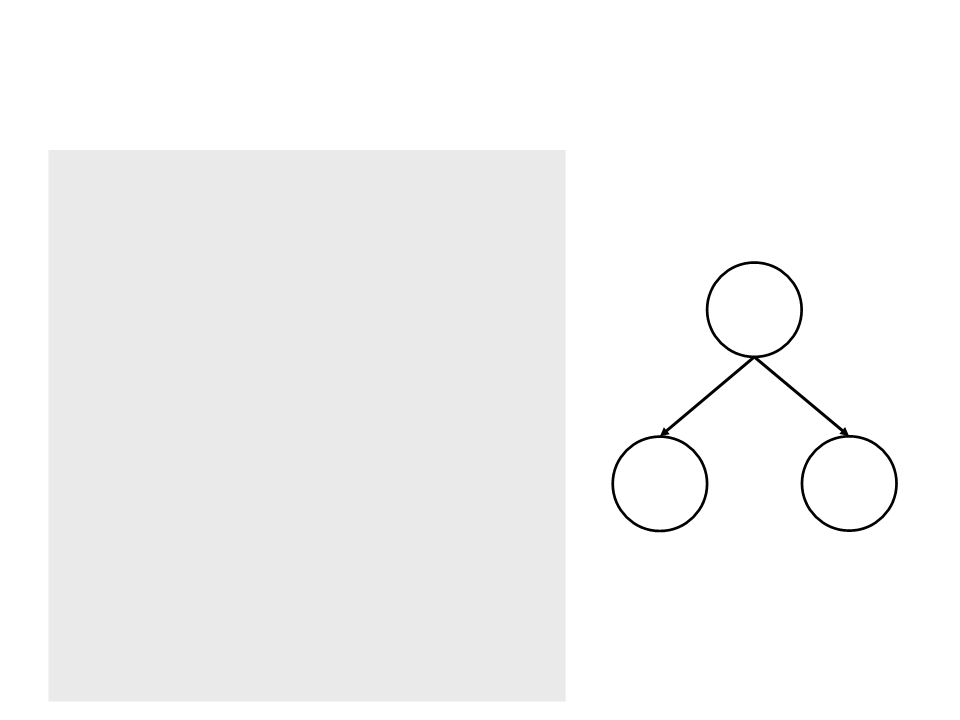
Binary Trees
•
A binary tree is a tree where each node has zero, one or two
children;
public class BTreeNode<T>
{
private T data;
private BTreeNode<T> left;
private BTreeNode<T> right;
.
..
}
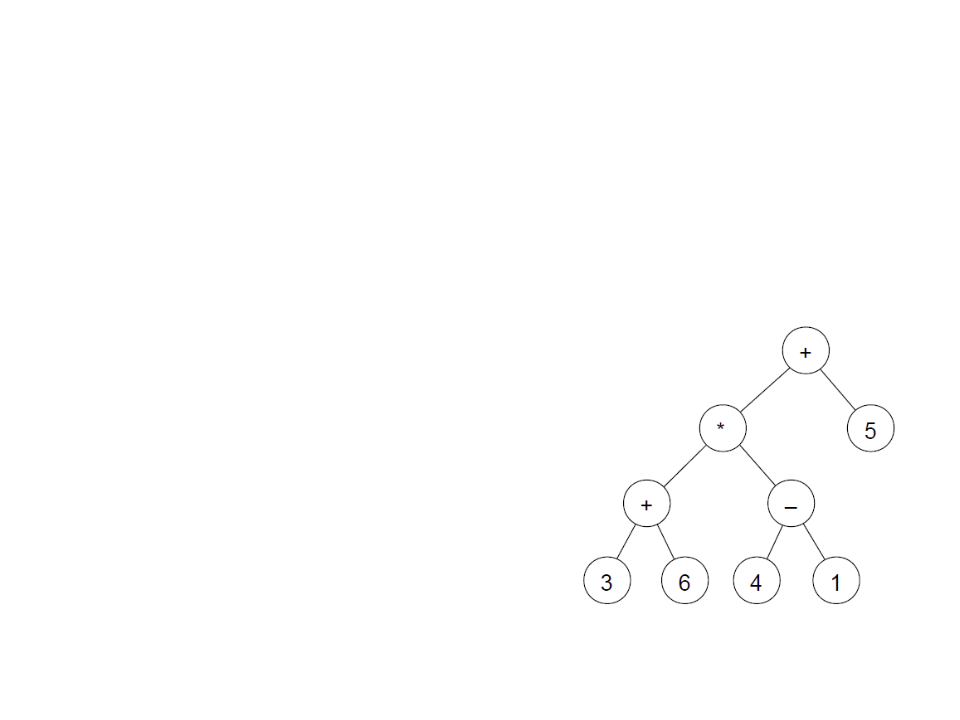
Binary Trees
•
Example: a binary tree can be used to represent
arithmetic expressions:
–
–
Leaf nodes represent operands;
Internal nodes operators;
–
Example: (3+6)*(4-1)+5

Binary Trees
Binary Tree – Structure
public class BTreeNode<T>{
private T data;
private BTreeNode<T> left;
private BTreeNode<T> right;
public BTreeNode<T> Left{
get { return left; }
set { left = value; }
}
Data
public BTreeNode<T> Right{
get { return right; }
set { right = value; }
}
Left
Right
public T Data{
get { return data; }
set { data = value; }
}
}
Binary Tree
•
Basic operations:
–
–
–
Create: creates a node.
IsEmpty: returns true if the tree is empty.
Traverse: iterates over the tree performing an operation over the
nodes (such as printing their values).
•
Different traversal orders are possible.
–
–
Search: checks if a value exists in the tree and returns its node.
Remove: removes a node from the tree.
Binary Tree
•
•
Tree operations:
–
Recursive implementation
–
Use of the recursive structure of the tree
A binary tree is:
–
An empty tree; or
–
A root node with two subtrees:
•
The left subtree (lst);
root
•
The right subtree (rst);
empty
lst
rst

Binary Tree – Create
•
•
Creates a root node given the information and the two
subtrees, the one on the left and the one on the right.
Constructor method of the BTreeNode class:
public BTreeNode(T t, BTreeNode<T> l, BTreeNode<T> r)
{
left = l;
right = r;
data = t;
}

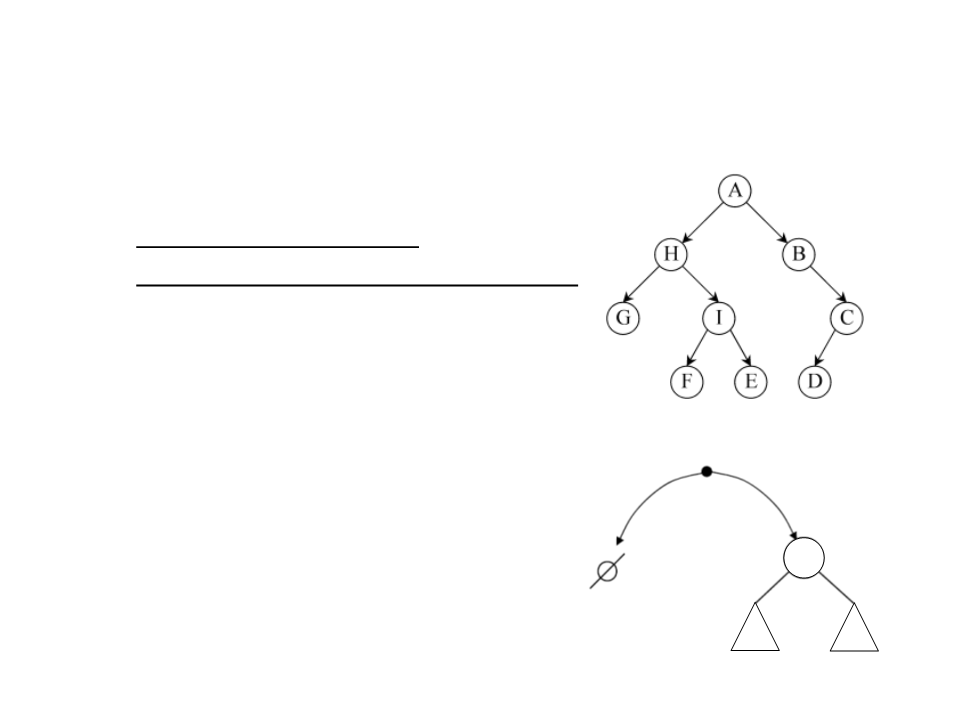
Binary Tree – IsEmpty
•
Indicates whether a given tree is empty or not.
–
The operation is not part of the generic node class, so a type for the
data must be defined (example: string).
public bool IsEmpty(BTreeNode<string> node)
{
if (node == null)
return true;
else
return false;
}

Binary Tree – Traverse
•
Recursively iterates over the tree, visiting all nodes and
performing an operation over the data (example: printing the
data).
–
The operation is not part of the generic node class, so a type for the
data must be defined (example: string).
public static void PrintTree(BTreeNode<string> node)
{
if (!IsEmpty(node))
{
Debug.Log(node.Data);
PrintTree(node.Left);
PrintTree(node.Right);
}
}
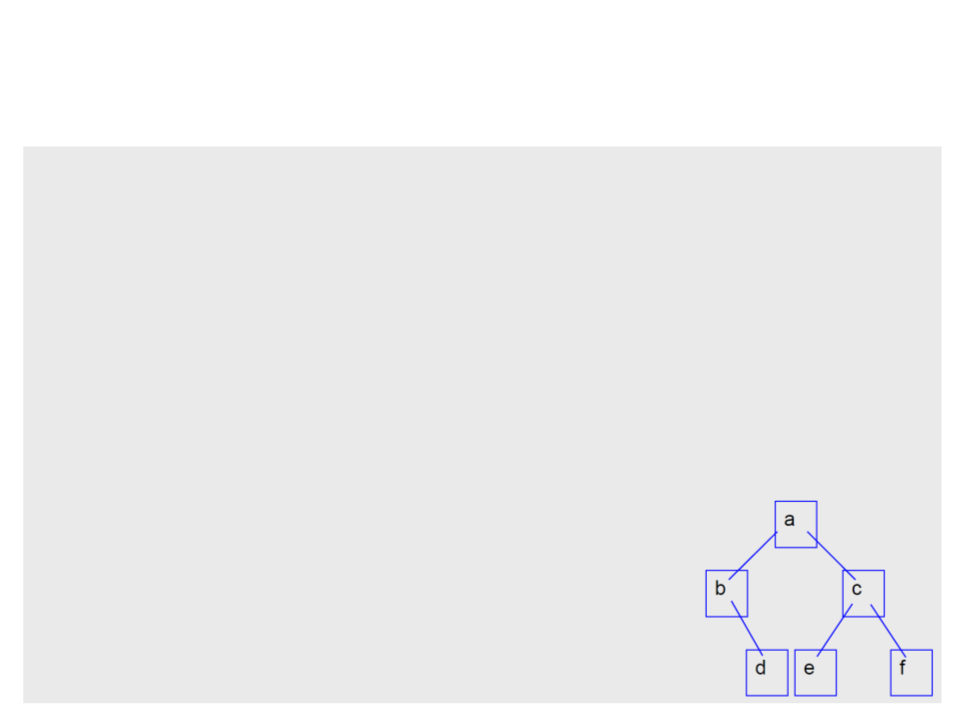
Binary Tree – Creating a Tree
/
* subtree "d" */
BTreeNode<string> a1 = new BTreeNode<string>("d", null, null);
* subtree "b" */
BTreeNode<string> a2 = new BTreeNode<string>("b", null, a1);
* subtree "e" */
BTreeNode<string> a3 = new BTreeNode<string>("e", null, null);
* subtree "f" */
BTreeNode<string> a4 = new BTreeNode<string>("f", null, null);
* subtree "c" */
BTreeNode<string> a5 = new BTreeNode<string>("c", a3, a4);
* subtree "a" */
BTreeNode<string> root = new BTreeNode<string>("a", a2, a5);
/
/
/
/
/
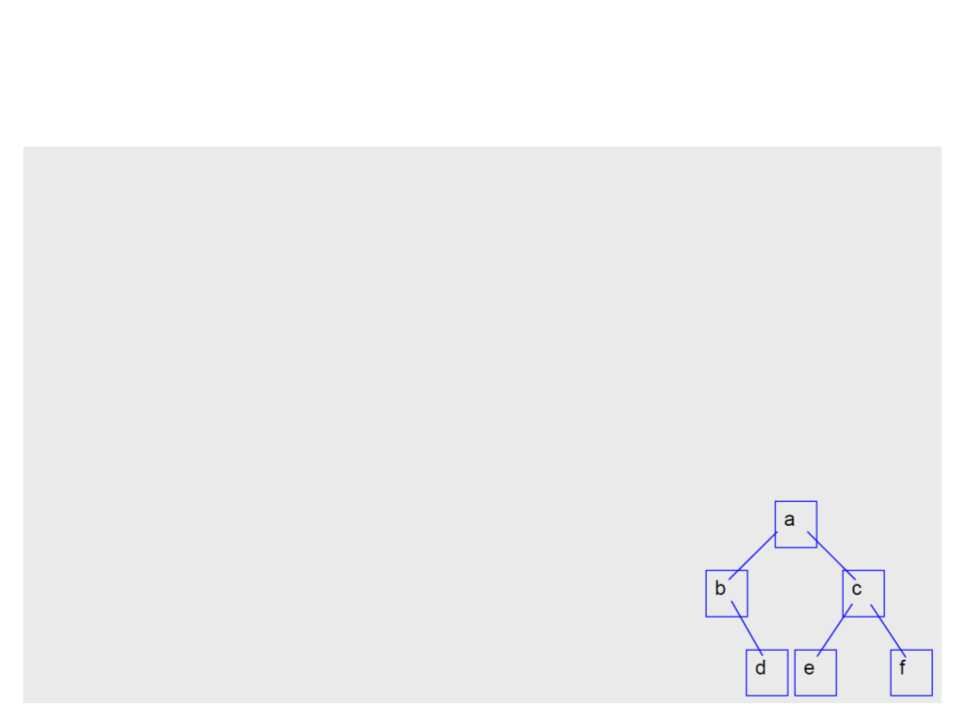
Binary Tree – Creating a Tree
BTreeNode<string> root = new BTreeNode<string>("a",
new BTreeNode<string>("b",
null,
new BTreeNode<string>("d", null, null)
),
new BTreeNode<string>("c",
new BTreeNode<string>("e", null, null),
new BTreeNode<string>("f", null, null)
));
Binary Tree – Traverse
•
It is possible to format the printing to better show the tree
structure.
public static void PrintTreeFormated(BTreeNode<string> node,
int level){
if (!IsEmpty(node))
{
PrintTreeFormated(node.Right, level + 1);
string spaces = "";
for (int i = 0; i < level; i++)
spaces += "\t";
Debug.Log(spaces + node.Data);
PrintTreeFormated(node.Left, level + 1);
Does not work
well on Unity
console
}
}

Binary Tree – Search
•
Checks for the occurrence of a string s in one of the nodes;
–
Returns a Boolean value indicating whether s exists or not in the tree.
public static bool SearchTree(BTreeNode<string> node, string s)
{
if (IsEmpty(node))
return false;
else{
if (node.Data.Equals(s))
return true;
else if (SearchTree(node.Left, s))
return true;
else if (SearchTree(node.Right, s))
return true;
else
return false;
}
}
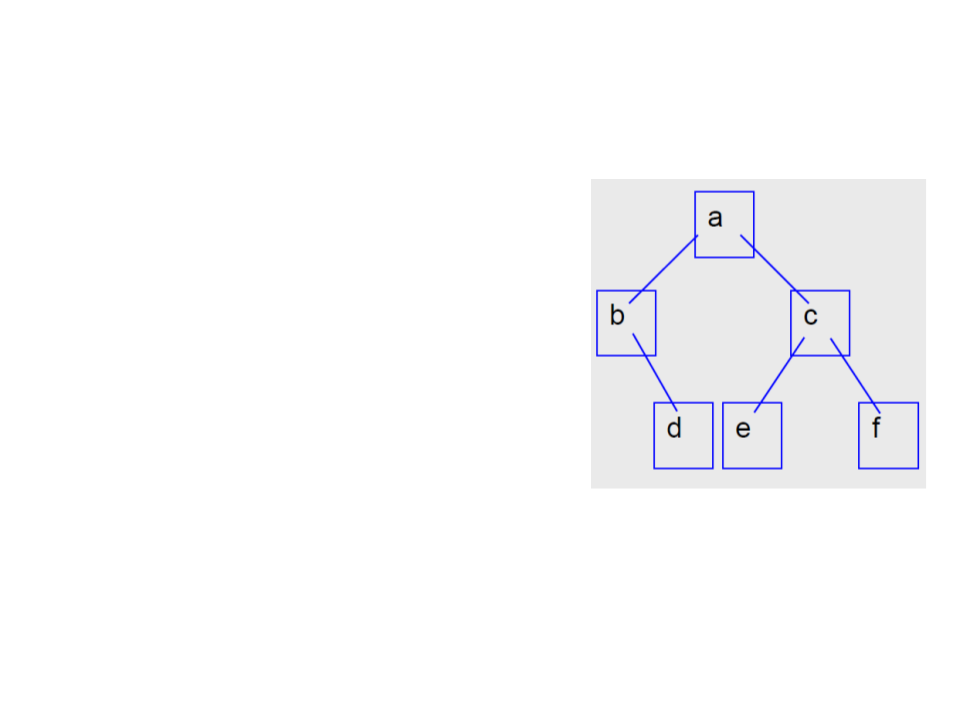
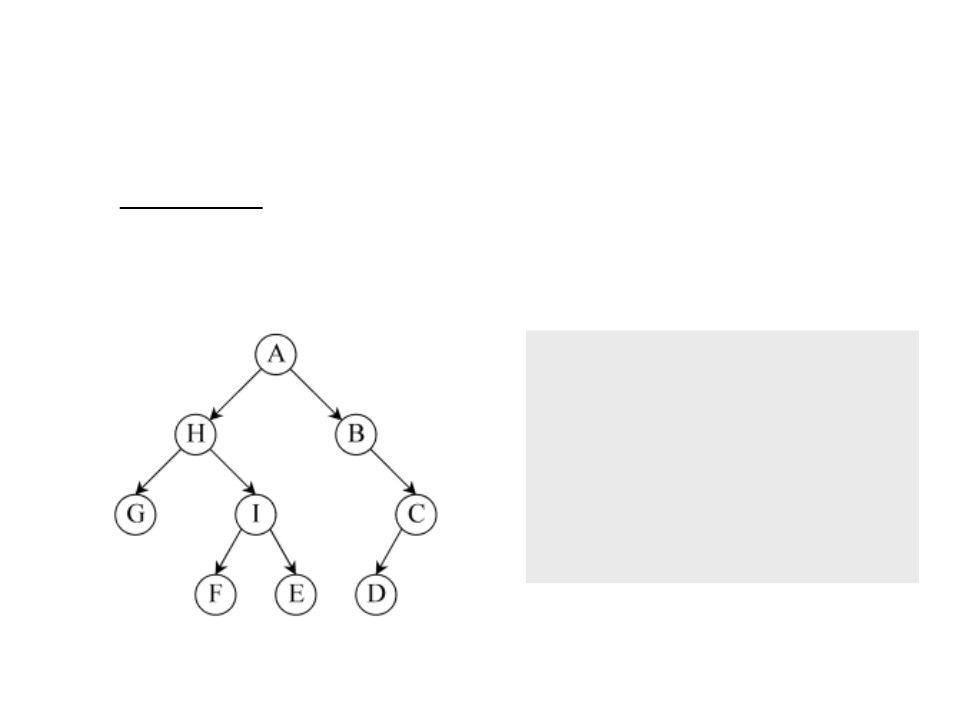
Binary Trees – Traverse Order
•
•
•
Pre-order:
–
Access data, traverse lst, traverse rst;
–
Example: a b d c e f
In-order:
–
Traverse lst, acess data, traverse rst;
–
Example: b d a e c f
Post-order:
–
Traverse lst, traverse rst, acess data;
–
Example: d b e f c a
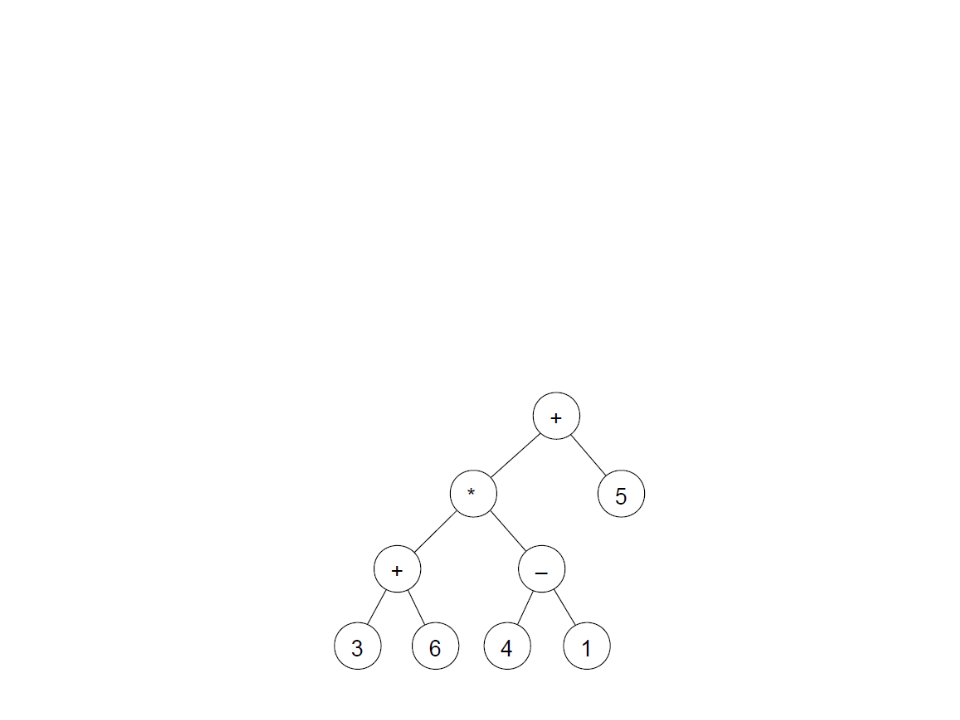
Binary Tree – Example
•
Considering a binary tree to represent arithmetic expressions:
–
Leaf nodes represent operands;
–
Internal nodes operators;
–
Example: (3 + 6) * (4 - 1) + 5
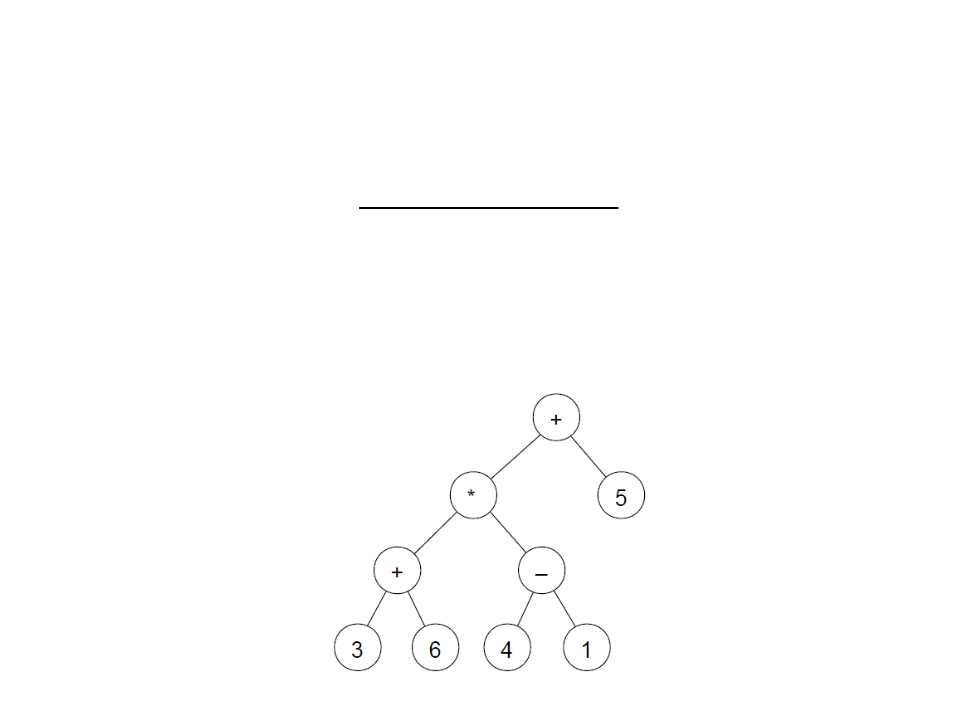
Binary Tree – Example
•
Create a function to print the expression that is encoded in a
binary tree.
•
For the tree example, the function must print the following
expression:
(((3+6)*(4-1))+5)

Binary Tree – Example
•
Create the tree:
BTreeNode<string> node1 = new BTreeNode<string>("3", null, null);
BTreeNode<string> node2 = new BTreeNode<string>("6", null, null);
BTreeNode<string> node3 = new BTreeNode<string>("4", null, null);
BTreeNode<string> node4 = new BTreeNode<string>("1", null, null);
BTreeNode<string> node5 = new BTreeNode<string>("5", null, null);
BTreeNode<string> node6 = new BTreeNode<string>("+", node1, node2);
BTreeNode<string> node7 = new BTreeNode<string>("-", node3, node4);
BTreeNode<string> node8 = new BTreeNode<string>("*", node6, node7);
BTreeNode<string> node9 = new BTreeNode<string>("+", node8, node5);

Binary Tree – Example
•
Print the expression:
public static string PrintTreeExp(BTreeNode<string> node){
string exp = "";
if (!IsEmpty(node)){
if ((IsEmpty(node.Left)) && (IsEmpty(node.Right)))
exp = node.Data;
else{
exp = "(";
exp += PrintTreeExp(node.Left);
exp += node.Data;
exp += PrintTreeExp(node.Right);
exp += ")";
}
}
return exp;
}
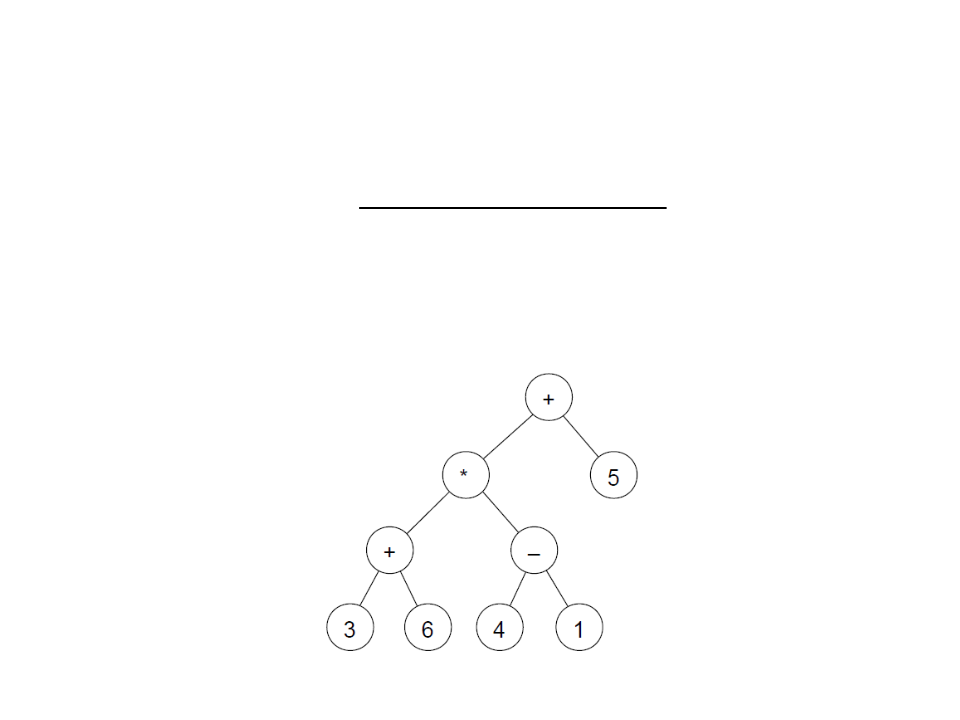
Binary Tree – Example
•
Create a function to evaluate the expression encoded in a
binary tree.
–
For the example, the result of the expression is: 32

Binary Tree – Example
•
Evaluate the expression:
public static float EvaluateTreeExp(BTreeNode<string> node)
{
if ((IsEmpty(node.Left)) && (IsEmpty(node.Right)))
return float.Parse(node.Data);
else{
if (node.Data.Equals("+"))
return EvaluateTreeExp(node.Left) + EvaluateTreeExp(node.Right);
else if (node.Data.Equals("-"))
return EvaluateTreeExp(node.Left) - EvaluateTreeExp(node.Right);
else if (node.Data.Equals("*"))
return EvaluateTreeExp(node.Left) * EvaluateTreeExp(node.Right);
else
return EvaluateTreeExp(node.Left) / EvaluateTreeExp(node.Right);
}
}
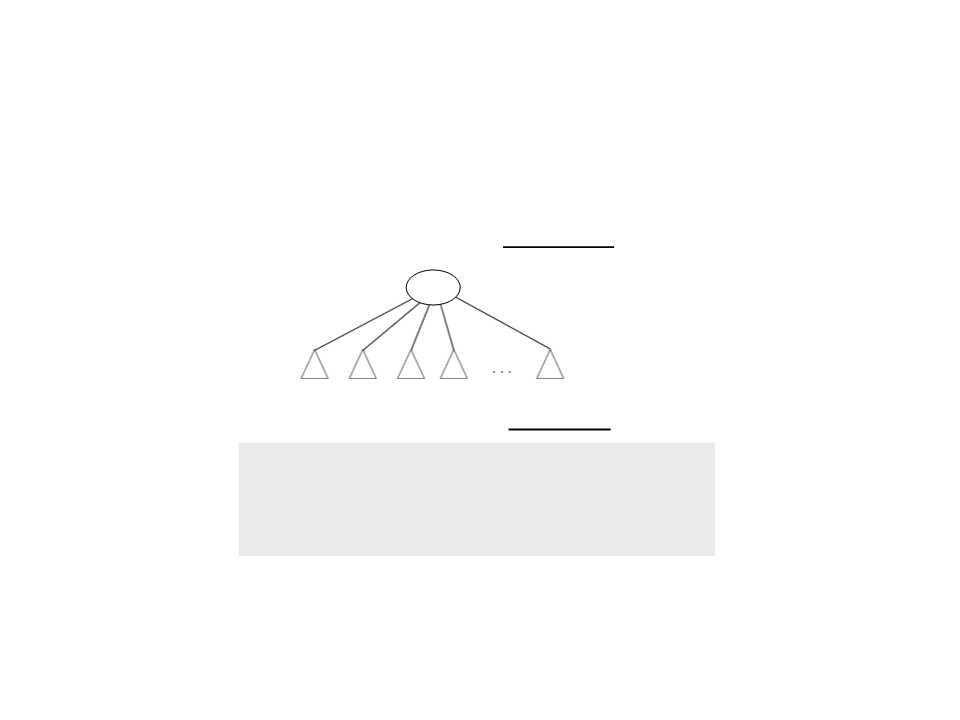
Assignment 1 – Tree
1) Create a class to represent a general tree data structure.
–
Every node of the tree can have N children.
root
subtrees
–
–
The children must be stored in a linked list:
public class TreeNode<T> : IComparable
{
private T data;
private LinkedList<TreeNode<T>> children;
...
The following operations must be implemented:
•
Create, IsEmpty, Print, and Search.
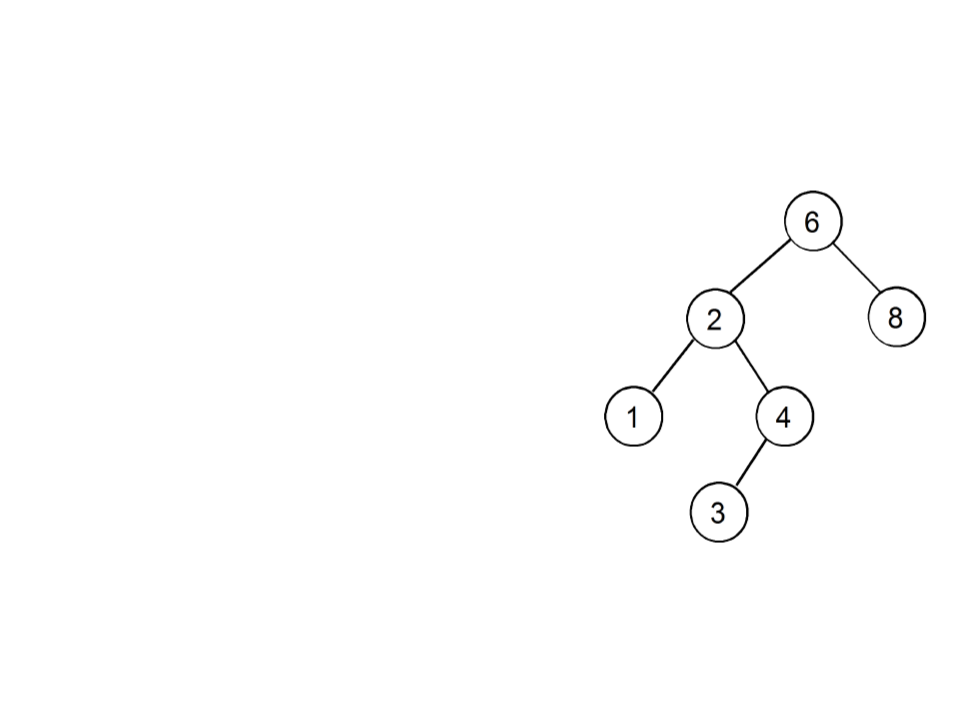
Binary Search Tree (BST)
•
•
The value associated with the root is
always greater than the value associated
with any node in the left subtree (lst);
The value associated with the root is
always less than or equal than the value
associated with any node in the right
subtree (rst);
•
When the tree is traversed in symmetrical
order (lst - root - rst), the values are
found in ascending order;
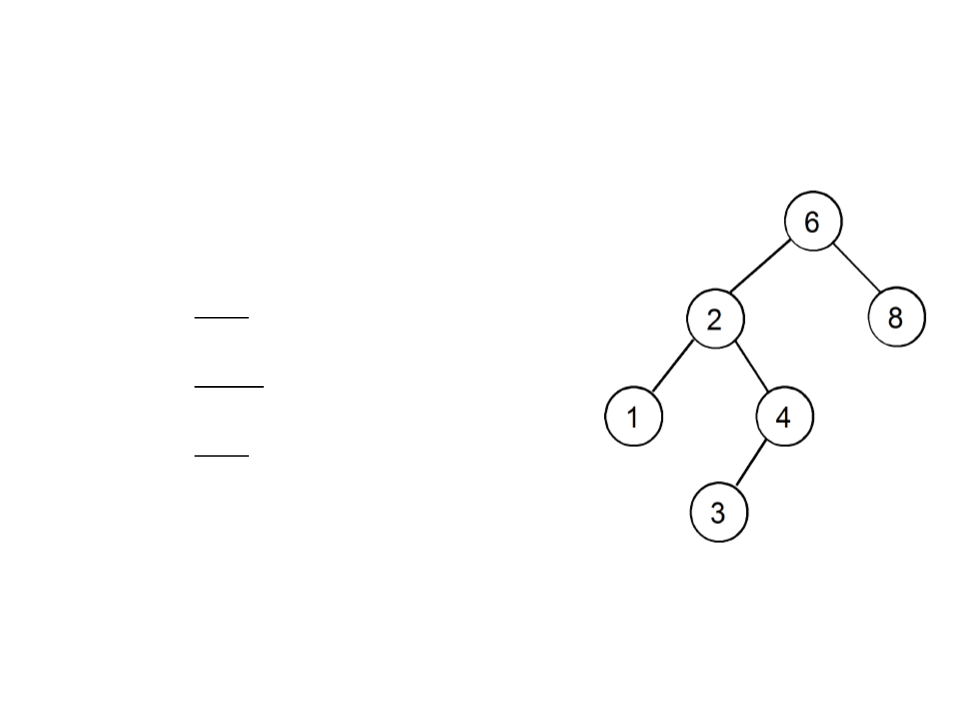
Search in a Binary Search Tree
•
Compare the given value with the value
associated with the root:
–
–
–
If it is equal, the value was found;
If it is smaller, the search continues on the lst;
If it is larger, the search continues on rst;
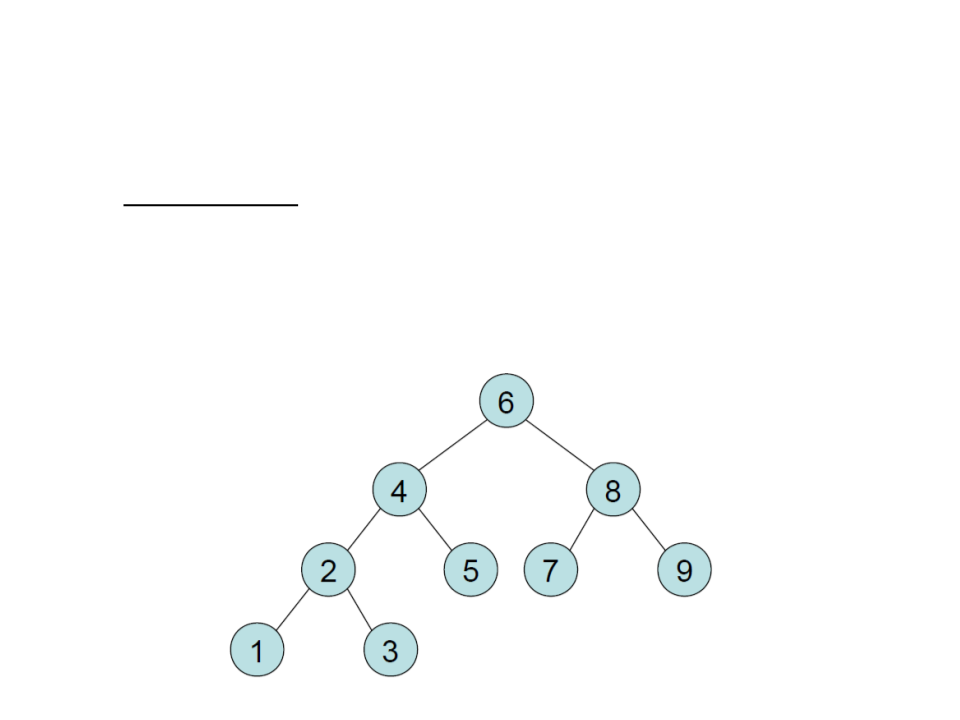
Search in a Binary Search Tree
•
•
In balanced trees the inner nodes have all, or almost all, 2
children;
Any node can be reached from the root in O(log n) steps;
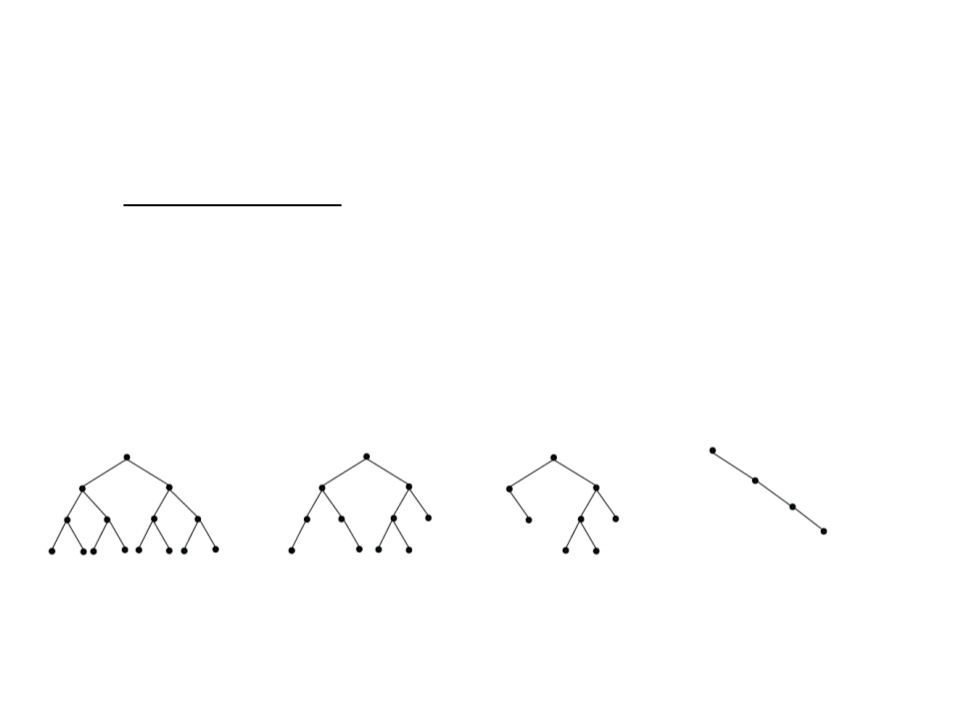
Search in a Binary Search Tree
•
•
In degenerated trees, all nodes have only 1 child, except for the
(single) leaf;
Any node can be reached from the root in O(n) steps;
Completly
Unbalanced
Degenerated)
Completly
Balanced
Balanced
Unbalanced
(

Binary Search Tree – Traverse
•
It is possible to print the values in ascending order, traversing
the nodes in symmetrical order:
public static void PrintBST(BTreeNode<int> node)
{
if (!IsEmpty(node))
{
PrintBST(node.Left);
Debug.Log(node.Data);
PrintBST(node.Right);
}
}

Binary Search Tree – Search
•
Explores the ordering property of the tree;
–
The computational performance is proportional to the height of the
tree;
public static BTreeNode<int> SearchBST(BTreeNode<int> node, int v)
{
if (node == null)
return null;
else if (node.Data > v)
return SearchBST(node.Left, v);
else if (node.Data < v)
return SearchBST(node.Right, v);
else
return node;
}

Binary Search Tree – Insert
•
•
Input: a value v to be inserted;
Output: a possible new root node for the tree/subtree;
•
To insert v on the correct position:
–
If the subtree is empty:
• Create a tree whose root contains v;
–
If the subtree is not empty:
•
Compare v with the value in the root;
•
Try to insert v in lst or rst, depending on the result of the comparison;

Binary Search Tree – Insert
public static BTreeNode<int> InsertBST(BTreeNode<int> node, int v)
{
if (node == null)
node = new BTreeNode<int>(v, null, null);
else if (node.Data > v)
node.Left = InsertBST(node.Left, v);
else
node.Right = InsertBST(node.Right, v);
return node;
}
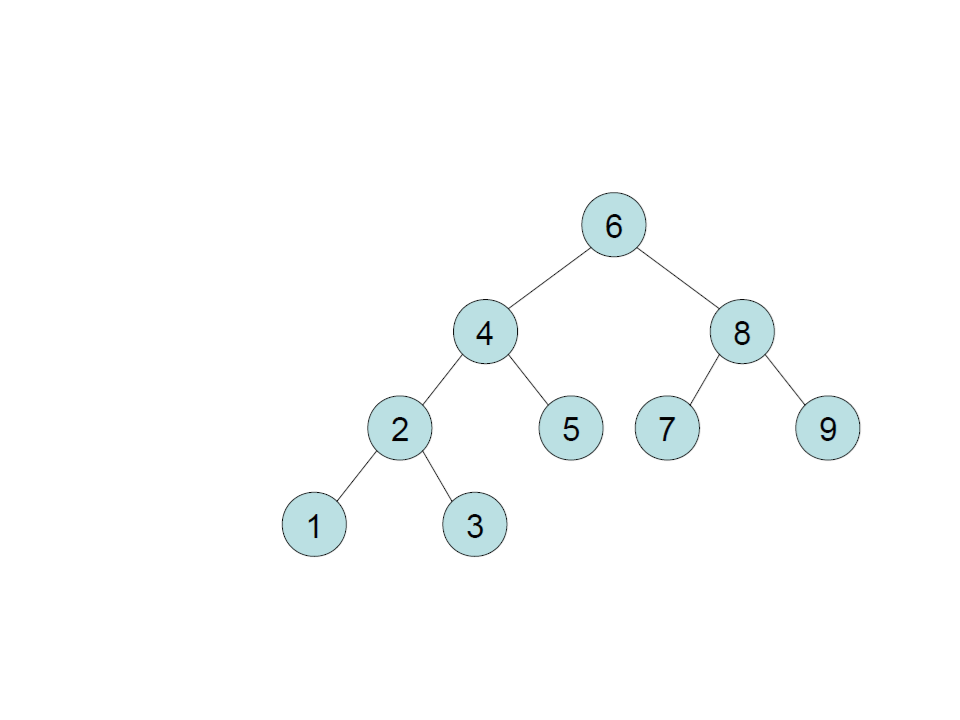
Binary Search Tree – Insert
create
insert 6
insert 4
insert 8
insert 2
insert 5
insert 1
insert 3
insert 7
insert 9
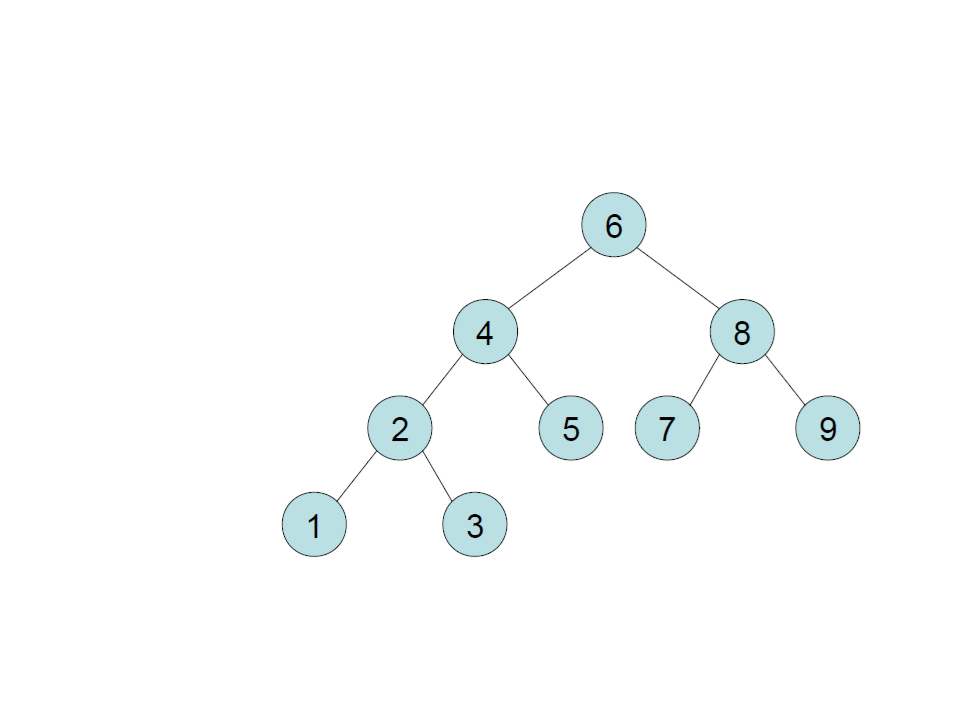
Binary Search Tree – Insert
create
insert 6
insert 4
insert 8
insert 2
insert 5
insert 1
insert 3
insert 7
insert 9
insert 6
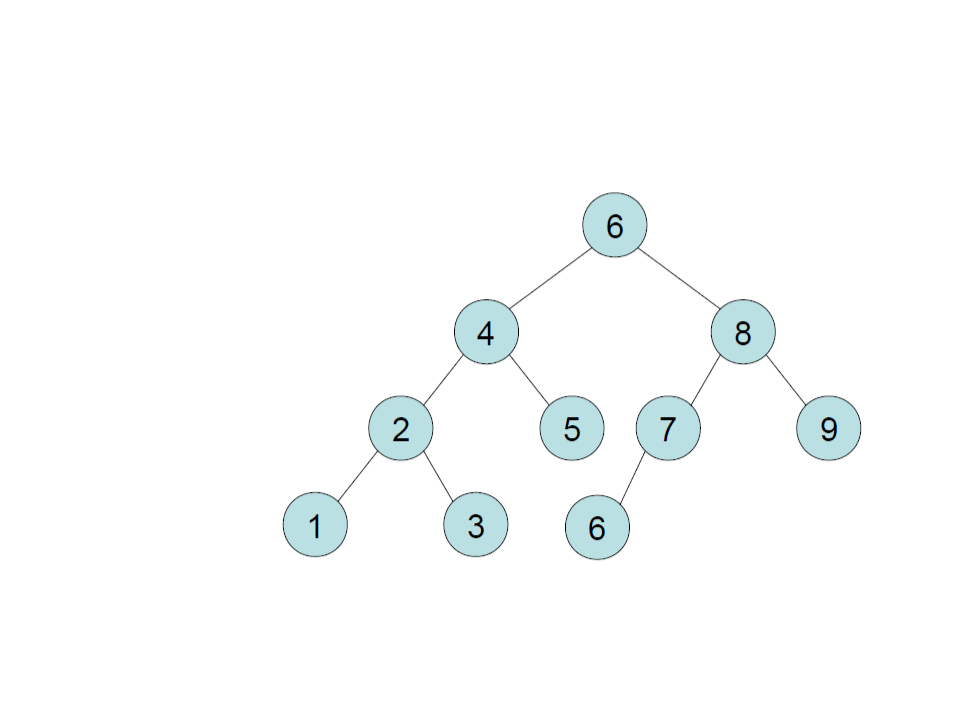
Binary Search Tree – Insert
create
insert 6
insert 4
insert 8
insert 2
insert 5
insert 1
insert 3
insert 7
insert 9
insert 6

Binary Search Tree – Insert
public static BTreeNode<int> InsertBST(BTreeNode<int> node, int v)
{
if (node == null)
node = new BTreeNode<int>(v, null, null);
else if (node.Data > v)
node.Left = InsertBST(node.Left, v);
else if(node.Data < v)
node.Right = InsertBST(node.Right, v);
return node;
}

Binary Search Tree – Remove
•
•
Input: a value v to be removed;
Output: a possible new root node for the tree/subtree;
•
To remove v:
–
If the subtree is empty:
•
nothing has to be done;
–
If the subtree is not empty:
•
•
•
•
compare the value stored at the root node with v:
if it is greater than v, remove the element from the left subtree;
if it is less than v, remove the element from the right subtree;
if it is equal to v, remove the root from the tree;

Binary Search Tree – Remove
•
To remove the root from the tree, there are 3 cases:
–
–
–
Case 1: the node to be removed is a leaf node;
Case 2: the node to be removed has a single child;
Case 3: the node to be removed has two children;
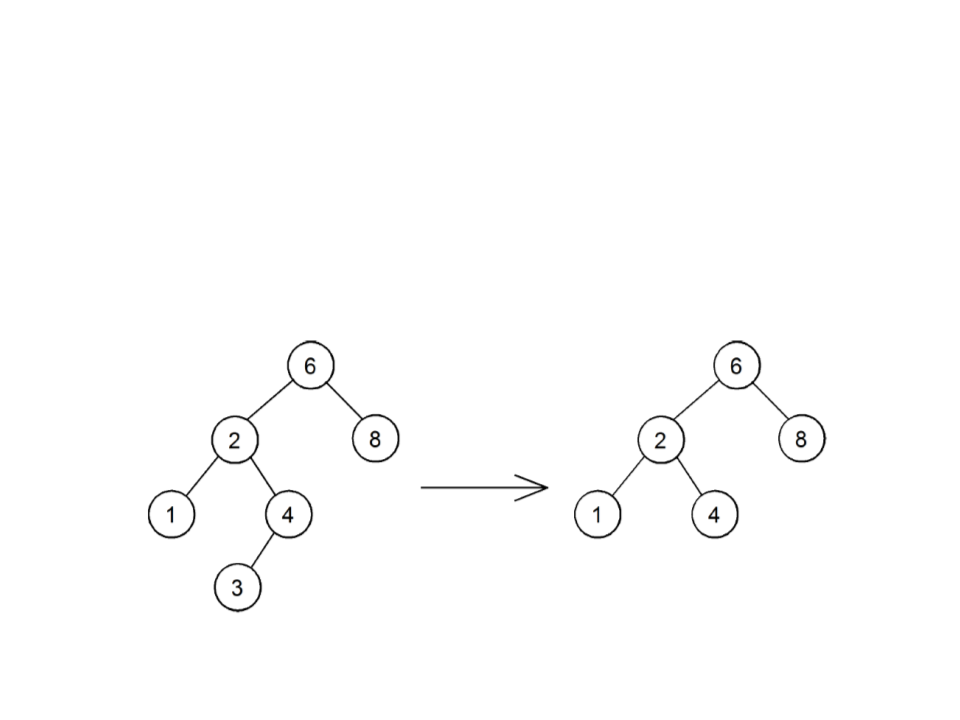
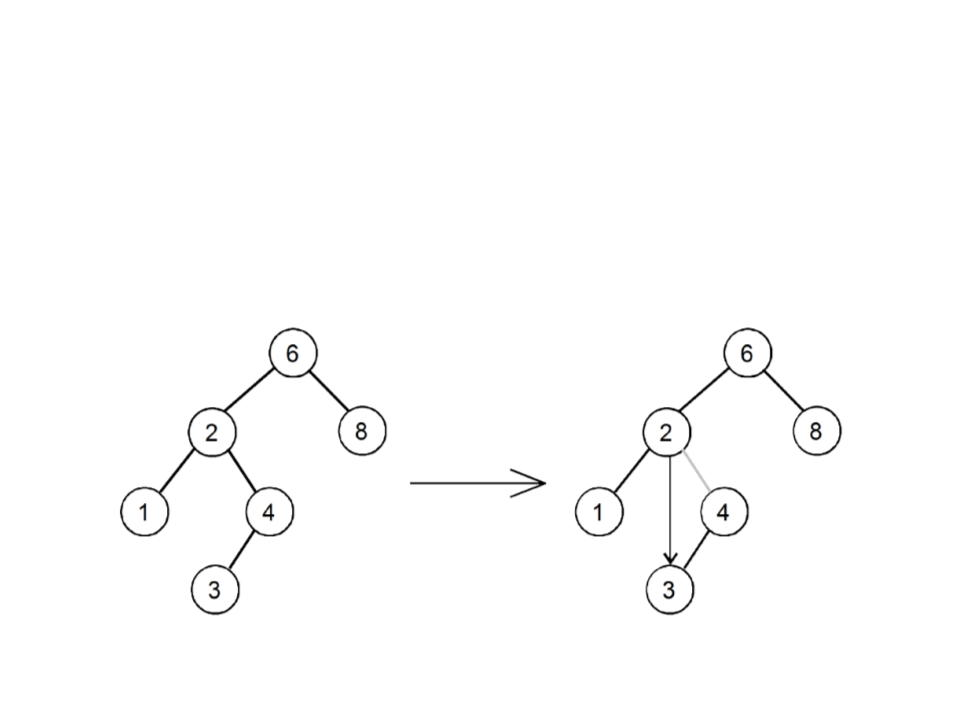
BST – Remove Leaf Node
•
Case 1: the node to be removed is a leaf node:
–
Remove the node by returning the updated node, which will be null
remove 3
remove
node 3
BST – Remove Single Child Node
•
Case 2: the node to be removed has a single child :
–
The child node becomes the child of the parent node;
remove 4
remove
node 4
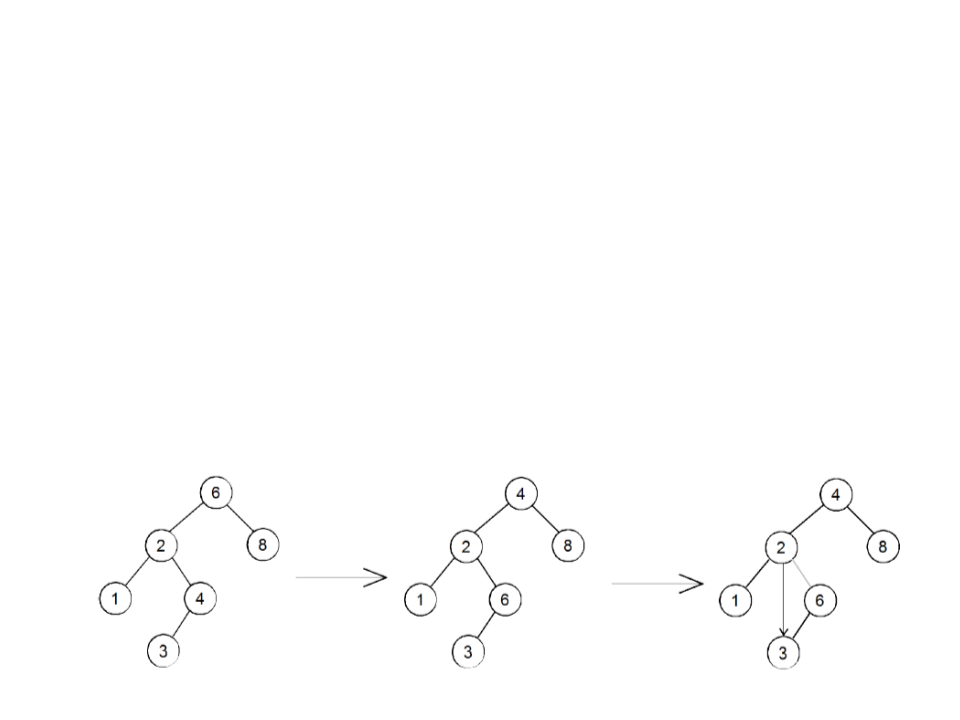
BST – Remove Two Children Node
•
Case 3: the node to be removed r has two children
–
find the node N that precedes r in the ordering (the rightmost element
of the left subtree)
–
–
swap the value of r with the value of N
remove N from the left subtree (which now contains the value to be
removed)
•
removing the rightmost node N is simple, as N is a leaf node or N is a node with a
single child (in this case, the right child never exists)
remove 6
swap 6
and 4
remove
node 6

public static BTreeNode<int> RemoveBST(BTreeNode<int> node, int v){
if (node == null)
return null;
else if (node.Data > v)
node.Left = RemoveBST(node.Left, v);
else if (node.Data < v)
node.Right = RemoveBST(node.Right, v);
else{
/* found the node to remove */
if (node.Left == null && node.Right == null) /* case 1: leaf node */
node = null;
else if (node.Left == null) /* case 2: single child to the left */
node = node.Right;
else if (node.Right == null) /* case 2: single child to the right */
node = node.Left;
else{
/* case 3: node has two children */
BTreeNode<int> f = node.Left;
while (f.Left != null) /* search for a single child or leaf node */
f = f.Right;
node.Data = f.Data; /* swap the values */
f.Data = v;
node.Left = RemoveBST(node.Left, v);
}
}
return node;
}

Applications in Game Programming
•
•
•
•
Branching narrative structures: each node represents a
narrative event or a sequence of events.
Dialog trees: branching nodes represent dialog choices that
lead to different dialogs.
Pathfinding: pathfinding algorithms use tree structures to
store the search data.
Decision trees, behavior trees, etc.
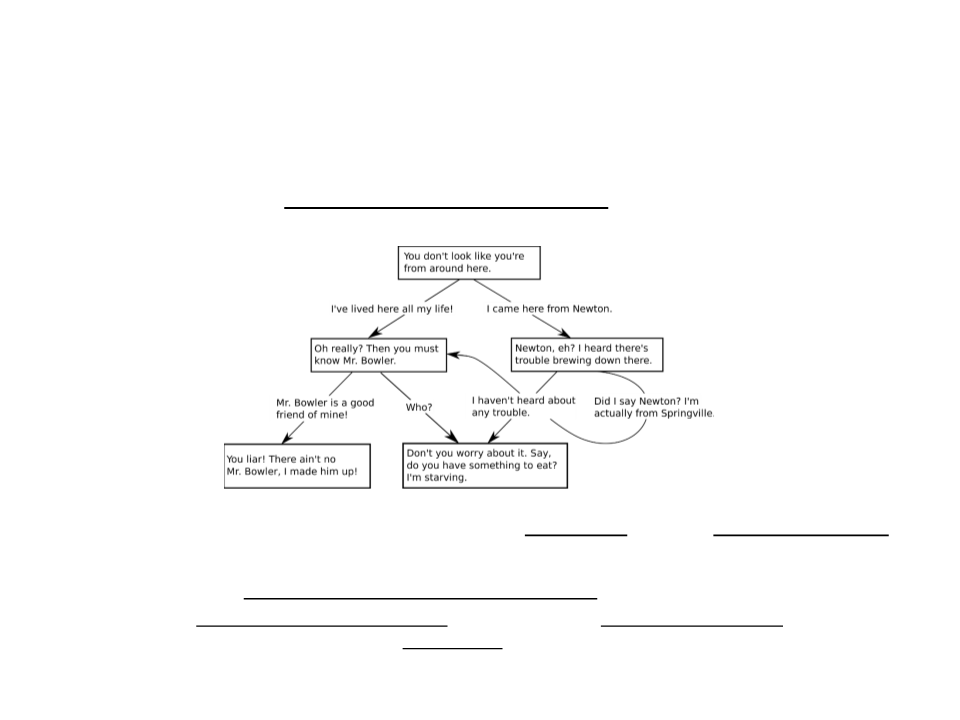
Assignment 2 – Tree
1
) Implement a tree-based dialog system to represent the
following dialog tree:
–
–
Every node of the tree must store the dialog text and the interaction option
that led to the node.
A way to see and interact with the dialog tree must be implemented.
•
No graphical interface is required. The dialogs can be displayed in the console and the player
interaction can be done by pressing keys (e.g.: 1 – selects the first child option; 2 – selects
the second child option).

Further Reading
•
•
Penton, R. (2002). Data Structures for Game Programmers.
Muska & Lipman/Premier-Trade. ISBN: 978-1931841948
–
–
–
Chapter 11: Trees
Chapter 12: Binary Trees
Chapter 13: Binary Search Trees
Sherrod, A. (2007). Data Structures and Algorithms for
Game Developers. Charles River Media. ISBN: 978-
1
584504955
–
Chapter 9: Trees
