
Data Structures
Lecture 02: Array Structures and Algorithms
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
Arrays
•
•
The most common form of data structure is the array.
Arrays are sequences of items (variables or objects) of the
same type.
–
Each item is identified by an index (integer).
–
With arrays, we can store in memory sequences of values (numbers,
imagens, objects, etc.), which are all associated with a single variable
(the array).

Arrays
•
•
Arrays can be used in any game programming every time a list
of objects with the same data type is needed.
–
Examples: array of characters, items, enemies, textures, sounds, etc.
C# arrays:
–
Arrays can be single-dimensional, multidimensional or jagged.
–
The number of dimensions and the length of each dimension are
established when the array instance is created.
–
–
Arrays are zero indexed: an array with n elements is indexed from 0 to
n-1.
Arrays are objects (not just addressable regions of contiguous memory
as in C and C++).

Single-Dimensional Arrays in C#
•
A single-dimensional array is instantiated using the new
operator specifying the array type and length:
int[] myArray = new int[5];
•
•
Arrays can store any element type (such as strings):
string[] myStringArray = new string[6];
Array elements are accessed using the index:
myArray[0] = 23;
myArray[4] = 8;
myStringArray[2] = "This is a string!";
myStringArray[0] = "Hello World!";

Single-Dimensional Arrays in C#
•
•
Arrays can be initialized when they are declared:
int[] myArray1 = new int[] { 1, 3, 5, 7, 9 };
string[] weekDays = new string[] { "Sun",
"
"
Mon", "Tue", "Wed", "Thu",
Fri", "Sat" };
The data of an array can be retrieved by use an index:
Debug.Log(weekDays[0]);
Debug.Log(weekDays[1]);
Debug.Log(weekDays[2]);
Debug.Log(weekDays[3]);
Debug.Log(weekDays[4]);
Debug.Log(weekDays[5]);
Debug.Log(weekDays[6]);

Multidimensional Arrays in C#
•
Arrays can have more than one dimension. Example of two
dimensions array (matrix):
int[,] my2DArray = new int[4, 4];
•
•
Example of an array of three dimensions (4, 2, and 3):
int[,,] my3DArray = new int[4, 2, 3];
Array elements are accessed using the indexes:
my2DArray[0, 0] = 15;
my2DArray[2, 1] = 25;
my3DArray[0, 0, 0] = 35;
my3DArray[3, 0, 1] = 45;

Multidimensional Arrays in C#
•
•
Multidimensional arrays can be initialized when they are
declared:
int[,] myArray2D = new int[,] { { 1, 2 },
{
{
{
3, 4 },
5, 6 },
7, 8 } };
The data of an array can be retrieved by use an index:
Debug.Log(myArray2D[0, 0]);
Debug.Log(myArray2D[0, 1]);
Debug.Log(myArray2D[1, 0]);
Debug.Log(myArray2D[1, 1]);
Debug.Log(myArray2D[2, 0]);
Debug.Log(myArray2D[2, 1]);
Debug.Log(myArray2D[3, 0]);
Debug.Log(myArray2D[3, 1]);

Jagged Arrays in C#
•
•
•
A jagged array is an array whose elements are arrays, possibly
of different sizes.
–
Also called an "array of arrays".
Example of an array that has three elements, each of which is
a single-dimensional array of integers:
int[][] myJaggedArray = new int[3][];
Before using the jagged array, its elements (arrays) must be
initialized:
jaggedArray[0] = new int[5];
jaggedArray[1] = new int[4];
jaggedArray[2] = new int[2];

Passing Arrays as Arguments
•
•
Arrays can be passed as arguments to method parameters.
–
Arrays are reference types, so the method can change the value of the
elements.
Example 1:
void PrintArray(int[] myArray)
{
for (int i = 0; i < myArray.Length; i++)
{
Debug.Log(myArray[i]);
}
}

Passing Arrays as Arguments
•
•
Arrays can be passed as arguments to method parameters.
–
Arrays are reference types, so the method can change the value of the
elements.
Example 2:
void DoubleArrayValues(int[] myArray)
{
for (int i = 0; i < myArray.Length; i++)
{
myArray[i] = myArray[i] * 2;
}
}

Foreach Loops
•
•
The foreach statement provides a simple way to iterate over
the elements of an array.
–
The foreach statement processes elements in increasing index order,
starting with index 0 and ending with index Length - 1.
Example:
void PrintArray(int[] myArray)
{
foreach (int item in myArray)
{
Debug.Log(item);
}
}

Algorithms for Array Operations
•
The basic operations commonly performed over arrays are:
–
–
–
–
–
Traverse: traverses through all the array elements (one by one).
Search: searches an element based on a given value or criteria.
Sort: arranges the array data in a particular order.
Insertion: adds an element at a given index.
Deletion: deletes an element at a given index.

Array – Traverse Algorithm
•
•
The traverse operation consists of iterating over the elements
the array one by one.
–
The operation to be performed over the elements depends on the task
(example: printing, adding, comparing, etc.)
Example:
void PrintArray(int[] myArray)
O(n)
{
}
for (int i = 0; i < myArray.Length; i++)
{
Debug.Log(myArray[i]);
}

Array – Search
•
Problem:
–
Input:
•
array a with n elements;
•
element d to search;
–
Output:
•
m if the searched element d is at a[m];
•
-1 if d is not in the array;
•
Search algorithms:
–
Linear search;
–
Binary search;

Array – Linear Search
•
Algorithm: iterate over the array a, element by element,
checking if d is equal to one of the elements of a:
int SearchArray(int[] a, int d)
O(n)
{
int i;
for (i = 0; i < a.Length; i++){
if (a[i] == d){
return i;
}
}
return -1;
}

Array – Linear Search (Sorted Array)
•
Algorithm: iterate over the array a, element by element,
checking if d is equal to one of the elements of a.
int SearchSortedArray(int[] a, int d)
O(n)
{
int i;
for (i = 0; i < a.Length; i++)
{
if (a[i] == d)
return i;
else if (a[i] > d)
return -1;
}
return -1;
}

Array – Binary Search Algorithm
•
Binary search algorithm:
–
–
–
Compare d with the element that is in the middle of a;
if d is less than the middle element, search in the first half of the array;
if d is greater than the middle element, search in the second half of
the array;
–
–
if d is equal to the middle element, retorn its index;
Continue the procedure subdividing the select part of the array until
finding the searched element or reaching the end of the array.

Array – Binary Search Algorithm
int BinarySearchArray(int[] a, int d)
{
int begin = 0;
int end = a.Length - 1;
int middle;
while (begin <= end) //while the remaining part is larger than 0
{
middle = (begin + end) / 2;
if (a[middle] > d)
end = middle - 1; //search in the first half of the array
else if (a[middle] < d)
begin = middle + 1; //search in the second half of the array
else
return middle; //element found
}
return -1;
}
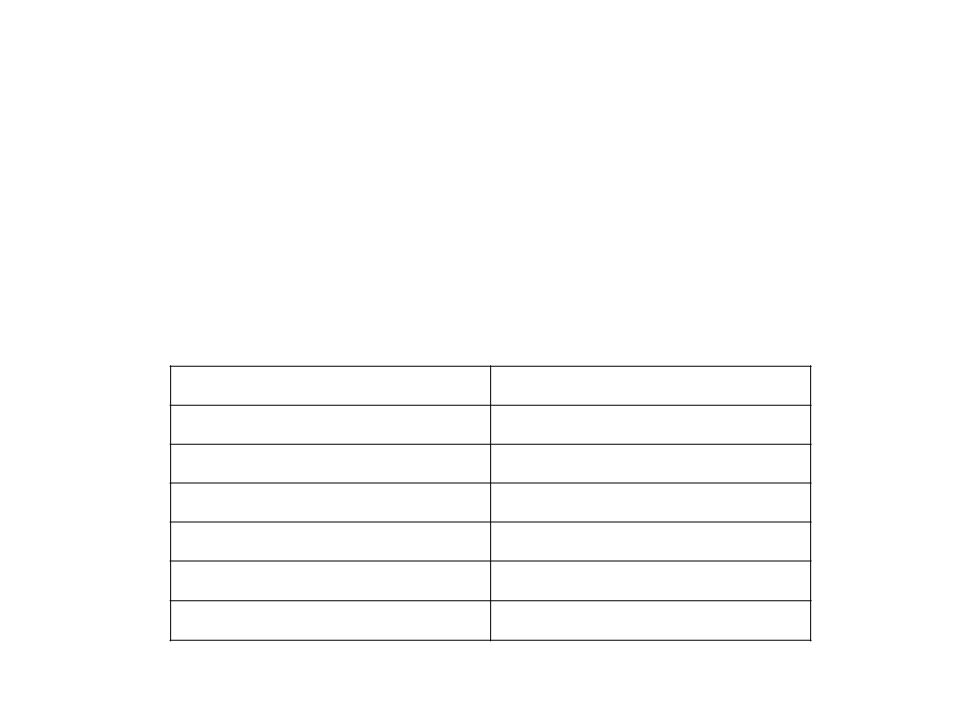
Array – Binary Search Algorithm
•
Worst Case: d is not in the array
–
–
–
2 tests are performed at every iteration;
At every iteration, the size of the search area is divided in half;
T(n) = O(log n)
Iteration
Size of the problem
1
2
n
n/2
n/4
n/8
…
3
4
…
log n
1

Assignment 1 – Arrays
1
) Write an algorithm that, given an array S of n
integers and another integer x, determines whether
or not there are two elements of S whose sum is
exactly x. Then analyze the complexity of this
algorithm.

Array – Sort
•
Problem:
–
Input: set of elements a1, a2, . . . , an;
–
Output: set of elements in an order ak1, ak2, . . . , akn, such
that, given a sorting function f, the following relation is
valid: f(ak1) < f(ak2) < . . . < f(akn).
•
•
Sorting is the process of rearranging a set of elements in
ascending or descending order.
The main purpose of sorting is to facilitate later retrieval of
elements from the ordered set.

Array – Sort
•
•
Main sorting algorithms:
–
–
–
–
–
Bubble Sort;
Selection Sort;
Insertion Sort;
Merge Sort;
Quick Sort;
The minimum asymptotic threshold for sorting algorithms
based on comparisons is: O(n log n)
Bubble Sort
•
Algorithm:
–
Iterates over the array, comparing adjacent elements, and
swapping them if they are in the wrong order.
–
The pass through the array is repeated until the entire
array is sorted.
Bubble Sort
162 162 2124 12842 1128772 1272
6
12 11844 184 1177 2222
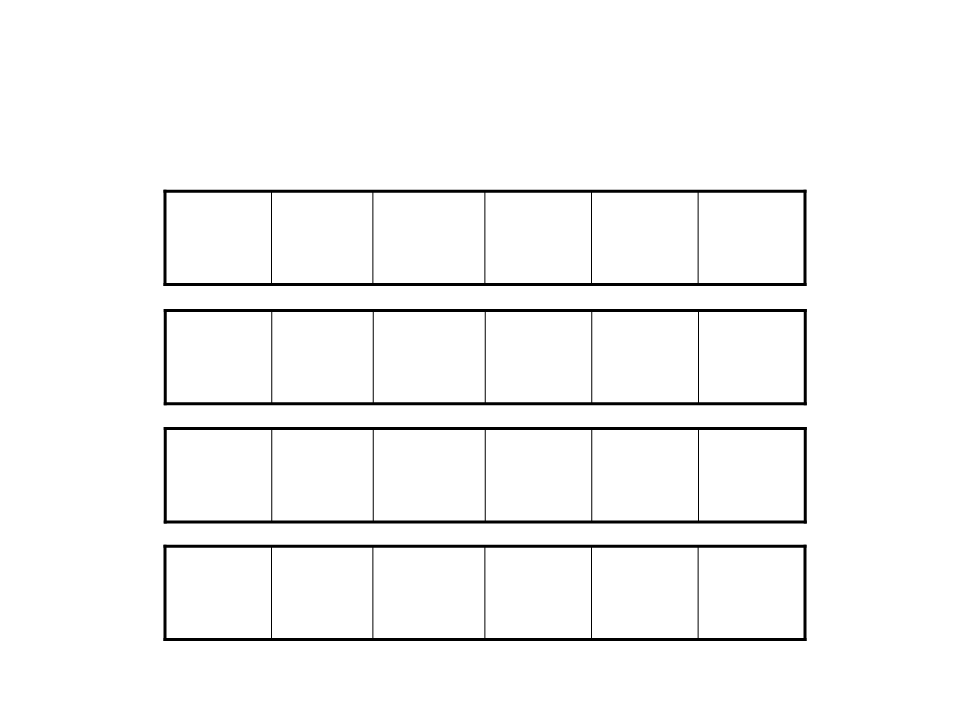
Bubble Sort
6
6
6
6
12 14 8 17 22
12 8 14 17 22
182 182 14 17 22
8 12 14 17 22

Bubble Sort Algorithm
void BubbleSort(int[] a)
{
int end, i, temp;
for (end = a.Length - 1; end > 0; end--)
{
for (i = 0; i < end; i++)
{
if (a[i] > a[i + 1])
{
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
}
}
}
}
Bubble Sort Algorithm
void BubbleSort(int[] a){
int end, i, temp;
bool changed;
for (end = a.Length - 1; end > 0; end--){
changed = false;
for (i = 0; i < end; i++){
if (a[i] > a[i + 1]){
temp = a[i];
a[i] = a[i + 1];
a[i + 1] = temp;
changed = true;
}
Optimized implementation: stop
the search when there is a full
pass without changes.
}
if (changed == false)
return;
}
}

Bubble Sort – Complexity
•
•
Computational complexity ≅ number of comparisons
≅
number of swaps
–
–
–
First pass: n-1 comparisons
Second pass: n-2 comparisons
Third pass: n-3 comparisons
Complexity:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Quadratic algorithm: O(n2)
ꢁ
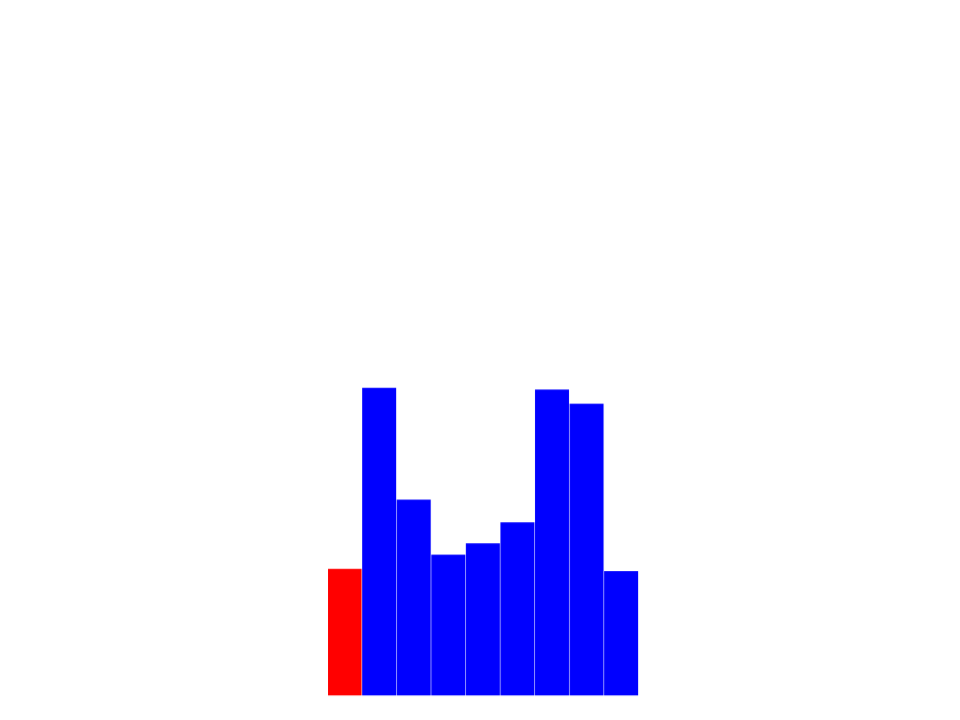
Selection Sort
•
Algorithm:
–
At each step, select the largest (or smallest) element and
place it in its correct position within the sorted array.
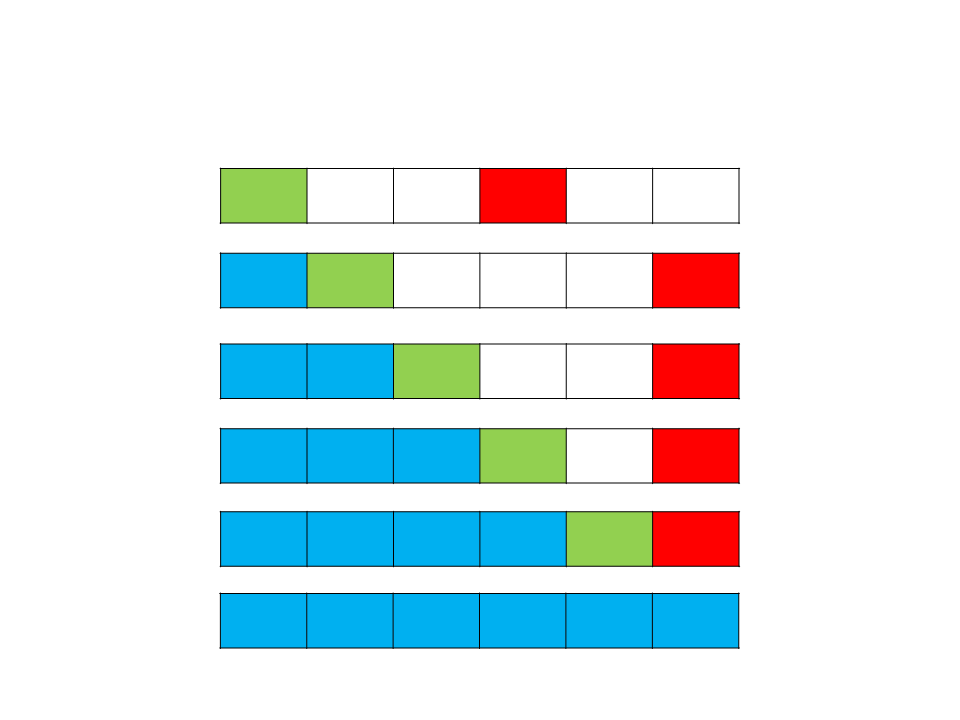
Selection Sort
8
1
5 7 1 9 3
5 7 8 9 3
1
1
1
1
3 7 8 9 5
3 5 8 9 7
3 5 7 9 8
3 5 7 8 9

Selection Sort – Algorithm
void SelectionSort(int[] a)
{
int min, temp, i, j;
for (i = 0; i < a.Length - 1; i++){
min = i;
for (j = i + 1; j < a.Length; j++){
if (a[j] < a[min])
min = j;
}
if (min != i){
temp = a[i];
a[i] = a[min];
a[min] = temp;
}
}
}

Selection Sort – Complexity
•
•
Computational complexity ≅ number of comparisons
≅
number of swaps
Complexity:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Quadratic algorithm: O(n2)
ꢁ
Insertion Sort
•
Algorithm:
–
In each step, starting from i = 2, the i-th item of the array is
picked up and transferred to its correct position.
–
The insertion of the element in the target location is done
by moving larger elements to the right and then inserting
the element in the final position.
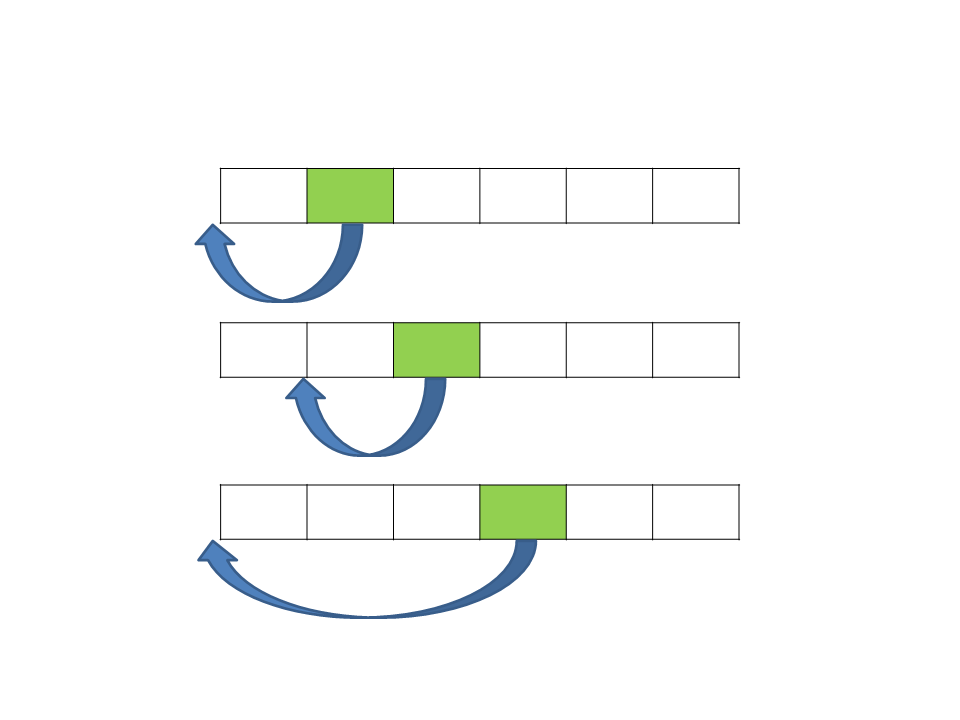
Insertion Sort
8
5
5 7 1 9 3
8 7 1 9 3
5
7 8 1 9 3
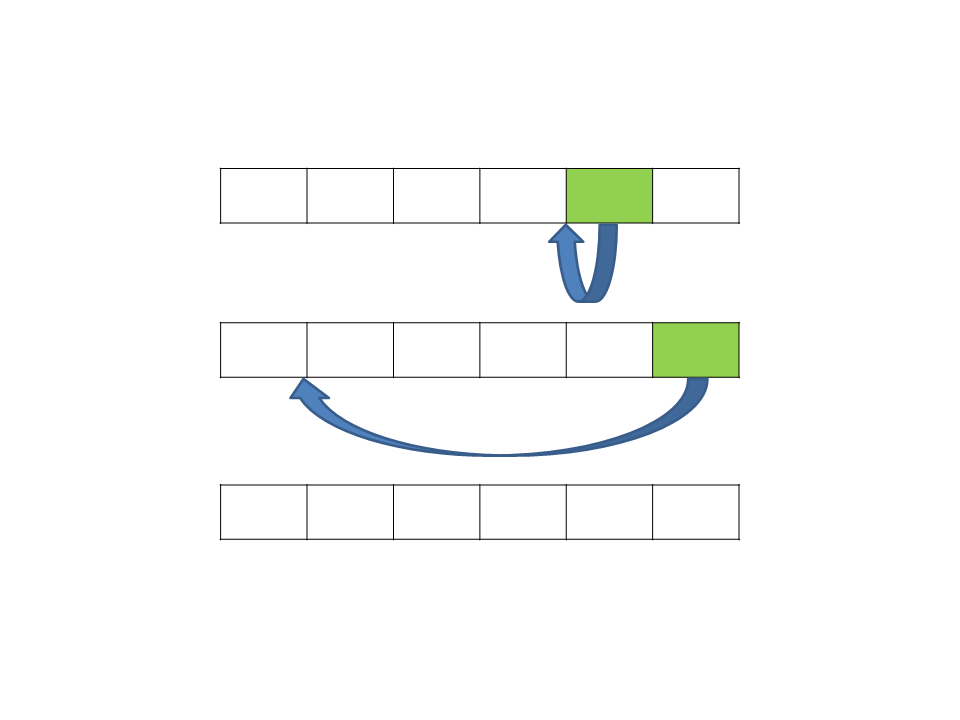
Insertion Sort
1
1
5 7 8 9 3
5 7 8 9 3
1
3 5 7 8 9

Insertion Sort – Algorithm
void InsertionSort(int[] a)
{
int j, i, temp;
for (i = 1; i < a.Length; i++)
{
j = i;
while (j > 0 && a[j] < a[j - 1])
{
temp = a[j];
a[j] = a[j - 1];
a[j - 1] = temp;
j--;
}
}
}

Insertion Sort – Complexity
•
•
Computational complexity ≅ number of comparisons
≅
number of swaps
Complexity:
–
T(n) = (n-1) + (n-2) + ... + 2 + 1
ꢀ2
− ꢀ
–
–
T(n) =
Quadratic algorithm: O(n2)
ꢁ

Merge Sort
•
•
Algorithm:
–
Divides the input array into two halves, calls itself for the two halves,
and then merges the two sorted halves.
Merge Sort is a Divide and Conquer algorithm:
–
–
–
Divide: recursively divide the problem into smaller problems;
Conquer: solve the smaller problems;
Combine: combine the solutions of the smaller problems to solve the
original problem.
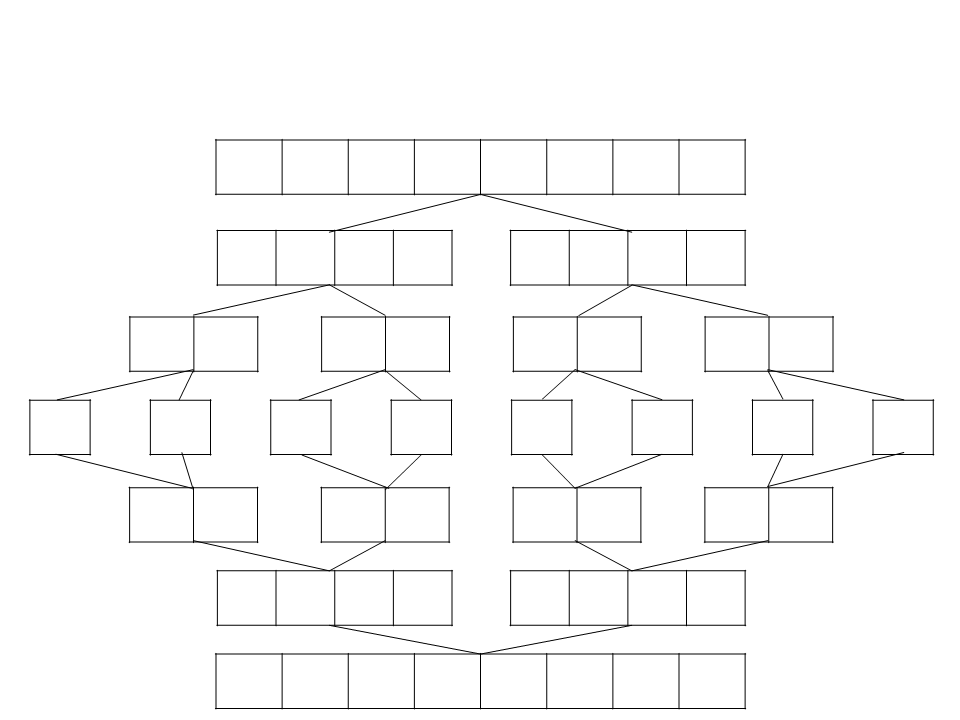
Merge Sort
8
8
5 7 1 9 3 2 4
5 7 1
7 1
9 3 2 4
9 3
8
5
5
8
2 4
2
8
5
7
1
9
3
4
1 7
3 9
2 4
1
1
5 7 8 2 3 4 9
2 3 4 5 7 8 9

Merge Sort – Algorithm
void MergeSort(int[] a, int left, int right)
{
if (left == right)
return;
int middle = (left + right) / 2;
MergeSort(a, left, middle);
MergeSort(a, middle + 1, right);
Merge(a, left, middle, right);
}

Merge Sort – Algorithm
void Merge(int[] a, int left, int middle, int right)
{
int i, j, k;
int lengthA = middle - left + 1;
int lengthB = right - middle;
int[] arrayA = new int[lengthA];
int[] arrayB = new int[lengthB];
for (i = 0; i < arrayA.Length; i++)
{
arrayA[i] = a[i + left];
}
for (i = 0; i < arrayB.Length; i++)
{
arrayB[i] = a[i + middle + 1];
}
...

Merge Sort – Algorithm
...
i = 0;
j = 0;
for (k = left; k <= right; k++)
{
if (i == arrayA.Length)
a[k] = arrayB[j++];
else if (j == arrayB.Length)
a[k] = arrayA[i++];
else if (arrayA[i] < arrayB[j])
a[k] = arrayA[i++];
else
a[k] = arrayB[j++];
}
}

Merge Sort – Complexity
•
Divide complexity: O(log n)
Iteration
Problem Size
1
2
n
n/2
n/4
…
3
…
log n
1
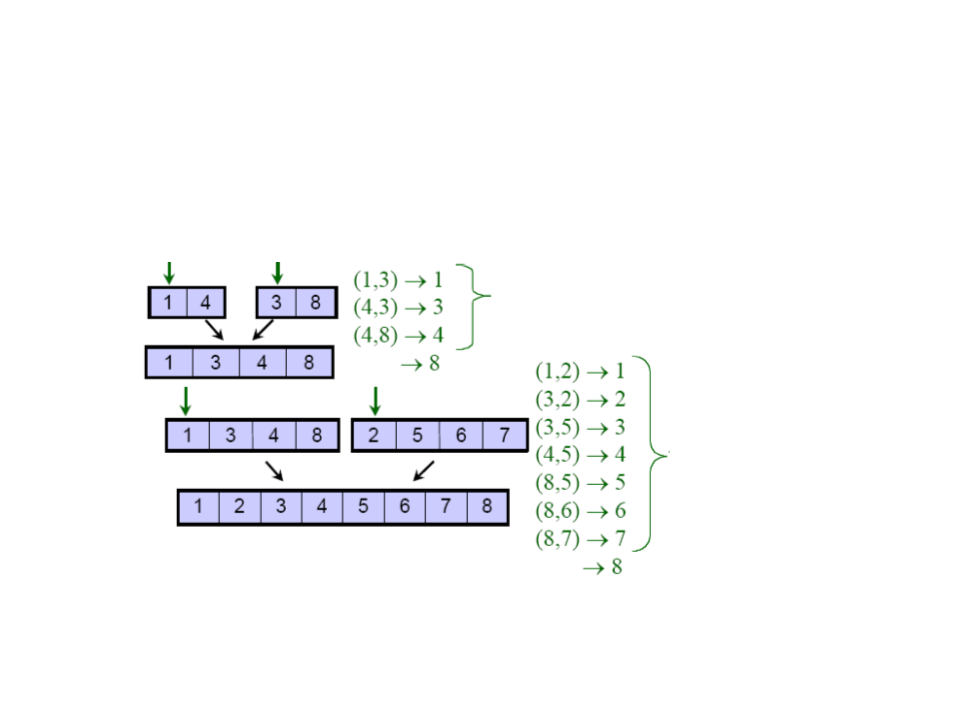
Merge Sort – Complexity
•
Merge complexity: O(n)
3
comparisons for 4
elements (n = 4)
7
comparisons
for n = 8
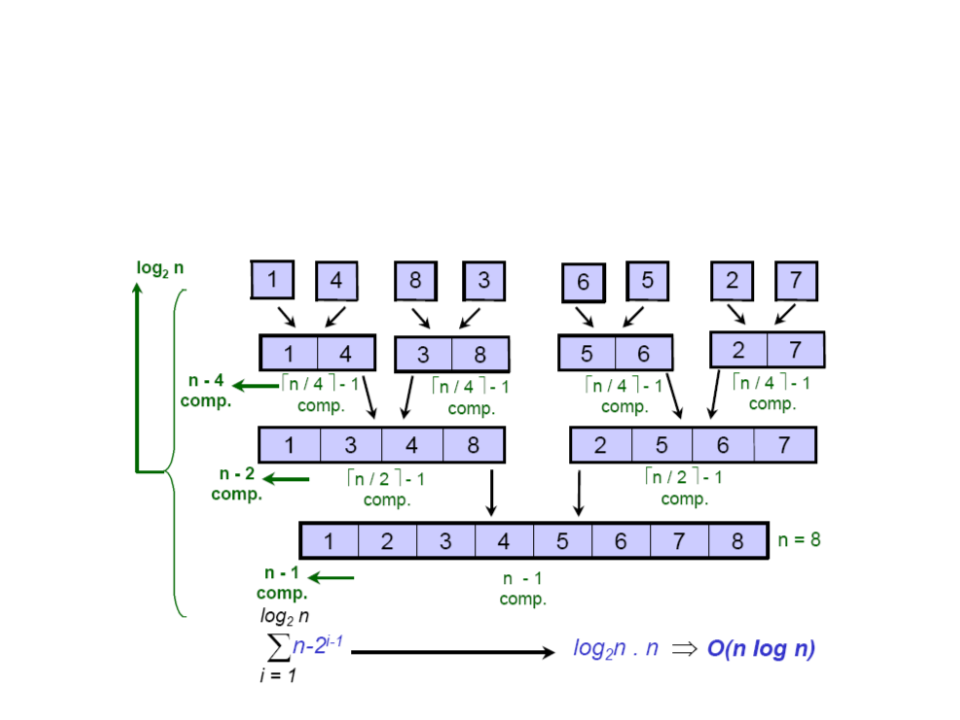
Merge Sort – Complexity
•
Complexity: O(n log n)
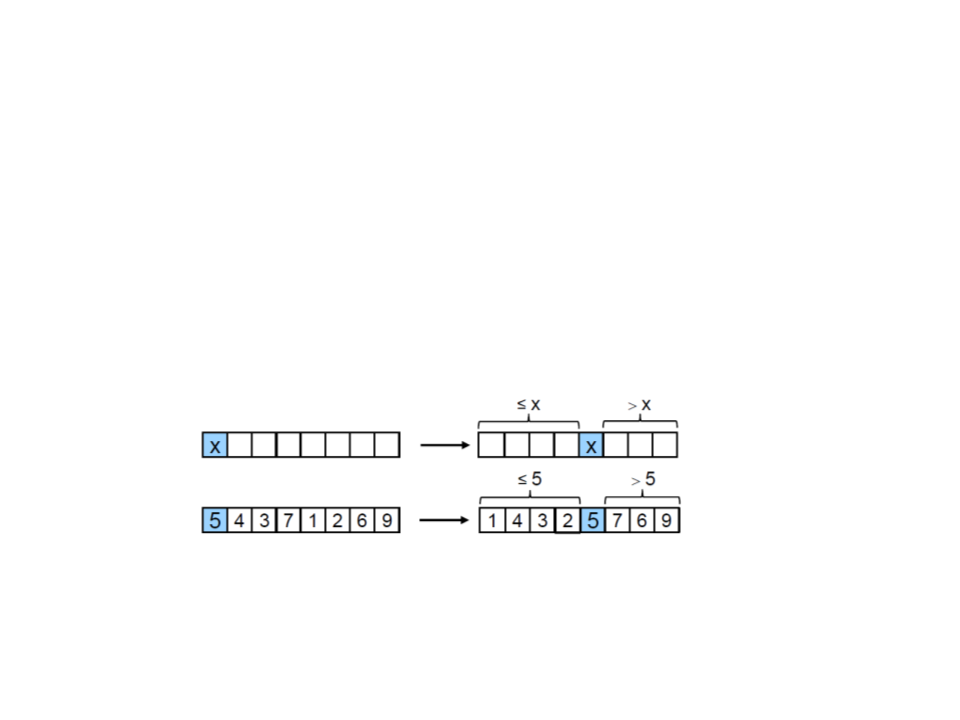
Quick Sort
•
Algorithm:
1
. Select an element x (arbitrarily), the pivot;
2
. Partition the array such that x is in the correct position a[i]:
•
x should occupy position i iff:
all elements v[0], … v[i-1] are smaller than x;
all elements v[i+1], …, v[n-1] are greater than x;
3
. Recursively call the algorithm to order the subarrays v[0], … v[i-1] and
v[i+1], …, v[n-1] (left array and right array)
•
continue until the arrays to be sorted have 0 or 1 element.

Quick Sort
quicksort of the array of length n
if n > 1 then
PARTITION with pivot x
quicksort of the left subarray of x
quicksort of the right subarray of x
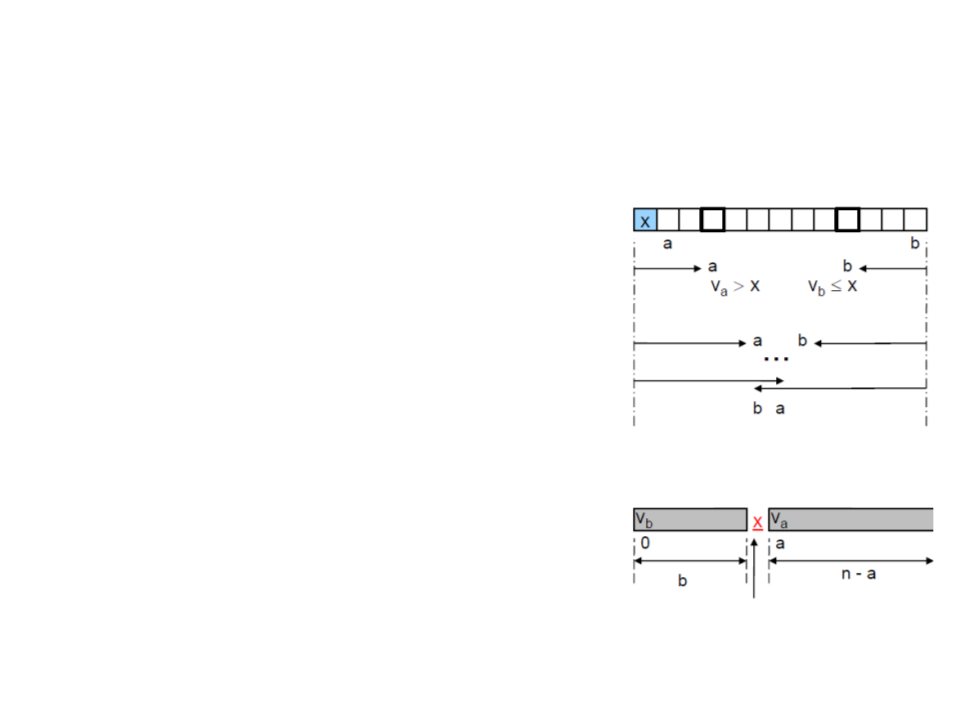
Quick Sort
•
Partition process:
1
. Walk with the index a from the start to the
end, comparing x with v[1], v[2], … until
v[a] > x is found
if a < b, swap and increment
2
. Walk with the index b from the end to the
start, comparing x with v[n-1], v[n-2], …
until v[b] <= x is found
region of ≤ x
region of > x
3
4
. Swap v[a] and v[b]
. Continue to the end from v[a+1] and to the
start from v[b-1]
if b < a, swap the pivot x with vb
subarray
subarray
5
. Finish the process when the index a and b
cross each other (b < a)
•
The correct position of x=v[0] is at index b,
therefore v[0] and v[b] are swapped.
correct
position
of x
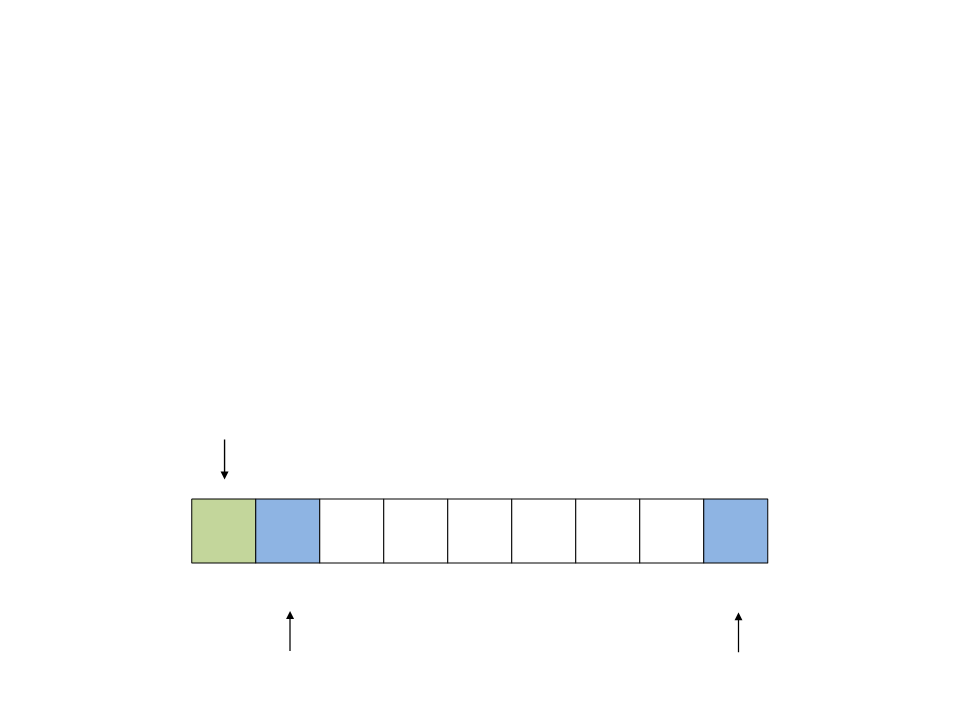
Quick Sort
•
Partition process:
–
Example:
pivot
40
20
10
80
60
50
7
30 100
[
0] [1]
[2] [3] [4]
[5]
[6] [7] [8]
a
b
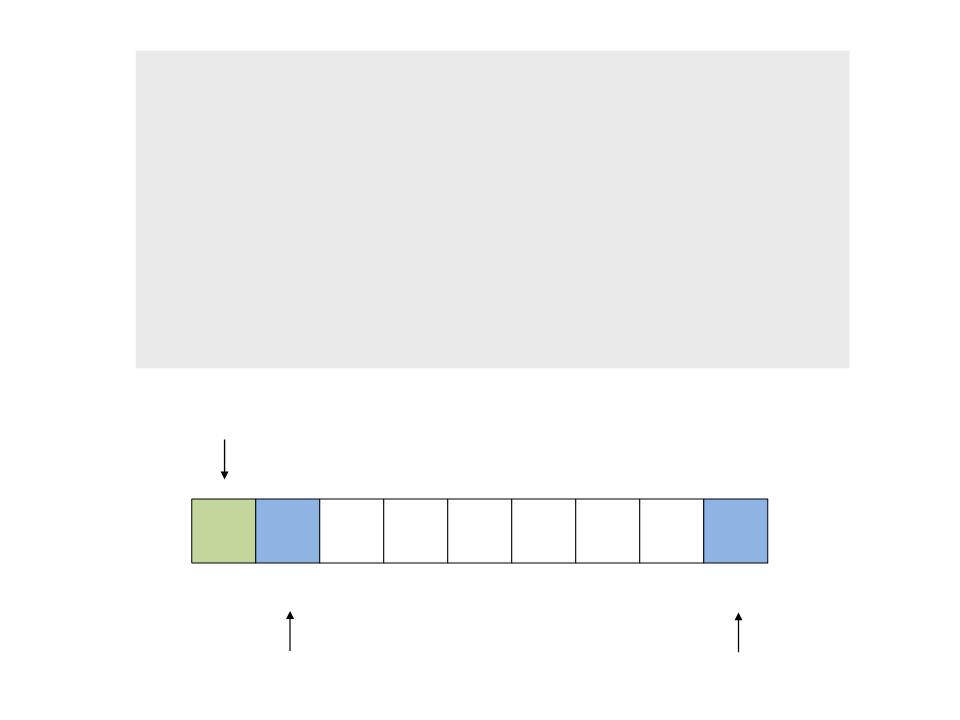
do{
while ((a <= b) && (v[a] <= pivot))
a++;
pivot
4
0 20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
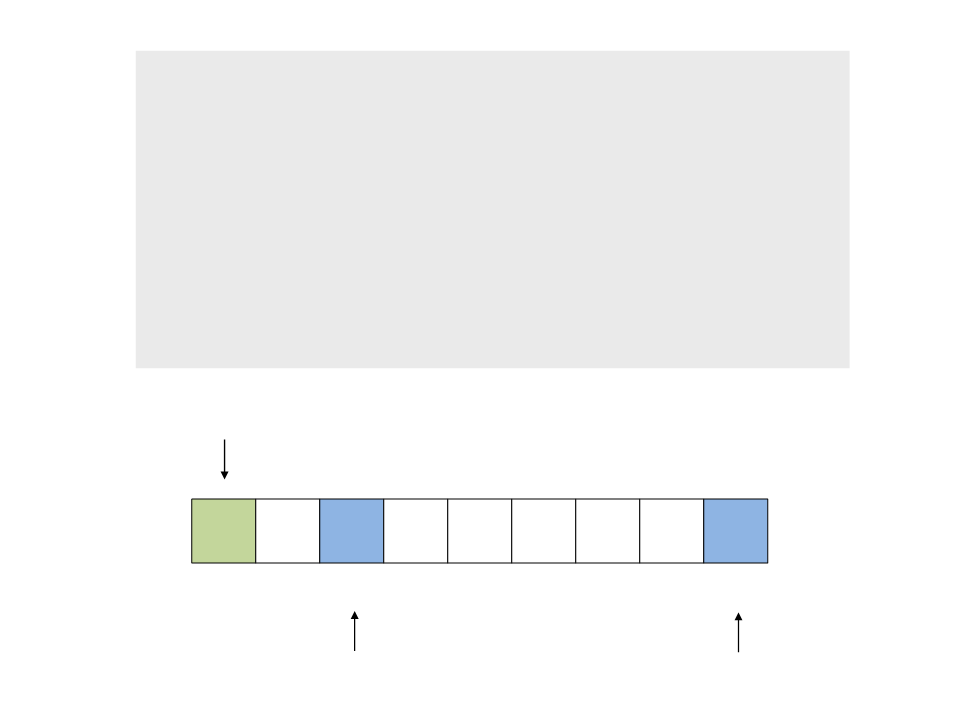
do{
while ((a <= b) && (v[a] <= pivot))
a++;
pivot
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3] [4] [5] [6]
a
b
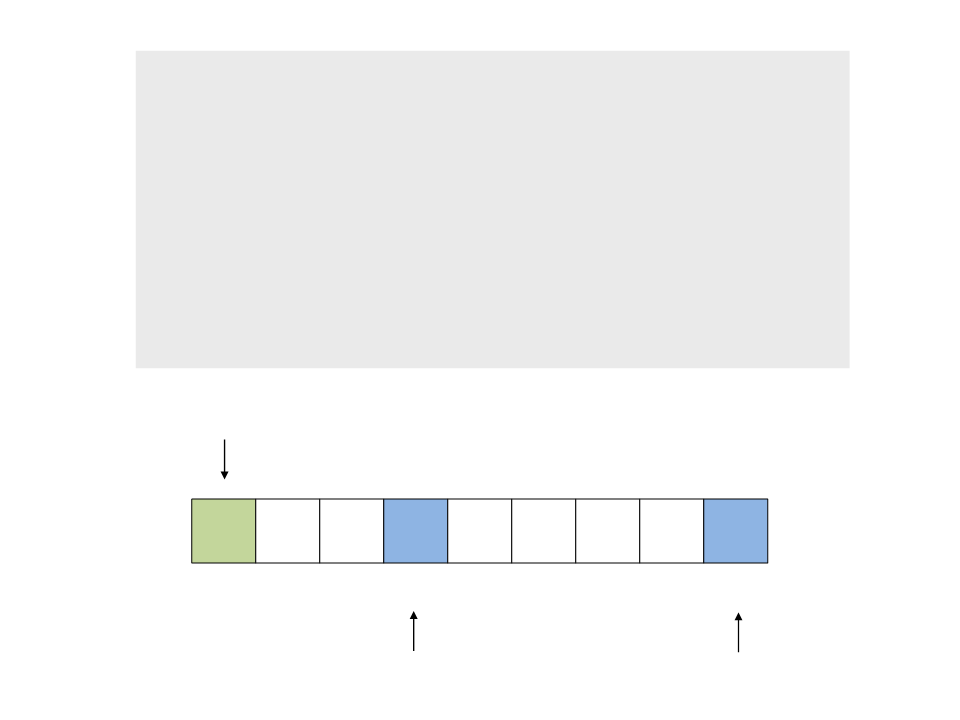
do{
while ((a <= b) && (v[a] <= pivot))
a++;
pivot
4
0 20 10
80
60
50
7
30 100
[7] [8]
[
0] [1] [2] [3] [4]
[5] [6]
a
b
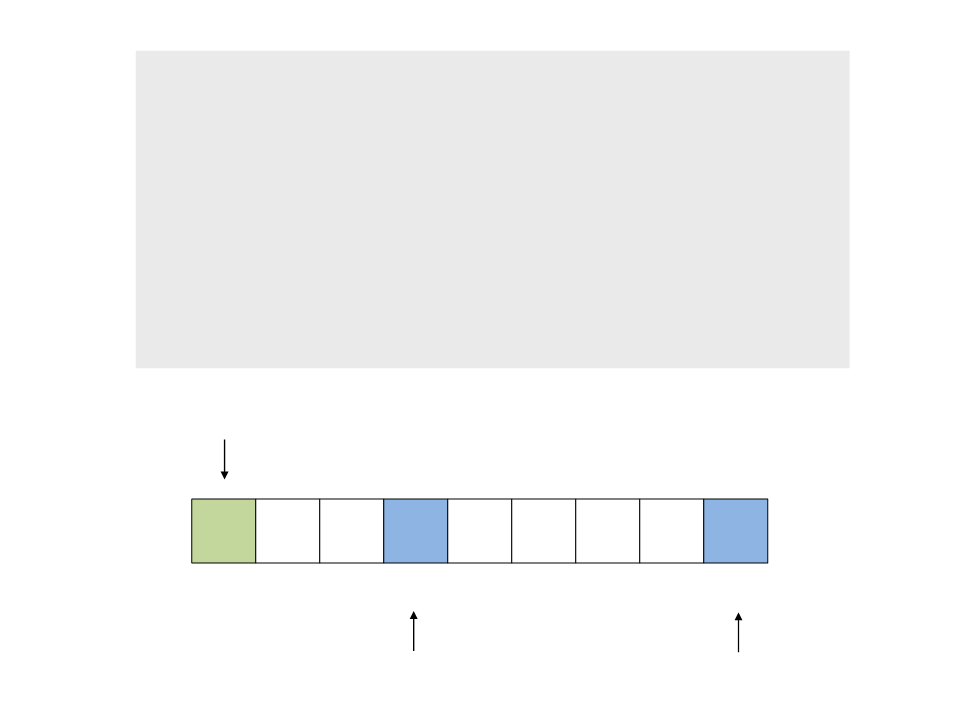
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
pivot
4
0
20
10
80
60
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
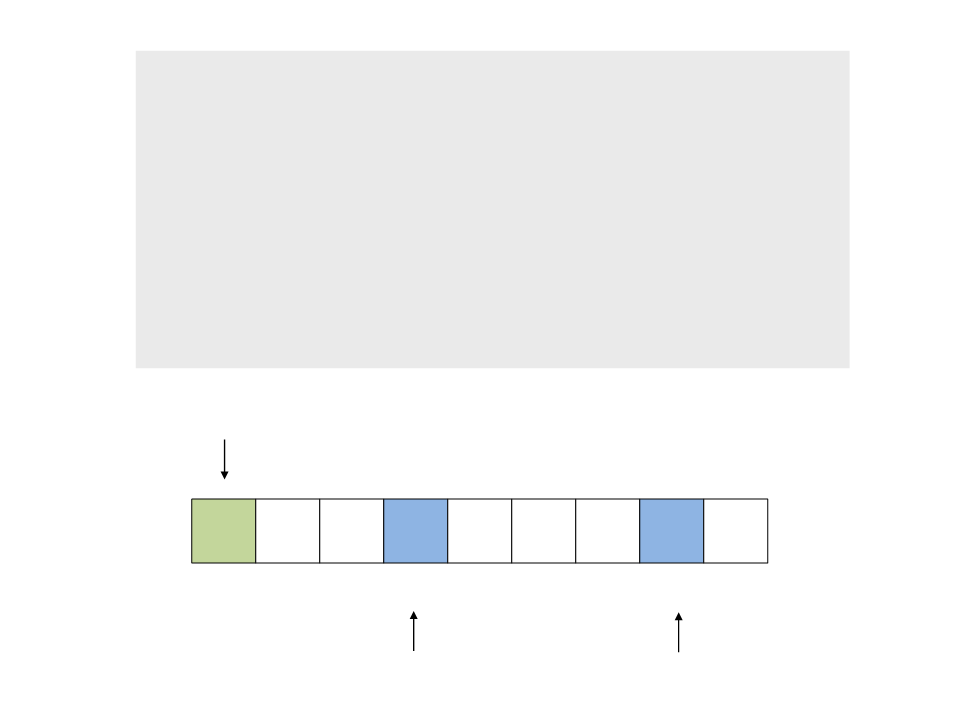
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
pivot
40 20 10
80 60 50 7 30 100
[
0] [1] [2] [3]
[4] [5] [6] [7] [8]
a
b
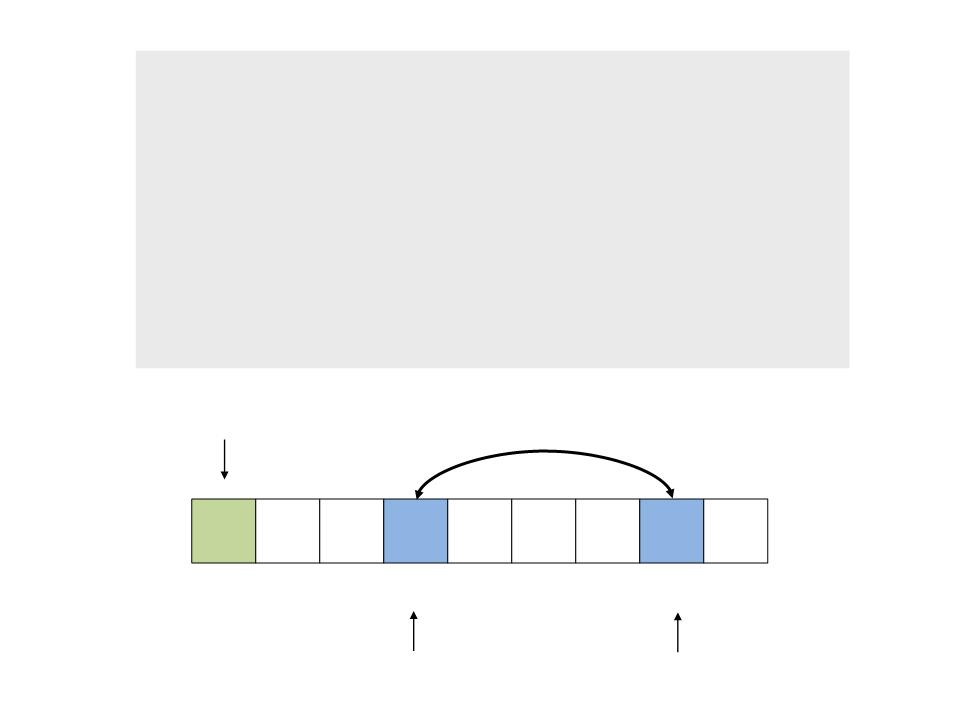
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
pivot
4
0
20
10
80 60
[4]
50
7
30 100
[7] [8]
[
0]
[1]
[2] [3]
[5]
[6]
a
b
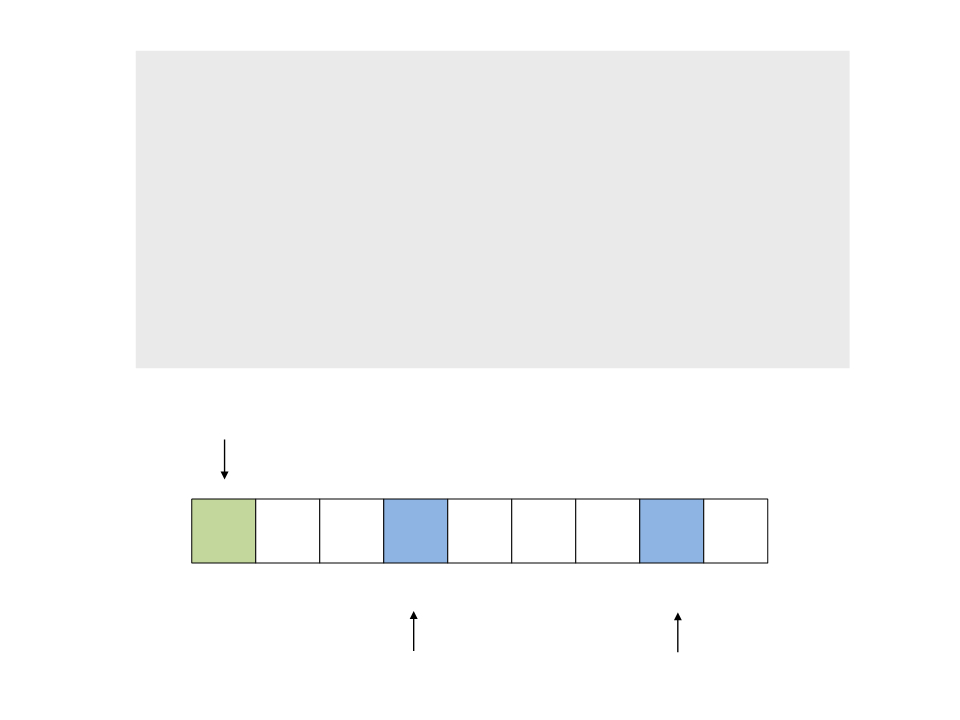
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
40 20 10 30 60 50
7
80 100
[
0] [1] [2] [3] [4] [5]
[6] [7] [8]
a
b
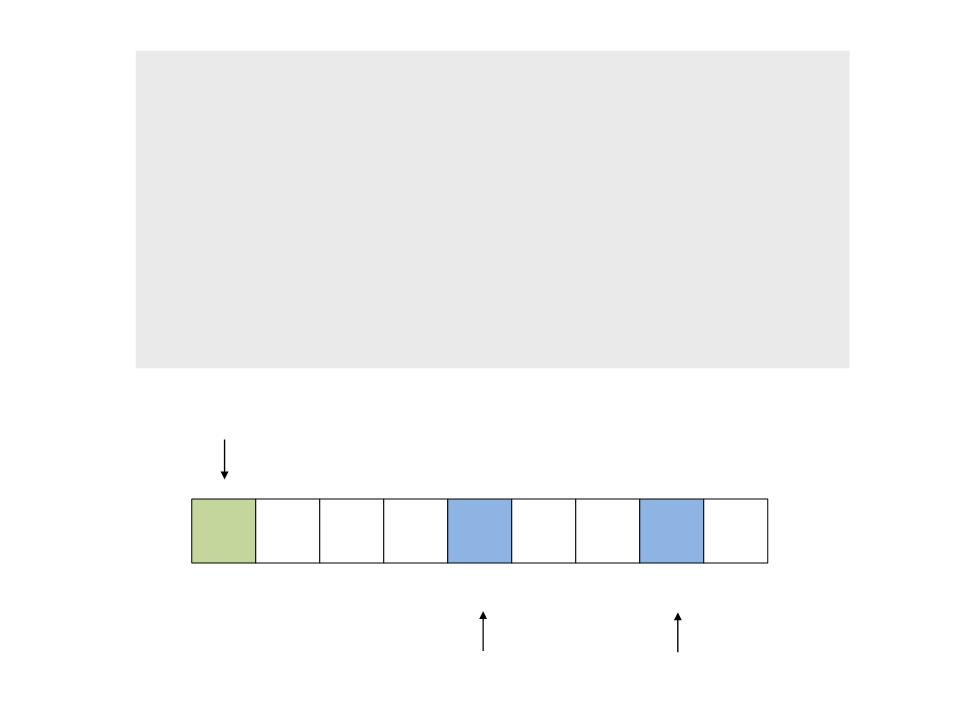
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
4
0
20
10
30
60
50
7
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
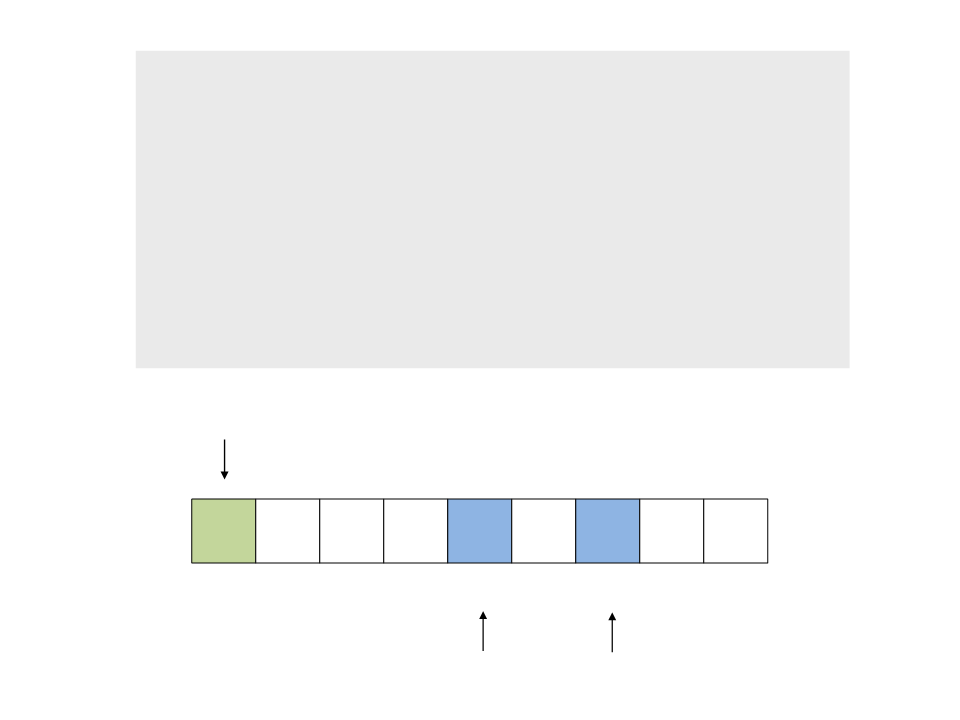
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
4
0 20
10
30
60 50
7
80 100
[7] [8]
[
0] [1] [2] [3]
[4] [5] [6]
a
b
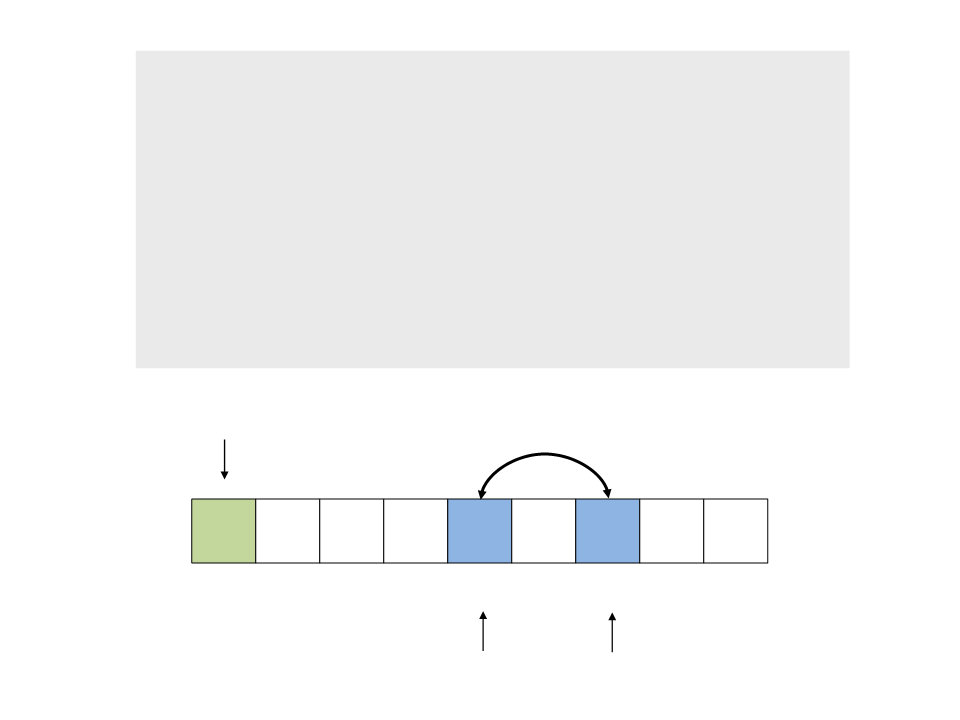
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
40 20
10 80 100
30
60
50
7
[
0] [1]
[2] [3] [4] [5] [6] [7] [8]
a
b
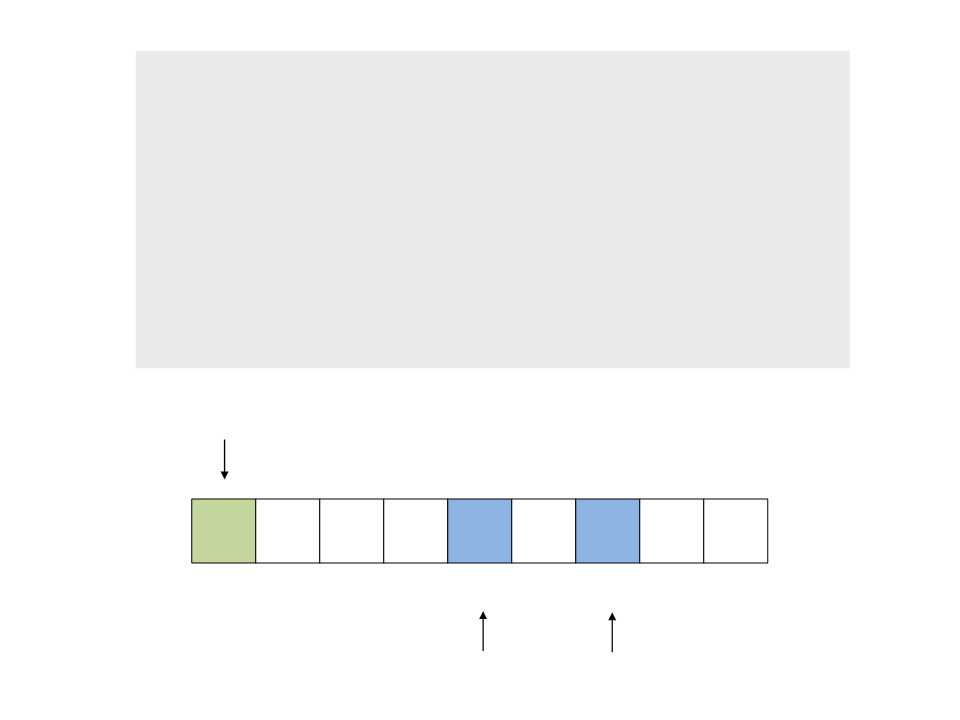
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
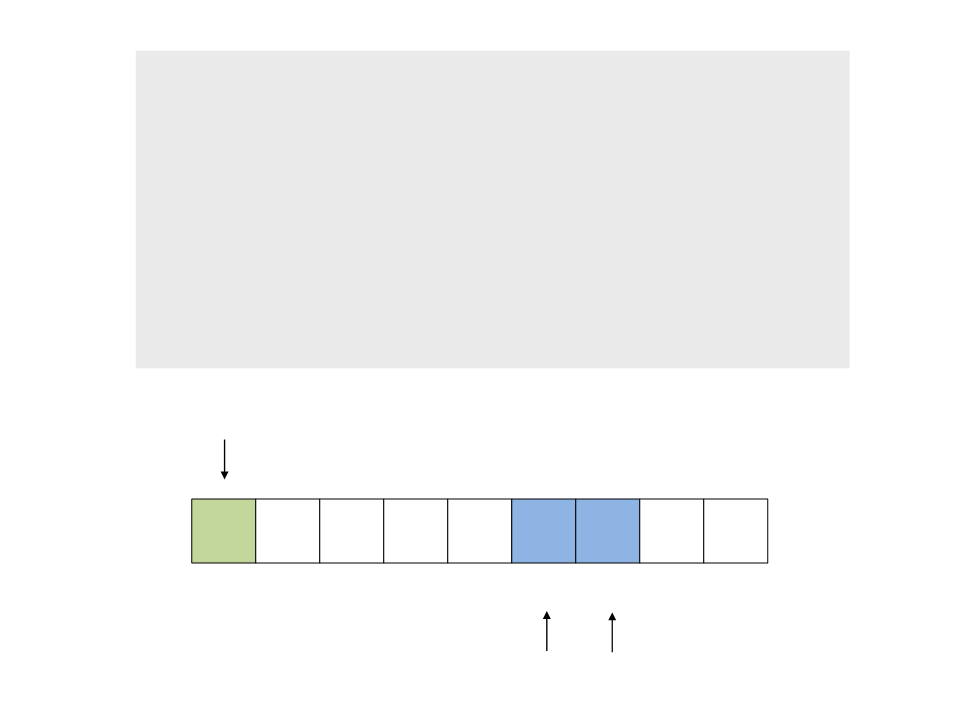
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
40 20 10 30
7
50 60 80 100
[
0] [1] [2] [3]
[4] [5] [6] [7] [8]
a
b
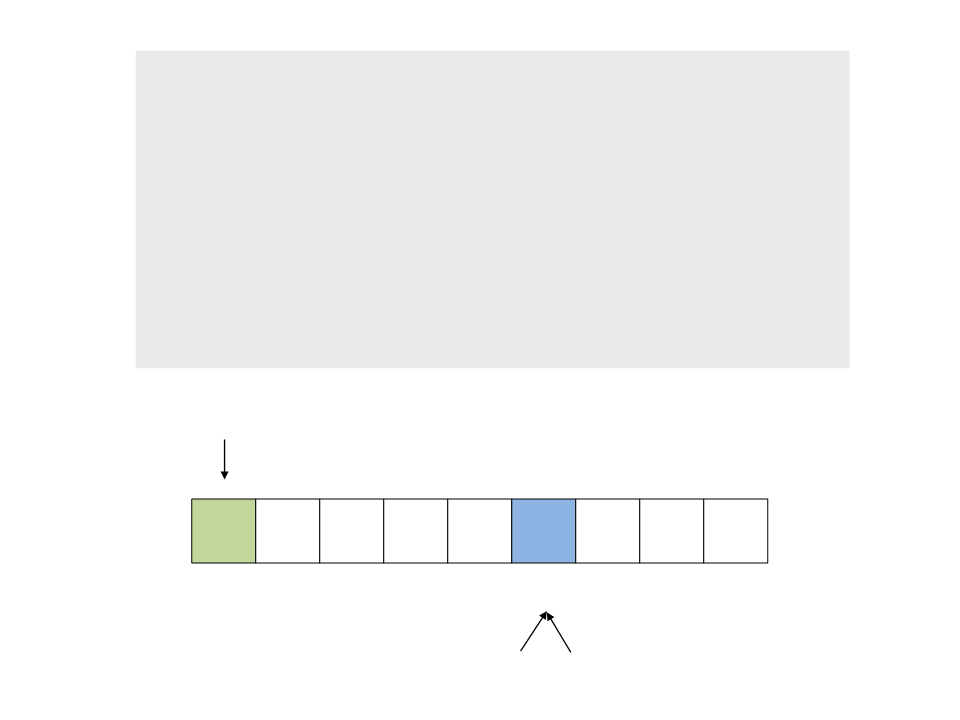
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
4
0
20 10 30
7
50
60
80 100
[7] [8]
[
0] [1] [2] [3] [4] [5] [6]
a
b
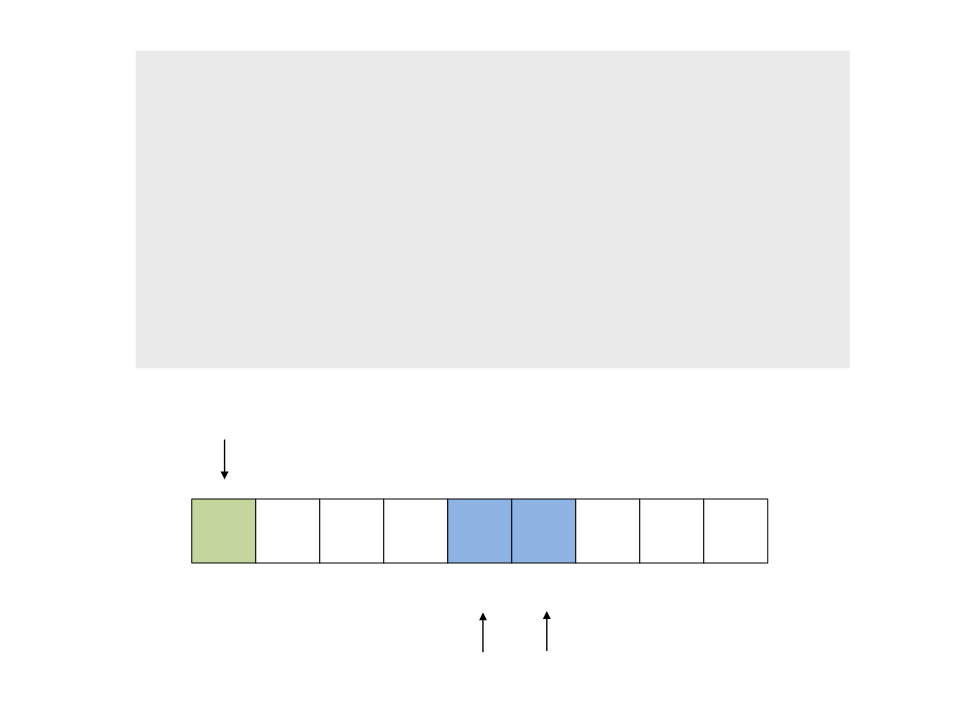
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
pivot
4
0 20
10
30
7
50
60
80 100
[7] [8]
[
0] [1]
[2] [3]
[4]
[5]
[6]
a
b
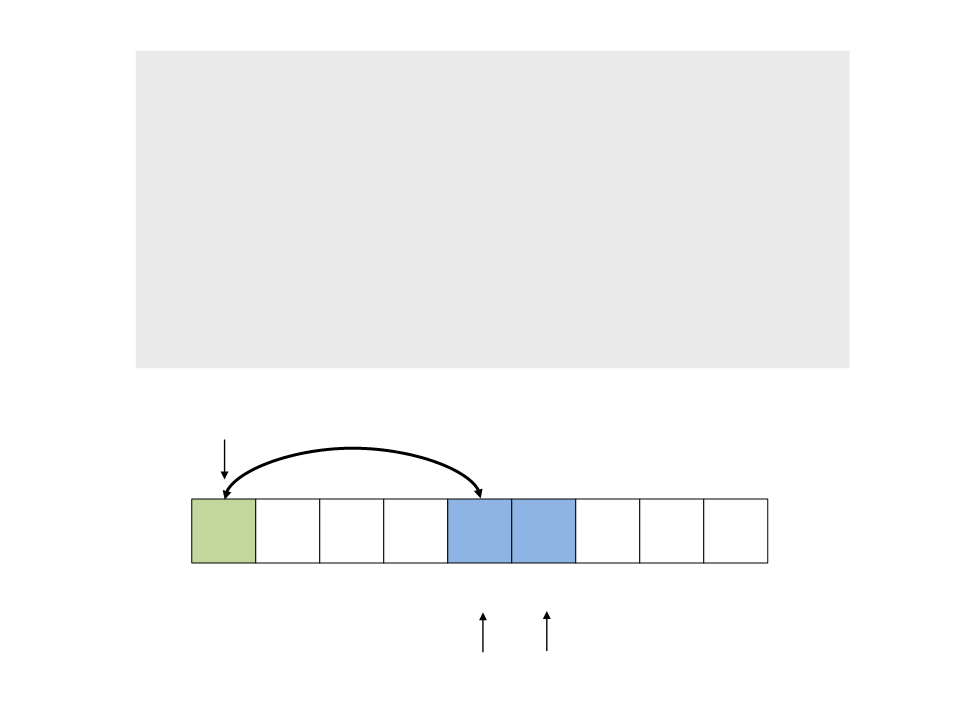
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
swap(v[pivot], v[b]);
pivot
4
0
20
10
30
7
50
60
80 100
[7] [8]
[
0]
[1]
[2] [3]
[4]
[5]
[6]
a
b
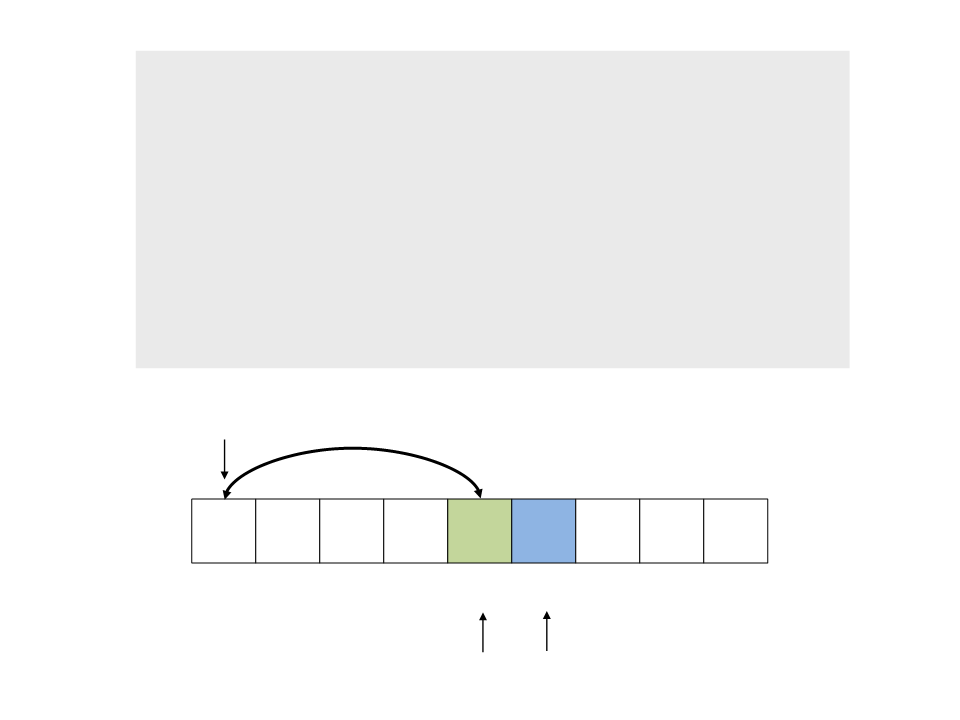
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
swap(v[a], v[b]);
while (a <= b);
}
swap(v[pivot], v[b]);
pivot
7
20 10 30
40 50
60
80 100
[7] [8]
[
0] [1] [2] [3] [4]
[5]
[6]
a
b
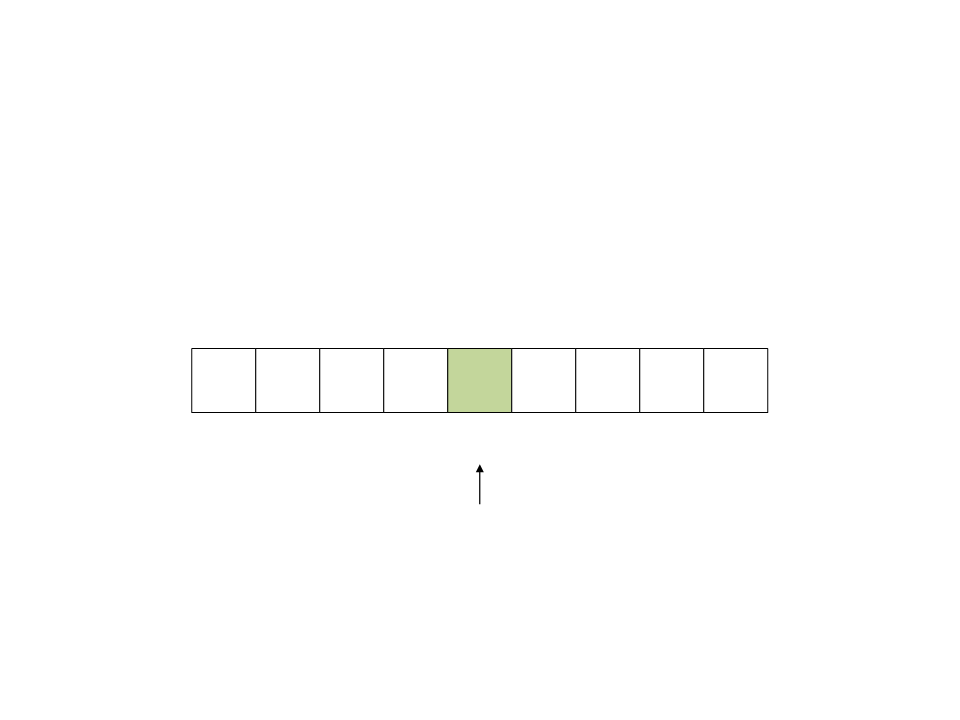
Quick Sort
•
Result of the partition process:
7
20 10 30 40 50 60 80 100
[1] [2] [3] [4] [5] [6] [7] [8]
[
0]
the pivot is on the final
position
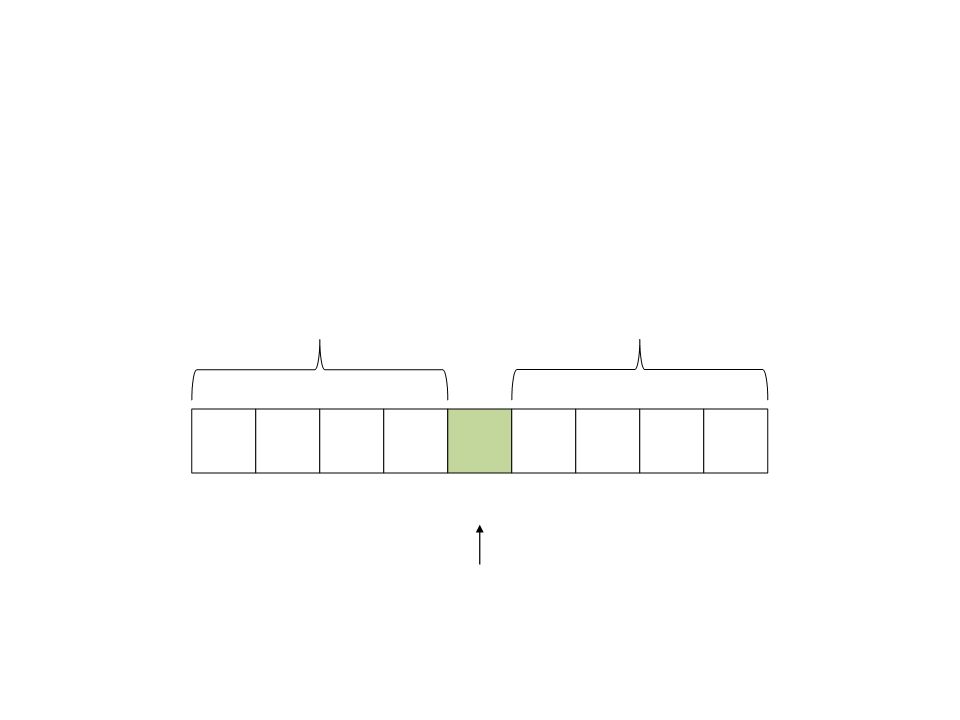
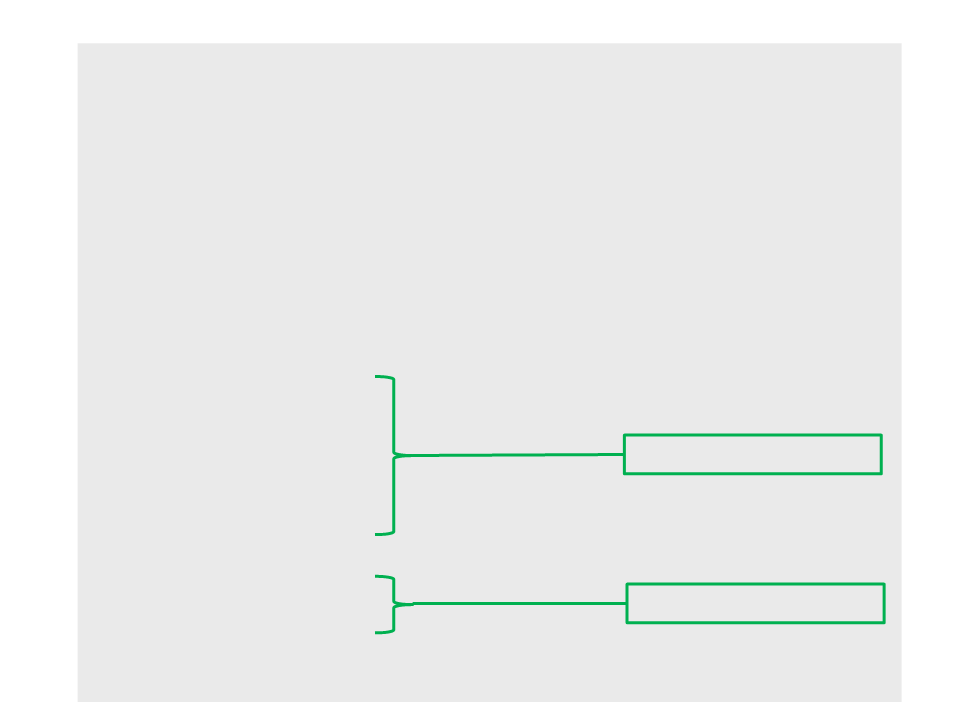
Quick Sort
•
Recursive calls to the subarrays:
left subarray
right subarray
7
20 10
30
40
50
60 80 100
[7] [8]
[
0]
[1]
[2] [3] [4]
[5] [6]
the pivot is on the final
position
int Partition(int[] v, int start, int end)
{
int pivot = v[start];
int a = start + 1;
int b = end;
do{
while ((a <= b) && (v[a] <= pivot))
a++;
while ((a <= b) && (v[b] >= pivot))
b--;
if (a <= b)
{
int temp = v[a];
v[a] = v[b];
v[b] = temp;
}
Swap a and b
}
while (a <= b);
v[start] = v[b];
v[b] = pivot;
return b;
Swap b and pivot
}

Quick Sort
void QuickSort(int[] v, int start, int end)
{
if (start < end)
{
int p = Partition(v, start, end);
QuickSort(v, start, p - 1);
QuickSort(v, p + 1, end);
}
}

Quick Sort – Algorithm
•
Best Case:
–
The pivot represents the median value of the array elements;
–
After moving the pivot to its final position, there are two subarrays left
to be sorted, both with the number of elements reduced by half, in
relation to the original array;
–
Complexity: T(n) = 2T(n/2)+n = n log n − n + 1 = O(n log n)

Quick Sort - Complexidade
•
Average Case:
–
According to Sedgewick and Flajolet (1996, p. 17), the number of
comparisons is approximately: T(n) ≈ 1.386 n log n − 0.846
–
Complexity: T(n) = O(n log n)
Quick Sort - Complexidade
•
Worst Case:
–
The pivot is the biggest element and algorithm falls into the same
procedure performed for the bubble sort algorithm;
–
Complexity: T(n) = O(n2)
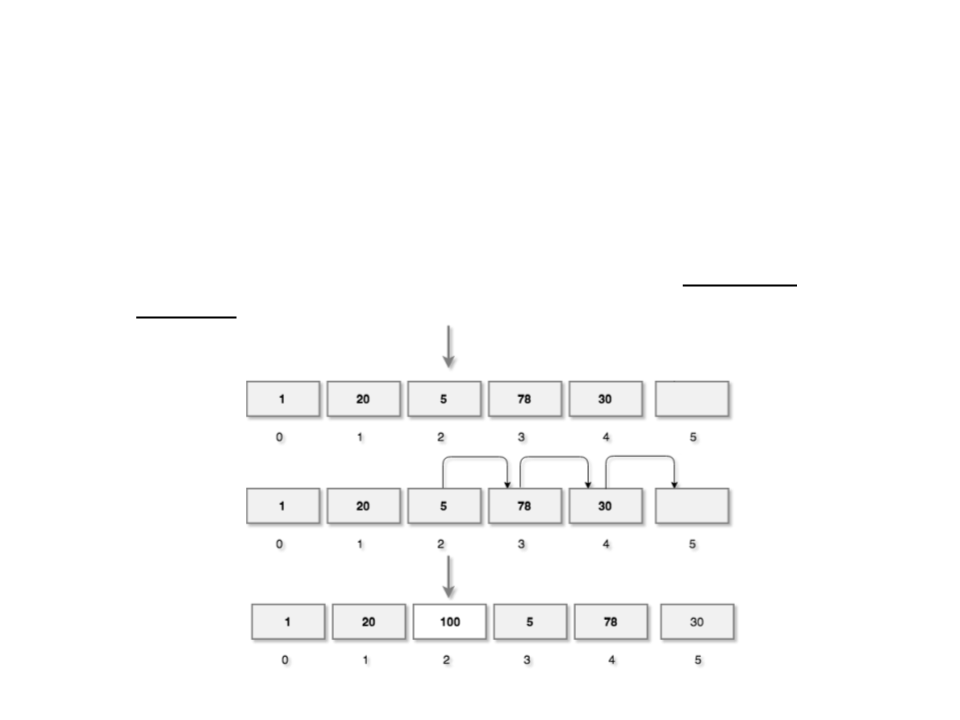
Array – Insertion Algorithm
•
•
The insertion operation inserts a new element at a given
index of the array.
–
Such dynamic insertion require a way to know the number of
elements in the array.
Example:

C# Generic Classes
•
•
Generic classes in C# encapsulate operations that are not
specific to a particular data type.
–
Operations such as adding and removing items from the collection are
performed in the same way regardless of the data type.
A type parameter T is used as placeholder for a particular type
specified when creating an instance of the generic type.
class DataStore<T>
{
public T Data;
}
DataStore<int> store = new DataStore<int>();

Generic Array Class
public class Array<T>
{
private T[] data;
private int count;
public T Get(int index)
{
return data[index];
}
public int Length
{
get { return data.Length; }
}
public Array(int length)
{
data = new T[length];
count = 0;
}
}

Generic Array Class – Add
•
A simple way to add a new element to the array is by inserting
it at end of the array:
–
The element data type is the generic type T.
–
Since the array has a maximum capacity (define when creating the
array), the operation can fail (returning false).
public bool Add(T value)
{
if (count < data.Length)
{
data[count] = value;
count++;
return true;
}
return false;
}

Generic Array Class – Traverse
•
The traverse operation consists of iterating over the elements
the array one by one.
–
We can implement the GetEnumerator method in the generic class to
allow us to iterate over the array using a foreach.
public IEnumerator<T> GetEnumerator()
{
for (int i = 0; i < count; i++)
{
yield return data[i];
}
}
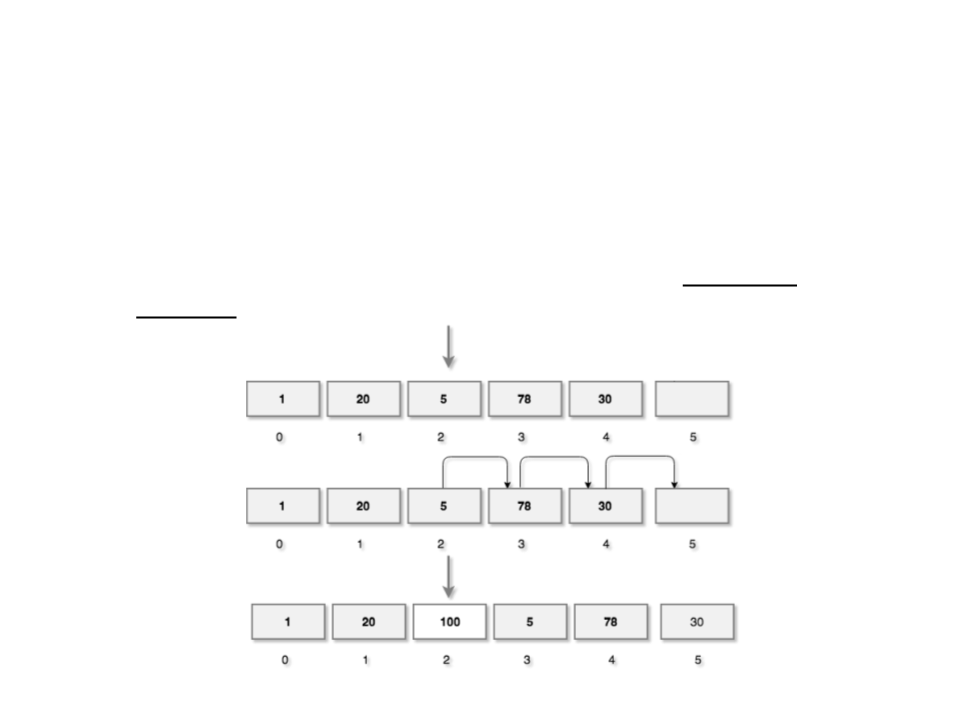
Back to the Insertion Algorithm
•
•
The insertion operation inserts a new element at a given
index of the array.
–
Such dynamic insertion require a way to know the number of
elements in the array.
Example:

Array – Insertion Algorithm
public bool InsertAt(T value, int index)
{
O(n)
if ((index < 0) || (index > count)) //check if index is valid
{
return false;
}
else if (index == count) //insert at the end
{
data[count] = value;
count++;
}
else //shift the elements to open space for the new element
{
count++;
for(int i = count - 1; i >= index; i--)
{
data[i + 1] = data[i];
}
data[index] = value;
}
return true;
}
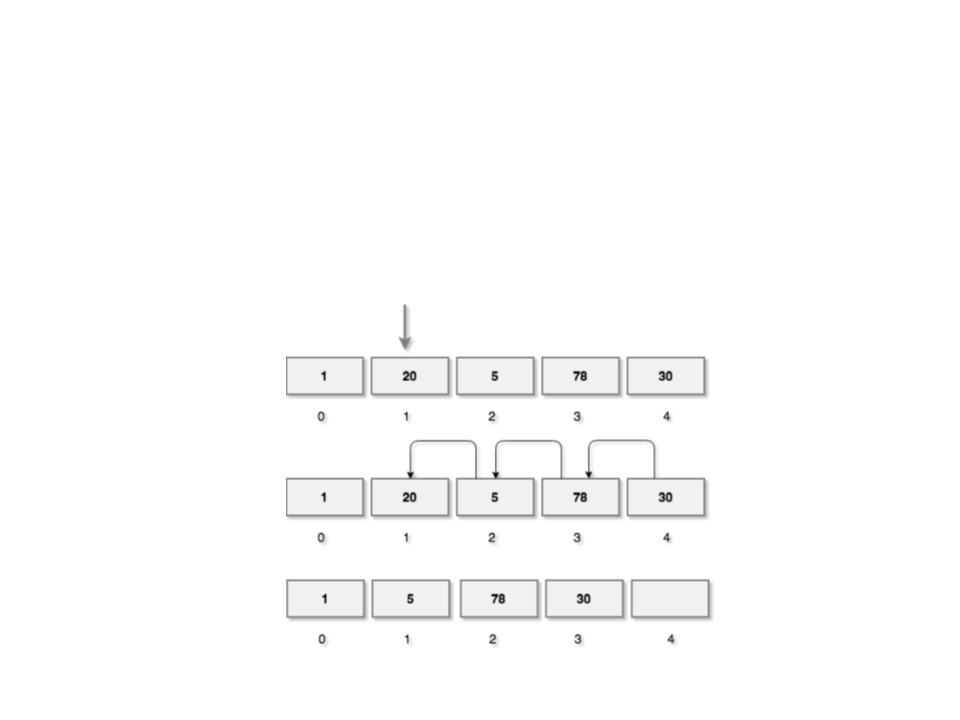
Array – Deletion Algorithm
•
•
The deletion operation removes an element from a given
index of the array.
Example:

Array – Deletion Algorithm
public bool RemoveFrom(int index)
{
O(n)
//check if index is valid
if ((index < 0) || (index >= count))
{
return false;
}
//shift the elements from index + 1 by one position to the left
for (int i = index; i < count - 1; i++)
{
data[i] = data[i + 1];
}
count--;
return true;
}

Assignment – Sort
Assignment List 02 – Sorting Algorithms
https://edirlei.com/aulas/data-structures/DS_Assignment_List_02.pdf

Further Reading
•
•
Penton, R. (2002). Data Structures for Game Programmers.
Muska & Lipman/Premier-Trade. ISBN: 978-1931841948
–
–
–
–
Chapter 3: Arrays
Chapter 4: Bitvectors
Chapter 5: Multi-Dimensional Arrays
Chapter 20: Sorting Data
Sherrod, A. (2007). Data Structures and Algorithms for
Game Developers. Charles River Media. ISBN: 978-
1
584504955
–
Chapter 2: Arrays
–
–
Chapter 4: Introduction to Sorting
Chapter 8: Advanced Sorting
