Introduction to Algorithm Analysis

Data Structures

Lecture 01: Introduction to Algorithm Analysis

Edirlei Soares de Lima

<edirlei.lima@universidadeeuropeia.pt>

What is an Algorithm?

•

A set of instructions to solve a problem.

–

The problem is the motivation for the algorithm.

–

In most cases, there are several algorithms to solve the same problem.

•

How can we choose the algorithm?

–

Algorithms can be expressed using a variety of notations,

including natural language, pseudocode, flowcharts, or directly in

a programming language.

What algorithms are important for game programming?

What is an Algorithm?

•

A computational problem is usually defined by a description

of its input and output.

Example: sorting

Input: a sequence {a₁; a₂; ... ; a_n} of n numbers

Output: a permutation of numbers {a'₁; a'₂; ... ; a’_n} such

that a'₁ ≤ a'₂ ≤ ... ≤ a'_n

Input: 6 3 7 9 2 4

Output: 2 3 4 6 7 9

Effectiveness and Efficiency

•

Effectiveness: the algorithm must be able to

correctly solve all instances of the problem.

Efficiency: the performance of the algorithm (time

and space) must be appropriate to target application.

Example: Effectiveness of an Algorithm

•

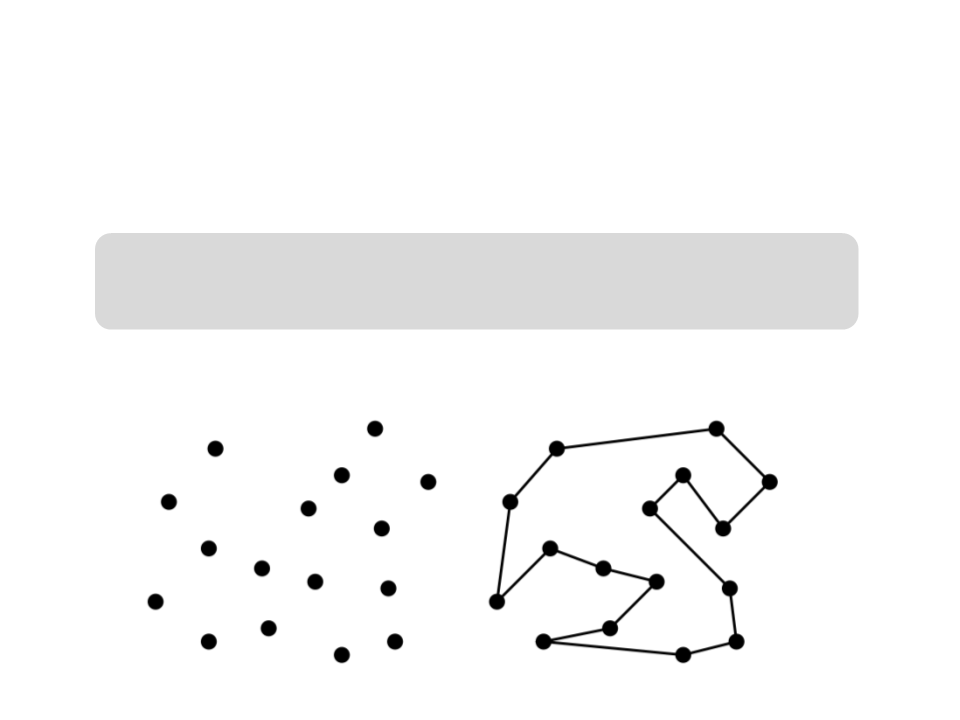
Traveling Salesman problem:

Input: a set S of n points in a plane

Output: the shortest cyclic path to visit all point of S

•

Example:

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

The first possible algorithm:

1. p₁ ← start point randomly selected

2

3

4

5

6

. i ← 1

. while (there are points to visit) do

. p_i ← the closest not visited neighbor of p_i

. i ← i + 1

. return path p₁ → p₂ → ... → p_n → p₁

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

It seems to work…

→

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

But it does not work for all the instances of the problem!

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

A second possible algorithm:

1. For i ← 1 to (n - 1) do

2

3

4

. Connect the closest pair of points that are part of

different connected components

. Connect the two points that are in the extremes of

the remaining connected component

. Return the cycle created with the points

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

It seems to work…

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

But it does not work for all the instances of the problem!

Example: Effectiveness of an Algorithm

•

Traveling Salesman problem

–

A third possible algorithm (brute force):

1. P_m_i_n ← any permutation of S

2

3

4

5

. For P_i ← every permutation of S do

.

if (cost(P_i) < cost(P_m_i_n)) then

P_m_i_n← P_i

. Return the path of P_m_i_n

–

The algorithm is effective (correct), but extremely slow!

•

P(n) = n! = n × (n - 1) × ... × 1 (n factorial!)

•

Example: P(20) = 2,432,902,008,176,640,000

Example: Effectiveness of an Algorithm

•

The Travelling Salesman Problem (TSP) is a classic problem in computer

science.

•

The problem has several applications that depend on its solutions.

–

Examples: industrial production, vehicle routes, genomic analysis ...

No efficient solution for this problem is known (some solutions generate

“approximated” results, but no one generates optimal results)

•

The temporal complexity of the brute force solution is: O(n!)

The TSP is part of class of problems known as NP-hard

–

There is decision version of the problem that is part of the class NP-complete

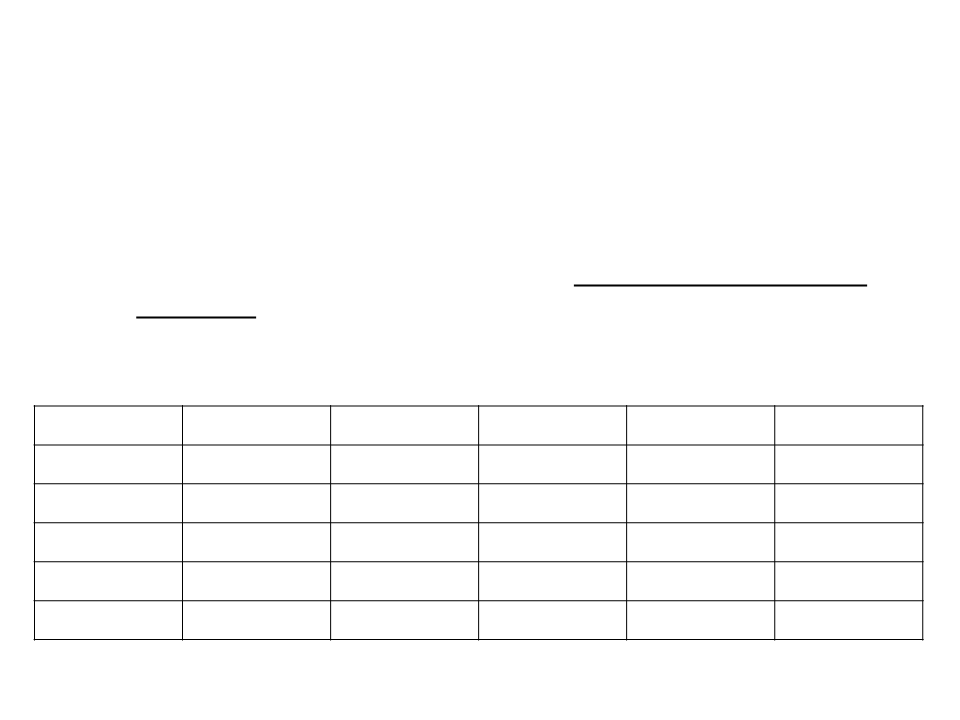
Efficiency of an Algorithm

•

How many simple operations a computer can perform per

second? (just an approximation)

–

Supposing that a computer can perform 1 million simple operations

per second, how much time it would take to perform the following

sets of operations?

Operations

100

< 1 sec

1 sec

1,000

< 1 sec

1 sec

10,000

< 1 sec

2 min

100,000

< 1 sec

1,000,000

1 sec

N

N²

N³

2^N

N!

3 hours

32 years

12 days

18 min

12 days

31,710 years

10¹⁷years

a lot of time a lot of time a lot of time a lot of time

a lot of time a lot of time a lot of time a lot of time a lot of time

a lot of time > 10²⁵ years

Efficiency of an Algorithm

•

Complexity of the Traveling Salesman brute force algorithm:

–

P(n) = n! = n × (n - 1) × ... × 1

Example of 6 permutations of {1, 2, 3}:

2 3

3 2

1

2

3

1 3

3 1

1 2

2 1

Efficiency of an Algorithm

•

How much time the algorithm would need to check all the

permutations of n numbers? (approximated time considering

around 10 permutations per second)

7

n = 8: 0,003s

n = 9: 0,026s

n = 10: 0,236s

n = 11: 2,655s

n = 12: 33,923s

…

n = 20: 5000 years !

Efficiency of an Algorithm

•

A faster computer can help?

•

if n = 20 = 5000 years, let’s use a faster computer:

–

10x faster would still need 500 years;

5,000x faster would need 1 year;

1,000,000x fast can solve the problem in 2 days… but:

•

n = 21 would take 1 month;

•

n = 22 would take 2 years!

•

The complexity growth of an algorithm is way more important

than a faster hardware!

Efficiency of an Algorithm

•

How can we predict how much time an algorithm will

take to solve a problem?

How can we compare two different algorithms?

Random Access Machine (RAM)

•

We need a model that is generic and independent of the

machine/language.

Random Access Machine (RAM)

–

Every simple operation (+, -, / , *) takes one time step;

All memory access takes exactly one time step;

Execution time: number of steps performed in a given input size (T(n)).

•

Simplified model (adding to integer numbers does not take

the same amount of time as dividing two float numbers, but

we will see that these differences do not affect the overall

estimation)

Example: Number of Operations

•

A simple program:

int count = 0;

int i;

for (i=0; i<n; i++)

if (v[i] == 0)

count++;

•

Number of basic operations:

Variable declarations

Sums

2

Comparisons “less than”

Comparisons “equal”

Array accesses

n + 1

n

Increments

Between n and 2n (depending o the number of zeros)

Example: Number of Operations

•

A simple program:

int count = 0;

int i;

for (i=0; i<n; i++)

if (v[i] == 0)

count++;

•

Total operations in the worst case:

T(n) = 2 + 2 + (n + 1) + n + n + 2n = 5 + 5n

•

Total operations in the best case:

T(n) = 2 + 2 + (n + 1) + n + n + n = 5 + 4n

Types of Algorithm Analysis

•

Worst Case Analysis:

–

T(n) = maximum time that an algorithm takes for any input

of size n.

Average Case Analysis:

–

T(n) = average time that an algorithm takes for all inputs of

size n.

•

Knowledge about the statistic distribution of the inputs is

necessary.

•

Best Case Analysis:

–

T(n) = naïve evaluation of the easiest inputs to be solved

by an algorithm.

Types of Algorithm Analysis

Asymptotic Analysis

•

To analyze algorithms, we need a mathematical method to

compare functions.

For algorithm analyzes, we use the Asymptotic Analysis

–

Study of the behavior of algorithms for arbitrarily large inputs

(complexity growth rate).

•

A specific notation is used: O, ꢀ, ꢁ (big O, omega, theta)

Allows us to "simplify" expressions focusing only on the

magnitude order.

Asymptotic Analysis – Notation

•

f(n) = O(g(n))

–

Means that C × g(n) describes the upper bound for f(n)

f(n) = ꢂ(g(n))

–

Means that C × g(n) describes the lower bound for f(n)

f(n) = ꢃ(g(n))

–

Means that C1 × g(n) describes the upper bound for f(n)

and C2 × g(n) describes the lower bound for f(n)

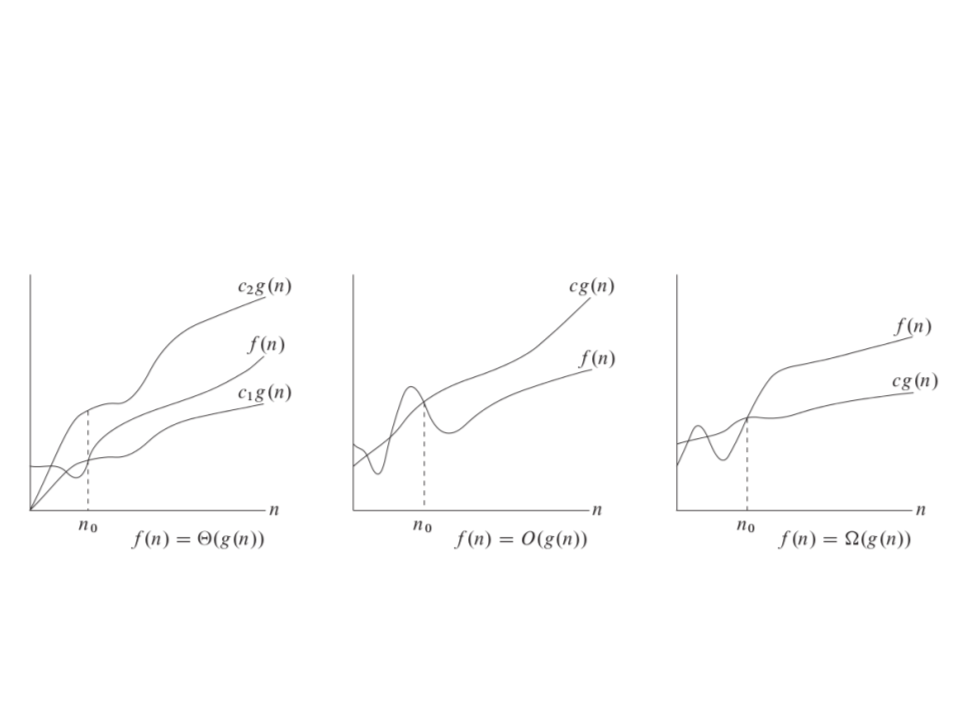
Asymptotic Analysis – Notation

ꢃ

O

ꢂ

Asymptotic Analysis – Formalization

•

f(n) = O(g(n)) if there are positive constants n₀ and c

such that f(n) ≤ c × g(n) for every n ≥ n₀

f(n) = 3n² - 100n + 6

2

–

f(n) = O(n )

f(n) = O(n³)

f(n) ≠ O(n)

Asymptotic Analysis – Formalization

•

f(n) = ꢂ(g(n)) if there are positive constants n₀ and c

such that f(n) ≥ c × g(n) for every n ≥ n₀

f(n) = 3n² - 100n + 6

2

–

f(n) = Ω(n )

f(n) ≠ Ω(n³)

f(n) = Ω(n)

Asymptotic Analysis – Formalization

•

f(n) = ꢃ(g(n)) if there are positive constants n₀, c₁and

c₂such that c₁ × g(n) ≤ f(n) ≤ c₂ × g(n) for every n ≥

n₀

f(n) = 3n² - 100n + 6

2

–

f(n) = Θ(n )

f(n) ≠ Θ(n³)

f(n) ≠ Θ(n)

•

f(n) = Θ(g(n)) means that f(n) = O(g(n)) and f (n) = Ω(g(n))

Asymptotic Analysis

•

The asymptotic analysis allows us to ignore constants and

terms that are not dominant.

For example, considering the function: f(n) = 3n² + 10n + 50

Asymptotic Analysis – Practical Rules

•

Multiplication by a constant does not change behavior of the

function:

–

Θ(c × f (n)) = Θ(f(n))

2 2

99 × n = Θ(n )

x

x-1

2

In a polynomial a n + a n + ... + a n + a₁n + a₀, we can focus on

x

x-1

the element with the highest exponent:

3 2 3

3n - 5n + 100 = Θ(n )

4 2 4

6n - 20 = Θ(n )

0.8n + 224 = Θ(n)

–

•

In an addition/subtraction, we can focus on the dominant element:

n

3

n

–

2 + 6n = Θ(2 )

2

n! - 3n = Θ(n!)

n log n + 3n = Θ(n²)

2

Asymptotic Analysis – Quick Exercise

•

T(n) = 32n² + 17n + 32

T(n) is:

2

–

O(n )? Yes

3

O(n )? Yes

Ω(n)? Yes

2

Ω(n )? Yes

O(n)? No

2

Θ(n )? Yes

3

Ω(n )? No

Θ(n)? No

4

Θ(n )? No

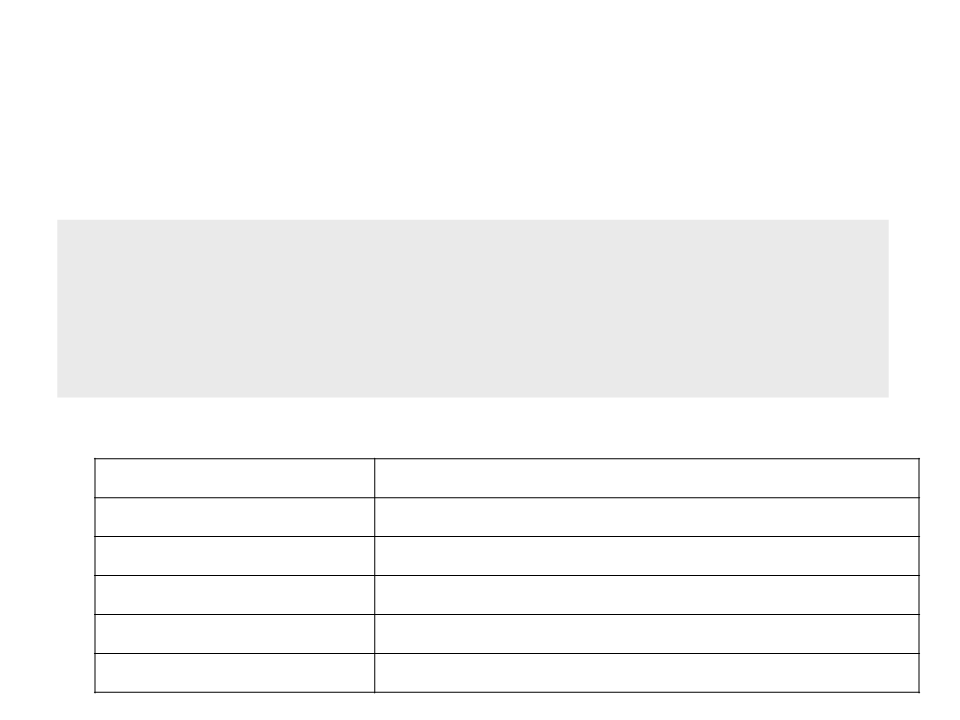
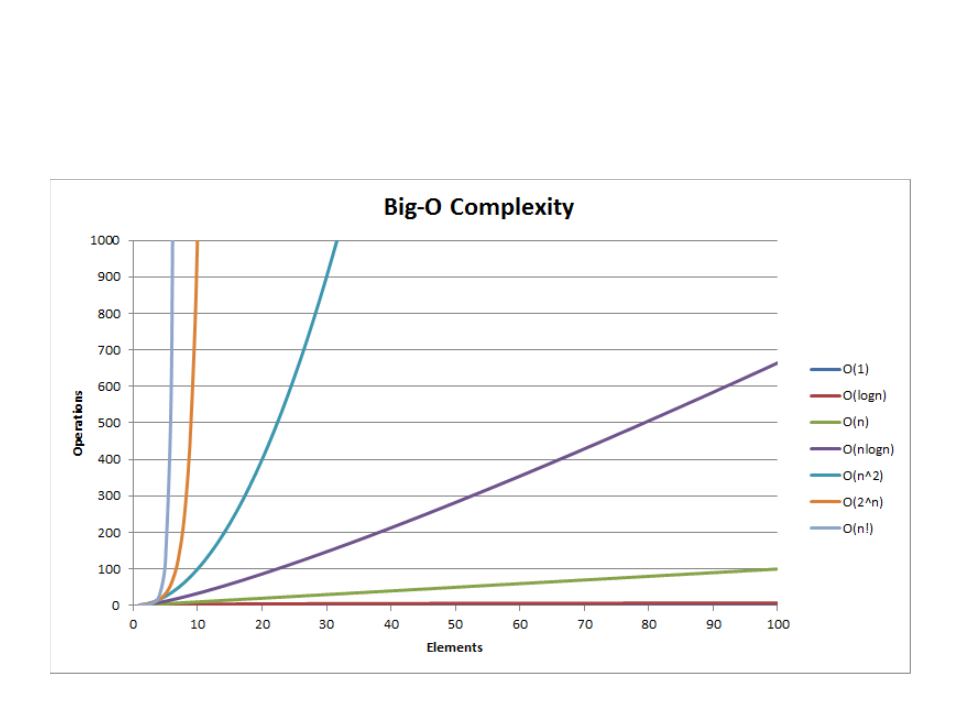
Asymptotic Complexity Growth

Function Name

Examples

1

log n

n

constant

logarithmic

linear

Add two numbers

Binary search, insert a value in a heap structure

Search a value in an array (one loop)

Sorting (merge sort, quick sort)

Sorting (bubble sort, selection sort) (two loops)

Floyd-Warshall (three loops)

n log n linearithymic

n²

n³

2ⁿ

n!

quadratic

cubic

exponential

factorial

Exhaustive search in subsets

Generate all permutations of a set

Asymptotic Complexity Growth

Asymptotic Analysis – Practical Examples

•

A program has two pieces of code A and B, executed one after the other,

2

with A running in O(n log n) and B in O(n ). What is the complexity of the

program?

2

O(n ) because n² > n log n

–

•

A program calls an O(log n) function n times, and then calls another O(log

n) function again n times. What is the complexity of the program?

–

O(n log n)

A program has 5 loops, called sequentially, each with complexity O(n).

What is the complexity of the program?

–

O(n)

A program P has a running time proportional to 100 × n log n. Another

1

2

program P is 2 × n . What is the most efficient program?

1

2

–

P is more efficient because n > n log n.

However, for a small n, P is faster and it might make sense to have a program

2

that calls P or P according to the value of n.

1

2

Quick Exercise 1

1

) Write an algorithm to check whether an array contains at

least two duplicate values (anywhere in the array). Then

analyze the complexity of the proposed algorithm.

bool hasDuplicate(int[] a){

int i, j;

for (i = 0; i < a.Length; i++){

for (j = 0; j < a.Length; j++){

if (i != j && a[i] == a[j]){

return true;

}

return false;

O(n²)

}

Quick Exercise 2

) What is the complexity of the following algorithm?

2

int i, j, k, x, result = 0;

for (i = 0; i < N; i++){

for (j = i; j < N; j++){

for (k = 0; k < M; k++){

x = 0;

while (x < N){

m

result++;

x += 3;

n

n²

}

for (k = 0; k < 2 * M; k++)

if (k % 7 == 4)

m

result++;

}

O(n²mn) = O(mn³)

}

Quick Exercise 3

3

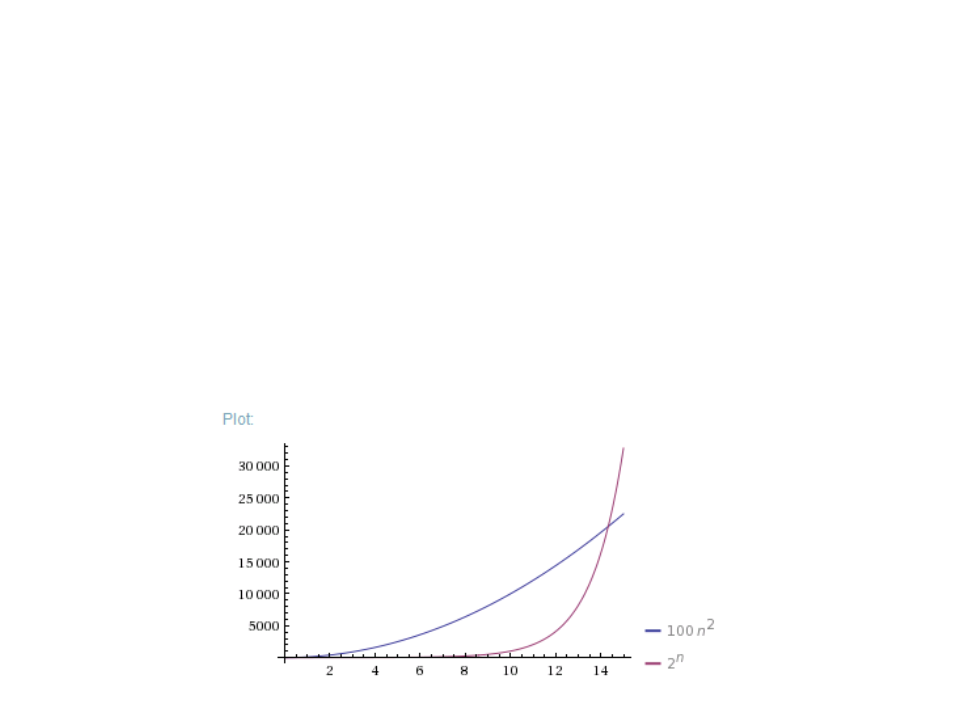
) What is the smallest value of n such that an algorithm whose

2

execution time is 100n works faster than an algorithm whose

n

execution time is 2 on the same machine?

Wolfram Alpha:

plot 100*n^2, 2^n from n=0 to 15

Assignment – Algorithms

Assignment List 01 – Algorithm Analysis

https://edirlei.com/aulas/data-structures/DS_Assignment_List_01.pdf