Compiladores - Sintaxe e Semântica

Compiladores

Aula 02 – Sintaxe e Semântica

Edirlei Soares de Lima

<edirlei.lima@universidadeeuropeia.pt>

Sintaxe e Semântica

•

A descrição de uma linguagem de programação envolve dois

aspectos principais:

–

Sintaxe: descreve a forma ou estrutura de expressões, comandos e

unidades de programa. É composto por um conjunto de regras que

determinam quais construções são corretas.

–

Semântica: descreve o significado das expressões, comandos e

unidades de programa. Define como as construções da linguagem

devem ser interpretadas e executadas.

•

Exemplo – IF na linguagem C:

–

Sintaxe: if (<expressão>) <instrução>

–

Semântica: se o valor atual da expressão for verdadeiro, a instrução

incorporada será selecionada para execução.

Sintaxe e Semântica – Exemplo

•

Analise o seguinte código em linguagem C e verifique se

existem erros:

int j=0, conta, V[10];

float i@;

conta = '0'

for (j=0, j<10; j++

{

V[j] = conta++;

}

•

O compilador tem a responsabilidade de reportar erros! É

necessário algum recurso para identificá-los.

Sintaxe e Semântica – Exemplo

•

Esses erros são verificados e diferenciados durante as fases de

análise da compilação:

•

Análise Léxica: reúne as unidades léxicas (tokens) do programa:

–

int, j, =, 0, conta, for, (, <, int, ++...

–

Erro: i@

•

Análise Sintática: realiza a combinação de tokens que formam o programa:

–

comando_for → for (expr1; expr2; expr3) {comandos}

Erros: ; for(j=0, ... )

–

Análise Semântica: verifica a adequação do uso:

–

Tipos semelhantes em comandos (atribuição, por exemplo), uso de

identificadores declarados...

–

Erro: conta = '0'

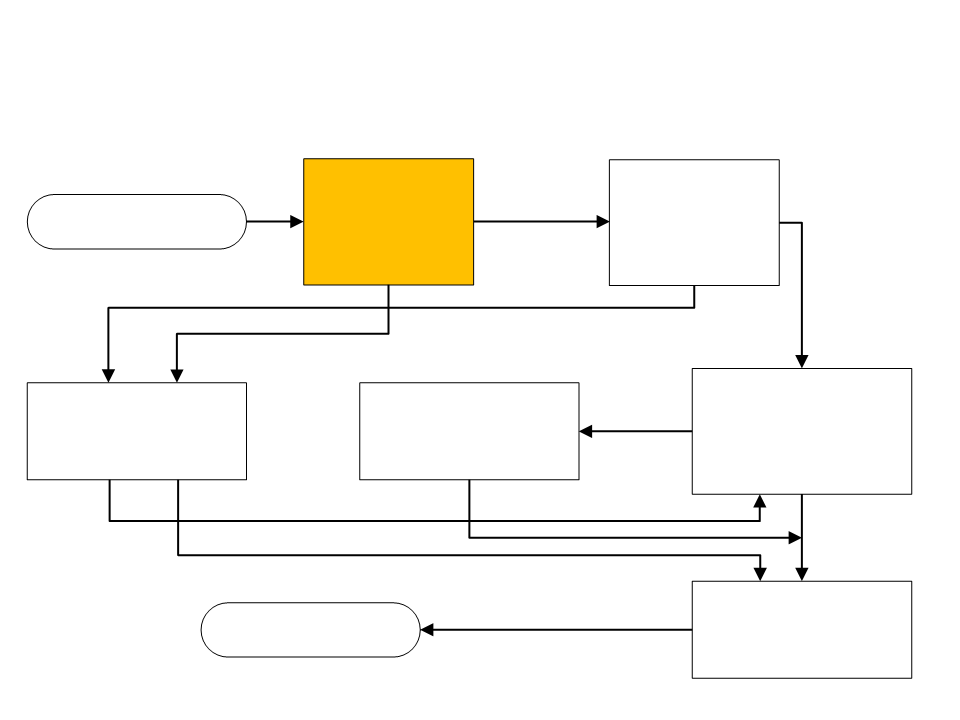
Processo de Compilação

unidades léxicas

Analisador

Léxico

Analisador

Sintático

Programa-fonte

árvores sintáticas

(opcional)

Gerador de Código

Intermediário e

Analisador

Tabela de Símbolos

Otimização

Semântico

código

intermediário

linguagem de máquina

Programa Objeto

Gerador de Código

Análise Léxica

•

A análise léxica é responsável por ler o código fonte e separá-

lo em partes significativas, denominadas tokens, instanciadas

por átomos.

Análise Léxica

•

A análise léxica pode ser feita através de autômatos finitos ou

expressões regulares.

–

Um autômato finito é uma máquina de estados finitos formada por

um conjunto de estados (um estado inicial e um ou mais estados

finais);

Simulador: JFLAP (http://www.jflap.org/jflaptmp/)

–

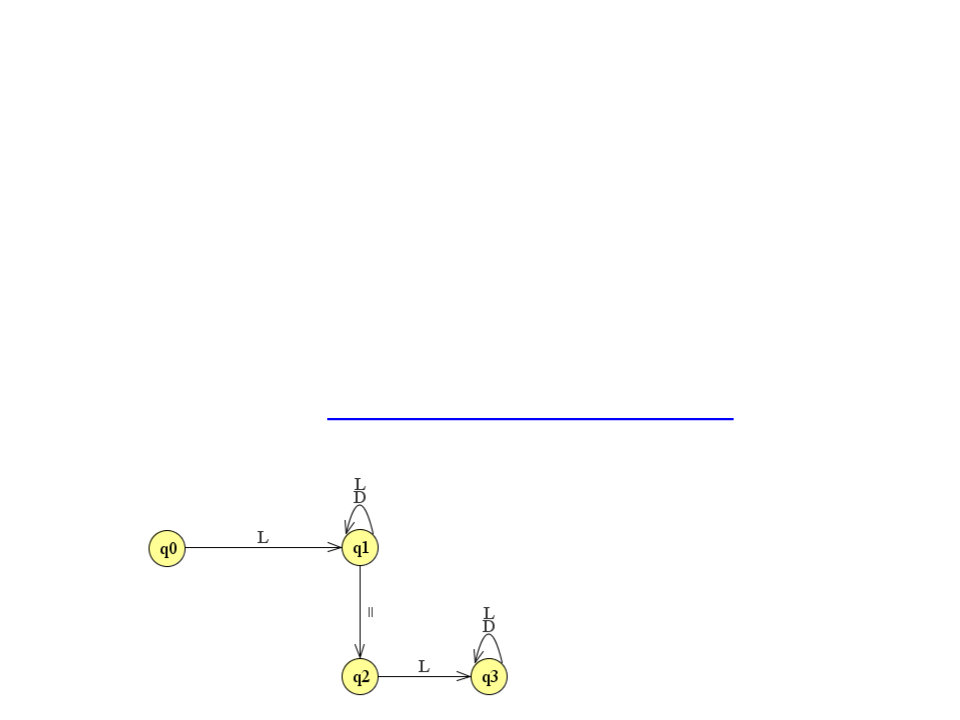
Exemplo de autômato para reconhecer atribuições entre variáveis:

L → a..z

D → 0..9

=

→ atribuição

Exercício 01

1

) Utilize o simulador JFLAP para construir e testar autômatos

finitos para os seguintes casos:

a) Cadeia de caracteres a, b, c.

b) Números inteiros (com ou sem sinal).

c) Números reais (com ou sem sinais).

d) Identificador.

e) Comparação (>, >=, <, <=, !=) entre dois identificadores.

f) Atribuição (=) entre dois identificadores.

g) Cadeias de caracteres entre aspas (exemplo: “teste”).

h) Expressões booleanas unidas pelos operadores lógicos && e ||

(exemplo: test > 8 && test < 2).

Análise Léxica

•

Classes de átomos mais comuns:

–

identificadores;

palavras reservadas;

números inteiros sem sinal;

números reais;

cadeias de caracteres;

sinais de pontuação e de operação;

caracteres especiais;

símbolos compostos de dois ou mais caracteres especiais;

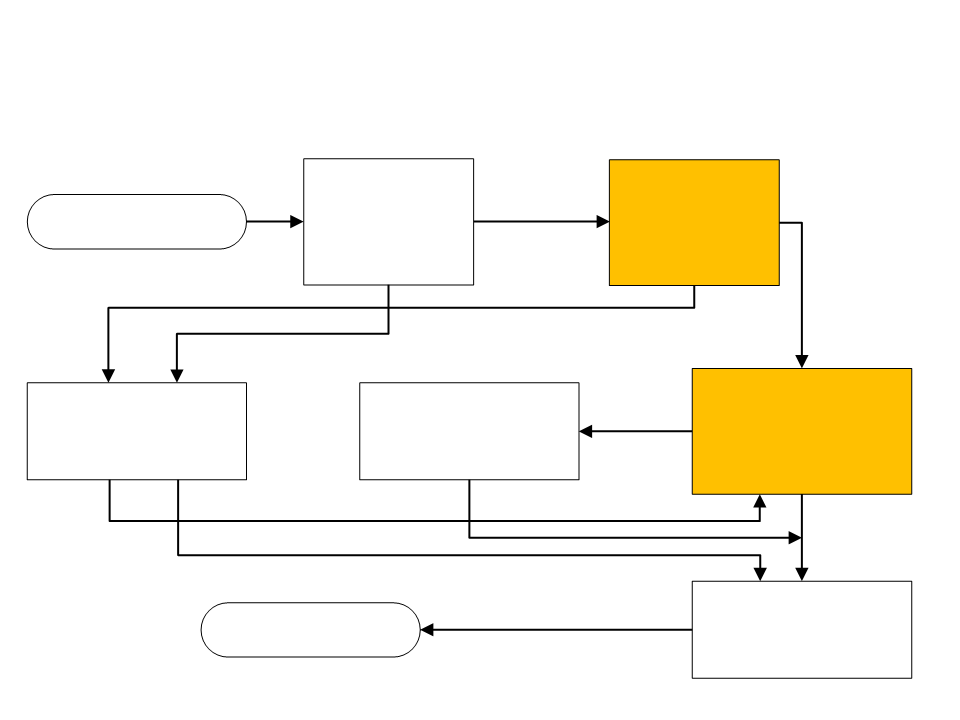
Processo de Compilação

unidades léxicas

Analisador

Léxico

Analisador

Sintático

Programa-fonte

árvores sintáticas

(opcional)

Gerador de Código

Intermediário e

Analisador

Tabela de Símbolos

Otimização

Semântico

código

intermediário

linguagem de máquina

Programa Objeto

Gerador de Código

Análise Sintática e Semântica

•

A análise sintática realiza verificação da formação do

programa.

–

Gramáticas livres de contexto;

<atribuição> → <var> = <expressão>

total = sub1 + sub2

A análise semântica realiza a verificação do uso adequado da

gramática.

–

Por exemplo, verificando se os identificadores estão sendo usados de

acordo com o tipo declarado;

Descrevendo a Sintaxe

•

Linguagens, sejam naturais ou artificiais, são conjuntos de

sequências de caracteres de algum alfabeto, onde:

–

Uma sentença é uma sequência de caracteres sobre um alfabeto;

Uma linguagem é um conjunto de sentenças;

Um lexema é a unidade sintática de menor nível em uma linguagem

(exemplo: *, sum, begin);

–

Um token é uma categoria de lexemas (exemplo: identificador,

números, caracteres, etc.);

•

Um programa pode ser visto como sendo uma sequência de

lexemas.

Descrevendo a Sintaxe

•

Exemplo:

index = 2 * count + 17;

Lexemas

Tokens

index

identificador

sinal_atribuicao

int_literal

=

2

*

mult_op

cont

+

identificador

soma_op

1

;

7

int_literal

ponto_e_virgula

Descrevendo a Sintaxe

•

As linguagens podem ser formalmente definidas de duas

maneiras:

Reconhecedores:

–

Um dispositivo de reconhecimento lê uma cadeia de entrada de uma

linguagem e decide se esta pertence ou não a linguagem;

–

Exemplo: Analisador sintático de um compilador.

•

Geradores:

–

Dispositivo que gera uma sentença da linguagem sempre que

acionado;

–

Pode-se determinar se a sintaxe de uma determinada sequência esta

correta comparando-a a estrutura de um gerador.

Métodos Formais para Descrever Sintaxe

•

Sintaxe → definida formalmente através de uma gramática.

•

Gramática → conjunto de definições que especificam uma

sequência válida de caracteres.

Duas classes de gramáticas são úteis na definição formal das

gramáticas:

–

Gramáticas livres de contexto;

–

Gramáticas regulares.

Métodos Formais para Descrever Sintaxe

•

Forma de Backus-Naur (1959) – BNF

–

Inventada por John Backus para descrever o Algol 58; modificada por

Peter Naur para descrever o Algol 60. É considerada uma gramática

livre de contexto.

•

A BNF é a forma mais popular de se descrever concisamente a

sintaxe de uma linguagem.

Embora simples é capaz de descrever a grande maioria das

sintaxes das linguagens de programação.

Forma de Backus-Naur (BNF)

•

Na BNF, abstrações são usadas para representar classes de

estruturas sintáticas.

<atribuição> → <var> = <expressão>

(

LHS)

(RHS)

Uma abstração é definida através de uma regra ou produção.

Esta é formada por:

–

Lado esquerdo (LHS) – abstração a ser definida (símbolo não-

terminal).

–

Lado direito (RHS) – definição da abstração, composta por símbolos,

lexemas e referências a outras abstrações.

•

Símbolos e lexemas são denominados símbolos terminais.

Forma de Backus-Naur (BNF)

•

< > indica um não-terminal (termo que precisa ser expandido);

Símbolos não cercados por < > são terminais;

–

Eles são representativos por si. Exemplo: if, while, (, =

•

O símbolo → significa é definido como;

Os símbolos cercados por {} indica que o termo pode ser

repetido n vezes (inclusive nenhuma);

•

O símbolo | significa or e é usado para separar alternativas.

Forma de Backus-Naur (BNF)

•

Uma descrição BNF ou Gramática de uma linguagem é

definida por um conjunto de regras.

Símbolos não-terminais podem ter mais de uma definição

distinta, representando duas ou mais formas sintáticas

possíveis na linguagem.

–

Regras diferentes:

<inst_if> → if ( <expr_logica> ) <inst>

<inst_if> → if ( <expr_logica> ) <inst> else <inst>

–

Mesa regra:

<inst_if> → if ( <expr_logica>) <inst>

|

if ( <expr_logica>) <inst> else <inst>

Forma de Backus-Naur (BNF)

Uma regra é recursiva se o LHS aparecer no RHS.

Exemplo – definição de listas de identificadores:

•

<ident_lista> → identificador

|

identificador, <ident_lista>

•

<ident_lista> é definido como um único símbolo ou um

símbolo seguido de virgula e de outra instancia de

<

ident_lista> .

Gramáticas e Derivações

•

A BNF é um dispositivo generativo para definir linguagens.

Sentenças da linguagem são geradas através de sequências de

aplicações das regras, iniciando-se pelo símbolo não terminal

da gramática chamado símbolo de início.

•

Uma geração de sentença é denominada derivação.

Gramáticas e Derivações

•

Exemplo de gramática de uma linguagem simples:

<

programa> → begin <lista_inst> end

lista_inst> → <inst> ; <lista_inst>

|

<inst> ;

<

inst> → <var> = <expressao>

var> → A | B | C

expressao> → <var> + <var>

|

|

<var>

Exemplo de Derivação

<

programa> → begin <lista_inst> end

lista_inst> → <inst> ; <lista_inst>

<inst> ;

Objetivo:

|

<

inst> → <var> = <expressao>

var> → A | B | C

expressao> → <var> + <var>

begin

A = B + C ;

B = C ;

end

|

<var>

<programa> => begin <lista_inst> end

=

> begin <inst> ; <lista_inst> end

> begin <var> = <expressão> ; <lista_inst> end

> begin A = <expressão> ; <lista_inst> end

> begin A = <var> + <var> ; <lista_inst> end

> begin A = B + <var> ; <lista_inst> end

> begin A = B + C ; <lista_inst> end

> begin A = B + C ; <inst> ; end

> begin A = B + C ; <var> = <expressão> ; end

> begin A = B + C ; B = <expressão> ; end

> begin A = B + C ; B = <var> ; end

> begin A = B + C ; B = C ; end

Gramáticas e Derivações

•

Cada uma das cadeias da derivação, inclusive <programa>, é

chamada de forma sentencial.

No exemplo anterior, o não-terminal substituído é sempre o

da extrema esquerda. Derivações que usam essa ordem são

chamadas de derivações à extrema esquerda (leftmost

derivations).

–

É possível realizar a derivação a extrema direita;

•

A derivação prossegue até que a forma sequencia não

contenha nenhum não-terminal.

Gramáticas e Derivações

Mais um exemplo de gramática:

•

<

atribuicao> → <id> = <expr>

id> → A | B | C

expr> → <id> + <expr>

|

( <expr> )

<id>

Derivando: A = B * ( A + C )

<

atribuicao> => <id> = <expr>

=

> A = <expr>

> A = <id> * <expr>

> A = B * <expr>

> A = B * ( <expr> )

> A = B * ( <id> + <expr> )

> A = B * ( A + <expr> )

> A = B * ( A + <id> )

> A = B * ( A + C )

Exercício 02

2

) Considere a seguinte gramática em notação BNF:

<

palavra> → <sílaba> <sílaba>

sílaba> → <vogal> <consoante> | <consoante> <vogal>

vogal> → a | e | i | o | u

consoante> → b | c | d | f | g | h | j | l | m | n | p

|

q | r | s | t | v | x | z

a) Indique os símbolos terminais e os símbolos não-terminais da

gramática.

b) Indique quais das expressões seguintes correspondem a palavras da

linguagem definida pela gramática. Justifique a sua resposta

apresentado a derivação da sentença.

•

lobo

cria

gato

•

leao

ovos

vaca

•

macaco

Exercício 03

3

) Considere a seguinte gramática em notação BNF:

<

operação> → (<argumento> <operador> <argumento>)

operador> → + | - | * | /

argumento> → <dígito>

dígito> → 2 | 4 | 6 | 8 | 0

a) Indique os símbolos terminais e os símbolos não-terminais da

gramática.

b) Indique quais das expressões seguintes pertencem à linguagem

definida pela gramática. Justifique a sua resposta apresentado a

derivação da sentença.

•

(1+2)

(2++)

(2*0)

•

(84+)

(0/0)

•

Exercício 04

4

) Escreva uma gramática em notação BNF para uma linguagem

que consiste em sequências de n cópias da letra “x” seguida

do mesmo número de cópias da letra “y”, onde n > 0.

–

Exemplos de sequências validas para a linguagem: xy, xxxyyy,

xxxxxyyyyy

Exemplos de sequências não-validas para a linguagem: x, yyy, xxy,

xxxyyyx, xxxyyyy

Exercício 05

5

) Escreva uma gramática em notação BNF para representar

programas no seguinte formato:

programa

inicio

x = 5 + 8;

y = 8 * x;

se (y >= 10)

inicio

x = y;

fim

–

Prove que a gramática é valida apresentando a derivação do programa

anterior.

Aplicando as Regras da Gramática

<

assignment> → <ID> = <expression> ;

<

expression> → <expression> + <term>

|

<term>

<

term> → <term> * <factor>

|

factor> → ( <expression> )

|

<ID>

<

ID> → x|y|z

NUMBER> → 0|1|2|3|4|5|6|7|8|9

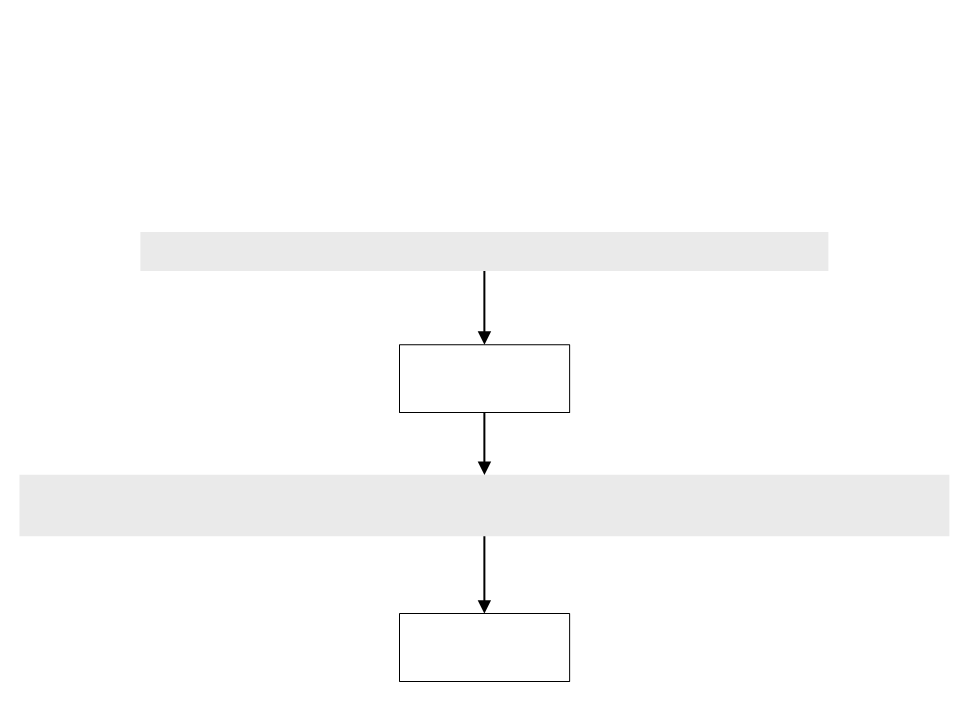
Aplicando as Regras da Gramática

•

Entrada:

z = (2*x + 5)*y - 7;

Analisador

Léxico

Tokens:

ID ASSIGNOP GROUP NUMBER OP ID OP NUMBER GROUP OP ID OP NUMBER DELIM

z

* - 7 ;

y

=

( 2

* x + 5

)

Analisador

Sintático

Aplicando as Regras da Gramática

ID = ( NUMBER * ID + NUMBER ) * ID - NUMBER ;

<assignment> → <ID> = <expression> ;

parser:ID

factor

factor =

expression> → <expression^r>^e^a+^d<⁽t^se^hrⁱm^f>^t⁾^fⁱ^r^s^t^t^o^k^eⁿ

<

reduce

shift

|

<term>

FAIL: Can't match any rules (reduce).

Backtrack and try again

<

term> → <term> * <factor>

ID = ( NUMBER

shift

reduce

sh/reduce

shift

|

ID = ( factor

ID = ( term *

ID = ( term * ID

<

factor> → ( <expression> )

ID = ( term * factor

reduce

shift

|

<ID>

ID = ( term

ID = ( term +

ID = ( expression + NUMBER

ID = ( expression + factor

reduce/sh

reduce

<

ID> → x|y|z

ID = ( expression + term

reduce

<

NUMBER> → 0|1|2|3|4|5|6|7|8|9

Aplicando as Regras da Gramática

ID = ( NUMBER * ID + NUMBER ) * ID - NUMBER ;

parser:ID

factor

factor =

read (shift) first token

reduce

shift

FAIL: Can't match any rules (reduce).

Backtrack and try again

ID = ( NUMBER

shift

reduce

ID = ( factor

ID = ( term *

ID = ( term * ID

sh/reduce

shift

ID = ( term * factor

ID = ( term

reduce

ID = ( term +

shift

ID = ( expression + NUMBER

ID = ( expression + factor

ID = ( expression + term

reduce/sh

reduce

Aplicando as Regras da Gramática

ID = ( NUMBER * ID + NUMBER ) * ID - NUMBER ;

<

assignment> → <ID> = <expression> ;

ID = ( expression

ID = ( expression )

reduce

shift

reduce

shift

reduce/sh

reduce

shift

<

expression> → <expression> + <term>

|

<term>

ID = factor

ID = factor *

ID = term * ID

<

term> → <term> * <factor>

ID = term * factor

|

ID = term

ID = term^<^f-^a^c^t^o^r^>

|

ID = expression -

reduce

shift

reduce

shift

<

factor> → ( <expression> )

|

ID = expression - NUMBER

<ID>

ID = expression - factor

|

ID = expression - term

ID = expression ;

<

ID> → x|y|z

assignment

reduce

<

NUMBER> → 0|1|2|3|4|5|6|7|8|9

Aplicando as Regras da Gramática

ID = ( NUMBER * ID + NUMBER ) * ID - NUMBER ;

ID = ( expression

ID = ( expression )

ID = factor

reduce

shift

reduce

shift

ID = factor *

ID = term * ID

ID = term * factor

ID = term

reduce/sh

reduce

shift

ID = term -

ID = expression -

ID = expression - NUMBER

ID = expression - factor

ID = expression - term

ID = expression ;

assignment

reduce

shift

reduce

shift

reduce

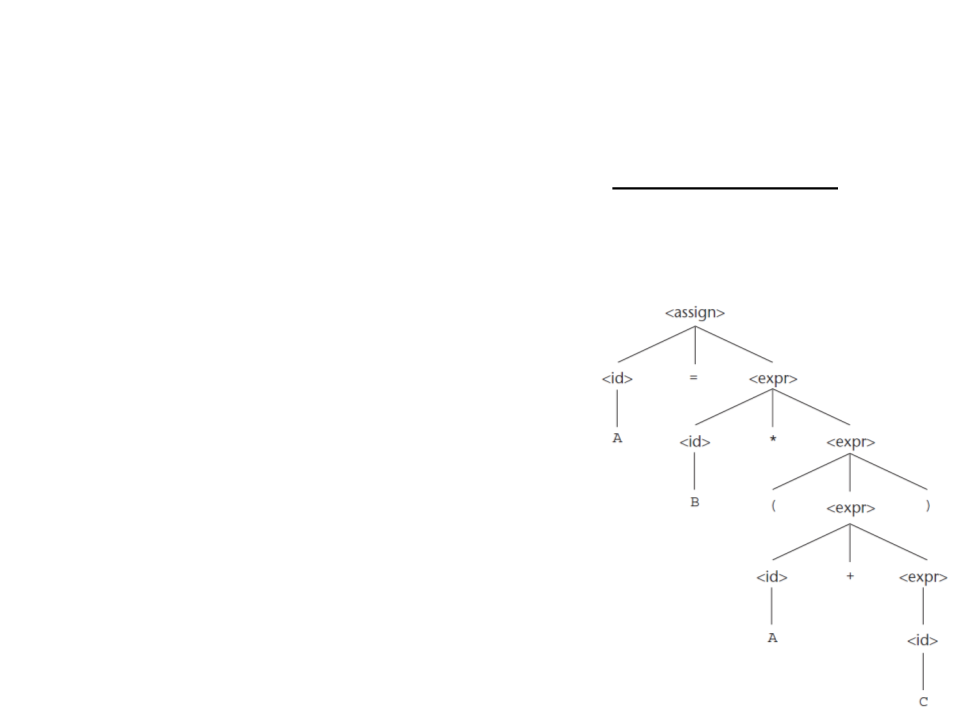
Árvores Sintáticas

•

As gramaticas descrevem naturalmente árvores sintáticas.

Uma árvore sintática é representação em forma de árvore da

derivação, onde:

•

Todo nó interno da árvore é um símbolo

não-terminal;

Toda folha é rotulada com um símbolo

terminal;

Toda sub-árvore descreve uma instância

de uma abstração na sentença.

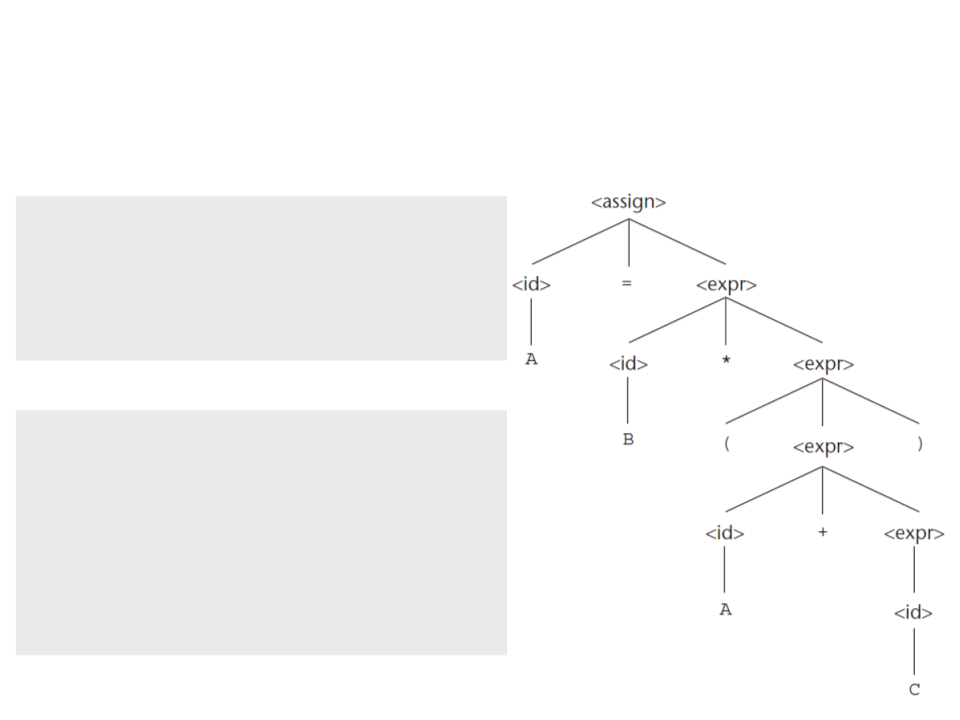
Árvores Sintáticas – Exemplo

<

assign> → <id> = <expr>

id> → A | B | C

expr> → <id> + <expr>

|

( <expr> )

<id>

=

> A = <expr>

> A = <id> * <expr>

> A = B * <expr>

> A = B * ( <expr> )

> A = B * ( <id> + <expr> )

> A = B * ( A + <expr> )

> A = B * ( A + <id> )

> A = B * ( A + C )

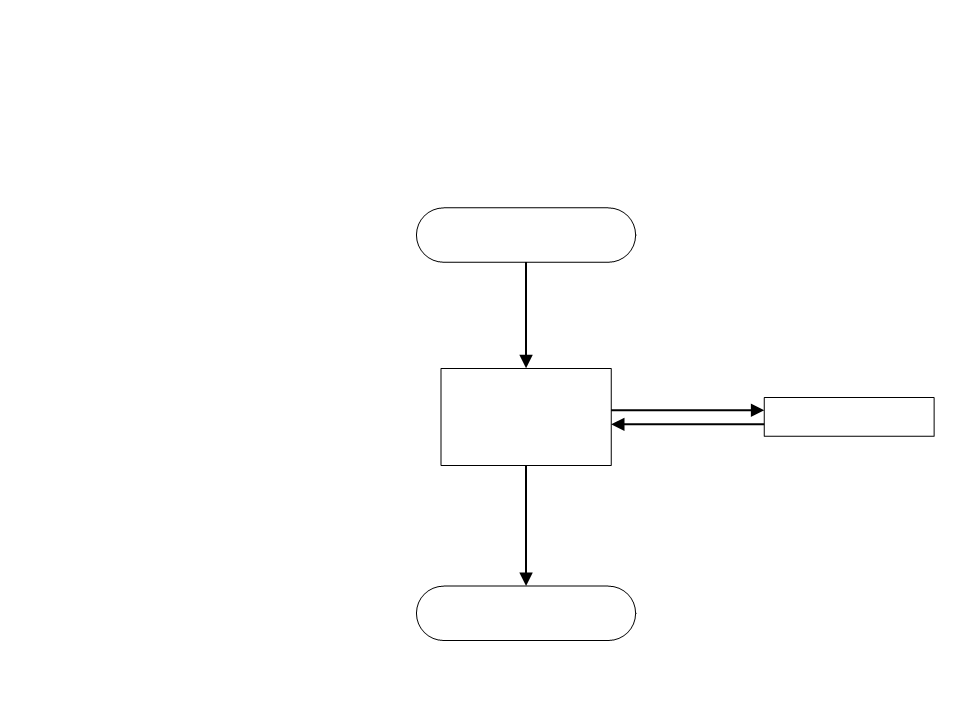
Árvores Sintáticas – Processo de

Compilação

•

Para utilizar uma árvore

Programa-fonte

sintática para gerar código de

máquina, o compilador

explora a árvore e gera

código conforme ele

reconhece sentenças.

Backwards

derivation

Compilador

Parse Tree

Busca em profundidade.

Traverse the

parse tree

to build

Programa Objeto

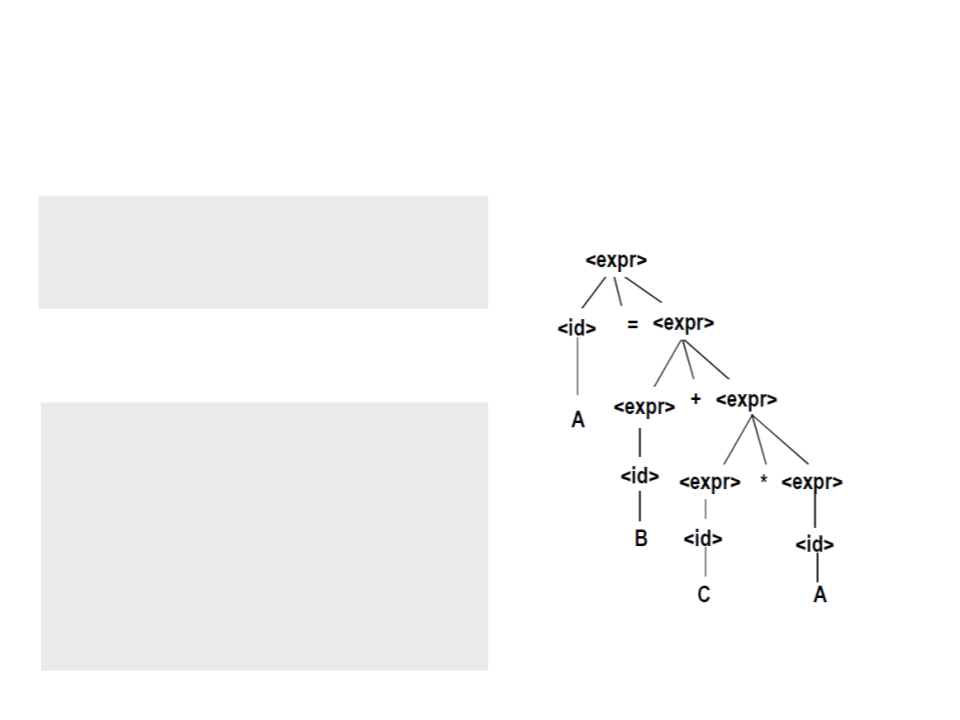
Árvores Sintáticas – Exemplo

|

A | B | C

<op> → * | +

A = B + C * A

=

> A = <expr>

> A = <expr> + <expr>

> A = <id> + <expr>

> A = B + <expr>

> A = B + <expr> * <expr>

> A = B + <id> * <expr>

> A = B + C * <expr>

> A = B + C * <id>

> A = B + C * A

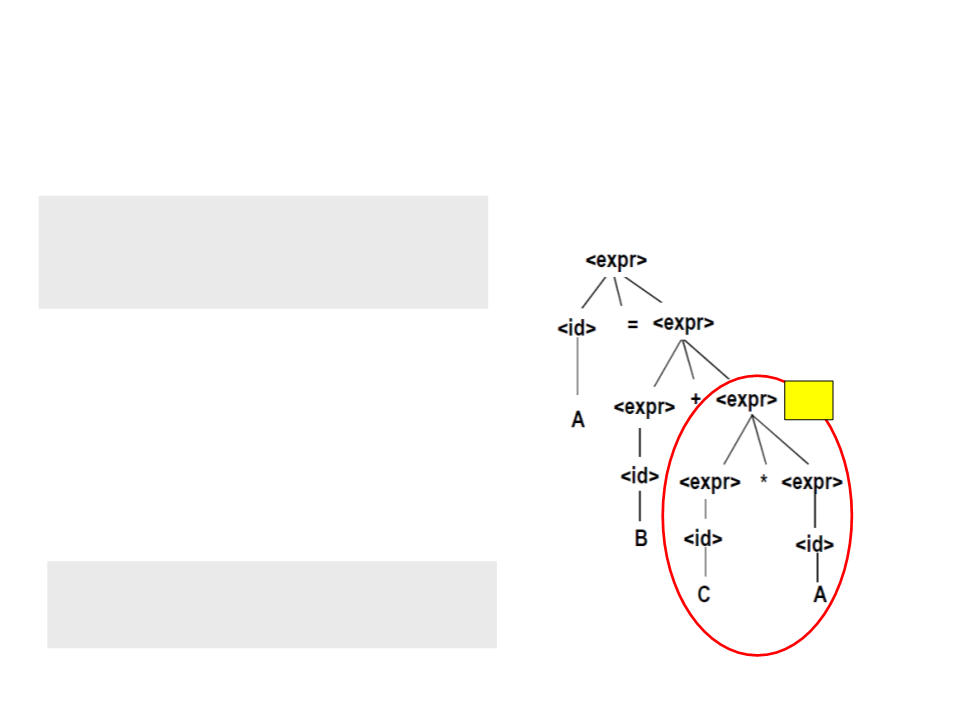
Árvores Sintáticas – Exemplo

|

A | B | C

<op> → * | +

•

A primeira expressão completamente

conhecida é "C * A";

T1

•

O compilador gera código para T1 = C * A,

substituindo <expr> por T1;

Código Gerado:

T1 = C * A;

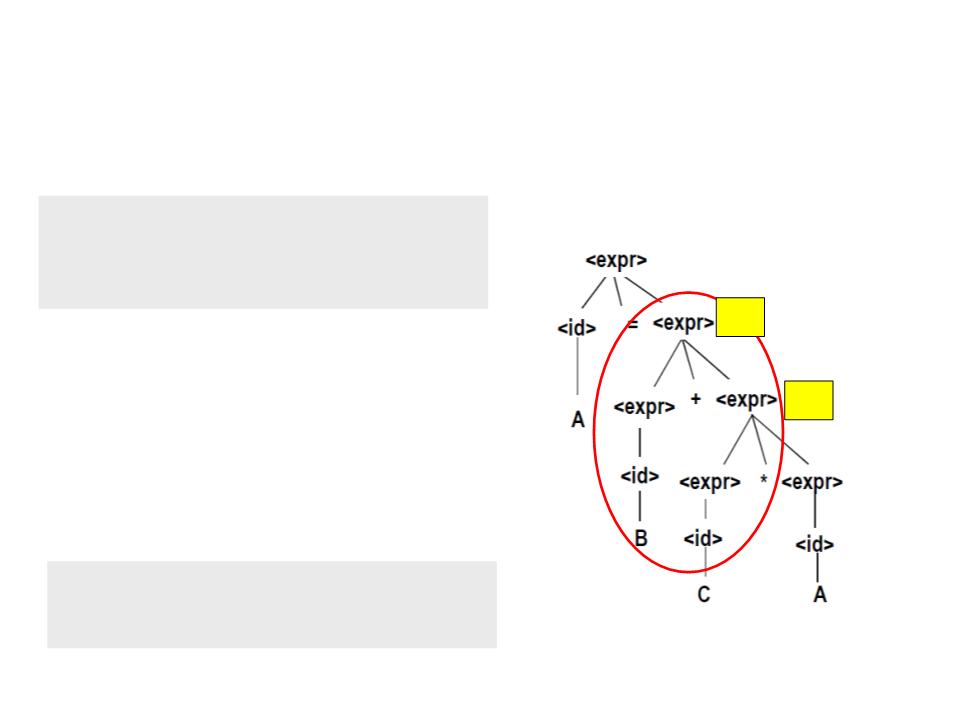
Árvores Sintáticas – Exemplo

|

A | B | C

<op> → * | +

T2

•

A expressão seguinte completamente

conhecida é "B + <expr>" onde <expr> é

igual a T1.

T1

Código Gerado:

T1 = C * A;

T2 = B + T1;

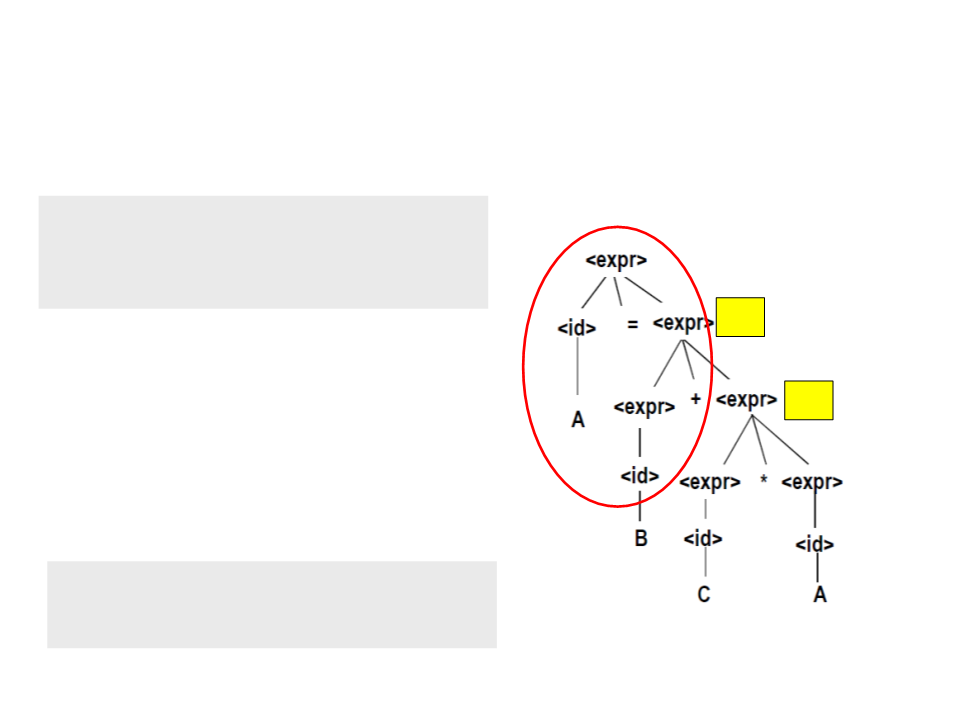
Árvores Sintáticas – Exemplo

|

A | B | C

<op> → * | +

T2

•

A última expressão completamente

conhecida é "A = <expr>" onde <expr> é T2.

T1

Código Gerado:

T1 = C * A;

T2 = B + T1;

A = T2;

Árvores Sintáticas

•

Após a análise, os detalhes de derivação não são necessários

para fases subsequentes do processo de compilação.

O Analisador Semântico remove as produções intermediárias

para criar uma árvore sintática abstrata (abstract syntax tree).

expr

term

Parse Tree:

Abstract Syntax Tree:

X

factor

X

Regras Gramaticais

•

É possível derivar significado (semântica) da árvore

de análise:

–

Operadores são avaliados quando uma sentença é

reconhecida;

As partes mais baixas da parse tree são completadas

primeiro;

Assim um operador gerado mais baixo em uma parse tree

é avaliado primeiro;

Em outras palavras, um operado gerado mais baixo na

parse tree tem precedência sobre um operador produzido

acima deste.

Exercício 06

6

) Considere a seguinte gramática em notação BNF:

<

assign> → <id> = <expr>

id> → A | B | C

expr> → <id> + <expr>

|

( <expr> )

<id>

–

Apresente uma derivação à extrema esquerda e construa a árvore de

análise para cada uma das seguintes sentenças:

a) A = A * (B + (C * A))

b) B = C * (A * C + B)

c)

A = A * (B + (C))

Precedência de Operadores

A ordem de produção afeta a ordem de computação.

Considerando a seguinte gramatica:

•

<

assignment> → <id> = <expression> ;

expression> → <id> + <expression>

|

<id>

<id> → A | B | C | D

<number> → 0|1|2|3|4|5|6|7|8|9

•

Qual o resultado da expressão: A = B + C * D?

Precedência de Operadores

•

A = B + C * D

<

assignment> → <id> = <expression>

expression> → <id> + <expression>

|

<id>

A = B + (C * D)

<id> → A | B | C | D

<

number> → 0|1|2|3|4|5|6|7|8|9

Recursão à direita

produz árvores

sintáticas associativas

á direita.

=

> A = <expression>

> A = <id> + <expression>

> A = B + <id> * <expression>

> A = B + C * <expression>

> A = B + C * <id>

> A = B + C * D

Precedência de Operadores

A = B + C * D

•

<

assignment> → <id> = <expression>

expression> → <expression> + <id>

|

<id>

<id> → A | B | C | D

A = (B + C) * D

<number> → 0|1|2|3|4|5|6|7|8|9

Recursão à esquerda

produz árvores

sintáticas associativas

á esquerda.

<

assignment> => <id> = <expression>

=

> A = <expression>

> A = <expression> * <id>

> A = <expression> + <id> * <id>

> A = <id> + <id> * <id>

> A = B + <id> * <id>

> A = B + C * <id>

> A = B + C * D

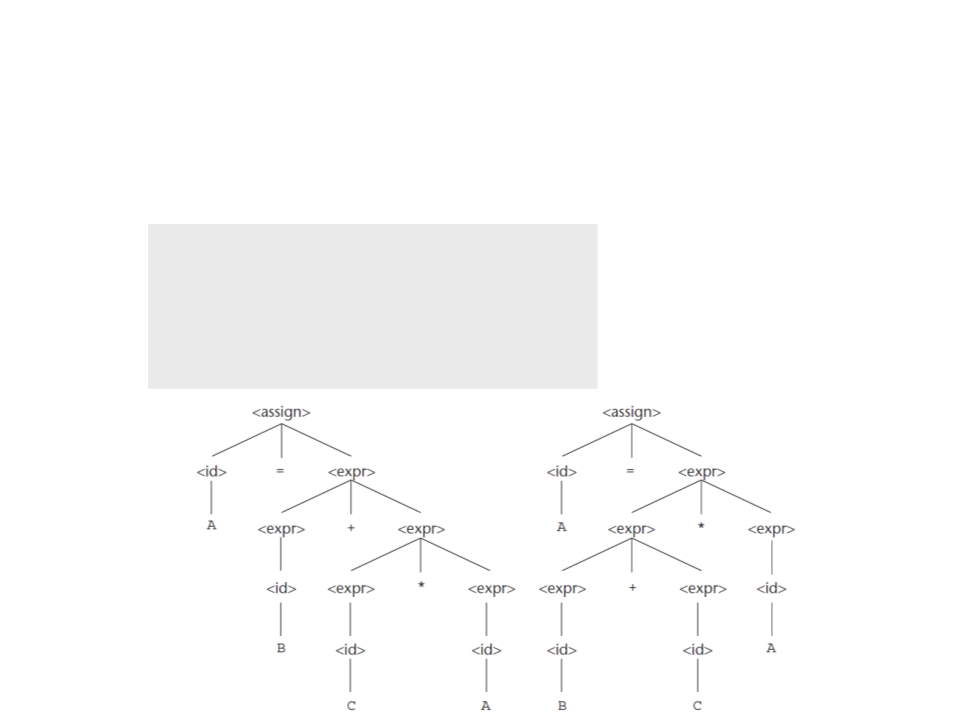
Gramaticas Ambíguas

•

Algumas gramáticas podem gerar árvores sintáticas diferentes.

<

assign> → <id> = <expr>

id> → A | B | C

expr> → <expr> + <expr>

A = B + C * A

|

( <expr> )

<id>

Gramaticas Ambíguas

•

Uma gramática é ambígua se ela gera formas sentenciais que

possuem duas ou mais árvores sintáticas distintas.

A ambiguidade ocorre porque a gramática especifica muito

pouco da estrutura sintática, permitindo que que a árvores

sintáticas cresça tanto para a direita como para esquerda.

•

Porque isso importa?

–

Compiladores geralmente baseiam a semântica das sentenças na sua

forma sintática.

•

O compilador decide qual código de máquina gerar examinando a árvore sintática;

•

Se uma sentença tem mais de uma árvore sintática, o significado da sentença não é

único!

Gramaticas Ambíguas

•

Soluções para gramáticas ambíguas:

–

Reescrever a gramática;

–

O algoritmo de análise pode utilizar informações não

gramaticais fornecidas pelo projetista para criar a árvore

correta:

•

Projetista provê uma tabela de precedência e associatividade dos

operadores;

•

Projetista pode impor regras de como a gramática deve ser usada.

“

utilizada em uma derivação”.

Sempre escolha a primeira regra quando mais de uma poder ser

Gramaticas Ambíguas

•

Soluções para gramáticas ambíguas – Exemplo:

<

assign> → <id> = <expr>

id> → A | B | C

expr> → <expr> + <expr>

|

( <expr> )

<id>

<

assign> → <id> = <expr>

id> → A | B | C

expr> → <expr> + <term>

|

<term>

term> → <term> * <factor>

factor> → ( <expr> )

<id>

<

|

Grafos de Sintaxe

•

As regras de uma BNF podem ser representadas

através de grafos de sintaxe (diagrama de sintaxe):

–

Grafo direcionado;

Um grafo é gerada para cada regra;

Símbolos não-terminais são representados através de

vértices retangulares;

–

Símbolos terminais são representados através de símbolos

elípticos.

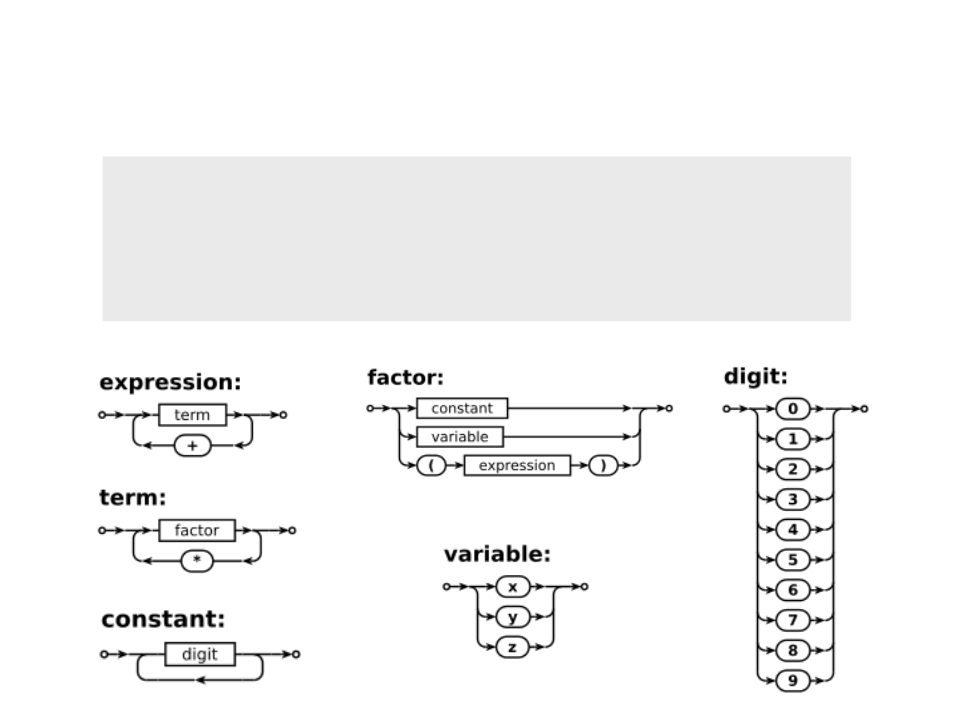
Grafos de Sintaxe

<

expression> → <term> | <term> + <expression>

term> → <factor> | <term> * <factor>

factor> → <constant> | <variable> | ( <expression> )

variable> → x | y | z

constant> → <digit> | <digit> <constant>

digit> → 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9

Limitações da BNF

•

Não é fácil impor limite de tamanho.

–

Exemplo: o tamanho máximo para nome de variável.

Não há como impor restrição de distribuição no código fonte.

–

Exemplo, uma variável deve ser declarada antes de ser usada.

•

Descreve apenas a sintaxe, não descreve a semântica.

EBNF (Extend BNF): não aumenta o poder descritivo, mas sim

sua legibilidade e capacidade de escrita.

Gramáticas e Reconhecedores

•

Há uma estreita ligação entre dispositivos de geração e de

reconhecimento.

Logo, dada uma gramática livre do contexto de uma dada

linguagem seu reconhecedor pode ser algoritmicamente

gerado.

•

Dentre os mais conhecidos geradores de analisadores

sintáticos estão:

–

yacc (yet another compiler-compiler);

–

antlr (another tool for language rocognition).

Exercício 07

7

) Prove que a seguinte gramática é ambígua:

<

S> → <A>

A> → <A> + <A> | <ID>

ID> → a | b | c

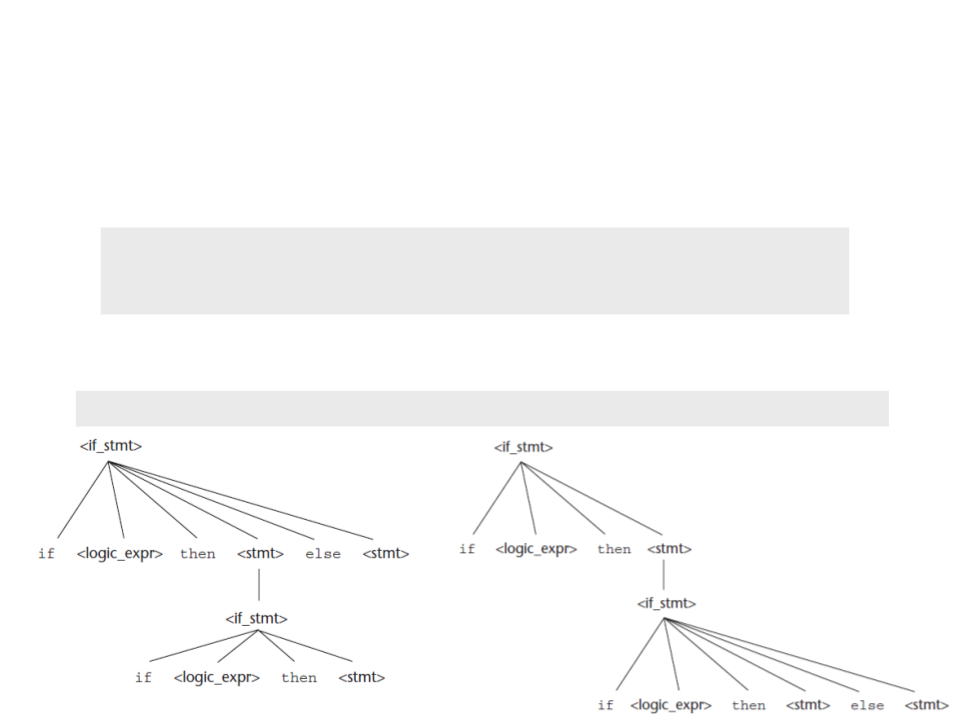
Exercício 08

8

) Reescreva a gramática abaixo corrigindo a sua ambiguidade:

<if_stmt> → if <logic_expr> then <stmt>

|

if <logic_expr> then <stmt> else <stmt>

Exemplo:

if <logic_expr> then if <logic_expr> then <stmt> else <stmt>

Leitura Complementar

•

Aho, A. V., Lam, M. S., Jeffrey, R. S.

Compiladores: Princípios, Técnicas e

Ferramentas. 2ª edição, Pearson, 2007.

ISBN: 978-8588639249.

–

Capítulo 2: A Simple Syntax-Directed Translator

Capítulo 3: Lexical Analysis

Capítulo 4: Syntax Analysis

Sebesta, R. W. Conceitos de Linguagens de

Programação. 9ª edição Editora Bookman,

2

–

011. ISBN: 978-8577807918.

Capítulo 3: Descrevendo a Sintaxe e a Semântica