
Computer Graphics
Lecture 03 – 2D and 3D Transformations
Edirlei Soares de Lima
<edirlei.lima@universidadeeuropeia.pt>
2
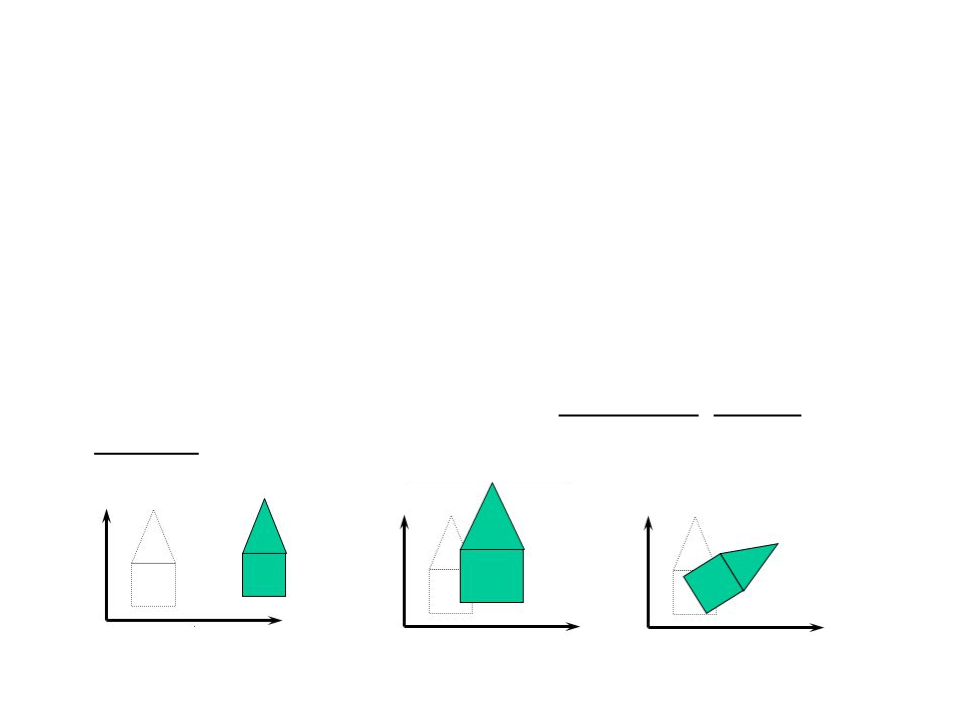
D Transformations
•
•
Transformations are a fundamental part of computer graphics.
They can be used to position objects, shape objects, change
viewing positions, and even to change how something is
viewed (projection transformation).
Let’s start with 2D transformations: translation, scaling and
rotation.
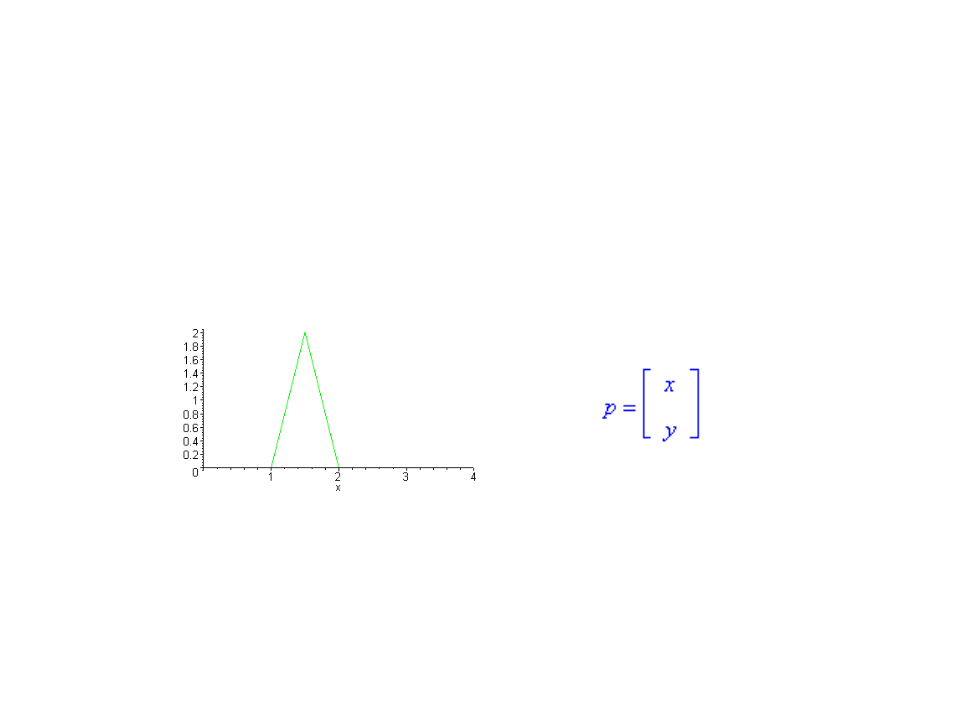
Representation of Points/Objects
•
2D objects are represented by a set of points (vertices), {p1,
p2, ..., pn}, and an associated set of edges {e1, e2, ..., em},
where each edge is a pair of points e = {pi, pj}.
•
We can use Unity to create a mesh with a triangle (ignoring
the z coordinate).

...
private Mesh mesh;
private Vector3[] vertices;
void Start(){
mesh = new Mesh();
GetComponent<MeshFilter>().mesh = mesh;
mesh.name = "MyMesh";
vertices = new Vector3[3];
vertices[0] = new Vector3(3, 0, 1);
vertices[1] = new Vector3(5, 0, 1);
vertices[2] = new Vector3(4, 2, 1);
mesh.vertices = vertices;
int[] triangles = new int[3];
triangles[0] = 0;
triangles[1] = 2;
triangles[2] = 1;
mesh.triangles = triangles;
}
...
2
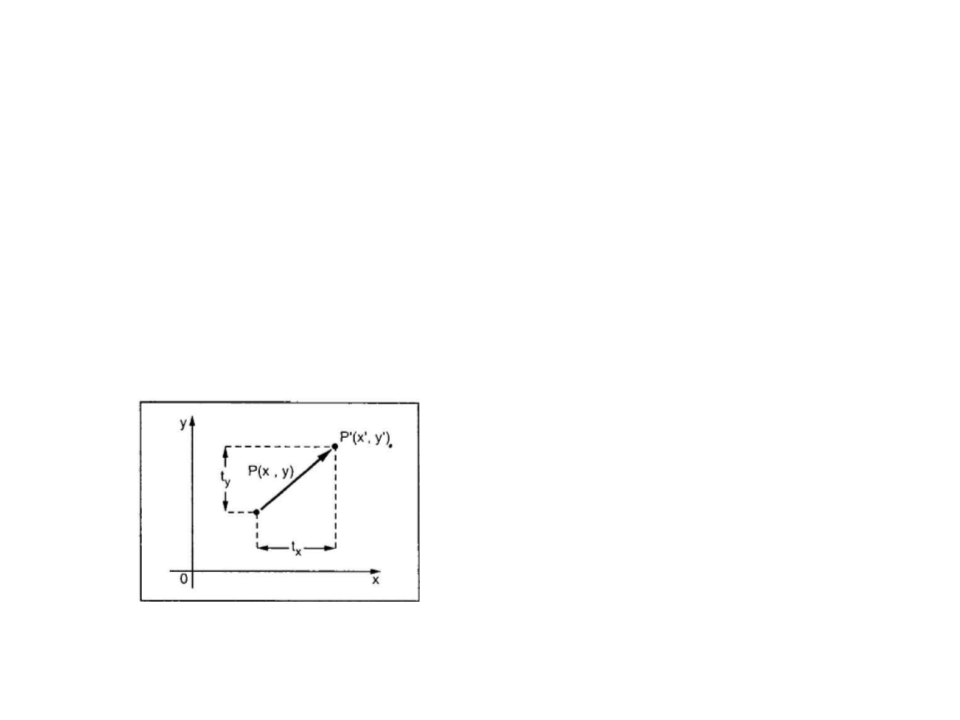
D Translation
•
A translation moves an object to a different position on the
screen. A point can be translated by adding a translation
coordinate (tx, ty) to the original coordinate (X, Y) to get the
new coordinate (X’, Y’).
ꢀ′
ꢃ′ = ꢃ + ꢁꢄ
= ꢀ + ꢁꢂ

2
D Translation
void Translate2D(float tx, float ty)
{
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = new Vector3(vertices[i].x + tx,
vertices[i].y + ty);
}
mesh.vertices = vertices;
}
void Update()
{
Translate2D(2 * Time.deltaTime, 0);
}
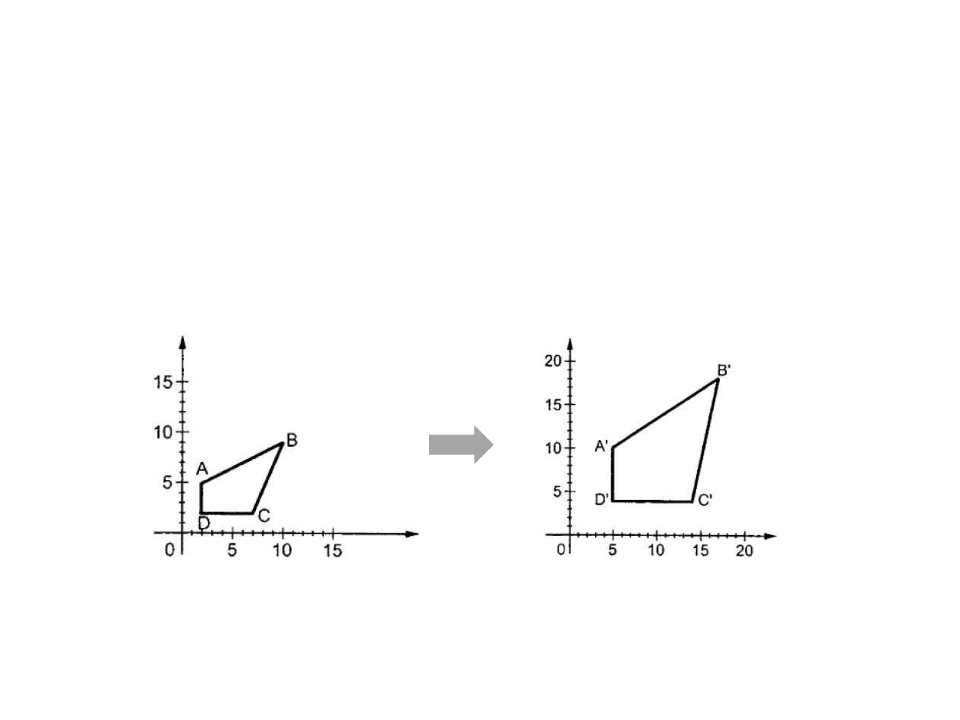
2
D Scaling
•
Scaling can be achieved by multiplying the original
coordinates of the object with the scaling factor (Sx, Sy) . The
object can be either expanded compressed.
ꢀ′
ꢃ′ = ꢃ × ꢅꢄ
= ꢀ × ꢅꢂ

2
D Scaling
void Scale2D(float tx, float ty)
{
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = new Vector3(vertices[i].x * sx,
vertices[i].y * sy);
}
mesh.vertices = vertices;
}
void Update()
{
Scale2D(1.01f, 1);
}

2
D Scaling – Matrix
•
•
We can also represent the scaling transformation using matrix
multiplication:
ꢀ′
ꢃ′ = ꢃ × ꢅꢄ
= ꢀ × ꢅꢂ
ꢅꢂ 0
0 ꢅꢄ
ꢀ
ꢃ´
´ =
ꢀ
ꢃ ×
How it works?
ꢅꢂ 0
ꢀ × ꢅꢂ + ꢀ × 0
=
ꢃ × 0 + ꢃ × ꢅꢄ
ꢀ
ꢃ ×
0
ꢅꢄ

2
D Scaling – Matrix
void Scale2DMat(float sx, float sy)
{
float[,] mat = new float[2, 2];
mat[0, 0] = sx; mat[0, 1] = 0;
mat[1, 0] = 0; mat[1, 1] = sy;
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = multiply(mat, vertices[i]);
}
mesh.vertices = vertices;
}
void Update()
{
Scale2DMat(1.01f, 1);
}

Point × Matrix
Vector3 multiply(float[,] matrix, Vector3 point)
{
Vector3 result = new Vector3();
for (int r = 0; r < matrix.GetLength(0); r++)
{
float s = 0;
for (int z = 0; z < matrix.GetLength(1); z++)
s += matrix[r, z] * point[z];
result[r] = s;
}
return result;
}
2
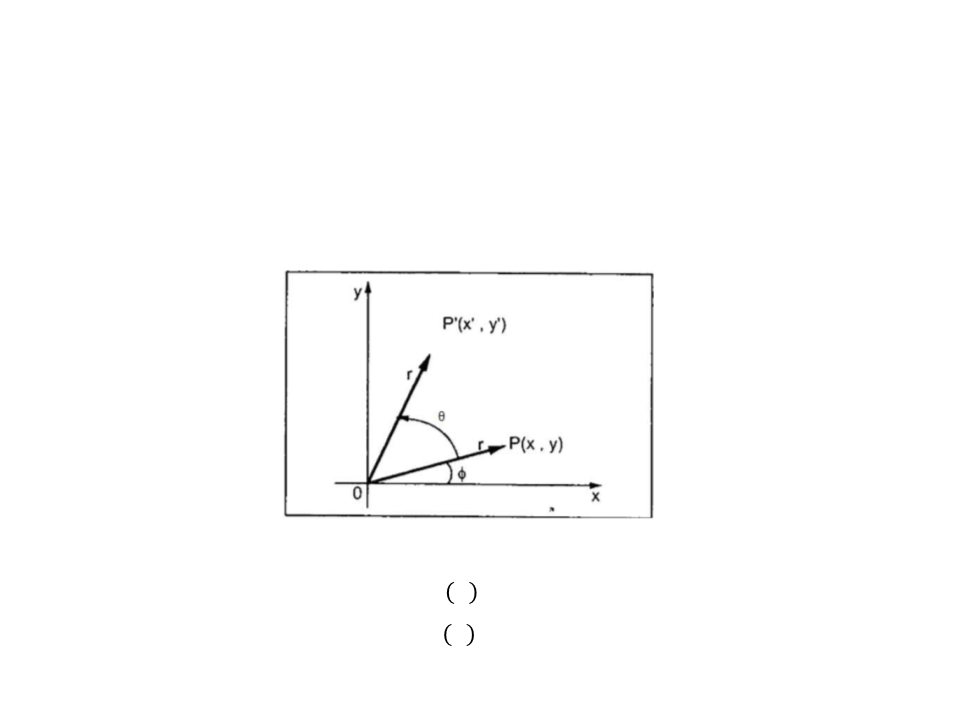
D Rotation
•
In rotation, we rotate the object at particular angle θ (theta)
from its origin.
ꢀ′
ꢃ′ = ꢀ × sin ꢆ + ꢃ × ꢊꢋꢇ(ꢆ)
= ꢀ × cos ꢆ − ꢃ × ꢇꢈꢉ(ꢆ)

2
D Rotation
void Rotate2D(float tx, float ty)
{
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = new Vector3(vertices[i].x * Mathf.Cos(angle)
-
vertices[i].y * Mathf.Sin(angle),
vertices[i].x * Mathf.Sin(angle)
vertices[i].y * Mathf.Cos(angle));
+
}
mesh.vertices = vertices;
}
void Update()
{
Rotate2D(20 * Mathf.Deg2Rad * Time.deltaTime);
}
2
D Rotation – Matrix
•
We can also represent rotation transformations using matrix
multiplication:
ꢀ′
= ꢀ × cos ꢆ − ꢃ × ꢇꢈꢉ(ꢆ)
ꢀ
ꢃ´
´ =
ꢀ
ꢊꢋꢇ ꢆ − ꢇꢈꢉ ꢆ
ꢃ × ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ
ꢃ′ = ꢀ × sin ꢆ + ꢃ × ꢊꢋꢇ(ꢆ)

2
D Rotation – Matrix
void Rotate2DMat(float angle)
{
float[,] mat = new float[2, 2];
mat[0, 0] = Mathf.Cos(angle); mat[0, 1] = -Mathf.Sin(angle);
mat[1, 0] = Mathf.Sin(angle); mat[1, 1] = Mathf.Cos(angle);
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = multiply(mat, vertices[i]);
}
mesh.vertices = vertices;
}
void Update()
{
Rotate2DMat(20 * Mathf.Deg2Rad * Time.deltaTime);
}

2
D Translation – Matrix
•
Can we represent translation using matrix multiplication?
ꢀ′
= ꢀ + ꢁꢂ
ꢃ′ = ꢃ + ꢁꢄ
ꢌ ꢎ
We need a 2 by 2 matrix, ꢊ ꢏ , such that ꢀ × ꢌ + ꢍ × ꢊ = ꢀ + ꢁꢂ.
There is no way to obtain the ꢁꢂ term!
–
–
•
It’s impossible to represent translation using a 2 by 2 matrix!

2
D Homogeneous Coordinates
•
•
What is required at this point is to change the setting (2D
coordinate space) in which we phrased our original problem.
–
In geometry, a common strategy to solve a problem in n space consists
in rephrasing it to a n+1 space.
ꢀ
ꢀ´
ꢀ
ꢃ
ꢃ → Transformation → ꢃ´ → ꢀ´
→
ꢃ´
1
1
In other words, the homogeneous coordinate system adds an
extra virtual dimension. Thus, 2D homogeneous coordinates
are actually 3D. This kind of transformation is called an affine
transformation.
2
D Homogeneous Coordinates
•
•
When using homogeneous coordinates to represent
transformations it is important to distinguish vectors that
represent positions and directions.
10
1
1
0 is a position.
1
1 is a direction.
0
This is important because vectors that represent directions or
offsets should not change when we translate an object.
–
If there is a scaling/rotation transformation in the upper-left 2 × 2
entries of the matrix, it will apply to the vector, but the translation still
multiplies with the zero and is ignored.

2
D Translation – Homogeneous Coordinates
•
Now we can represent translations as a matrix multiplication:
1
ꢃ´ = ꢃ × 0
0 ꢁꢂ
1 ꢁꢄ
ꢀ
´
ꢀ
1
1
0 0 1
void Translate2DMatHM(float tx, float ty){
float[,] mat = new float[3, 3];
mat[0, 0] = 1; mat[0, 1] = 0; mat[0, 2] = tx;
mat[1, 0] = 0; mat[1, 1] = 1; mat[1, 2] = ty;
mat[2, 0] = 0; mat[2, 1] = 0; mat[2, 2] = 1;
for (int i = 0; i < vertices.Length; i++){
vertices[i] = multiply(mat, vertices[i]);
}
mesh.vertices = vertices;
}

2
D Scale – Homogeneous Coordinates
•
We can also represent scale as a matrix multiplication in
homogeneous coordinates:
ꢅꢂ 0 0
ꢅꢄ 0
0 0 1
ꢀ
´
ꢀ
ꢃ´ = ꢃ ×
1
0
1
void Scale2DMatHM(float sx, float sy){
float[,] mat = new float[3, 3];
mat[0, 0] = sx; mat[0, 1] = 0; mat[0, 2] = 0;
mat[1, 0] = 0; mat[1, 1] = sy; mat[1, 2] = 0;
mat[2, 0] = 0; mat[2, 1] = 0; mat[2, 2] = 1;
for (int i = 0; i < vertices.Length; i++){
vertices[i] = multiply(mat, vertices[i]);
}
mesh.vertices = vertices;
}

2
D Rotation – Homogeneous Coordinates
•
We can also represent rotation as a matrix multiplication in
homogeneous coordinates:
ꢀ
´
ꢀ
ꢊꢋꢇ ꢆ − ꢇꢈꢉ ꢆ 0
ꢃ´ = ꢃ × ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ 0
1
1
0
0
1
void Rotate2DMatHM(float angle){
float[,] mat = new float[3, 3];
mat[0,0]=Mathf.Cos(angle); mat[0,1]=-Mathf.Sin(angle); mat[0,2]=0;
mat[1,0]=Mathf.Sin(angle); mat[1,1]=Mathf.Cos(angle); mat[1,2]=0;
mat[2,0]=0;
mat[2,1]=0;
mat[2,2]=1;
for (int i = 0; i < vertices.Length; i++){
vertices[i] = multiply(mat, vertices[i]);
}
mesh.vertices = vertices;
}
Combining Transformations
•
•
Using homogeneous coordinates, every rotation, translation,
and scaling operation can be represented by a matrix
multiplication.
The advantages of the homogeneous coordinates became
clear when we need to combine more than one
transformation at once.
–
Applying transformation matrices in sequence is the same as applying
the product of those matrices once.
•
This is a key concept that underlies most graphics hardware
and software.
Combining Transformations – Example 1
•
For example, suppose we wish to first rotate an object 90
degrees and then scale the object by 2 along the x axis.
ꢅꢂ 0 0
scale(2,1) = 0 ꢅꢄ 0
0 0 1
ꢊꢋꢇ ꢆ − ꢇꢈꢉ ꢆ 0
rotate(90) = ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ 0
0
0
1
0
−1 0
rotate(90) = 1 0 0
0 1
2 0 0
scale(2,1) = 0 1 0
0 0 1
0
–
When combining transformations, it is very important to remember that
matrix multiplication is not commutative. So, the order of transforms
does matter. The transforms are applied from the right side first.
2
0
0
0 0 0 −2 0
1 0 × 1 0 0 = 1 0 0
0 1 0 0 1 0 0 1
0 −1 0
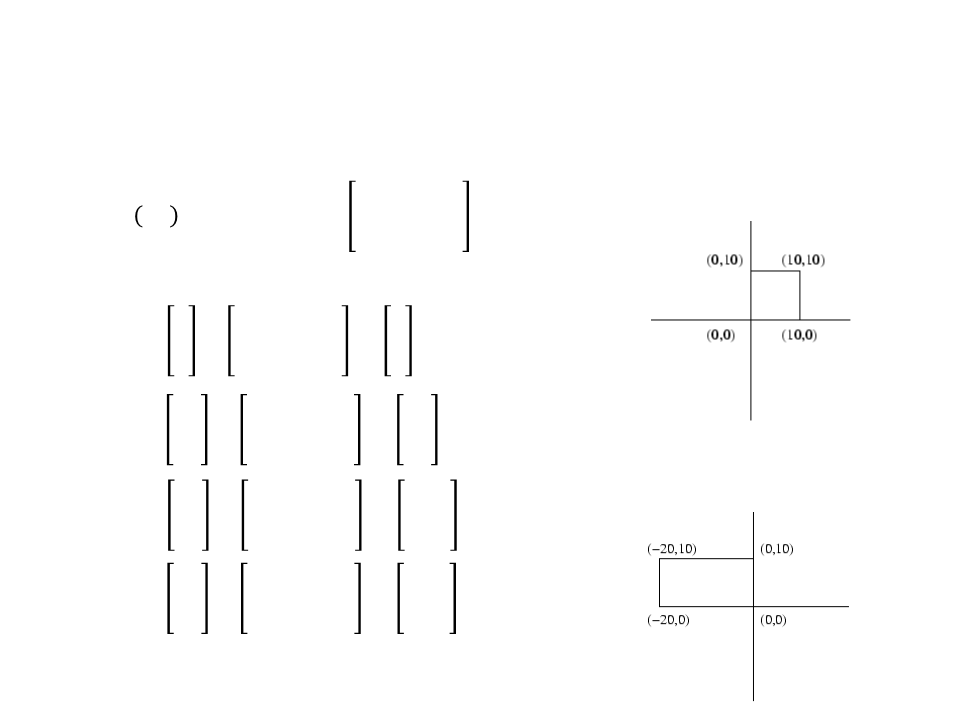
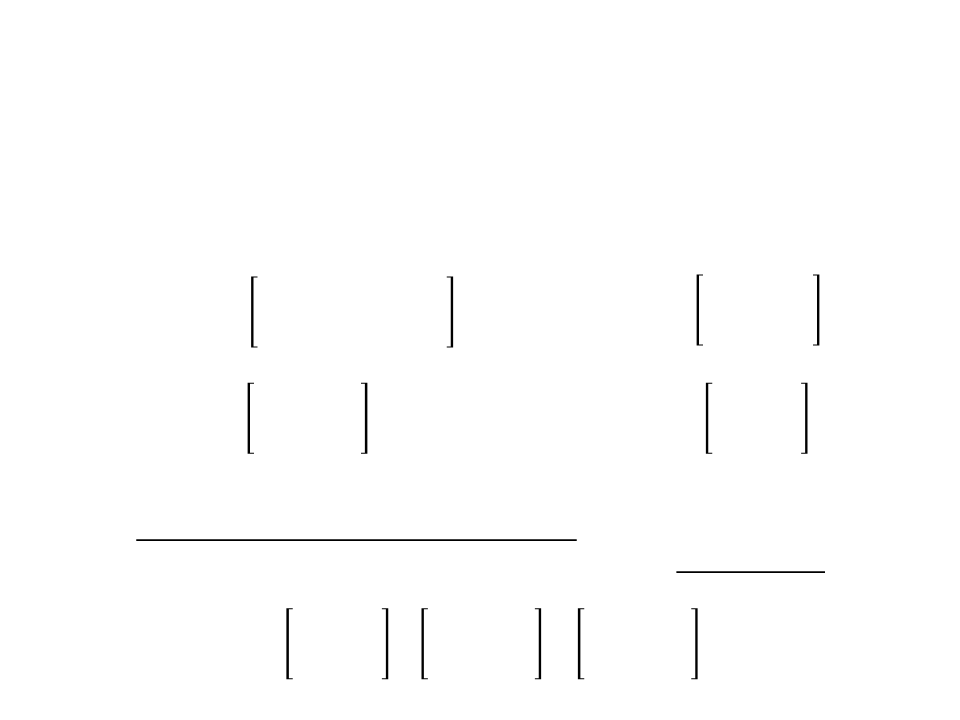
Combining Transformations – Example 1
0
−2 0
ꢐꢋꢁꢌꢁꢑ 90 + ꢇꢊꢌꢒꢑ(2,1) = 1 0 0
0 1
Square object:
P3
P4
0
0
0 −2 0
0
ꢓ1 = 0 × 1 0 0 = 0
P1
P2
1
0 0 1
0 −2 0
1
10
0
ꢓ2 = 0 × 1 0 0 = 10
1
0
0 0 1
0 −2 0
1
−20
Rotated and scaled square:
ꢓ3 = 10 × 1 0 0 = 0
P4
P2
1
0 0 1
0 −2 0
1
−20
10
ꢓ4 = 10 × 1 0 0 = 10
1
0 0 1
1
P3
P1

Combining Transformations – Example 1
float[,] multiply(float[,] matrix1, float[,] matrix2)
{
float[,] result = new float[matrix1.GetLength(0),
matrix2.GetLength(1)];
for (int i = 0; i < matrix1.GetLength(0); i++)
{
for (int j = 0; j < matrix2.GetLength(1); j++)
{
float s = 0;
for (int k = 0; k < matrix1.GetLength(1); k++)
{
s += matrix1[i, k] * matrix2[k, j];
}
result[i, j] = s;
}
}
return result;
}

Combining Transformations – Example 1
void RotateScale(float angle, float sx, float sy)
{
float[,] rmat = new float[3, 3];
rmat[0,0]=Mathf.Cos(angle);rmat[0,1]=-Mathf.Sin(angle);rmat[0,2]=0;
rmat[1,0]=Mathf.Sin(angle);rmat[1,1]=Mathf.Cos(angle); rmat[1,2]=0;
rmat[2,0]=0;
rmat[2,1]=0;
rmat[2,2]=1;
float[,] smat = new float[3, 3];
smat[0,0] = sx; smat[0,1] = 0; smat[0,2] = 0;
smat[1,0] = 0; smat[1,1] = sy; smat[1,2] = 0;
smat[2,0] = 0; smat[2,1] = 0; smat[2,2] = 1;
float[,] finalmat = multiply(scalemat, rmat);
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = multiply(finalmat, vertices[i]);
}
mesh.vertices = vertices;
}
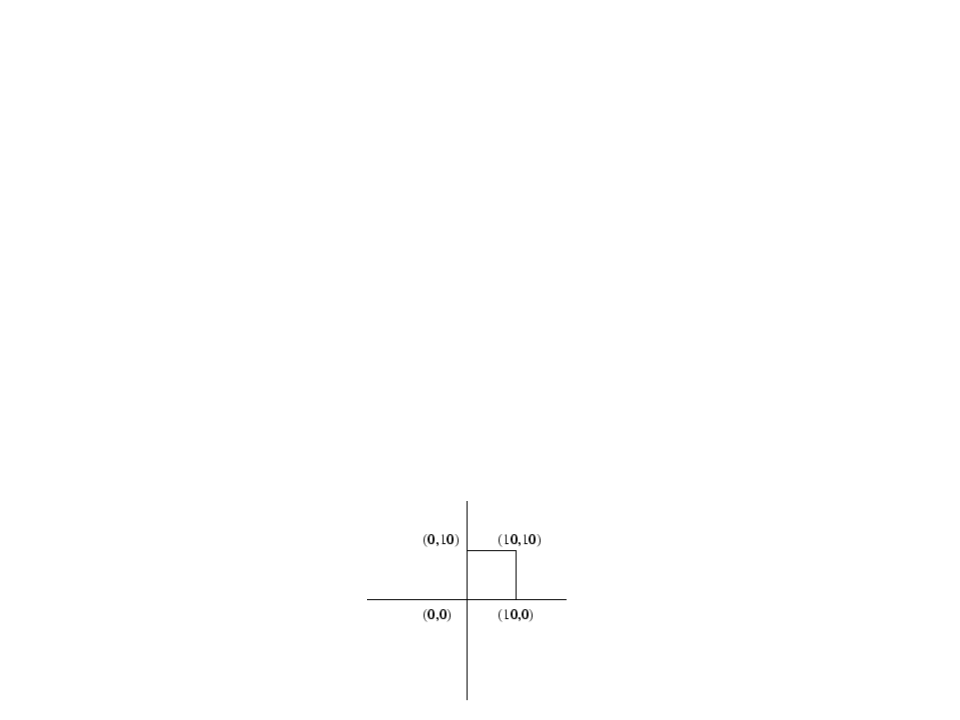
Combining Transformations – Example 2
•
In order to rotate an object around a specific point (such as its
center or a corner). We need to perform 3 operations:
–
–
–
(1) translate the object to the origin;
(2) rotate the object;
(3) translate the object back to its initial position.
•
Suppose we wish to rotate our object 90 degrees around its
upper right corner (P4).
P3
P4
P1
P2
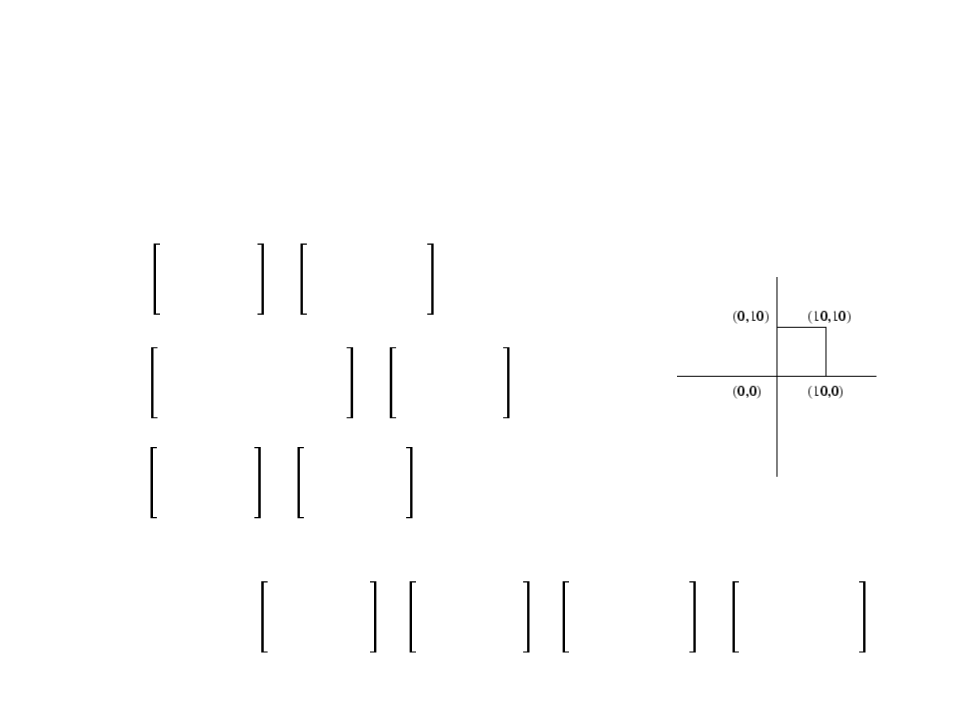
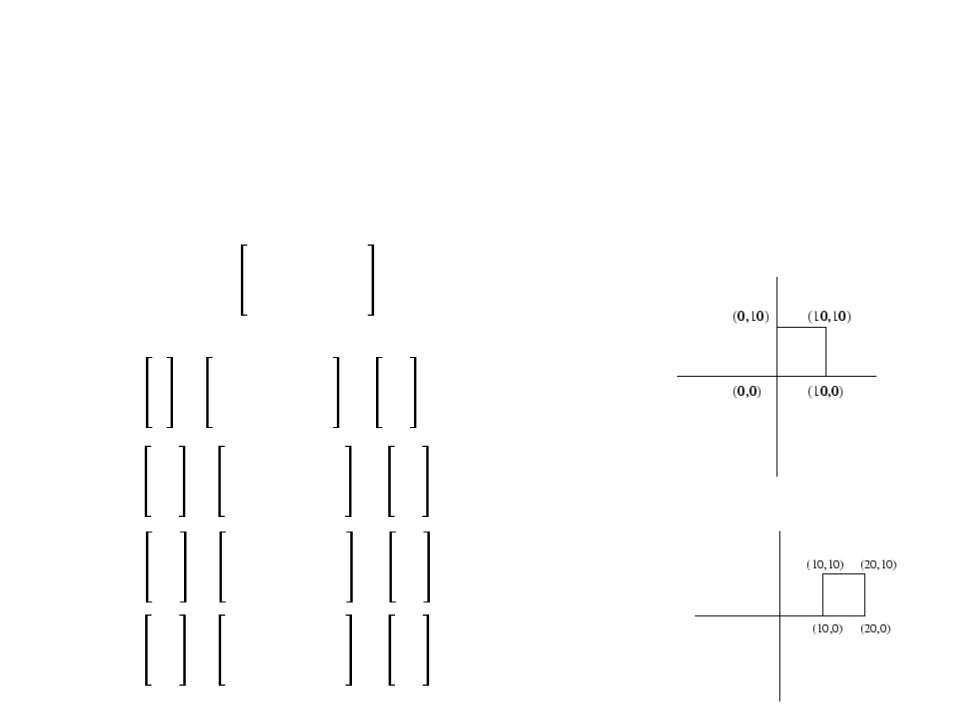
Combining Transformations – Example 2
•
Rotation of 90 degrees around the upper right corner (P4 = (10, 10)):
1
0 ꢁꢂ
ꢔꢕ = 0 1 ꢁꢄ = 0 1 −10
0 1
1
0 −10
P3
P1
P4
P2
0
0
0 1
ꢊꢋꢇ ꢆ − ꢇꢈꢉ ꢆ 0
ꢖ = ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ 0 = 1 0 0
0 0 1
0 −1 0
0
0
1
1
0 ꢁꢂ
1
0 10
ꢔꢗ = 0 1 ꢁꢄ = 0 1 10
0 1
0
0
0 1
1
0 10 0 −1 20
ꢔꢕ × ꢖ × ꢔꢗ = 0 1 10 × 1 0 0 × 0 1 −10 = 1 0 0
0 1 0 0 1 0 0 1 0 0 1
0 −1 0
1 0 −10
0
Combining Transformations – Example 2
•
Rotation of 90 degrees around the upper right corner (P4 = (10, 10)):
Square object:
0
−1 20
ꢔꢕ × ꢖ × ꢔꢗ = 1 0 0
0 1
P3
P1
P4
P2
0
0
0 −1 20
ꢓ1 = 0 × 1 0 0 = 0
0 0 1
0 −1 20
20
1
1
10
20
ꢓ2 = 0 × 1 0 0 = 10
1
0
0 0 1
0 −1 20
ꢓ3 = 10 × 1 0 0 = 0
1
10
Rotated square:
P4 P2
1
0 0 1
0 −1 20
ꢓ4 = 10 × 1 0 0 = 10
1
10
10
P3 P1
1
0 0 1
1

Combining Transformations – Example 2
void RotateAroundPoint(float angle, float px, float py)
{
float[,] rmat = new float[3, 3];
rmat[0,0]=Mathf.Cos(angle);rmat[0,1]=-Mathf.Sin(angle);rmat[0,2]=0;
rmat[1,0]=Mathf.Sin(angle);rmat[1,1]=Mathf.Cos(angle); rmat[1,2]=0;
rmat[2,0]=0;
rmat[2,1]=0;
rmat[2,2]=1;
float[,] tran1mat = new float[3, 3];
t1mat[0, 0] = 1; t1mat[0, 1] = 0; t1mat[0, 2] = -px;
t1mat[1, 0] = 0; t1mat[1, 1] = 1; t1mat[1, 2] = -py;
t1mat[2, 0] = 0; t1mat[2, 1] = 0; t1mat[2, 2] = 1;
float[,] tran2mat = new float[3, 3];
t2mat[0, 0] = 1; t2mat[0, 1] = 0; t2mat[0, 2] = px;
t2mat[1, 0] = 0; t2mat[1, 1] = 1; t2mat[1, 2] = py;
t2mat[2, 0] = 0; t2mat[2, 1] = 0; t2mat[2, 2] = 1;
float[,] finalmat = multiply(multiply(t2mat, rmat), t1mat);
for (int i = 0; i < vertices.Length; i++)
{
vertices[i] = multiply(finalmat, vertices[i]);
}
mesh.vertices = vertices;
}
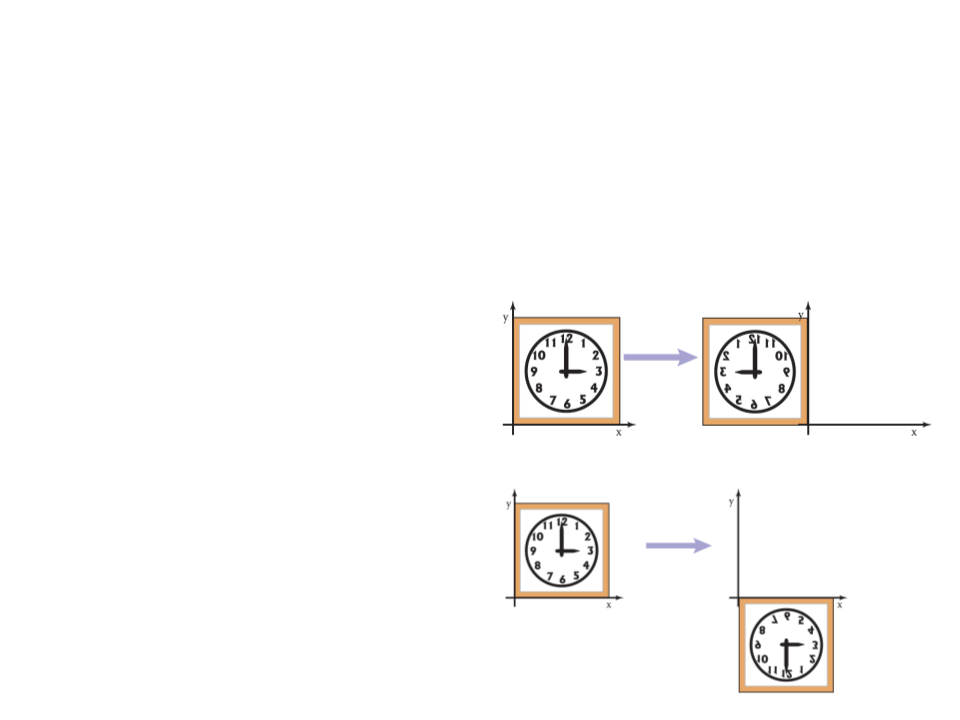
Exercise 1
1
) Reflection is a transformation that flips the object over the
axis of reflection (x or y).
Reflection over the x-axis:
a) What is the reflection matrix
for the x-axis?
b) What is the reflection matrix
for the y-axis?
Reflection over the y-axis:
c) Implement and apply the
reflection transformation.
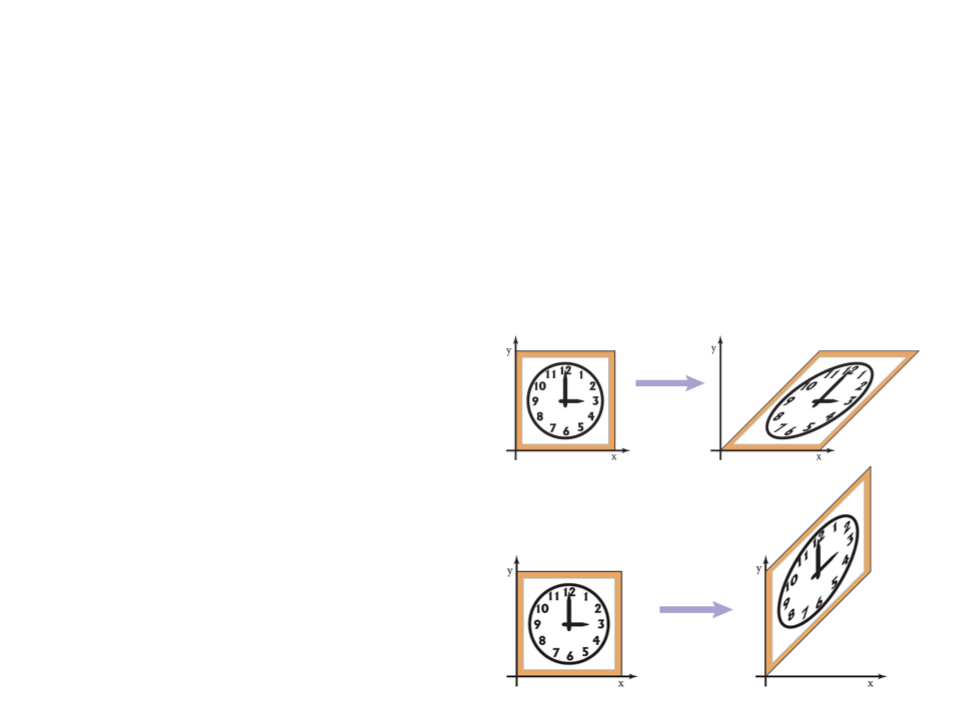
Exercise 2
2
) Shearing is a transformation that displaces each point in a
fixed direction, by an amount proportional to its signed
distance from a line that is parallel to that direction.
Shear over the x-axis:
a) What is the shearing matrix
for the x-axis?
b) What is the shearing matrix
for the y-axis?
Shear over the y-axis:
c) Implement and apply the
shearing transformation.
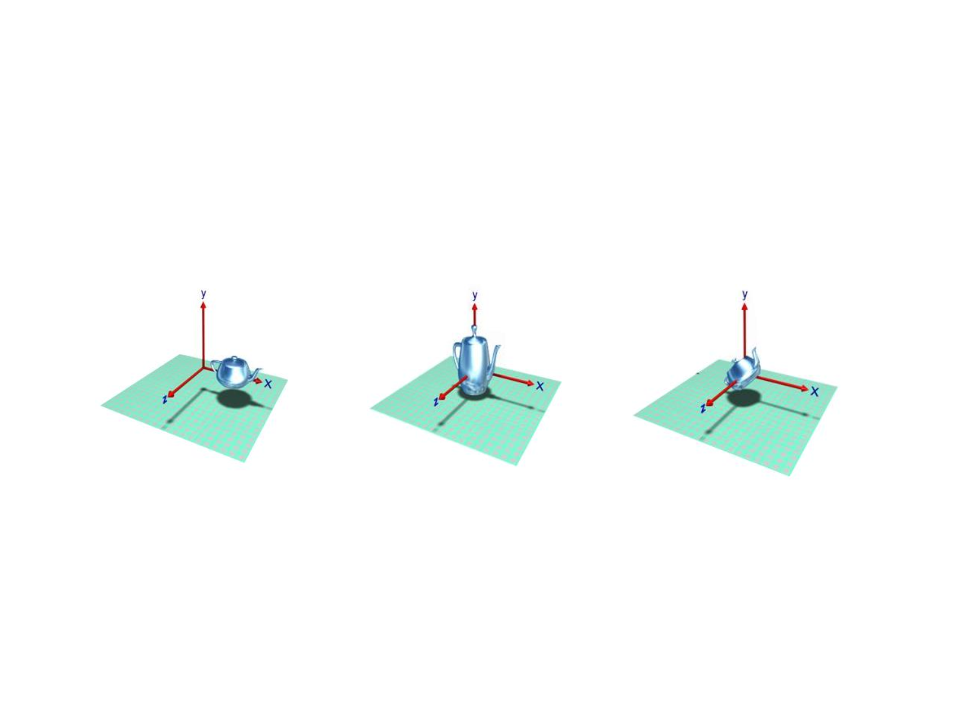
3
D Transformations
•
3D Transformations are an extension of the 2D transformations.
•
We can also use homogeneous coordinates in 3D by adding a
fourth coordinate to the transformation matrices.
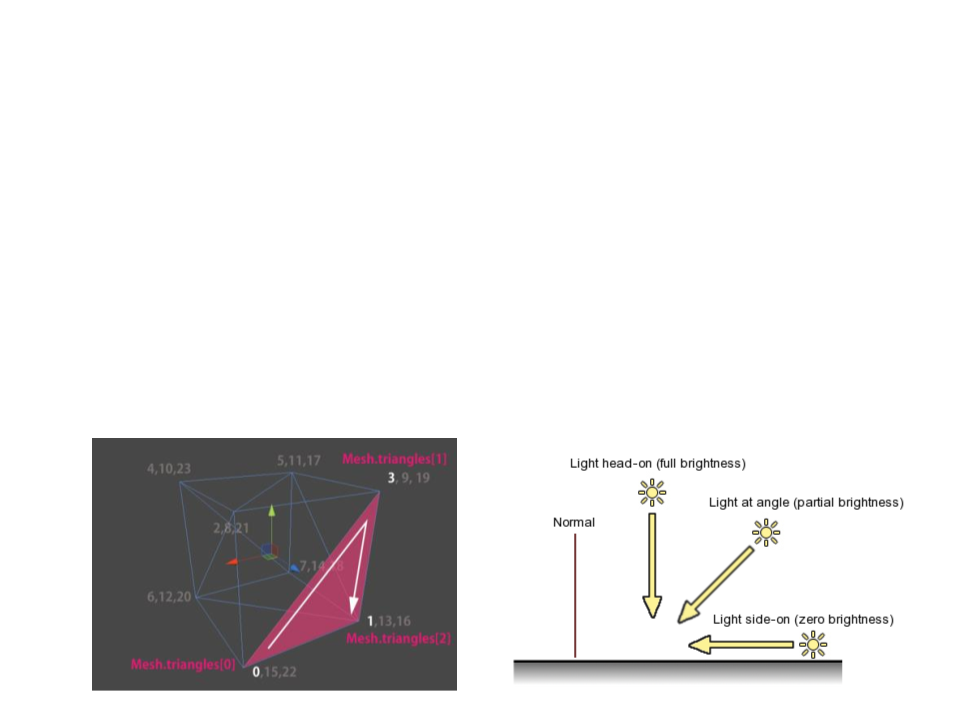
Representation of 3D Objects
•
3D objects are represented by a set of triangles. Each triangle
is defined by three vertices. In addition, each vertex has a
normal vector, which usually points outward (perpendicular
to the mesh surface).
–
The vertices and triangles define the spatial structure of the object.
–
The normals define how light affects the surface of the object.

vertices = new Vector3[18];
/back triangle vertices
/
vertices[0] = new Vector3(-10, 0, -10);
vertices[1] = new Vector3(10, 0, -10);
vertices[2] = new Vector3(0, 10, 0);
//front triangle vertices
vertices[3] = new Vector3(-10, 0, 10);
vertices[4] = new Vector3(10, 0, 10);
vertices[5] = new Vector3(0, 10, 0);
//left triangle vertices
vertices[6] = new Vector3(-10, 0, 10);
vertices[7] = new Vector3(-10, 0, -10);
vertices[8] = new Vector3(0, 10, 0);
//right triangle vertices
vertices[9] = new Vector3(10, 0, 10);
vertices[10] = new Vector3(10, 0, -10);
vertices[11] = new Vector3(0, 10, 0);
//botton triangle 1 vertices
vertices[12] = new Vector3(-10, 0, -10);
vertices[13] = new Vector3(10, 0, -10);
vertices[14] = new Vector3(-10, 0, 10);
//botton triangle 2 vertices
vertices[15] = new Vector3(10, 0, 10);
vertices[16] = new Vector3(10, 0, -10);
vertices[17] = new Vector3(-10, 0, 10);

int[] triangles = new int[18];
/back triangle
/
triangles[0] = 0;
triangles[1] = 2;
triangles[2] = 1;
//front triangle
triangles[3] = 4;
triangles[4] = 5;
triangles[5] = 3;
//left triangle
triangles[6] = 6;
triangles[7] = 8;
triangles[8] = 7;
//right triangle
triangles[9] = 10;
triangles[10] = 11;
triangles[11] = 9;
//botton triangle 1
triangles[12] = 13;
triangles[13] = 14;
triangles[14] = 12;
//botton triangle 2
triangles[15] = 15;
triangles[16] = 17;
triangles[17] = 16;

Vector3[] normals = new Vector3[18];
normals[0] = Vector3.back + Vector3.up;
normals[1] = Vector3.back + Vector3.up;
normals[2] = Vector3.back + Vector3.up;
normals[3] = Vector3.forward + Vector3.up;
normals[4] = Vector3.forward + Vector3.up;
normals[5] = Vector3.forward + Vector3.up;
normals[6] = Vector3.left + Vector3.up;
normals[7] = Vector3.left + Vector3.up;
normals[8] = Vector3.left + Vector3.up;
normals[9] = Vector3.right + Vector3.up;
normals[10] = Vector3.right + Vector3.up;
normals[11] = Vector3.right + Vector3.up;
normals[12] = Vector3.down;
normals[13] = Vector3.down;
normals[14] = Vector3.down;
normals[15] = Vector3.down;
normals[16] = Vector3.down;
normals[17] = Vector3.down;
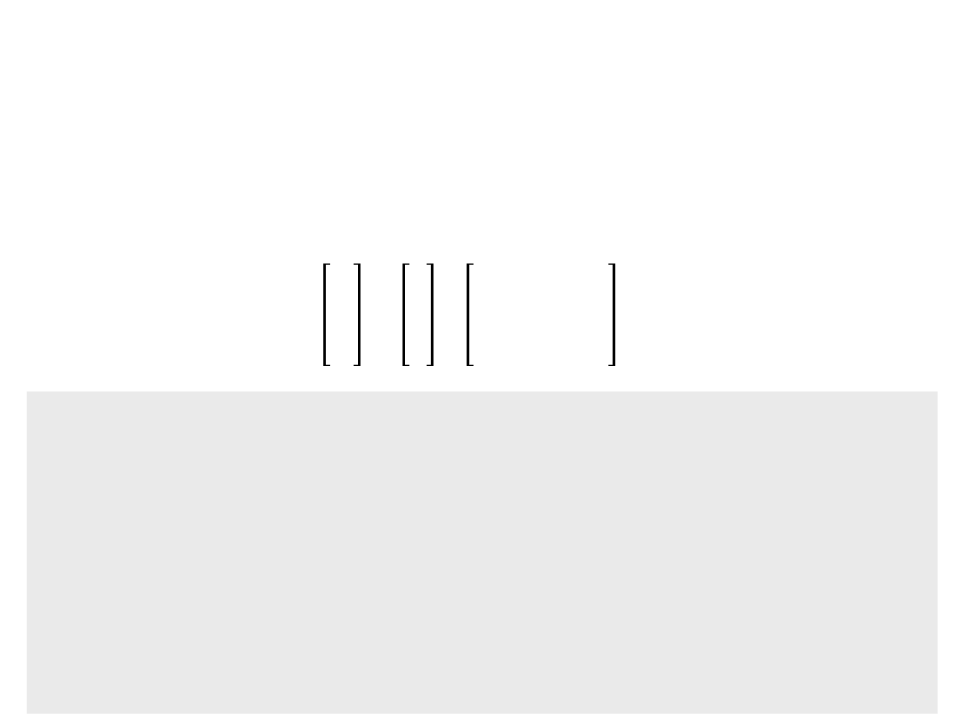
3
D Translation – Homogeneous Coordinates
•
Using homogeneous coordinates, we can also represent 3D
translation as a matrix multiplication:
1
0 0 ꢁꢂ
ꢀ
´
ꢀ
0
ꢁꢄ
ꢃ´
ꢘ´
1
ꢃ
ꢘ
1
0 1
0
0
=
×
0 1 ꢁꢙ
0 0 1
void Translate3D(float tx, float ty, float tz){
Matrix4x4 translation_matrix = new Matrix4x4();
translation_matrix.SetRow(0, new Vector4(1f, 0f, 0f, tx));
translation_matrix.SetRow(1, new Vector4(0f, 1f, 0f, ty));
translation_matrix.SetRow(2, new Vector4(0f, 0f, 1f, tz));
translation_matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
for (int i = 0; i < vertices.Length; i++){
vertices[i]=translation_matrix.MultiplyPoint(vertices[i]);
}
mesh.vertices = vertices;
}

3
D Scale – Homogeneous Coordinates
•
We can also represent 3D scale as a matrix multiplication:
ꢀ
´
ꢀ
ꢃ
ꢘ
ꢅꢂ 0 0 0
0
ꢅꢄ 0 0
0 ꢅꢙ 0
0 0 1
ꢃ´
ꢘ´
1
=
×
0
0
1
void Scale3D(float sx, float sy, float sz){
Matrix4x4 scale_matrix = new Matrix4x4();
scale_matrix.SetRow(0, new Vector4(sx, 0f, 0f, 0));
scale_matrix.SetRow(1, new Vector4(0f, sy, 0f, 0));
scale_matrix.SetRow(2, new Vector4(0f, 0f, sz, 0));
scale_matrix.SetRow(3, new Vector4(0f, 0f, 0f, 1f));
for (int i = 0; i < vertices.Length; i++){
vertices[i]=scale_matrix.MultiplyPoint(vertices[i]);
}
mesh.vertices = vertices;
}
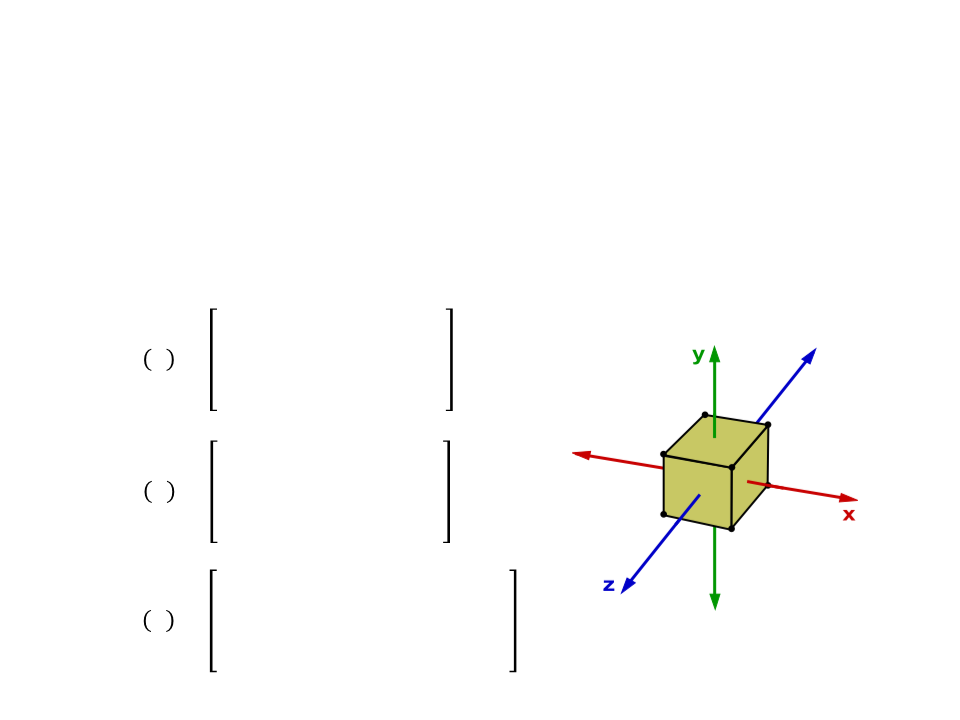
3
D Rotation – Homogeneous Coordinates
•
3D rotations are not exactly same as 2D rotations. In 3D, we
have to specify the angle of rotation along with the axis of
rotation (we can perform 3D rotations about X, Y, and Z axes).
1
0
0
0
0
ꢊꢋꢇ θ − ꢇꢈꢉ ꢆ 0
ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ 0
0
0
ꢖꢂ ꢆ =
ꢖꢄ ꢆ =
ꢖꢙ ꢆ =
0
0
1
ꢊꢋꢇ θ 0 ꢇꢈꢉ ꢆ 0
0
1
0
0
−
ꢇꢈꢉ ꢆ 0 ꢊꢋꢇ ꢆ 0
0
0
0
1
ꢊꢋꢇ θ −ꢇꢈꢉ ꢆ
ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ
0
0
1
0
0
0
0
0
0
0
0
1

3
D Rotation – Homogeneous Coordinates
1
0
0
0
0
ꢊꢋꢇ θ − ꢇꢈꢉ ꢆ 0
ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ 0
0
0
ꢖꢂ ꢆ =
0
0
1
void RotateX3D(float angle)
{
Matrix4x4 rxmat = new Matrix4x4();
rxmat.SetRow(0,new Vector4(1f,0f,
0f,
0f));
rxmat.SetRow(1,new Vector4(0f,Mathf.Cos(angle),-Mathf.Sin(angle),0f));
rxmat.SetRow(2,new Vector4(0f,Mathf.Sin(angle),Mathf.Cos(angle), 0f));
rxmat.SetRow(3,new Vector4(0f,0f,
0f,
1f));
for (int i = 0; i < vertices.Length; i++){
vertices[i] = rxmat.MultiplyPoint(vertices[i]);
normals[i] = rxmat.MultiplyPoint(normals[i]);
}
mesh.vertices = vertices;
mesh.normals = normals;
}
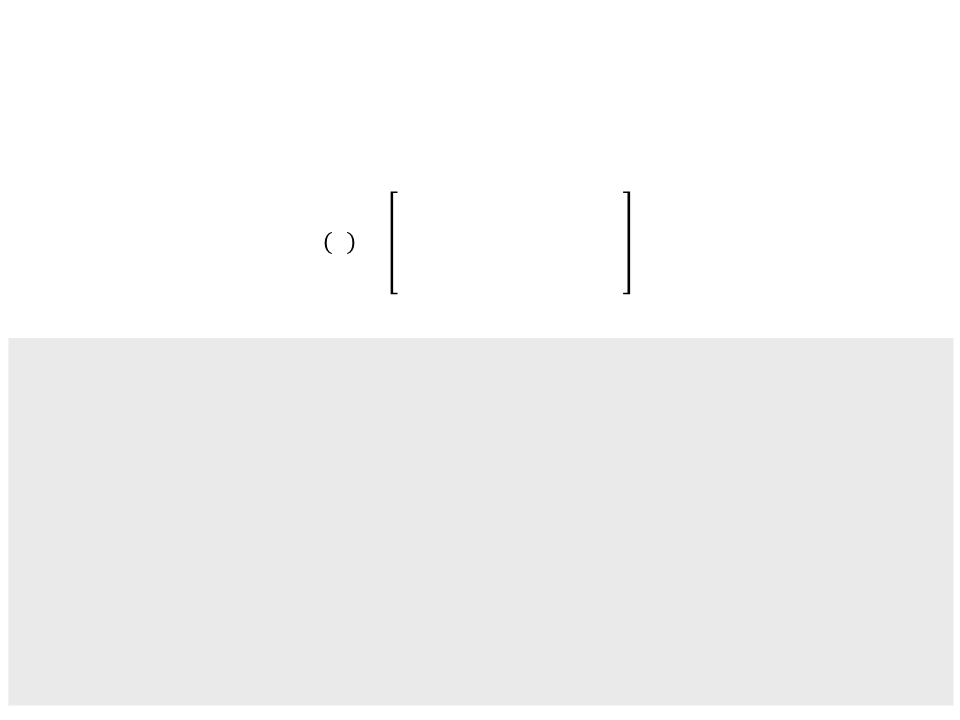
3
D Rotation – Homogeneous Coordinates
ꢊꢋꢇ θ 0 ꢇꢈꢉ ꢆ 0
0
ꢇꢈꢉ ꢆ 0 ꢊꢋꢇ ꢆ 0
1
0
0
ꢖꢄ ꢆ =
−
0
0
0
1
void RotateY3D(float angle)
{
Matrix4x4 rymat = new Matrix4x4();
rymat.SetRow(0,new Vector4(Mathf.Cos(angle), 0f,Mathf.Sin(angle),0f));
rymat.SetRow(1,new Vector4(0f, 1f,0f, 0f));
rymat.SetRow(2,new Vector4(-Mathf.Sin(angle),0f,Mathf.Cos(angle),0f));
rymat.SetRow(3,new Vector4(0f,
0f,0f,
1f));
for (int i = 0; i < vertices.Length; i++){
vertices[i] = rymat.MultiplyPoint(vertices[i]);
normals[i] = rymat.MultiplyPoint(normals[i]);
}
mesh.vertices = vertices;
mesh.normals = normals;
}
3
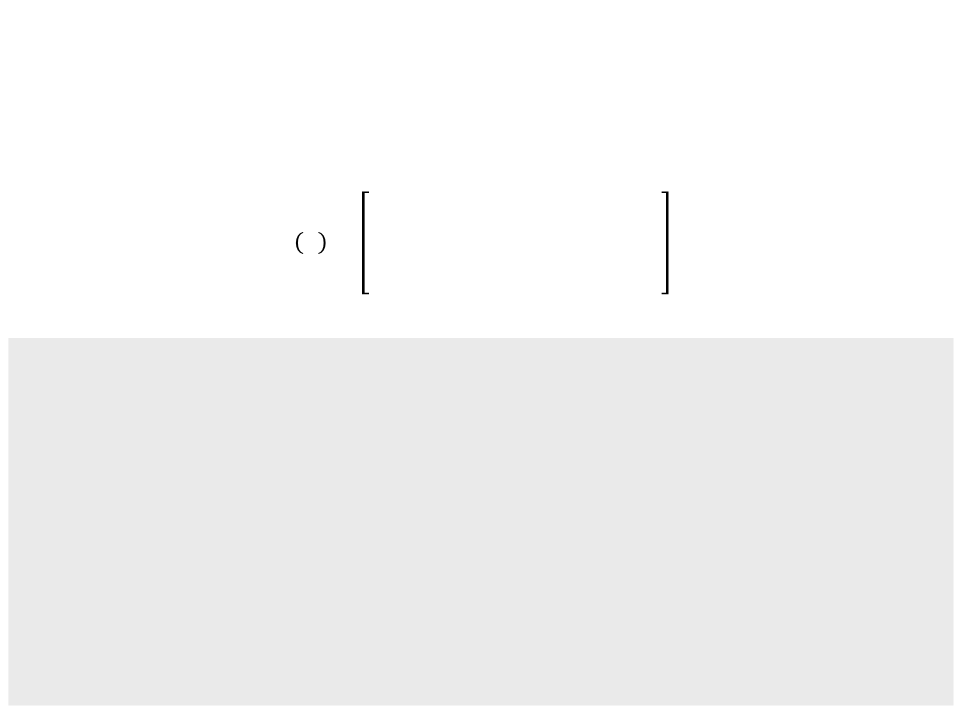
D Rotation – Homogeneous Coordinates
ꢊꢋꢇ θ −ꢇꢈꢉ ꢆ
ꢇꢈꢉ ꢆ ꢊꢋꢇ ꢆ
0
0
1
0
0
0
ꢖꢙ ꢆ =
0
0
0
0
0
1
void RotateZ3D(float angle)
{
Matrix4x4 rzmat = new Matrix4x4();
rzmat.SetRow(0,new Vector4(Mathf.Cos(angle),-Mathf.Sin(angle),0f,0f));
rzmat.SetRow(1,new Vector4(Mathf.Sin(angle), Mathf.Cos(angle),0f,0f));
rzmat.SetRow(2,new Vector4(0f,
rzmat.SetRow(3,new Vector4(0f,
0f,
0f,
1f,0f));
0f,1f));
for (int i = 0; i < vertices.Length; i++){
vertices[i] = rzmat.MultiplyPoint(vertices[i]);
normals[i] = rzmat.MultiplyPoint(normals[i]);
}
mesh.vertices = vertices;
mesh.normals = normals;
}

3
D Rotation – Homogeneous Coordinates
•
•
When we rotate a 3D object, we also need to apply the same
rotation to the normal vectors of the object:
.
..
for (int i = 0; i < vertices.Length; i++){
vertices[i] = rxmat.MultiplyPoint(vertices[i]);
normals[i] = rxmat.MultiplyPoint(normals[i]);
}
mesh.vertices = vertices;
mesh.normals = normals;
.
..
We can visualize the normals in the Unity editor:
private void OnDrawGizmos(){
if (vertices == null) return;
for (int i = 0; i < vertices.Length; i++){
Gizmos.color = Color.yellow;
Gizmos.DrawRay(vertices[i], normals[i]);
}
}

Exercise 3
3
) Rotations in 3D are performed around the origin of the
coordinates system (0, 0, 0). How can we rotate a 3D
object around a specific position?
Implement in Unity the functions to rotate objects around
specific positions (such as the center of the object) in the X,
Y, and Z axes.
Homogeneous Coordinates
•
•
Homogeneous coordinates are used nearly universally to
represent transformations in graphics systems.
–
They underlie the design and operation of renderers implemented in
all graphics hardware.
Homogeneous coordinates not only clean up the code for
transformations, but they also simplify the composition of
complex transformations.
Further Reading
•
Hughes, J. F., et al. (2013). Computer Graphics: Principles and Practice
(
0
3rd ed.). Upper Saddle River, NJ: Addison-Wesley Professional. ISBN: 978-
-321-39952-6.
–
Chapter 10: Transformations in Two Dimensions
Chapter 11: Transformations in Three Dimensions
–
•
Marschner, S., et al. (2015). Fundamentals of Computer Graphics (4th
ed.). A K Peters/CRC Press. ISBN: 978-1482229394.
–
Chapter 6: Transformation Matrices
